Сумма нескольких векторов
Вам уже известны правила сложения двух векторов.

Cегодня мы будем учиться складывать несколько векторов.
Построим
вектор суммы векторов  ,
,  ,
,  .
От некоторой точки А отложим вектор
.
От некоторой точки А отложим вектор  . Далее от точки B
отложим вектор
. Далее от точки B
отложим вектор 
 .
.Будем последовательно складывать наши векторы, пользуясь правилом треугольника.

Сумма
векторов  ,
, 
 .
.Теперь
к вектору  добавим
вектор
добавим
вектор  . В результате мы
получаем вектор
. В результате мы
получаем вектор  .
.
Тогда
можем сказать, что сумма 
Так, последовательно складывая первый вектор со вторым, затем их сумму с третьим и так далее, можно найти суммы четырёх, пяти и большего числа векторов.
Такое правило построения суммы векторов называют правилом многоугольника.
Сформулируем его в общем виде.
Если А1, А2,
…, An — произвольные точки
плоскости, то сумма векторов 
.

Это равенство справедливо для любых точек А1, А2, …, An. И, в частности, для случая, когда некоторые из них совпадают.

Например, если начало первого вектора совпадает с концом последнего, то сумма данных векторов равна нулевому вектору.

Задача.
Построить
вектор суммы попарно неколлинеарных векторов 
 ,
,  ,
,  и
и  .
.
Построение






 .
.
Задача. В соответствии с правилом многоугольника составить равенство,выражающее сумму нескольких векторов.

Посмотрим на первый рисунок. Мы
видим, что последовательно складывают векторы  . Но, так как
начало вектора
. Но, так как
начало вектора 
 ,
то сумма данных векторов равна нулевому вектору
,
то сумма данных векторов равна нулевому вектору  .
.Перейдём к следующему случаю.
Видим, что сумма состоит
из векторов  .
А вот вектор
.
А вот вектор 
На рисунке в
последовательно, друг за другом, отложены векторы  Ну, а вектор
Ну, а вектор
 равен их
сумме.
равен их
сумме.
На последнем рисунке
последовательно, друг за другом, отложены векторы 

 .
.Задача.  равнобокая
трапеция.
равнобокая
трапеция. и
и

 . Построить вектор
. Построить вектор
 и найти его
длину.
и найти его
длину.
Построение

Решение.

Ответ:

А теперь подведём итоги нашего урока.
Сегодня мы познакомились с правилом многоугольника, которое позволяет строить вектор суммы нескольких векторов.
Его суть заключается в том, что векторы-слагаемые последовательно откладывают друг от друга, суммой является вектор, начало которого совпадает с началом первого вектора-слагаемого, а конец совпадает с концом последнего вектора-слагаемого.
Сумма нескольких векторов
Материал урока.
Вам уже известны правила сложения и вычитания двух векторов.
Чтобы
сложить два неколлинеарных вектора  и
и
 по
правилу треугольника, нужно от некоторой точки А отложить вектор
по
правилу треугольника, нужно от некоторой точки А отложить вектор  ,
равный вектору
,
равный вектору  .
Далее от точки B отложить вектор
.
Далее от точки B отложить вектор
 ,
равный вектору
,
равный вектору  .
Вектор
.
Вектор  является
вектором суммы двух векторов
является
вектором суммы двух векторов  и
и
 .
.
Чтобы
сложить два вектора по правилу параллелограмма, нужно отложить от произвольной
точки А векторы  и
и
 ,
равные векторам
,
равные векторам  и
и
 соответственно,
и построить на них параллелограмм ABCD.
Тогда вектор
соответственно,
и построить на них параллелограмм ABCD.
Тогда вектор  равен
сумме векторов
равен
сумме векторов  и
и
 .
.

Также вам уже знакомы законы сложения векторов: переместительный и сочетательный.
Ну,
а убедившись в том, что разность векторов  и
и
 равна
сумме вектора
равна
сумме вектора  и
вектора, противоположного вектору
и
вектора, противоположного вектору  ,
мы получили два способа построения вектора разности двух векторов.
,
мы получили два способа построения вектора разности двух векторов.

Сегодня мы будем учиться складывать несколько векторов в пространстве. Но сначала вспомним, как мы это делали на плоскости.
Построим
вектор суммы векторов  ,
,
 и
и
 .
.
От
некоторой точки А отложим вектор  ,
равный вектору
,
равный вектору  .
Далее от точки B отложим вектор
.
Далее от точки B отложим вектор  ,
равный вектору
,
равный вектору  .
А от точки C отложим вектор
.
А от точки C отложим вектор  ,
равный вектору
,
равный вектору  .
.
Будем последовательно складывать наши векторы, пользуясь правилом треугольника.
Сумма
векторов  и
и
 равна
вектору
равна
вектору  .
.
Теперь
к вектору  добавим
вектор
добавим
вектор  .
В результате мы получаем вектор
.
В результате мы получаем вектор  .
.
Тогда
можем сказать, что сумма векторов  ,
,
 и
и
 .
равна вектору
.
равна вектору  .
.

Так, последовательно складывая первый вектор со вторым, затем их сумму с третьим и так далее, можно найти суммы четырёх, пяти и большего числа векторов.
Такое правило построения суммы векторов называют правилом многоугольника, и оно позволяет построить вектор суммы неограниченного количества векторов.
Задача. Построить
вектор суммы попарно неколлинеарных векторов  ,
,
 ,
,
 ,
,
 и
и
 .
.

Построение.



Примеры, приведённые нами, подходят для векторов, лежащих в одной плоскости. А мы, изучая стереометрию, находимся в пространстве, поэтому правило многоугольника сложения векторов в пространстве может иметь и другую иллюстрацию.
Задача.
Рассмотрим векторы  ,
,
 и
и
 ,
такие, что
,
такие, что  ,
,
 лежат
в одной плоскости, а вектор
лежат
в одной плоскости, а вектор  не
лежит в этой плоскости. Найдём сумму этих векторов.
не
лежит в этой плоскости. Найдём сумму этих векторов.

Решение.
Выберем
любую удобную точку О в пространстве и отложим от неё вектор  ,
равный вектору
,
равный вектору  ,
а от точки А отложим вектор
,
а от точки А отложим вектор  ,
равный вектору
,
равный вектору  .
Понятно, что через проведённые векторы можно провести плоскости. Далее, от
точки B отложим вектор
.
Понятно, что через проведённые векторы можно провести плоскости. Далее, от
точки B отложим вектор  ,
равный вектору
,
равный вектору  .
Вектором суммы данных векторов является вектор
.
Вектором суммы данных векторов является вектор  .
.
Вы видите, что многоугольник сложения в данном случае является пространственным, то есть не все его вершины лежат в одной плоскости.
Сформулируем правило многоугольника для произвольных точек пространства А1, А2 ,…, Аn.


Это равенство справедливо для любых точек А1, А2, …, An. И, в частности, для случая, когда некоторые из них совпадают.
Например,
если начало первого вектора совпадает с концом последнего, то сумма данных
векторов равна  .
.
Задача. Упростить выражения
Выполним задание, где, пользуясь данной формулировкой, упростим выражения.
а)

б)

в)


г)
 =
=

Так мы с вами рассмотрели примеры преобразования выражений с векторами, представленных в виде алгебраической суммы.
Задача.
 ,
,
 ,
,
 ,
,
 произвольные
точки пространства.
произвольные
точки пространства.
Представить
вектор  в
виде алгебраической суммы векторов:
в
виде алгебраической суммы векторов:
а)
 ,
,
 ,
,
 б)
б)  ,
,
 ,
,
 в)
в)  ,
,
 ,
,

Решение.
 В
последнем задании рассмотрим параллелепипед ABCDA1B1C1D1.
В
последнем задании рассмотрим параллелепипед ABCDA1B1C1D1.

Нужно
указать вектор  ,
начало и конец которого являются вершинами параллелепипеда. И чтобы истинными
были данные равенства.
,
начало и конец которого являются вершинами параллелепипеда. И чтобы истинными
были данные равенства.
Сумма
векторов  .
.
По
рисунку понятно, чтобы восстановить правило многоугольника, не достает вектора  .
Значит, вектор
.
Значит, вектор  .
.
Далее
рассмотрим выражение, где сумма векторов  .
.

По
рисунку понятно, что сумма известных векторов из левой части равенства равна
вектору  .
И чтобы вся сумма равнялась вектору
.
И чтобы вся сумма равнялась вектору  ,
вектор
,
вектор  должен
быть равен вектору
должен
быть равен вектору  .
.
Перейдём
к следующему равенству. 

Чтобы
восстановить правило многоугольника, вектор  удобнее
заменить равным ему вектором
удобнее
заменить равным ему вектором  .
Тогда становится понятно, что вектор «-
.
Тогда становится понятно, что вектор «- »
равен вектору
»
равен вектору  .
А вектор
.
А вектор  отсюда
равен вектору
отсюда
равен вектору  .
.
Разберёмся
с последним равенством.  .
.

Левую
часть представим в виде суммы и заменим вектор «–  »
на
»
на  .
.
Изобразим
данные векторы. Видим, что искомый вектор  равен
вектору
равен
вектору  .
.
Подведём итоги урока.
Сегодня мы сформулировали правило многоугольника сложения нескольких векторов в пространстве. И нашли его отличие от того же правила на плоскости.
Оно заключается в том, что полученный многоугольник может являться пространственным, то есть не все его вершины лежат в одной плоскости.
Также мы сформулировали правило многоугольника для произвольных точек пространства А1, А2 …, Аn.
Сумма
векторов  +
+
 ,+
,+ =
=
 ,.
,.
И
если начало первого вектора совпадает с концом последнего, то сумма данных
векторов равна  .
.
Эти знания мы смогли применить при выполнении заданий.
Сумма двух векторов / Векторы / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Векторы
- Сумма двух векторов
Рассмотрим два вектора и 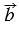 и найдем их сумму. Для этого отметим произвольную точку А и отложим от этой точки вектор , равный . Затем от точки В отложим вектор
и найдем их сумму. Для этого отметим произвольную точку А и отложим от этой точки вектор , равный . Затем от точки В отложим вектор 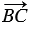 , равный
, равный 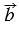 . Вектор , равный вектору
. Вектор , равный вектору 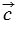 , называется суммой векторов и
, называется суммой векторов и 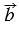 .
.
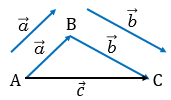
Данное правило сложения векторов называется правилом треугольника (рисунок поясняет это название).
Сумма векторов и 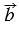 обозначается так: +
обозначается так: + 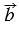 .
.
Результат 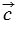 сложения (сумма) векторов и сложения (сумма) векторов и 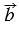 не зависит от выбора точки, от которой откладывается вектор . не зависит от выбора точки, от которой откладывается вектор . |
Доказательство
Дано: = 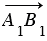 ,
, 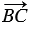 =
= 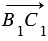 .
.
Доказать: = .
Доказательство:

Допустим, что точки А, В, А1, точки В, С, В1 и точки А, С, А1 не лежат на одной прямой. Из равенства = 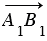 следует, что стороны АВ и А1В1 четырехугольника АВВ1А1 равны и параллельны, т.к. равные векторы сонаправлены и их длины равны, поэтому этот четырехугольник — параллелограмм. Поэтому АА1 = ВВ1, значит, и
следует, что стороны АВ и А1В1 четырехугольника АВВ1А1 равны и параллельны, т.к. равные векторы сонаправлены и их длины равны, поэтому этот четырехугольник — параллелограмм. Поэтому АА1 = ВВ1, значит, и 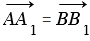 . Аналогично из равенства
. Аналогично из равенства 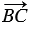 =
= 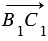 следует, что четырехугольник ВСС1В1 — параллелограмм. Поэтому .
следует, что четырехугольник ВСС1В1 — параллелограмм. Поэтому .
Итак, 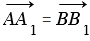 , , следовательно,
, , следовательно, 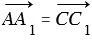 . Поэтому АА1С1С — параллелограмм, и, значит, = . Что и требовалось доказать.
. Поэтому АА1С1С — параллелограмм, и, значит, = . Что и требовалось доказать.
Складывая по правилу треугольника произвольный вектор с нулевым вектором, получаем, что для любого вектора справедливо равенство + = .
Правило треугольника можно сформулировать и так:
Если А, В и С — произвольные точки, то + 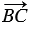 = . = . |
Данное правило справедливо для произвольных точек А, В и С, даже в том случае, когда две из них или даже все три совпадают.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие вектора
Равенство векторов
Откладывание вектора от данной точки
Законы сложения векторов. Правило параллелограмма
Сумма нескольких векторов
Вычитание векторов
Произведение вектора на число
Применение векторов к решению задач
Средняя линия трапеции
Векторы
Правило встречается в следующих упражнениях:
7 класс
Задание 756, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 764, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 768, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 776, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 7, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 803, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 804, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 805, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 807, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1074, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Лекция по математике на тему «Сумма нескольких векторов»
Лекция по теме «Сумма нескольких векторов»
Сложение нескольких векторов в пространстве выполняется так: первый вектор складывается со вторым, затем их сумма – с третьим вектором и так далее. Это правило нам известно как правило многоугольника. На рисунке показано сложение трех векторов в пространстве.От точки О отложен вектор ОА равный вектору а, затем от точки А вектор АВ равный бэ, от точки В отложен следующий вектор ВС равный це, и соединяем первую и последнюю точки О с С получаем вектор ОС равный сумме векторов а, бэ и це.
Текст
Сумма нескольких векторов
Рисунок: сложение трех векторов
Текст
Сформулируем правило многоугольника.
ЕслиА1, А2, А3 и так далее Аn – произвольные точки, то вектор А1А2 плюс вектор А2А3 плюс вектор А3А4 и так далее плюс Аn-1 An, то в результате получится вектор А1Аn.
На рисунке показана сумма шести векторов.
Текст
Правило многоугольника
Рисунок
Текст

Если начало вектора совпадает с концом последнего, то сумма равна нулевому вектору.
Рассмотрим сумму векторов
Выполнив сложение по правилу многоугольника, получаем вектор АА или нулевой вектор.
Текст
Сумма нескольких векторов
Рисунок параллелепипеда
Текст
Решим задачу №337 (в)
Упростите выражение
Решение: Заменим в выражении вычитание на сумму. Для этого заменим отрицательные векторы на противоположные. Вектор минус ВС равен вектору СВ, минус вектор РМ равен вектору МР. Минус вектор АР равен вектору РА. Вектор АС в сумме с вектором СВ дают вектор АВ. Векторы МР и РА дают вектор МА. Затем, складывая векторы АВ и ВМ, получаем вектор АМ. В итоге сумма векторов АМ и МА дают нулевой вектор. Выражение упрощено.
Текст
Задача 337(в)
Упростите:
Решение:
Решим задачу на доказательство №338.
Дан параллелепипед АВСDA1B1C1D1. Докажите, что , где О – произвольная точка пространства.
, где О – произвольная точка пространства.
Доказательство. Преобразуем левую часть равенства. Вектор ОА представим как сумму векторов ОА1 и А1А по правилу треугольника. Вектор А1А равен вектору С1С как противоположные ребра параллелепипеда. Складывая векторы ОС1 и С1С, получаем ОС. В результате преобразований получили правую часть равенства. Доказательство окончено.
Текст
Задача №338
Рисунок параллелепипеда и внешняя точка О.

Текст
Дано: АВСDA1B1C1D1,
Oпараллелепипеду.
Доказать: 
Доказательство:
Разработка урока и презентация «Сумма нескольких векторов»
Муниципальное автономное общеобразовательное учреждение
средняя общеобразовательная школа № 45
Разработка урока по теме
«Сумма нескольких векторов»,
геометрия, 8 класс.
Автор: учитель математики
первой категории
МАОУ СОШ №45 г. Калининграда
Борисова Алла Николаевна.
г. Калининград
2016 – 2017 учебный год
Автор – Борисова Алла Николаевна
Образовательное учреждение – муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа № 45 города Калининграда
Предмет – математика (геометрия)
Класс – 8
Тема – «Сумма нескольких векторов»
Учебно-методическое обеспечение:
Геометрия, 7 — 9: учебник для общеобразовательных учреждений/ Л. С. Атанасян и др., — 17 — е изд., — М.: Просвещение, 2015 г.
Рабочая тетрадь «Геометрия, 8 класс», авторы Л. С. Атанасян, В. Ф. Бутузов, Ю.А. Глазков, И.И. Юдина/ учебное пособие для учащихся общеобразовательных учреждений/ — М. Просвещение, 2016 г.
Данные о программах, в которых выполнена мультимедийная составляющая работы — Microsoft Office Power Point 2010
Цель: ознакомить учащихся с правилом построения суммы нескольких векторов, правилом многоугольника и со свойством сложения нескольких векторов.
Задачи урока:
Образовательные:
повторение теоретических сведений по теме «Векторы»;
научить учащихся выполнять сложение нескольких векторов;
выработать у учащихся умение применять свойства сложения нескольких векторов в решении простейших задач.
Развивающие:
развитие познавательного интереса к предмету;
формирование ключевых и предметных компетентностей;
развитие пространственного воображения и логического мышления;
развитие памяти, математической речи, наблюдательности, развитие графических навыков у учащихся;
развитие творческих способностей;
развивать у учащихся навыки самостоятельной работы и работы в парах.
Воспитательные:
воспитание интереса к предмету и потребности в приобретении знаний.
воспитание инициативы и творчества;
воспитание ответственного отношения к учебному труду;
воспитание уважительного отношения к сверстникам.
Оборудование и материалы для урока: мультимедийный проектор, презентация, раздаточный материал.
Тип урока: урок изучения нового материала.
Структура урока:
1) Учащимся сообщается тема урока и цели (слайд №1).2) Объявляется план урока.
1. Проверка домашнего задания.
2. Повторение.
3. Открытие нового знания.
4. Закрепление.
II. Проверка домашнего задания.
1) 2 уч-ся оформляют самостоятельно на доске номера из домашней работы: № 763(б,в).
C D
B A
б)
(по теореме Пифагора).
в)
по правилу параллелограмма .
В параллелограмме ABCD угол В равен 90°, значит, ABCD— прямоугольник, тогда BD = AC = 10. Поэтому,
2) Остальные работают в это время устно с целью повторения пройденного материала.
а) Установите соответствие (слайд №2).
б) Решение задач на готовых чертежах (слайды № 3 — 5).
в) (слайд №6).
III. Введение нового материала.
1) Выполнение практической работы с целью подготовки учащихся к восприятию нового материала (смотри приложение 1).
Возникает проблема: не хватает имеющихся знаний для решения данной задачи.
2) Объяснение учителя (слайд №7).
3) Сделайте вывод, как сложить несколько векторов.
Вывод.
Первый вектор складывается со вторым, затем их сумма — с третьим вектором и т. д.
Это правило сложения векторов называется правилом многоугольника.
Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.
IV. Закрепление изученного материала.
1) Возвращаемся к практической части и выполняем сложение трёх векторов. Наиболее подготовленным учащимся предлагается дополнительно решить вариант 3 (сложение трёх коллинеарных векторов)
2) Фронтальная работа.
Задача № 121 в рабочей тетради (слайд №8).
3) Разобрать решение задачи № 1(слайд №9).
V. Физкультминутка.
Упражнения для глаз.
VI. Самостоятельное решение задач.
а) 1 уровень. Решают задачу № 2. Работают самостоятельно, учитель при необходимости консультирует учащихся, анализирует результаты выполнения учащимися заданий
Задача №2.
ABCD, ADEF −параллелограммы.
Укажите такой вектор а, что CD + AB + AF + AD + a = AF.

б) 2 уровень (более подготовленные учащиеся).
Работают самостоятельно (по необходимости пользуются помощью учителя или соседа по парте).
После окончания работы взаимопроверка.
Задача № 3.
В трапеции ABCD AD║BC, угол АВС равен 120°, AD = 6 см, АВ = 3 см. Найдите
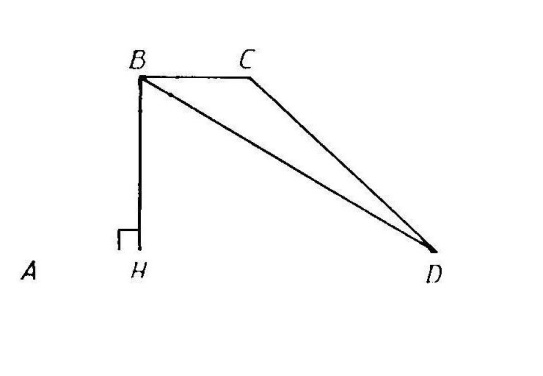
VII. Подведение итогов урока, рефлексия деятельности
Подведение итогов урока, мобилизация учащихся на самооценку своей деятельности;
— Итак, что вы узнали сегодня на уроке?
— Чему научились сегодня на уроке?
Выставление отметок за урок.
VIII. Домашнее задание (слайд №10)
п.81, контрольные вопросы № 11 стр. 201-202.
№ 755, 760, 761.
Приложение 1.
Практическая работа.Вариант №1.
Даны векторы и точка А.
Найдите сумму этих векторов, откладывая их от точки А.
A
Практическая работа.
Вариант№2.
Даны векторы и точка А.
Найдите сумму этих векторов, откладывая их от точки А.
A
Практическая работа.
Вариант №3.
Даны векторы и точка А.
Найдите сумму этих векторов, откладывая их от точки А.
A
Вычитание векторов / Векторы / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Векторы
- Вычитание векторов
Разность векторов 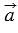 и и 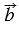 — вектор, сумма которого с вектором — вектор, сумма которого с вектором 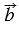 равна вектору равна вектору 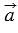 . . |
Разность векторов 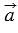 и
и 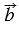 обозначается так:
обозначается так: 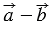 .
.
Задача на построение разности векторов (1 способ)
Даны векторы 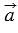 и
и 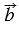 . Построить вектор
. Построить вектор 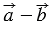 .
.
Дано: 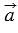 и
и 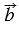 .
.
Построить: 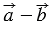 .
.
Решение:
От произвольной точки О откладываем векторы = 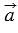 и
и  =
= 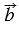 .
.
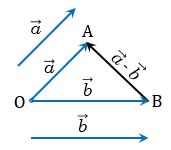
По правилу треугольника  + = или
+ = или 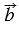 + =
+ = 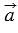 , то есть сумма векторов и
, то есть сумма векторов и 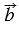 равна
равна 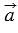 . По определению разности векторов это означает, что =
. По определению разности векторов это означает, что = 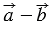 , следовательно, вектор — искомый.
, следовательно, вектор — искомый.
Противоположный вектор
Пусть 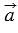 — произвольный ненулевой вектор.
— произвольный ненулевой вектор.
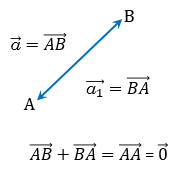
Вектор = является противоположным вектору 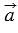 =
= 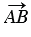 . Вектором, противоположным нулевому вектору, считается нулевой вектор.
. Вектором, противоположным нулевому вектору, считается нулевой вектор.
Вектор, противоположный вектору 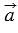 , обозначается так:
, обозначается так: 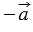 .
.
Теорема
Для любых векторов 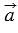 и и 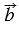 справедливо равенство . справедливо равенство . |
Доказательство
Дано: 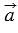 и
и 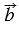 .
.
Доказать: .
Доказательство:
По определению разности векторов . Прибавим к обеим частям этого равенства вектор , получим:
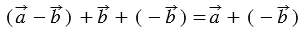 или (т.к. ), следовательно, . Теорема доказана.
или (т.к. ), следовательно, . Теорема доказана.
Задача на построение разности векторов (2 способ)
Даны векторы 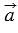 и
и 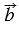 . Построить вектор
. Построить вектор 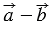 .
.
Дано: 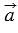 и
и 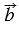 .
.
Построить: 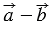 .
.
Решение:
От произвольной точки О откладываем векторы = 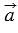 . Затем от точки А отложим
. Затем от точки А отложим 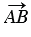 =.
=.
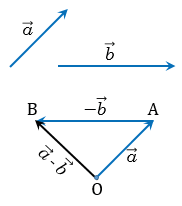
По теореме о разности векторов , поэтому , следовательно, вектор  — искомый.
— искомый.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие вектора
Равенство векторов
Откладывание вектора от данной точки
Сумма двух векторов
Законы сложения векторов. Правило параллелограмма
Сумма нескольких векторов
Произведение вектора на число
Применение векторов к решению задач
Средняя линия трапеции
Векторы
Правило встречается в следующих упражнениях:
7 класс
Задание 764, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 770, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 773, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 776, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 785, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 905, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 906, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 908, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 925, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1050, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Сумма векторов, длина вектора

Сумма векторов. Длина вектора. Дорогие друзья, в составе типов задний экзамена присутствует группа задач с векторами. Задания довольно широкого спектра (важно знать теоретические основы). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения. Так же много заданий, при решении которых необходимо осуществить действия с координатами векторов.
Теория касающаяся темы векторов несложная, и её необходимо хорошо усвоить. В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:
Понятие вектора
Вектор — это направленный отрезок.

Все векторы, имеющие одинаковое направление и равные по длине являются равными.

*Все представленные выше четыре вектора равны!
То есть, если мы будем при помощи параллельного переноса перемещать данный нам вектор, то всегда получим вектор равный исходному. Таким образом, равных векторов может быть бесчисленное множество.
Обозначение векторов
Вектор может быть обозначен латинскими заглавными буквами, например:

При данной форме записи сначала записывается буква обозначающая начало вектора, затем буква обозначающая конец вектора.
Ещё вектор обозначается одной буквой латинского алфавита (прописной):

Возможно также обозначение без стрелок:

Сумма векторов

Суммой двух векторов АВ и ВС будет являться вектор АС.
Записывается как АВ+ВС=АС.
Это правило называется – правилом треугольника.
То есть, если мы имеем два вектора – назовём их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то суммой этих векторов будет вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).
Вывод: если мы имеем на плоскости два вектора, то всегда сможем найти их сумму. При помощи параллельного переноса можно переместить любой из данных векторов и соединить его начало с концом другого. Например:

Перенесём вектор b, или по-другому – построим равный ему:

Как находится сумма нескольких векторов? По тому же принципу:

* * *
Правило параллелограмма
Это правило является следствием изложенного выше.
Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a, и мы можем построить вектор, который будет являться их суммой:

Ещё немного важной информации, необходимой для решения задач.
Вектор, равный по длине исходному, но противоположно направленный, обозначается также но имеет противоположный знак:

Эта информация крайне полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов это та же сумма в изменнёном виде.
Пусть даны два вектора, найдём их разность:


Мы построили вектор противоположный вектору b, и нашли разность.
Координаты вектора
Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала:

То есть, координаты вектора представляют собой пару чисел.
Если

И координаты векторов имеют вид:

То c1= a1+ b1 c2= a2+ b2
Если

То c1= a1– b1 c2= a2– b2
Модуль вектора
Модулем вектора называется его длина, определяется по формуле:

Формула для определения длины вектора, если известны координаты его начала и конца:

Рассмотрим задачи:

Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО.

Найдём вектор, который будет являться результатом АО–ВО:
АО–ВО=АО+(–ВО)=АВ
То есть разность векторов АО и ВО будет являться вектор АВ. А его длина равна восьми.
Ответ: 8

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ+AD.

Найдём вектор, который будет являться суммой векторов AD и AB. Вектор BC равен вектору AD. Значит AB+AD=AB+BC=AC
Длина вектора AC это длина диагонали ромба АС, она равна 16.
Ответ: 16

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО+ВО.

Найдём вектор, который будет являться суммой векторов АО и ВО. Вектор ВО равен вектору OD, значит

Длина вектора AD это длина стороны ромба. Задача сводится к нахождению гипотенузы в прямоугольном треугольнике AOD. Вычислим катеты:

По теореме Пифагора:

Ответ: 10

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО–ВО.

Найдём вектор, который будет являться результатом АО–ВО:

Длина вектора АВ это длина стороны ромба. Задача сводится к нахождению гипотенузы АВ в прямоугольном треугольнике AOB. вычислим катеты:

По теореме Пифагора:

Ответ: 10

Стороны правильного треугольника ABC равны 3.
Найдите длину вектора АВ–АС.

Найдём результат разности векторов:

Длина вектора СВ равна трём, так как в условии сказано, что треугольник равносторонний и его стороны равны 3.
Ответ: 3

27663. Найдите длину вектора а(6;8).

Посмотреть решение
27664. Найдите квадрат длины вектора АВ.

Посмотреть решение
27707. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину вектора АС.

Посмотреть решение
27708. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину суммы векторов AB и AD.

Посмотреть решение
27709. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов AB и AD.

Посмотреть решение
27711. Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов АО и ВО.

Посмотреть решение
27713. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ.

Посмотреть решение
27715. Диагонали ромба ABCD равны 12 и 16.
Найдите длину вектора АВ–AD.

Посмотреть решение
27716. Диагонали ромба ABCD равны 12 и 16.
Найдите длину вектора АВ–АС.

Посмотреть решение
Стороны правильного треугольника ABC равны 2√3. Найдите длину вектора АВ+АС.

Посмотреть решение
В будущем мы продолжим рассматривать задачи с векторами, не пропустите! Задания будут связаны с координатами векторов, скалярным произведением.
На этом всё. Успеха вам!
С уважением, Александр
Вступительный экзамен по математике. Преподаватели приглашают первого абитуриента:
— Сколько будет два плюс два?
— Три! — Нет! — Пять! — Нет! — Шесть!
— Неправильно! Да… дурак, но ищущий… берем!
Заходит второй абитуриент:
— Сколько будет два плюс два?
— Три! — Нет! — Три! — Нет! — Три!
— Неправильно! Да… дурак, но настырный… берем!
Заходит третий абитуриент:
— Сколько будет два плюс два?
— Четыре, конечно!
— Да… умный. Но мест уже нет!
P.S: Буду благодарен, если расскажете о статье в социальных сетях.

