Сумма ⭐ двух векторов: определение, правило, координаты
Основные понятия
Определение 1Направленный отрезок, то есть отрезок, который имеет длину и определенное направление, носит название вектора.
Обозначается буквенным символом со стрелкой над ним:
Определение 2
Сонаправленные векторы — это векторы, направления которых совпадают (одинаковые по направлению).
Определение 3Противоположно направленные векторы — это векторы, которые направлены в разные стороны.
С векторами можно производить такие операции, как:
- сложение;
- вычитание;
- умножение на число.
Для начала, рассмотрим подробно сложение.
Сложение (сумма) векторов «a + b» — это операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:
c=a+b
Вычитание (разность) векторов «a — b» — это операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:
c=a-b
Сложение векторов может осуществляться по трем правилам:
- Правило параллелограмма.
 Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов.
Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов. - Правило многоугольника. Из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее. Когда все векторы отложены, соединим начальную точку с концом последнего вектора и получим сумму нескольких векторов.
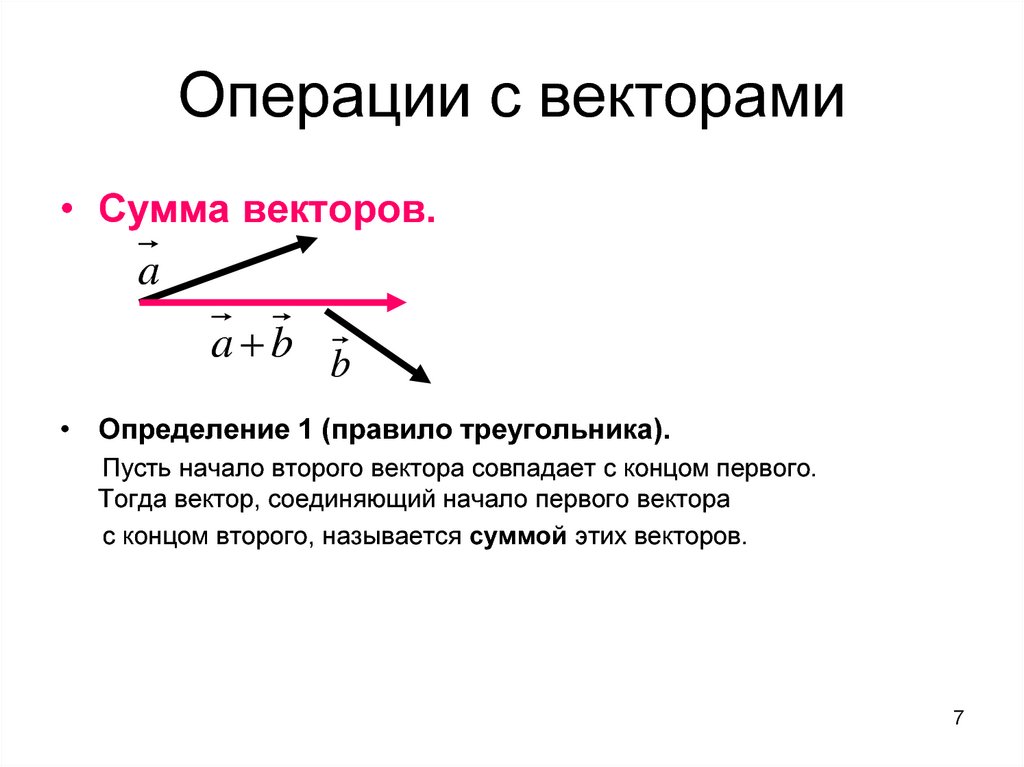
- Правило треугольника.
Сумма сонаправленных и противоположно направленных векторов, правило треугольника
Правило треугольника заключается в следующем: для того чтобы сложить два сонаправленных вектора, необходимо из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго. Конечный вектор и будет суммой двух векторов.
Чертеж поможет наглядно объяснить правило:
a+b=AB+BC=AC
AC — сумма векторов.
Разность векторов a и b является суммой векторов a и -b.
Как вычислить координаты суммы двух векторов, пояснение на примерах
Кроме геометрического способа сложения (вычитания) векторов (правила треугольника, параллелограмма, многоугольника), существует способ сложения координат векторов.
Для того чтобы найти координаты суммы двух векторов, нужно сложить их соответствующие координаты по следующей формуле:
Пример 1Найти сумму векторов a(7;5) и b(3;8)
Решение: a+b=(7+3;5+8)=(10;13)
Пример 2Найти сумму координат векторов a(-7;2), b(-3;6), c(6;-5)
Решение: a+b+c=(-7-3+6;2+6-5)=(-4;3)
Примеры решения задач
Пример 3Найти сумму векторов a(1;2), b(7;9)
Решение:a+b=(1+7;2+9)=(8;11)
Пример 4Найти разность координат векторов a(4;-6), b(5;-1)
Решение: a-b=(4-5;-6-(-1))=(-1;-5)
3 Сложение векторов
Определение
3.1. Суммой
двух векторов и называется
вектор ,
где , , —
произвольная точка, — точки,
полученные после откладывания
векторов и .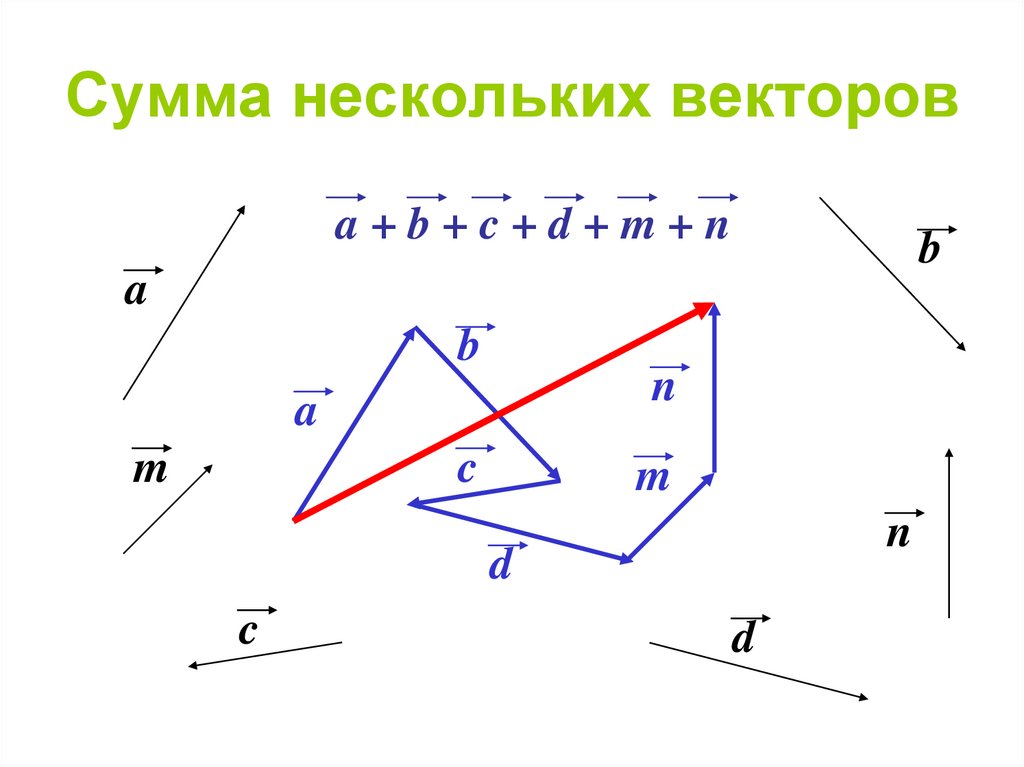
Покажем, что сумма векторов не зависит от выбора точки . Действительно, пусть — любая точка, отличная от точки . Строим векторы . Докажем, что . Так как и , то по лемме 2.1. и , то есть . Следовательно, по той же лемме . Замечание 3.1. Для нахождения суммы неколлинеарных векторов приходится строить треугольник . Поэтому правило сложения векторов называется правилом треугольника. Из этого правила следует, что для любых трех точек справедливо равенство
В частности, это правило справедливо и для коллинеарных точек.
Свойства сложения векторов.
ТЕОРЕМА 3.1. Для произвольных векторов справедливы следующие равенства:
 Согласно построению ,
поэтому по
лемме 2.1. получаем ,
т.е. .
По
правилу треугольника и ,
следовательно, .
Отсюда получаем, что . 2. Пусть и —
произвольные векторы. Возьмем какую-нибудь
точку и
отложим последовательно векторы
.
По
правилу треугольника ,
поэтому .
С другой стороны ,
поэтому .
Отсюда получаем требуемое.
Согласно построению ,
поэтому по
лемме 2.1. получаем ,
т.е. .
По
правилу треугольника и ,
следовательно, .
Отсюда получаем, что . 2. Пусть и —
произвольные векторы. Возьмем какую-нибудь
точку и
отложим последовательно векторы
.
По
правилу треугольника ,
поэтому .
С другой стороны ,
поэтому .
Отсюда получаем требуемое. 
4 Разность векторов.
 Тогда .
Прибавим к обеим частям этого равенства
вектор .
Получим Таким
образом, доказано существование и
единственность разности любых двух
векторов, при этом эта разность
обозначается .
Тогда .
Прибавим к обеим частям этого равенства
вектор .
Получим Таким
образом, доказано существование и
единственность разности любых двух
векторов, при этом эта разность
обозначается . Отметим еще равенство В самом деле,
Вопрос Видео: Нахождение суммы трех векторов в компонентной форме
Стенограмма видео
Учитывая, что 𝐮 — это вектор два, минус три, а 𝐯 — вектор три, два и 𝐰 — отрицательный вектор один, минус пять, найдите компоненты 𝐮 плюс 𝐯 плюс 𝐰.
В этом вопросе нам даны три вектора 𝐮, 𝐯 и 𝐰, и нас просят найти сумму этих трех векторов. И мы знаем много разных способов сложения двух векторов. Например, мы могли бы изобразить все три этих вектора графически, а затем графически сложить их вместе. И это сработает; однако нам даны эти три вектора с точки зрения их компонентов, поэтому будет проще сложить их вместе по компонентам.
И это сработает; однако нам даны эти три вектора с точки зрения их компонентов, поэтому будет проще сложить их вместе по компонентам.
Итак, мы начнем с того, что напишем нашу сумму полностью. У нас 𝐮 плюс 𝐯 плюс 𝐰 равно вектору два, минус три прибавляется к вектору три, два добавляется к вектору минус один, минус пять. И мы помним, чтобы сложить два вектора одной размерности вместе, нам просто нужно сложить вместе соответствующие компоненты. Итак, мы начнем со сложения наших векторов 𝐮 и 𝐯 вместе. Когда мы сложим эти два вектора вместе, первый компонент будет суммой первых компонентов наших векторов. Это два плюс три. И наш второй компонент будет суммой вторых компонентов наших двух векторов. Это минус три плюс два.
И не забудьте, нам еще нужно добавить наш вектор 𝐰. Это дает нам следующее выражение. И мы можем упростить это выражение, вычислив компоненты нашего первого вектора. У нас два плюс три равно пяти, а минус три плюс два равен минус единице, что дает нам 𝐮 плюс 𝐯 плюс 𝐰 — это вектор пять, минус один добавляется к вектору минус один, минус пять. Но теперь мы видим, что нам все еще нужно сложить два вектора вместе. Поэтому нам нужно будет повторить этот процесс. Мы складываем вместе первые компоненты наших векторов и вторые компоненты наших векторов вместе. Это дает нам вектор пять плюс минус один, минус один плюс минус пять.
Но теперь мы видим, что нам все еще нужно сложить два вектора вместе. Поэтому нам нужно будет повторить этот процесс. Мы складываем вместе первые компоненты наших векторов и вторые компоненты наших векторов вместе. Это дает нам вектор пять плюс минус один, минус один плюс минус пять.
И мы можем вычислить каждое из выражений в наших компонентах. Пять плюс минус один равно четырем, а минус один плюс минус пять равно минус шесть. Итак, мы показали, что 𝐮 плюс 𝐯 плюс 𝐰 — это вектор четыре минус шесть. И мы могли бы остановиться здесь. Тем не менее, есть кое-что, на что стоит обратить внимание. Когда мы оценивали это выражение, мы начали с нахождения вектора 𝐮 плюс 𝐯, а затем добавили результат к вектору 𝐰. Однако это не единственный вариант. Мы могли бы также добавить вектор 𝐯 к вектору 𝐰, а затем добавить результат к вектору 𝐮.
Если бы мы сделали это, нам нужно было бы сложить компоненты вектора 𝐯 и вектора 𝐰 вместе. Это дает нам вектор два, минус три, добавленный к вектору три плюс минус один, два плюс минус пять, который мы можем упростить, чтобы получить вектор два, минус три, добавленный к вектору два, минус три.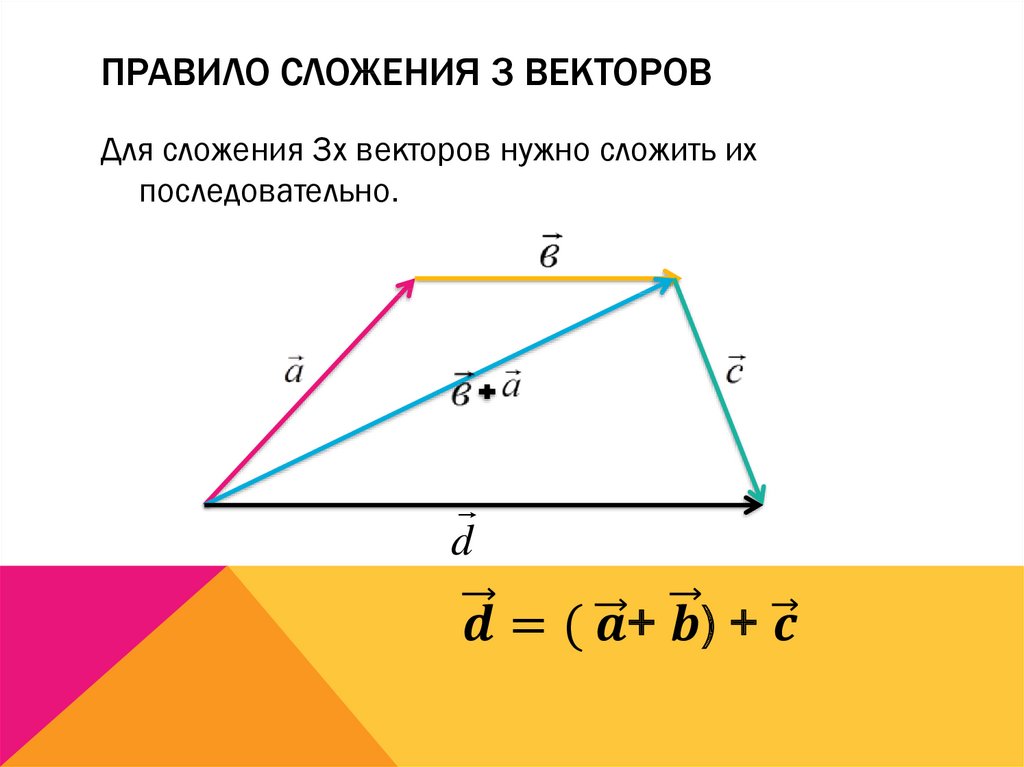 И затем мы можем сложить эти два вектора вместе по компонентам. И если бы мы сделали это, первая составляющая нашего вектора была бы два плюс два, то есть четыре, а вторая составляющая нашего вектора была бы минус три плюс минус три, что минус шесть.
И затем мы можем сложить эти два вектора вместе по компонентам. И если бы мы сделали это, первая составляющая нашего вектора была бы два плюс два, то есть четыре, а вторая составляющая нашего вектора была бы минус три плюс минус три, что минус шесть.
Таким образом, мы также получаем вектор четыре, минус шесть. Итак, мы только что показали, что в данном случае не имеет значения, в каком порядке мы складывали наши векторы 𝐮, 𝐯 и 𝐰 вместе. На самом деле это верно вообще для любых трех векторов. Мы всегда можем сложить их вместе в любом порядке. Это называется ассоциативностью сложения векторов. И это очень похоже на другое свойство, о котором вы, возможно, слышали, называемое коммутативностью, что означает, что мы можем менять порядок наших векторов. И очень полезно помнить об этих свойствах, потому что часто их можно использовать для упрощения задач, связанных с векторами.
Следовательно, в этом вопросе мы смогли показать, если 𝐮 — это вектор два, минус три, а 𝐯 — вектор три, два, а 𝐰 — вектор минус один, минус пять, то 𝐮 плюс 𝐯 плюс 𝐰 — это вектор четыре, минус шесть.
Видео с вопросом: графическое сложение трех векторов
Стенограмма видео
Какой из векторов 𝐏, 𝐐, 𝐑, 𝐒 и 𝐓, показанных на диаграмме, равен 𝐀 плюс 𝐁 плюс 𝐂?
Упомянутая диаграмма представляет собой набор декартовых осей с несколькими векторами, представленными в виде стрелок. Нас особенно интересуют векторы 𝐀, 𝐁 и 𝐂. И перед нами стоит задача определить, какой из других векторов на диаграмме равен сумме этих трех векторов. Когда мы представляем вектор стрелкой, заостренный конец называется головой, а другой конец называется хвостом. Чтобы добавить второй вектор, мы просто рисуем этот вектор так, чтобы его хвост находился в начале первого. Сумма этих двух векторов — это вектор, хвост которого находится в хвосте первого вектора, а голова — в начале второго вектора.
Однако для нашего вопроса мы ищем сумму трех векторов, а не двух. К счастью, сложение векторов ассоциативно. Это означает, что мы можем сгруппировать различные части расчета так, как мы хотим, не изменяя окончательный ответ. Допустим, мы добавляем три вектора 𝐔, 𝐕 и 𝐖. Чтобы сложить все три этих вектора вместе, мы можем сначала сложить два вектора 𝐔 и 𝐕, а затем добавить 𝐖.
Допустим, мы добавляем три вектора 𝐔, 𝐕 и 𝐖. Чтобы сложить все три этих вектора вместе, мы можем сначала сложить два вектора 𝐔 и 𝐕, а затем добавить 𝐖.
Как видно из нашей диаграммы, 𝐔 плюс 𝐕 — это просто еще один вектор, поэтому 𝐔 плюс 𝐕 в скобках плюс 𝐖 — это просто сумма этого нового вектора 𝐔 плюс 𝐕 с третьим вектором 𝐖. И мы знаем, как это сделать. Мы просто рисуем 𝐖 с хвостом во главе 𝐔 плюс 𝐕. Теперь мы рисуем вектор, хвост которого находится в хвосте 𝐔 плюс 𝐕, а голова в начале 𝐖. И это дает нам сумму трех векторов 𝐔 плюс 𝐕 плюс 𝐖. Обратите внимание, что мы могли бы фактически стереть промежуточный шаг вычисления 𝐔 плюс 𝐕 и все равно получить тот же ответ.
Таким образом, мы можем вычислить сумму 𝐔 плюс 𝐕 плюс 𝐖, нарисовав каждую стрелку так, чтобы ее конец находился в начале предыдущей стрелки, а затем соединив оставшийся конец и оставшуюся часть, чтобы сформировать окончательный вектор. На самом деле это работает для любого количества векторов, и мы всегда будем получать один и тот же ответ независимо от порядка, который мы используем при отрисовке векторов.
Итак, чтобы найти искомую сумму, нам просто нужно перерисовать 𝐀, 𝐁 и 𝐂 так, чтобы их головы и решки соприкасались. Давайте начнем с перерисовки 𝐁 с хвостом в голове 𝐀. Стрелка 𝐁 проходит на две единицы вправо и на три единицы вверх. Нарисовав стрелку с хвостиком в начале 𝐀 и удлинив ее на две единицы вправо и на три единицы вверх, мы подошли к этому моменту. Теперь нам нужно добавить стрелку для 𝐂. Эта стрелка простирается на четыре единицы влево и на одну единицу вверх. Соединив эту стрелку с двумя, которые мы уже нарисовали, мы перенесемся из предыдущей головы в эту точку, которая является головой вектора, помеченного 𝐐.
Теперь, чтобы найти искомую сумму, нам нужно найти вектор, у которого хвост находится в хвосте 𝐀, а голова — в начале 𝐂. И мы видим, что 𝐐 действительно имеет голову во главе 𝐂. И поскольку и 𝐀, и 𝐐 имеют свои хвосты в начале координат, 𝐐 также имеет свой хвост в хвосте 𝐀.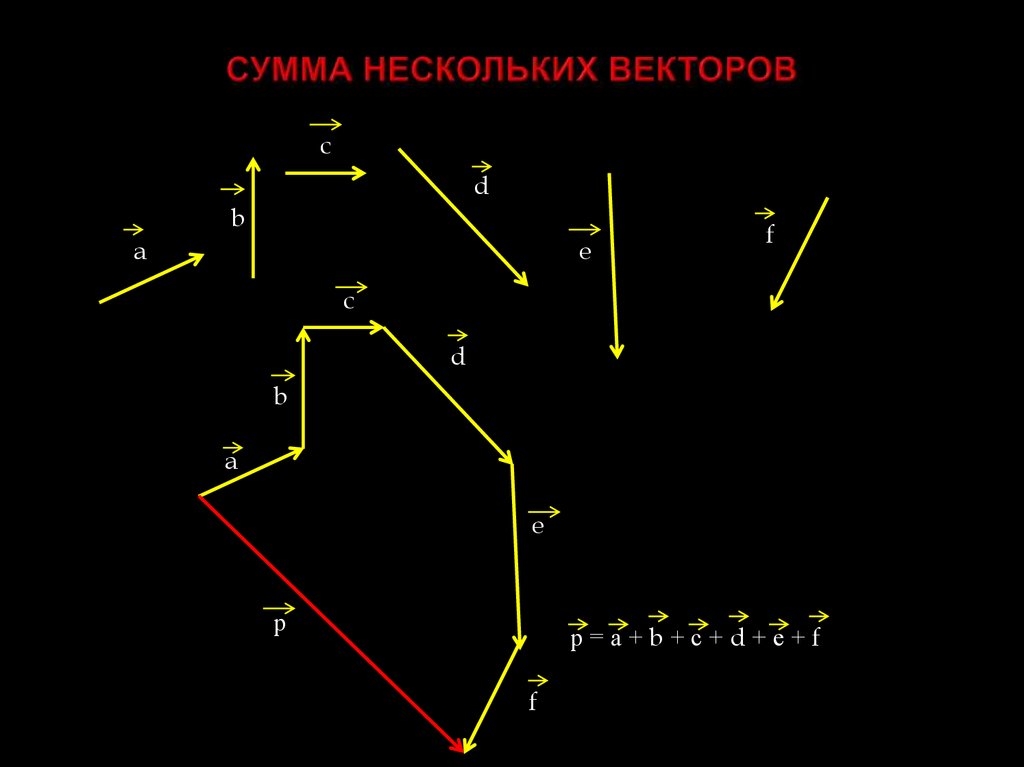


 Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов.
Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов.