Среднеквадратичное значение — frwiki.wiki

Корень средний квадрат из мультимножествя чисел является корнем квадратным из средних арифметических из квадратов этих чисел. Например, стандартное отклонение в генеральной совокупности — это среднеквадратическое значение расстояний от среднего значения. Среднеквадратичное значение больше или равно среднему арифметическому. В серии значений особенно высокое значение по сравнению с другими будет иметь большее влияние на среднеквадратическое значение ряда, чем на среднее арифметическое. Его эквивалентом для стационарного сигнала является среднеквадратичное значение .

Резюме

• 1 Рейтинг
• 2 Определение
• 3 использования
• 4 Среднеквадратичная непрерывность пространственного процесса
• 5 Среднеквадратичная дифференцируемость одномерного процесса
• 6 Ссылки
• 7 Связанная статья

Рейтинг

Пусть конечное семейство чисел. Квадратичное среднее значение х затем отмечено (как в среднем в целом),

Q ( х ), или снова (обозначение в общем пользовании в физике, где ⟨⟩ обозначает среднее арифметическое). {2}.} Мы можем попытаться оценить скорость v, которая, приложенная к тому же количеству частиц, дала бы ту же кинетическую энергию. Эта скорость является среднеквадратическим из всех скоростей.

В области постоянного тока мы обнаруживаем ту же проблему при вычислении эффективного значения электрического тока.

Среднеквадратичная непрерывность пространственного процесса

Определение  —  второй порядок процесс Й на пространственное множества S ⊂ ℝ ^D является непрерывной в среднеквадратичном, если для любой сходящейся последовательности S

сек _п → s, Е ( Х ( ы _л ) — Х ( ы )) ² → 0 .

Характеристика  —  по центру L ² Процесса непрерывно в среднеквадратичной всюду тогда и только тогда его ковариационной непрерывна на диагонали его пространственного набора.

Непрерывность по диагонали означает, что C ( s, s ) непрерывна для всех s в пространственном множестве, где C — ковариация.

Теорема  —  Если внутренний гауссовский процесс в вариограммах гамма удовлетворяют гамма (

ч ) ≤ | log∥ ч ∥ | ^{— (1 + ε)} в окрестности начала координат, то почти наверное непрерывно .

Это справедливо для всех стандартных моделей вариограмм, за исключением модели эффекта самородка.

Теорема  —  присущий процесс является среднеквадратическим непрерывным, если его вариограмма первоначально непрерывно.

Стационарный процесс второго порядка является среднеквадратичным квадрат непрерывным, если его ковариационная непрерывна в нуле.

Среднеквадратичная дифференцируемость одномерного процесса

Определение

 —  пространственный процесс Х на одномерное пространственное множестве S ⊂ ℝ является дифференцируемым в среднеквадратичном в сек, если существует X _с таким образом, чтоLimчас→0Икс(s+час)-Икс(s)часзнак равноИксs в L2{\ displaystyle \ lim _ {h \ to 0} {\ frac {X \ left (s + h \ right) -X \ left (s \ right)} {h}} = X_ {s} {\ text {in }} \ mathbf {L} ^ {2}}.

Свойство  —  Если ковариация С процессом X из L ² центрированного таково, что вторая поперечная производная D ( s, т ) = ^{∂ 2} / _{∂ s ∂ T} C ( s, т ) существует и конечна для всех s = т, то X везде среднеквадратично дифференцируемо, D существует всюду и ковариантность производного процесса равна Cov ( Ẋ ( s ), Ẋ ( t )) = D ( s, t ) .

Производная  —  Поле Х над ℝ является корнем среднеквадратичного дифференцируемым, если вторая производная γ «(0) от вариограммы существует. В этом случае γ ″ существует всюду, а X стационарно с ковариацией γ ″  ; X ( s ) и X ( s ) некоррелированны для всех х, и независимых, если X является гауссовым .

Рекомендации

1. ↑ Среднее квадратичное на изображениях математики — Cnrs
2. ↑ Среднее квадратичное на Educatim. fr

Связанная статья

Стандартное отклонение

Вероятности и статистика индекса проекта

Теория вероятности Теоретические основы Общие принципы Аксиомы вероятностей  · Пространство  вероятностей · Вероятность  · Событие  · Племя · Независимость · Случайная величина · Ожидание · iid-переменные        Сходимость законов Центральная предельная теорема  · большие числа Ло  · лемма Бореля-Кантелли Стохастическое исчисление Случайное блуждание  · Марковская цепь  · Стохастические процессы  · Марковские процессы  · Мартингал  · Броуновское движение  · Стохастическое дифференциальное уравнение Законы вероятности Непрерывные законы Экспоненциальный  · Нормальное распределение · Единый закон · Студент юридического факультета · Закон Фишера · Закон хи-квадрат        Дискретные законы Бернулли  · Бином по Акту · Пуассон по Акту · Геометрическое распределение · Гипергеометрическое распределение      Смесь статистики и вероятностей Доверительный интервал Статистическая теория Описательная статистика Теоретические основы Статистика Персонаж Образец Стандартная ошибка Доверительный интервал Эмпирическая функция распределения Теорема Гливенко-Кантелли Байесовский вывод Линейная регрессия Метод наименьших квадратов Анализ данных Корреляция Картины Таблица сопряженности Полная дизъюнктивная таблица Стол Берта Визуализация данных Гистограмма Гистограмма Диаграмма с областями Круговая диаграмма Древовидная карта Boxplot Облако точек Пузырьковая диаграмма Схема водопада Диаграмма-воронка Диаграмма Кивиат Коррелограмма Лесная графика Ветвисто-листовая диаграмма Тепловая карта Спарклайн Настройки положения Среднее арифметическое Мода Медиана Квантиль Квартиль Дециль Процентиль Параметры дисперсии Сфера Средняя разница Дисперсия Стандартное отклонение Межквартильный размах Коэффициент вариации Настройки формы Коэффициент асимметрии Коэффициент эксцесса Индуктивная статистика Теоретические основы Статистическая гипотеза  · Нулевая гипотеза  · Оценщик  · Статистическая значимость  · Чувствительность и специфичность  · Кривая ROC  · Требуемое количество испытуемых  · Значение p  · Контраст (статистика)  · Статистика теста  · Эффект размера  · Статистическая мощность Параметрические тесты Проверка гипотезы  · Тест Бартлетта  · Тест нормальность  · Тест Фишер равенство двух отклонениях  · Хаусман испытание  · Испытание Андерсон-Дарлинг  · Тест Банерджи  · Тест Дарбина-Уотсон  · Тест Голдфельд и Quandt  · Теста Харка-Бер  · Тест Настроение  · критерий лиллиефорс  · Wald тест  · T-тест для независимых выборок  · T-тест парных выборок  · корреляционный тест Пирсона Непараметрические тесты Тест У Манна-Уитни  · Тест Краскала-Уоллиса  · Точный тест Фишера  · Тест Колмогорова-Смирнова  · Тест Шапиро-Уилка  · Тест Чоу  · Тест МакНемара  · Тест Спирмена  · Тау Кендалл  · Тест Гамма  · Наборы тестов Вальда-Вольфовица  · Медианный тест  · Признаки Тест  · ANOVA Фридмана  · Соответствие Кендалла  · Тест Q Кокрана  · Тест Уилкоксона подписанные ранги  · Тест Саргана Заявление Эконометрика  · Статистическая механика  · Азартные игры  · Биоматематика  · Биостатистика  · Финансовая математика

Середина
Исчерпывающий	Арифметика взвешенный Геометрический взвешенный Арифметико-геометрический Гармонический взвешенный Квадратичный Обобщенный Квазиарифметика по Muirhead
Частичное	Усечено или уменьшено Подвижный или скользкий
Полученные результаты	Арифметико-геометрическое неравенство Неравенство Мюрхеда Лемма Чезаро. Неравенство среднего

<img src=»//fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

где

s² – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Расчет дисперсии в Excel

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

D(A) = 0

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А² раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

D(AX) = А² D(X)

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

D(A + X) = D(X)

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

D(X+Y) = D(X) + D(Y)

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

D(X-Y) = D(X) + D(Y)

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

 

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

=СТАНДОТКЛОН.В()/СРЗНАЧ()

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных. 

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Поделиться в социальных сетях:

среднеквадратических значений

среднеквадратичное значение

Среднеквадратичное значение:

Среднеквадратичное значение функции часто используется в физике и электронике.

За например, мы можем захотеть рассчитать мощность P рассеивается электрическим проводником сопротивлением Ом Ом. Легко сделать расчет, когда постоянный ток I течет по проводнику. Это просто,

Р = I ² Ч

Но что, если ток представляет собой переменную функцию I ( t )? Вот тут-то и появляется среднеквадратичное значение. Можно тривиально показать, что среднеквадратичное значение значение I ( t ) можно заменить на постоянный ток I в приведенном выше уравнении чтобы дать среднюю рассеиваемую мощность:

	( R является постоянным, поэтому мы можем взять его за пределы среднего)
	(по определению RMS)

Мы также можем показать тем же методом

Извлекая из обоих этих уравнений квадратный корень и перемножая их вместе, мы получаем уравнение

Однако важно подчеркнуть, что это основано на предположении, что напряжение и ток пропорциональны (то есть нагрузка резистивная) и НЕ верно в общем случае (дополнительную информацию см.

в разделе «Питание переменного тока»).

В общем случае переменного тока, когда I ( t ) представляет собой синусоидальный ток, что приблизительно соответствует мощности сети, среднеквадратичное значение легко вычислить из приведенного выше уравнения (2). Результат:

где I _p пик амплитуда.

Среднеквадратичное значение можно рассчитать с помощью уравнения (2) для сигнала любой формы, для например аудио- или радиосигнал. Это позволяет вычислить среднюю мощность доставлено в указанную загрузку. По этой причине указанные напряжения для питания розеток (например, 110 В или 240 В) почти всегда указаны в среднеквадратичных значениях, а не пиковые значения.

В аудиотехнике среднюю мощность часто (ошибочно) называют RMS. сила. Вероятно, это связано с тем, что его можно получить из среднеквадратичного значения напряжения или среднеквадратичного значения. Текущий. Кроме того, поскольку среднеквадратичное значение подразумевает некоторую форму усреднения, выражения такие как «пиковая среднеквадратичная мощность», иногда используемая в рекламе аудиоусилителей, бессмысленны.

В химии среднеквадратичная скорость

определяется как квадрат корень из квадрата средней скорости молекул в газе. Среднеквадратическая скорость газа рассчитывается по следующему уравнению:

где R представляет постоянную идеального газа (в данном случае 8,314 Дж/(моль⋅К)), Тл температура газа в кельвинах, а M равно молярная масса соединения в килограммах на моль.

 

Ссылка: Википедия, свободная энциклопедия

Важные темы физики: среднеквадратичное значение

Введение:

Среднеквадратичное значение: Среднеквадратичное значение — это сокращение от Root Mean Square. Среднеквадратичное значение напряжения обычно выражается в виде среднего квадрата мгновенных значений сигнала напряжения. Среднеквадратичное значение — это другое название среднеквадратичного значения.

Интеграл квадратов среднеквадратичного значения в течение цикла также может использоваться для определения среднеквадратичного значения напряжения для постоянно колеблющегося напряжения. Как и в случае сигнала переменного тока, решающее значение имеет среднеквадратичное значение. Мгновенное значение сигнала переменного тока постоянно изменяется во времени. В отличие от сигнала постоянного тока, который очень устойчив. В результате непосредственное значение напряжения нельзя использовать непосредственно в расчете.

Поскольку среднеквадратичное значение показывает количество мощности переменного тока, потребляемого резистором, которое идентично мощности, потребляемой источником постоянного тока, оно также называется эквивалентным напряжением постоянного тока.

Среднеквадратичное значение (RMS) является мерой величины изменяющейся величины. В цепи переменного тока квадрат среднего значения используется для обозначения среднего тока или напряжения. Пиковое напряжение и ток, превышающие квадратный корень из двух, представляют собой среднеквадратичное значение напряжения и тока (для синусоидальных систем). В цепи переменного тока средняя мощность прямо пропорциональна произведению среднеквадратичного напряжения и среднеквадратичного тока.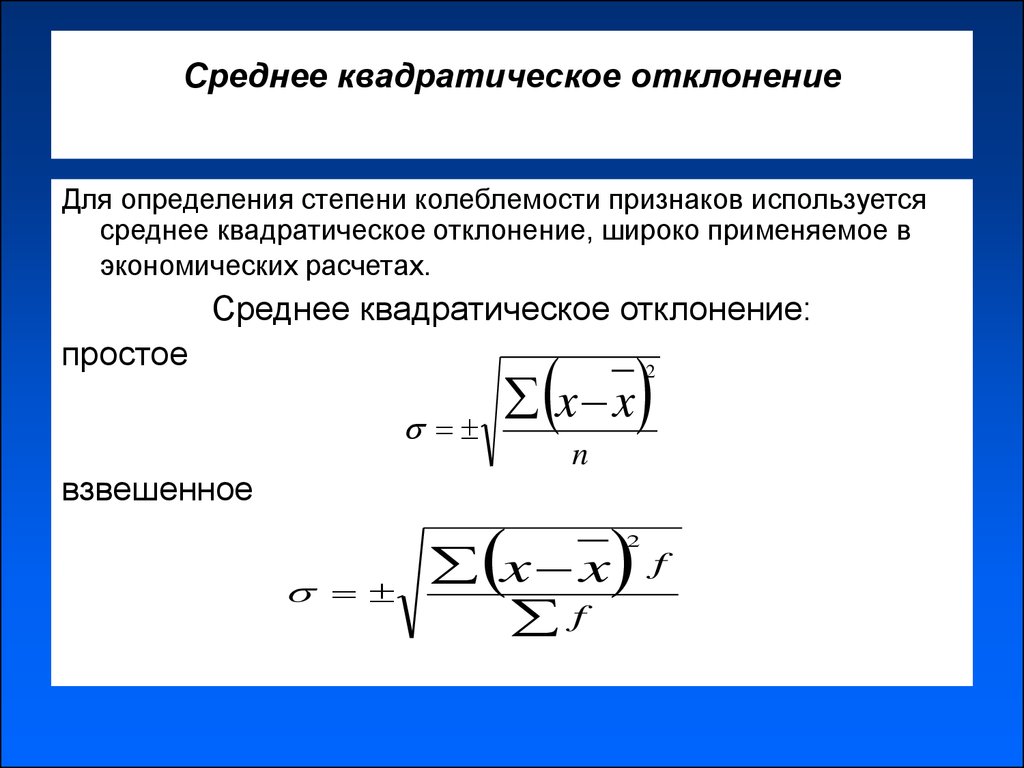 Сигналы тока и напряжения могут быть представлены как постоянными, так и переменными сигналами, хотя и разными способами. Положительные и отрицательные циклы чередуются в формах сигналов переменного тока. Напряжение постоянного тока — это просто фиксированное значение. Их трудно сравнивать из-за этого различия. Однако среднеквадратичное значение дает нам ориентир, с которым мы можем сравнить сумму.

Краткое описание:

Что такое среднеквадратичное напряжение и как его рассчитать?

Среднеквадратичное значение оценивается только для изменяющихся во времени сигналов, в которых величина величины изменяется во времени. Поскольку форма сигнала постоянного тока имеет постоянное значение в каждый момент времени, мы не можем найти среднеквадратичное значение.

Среднеквадратичное значение можно рассчитать двумя способами.

• Аналитический метод
• Графический метод

Графический подход:

Для получения среднеквадратичного значения в этом подходе мы используем форму волны. Когда сигнал не является симметричным или синусоидальным, более полезен графический метод. Количество точек, извлеченных из сигнала, определяет точность метода. Низкая точность обусловлена ​​малым количеством точек, а высокая точность обусловлена ​​большим количеством точек. Среднеквадратичное значение представляет собой квадратный корень из квадрата среднего значения функции.

Аналитические методы:

Среднеквадратичное значение напряжения можно оценить таким образом, используя математическую процедуру. Для чисто синусоидального сигнала этот подход является более точным.

Важные понятия:

Подстановка текущего среднеквадратичного значения:

Среднеквадратичное значение мгновенной приведенной стоимости известно как среднеквадратичное значение. Постоянный ток, протекающий через препятствие, дает RMS преимущество вращающегося тока. AC имеет оценку RMS, которая выше, чем обычно. Область, охваченную полупериодом, можно использовать для определения среднеквадратичного значения синусоидальной волны тока. Это остается постоянным для всех волн, включая синусоидальные, несинусоидальные, сбалансированные и перевернутые волны. Он упоминается как Irms или Iv.

Функциональное значение синусоидальной формы волны, которая производит такой же эффект нагрева, как и аналогичный источник постоянного тока, называется среднеквадратичным значением. В результате среднеквадратичное значение переменного тока вычисляется путем деления максимального значения тока на квадратный корень из двух.

I _{R MS} = I _M /√2

«Корневые квадраты»-это аббревация для «корневого». «Количество мощности переменного тока, которое вызывает тот же эффект нагрева, что и сравнимая мощность постоянного тока» или что-то в этом роде, является наиболее распространенным определением, но среднеквадратичное значение — это нечто большее.

Чем больше тепла поглощается, тем выше средние значения тока при одинаковых среднеквадратичных значениях; влияние среднего значения тока зависит от среднеквадратичных значений. Очень важно помнить, что то, что ток представлен как среднее или среднеквадратичное значение, не означает, что одно и то же среднее или среднеквадратичное значение производит одинаковое количество тепла.

Во избежание недоразумений следует поднять еще один вопрос: разница между средним и среднеквадратичным значением знака (например, тока) и, как следствие, разделение сигнала на постоянную и переменную составляющие. Текущий сигнал не описывается суммой средних и среднеквадратичных значений компонентов постоянного и переменного тока соответственно.

Поскольку напряжение и ток в системе постоянного тока постоянны, определить их величину не составляет труда. Однако в системе переменного тока переменное напряжение меняется от момента к моменту, что затрудняет определение величины.

Понятие среднеквадратичного значения было разработано для передачи величин переменного тока в простой и понятной форме. Они также могут быть выражены как пиковое или среднее значение; однако эти значения не отражают эффективность количества AC.

Среднеквадратичное значение переменного тока — это величина постоянного тока, которая создает такое же тепловое воздействие при протекании через одно и то же сопротивление в течение того же периода времени.

При работе с переменными напряжениями (или токами) мы должны учитывать, как описать величину напряжения или сигнала. Одним из простых методов было бы использование пиковых значений сигнала.

Значение переменного тока в экзамене NEET:

Физическая наука занимается исследованием оценки RMS. Эти пункты покрываются тестом NEET. Чтение курса физики NCERT, которое было сделано специально для теста NEET, проходит внутри и снаружи. Посещая бесконечный учебный сайт, дублеры могут узнать о таких идеях, а также о выводе различных уравнений, связанных с ними.

Кроме того, в поручениях части есть несколько проблем, которые помогут вам попрактиковаться и справиться с приложением субъекта. Дублеры также могут сосредоточиться на материалах для чтения по физике от разных распространителей.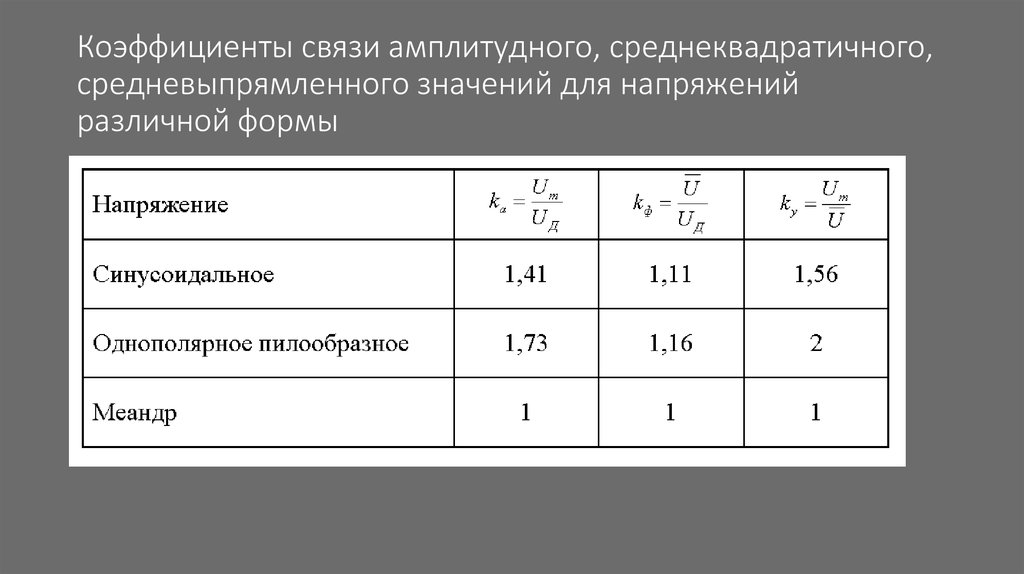

Boundless Learn предлагает широкий спектр ресурсов, которые помогут дублерам в изучении каждого предмета в организованном порядке. Дублеры также могут узнать больше о предмете, используя предоставленные материалы обзора.

Доступны наборы тестовых вопросов, которые можно использовать для репетиции дополнительных вопросов и дальнейшего планирования тестирования. Любой дублер может получить доступ к этим активам, зарегистрировавшись на сайте, что совершенно бесплатно. Дополнительные руководства по обзору также можно загрузить бесплатно.

Читайте также: Важная тема физики: Закон Фарадея

Часто задаваемые вопросы (часто задаваемые вопросы):

Вопрос 1: Каково определение пикового значения?

Ответ: Пиковое значение определяется как максимальное значение, полученное переменной величиной за один цикл, известное как Пиковое значение.

Вопрос 2: Что означает указание среднего значения?

Ответ: Среднее значение берется как среднее всех мгновенных значений переменного тока и напряжения за один полный цикл.