Среднее квадратическое значение: Среднее квадратическое — Википедия – Среднее квадратическое | Расчет онлайн, определение среднего квадратического значения, формула — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Среднее квадратическое — Википедия

Материал из Википедии — свободной энциклопедии

Среднее квадратическое (квадратичное)^[1] — число s{\displaystyle s}, равное квадратному корню из среднего арифметического квадратов данных чисел a1,a2,…,an{\displaystyle a_{1},a_{2},…,a_{n}}:

s=a12+a22+…+an2n{\displaystyle s={\sqrt {\frac {a_{1}^{2}+a_{2}^{2}+\ldots +a_{n}^{2}}{n}}}}

Среднее квадратическое — частный случай среднего степенного и потому подчиняется неравенству о средних. В частности, для любых чисел оно не меньше среднего арифметического:

a1+a2+…+ann⩽a12+a22+…+an2n{\displaystyle {\frac {a_{1}+a_{2}+\ldots +a_{n}}{n}}\leqslant {\sqrt {\frac {a_{1}^{2}+a_{2}^{2}+\ldots +a_{n}^{2}}{n}}}}

Среднее квадратическое находит широкое применение во многих науках. В частности, через него определяется основное понятие теории вероятностей и математической статистики — дисперсия (квадратный корень из которой называется среднеквадратическим отклонением). Также тесно связан с этим понятием метод наименьших квадратов, имеющий общенаучное значение.

Среднее квадратическое набора неотрицательных чисел лежит между минимальным и максимальным числами из этого набора.

Среднее квадратическое — Википедия. Что такое Среднее квадратическое

Материал из Википедии — свободной энциклопедии

s=a12+a22+…+an2n{\displaystyle s={\sqrt {\frac {a_{1}^{2}+a_{2}^{2}+\ldots +a_{n}^{2}}{n}}}}

a1+a2+…+ann⩽a12+a22+…+an2n{\displaystyle {\frac {a_{1}+a_{2}+\ldots +a_{n}}{n}}\leqslant {\sqrt {\frac {a_{1}^{2}+a_{2}^{2}+\ldots +a_{n}^{2}}{n}}}}

Примечания

Свойства

Среднее квадратическое набора неотрицательных чисел лежит между минимальным и максимальным числами из этого набора.

Средняя квадратическая

Используется в тех случаях, когда при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин.

Главная сфера её использования – измерение степени колеблемости индивидуальных значений признака относительно средней арифметической (среднее квадратическое отклонение). Кроме этого, средняя квадратическая применяется в тех случаях, когда необходимо вычислить средний величину признака, выраженного в квадратных или кубических единицах измерения (при вычислении средней величины квадратных участков, средних диаметров труб, стволов и т. д.).

Средняя квадратическая рассчитывается в двух формах:

— как простая

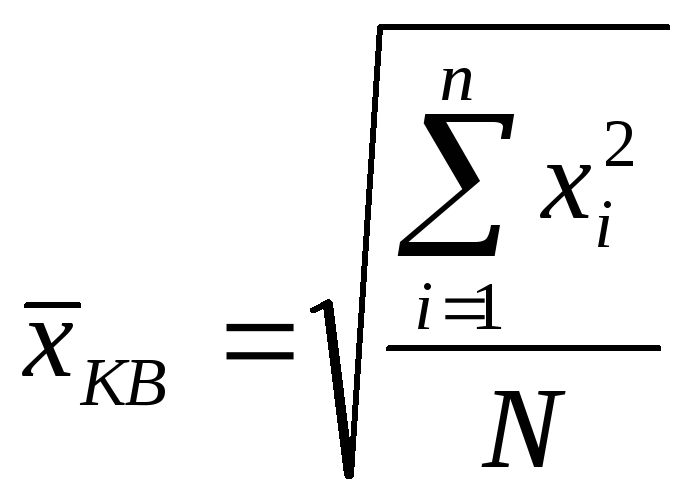(4.21)

как взвешенная

(4.22)

Все степенные средние различаются между собой значениями показателя степени.При этом, чем выше показатель степени, тем большеколичественное значение среднего показателя:

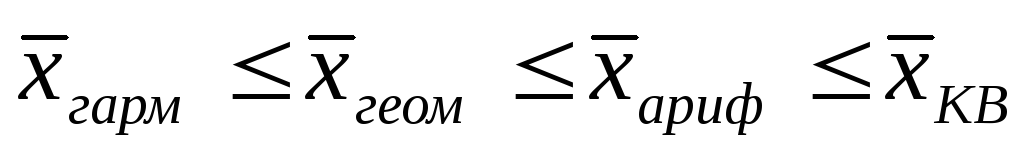(4.23)

Это свойство степенных средних называется свойством мажорантности средних.

Таким образом, выбор вида среднего показателя оказывает существенное влияние на его численную величину. Выбор вида средней определяется в каждом отдельном случае путем анализа исследуемой совокупности,

изучения содержания явления. Степенная средняя выбрана правильно, если на всех этапах вычислений не меняется её логическая формула, т.е. реально сохраняется социально-экономическое содержание усредняемого признака.

Особый вид средних показателей – структурные средние. Они используются при изучении внутреннего строения рядов распределения значений признака. К ним относятся мода и медиана.

Мода и медиана характеризуют значение признака у статистической единицы, занимающей определенное положение в вариационном ряду.

Мода (Mo

) — наиболее часто встречаемое значение признака в совокупности. Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и др.

Медиана (Me) — значение признака у статистической единицы, стоящей в середине ранжированного ряда и делящей совокупность на две равные по численности части.

Для дискретных вариационных рядов Mo и Me выбираются в соответствии с определениями: мода — как значение признака с наибольшей частотой\ n_i ; положение медианы при нечетном объеме совокупности определяется ее номером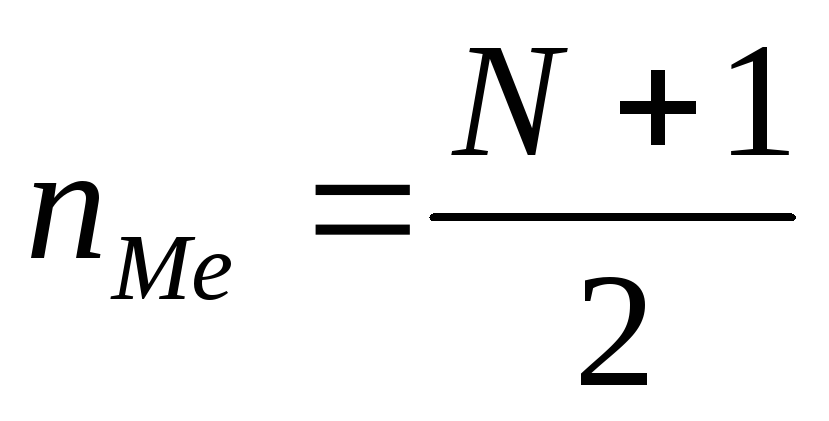

, гдеN – объем статистической совокупности. При четном объеме ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

Медиану используют как наиболее надежный показатель типичного значения неоднородной совокупности, так как она нечувствительна к крайним значениям признака, которые могут значительно отличаться от основного массива его значений. Кроме этого, медиана находит практическое применение вследствие особого математического свойства: .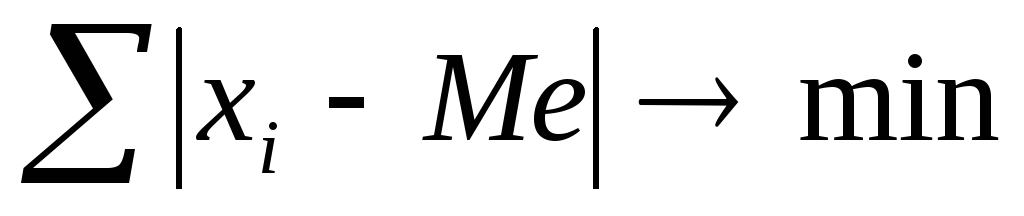

Рассмотрим определение моды и медианы на следующем

примере:

Имеется ряд распределения рабочих участка по уровню квалификации. Данные приведены в таблице 4.4.

Таблица 4.4 — Распределения рабочих участка по уровню квалификации

№ группы	Разряд рабочих	Число рабочих	Накопленная частота
1	1	3	3
2	2	5	8
3	3	9	17
4	4	14	31
5	5	10	41
6	6	9	50
Всего	—	50	—

Мода выбирается по максимальному значению частоты: при n_max = 14, Mo = 4, т.е. чаще всего встречается 4-ый разряд. Для нахождения медианы Me определяются центральные единицы (N +1)/2 . Это 25 и 26-ая единицы. По накопленным частотам определяется группа, в которую попадают эти единицы. Это 4-ая группа, в которой значение признака равно 4. Таким образом,

Me = 4, это означает, что у половины рабочих разряд ниже 4-го, а у другой – выше четвертого.

В интервальном ряду значения Mo и Me вычисляются более сложным путем.

Мода определяется следующим образом:

• По максимальному значению частоты определяется интервал, в котором находится значение моды. Он называется модальным.

• Внутри модального интервала значение моды вычисляется по формуле:

(4.24)

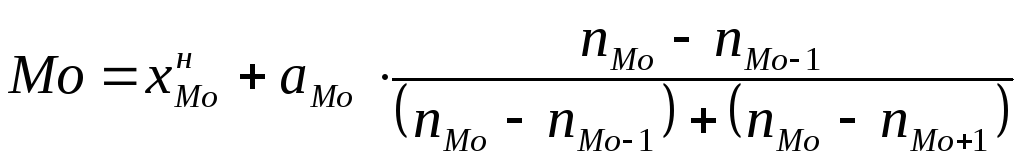
где 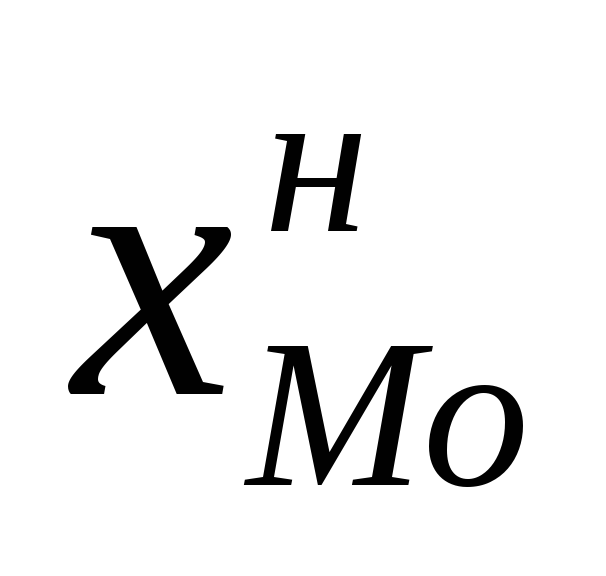— нижняя граница модального интервала;

a_Мо — ширина модального интервала;

n_Мо , n_Мо-1, n_Мо+1 — соответственно частоты модального, предмодального (предшествующего модальному) и постмодального (следующего за модальным) интервалов.

Для расчета медианы в интервальных рядах используется следующий подход:

• По накопленным частотам находится медианный интервал.

Медианным называется интервал, содержащий центральную единицу.

• Внутри медианного интервала значение Me определяется по формуле:

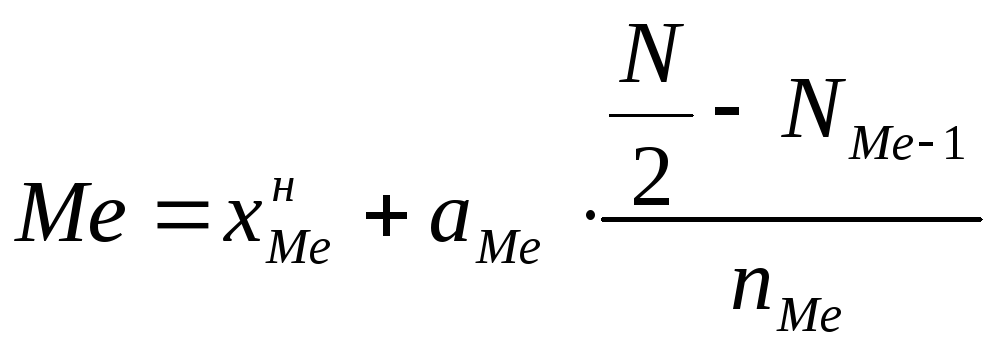(4.25)

где 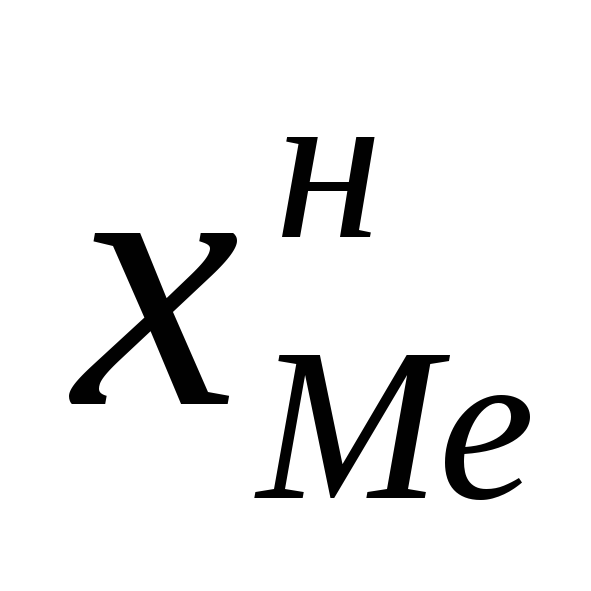— нижняя граница медианного интервала;

a_Ме -ширина медианного интервала;

N – объем статистической совокупности;

N _Ме-1— накопленная частота предмедианного интервала;

n_Ме — частота медианного интервала.

Расчет моды и медианы для интервального ряда распределения рассмотрим на примере ряда распределения рабочих по стажу (табл. 4.5).

Таблица 4.5 — Распределение рабочих участка по стажу

№ группы	Интервал		а_i	n i	N_i
№ группы			а_i	n i	N_i
1	0	4	4	6	6
2	4	8	4	8	14
3	8	12	4	11	25
4	12	16	4	13	28
5	16	20	4	6	44
6	20	24	4	4	48
7	24	28	4	2	50
Всего	0	28	28	50	—

Расчет Mo:

• Максимальная частота n_max = 13, она соответствует четвертой группе, следовательно, модальным является интервал с границами 12 – 16 лет.

• Моду рассчитаем по формуле:

Чаще всего встречаются рабочие со стажем работы около 13 лет.

Мода не находится в середине модального интервала, она смещена к его нижней границе, связано это со структурой данного ряда распределения (частота предмодального интервала значительно больше частоты постмодального интервала).

Расчет медианы:

• По графе накопленных частот определяется медианный интервал. Он содержит 25 и 26-ую статистические единицы, которые находятся в разных группах – в 3-ей и 4-ой. Для нахождения Me можно использовать любую из них. Расчет проведем по 3-ей группе:

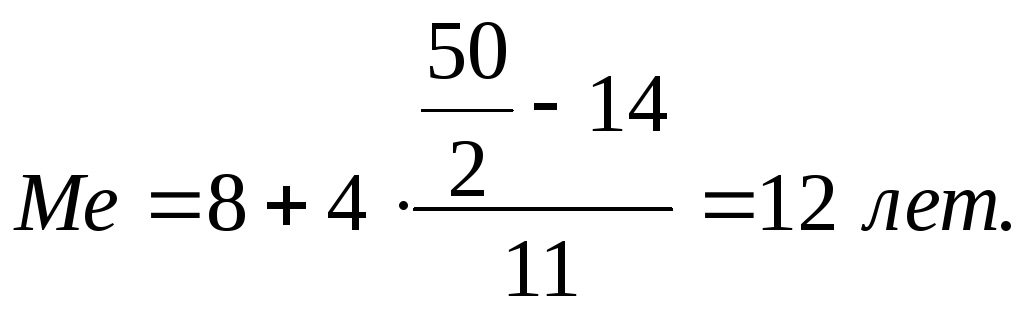
Такое же значение Me можно получить при её расчете по 4-ой группе:

При сдвоенном центре Me всегда находится на стыке интервалов, содержащих центральные единицы. Вычисленное значениеMe показывает, что у первых 25 рабочих стаж работы – менее 12 лет, а у оставшихся 25-ти, следовательно, — более 12 лет.

Моду можно определить графически по полигону распределения в дискретных рядах, по гистограмме распределения – в интервальных, а медиану — по кумуляте.

Для нахождения моды в интервальном ряду правую вершину модального прямоугольника нужно соединить с правым верхним углом предыдущего прямоугольника, а левую вершину – с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.

Для определение медианы высоту наибольшей ординаты кумуляты, соответствующей общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.

Кроме Mo иMe в вариантных рядах могут быть определены и другие структурные характеристики – квантили. Квантили предназначены для более глубокого изучения структуры ряда распределения.Квантиль – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности. Различают следующие виды квантилей:

— квартили – значения признака, делящие упорядоченную совокупность на 4 равные части;

— децили – значения признака, делящие совокупность на 10 равных частей;

— перцентели — значения признака, делящие совокупность на 100 равных частей.

Таким образом, для характеристики положения центра ряда распределения можно использовать 3 показателя: среднее значениепризнака,мода, медиана.

При выборе вида и формы конкретного показателя центра распределения необходимо исходить из следующих рекомендаций:

— для устойчивых социально-экономических процессов в качестве показателя центра используют среднюю арифметическую. Такие процессы характеризуются симметричными распределениями, в которых

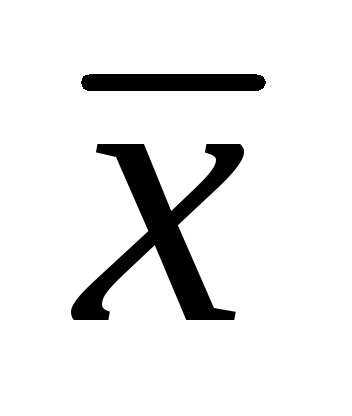= Me = Mo;

— для неустойчивых процессов положение центра распределения характеризуется с помощью Mo илиMe. Для асимметричных процессов предпочтительной характеристикой центра распределения является медиана, поскольку она занимает положение между средней арифметической и модой.

Среднее квадратичное — это… Что такое Среднее квадратичное?

Среднее квадратичное

Wikimedia Foundation. 2010.

Среднее квадратическое отклонение
Среднее квадратичное отклонение

Смотреть что такое «Среднее квадратичное» в других словарях:

СРЕДНЕЕ, КВАДРАТИЧНОЕ — Среднее арифметическое набора квадратов отклонений от среднего; то есть варианса. Корень из среднего квадратичного – квадратный корень из среднего квадратичного или стандартное отклонение … Толковый словарь по психологии
среднее квадратичное значение — kvadratinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, lygus kvadratinei šakniai iš tam tikro dydžio verčių kvadratų sumos, padalytos iš tų verčių skaičiaus. atitikmenys: angl. mean effective value; root mean… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
среднее квадратичное расстояние — vidutinis kvadratinis nuotolis statusas T sritis fizika atitikmenys: angl. root mean square distance vok. mittlerer quadratischer Abstand, m rus. среднее квадратичное расстояние, n; среднеквадратичное расстояние, n pranc. distance moyenne… … Fizikos terminų žodynas
Среднее квадратичное отклонение — … Википедия
среднее квадратичное отклонение — То же, что и стандартное отклонение. Примечание. Говорят также «среднеквадратичное отклонение». Кроме того, в том же смысле используют термины квадратичная ошибка, средняя квадратичная ошибка … Словарь социологической статистики
СРЕДНЕЕ ЗНАЧЕНИЕ — числовая характеристика группы чисел или функций. Для группы чисел наиб. употребительными С. з. являются: арифметическое среднее, гармоническое среднее, геометрическое среднее, квадратичное среднее. С. з. случайной величины то же, что… … Естествознание. Энциклопедический словарь
Квадратичное среднее — Среднее квадратическое (квадратичное) число s, равное квадратному корню из среднего арифметического квадратов данных неотрицательных чисел a1,a2,…,an: Среднее квадратическое частный случай среднего степенного и потому подчиняется неравенству… … Википедия
КВАДРАТИЧНОЕ СРЕДНЕЕ — величина (s), равная корню квадратному из среднего арифметического квадратов данных величин () … Большой Энциклопедический словарь
Среднее квадратическое — (квадратичное) число , равное квадратному корню из среднего арифметического квадратов данных чисел : Среднее квадратическое частный случай среднего степенного и потому подчиняется неравенству о средних. В частности, для любых чисел… … Википедия
СРЕДНЕЕ — (1) арифметическое числовая характеристика совокупности чисел, которая получается в результате сложения данных величин, напр. а и b и деления суммы на число этих величин, т.е , для n величин a1, a2 ,… an среднее арифметическое,(2) геометрическое … Большая политехническая энциклопедия

СРЕДНЕЕ КВАДРАТИЧЕСКОЕ — это… Что такое СРЕДНЕЕ КВАДРАТИЧЕСКОЕ?

СРЕДНЕЕ КВАДРАТИЧЕСКОЕ: — англ. mean, quadratic; нем. Mittel, quadratisches. Измерение центральной тенденции ряда данных, представляющее собой корень квадратный из среднего арифметического квадратов величин ряда.

СРЕДНЕЕ ГАРМОНИЧЕСКОЕ
СРЕДНИЙ ВОЗРАСТ

Смотреть что такое «СРЕДНЕЕ КВАДРАТИЧЕСКОЕ» в других словарях:

Среднее квадратическое — (квадратичное) число , равное квадратному корню из среднего арифметического квадратов данных чисел : Среднее квадратическое частный случай среднего степенного и потому подчиняется неравенству о средних. В частности, для любых чисел… … Википедия
СРЕДНЕЕ КВАДРАТИЧЕСКОЕ — англ. mean, quadratic; нем. Mittel, quadratisches. Измерение центральной тенденции ряда данных, представляющее собой корень квадратный из среднего арифметического квадратов величин ряда … Толковый словарь по социологии
среднее квадратическое отклонение — 2.7. среднее квадратическое отклонение (далее СКО) нестабильности метрологической характеристики эталона: Показатель нестабильности метрологической характеристики эталона, отражающий рассеяние нестабильности в группе эталонов одного типа или в… … Словарь-справочник терминов нормативно-технической документации
Среднее квадратическое значение колеблющейся величины — 14. Среднее квадратическое значение колеблющейся величины Квадратный корень из среднего арифметического или среднего интегрального значения квадрата колеблющейся величины в рассматриваемом интервале времени Источник … Словарь-справочник терминов нормативно-технической документации
среднее квадратическое отклонение воспроизводимости — 3.11 среднее квадратическое отклонение воспроизводимости: Среднее квадратическое отклонение результатов измерений, полученных в условиях воспроизводимости. Источник … Словарь-справочник терминов нормативно-технической документации
среднее квадратическое (стандартное) отклонение воспроизводимости — 3.17 среднее квадратическое (стандартное) отклонение воспроизводимости: Среднее квадратическое отклонение результатов анализа, полученных в условиях воспроизводимости (с учетом [1]). Источник … Словарь-справочник терминов нормативно-технической документации
среднее квадратическое (стандартное) отклонение повторяемости — 3.15 среднее квадратическое (стандартное) отклонение повторяемости: Среднее квадратическое отклонение результатов единичного анализа, полученных по методике в условиях повторяемости (с учетом [1]). Источник … Словарь-справочник терминов нормативно-технической документации
среднее квадратическое значение спектральной (-го) полосы (интервала), — 3.10 среднее квадратическое значение спектральной ( го) полосы (интервала), Dlrms: Среднее квадратическое значение Dlrms определяют по формуле где λi длина волны i й спектральной линии или i й моды излучения; Ii относительное значение мощности… … Словарь-справочник терминов нормативно-технической документации
Среднее квадратическое напряжение шума ФППЗ — 42. Среднее квадратическое напряжение шума ФППЗ Среднее квадратическое значение временной флюктуации выходного или темнового сигнала фоточувствительного поля ФППЗ или его части, в том числе одного фоточувствительного элемента, в заданной полосе… … Словарь-справочник терминов нормативно-технической документации
среднее квадратическое отклонение воспроизводимости, СКО воспроизводимости — 3.15 среднее квадратическое отклонение воспроизводимости, СКО воспроизводимости: Среднее квадратическое отклонение результатов анализа, полученных в условиях воспроизводимости (ГОСТ Р ИСО 5725 1). Источник … Словарь-справочник терминов нормативно-технической документации

18. Среднее квадратическое отклонение, методика расчета, значение.

Приближенный метод оценки колеблемости вариационного ряда — определение лимита и амплитуды, однако не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного признака в пределах вариационного ряда является среднее квадратическое отклонение (σ — сигма). Чем больше среднее квадратическое отклонение, тем степень колеблемости данного ряда выше.

Методика расчета среднего квадратического отклонения включает следующие этапы:

1. Находят среднюю арифметическую величину (Μ).

2. Определяют отклонения отдельных вариант от средней арифметической (d=V-M). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех отклонений равняется нулю.

3. Возводят каждое отклонение в квадрат d².

4. Перемножают квадраты отклонений на соответствующие частоты d²*p.

5. Находят сумму произведений ( d²*p)

6. Вычисляют среднее квадратическое отклонение по формуле:

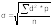при n больше 30, или 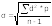при n меньше либо равно 30, где n — число всех вариант.

Значение среднего квадратичного отклонения:

1. Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше.

2. Среднее квадратичное отклонение используется для сравнительной оценки степени соответствия средней арифметической величины тому вариационному ряду, для которого она вычислена.

Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм.

Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат — частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями.

Установлено, что при нормальном распределении признака:

— 68,3% значений вариант находится в пределах М1

— 95,5% значений вариант находится в пределах М2

— 99,7% значений вариант находится в пределах М3

3. Среднее квадратическое отлонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М1 обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1 указывает на отклонение изучаемого параметра от нормы.

4. В медицине правило трех сигм применяется в педиатрии для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды

5. Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины.

Величина среднего квадратического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратическое отклонение — именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv), представляющий собой относительную величину: процентное отношение среднего квадратического отклонения к средней арифметической.

Коэффициент вариации вычисляется по формуле:

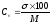
Чем выше коэффициент вариации, тем большая изменчивость данного ряда. Считают, что коэффициент вариации свыше 30 % свидетельствует о качественной неоднородности совокупности.

Как найти среднеквадратическое отклонение

В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом 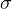$\sigma$ (греческая буква «сигма»).

Формула для расчета 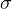$\sigma$ довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

Определите среднее (простое среднее арифметическое ряда значений).
Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Порода собаки	Рост в миллиметрах
Ротвейлер	600
Бульдог	470
Такса	170
Пудель	430
Мопс	300

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее 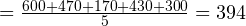$=\frac{600+470+170+430+300}{5} = 394$ мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить отклонение роста каждой из собак от среднего:

$\begin{array}{l} 1: 600-394 = 206 \\ 2: 470-394 = 76 \\ 3: 170-394 = -224\\ 4: 430-394 = 36\\ 5: 300-394 = -94 \end{array}$

Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Дисперсия 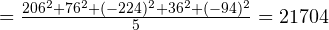$= \frac{206^2+76^2+(-224)^2+36^2+(-94)^2}{5} = 21704$ мм².

Таким образом, дисперсия составляет 21704 мм².

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

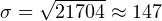$\sigma = \sqrt{21704} \approx 147$ мм (округлено до ближайшего целого значения в мм).

Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть 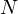значений, то:

Когда мы имеем дело с генеральной совокупностью при вычислении дисперсии, мы делим на (как и было сделано в рассмотренном нами примере).
Когда мы имеем дело с выборкой, при вычислении дисперсии делим на .

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

Дисперсия выборки = 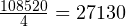$\frac{108520}{4}=27130$ мм².

При этом стандартное отклонение по выборке равно 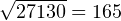$\sqrt{27130} = 165$ мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Примечание. Почему именно квадраты разностей?

Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:

$\frac{4+4-4-4}{4}=0$ .

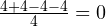Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?

$\frac{4+4+$ .

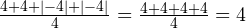На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:

$\frac{7+1+$ .

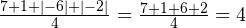Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.

А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).

Для первого примера получится:

$\sqrt{\frac{4^2+4^2+(-4)^2+(-4)^2}{4}}=4$ .

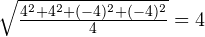Для второго примера получится:

$\sqrt{\frac{7^2+1^2+(-6)^2+(-2)^2}{4}}=4.74$ .

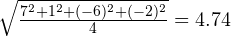Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.

Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.

И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.

О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич
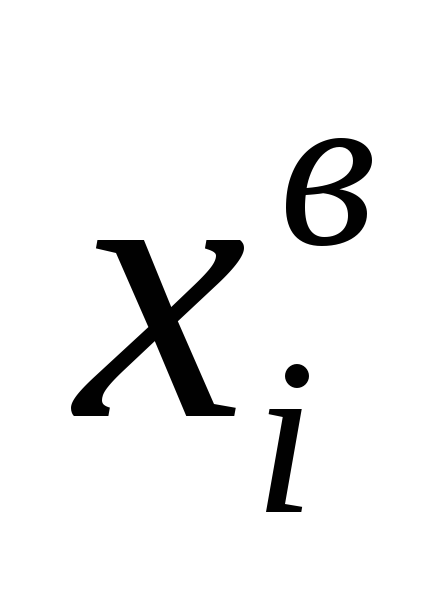
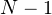