Проектирование векторов на оси | LAMPA

Проектирование вектора на ось, когда задан угол между вектором и осью

Очень часто (а вернее — почти всегда) бывает так, что задан угол между вектором и осью, а также длина вектора, а на оси нет никаких обозначений координат. Тогда проекцию вектора ищут с помощью косинуса или синуса. Рассмотрим все на конкретном примере.

Пусть у нас есть вектор a⃗\vec{a}a⃗.

Из его начала проведем нужные нам оси XXX и YYY, на которые будем проектировать наш вектор.

Из конца вектора опускаем перпендикуляры на оси XXX и YYY.

Получается прямоугольник. Стороны этого прямоугольника и есть проекции вектора a⃗\vec{a}a⃗: axa_{x}ax​ и aya_{y}ay​. 

Видно, что у нас получился прямоугольный треугольник.

Его стороны как раз проекции нашего вектора. Наверняка вы помните (а тем, кто не помнит, я напоминаю), что в прямоугольном треугольнике

cosα=прилежащий катетгипотенуза\cos \alpha=\frac{\text{прилежащий катет}}{\text{гипотенуза}}cosα=гипотенузаприлежащий катет​

sinα=противолежащий катетгипотенуза\sin \alpha=\frac{\text{противолежащий катет}}{\text{гипотенуза}}sinα=гипотенузапротиволежащий катет​.

В нашем треугольнике то же самое:

cosα=axa\cos \alpha=\frac{a_{x}}{a}cosα=aax​​

sinα=aya\sin \alpha = \frac{a_{y}}{a}sinα=aay​​.

Или:

ax=a⋅cosαa_{x}=a\cdot \cos \alphaax​=a⋅cosα;

ay=a⋅sinαa_{y}=a\cdot \sin \alphaay​=a⋅sinα.

Итак:

Проекция на прилежащую ось — это умножение на косинус.
Проекция на противолежащую ось — это умножение на синус.

Проекция вектора на ось (Лекция №16)

Пусть в пространстве даны два вектора и . Отложим от произвольной точки O векторы и . Углом между векторами и называется наименьший из углов . Обозначается .

Рассмотрим ось l и отложим на ней единичный вектор (т.е. вектор, длина которого равна единице).

Под углом между вектором и осью l понимают угол между векторами и .

Итак, пусть l – некоторая ось и – вектор.

Обозначим через A₁ и B₁ проекции на ось lсоответственно точек A и B. Предположим, что A₁ имеет координату x₁, а B₁ – координату x₂ на оси l.

Тогда проекцией вектора на ось l называется разность x₁ – x₂ между координатами проекций конца и начала вектора на эту ось.

Проекцию вектора на ось

l будем обозначать .

Ясно, что если угол между вектором и осью l острый, то x₂> x₁, и проекция x₂ – x₁> 0; если этот угол тупой, то x₂< x₁ и проекция x₂ – x₁< 0. Наконец, если вектор перпендикулярен оси l, то x₂= x₁ и x₂– x₁=0.

Таким образом, проекция вектора на ось l – это длина отрезка A₁B₁, взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр.

Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор.

Рассмотрим некоторые основные свойства проекций.

1. Проеция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью:

   Доказательство. Ясно, что проекция вектора не изменится при его параллельном переносе, поэтому достаточно рассмотреть случай, когда начало вектора совпадает с началом отсчёта O оси l. Так как координата проекции начала равна нулю, то обозначим .

   1. Если угол φ острый, то из прямоугольного получаем . Откуда или
   2. Если угол φ тупой, то x< 0, . Тогда из или . Т.е. .

2. Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось: .

   Доказательство. Пусть . Обозначим через x₁, x₂ и x₃ координаты проекций A₁, B₁, C₁ на ось l точек A, B и C. Тогда . Но .

   Это свойство можно обобщить на случай любого числа слагаемых.

3. Если вектор умножается на число λ, то его проекция на ось также умножается на это число:
   .

   Доказательство. Пусть угол между вектором и осью .

   Если λ > 0, то вектор имеет то же направление, что и , и составляет с осью такой же угол .

   При λ > 0 .

   Если же λ < 0, то и имеют противоположные направления и вектор составляет с осью угол π – φ и .

   Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось.

ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ

Рассмотрим несколько векторов .

Линейной комбинацией данных векторов называется любой вектор вида , где — некоторые числа. Числа называются коэффициентами линейной комбинации. Говорят также, что в этом случае линейно выражается через данные векторы , т.е. получается из них с помощью линейных действий.

Например, если даны три вектора то в качестве их линейной комбинации можно рассматривать векторы:

Если вектор представлен как линейная комбинация каких-то векторов, то говорят, что он разложен по этим векторам.

Векторы называются линейно зависимыми, если существуют такие числа, не все равные нулю, что . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.

В противном случае, т.е. когда соотношение выполняется только при , эти векторы называются линейно независимыми.

Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Доказательство:

1. Действительно, пусть имеем два коллинеарных вектора и . Тогда либо оба они равны нулю, и следовательно, любая их линейная комбинация при любых λ₁ и λ₂, либо один из них не нуль, тогда другой отличается от него на числовой множитель, например, . Но отсюда , а это и означает линейную зависимость векторов и .
2. Докажем обратное, т.е. если два вектора линейно зависимы, то они коллинеарны. Пусть векторы и линейно зависимы. Тогда найдутся числа λ
   1 и λ₂ такие, что , причём, например, λ₂ ≠ 0. Тогда , т.е. векторы коллинеарны.

   Таким образом, теорема утверждает, что линейно независимыми на плоскости могут быть только те векторы, которые неколлинеарны.

Аналогично можно доказать следующую теорему.

Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Доказательство.

1. Пусть три вектора линейно зависимы, т.е. , где, например, λ₃ ≠ 0. Тогда .

   Отнесём векторы и к одному началу и проведём через них плоскость. Тогда и будут лежать в той же плоскости, а потому и их сумма, т.е. будет лежать в той же плоскости, т.е. – компланарны.

2. Пусть теперь векторы – компланарны. Тогда они будут лежать в одной плоскости. Отнесём все три вектора к одному началу.

   Если векторы и не коллинеарны, то очевидно, вектор можно предствить в виде . Действительно из рисунка видно, что , где и , а значит найдутся числа и такие, что .

   Если же вектор коллинеарен вектору , то один из них линейно выражен через другой, т.е. . Что и требовалось доказать.

   Таким образом, три некомпланарных вектора всегда линейно независимы. Кроме того, можно показать, что каждые четыре вектора линейно зависимы.

БАЗИС

Базисом называется совокупность отличных от нулей линейно независимых векторов. Элементы базиса будем обозначать .

В предыдущем пункте мы видели, что два неколлинеарных вектора на плоскости линейно независимы. Поэтому согласно теореме 1, из предыдущего пункта, базисом на плоскости являются любые два неколлинеарных вектора на этой плоскости.

Аналогично в пространстве линейно независимы любые три некомпланарных вектора. Следовательно, базисом в пространстве назовём три некомпланарных вектора.

Справедливо следующее утверждение.

Теорема. Пусть в пространстве задан базис . Тогда любой вектор можно представить в виде линейной комбинации , где x, y, z – некоторые числа. Такое разложение единственно.

Доказательство.

1. Докажем сначала существование такого представления.
   1. Предположим, что коллинеарен какому-либо из векторов базиса, например, .
      Тогда по доказанному выше . Следовательно, , где x = l, y = z = 0.
   2. Пусть компланарен с какой-либо парой базисных векторов, например, с и . Отложим три вектора от одной точки O. Через точку A проведём прямые, параллельные векторам и . Тогда , причём векторы и коллинеарны соответственно векторам и . Поэтому найдутся числа x и y такие, что , а значит .
   3. Пусть некомпланарен ни с одной парой базисных векторов.
      Отложим от одной точки и проведём через конец вектора прямую, параллельную вектору . Она пересечёт плоскость в точке A₁. Очевидно, что . Но вектор компланарен векторам и , следовательно, по доказанному выше, , а вектор коллинеарен , поэтому . Таким образом, .
2. Докажем теперь единственность такого представления.

   Допустим, что возможны два представления вектора и . Причём, например, . Тогда должны иметь , т.к. иначе мы имели бы две прямые, проходящие через точку

   A₁ параллельно . Из последнего равенства вытекает, что . Получили противоречие с нашим предположением, что и доказывает теорему.

   В качестве частного случая из этой же теоремы можно сформировать следующее утверждение:

   Если задан базис на плоскости, то любой вектор, компланарный с векторами можно представить в виде , причём такое разложение единственно.

Таким образом, базис позволяет однозначно сопоставить каждому вектору тройку чисел – коэффициенты разложения этого вектора по векторам базиса: . Верно и обратное, каждой тройке чисел x, y, z при помощи базиса можно сопоставить вектор, если составить линейную комбинацию .

Если базис и , то числа x, y, z называются координатами вектора в данном базисе. Координаты вектора обозначают .

ДЕКАРТОВА СИСТЕМА КООРДИНАТ

Пусть в пространстве задана точка O и три некомпланарных вектора .

Декартовой системой координат в пространстве (на плоскости) называется совокупность точки и базиса, т.е. совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.

Точка O называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат – осью абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями.

Рассмотрим в выбранной системе координат произвольную точку M. Введём понятие координаты точки M. Вектор , соединяющий начало координат с точкой M. называется радиус-вектором точки M.

Вектору в выбранном базисе можно сопоставить тройку чисел – его координаты: .

Координаты радиус-вектора точки M. называются координатами точки M. в рассматриваемой системе координат. M(x,y,z). Первая координата называется абсциссой, вторая – ординатой, третья – аппликатой.

Аналогично определяются декартовы координаты на плоскости. Здесь точка имеет только две координаты – абсциссу и ординату.

Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся единственная точка, имеющая эти числа в качестве координат.

Если векторы, взятые в качестве базиса, в выбранной системе координат, имеют единичную длину и попарно перпендикулярны, то система координат называется декартовой прямоугольной системой координат. В этом случае основные векторы принято обозначать буквами , а оси координат Ox, Oy и Oz.

Таким образом, любой вектор в декартовой прямоугольной системе координат можно записать в виде: .

Примеры.

1. Построить на плоскости в декартовой системе координат вектор . Вектор примем в качестве радиус-вектора точки

   М(-1;3).

2. Построить вектор . Вектор примем в качестве радиус-вектора точки N(2; -1; 3).

   В дальнейшем мы в основном будем использовать только декартову прямоугольную систему координат.

НАПРАВЛЯЮЩИЕ КОСИНУСЫ ВЕКТОРА

Пусть в декартовой прямоугольной системе координат задан вектор . Направление вектора в пространстве определяется углами α, β, γ которые вектор составляет с осями координат. Косинусы этих углов cos α, cos β, cos γ называются направляющими косинусами вектора.

Найдем выражение для направляющих косинусов вектора.

Пусть вектор задан в координатной форме .

Тогда , откуда.

Несложно показать, что .

Направляющие косинусы вектора полностью определяют его направление, но ничего не говорят о его длине.

Проекция вектора на ось, формула и примеры

Определение и формула проекции вектора на ось

Под осью понимается прямая, для которой указано направление.

Чтобы построить проекцию вектора на ось , нужно из точек и (начало и конец вектора соответственно) опустить перпендикуляры на направленную прямую , основания этих перпендикуляров будут началом и концом искомой проекции (рис. 1).

Числовой характеристикой проекции вектора на ось является числовая проекция этого вектора на данную ось – число, которое равно произведению длины данного вектора на косинус угла между этим вектором и вектором, определяющим направление оси.

Если направление оси определяется вектором , то числовая проекция вектора на эту ось обозначается как , причем

   

Примеры нахождения проекции вектора на ось

Из определения скалярного произведения двух векторов и :

   

получаем, что

   

В результате формула (1) принимает вид:

   

То есть числовой проекцией вектора на ось, направление которой совпадает с направлением вектора , есть отношение скалярного произведения векторов и к модулю вектора :

   

Понравился сайт? Расскажи друзьям!

Что такое проекция вектора на ось координат?

отрезок на оси координат, соединяющий перпендикуляры, опущенные из начала и конца вектора на ось координат. легкая херня непонятнее всего объясняетсЯ)

отрезок соединяющий проекцию начала вектора с проекцией конца вектора, взяты по модулю со знаком плюс или минус

Это скалярное произведение вектора на орт оси.

симпо-тяффка ты ваще ф сколи че деляись

Если есть вектор А и ось х, то проекция вектора А на ось х, обозначаемая Ax = A * cos (alfa) где alfa — угол между осью х и векторм A

3. Проекция вектора на ось

3.1. Основные определения

Определение 3.1 Проекцией точки на прямую или плоскость называется основание перпендикуляра, проведенного из данной точки на прямую или плоскость (на рис. 3.1 точка– проекция точкиA, точка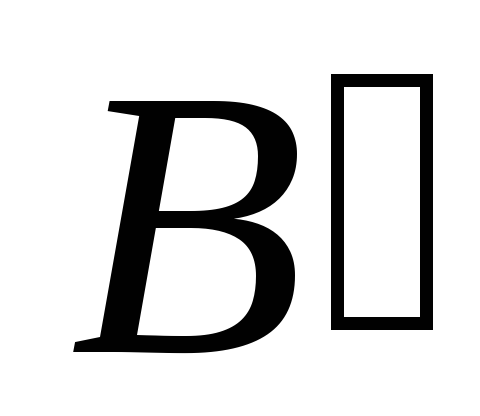– проекция точкиB).

Определение 3.2. Составляющей (компонентой) вектора по прямой (плоскости) называется вектор, лежащий на данной прямой (плоскости), начало и конец которого совпадают, соответственно, с проекциями начала и конца этого вектора (на рис. 3.1 вектор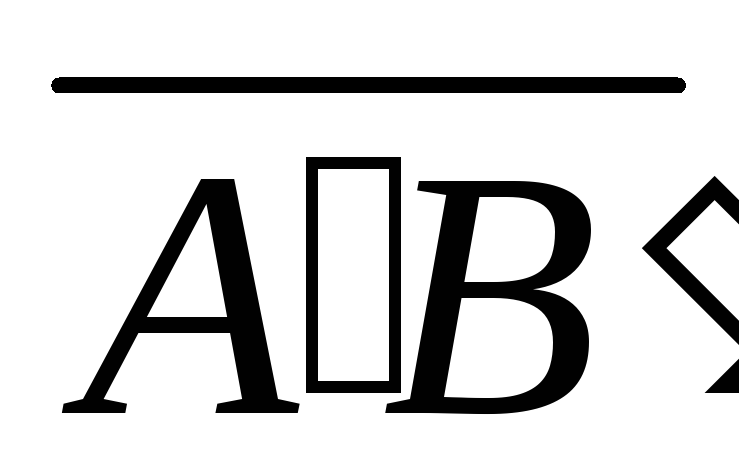– составляющая вектора).

Определение 3.3. Проекцией вектора на ось называется скаляр, равный модулю составляющей вектора по этой оси, взятому со знаком плюс, если направление составляющей совпадает с направлением оси, и со знаком минус, если эти направления противоположны (рис. 3.2).

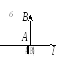
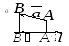
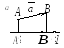
Рис. 3.2

Проекция вектора на ось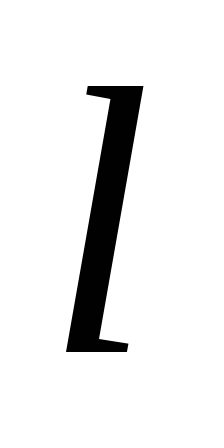обозначается символом:

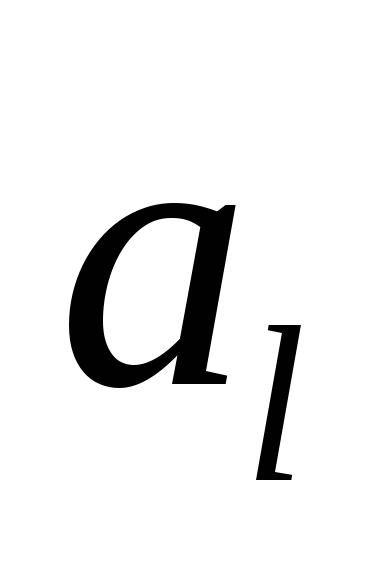или.

На рис. 3.2 (а) проекция векторана ось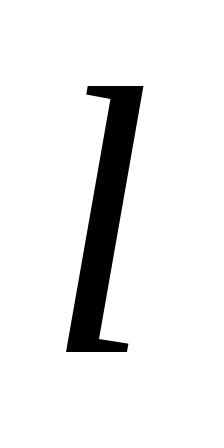положительна, т.к. составляющая данного вектора по осисовпадает по направлению с осью,.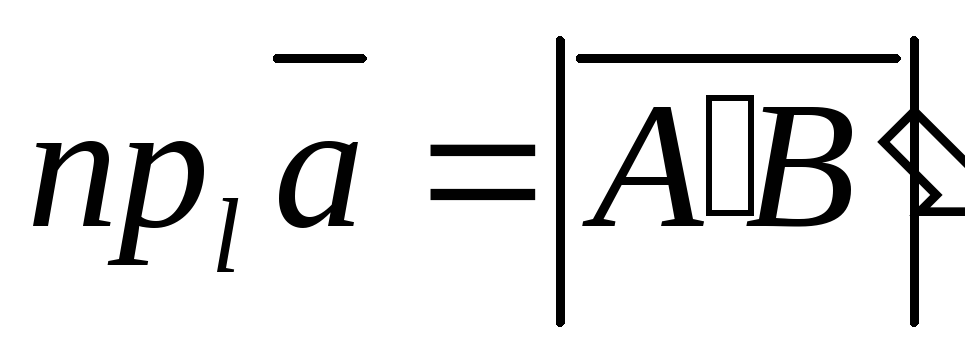

На рис. 3.2 (б) проекция равна нулю, т.к. начало и конец составляющей вектора совпадают,.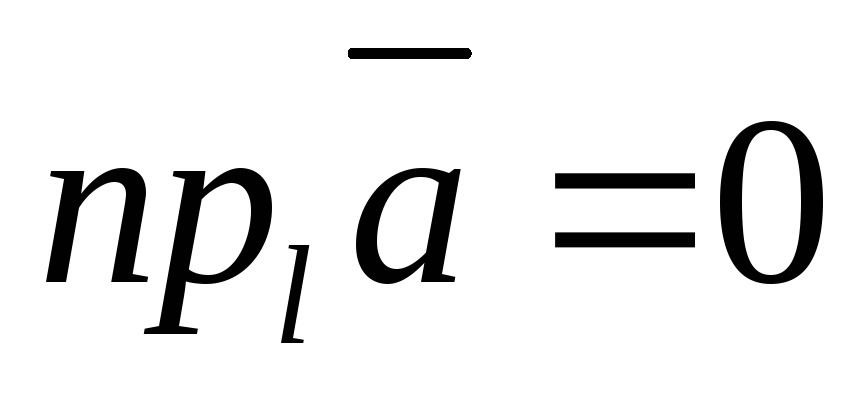

На рис. 3.2 (в) проекция вектора отрицательна, т.к. составляющая вектора направлена противоположно направлению оси,.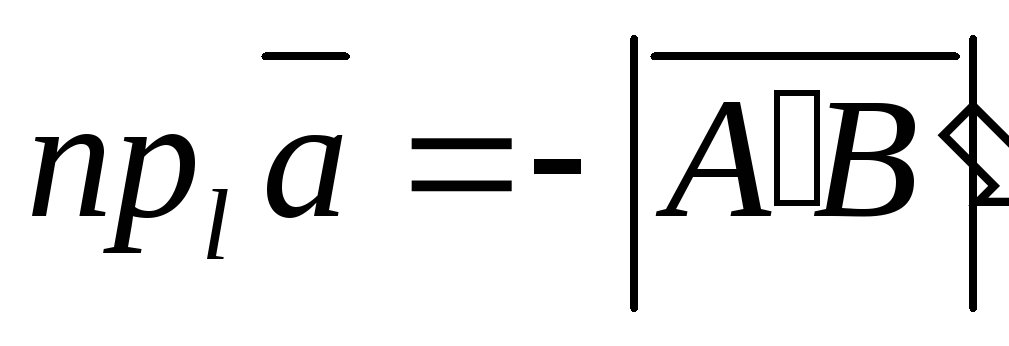

3.2. Свойства проекции вектора на ось

Проекция вектора на ось не изменится при параллельном переносе вектора.

Аддитивность проекции. Проекция суммы векторов на некоторую ось равна сумме проекций данных векторов на эту ось.

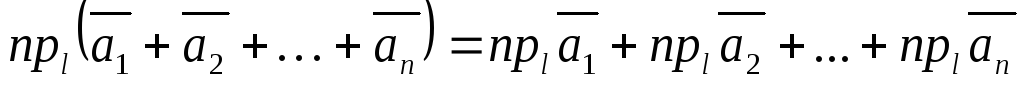. (3.1)

.Однородность проекции. Скалярный множитель можно вынести за знак проекции вектора на ось,

. (3.2)

Следующему свойству предпошлем определение угла между вектором и осью.

Определение 3.4.Углом между вектором и осью 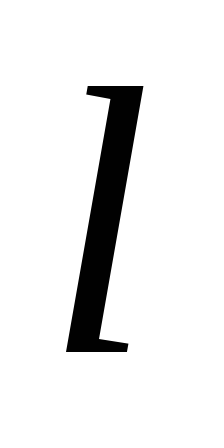называется угол между вектором и положительным направлением оси, отсчитываемый в направлении от оси против движения часовой стрелки(рис. 3.4).

.Проекция вектора на ось равна произведению модуля этого вектора на косинус угла между вектором и осью,(рис. 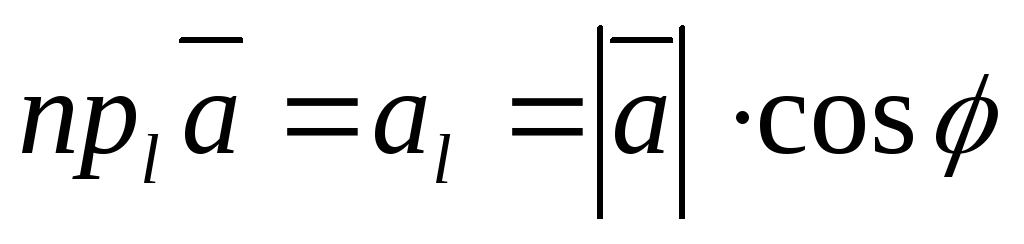3.3).

(3.3)

Рис. 3.3

Проиллюстрируем применение свойств проекции вектора на ось к решению задачи.

Задача 3.1.Дано:,,,.

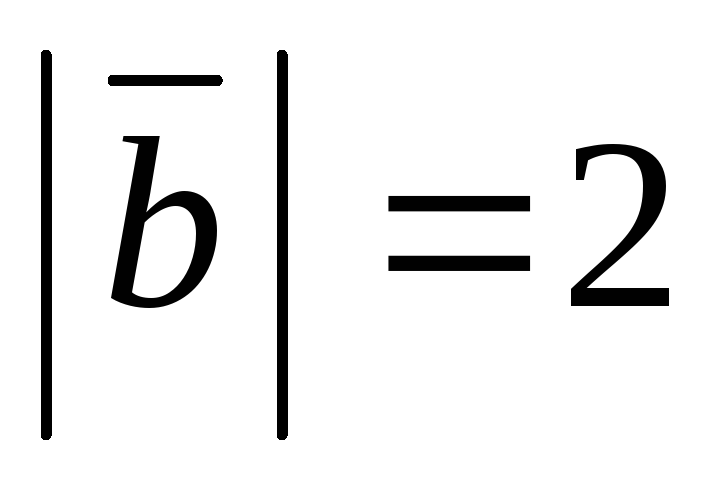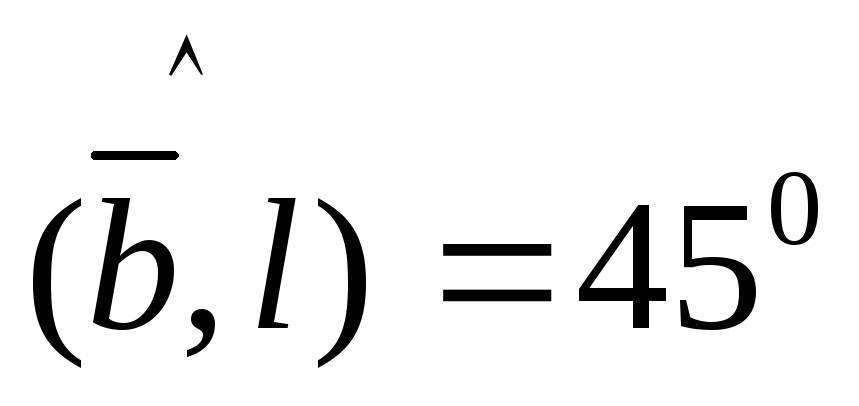Найти: _.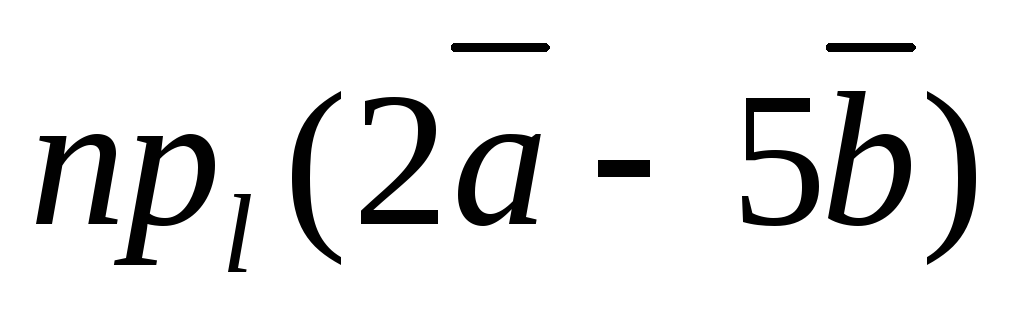

Решение. Применим свойства аддитивности и однородности проекции вектора на ось и формулу (3.2).

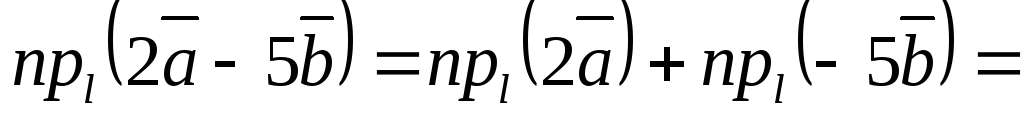
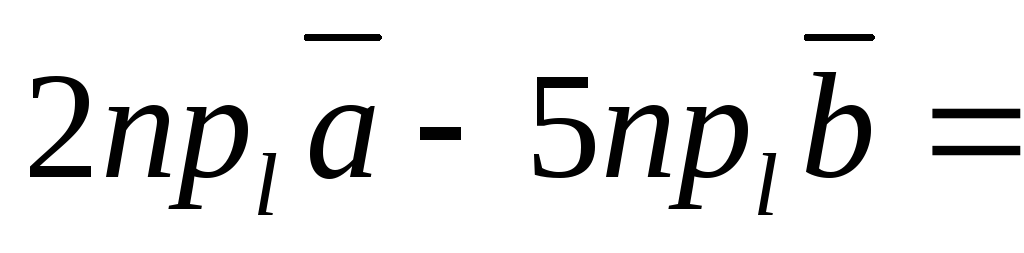
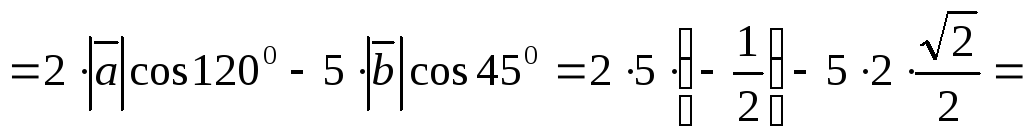
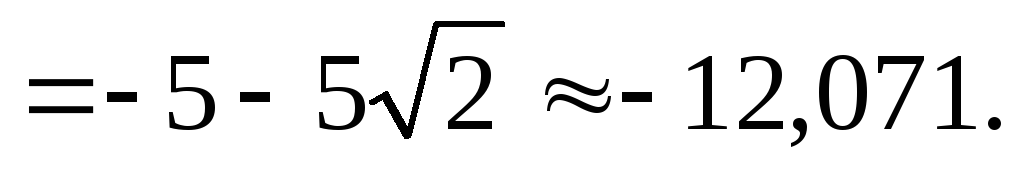
Ответ.

Эффективное практическое применение векторов, в том числе и с использованием компьютеров, связано с использованием пространственной системы координат.

4. Декартова прямоугольная система координат в пространстве

4.1. Общие определения, координаты вектора

Декартова прямоугольная система координат в пространстве определяется заданием трех взаимно перпендикулярных осей с общим началом отсчета (начало системы координат) и одинаковой для всех осей масштабной единицей (рис. 4.1). Оси носят название:

• Ох– ось абсцисс;

• Оy– ось ординат;

• Оz– ось аппликат.

Плоскости xОy,xОz,yOzназываются координатными плоскостями.

Единичные векторы ,,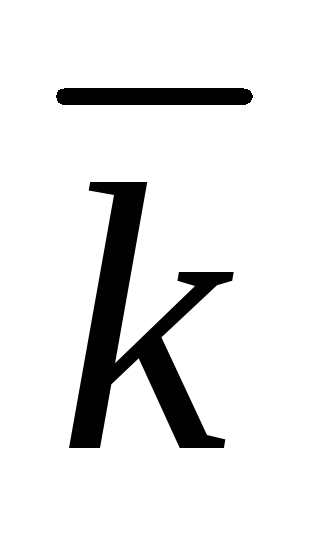 сонаправленные с осямиOx,Oy,Oz, носят названиеортов осей.

Если орты образуют правую тройку, то система координат называется правой, если левую, то – левой.

Мы будем работать только с правой системой координат (рис. 4.1).

Определим понятие координат вектора. Рассмотрим произвольный вектор . Приведем его к началу координат, точке(рис. 4.1). Спроектируем этот вектор на координатные оси. Составляющими векторапо координатным осям являются векторы: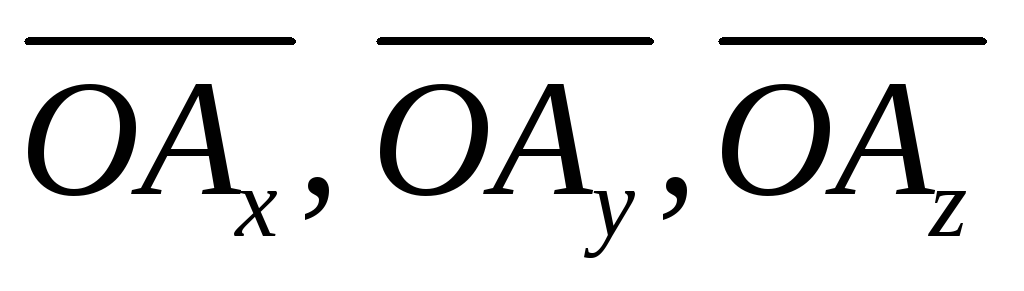, а проекциями на координатные оси – числа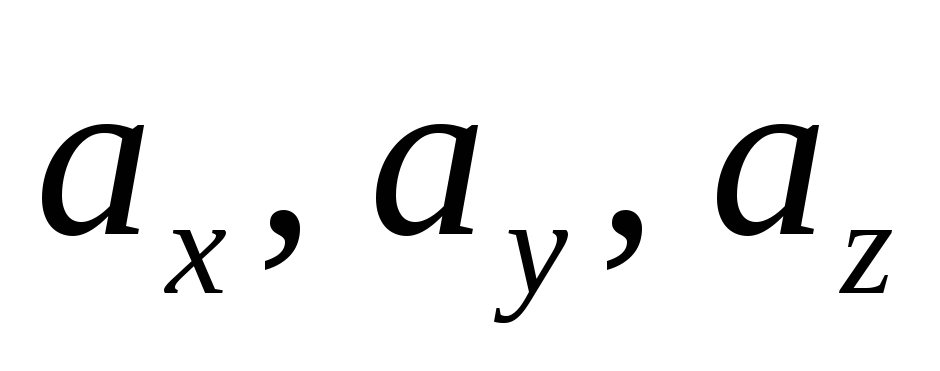. Эти проекции носят названия координатами вектора.

Определение 4.1. Координатами вектора называются его проекциина координатные оси. При этом пишут:

(4.1)

где 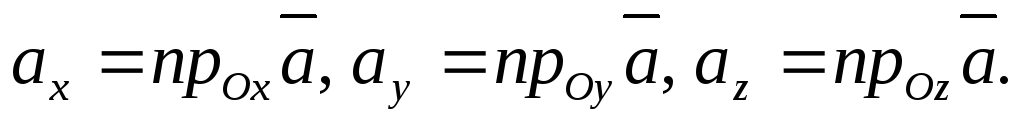Очевидно, координаты нулевого вектора равны 0:

(4.2)

знаки проекции вектора? Это что?

Если проекция по оси — знак плюс, если против оси — знак минус.

Когда проектируешь вектор на ось, то необходимо правильно выставлять знаки у проекций. Для того, чтобы найти проекцию вектора на ось, необходимо из конца вектора и из начала вектора отложить перпендикуляры на ось. Если проекция вектора на ось совпадает по направлению с осью то у проекции ставят знак плюс, если проекция вектора направлена противоположно оси, то у проекции вектора ставят знак минус

Это «+», «-» В следующей формулировке, на мой взгляд, исчерпывающий ответ «Алгебраическим значением проекции вектора на направленную ось называется модуль проекции вектора на эту ось, взятый со знаком «+», если направление проекции вектора совпадает с положительным направлением оси, и со знаком «–», в противном случае. » ps: Гугл тебе в помощь

§ 6. Проекция вектора на ось. Теоремы о проекциях

27

Определение. Углом между векторами a и b называется наименьший угол ϕ ( 0 ≤ϕ ≤ π ), на который надо повернуть один из векторов относительно общей начальной точки до его совпадения со вторым.

Определение. Рассмотрим ось l , положительное направление которой совпадает с направлением единичного вектора e , расположенного на

оси. Под углом между вектором a и осью l понимают угол ϕ между векторами er и ar.

→

Пусть l – некоторая ось, а AB – вектор, произвольно расположенные в пространстве. Обозначим через A1 и B1 проекции на ось l соответственно

начала A и конца B этого вектора. Предположим, что A1 на оси l имеет координату x1 , а B1 – координату x2 (рис. 1.6).

Определение. Разность x2 − x1 между координатами проекций конца

				и начала вектора		→	на-
	B					AB на ось l
				зывается проекцией вектора			→
							AB
	B1		l	на эту ось.
				Если вектор		→
x2						AB образует с
				осью l острый угол, то x2 > x1 , и
Рис. 1.6				проекция	x2 − x1 > 0 , если угол
						→
				между осью l и вектором AB –
				→	l , то проекция равна 0.
и проекция отрицательна. Если AB

Теорема 1. Проекция вектора a на ось l равна модулю вектора a , умноженному на косинус угла ϕ между вектором и осью:

прl a = a cosϕ .

Доказательство. Проекция вектора a не изменится при любом его переносе параллельно самому себе, т.к. при этом x2 и x1 изменяются на одну и ту же

величину. Поэтому достаточно рассмотреть случай, когда начало вектора совпадает с началом O оси l .

	ar	B	B				B
			a	ϕ		ar
	ϕ		π −ϕ
O		B1 l	B1	O	l	O			l

Рис. 1.7

Рис. 1.8

Рис. 1.9

28

Если угол ϕ между вектором и осью острый ( 0 ≤ϕ ≤π2 ) (рис. 1.7), то

прl ar =		→
	OB1 =	OB cosϕ = ar cosϕ .

Если же угол ϕ тупой (π 2 ≤ϕ ≤π ) (рис. 1.8), то

прl ar = − B1O = − OB cos(π −ϕ) = OB cosϕ = ar cosϕ .

Наконец, если ϕ = π2 (рис. 1.9), то прl a = 0 и cosϕ = 0. Таким образом,

снова имеем соотношение

прl a = a cosϕ .

Теорема 2. Проекция суммы двух векторов на ось равна сумме проекций слагаемых векторов на ось.

Доказательство. Пусть

B

A

x1

O x2

Рис. 1.10

→	→ →
AC = AB+ BC . Обозначим через x1 , x2 и x3 коор-
				динаты проекций A1 , B1 и C1 на
				ось l точек A , B , C (рис.1.10).
				Тогда
				→	→
	C			прl AB = x2	− x1 , прl BC	= x3 − x2 ,
				→
				прl AC = x3	− x1 , т.е.
		l		→	→	→
x3				прl AC	= прl AB+ прl	BC .

Замечание. Эту теорему можно обобщить на случай любого числа слагаемых.

Теорема 3.

прl (λ a)= λ прl a .

Доказательство. Прежде всего заметим, что если вектор ar составляет с осью угол ϕ и λ > 0 , то вектор λa имеет то же направление, что и вектор a , и составляет с осью также угол ϕ . Если же λ < 0 , то направление вектора λa

противоположно направлению a и вектор λa составляет с осью угол

π −ϕ =ϕ1 .

По теореме 1 имеем:

1)

λ > 0 ;

прl (λar)=

λar

cosϕ =

λ

a

cosϕ = λ

ar

cosϕ = λ прl a ;

2)

λ < 0 ;

прl (λar)=

λar

cosϕ1 =

λ

a

cosϕ1 = −λ

ar

cos(π −ϕ)=

= λ

ar

cosϕ = λ прl a .

Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на эту же ось.