11. Частотный спектр импульсного сигнала.
Ранее отмечалось, что любой электрический сигнал может быть представлен в виде суммы синусоид, каждая синусоида имеет свою амплитуду, частоту и фазу.
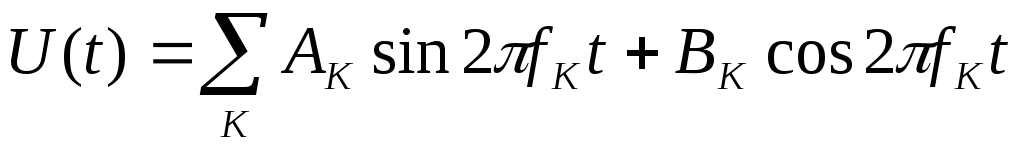где
Ак – амплитуда fк – частота к – фаза.
Если построить график, показывающий, как зависит амплитуда синусоиды от частоты, то это будет частотный спектр данного сигнала.
U(t)
– сигнал, имеющий периодический
характер.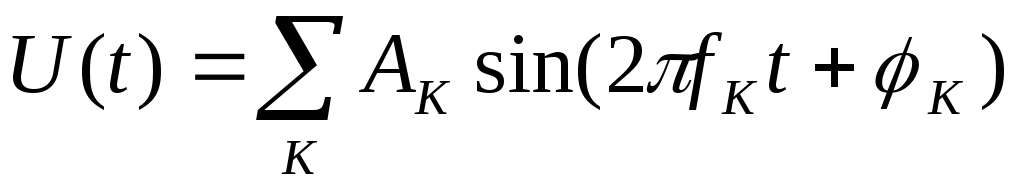
Частотный спектр – зависимость Ак от fк.
Можно вместо синусоиды брать косинусоиду, частотный спектр от этого не изменится. Выбор разложения по синусоиде или косинусоиде зависит от выбора начала отсчета (симметричный).
Каждая синусоида носит название гармоника. Поэтому представление в виде суммы гармоник называется гармоническим рядом.
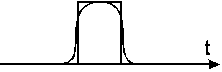
Пусть импульсы прямоугольной формы периодически повторяются, амплитуда, период и длительность – постоянны.
В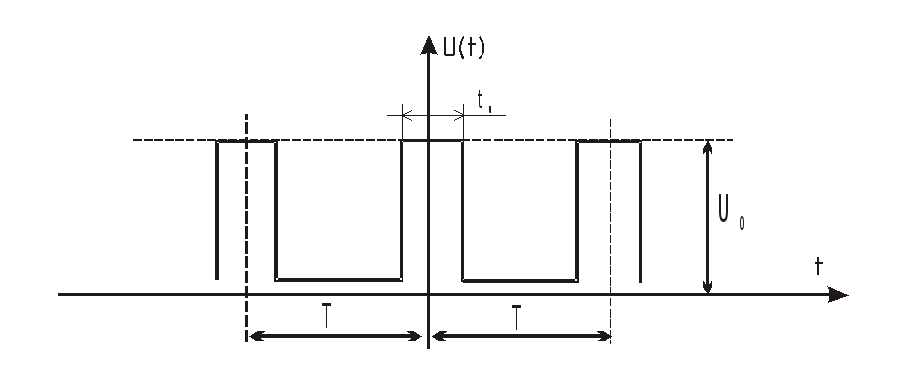
ыберем
начало отсчета времениt
= 0 так, чтобы картина была симметричной
относительно начала отсчета.
Тогда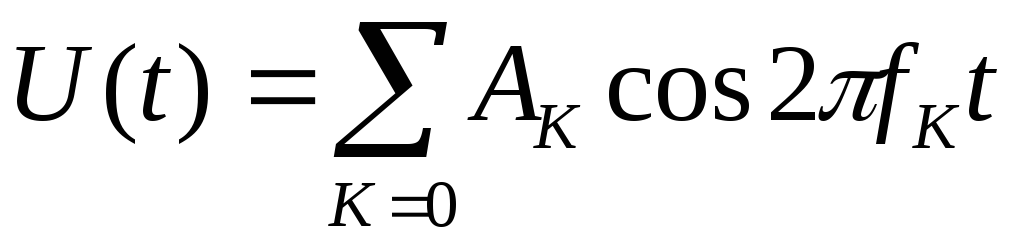 
— т.е. будут одни косинусоиды,
где k 2 f k = k— частота гармоники.
Отсутствует к , т.е. все гармоники имеют нулевой фазовый сдвиг.
Существует косинусоида, у которой к = 0, f0 = 0, нулевая гармоника, ей соответствует постоянная составляющая U(t).
Частоты гармоник:
К = 0, f 0 = 0 — нулевая гармоника
К = 1, f 1 = 1/T — первая гармоника
К = 2, f 2 = 2/T — вторая гармоника и т.д.
Если Т постоянно, т.е. сигнал периодический
Частоты
гармоник: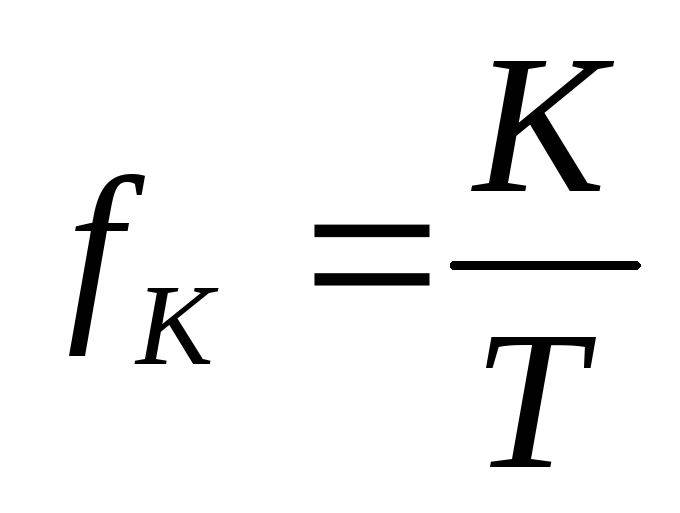 
Амплитуды гармоник.
Определяются из теории рядов Фурье.
Для прямоугольных импульсов:
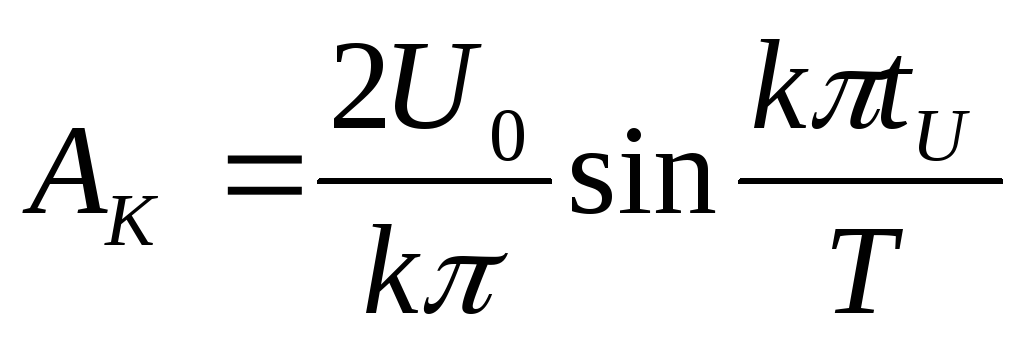где
U0 – амплитуда импульса,
К – номер гармоники (чем больше к, тем меньше U0).
.
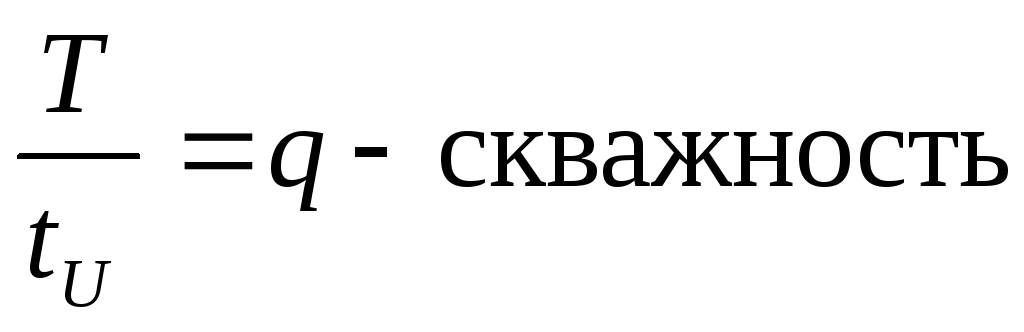Как следует из формулы для Ak амплитуды гармоник идеальных прямоугольных импульсов имеют тенденцию с ростом k (частоты) убывать асимптотически, т.е. формально ширина частотного спектра идеальных прямоугольных импульсов неограниченна.
Реальные импульсы имеют отклонения от прямоугольной формы и ширина их спектра не бесконечна.
Отдельно вычисляется амплитуда нулевой гармоники.
Если к = 0 , знаком синуса можно пренебречь и тогда:
-это
не что иное, как постоянная составляющая
напряжения U(t).
И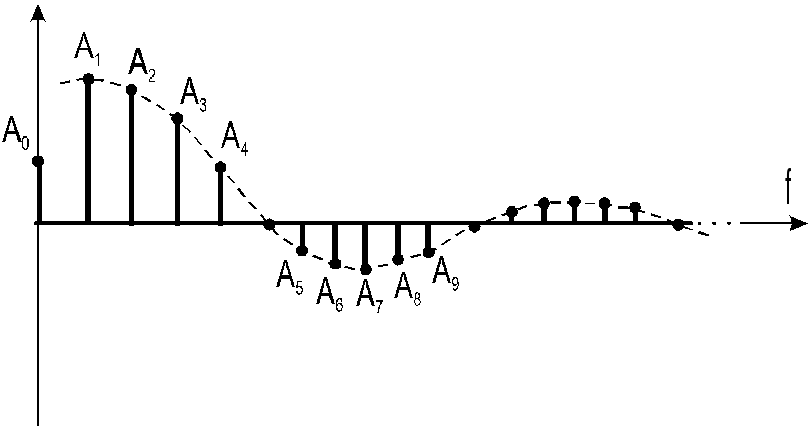
зобразим
график частотного спектра.
Для упрощения далее будет изображаться только первая полуволна графика частотного спектра — основной частотный спектр.
Амплитуды гармоник уменьшаются с увеличением частоты, при этом наблюдается колебательный характер.
Участок до первого нуля (первая полуволна) – это основной спектр.
Частотная граница основного спектра определяет ширину частотного спектра из условия:
откуда
k=kосн=
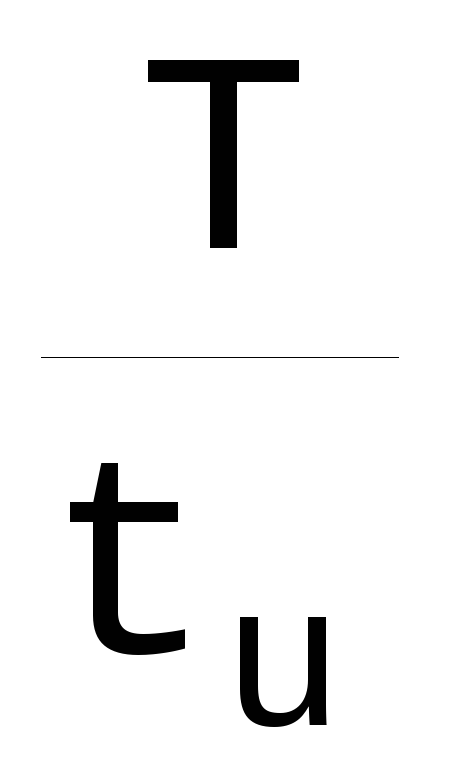илиk
kосн – количество линий в основном спектре.
Величина
Fосн=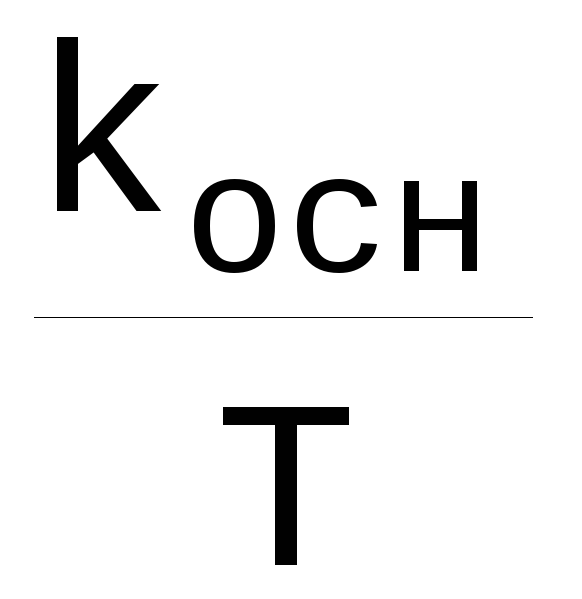
— ширина основного спектра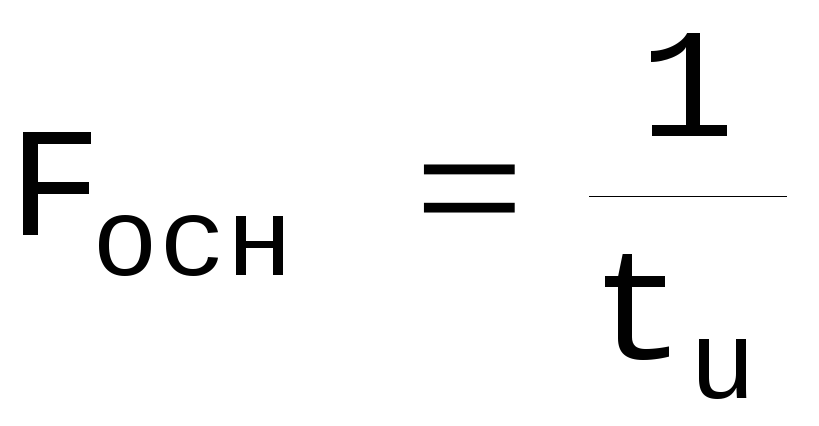 
Часто требуется количественная оценка ширины частотного спектра Fc . Для идеальных прямоугольных импульсов, её условно принимают равной
Fc=(1..3)Fосн или 
.
Свойства частотного спектра.
Чем больше период повторения импульсов, тем больше линий в основном частотном спектре – чаще расположены линии в частотном спектре.
Чем короче импульс, тем больше ширина частотного спектра.
Ширина ЧС определяется для прямоугольного импульса соотношением:
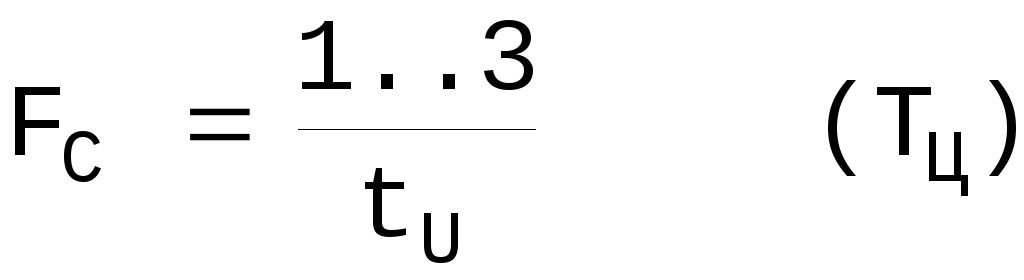
Это соотношение справедливо для идеальных прямоугольных импульсов.
Реальный импульс отличается от идеального более пологими фронтами.
Общая формула вычисления амплитуды гармоник для любого случая:
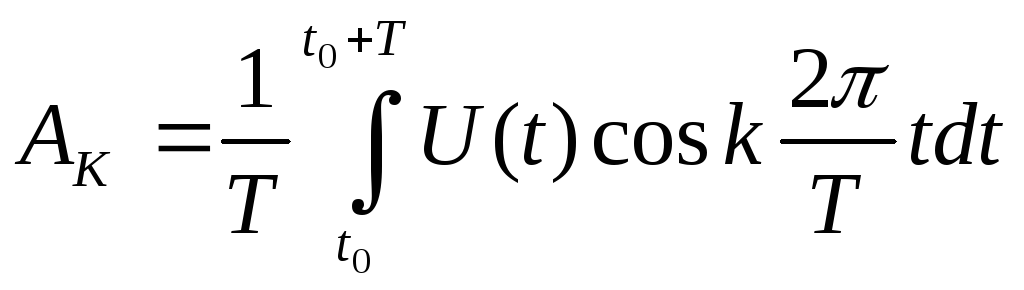
По сравнению с идеальным прямоугольным импульсом для реального импульса ЧС имеет более определенную частотную границу. Убывание амплитуд гармоник с частотой может иметь монотонный характер.
Гармоника (спектр звука) Википедия
Запрос «Гармоника (колебания)» перенаправляется сюда; также см. Гармоника. Колебания струны: 1 — колебание по всей длине образует основной тон, 2 — колебание половинок образует первый обертон, 3 — колебание третей — второй обертон и т. д. 15 обертонов от ноты До большой октавы (16 гармоник), озвученные как нажатие клавиш фортепианоОберто́ны (нем. ober — высокий,
Обертоны бывают гармоническими и негармоническими. Частоты гармонических обертонов больше частоты основного тона в 2, 3, 4, 5 и т. д. раз (кратность равна натуральному числу). Гармонические обертоны вместе с основным тоном называются гармониками и образуют натуральный звукоряд:
В реальных физических ситуациях (например, при колебаниях массивной и жесткой струны) частоты обертонов могут заметно отклоняться от величин, кратных частоте основного тона — такие обертоны называются негармоническими. Присутствие негармонических обертонов в колебаниях струн музыкальных инструментов приводит к феномену неточного равенства между рассчитанными частотами равномерно темперированного строя и реальными частотами правильно настроенного фортепиано (см. Кривые Рейлсбека).
Ввиду исключительной важности для музыки именно гармонических обертонов (и относительной малозначимости негармонических) вместо «гармонический обертон» в музыкально-теоретической (но не в физической) литературе часто пишут «обертон» без каких-либо уточнений.
Обертон может быть колебанием частей звучащего тела, выраженных как аликвотными дробями (
Начальные 10 обертонов прослушиваются по высоте и сливаются друг с другом в аккорды. Остальные прослушиваются плохо или не прослушиваются вообще.
Использование обертонов в музыке
Примечания
Литература
- Обертоны // Музыкальная энциклопедия. — М.: Советская энциклопедия, 1976. — Т. 3. — С. 1066—1067. — 1104 с.
- Обертоны // Музыкальный энциклопедический словарь. — М.: Советская энциклопедия, 1990. — С. 389. — 672 с.
Гармоника (спектр звука) Википедия
Запрос «Гармоника (колебания)» перенаправляется сюда; также см. Гармоника.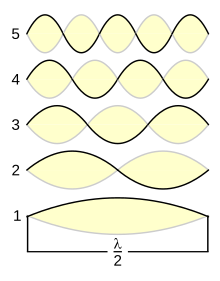
Оберто́ны (нем. ober — высокий, Ton — звук[1]) в акустике — призвуки, входящие в спектр музыкального звука; высота обертонов выше основного тона (отсюда название). Наличие обертонов обусловлено сложной картиной колебаний звучащего тела (струны, столба воздуха, мембраны, голосовых связок и т. д.): частоты обертонов соответствуют частотам колебания его частей.
Обертоны бывают гармоническими и негармоническими. Частоты гармонических обертонов больше частоты основного тона в 2, 3, 4, 5 и т. д. раз (кратность равна натуральному числу). Гармонические обертоны вместе с основным тоном называются гармониками и образуют натуральный звукоряд:
| Обертон | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| Гармоника | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| Нотация |   d2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
11. Частотный спектр импульсного сигнала.
Ранее отмечалось, что любой электрический сигнал может быть представлен в виде суммы синусоид, каждая синусоида имеет свою амплитуду, частоту и фазу.
где Ак – амплитуда fк – частота к – фаза.
Если построить график, показывающий, как зависит амплитуда синусоиды от частоты, то это будет частотный спектр данного сигнала.
U(t)
– сигнал, имеющий периодический
характер.
Частотный спектр – зависимость Ак от fк.
Можно вместо синусоиды брать косинусоиду, частотный спектр от этого не изменится. Выбор разложения по синусоиде или косинусоиде зависит от выбора начала отсчета (симметричный).
Каждая синусоида носит название гармоника. Поэтому представление в виде суммы гармоник называетсягармоническим рядом.
Пусть импульсы прямоугольной формы периодически повторяются, амплитуда, период и длительность – постоянны.
В
ыберем
начало отсчета времениt
= 0 так, чтобы картина была симметричной
относительно начала отсчета.
Тогда 
— т.е. будут одни косинусоиды,
где k 2 f k = k— частота гармоники.
Отсутствует к , т.е. все гармоники имеют нулевой фазовый сдвиг.
Существует косинусоида, у которой к = 0, f0 = 0, нулевая гармоника, ей соответствует постоянная составляющая U(t).
Частоты гармоник:
К = 0, f 0 = 0 — нулевая гармоника
К = 1, f 1 = 1/T — первая гармоника
К = 2, f 2 = 2/T — вторая гармоника и т.д.
Если Т постоянно, т.е. сигнал периодический
Частоты
гармоник: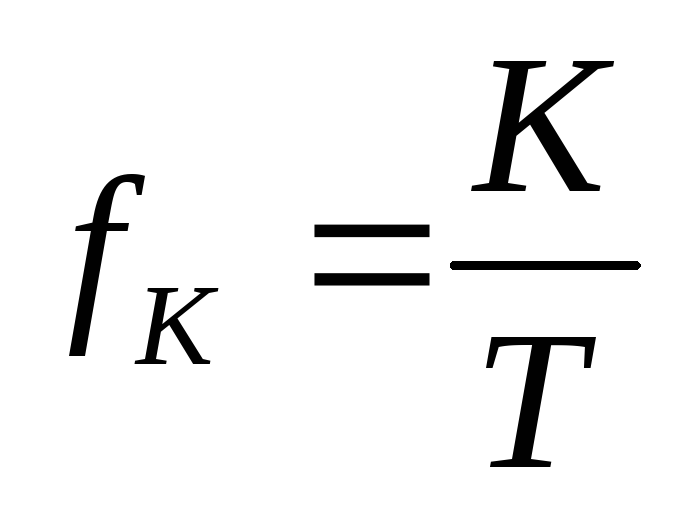 
Амплитуды гармоник.
Определяются из теории рядов Фурье.
Для прямоугольных импульсов:
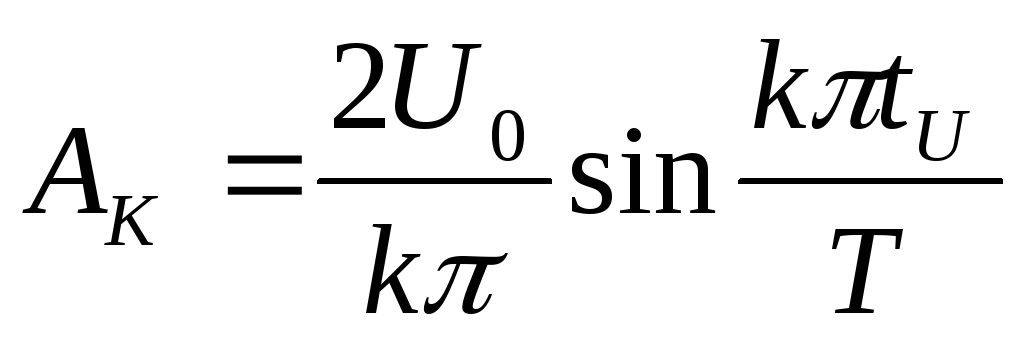где U0 – амплитуда импульса,
К – номер гармоники (чем больше к, тем меньше U0).
.
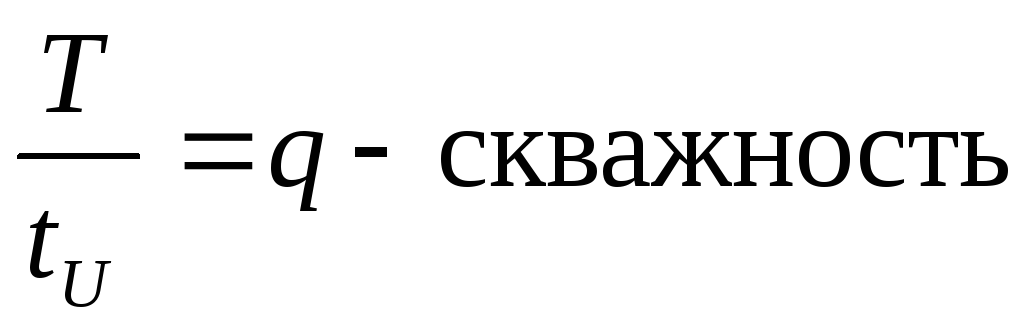Как следует из формулы для Ak амплитуды гармоник идеальных прямоугольных импульсов имеют тенденцию с ростом k (частоты) убывать асимптотически, т.е. формально ширина частотного спектра идеальных прямоугольных импульсов неограниченна.
Реальные импульсы имеют отклонения от прямоугольной формы и ширина их спектра не бесконечна.
Отдельно вычисляется амплитуда нулевой гармоники.
Если к = 0 , знаком синуса можно пренебречь и тогда:
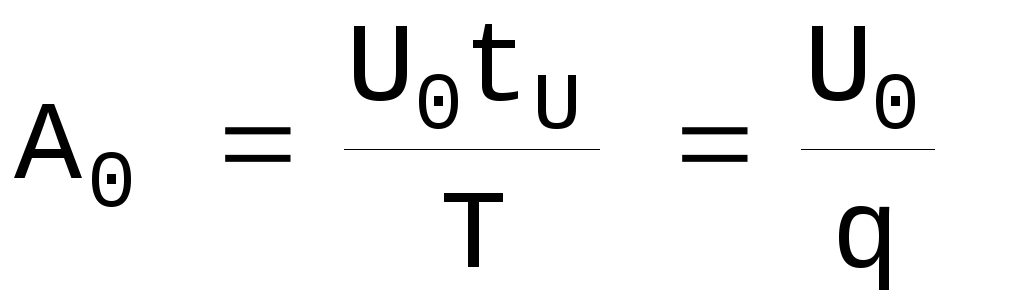-это
не что иное, как постоянная составляющая
напряжения U(t).
И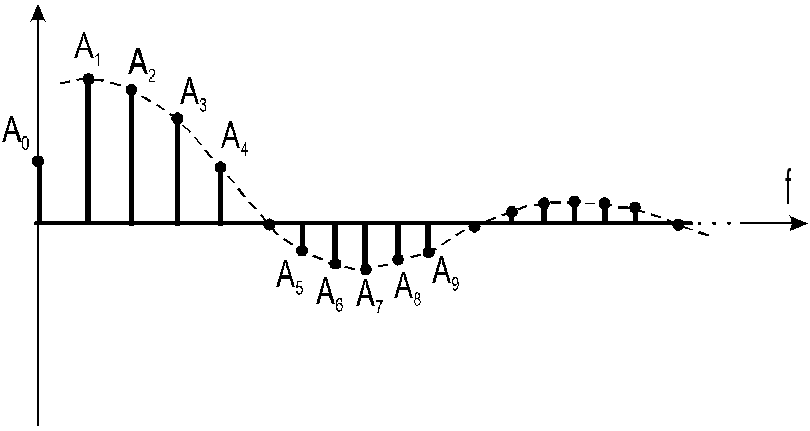
зобразим
график частотного спектра.
Для упрощения далее будет изображаться только первая полуволна графика частотного спектра — основной частотный спектр.
Амплитуды гармоник уменьшаются с увеличением частоты, при этом наблюдается колебательный характер.
Участок до первого нуля (первая полуволна) – это основной спектр.
Частотная граница основного спектра определяет ширину частотного спектра из условия:
откуда
k=kосн=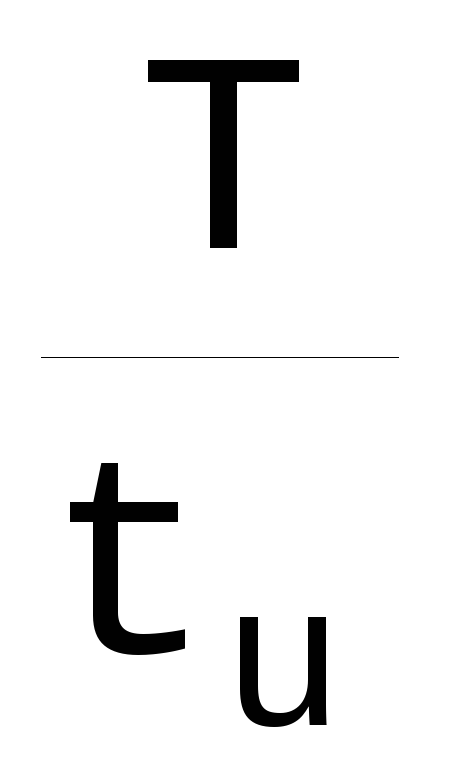
илиkосн=q
kосн – количество линий в основном спектре.
Величина Fосн=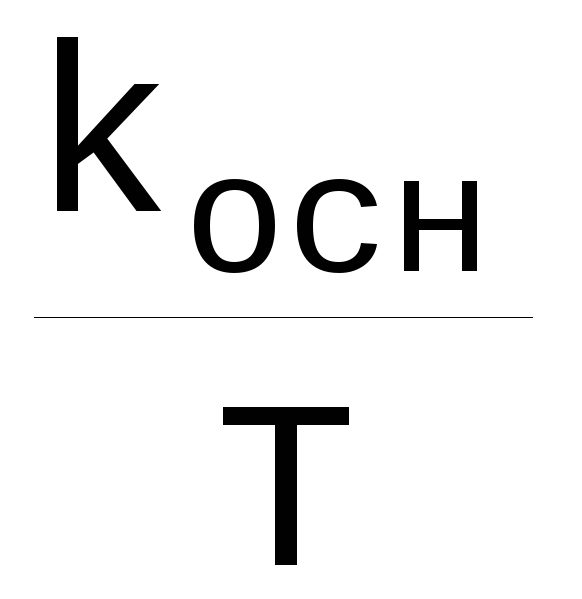
— ширина основного спектра 
Часто требуется количественная оценка ширины частотного спектра Fc . Для идеальных прямоугольных импульсов, её условно принимают равной
Fc=(1..3)Fосн или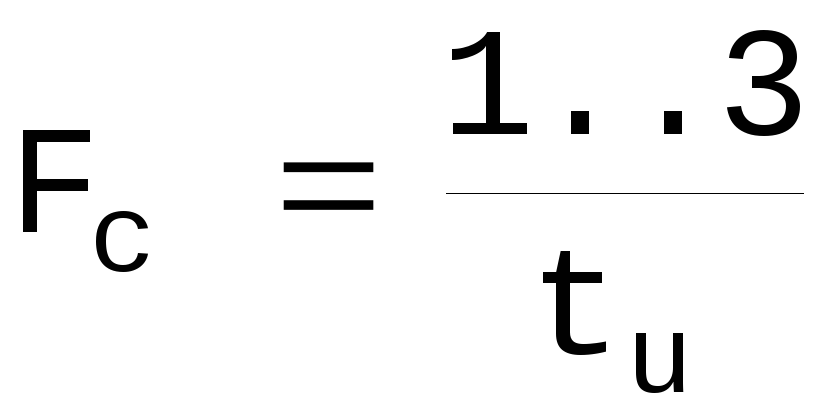 
.
Свойства частотного спектра.
Чем больше период повторения импульсов, тем больше линий в основном частотном спектре – чаще расположены линии в частотном спектре.
Чем короче импульс, тем больше ширина частотного спектра.
Ширина ЧС определяется для прямоугольного импульса соотношением:
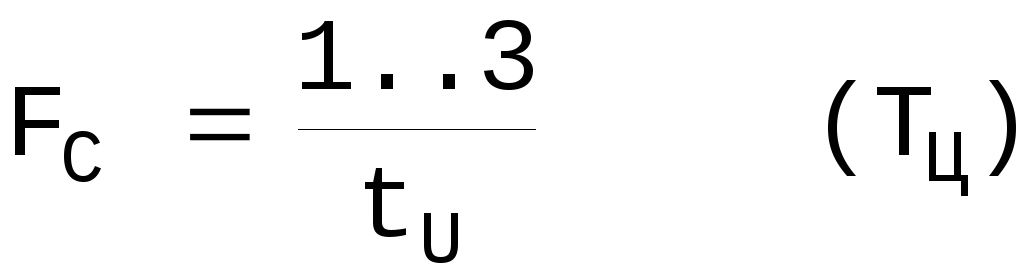
Это соотношение справедливо для идеальных прямоугольных импульсов.
Реальный импульс отличается от идеального более пологими фронтами.
Общая формула вычисления амплитуды гармоник для любого случая:
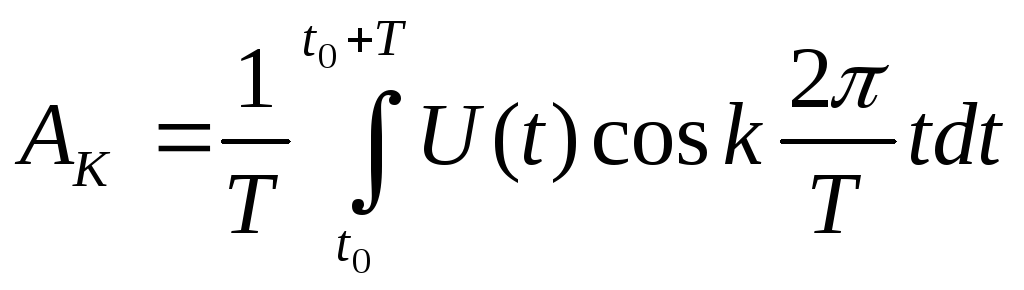
По сравнению с идеальным прямоугольным импульсом для реального импульса ЧС имеет более определенную частотную границу. Убывание амплитуд гармоник с частотой может иметь монотонный характер.
Эксперимент 2. Спектр гармонического сигнала с постоянным смещением.
Откройте файл с1_002 (рис. 1.2).
Для получения изображения спектральной характеристики гармонического сигнала, смещенного на постоянный уровень, необходимо на генераторе с помощью органа управления Off Set установить требуемое смещение, например равное 10 В, как показано на рис. 1.2а. Изображение такого сигнала на осциллографе приведено на рис. 1.26. После задания смещения, по команде Анализ > Запустить > Фурье…, получим на экране монитора изображение спектра сигнала в виде двух спектральных линий: постоянного смещения 10 В и гармоники с амплитудой 10 В и частотой 1 кГц, как показано на рис. 1.2в.
а)
Рис. 1.2, а. Результаты анализа по Фурье гармонического сигнала с постоянной составляющей: установка генератора
б)
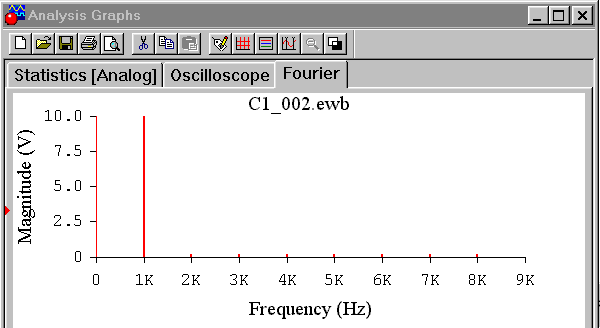в)
Рис. 1.2б, в. Результаты анализа по Фурье гармонического сигнала с постоянной составляющей: изображение на осциллографе (б), изображение спектра (в)
Эксперимент 3. Спектр симметричных импульсов прямоугольной формы.
Откройте файл с1_003 (рис. 1.3).
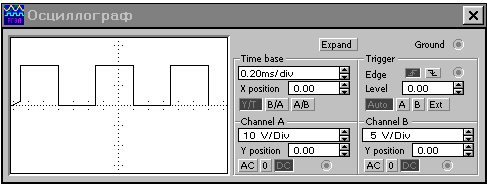
Теперь выполним разложение в ряд Фурье симметричного периодического напряжения прямоугольной формы. Для этого на генераторе функций установим соответствующее выходное напряжение с амплитудой 10 В и частотой 1 кГц, как показано на рис. 1.3а. Изображение этого напряжения можно увидеть на осциллографе, как показано на рис. 1.3б.
После подачи команды Анализ > Запустить > Фурье… в окне Analysis Graphs появится изображение спектральной характеристики сигнала, которое приведено на рис. 1.3в. Из этого рисунка видно, что спектр прямоугольного импульса состоит из набора нечетных гармоник, амплитуды которых убывают обратно пропорционально номеру гармоники. Так, например, первая гармоника имеет частоту 1 кГц и амплитуду, равную 12,74 В. Третья гармоника с частотой 3 кГц имеет амплитуду 4,25 В (т. е. в три раза меньше амплитуды первой гармоники). Пятая гармоника с частотой 5 кГц имеет амплитуду 2,55 В, а седьмая гармоника с частотой 7 кГц — 1,82 В. Четные гармоники в спектре сигнала отсутствуют. В спектре сигнала нет также постоянной составляющей.
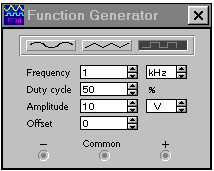
а) б)
в)
Рис. 1.3. Анализ по Фурье прямоугольного симметричного напряжения: установка генератора (а), изображение сигнала (б), спектральный состав (в)
Эксперимент 4. Спектр симметричных импульсов прямоугольной формы с постоянным смещением.
Откройте файл с1_004 (рис. 1.4).
Для получения однополярных симметричных прямоугольных импульсов нужно на генераторе функций установить постоянное напряжение смещения Off Set, например равное 10 В, как показано на рис. 1.4а. Изображение этого напряжения, которое появится на экране осциллографа, показано на рис. 1.4б.
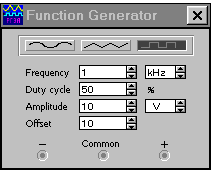
а) б)
i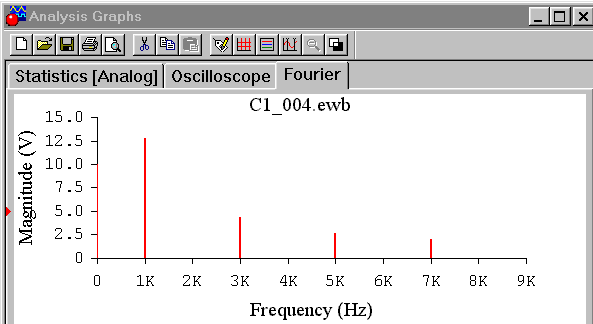
в)
Рис. 1.4. Анализ по Фурье смещенных прямоугольных импульсов: установка генератора (а), изображение сигнала (б) и его спектр (в)
После подачи команды Анализ > Запустить > Фурье… в окне Analysis Graphs можно увидеть частотный спектр этого сигнала, который отличается от рассмотренного выше спектра прямоугольных импульсов тем, что в нем присутствует постоянная составляющая, равная 10 В. Остальные спектральные составляющие не изменились.
Сравнение этих разложений в ряд Фурье с теоретическими значениями можно произвести, если воспользоваться данными теории. Так, для прямоугольных симметричных импульсов (эксперимент 3), спектральный состав которых определяется по формулам (1.1), имеем:
амплитуда первой гармоники Um1 = 4Am/ = 40/ =12,74 В;
амплитуда третьей гармоники Um3 = 4Am/(3) = 4,25 В;
амплитуда пятой гармоники Um5 = 4Am/(5) = 2,55 В.
Аналогичный расчет можно выполнить для смещенных прямоугольных импульсов (эксперимент 4), которые содержат постоянную составляющую Uo = Ат /2= 10 В. Расчетные формулы для этого сигнала приведены в (1.2). Эти значения полностью совпадают со значениями спектральных составляющих, полученных путем моделирования, что подтверждает корректность выполненного решения.
Спектр FM и PM
Содержание
Аналитическое выражение спектра сигналов с однотональной угловой модуляцией Анализ спектра сигнала с однотональной угловой модуляцией Общий случай спектра сигнала с угловой модуляциейВведение
В данной статье речь пойдет о спектре сигнала с угловой модуляцией. Сначала рассмотрим однотональную угловую модуляцию, после чего рассмотрим более общий случай при произвольном модулирующем сигнале. Необходимо отметить, что в аналитическом виде можно получить выражение для спектра только в случае однотональной угловой модуляции.Предварительно приведем некоторые математические соотношения из теории функций Бесселя и комплексных чисел, которые будут нам необходимы при анализе.
В математике доказывается, что функция раскладывается в бесконечный ряд:
| (1) |
где - функция Бесселя первого рода целого порядка аргумента , — мнимая единица. Аналогично функция представляется рядом:
| (2) |
Функции Бесселя также удовлетворяют соотношению:
| (3) |
Вспомним из теории комплексных функций что:
| (4) |
Аналитическое выражение спектра сигналов с однотональной угловой модуляцией
Итак, переходим к сигналам с угловой модуляцией. Сигнал с фазовой модуляцией может быть представлен выражением:| (5) |
где — модулирующий сигнал, — индекс фазовой модуляции, — несущая частота, — случайная начальная фаза несущего колебания. Рассмотрим случай однотональной фазовой модуляции, когда где — частота модулирующего сигнала, — начальная фаза модулирующего сигнала. Тогда
| (6) |
Учтем в (6) разложение (1) получим:
| (7) |
Разложим на три суммы:
| (8) |
Первое слагаемое (8) может быть представлено с учетом выражений (3) и (4):
| (9) |
Тогда
| (10) |
Представим экспоненты по формуле и Эйлера раскроем скобки:
| (11) |
Возьмем теперь реальную часть:
| (12) |
Анализ спектра сигнала с однотональной угловой модуляцией
Теперь разбираемся. Спектр бесконечен и состоит из гармоник кратных частоте модулирующего сигнала вправо и влево от центральной частоты. Амплитуды гармоник зависят от индекса модуляции . При этом пять слагаемых показывают поведение спектра.Первое слагаемое показывает, что амплитуды четных гармоник ниже центральной частоты равны , при этом фаза этих гармоник равна , при этом каждая четвертая гармоника, начиная со второй (2,6,10,14,18… гармоники) приобретает сдвиг на из-за множителя . Амплитудный и фазовый спектры для первого слагаемого сигнала представлены на рисунке 1 малиновым цветом.
Второе слагаемое показывает амплитуды и фазы нечетных гармоник ниже центральной частоты. Амплитуды нечетных гармоник ниже центральной частоты равны , а фазы . Сдвиг фазы на из-за того, что во вторую сумму входят синусы, а не косинусы. Как и в первом слагаемом каждая четвертая гармоника, начиная с первой (1,5,9,13,17…) приобретает сдвиг на из-за множителя . Амплитудный и фазовый спектры для второго слагаемого сигнала представлены на рисунке 1 синим цветом.
Третье слагаемое показывает гармонику несущей частоты. Ее амплитуда , фаза . На рисунке 1 гармоника центральной частоты — черная.
Четвертое слагаемое показывает амплитуды и фазы четных гармоник выше центральной частоты . Амплитуды такие же как и у четных гармоник ниже центральной частоты, а фазы равны , причем уже известный множитель сдвигает каждую четвертую фазу на , начиная со второй. На рисунке 1 гармоники четвертого слагаемого показаны красным цветом.
И наконец последнее пятое слагаемое соответствует нечетным гармоникам выше центральной. Амплитуды те же что и у нечетных гармоник ниже центральной частоты, фазы равны . Сдвиг фазы на из-за того, что в сумму входят синусы, а не косинусы, ну и конечно же каждая четвертая гармоника сдвинута на начиная с первой. На рисунке 1 гармоники пятого слагаемого показаны зеленым.
Рисунок 1: Амплитудный и фазовый спектры сигнала с фазовой модуляцией при m = 10
Несколько комментариев к рисунку 1. Полоса сигнала с угловой модуляцией по уровню 0,5 (-3 дБ) зависит от индекса модуляции и частоты модулирующего сигнала:
| (13) |
где — девиация частоты. Чем выше частота модулирующего сигнала и чем выше индекс модуляции, тем полоса сигнала шире. Из рисунка 1 хорошо видно, что при ровно 10 гармоник справа и слева имеют амплитуду выше половины максимума. На фазовом спектре показаны параллельные прямые проведенные через фазовый спектр касающиеся каждую четвертую гармонику и показывающие сдвиг фаз при изменении номера гармоники. При этом необходимо отметить, что приведенный на рисунке 1 фазовый спектр не учитывается периодичность фазы. Фазовый спектр с учетом периодичности фазы представлен на рисунке 2.
Рисунок 2: Фазовый спектр с учетом периодичности фазы
При этом полученный спектр с однотональной фазовой модуляцией при частоте модулирующего сигнала и индексе модуляции соответствует спектру сигнала с однотональной частотной модуляцией при девиации частоты Таким образом, однотональная фазовая и частотная модуляции неотличимы. Различия будут наблюдаться если частота модулирующего сигнала будет меняться. Рассмотрим это на конкретном примере.
Пусть имеется модулирующий сигнал с частотой 10 кГц.
| (14) |
Рассмотрим два сигнала — PM сигнал и — FM сигнал. Девиацию фазы при PM зададим , девиацию частоты при FM зададим . Несущую частоту обоих сигналов зададим равной
Амплитудные спектры FM и PM сигналов при данных параметрах приведены на рисунке 3.
Рисунок 3: Спектры FM и PM сигналов при частоте модулирующего сигнала 10 кГц
Амплитудные спектры получились одинаковые, так как при заданных параметрах FM сигнала получаем девиацию фазы FM сигнала как у PM . Таким образом, получили сигналы в полосе 200 кГц с одинаковым количеством гармоник справа и слева от несущей .
Теперь уменьшим частоту модулирующего сигнала в 2 раза, то есть Несущую частоту, а также девиацию частоты и фазы не меняем. Амплитудные спектры в этом случае приведены на рисунке 4.
Рисунок 4: Спектры FM и PM сигналов при частоте модулирующего сигнала 5 кГц
Спектры изменились. Давайте разберемся. Шаг между гармониками уменьшился в 2 раза (по сравнению с рисунком 3), так как шаг между гармониками равен частоте модулирующего сигнала, а она уменьшилась в 2 раза.
Поскольку при FM задается девиация частоты, то полоса FM сигнала не изменилась по сравнению с полосой FM сигнала на рисунке 3. Поскольку девиация частоты и девиация фазы связаны соотношением то девиация фазы при FM выросла в 2 раза за счет уменьшения частоты модулирующего сигнала (девиация частоты при FM не может изменятся).
Действительно, количество гармоник в полосе сигнала FM увеличилось в 2 раза. В PM, наоборот, задается девиация фазы, то есть количество гармоник в спектре, поэтому при уменьшении расстояния между гармониками девиация частоты PM сигнала уменьшается, в данном случае в 2 раза по сравнению с рисунком 3. Спектр PM как бы сжался по оси частот, не изменив формы, а спектр FM наоборот приобретает больше гармоник. Если же еще уменьшить частоту модулирующего колебания например до 2 кГц, то спектр FM останется таким же широким, так как девиация частоты не изменилась, но будет еще более насыщен гармониками, так как девиация фазы будет равна спектр PM же еще более «сожмется» оставив тоже количество гармоник. Девиация частоты при PM будет всего В этом можно убедится рассмотрев рисунок 5.
Рисунок 5: Спектры FM и PM сигналов при частоте модулирующего сигнала 2 кГц
Общий случай спектра сигнала с угловой модуляцией
В случае однотональной угловой модуляции спектр сигнала симметричен, однако в общем случае спектр сигнала с угловой модуляцией не является симметричным. Симметричность спектра возникает в том случае, когда форма модулирующего сигнала сверху и снизу будет одинакова на рисунке приведен пример модулирующего сигнала, угловая модуляция которого приведет к несимметричному относительно центральной частоты спектру. В обоих случаях центральная частота равна 200кГц.Рисунок 6: Несимметричный спектр FM и PM сигнала
Из рисунка явно видно, что спектры FM и PM сигналов несимметричны относительно 200 кГц, также формы спектров явно различаются. Несимметричность спектров сигналов с угловой модуляцией приводит к тому, что невозможно осуществить однополосную угловую модуляцию.
Выводы
Таким образом, мы получили аналитическое выражение для спектра сигнала с угловой модуляцией рассмотрели разницу FM и PM сигналов при изменении частоты модулирующего сигнала, а также показали несимметричность спектра сигнала с угловой модуляции при произвольном модулирующим сигнале.4. Подробнее о спектральном анализе сигналов | 7. Смешивание частот | Часть2
4. Подробнее о спектральном анализе сигналов
Подробнее о спектральном анализе сигналов
Компьютерный анализ Фурье (в частности алгоритм БПФ) является мощным инструментом, позволяющим лучше понять сигналы и связанные с ними спектральные компоненты. Математический алгоритм этого анализа запрограммирован в программе SPICE (в качестве параметра .fourier), а так же в различных измерительных приборах, которые выполняют анализ Фурье измеренных сигналов в режиме реального времени. Данная статья посвящена использованию таких инструментов и анализу различных сигналов.
Давайте начнем с простого синусоидального сигнала, частота которого составляет 523,25 Гц. В качестве примера мы взяли ноту «До» пианино, которая на одну октаву выше «middle C». На самом деле сигнал, измеренный для этой демонстрации, был создан клавишным электронным музыкальным инструментом, позволившим получить наиболее идеальную синусоиду. Нижеприведенный рисунок представляет собой экран осциллографа, показывающий амплитуду (напряжение) данного сигнала в течении длительного времени:
На экране осциллографа синусоида выглядит как волнистая кривая. Горизонтальная ось экрана обозначена словом «Время» и стрелкой в направлении увеличения времени. Сама кривая, конечно же, представляет собой циклическое увеличение и уменьшение напряжения с течением времени.
Приглядевшись внимательно к рисунку можно заметить неидеальность синусоидальной волны. Это обусловлено особенностями конкретного измерительного оборудования, используемого для анализа сигнала.
Если мы посмотрим на этот же сигнал в анализаторе спектра, то увидим совершенно другой результат:
Как видите, горизонтальная ось данного экрана обозначена словом «Частота», показывающим какой параметр мы анализируем. Единственный пик на кривой говорит нам о том, что в анализируемом сигнале преобладает только одна частота (фундаментальная). Если бы сетка экрана была помечена цифрами, то мы бы увидели, что этот пик приходится на частоту 523.25 Гц. Высота пика представляет собой амплитуду сигнала (напряжение).
Если мы смешаем три разных синусоидальных тона электронного клавишного инструмента (ноты До-Ми-Соль или До-мажорный аккорд) и измерим результат, то экраны осциллографа и анализатора спектра отобразят этот сложный сигнал следующим образом:
Экран осциллографа показывает волну с большим количеством пиков, чем в предыдущем примере, что является прямым результатом смешивания трех частот. Как вы наверное заметили, некоторые из этих пиков превышают пиковые значения однотонового сигнала, а некоторые наоборот, имеют меньшие значения. Все это происходит потому, что три различных сигнала поочередно усиливают и ослабляют друг друга в соответствии с изменениями их фазовых сдвигов во времени.
Показания анализатора спектра интерпретировать гораздо легче: каждый «тон» здесь представлен собственным пиком на кривой. Различие в высотах этих пиков объясняется «особенностями» испытательного оборудования, а не характеристиками самого музыкального аккорда.
Как уже было сказано ранее, устройство, используемое для создания этих сигналов, представляет собой клавишный электронный музыкальный инструмент. Для первых экспериментов данный инструмент был выбран в связи с тем, что производимые им сигналы наиболее близко напоминают синусоиду. Сигнал, производимый другим музыкальным инструментом — трубой — не так прост, как рассмотренные выше:
Фундаментальная (основная) частота этого сигнала такая же, как и в первом примере — 523,25 Гц, но его форма далека от чистой синусоиды. Зная, что любой повторяющийся несинусоидальный сигнал эквивалентен последовательности синусоидальных сигналов с различными амплитудами и частотами, мы ожидали, что увидим несколько пиков на экране анализатора спектра:
Наши ожидания оправдались! Фундаментальная частота 523,25 Гц представлена крайним левым пиком, а каждая последующая гармоника представлена собственным пиком на экране анализатора спектра. Вторя гармоника двукратна фундаментальной частоте (1046,5 Гц), третья гармоника трехкратна фундаментальной частоте (1569,75 Гц), и так далее. Этот рисунок показывает только первые шесть гармоник сложного сигнала, но на самом деле их гораздо больше.
Давайте проанализируем другой сложный сигнал, произведенный таким музыкальным инструментом, как аккордеон. Показания осциллографа и анализатора спектра в этом случае будут следующими:
Обратите внимание на различия в величинах амплитуд гармоник (высот пиков) трубы и аккордеона, отображенные на соответствующих экранах анализаторов спектров. Оба прибора отображают с первой (фундаментальной) по шестую гармоники, но их пропорции не совпадают. Это говорит о том, что каждый инструмент имеет уникальную гармоническую сигнатуру в своем тоне. Примите во внимание, что эти сложные сигналы представляют собой одну ноту, проигранную двумя разными инструментами. Несколько нот, сыгранных, например, на аккордеоне, создадут гораздо более сложную смесь частот, чем представлено здесь.
Аналитические возможности осциллографа и анализатора спектра позволяют нам сформировать общие представления о сигналах и их гармонических спектрах на примерах реальных осциллограмм. Мы уже знаем, что любое отклонение сигнала от синусоидальной формы приводит к эквивалентной смеси нескольких синусоидальных сигналов различных амплитуд и частот. Однако, анализ большего количества сигналов, имеющих разные формы, позволяет получить нам больше конкретики. Обратите внимание на временной и частотный анализ сигнала, форма которого близка к прямоугольной:
Согласно показаниям анализатора спектра, этот сигнал не содержит четных гармоник, в его составе есть только нечетные гармоники. Несмотря на то, что экран прибора не показывает частоты дальше шестой гармоники, последовательность нечетных гармоник в порядке убывания амплитуды будет продолжаться бесконечно. Это не должно вас удивлять, так как ранее при помощи SPICE анализа мы с вами убедились, что прямоугольный сигнал состоит из бесконечности нечетных гармоник. Однако, тоны трубы и аккордеона содержат как четные, так и нечетные гармоники. Эта разница в содержании гармоник заслуживает внимания. Давайте продолжим наше исследование и проанализируем треугольный сигнал:
В этом сигнале практически отсутствуют четные гармоники, все значимые пики частот на экране анализатора спектра принадлежат нечетным гармоникам. Крошечные пики можно увидеть на второй, четвертой и шестой гармониках, но они обусловлены неидеальностью конкретного треугольного сигнала. Идеальный треугольный сигнал не производит четных гармоник, точно так же, как их не производит идеальный прямоугольный сигнал. Из проведенных исследований очевидно, что гармонический спектр треугольного сигнала не идентичен спектру прямоугольного сигнала: соответствующие гармонические пики имеют разную высоту. Тем не менее, два этих сигнала идентичны в том, что у них отсутствуют четные гармоники.
Давайте исследуем еще один сигнал, очень похожий на треугольный. Называется этот сигнал пилообразным, и отличается от треугольного тем, что время его нарастания превышает время падения. На экране осциллографа данный сигнал будет выглядеть подстать своему названию:
Когда мы проведем спектральный анализ этого сигнала, то увидим результат, довольно сильно отличающийся от спектрального анализа треугольного сигнала. Здесь мы увидим довольно сильное присутствие четных гармоник (второй и четвертой):
Отличие сигналов имеющих четные гармоники от сигналов не имеющих четных гармоник заключается в различии форм этих сигналов. Данное различие определяется симметрией выше и ниже горизонтальной центральной (осевой) линии. Сигнал, который симметричен выше и ниже центральной линии не будет содержать четных гармоник:
Все вышепоказанные сигналы (прямоугольный, треугольный, синусоидальный) обладают такой симметрией, а следовательно, не содержат четных гармоник. Сигналы, производимые трубой и аккордеоном, а также пилообразные сигналы не симметричны относительно центральной линии, а значит, они содержат четные гармоники.
Не стоит путать принцип симметрии центральной линии с симметрией вокруг нулевой линии. Во всех рассмотренных примерах центральная линия на экране осциллографа совпадает с нулевой (0 вольт). Если нулевая линия будет смещена вверх или вниз, то это никак не отразится на гармоническом содержании сигнала. Для примера мы покажем те же самые сигналы, нулевая линия в которых смещена относительно осевой:
Почему это эмпирическое правило гармоник так важно знать? Оно может помочь вам понять взаимоотношения между гармониками в цепях переменного тока и конкретными компонентами схемы. Поскольку большинство источников искажения синусоидальных сигналов в силовых цепях переменного тока, как правило, симметричны, четные гармоники в них можно увидеть достаточно редко. Это полезно знать, если вы проектируете системы энергоснабжения и заранее планируете устранение или минимизацию гармоник. В этом случае вам нужно будет позаботиться только о нечетных гармониках. Кроме того, если вам придется измерять гармоники в цепи переменного тока при помощи анализатора спектра или частотомера, вы будете знать, что что-то в этой цепи дает несимметричные искажения синусоидального сигнала напряжения или тока, и эта подсказка может быть полезной в локализации источника проблемы (вам нужно искать компоненты или условия, которые наиболее вероятно искажают один полупериод сигнала больше, чем другой).
Теперь вам должно быть понятно, почему сигнал, произведенный схемой выпрямителя из предыдущей статьи, содержит такие сильные четные гармоники. У этого сигнала вообще нет никакой симметрии относительно центральной (осевой) линии.
