Построение таблиц истинности и логических функций

Похожие презентации:

Пиксельная картинка

Информационная безопасность. Методы защиты информации

Электронная цифровая подпись (ЭЦП)

Этапы доказательной медицины в работе с Pico. Первый этап

История развития компьютерной техники

От печатной книги до интернет-книги

Краткая инструкция по CIS – 10 шагов

Информационные технологии в медицине

Информационные войны

Моя будущая профессия. Программист

1. Построение таблиц истинности и логических функций

Автор: Воронова Светлана Аркадьевна,
преподаватель ГБПОУ ВО «ВАМК»

2. Алгоритм построения таблиц истинности для сложных выражений

1. Определить количество строк:
количество строк = 2n + строка для заголовка
n — количество простых высказываний
2. Определить количество столбцов:
количество столбцов = количество переменных +
количество логических операций
3. Заполнить столбцы результатами
выполнения логических операций в
обозначенной последовательности с
учетом таблиц истинности основных
логических операций.

3. ПРИМЕР

Составить таблицу истинности логического
выражения: D = ¬ А & (B V C)
1. Определить количество строк: на входе три
простых высказывания: А, В, С поэтому n=3 и
количество строк = 23 +1 = 9
9 строк
2. Определить количество столбцов:
А, В, С, ¬ А, B V C, D
6 столбцов
3. Заполнить столбцы с учетом таблиц истинности
логических операций
A
B
C
¬А
BVC
¬ А & (B V C)
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
1
1
1
0
0
0
0
0
1
1
1
0
1
1
1
0
1
1
1
0
0
0
0

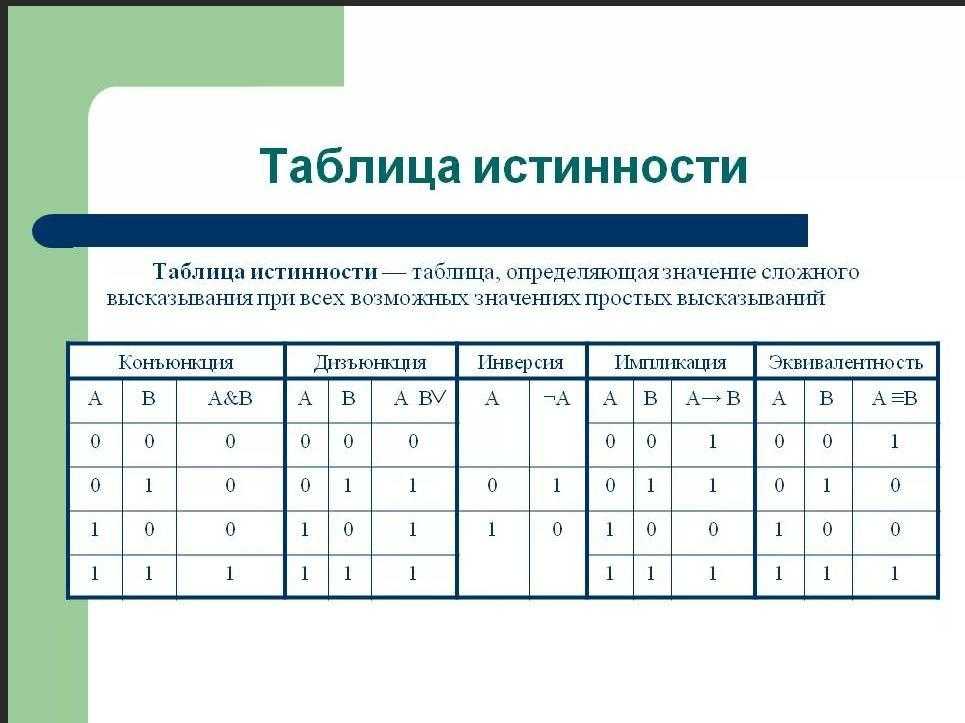
5. Алгоритм построения логической функции по таблице истинности

1. Выделить в таблице истинности те строки, в
которых значение функции равно 1
2. Выписать искомую формулу в виде дизъюнкции
нескольких логических элементов. Число этих
элементов равно числу выделенных строк.
3. Каждый логический элемент в этой дизъюнкции
записать в виде конъюнкции аргументов
функции.
4. Если значение какого-либо аргумента функции в
соответствующей строке таблице равно 0, то этот
аргумент взять с отрицанием.
Пусть дана таблица истинности для некоторой
логической функции Z(X,Y)
X
Y
Z
0
0
1
0
1
0
1
0
1
1
1
0
В первой и третьей строках таблицы истинности
значение функции равно 1.
1. В первой и третьей строках таблицы истинности
значение функции равно 1.
2. Так как строки две, получаем дизъюнкцию двух
элементов: ( ) V ( ).
3. Каждый логический элемент в этой дизъюнкции
запишем в виде конъюнкции аргументов
функции X и Y: (X & Y) V (X & Y).
4. Берем аргумент с отрицанием если его значение в
соответствующей строке таблицы равно 0 и

получаем искомую функцию:
Z (X, Y) =(¬ X & ¬Y) V (X & ¬Y).

English     Русский Правила

404 Cтраница не найдена

Размер:

AAA

Цвет: C C C

Изображения Вкл. Выкл.

Обычная версия сайта

Контакты Версия для слабовидящих Версия для слабовидящих

Санкт-Петербургский техникум железнодорожного транспорта

структурное подразделение федерального государственного бюджетного образовательного учреждения высшего образования «Петербургский государственный университет путей сообщения Императора Александра I»

• О техникуме
  • Сведения об образовательной организации
  • История
  • Структура
  • Руководство
  • Преподаватели и сотрудники
  • Лицензии
  • Новости
  • Фотогалерея
  • Видеогалерея
  • Контакты
  • Противодействие коррупции
  • Напишите нам
• Абитуриенту
  • Приемная комиссия
  • Часто задаваемые вопросы
  • Платное обучение
  • Специальности
  • Учебные корпуса
  • Жилье иногородним
  • Фотогалерея
  • Видеогалерея
  • Одежда обучающихся
• Студенту
  • Расписание
  • Консультации
  • Государственная итоговая аттестация
  • Система дистанционного обучения
  • Учебно-методические материалы
  • Библиотека
  • Заочное отделение
  • Олимпиада профессионального мастерства
  • Демонстрационный экзамен
  • Производственная практика
  • Чемпионаты профессионального мастерства
  • Региональный этап Чемпионата по профессиональному мастерству «Профессионалы» (10-28 апреля 2023 г. )
  • Общежитие
  • Стипендии
  • Платное обучение
  • Социальная поддержка
  • Студенческая жизнь
  • Спортивная жизнь
  • Студенческое самоуправление
  • Одежда обучающихся
  • Единый государственный экзамен
• Сотруднику
  • Коллективный договор
  • Локальные нормативные акты
  • Педагогический совет
  • Профсоюзная организация
  • Медицинский осмотр
  • Система дистанционного обучения
• Контакты

• Главная

Таблицы истинности — KnowItAllNinja

Мы рассмотрели, как можно изобразить логические схемы в виде диаграмм с входами и выходами. Другой способ представить их — нарисовать схему в виде таблицы истинности.

Таблица истинности представляет собой простую сетку, которая показывает все входные данные и все возможные выходные данные. Мы можем использовать их, чтобы понять, что делает наша схема. Это особенно полезно, когда мы начинаем комбинировать логические вентили.

Мы также можем выразить наши логические вентили с помощью булевой алгебры, где мы записываем логику наших вентилей в виде логического выражения.

В этом уроке мы узнаем о:

1. Что такое таблицы истинности
2. Таблица истинности для вентиля НЕ
3. Таблица истинности для вентиля И
4. Таблица истинности для вентиля ИЛИ

Медиа Приложения: Презентационное видео

1. Что такое таблицы истинности

Таблицы истинности используются для отображения выходных данных логического элемента и логических схем (где мы объединяем более одного логического элемента вместе).

Мы создаем их, рисуя таблицу со столбцами для каждого из входов и выходов в нашей логической схеме. В таблице также должно быть достаточно строк для представления всех возможных комбинаций входных данных.

Например, если у вас есть два входа (которые всегда являются двоичными числами), то у нас могут быть следующие комбинации: четыре строки в нашей таблице истинности.

Таблицы истинности становятся чрезвычайно важными, когда мы начинаем проектировать более крупные схемы, чтобы помочь нам точно определить, какие выходные данные производятся этими комбинациями вентилей.

Дополнительные мысли

Мы часто выражаем схемы булевой логики с помощью булевой алгебры. Изучите, что это такое.

2. Таблица истинности для вентиля НЕ

Мы видели, как вентиль НЕ представлен в виде логической схемы. Это выглядит как на рисунке 1 ниже.

Рисунок 1. Шлюз НЕ.

Существует только ОДИН возможный вход, который может быть либо 1, либо 0.

Мы рисуем это в виде таблицы истинности следующим образом: 1 0 0 1

Вот и все. Если вы введете 1, на выходе будет 0. Если вы введете 0, на выходе будет 1.

Таблица истинности имеет ОДИН вход, который может иметь ДВЕ ВОЗМОЖНЫЕ КОМБИНАЦИИ, поэтому в таблице истинности есть ДВЕ строки.

Если бы мы хотели записать это как логическое выражение, мы могли бы написать это как Q = NOT X.

Дополнительные мысли

Что произойдет, если вы объедините логический элемент НЕ с логическим элементом И или ИЛИ?

3. Таблица истинности для вентиля И

Мы видели, что схема И представляет собой два переключателя один за другим.

Свет будет гореть, только если ОБА переключателя замкнуты.

Рисунок 2 – схема И с обоими замкнутыми переключателями.

Если свет горит, это означает, что у нас есть выход 1.

Мы нарисовали это как логический элемент И на логической схеме, как показано на рисунке 3.

Рисунок 3 – логический элемент И

Для этой таблицы истинности мы можем видим, что у нас есть два входа с двумя возможными комбинациями, поэтому у нас есть ЧЕТЫРЕ строки в таблице истинности.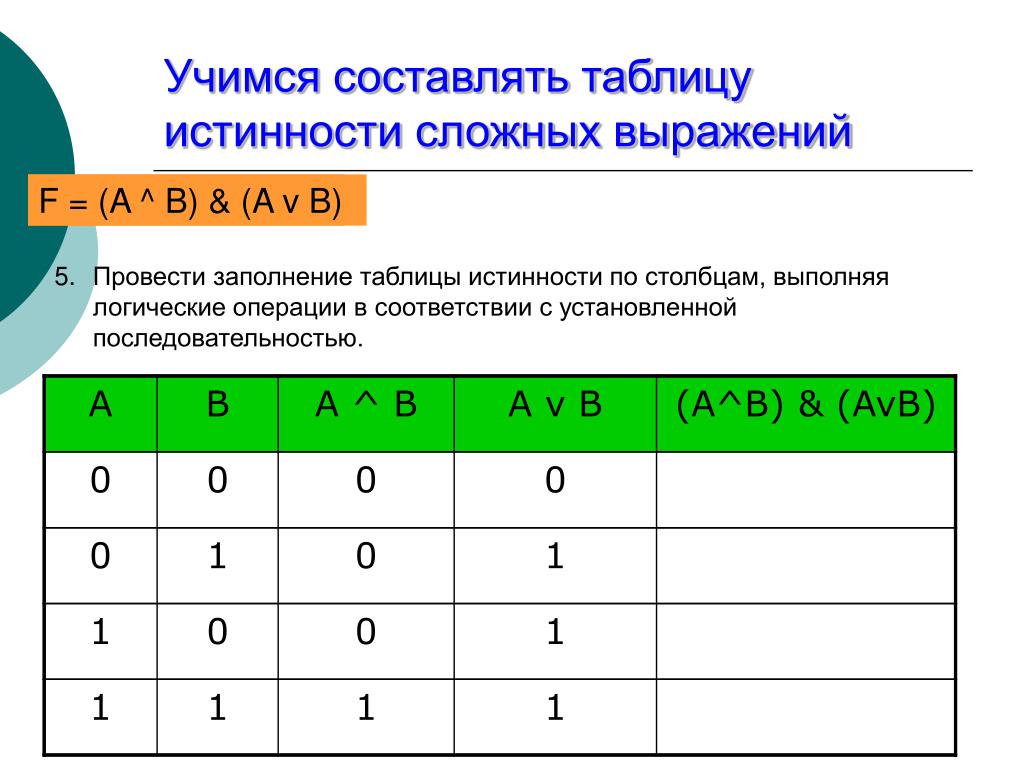

Чтобы построить таблицу истинности, нужно записать все возможные комбинации входных данных. Поскольку у нас есть два входа двоичных чисел, каждое из них может быть 1 или 0. Таким образом, все комбинации следующие:

188

Вход X	Вход Y	Выход Q
1
1	0
0	1
0	0

После того, как мы настроили нашу таблицу истинности с нашими входными данными, мы можем записать наши выходные данные. Помните, что с логическим элементом И мы получаем выход 1 только в том случае, если ОБА входа равны 1.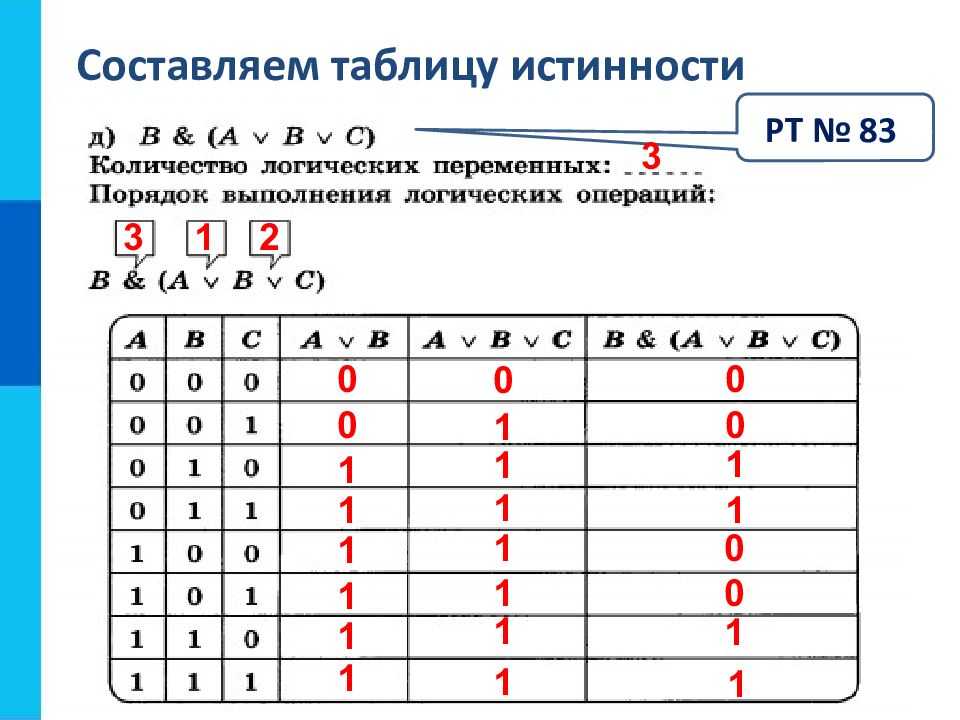 В противном случае выход равен 0. 1 1 1 0 0 0 1 0 0 0 0

, если мы хотели написать это как выпускное выражение.

Сколько строк у вас было бы, если бы у вас было 3 входа?

4. Таблица истинности для схемы ИЛИ

Мы видели, что схема ИЛИ представляет собой два переключателя, включенных параллельно.

Если замкнут ОДИН из выключателей, загорится свет.

Рисунок 4 – схема ИЛИ с одним замкнутым переключателем и одним разомкнутым переключателем.

Мы нарисовали это как вентиль ИЛИ на логической схеме, как показано на рисунке 5.

Рисунок 5 – Логический вентиль ИЛИ

Для этой таблицы истинности нам снова нужно записать все возможные комбинации входных данных. Поскольку он имеет два входа, он имеет те же комбинации, что и для логического элемента И.

Вход X	Вход Y	Выходные0121
0	1
0	0

. Помните, что с вентилем ИЛИ мы получаем на выходе 1, если ОДИН ИЛИ ОБА входа равны 1. В противном случае выход равен 0. 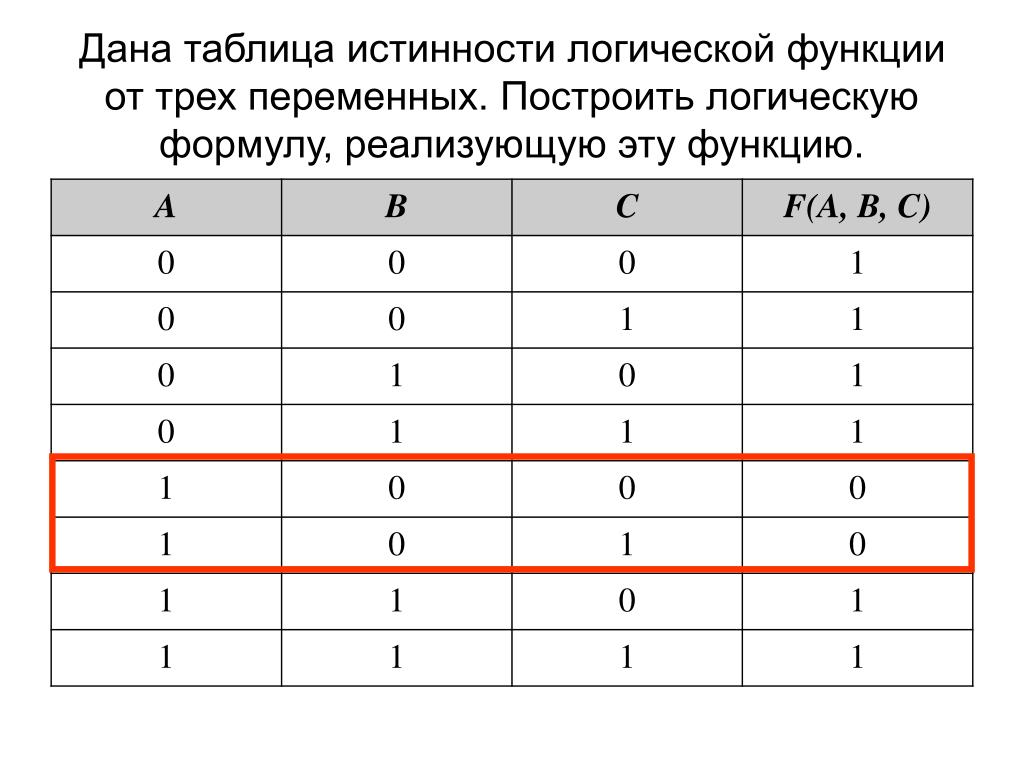1 1 1 0 1 0 1 1 0 0 0 0 0 0 0 0. как Q = X OR Y.

Дополнительные мысли

Существует такая вещь, как вентиль исключающее ИЛИ. Чем это отличается от стандартных ворот ИЛИ?

Итоги урока

Итак, подведем итог тому, что мы узнали на этом уроке:

• Таблицы истинности — это способы суммирования вывода любого входа в логическую схему.
• При заполнении таблицы истинности мы должны сначала определить все возможные комбинации входных данных.
• Вывод таблицы истинности НЕ противоположен вводу.
• Выход таблицы истинности по И равен 1, когда оба входа равны 1, в противном случае он равен 0.
• Выход таблицы истинности по ИЛИ равен 0, когда оба входа равны 0, иначе он равен 1.

Продолжить …

Таблицы истинности булевой алгебры — Electronics-Lab.com

Таблицы истинности булевой алгебры

Цифровая логическая схема может быть представлена ​​уравнением в форме Логическое выражение

, которое описывает взаимосвязь входов и выходов каждого логического элемента с другими. Общая функция логического выражения и каждой отдельной логики также может быть выражена в форме таблицы, которая называется таблицей истинности. Логическое выражение цифровой схемы используется для построения таблицы истинности для соответствующей функции. Таблица истинности состоит из входов и выходов. Общее количество входов, доступных для цифровой логической схемы, составляет входы и строится для каждого возможного состояния или комбинации. Функция каждого логического элемента и всей цифровой схемы представляет собой выход. Эти выходы определяются для каждого возможного состояния или комбинации входов.

Количество возможных состояний или комбинаций можно рассчитать по следующей формуле:

Количество входных состояний или комбинаций = 2 ⁿ

Где «n» представляет общее количество входов цифровую логику ворота или цепь.

Например, используя приведенную выше формулу, всего возможно четыре (4) комбинации состояний для двух входов.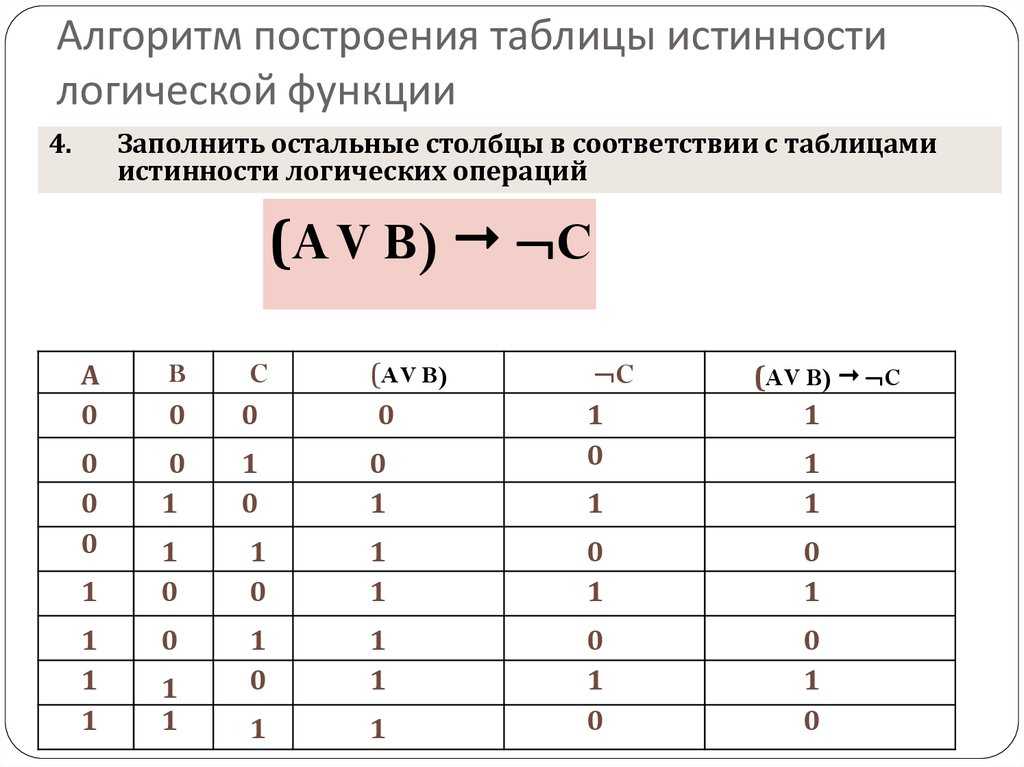 Как уже известно из предыдущих статей, состояния входа и выхода логических элементов представлены в виде данных логической логики, который имеет только два состояния, т. е. «ВКЛ» = «1» = «ИСТИНА» и «ВЫКЛ» = «0» = « ЛОЖЬ». Однако в таблицах истинности чаще всего состояния представлены логическими типами «1» и «0», которые также равны битовым значениям. Комбинации состояний для двух входов (X и Y):

Комбинация входных данных 1 = [X=0, Y=0]

Комбинация входов 2 = [X=0, Y=1]

Комбинация входных данных 3 = [X=1, Y=0]

Комбинация ввода 4 = [X=1, Y=1]

Для логического элемента или схемы с тремя входами всего восемь (8) комбинаций , используя приведенную выше формулу. Комбинации состояний для двух входов (X, Y и Z):

Комбинация входов 1 = [X=0, Y=0, Z=0]

Комбинация входных данных 2 = [X=0, Y=0, Z=1]

Комбинация входных данных 3 = [X=0, Y=1 Z=0]

Комбинация входных данных 4 = [X=0, Y=1, Z=1]

Комбинация входных данных 5 = [X=1, Y=0, Z=0]

Комбинация ввода 6 = [X=1, Y=0, Z=1]

Комбинация входных данных 7 = [X=1, Y=1, Z=0]

Комбинация ввода 8 = [X=1, Y=1, Z=1]

Аналогично, логический элемент или схема с четырьмя входами может иметь всего 16 возможных комбинаций . Однако в этой статье для простоты не используется логический элемент или схема с более чем тремя входами. Таблицы истинности, построенные для двух и трех входов, представляют собой логику, которую можно использовать для построения таблиц истинности для цифровой схемы, имеющей любое количество входов.

Таблицы истинности логических вентилей вместе с их символами и выражениями приведены ниже.

Строб NOT

Это вентиль с одним входом, который инвертирует или дополняет вход. Например, он выводит «ИСТИНА» или «1», когда ввод «ЛОЖЬ» или «0», и наоборот.

Элемент ИЛИ

Элемент ИЛИ выводит «ИСТИНА» или «1» для всех комбинаций входов, за исключением случаев, когда все его входы равны «ЛОЖЬ» или «0».

Для двухвходовых вентилей ИЛИ:

Для логического элемента ИЛИ с тремя входами:

логического элемента И

Логический элемент И выводит «ИСТИНА» или «1», только если все его входы имеют значение «ИСТИНА» или «1».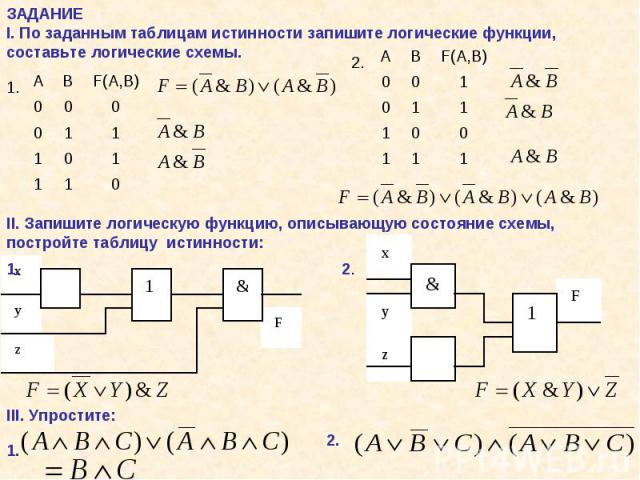

Для вентиля И с двумя входами:

Для вентиля И с тремя входами:

Вентиль ИЛИ-НЕ

Вентиль ИЛИ-НЕ расположен в перевернутой форме вентиля ИЛИ, т.е. в воротах ИЛИ составляют ворота ИЛИ. Он выводит «ЛОЖЬ» или «0» для всех комбинаций входов, за исключением случаев, когда все его входы равны «ЛОЖЬ» или «0».

Для вентиля ИЛИ с двумя входами:

Для вентиля ИЛИ с тремя входами:

Вентиль И-НЕ

Вентиль И-НЕ расположен в инвертированном вентиле И. вентиля И, составляющего вентиль И-НЕ. Он выводит «ЛОЖЬ» или «0» только тогда, когда все его входы «ИСТИНА» или «1».

Для вентиля И-НЕ с двумя входами:

Для вентиля И-НЕ с тремя входами:

Кроме того, упомянутые выше логические элементы, исключающее ИЛИ (XOR) и исключающее ИЛИ (XNOR), представляют собой наиболее широко и часто используемую логику. Эти логические схемы используются в арифметических вычислениях, схемах проверки данных и т. д. Из-за их важности в логических схемах они доступны в цифровых микросхемах. пакеты и настоящим включены в статью.

Логический элемент исключающее ИЛИ (исключающее ИЛИ)

Логический элемент исключающее ИЛИ (исключающее ИЛИ) выводит «ИСТИНА» или «1», если любой из входов находится в состоянии «ИСТИНА» или «1». Его выход «ЛОЖЬ» или «0», когда входы находятся в одинаковом состоянии.

Для логического элемента XOR с двумя входами:

Для логического элемента XOR с тремя входами:

Строб Exclusive-NOR (XOR)

(XOR) ворота. Его выход «FLASE» или «0», если любой из входов находится в состоянии «TRUE» или «1». Его выход «ИСТИНА» или «1», когда входы находятся в одном и том же состоянии.

Для логического элемента XNOR с двумя входами:

Для логического элемента XNOR с тремя входами:

Пример таблицы истинности

На следующем рисунке таблица истинности построена из данной логической схемы.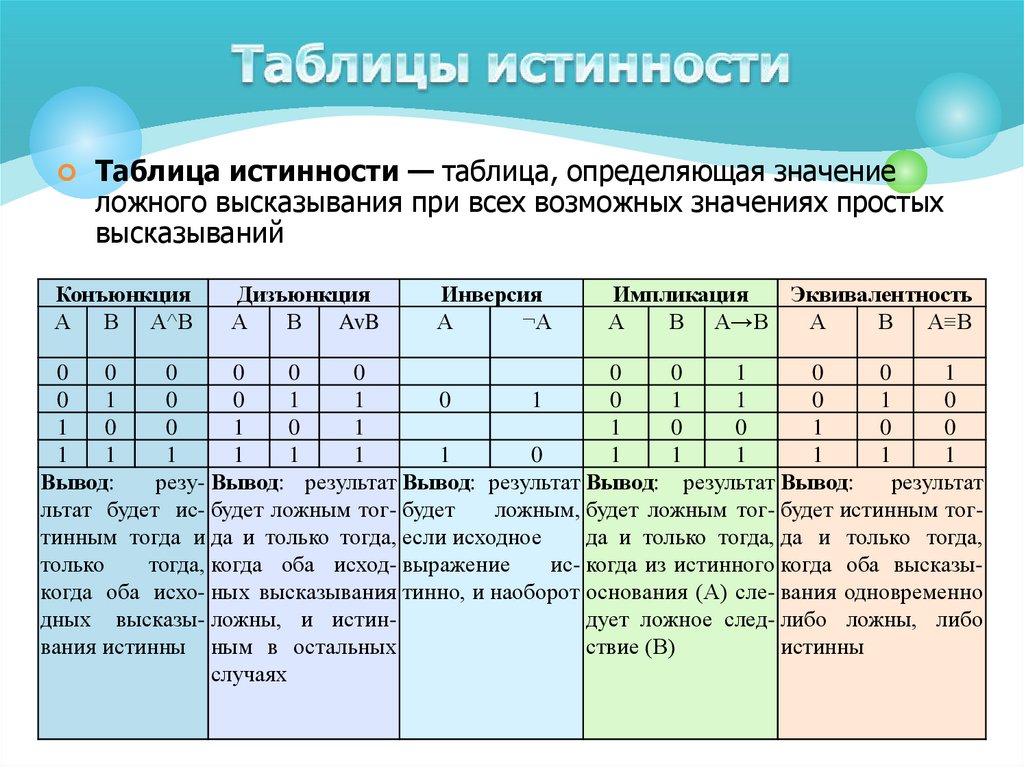