Элементарный учебник физики Т2
Элементарный учебник физики Т2
ОглавлениеИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮГлава I. Электрические заряды § 1. Электрическое взаимодействие. § 2. Проводники и диэлектрики. § 3. Разделение тел на проводники и диэлектрики § 4. Положительные и отрицательные заряды § 5. Что происходит при электризации? § 6. Электронная теория. § 7. Электризация трением. § 8. Электризация через влияние. § 9. Электризация под действием света. § 10. Закон Кулона. § 11. Единица заряда. Глава II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ § 12. Действие электрического заряда на окружающие тела. § 13. Понятие об электрическом поле. § 14. Напряженность электрического поля. § 16. Электрическое поле в диэлектриках и в проводниках. § 17. Графическое изображение полей. § 18. Основные особенности электрических карт. § 19. Применение метода линий поля к задачам электростатики. § 20. Работа при перемещении заряда в электрическом поле.  § 21. Разность потенциалов (электрическое напряжение). § 22. Эквипотенциальные поверхности. § 23. В чем смысл введения разности потенциалов? § 24. Условия равновесия зарядов в проводниках. § 25. Электрометр. § 26. В чем различие между электрометром и электроскопом? § 28. Измерение разности потенциалов в воздухе. Электрический зонд. § 29. Электрическое поле Земли. § 30. Простейшие электрические поля. § 31. Распределение зарядов в проводнике. Клетка Фарадея. § 32. Поверхностная плотность заряда. § 33. Конденсаторы. § 34. Различные типы конденсаторов. § 35. Параллельное и последовательное соединение конденсаторов. § 36. Диэлектрическая проницаемость. § 37. Почему электрическое поле ослабляется внутри диэлектрика? § 38. Энергия заряженных тел. Энергия электрического поля. Глава III. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 39. Электрический ток и электродвижущая сила.  § 41. Направление тока. § 42. Сила тока. § 43. «Скорость электрического тока» и скорость движения носителей заряда. § 44. Гальванометр. § 45. Распределение напряжения в проводнике с током. § 46. Закон Ома. § 47. Сопротивление проводов. § 48. Зависимость сопротивления от температуры. § 49. Сверхпроводимость. § 50. Последовательное и параллельное соединение проводников. § 51. Реостаты. § 52. Распределение напряжения в цепи. § 53. Вольтметр. § 54. Каким должно быть сопротивление вольтметра и амперметра? Глава IV. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА § 56. Нагревание током. Закон Джоуля-Ленца. § 57. Работа, совершаемая электрическим током. § 58. Мощность электрического тока. § 59. Контактная сварка. § 60. Электрические нагревательные приборы. Электрические печи. § 61. Понятие о расчете нагревательных приборов. § 62. Лампы накаливания. § 63. Короткое замыкание. § 64.  Электрическая проводка.Глава V. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ЭЛЕКТРОЛИТЫ § 65. Первый закон Фарадея. § 66. Второй закон Фарадея. § 67. Ионная проводимость электролитов. § 69. Элементарный электрический заряд. § 70. Первичные и вторичные процессы при электролизе. § 71. Электролитическая диссоциация. § 72. Градуировка амперметров при помощи электролиза. § 73. Технические применения электролиза. Глава VI. ХИМИЧЕСКИЕ И ТЕПЛОВЫЕ ГЕНЕРАТОРЫ ТОКА § 74. Введение. Открытие Вольты. § 75. Правило Вольты. Гальванический элемент. § 76. Как возникают э. д. с. и ток в гальваническом элементе? § 77. Поляризация электродов. § 78. Деполяризация в гальванических элементах. § 79. Аккумуляторы. § 80. Закон Ома для замкнутой цепи. § 81. Напряжение на зажимах источника тока и э. д. с. § 83. Термоэлементы. § 84. Термоэлементы в качестве генераторов.  § 85. Измерение температуры с помощью термоэлементов. Глава VII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ МЕТАЛЛЫ § 86. Электронная проводимость металлов. § 87. Строение металлов. § 88. Причина электрического сопротивления. § 89. Работа выхода. § 90. Испускание электронов накаленными телами. Глава VIII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ГАЗЫ § 91. Самостоятельная и несамостоятельная проводимость газов. § 92. Несамостоятельная проводимость газа. § 94. Молния. § 95. Коронный разряд. § 96. Применения коронного разряда. § 97. Громоотвод. § 98. Электрическая дуга. § 99. Применения дугового разряда. § 100. Тлеющий разряд. § 101. Что происходит при тлеющем разряде? § 102. Катодные лучи. § 103. Природа катодных лучей. § 104. Каналовые лучи. § 105. Электронная проводимость в высоком вакууме. § 106. Электронные лампы. § 107. Электроннолучевая трубка. Глава IX. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ПОЛУПРОВОДНИКИ § 108.  Природа электрического тока в полупроводниках.§ 110. Полупроводниковые выпрямители. § 111. Полупроводниковые фотоэлементы. Глава X. ОСНОВНЫЕ МАГНИТНЫЕ ЯВЛЕНИЯ § 112. Естественные и искусственные магниты. § 113. Полюсы магнита и его нейтральная зона. § 114. Магнитное действие электрического тока. § 115. Магнитные действия токов и постоянных магнитов. § 116. Происхождение магнитного поля постоянных магнитов. § 117. Гипотеза Ампера об элементарных электрических токах. Глава XI. МАГНИТНОЕ ПОЛЕ § 118. Магнитное поле и его проявления. Магнитная индукция. § 119. Магнитный момент. Единица магнитной индукции. § 120. Измерение магнитной индукции поля с помощью магнитной стрелки. § 122. Линии магнитного поля. § 123. Приборы для измерения магнитной индукции. Глава XII. МАГНИТНЫЕ ПОЛЯ ЭЛЕКТРИЧЕСКИХ ТОКОВ § 124. Магнитное поле прямолинейного проводника и кругового витка с током.  § 125. Магнитное поле соленоида. Эквивалентность соленоида и полосового магнита. § 126. Магнитное поле внутри соленоида. Напряженность магнитного поля. § 127. Магнитное поле движущихся зарядов. Глава XIII. МАГНИТНОЕ ПОЛЕ ЗЕМЛИ § 128. Магнитное поле Земли. § 129. Элементы земного магнетизма. § 131. Изменение элементов земного магнетизма с течением времени. Магнитные бури. Глава XIV. СИЛЫ, ДЕЙСТВУЮЩИЕ В МАГНИТНОМ ПОЛЕ НА ПРОВОДНИКИ С ТОКОМ § 132. Введение. § 133. Действие магнитного поля на прямолинейный проводник с током. Правило левой руки. § 134. Действие магнитного поля на виток или соленоид с током. § 135. Гальванометр, основанный на взаимодействии магнитного поля и тока. § 136. Сила Лоренца. § 137. Сила Лоренца и полярные сияния. Глава XV. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 138. Условия возникновения индукционного тока. § 139. Направление индукционного тока.  § 140. Основной закон электромагнитной индукции. § 141. Электродвижущая сила индукции. § 142. Электромагнитная индукция и сила Лоренца. § 143. Индукционные токи в массивных проводниках. Токи Фуко. Глава XVI. МАГНИТНЫЕ СВОЙСТВА ТЕЛ § 144. Магнитная проницаемость железа. § 145. Магнитная проницаемость различных веществ. Вещества парамагнитные и диамагнитные. § 146. Движение парамагнитных и диамагнитных тел в магнитном поле. Опыты Фарадея. § 147. Молекулярная теория магнетизма. § 148. Магнитная защита. § 149. Особенности ферромагнитных тел. § 150. Основы теории ферромагнетизма. § 151. Постоянная и переменная электродвижущая сила. § 152. Опытное исследование формы переменного тока. Осциллограф. § 153. Амплитуда, частота и фаза синусоидального переменного тока и напряжения. § 154. Сила переменного тока. § 155. Амперметры и вольтметры переменного тока. § 156. Самоиндукция. § 157. 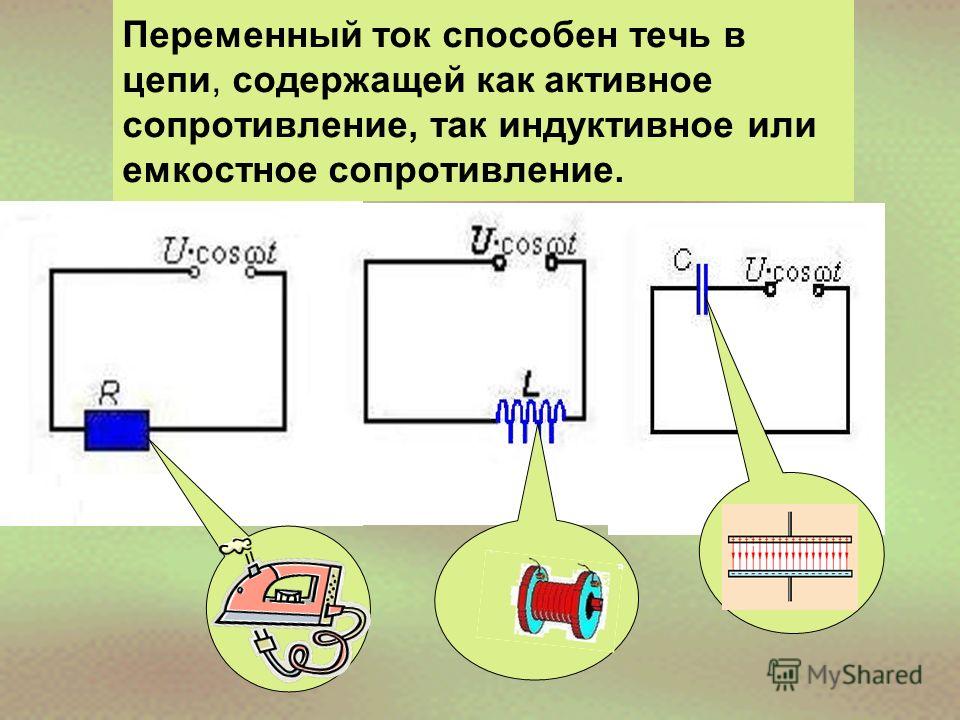 Индуктивность катушки.§ 158. Прохождение переменного тока через конденсатор и катушку с большой индуктивностью. § 159. Закон Ома для переменного тока. Емкостное и индуктивное сопротивления. § 160. Сложение токов при параллельном включении сопротивлений в цепь переменного тока. § 161. Сложение напряжений при последовательном соединении сопротивлений в цепи переменного тока. § 162. Сдвиг фаз между током и напряжением. § 163. Мощность переменного тока. § 164. Трансформаторы. § 165. Централизованное производство и распределение электрической энергии. § 166. Выпрямление переменного тока. Глава XVIII. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ: ГЕНЕРАТОРЫ, ДВИГАТЕЛИ, ЭЛЕКТРОМАГНИТЫ § 167. Генераторы переменного тока. § 168. Генераторы постоянного тока. § 169. Генераторы с независимым возбуждением и с самовозбуждением. § 170. Трехфазный ток. § 171. Трехфазный электродвигатель. § 172. Электродвигатели постоянного тока. § 173. Основные рабочие характеристики и особенности двигателей постоянного тока с параллельным и последовательным возбуждением.  § 174. Коэффициент полезного действия генератора и двигателя. § 175. Обратимость электрических генераторов постоянного тока. § 176. Электромагниты. § 177. Применение электромагнитов. § 178. Реле и их применения в технике и автоматике. Ответы и решения к упражнениям Приложения Предметный указатель Таблицы |
Физика Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока
Материалы к уроку
12. Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока.
doc55 KBСкачать12. Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока.ppt
2.78 MBСкачать
doc55 KBСкачатьКонспект урока
Огромное практическое значение имеют незатухающие вынужденные колебания. Свободные электромагнитные колебания в контуре быстро затухают и поэтому практически не используются. Переменный ток, используемый потребителями, представляет собой не что иное, как вынужденные электромагнитные колебания. Частота переменного тока показывает число колебаний за 1 секунду. Стандартная частота промышленного тока равна 50 Герц. Значит, на протяжении 1 с ток 50 раз течет в одну сторону и 50 раз в другую. Частота 50 Герц принята для промышленного тока во многих странах мира. Сила тока и напряжение меняются со временем по гармоническому закону. Это вытекает из следующих рассуждений. Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводников будет также меняться гармонически.
Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц и, следовательно, гармонические колебания силы тока. При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Если время распространения изменений поля в цепи гораздо меньше периода колебаний напряжения, то можно считать, что электрическое поле во всей цепи меняется почти мгновенно при изменении напряжения на концах цепи. Переменное напряжение, использующее потребителями в осветительной сети, создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генераторов переменного тока. Поток магнитной индукции, который пронизывает проволочную рамку, пропорционален косинусу угла альфа между нормалью к рамке и вектором магнитной индукции. При равномерном вращении рамки угол альфа увеличивается прямо пропорционально времени. Поэтому поток магнитной индукции меняется гармонически.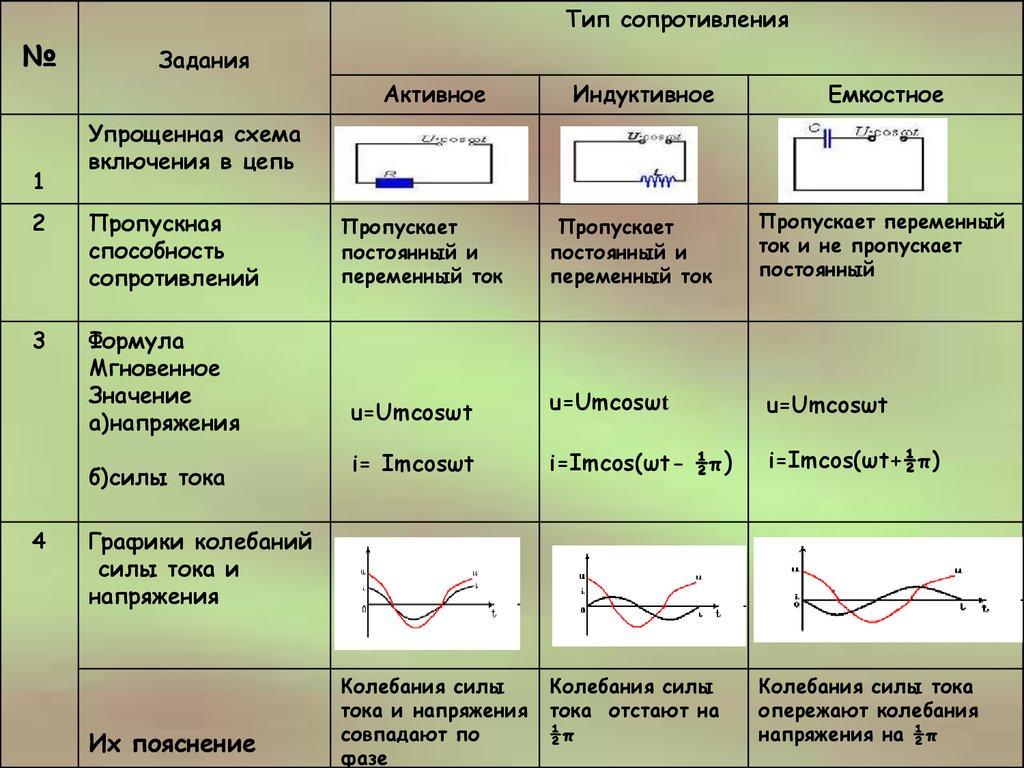
Согласно закону электромагнитной индукции, ЭДС индукции в рамке равна взятой со знаком минус скорости изменения потока магнитной индукции по времени. Иначе ЭДС электромагнитной индукции равна производной потока магнитной индукции по времени. При изменении напряжения по гармоническому закону напряженность электрического поля в проводнике изменяется по такому же закону. Под действием переменного электрического поля в проводнике возникает переменный электрический ток, частота и фаза колебаний которого совпадает с частотой и фазой колебаний напряжения. Цепи с резистором. Цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением, называемым активным сопротивлением. При наличии нагрузки, обладающей активным сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются. В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения. В цепи переменного тока промышленной частоты, равной 50 Герц, сила тока и напряжение изменяются сравнительно быстро.
Мощность в цепи постоянного тока на участке с сопротивлением равна по определению произведению квадрата силы тока на сопротивление. На протяжении очень малого интервала времени переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление, определяется произведением квадрата мгновенного значения силы тока на сопротивление. Под средней за период мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду. Человеку необходимо знать среднюю мощность тока на участке цепи за большой промежуток времени, включающий много периодов.
Здесь изображен график зависимости мгновенной мощности от времени. На протяжении одной четверти периода мощность больше половины амплитудного значения. Но на протяжении следующей четверти периода мощность меньше этой величины. На протяжении одной четверти периода эта функция пробегает ряд положительных значений. Половина квадрата амплитуды силы тока в колебательном электромагнитном контуре есть среднее за период значение квадрата силы тока.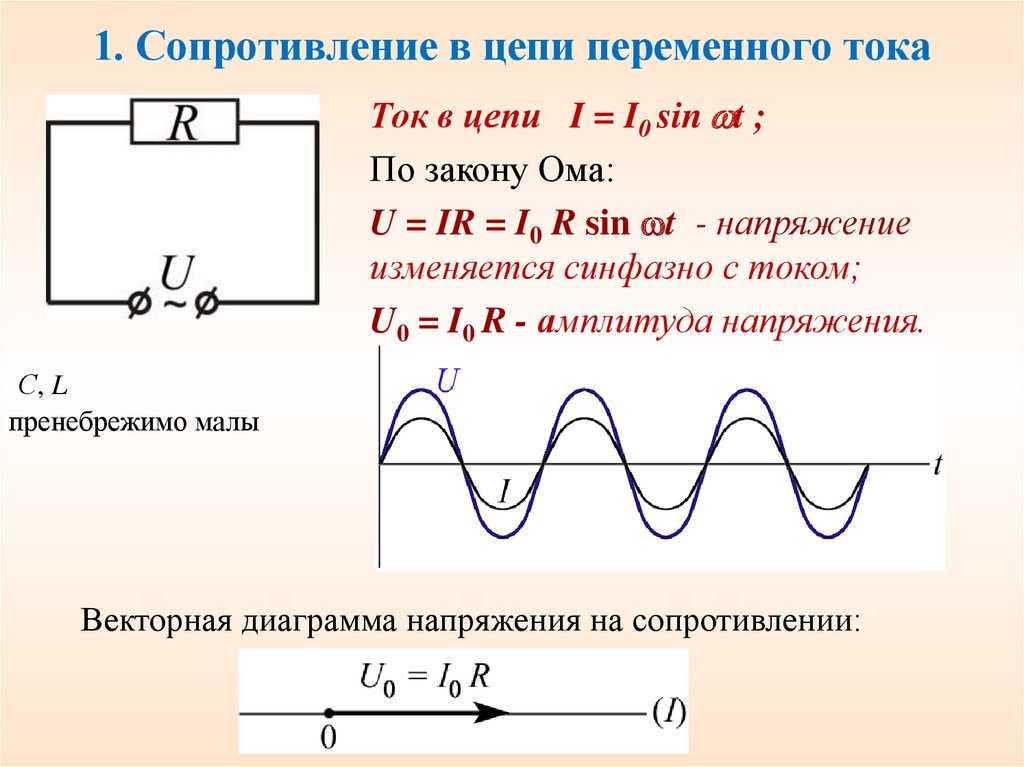
Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока. Всегда можно подобрать такое значение силы постоянного тока, чтобы энергия, выделяемая за некоторое время этим током, равнялась энергии, выделяемой за то же время переменным током. Действующее значение силы переменного тока равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время. Нам важны общие характеристики колебаний, такие как амплитуда, период, частота, действующие значения силы тока и напряжения и средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока. Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения. Мощность в цепи переменного тока определяется действующими значениями силы тока и напряжения. Мощность равна произведению силы тока и напряжения. Фактически цепь, содержащая конденсатор, оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком.
Поэтому постоянный ток не может существовать в цепи, содержащей конденсатор. Переменный ток способен течь в цепи, содержащей конденсатор. Проведем опыт. Составим последовательную цепь из конденсатора и лампы накаливания. Постоянное напряжение на зажимах источника равно действующему значению переменного напряжения. При включении постоянного напряжения лампа не светится. Но при включении переменного напряжения лампа загорается. При этом емкость конденсатора достаточно велика. Происходит периодическая зарядка и разрядка конденсатора под действием переменного напряжения. Ток, текущий в цепи при перезарядке конденсатора, нагревает нить лампы. Рассмотрим цепь, содержащую только конденсатор, где сопротивлением проводов и обкладок конденсатора можно пренебречь. Напряжение на конденсаторе совпадает по значению с напряжением на концах цепи. Следовательно, заряд конденсатора меняется по гармоническому закону. Сила тока представляет собой производную заряда по времени. Приведем графики зависимости силы тока и напряжения от времени.
Видно, что колебания силы тока опережают колебания напряжения на конденсаторе на пи вторых. Амплитуда силы тока равна произведению максимального напряжения емкости конденсатора и циклической частоты колебаний. Величину икс-цэ, равную обратному произведению циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления в законе Ома. Это и позволяет рассматривать емкостное сопротивление как сопротивление конденсатора переменному току. Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. С увеличением емкости конденсатора емкостное сопротивление уменьшается. Уменьшается оно и с увеличением частоты.
Индуктивность в цепи влияет на силу переменного тока. Это можно доказать с помощью простого опыта. Составим цепь из катушки большой индуктивности и электрической лампы накаливания. С помощью переключателя можно подключить эту цепь или к источнику постоянного напряжения, или к источнику переменного напряжения с равными значениями.
Лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы переменного тока в рассматриваемой цепи меньше силы постоянного тока. Здесь проявляется самоиндукция. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь со временем сила тока достигает наибольшего установившегося значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет достигать тех значений, которые оно бы приобрело с течением времени при постоянном напряжении. Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения. При изменении силы тока по гармоническому закону ЭДС самоиндукции будет равна противоположному значению производной индуктивности. Так как удельная работа кулоновского поля равна напряжению на концах катушки, то напряжение на концах катушки оказывается гармонически связанным с амплитудным значением напряжения контура.
Следовательно, колебания напряжения на катушке опережают колебания силы тока на пи-пополам. В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю. В момент, когда напряжение становится равным нулю, сила тока будет максимальной. Величину икс-эл, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением. Амплитуда силы тока в катушке можно найти отношением амплитуды напряжения на индуктивное сопротивление. Так выглядит закон Ома для цепи постоянного тока с катушкой. Индуктивное сопротивление увеличивается с ростом частоты, значит, катушка хорошо проводит низкочастотные колебания и плохо – высокочастотные, а для постоянного тока оно равно нулю. Рассмотрим использование частотных свойств конденсатора и катушки индуктивности. Реальные электрические цепи содержат все виды сопротивлений: активное, индуктивное, емкостное, поэтому ток в реальной цепи зависит от ее полного эквивалентного сопротивления.
Конденсатор хорошо проводит высокочастотные колебания и плохо – низкочастотные колебания.
Катушка наоборот: хорошо проводит низкочастотные колебания и плохо – высокочастотные колебания. Эти свойства позволяют создать различные частотные фильтры – схемы, позволяющие выделить из всего сигнала низкочастотные и высокочастотные составляющие.
Колебательный контур обладает замечательным свойством – пропускать колебания только определенной частоты, зависящей от емкости конденсатора и индуктивности катушки, под действием резонанса. Эти свойства контура широко применяются в радио- и телеприёмной и передающей аппаратуре для селекции сигналов.
Задача
Конденсатор включен в цепь переменного тока с частотой 200 Герц. Напряжение в цепи 40 Вольт, сила тока 0,64 Ампера. Какова емкость конденсатора?
Вспомнив закон Ома для цепи с колебательным контуром, выразим емкость конденсатора как отношение силы тока к напряжению и циклической частоте. Чтобы определить циклическую частоту, необходимо частоту переменного тока разделить на два-пи. Получаем результат 0,5 микрофарад есть емкость конденсатора.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
Сопротивление в цепях переменного тока — Цепи переменного тока
Цепи переменного тока
Введение
Как правило, формы сигналов переменного напряжения и тока ряда электронных устройств существенно не отличаются от синусоиды. Дальше, несинусоидальные сигналы могут быть разделены на синусоидальные для целей анализ. Поэтому во всех обсуждениях напряжений и токов в следующем сечения, синусоида будет использоваться как основа математического анализа.
В следующих разделах влияние свойств электрической цепи
будут осмотрены. Эти свойства схемы или параметры схемы
сопротивление, индуктивность и емкость.
Необходимо указать, что это
невозможно построить чисто резистивный, чисто индуктивный или чисто
емкостная цепь. При обсуждении чистого сопротивления, чистой индуктивности или
чистая емкость, мы рассматриваем гипотетические схемы.
Чистая резистивная цепь
Чистая резистивная цепь.
Синусоидальное напряжение подается на сопротивление, как показано на рисунке выше.
Показаны результирующие временные вариации форм тока и напряжения.
на рисунке ниже. По этим формам сигналов можно сделать следующие выводы:
1. Обе волны синусоидальные и имеют одинаковую частоту.
2. Волны совпадают по фазе.
Синфазный ток и напряжение.
Соотношения формы сигнала на рисунке выше могут быть выражены математически. Напряжение, приложенное к сопротивлению цепи чистого сопротивления, равно
Применяя закон Ома в любой момент,
где
На рисунке ниже показаны две векторные диаграммы. В одном фазор тока и напряжение
phasor показаны как максимальные значения.
В другом они показаны как эффективные
ценности. Поскольку эти вращающиеся векторы времени представляют собой синусоиды, было бы
правильнее использовать максимальные значения. На практике удобнее
использовать эффективные значения, и, кроме того, эффективные значения
на это указывают традиционные показания счетчика.
Векторная диаграмма максимальных и эффективных значений.
Таким образом, закон Ома можно применить к эффективным величинам фазора. ток и векторное напряжение. Проводимость G можно использовать в Уравнения закона Ома для векторного тока и напряжения, как и при постоянном токе. схемы.
Для демонстрации зависимости переменного тока и напряжения по закону Ома от сопротивления приведен следующий пример.
Пример 1: Напряжение, приложенное к сопротивлению чистого
цепь сопротивления v = 150 sin 377 t .
Сопротивление 800 Ом. Рассчитайте (1) максимальное значение тока,
(2) мгновенный ток при t = 0,002 с, и (3) действующее значение
тока.
Решение:
1.
2. Расчет мгновенного напряжения при t = 0,002 с,
Мгновенный ток
Мгновенный ток также можно рассчитать напрямую
3.
Также
Средняя мощность, рассеиваемая на сопротивлении, определяется уравнением
В этом уравнении напряжение и ток даны как эффективные значения. Это здесь следует отметить, что В и I указывают действующие значения переменного тока напряжение и ток, соответственно, если только они не указаны для обозначения максимальные или средние значения. Cos θ — коэффициент мощности, а θ — фазовый угол между током и напряжением. Поскольку в цепь чистого сопротивления ток и напряжение совпадают по фазе, угол θ = 0 и cos θ = 1. Предыдущее уравнение поэтому сводится к уравнению для чисто резистивной цепи
Калькулятор сопротивления переменному току круглого провода
Калькулятор сопротивления переменному току круглого провода Логотип Chemandy Electronics Логотип Chemandy Electronics CHEMANDY ELECTRONICSПоставщики необычного Вычисляет сопротивление переменному току круглого прямого провода для обычных проводящих материалов, используя уравнение и данные, указанные ниже, или данные материала, введенные вручную.
| ВХОДНЫЕ ДАННЫЕ | |
| Материал проводника: | Введите данныеAluminiumCopperGoldNickelSilver |
| Частота: | МГц |
| Длина: | мм |
| Диаметр: | мм |
| Результаты | ||||
| Удельное сопротивление (ρ): | x 10 -8 ω.m | |||
| Относительная достоверность (µ R ) | (µ R ):111165):1110109 | (µ R ). | ||
| Глубина скин-эффекта (δ): | мкм | |||
| переменный ток Сопротивление: | Ом | |||
Примечание. Чтобы использовать разные значения удельного сопротивления и относительной проницаемости, выберите «Ввести данные» в текстовом поле «Выбор материала проводника», а затем введите соответствующие значения в поля, выделенные желтым цветом.
Этот калькулятор использует JavaScript и будет работать в большинстве современных браузеров. Подробнее см. О наших калькуляторах
.сопротивление для длины круглого прямого провода рассчитывается с использованием удельного сопротивления проводника, длины проводника и эффективной площади поперечного сечения, используемой скин-эффектом.
Где ρ — удельное сопротивление проводника в Ом·м
l — длина проводника в мм
A eff — используемая эффективная площадь поперечного сечения в мм
Площадь поперечного сечения, используемая скин-эффектом, определяется путем первоначального расчета номинальной глубины проникновения проводника.
Из «Линий и сетей передачи» Уолтера С. Джонсона, McGraw-Hill, 1963, стр. 58.
Где ρ — удельное сопротивление проводника в Ом·м
f — частота в Герцах
μ — абсолютная магнитная проницаемость проводника
Абсолютная магнитная проницаемость (μ) = μ o x μ r
μ o = 4π x 10 -7 Гн/м
Значения для μ r взяты из Справочник по проектированию линий электропередач Брайана С Уоделла, Artech House 1991 Таблица 9.
3.2 стр.
446.
Значения ρ взяты из CRC Handbook of Chemistry and Physics 1st Student Edition 1998 page F-88 и относятся к элементам высокой чистоты при 20°C.
Фактическая площадь поперечного сечения, используемая из-за скин-эффекта, может быть рассчитана несколькими методами с разной степенью точности. Самый простой способ — умножить глубину скин-слоя на длину окружности проводника.
Где d — диаметр проводника
Этот метод делает используемую площадь поперечного сечения слишком большой от высоких частот до точки, где глубина поверхностного слоя становится примерно половиной радиуса проводника, после чего увеличиваются погрешности, и в конечном итоге расчетная используемая площадь становится больше фактической площади проводника. Сделать метод расчета только приблизительным и использовать его только тогда, когда r >> δ.
Второй простой метод заключается в вычислении общей площади проводника, а затем вычитании площади круга, представляющего центральную область без использования скин-эффекта.
Где r — радиус проводника
Этот метод является более точным, чем первый метод, когда r >> δ, но становится очень неточным ниже точки, где d/δ = π, и может иметь огромные положительные или отрицательные колебания значения.
Гораздо более точный метод описан Дэвидом Найтом в очень подробной статье под названием Zint.pdf, которую можно найти по адресу http://www.g3ynh.info/zdocs/comps/part_1.html. В этом методе используется метод усеченного экспоненциального затухания. для устранения ошибок, возникающих, когда фактическая площадь проводника становится меньше, чем расчетная площадь толщины скин-слоя в простом методе, описанном выше, и модифицированная коррекция Лоренца, которая устраняет ошибку, возникающую, когда вычисленная площадь скин-слоя приближается к фактической площади проводника. Автор называет это уравнение Rac — TED — ML и указывает максимальную ошибку 0,09.%.
Метод расчета предполагает наличие одного изолированного проводника и не учитывает обратный путь.
