Ток, напряжение и сопротивление в комплексном виде.

Ток, напряжение и сопротивление в комплексном виде

Если ток и напряжение изменяются по синусоидальному зако­ну то, как указывалось вышеих можно изобразить векторами и, следовательно, записать комп­лексными числами:

(14.6)

где — комплексы тока и напряжения. Точка над комплексами указывает, что ток и напряжение изменяются по синусо­идальному закону с определенной частотой ώ; I и U — модули i комплексов тока и напряжения, они же действующие значения

тока и напряжения — аргументы комплексов тока и напряжения, они же начальные фазы тока ψ_i и на­пряжения ψ_u.

Для неразветвленной цепи с R и L (рис. 12.1а) мгновенные зна­чения синусоидального тока и напряжения можно записать так:

Тогда комплексы тока и напряжения

(14. 7)

Комплекс полного сопротивления цепи Z определяется отно­шением комплекса напряжения к комплексу тока, т. е.

(14.8)

Комплексные величины, не зависящие от времени, обознача­ются прописными буквами с черточкой внизу. Модулем комплекса полного сопротивления является кажущееся

сопротивление цепи а аргументом — угол сдвига фаз между током и напряжением φ.

Алгебраическая форма записи комплекса полного сопротивле­ния Z

(14.9)

Вещественная часть комплекса полного сопротивления есть ак­тивное сопротивление

R, а коэффициент при мнимой единице j » реактивное сопротивление X. Знак перед поворотным множите­лем (мнимой единицей) указывает на характер цепи. Знак «плюс» соответствует цепи индуктивного характера, а знак «минус» — цепи емкостного характера.

Выражения комплексов сопротивлений различных цепей при­ведены в Приложении 7.

О братная величина комплекса сопротивления — комплекс про­водимости

Любую цепь переменного тока можно рассчитывать по зако­нам постоянного тока, если все величины представить в комплек­сной форме. В этом и заключается достоинство символического метода расчета.

Мощность в комплексном виде

§Для неразветвленной цепи с Я и С (рис. 12.3а) мгновенные зна­чения тока и напряжения можно записать как

Комплексы напряженияi тока соответственно равны

К омплекс полной мощности цепи S определяется произве­дением комплекса напряжения U и сопряженного комплекса тока (над сопряженным комплексом синусоидальной величины ставят «звёздочку»»)

(14.10)

Таким образом, модулем комплекса полной мощности S являет­ся кажущаяся мощность цепи S=UI, а аргументом — угол сдвига фаз между током и напряжением.

Если комплекс полной мощности S перевести из показатель­ной формы в алгебраическую, то получится

(14.11)

То есть вещественная часть комплекса полной мощности — ак­тивная мощность Р, а коэффициент при мнимой единице — реак­тивная мощность Q

.

Знак перед поворотным множителем j указывает на характер Цепи. В рассматриваемой цепи реактивная мощность емкостно­го характера

Комплексы величин токов, напряжений, сопротивлений, мощ­ностей и других параметров цепи синусоидального тока необхо­димо выражать в двух видах записи комплексного числа: показа­тельной и алгебраической. В этом случае сразу определяются Действующие значения тока, напряжения, кажущееся сопротив­ление, его активные и реактивные части (R и X), угол сдвига фаз ср Между током и напряжением, характер цепи, кажущаяся S, актив­ная Р и реактивная Q

мощности. Кроме того, в неразветвленной цепи напряжения на участках складываются, суммируются токи в разветвленных цепях, а сложение комплексов можно производить только в алгебраической форме записи. В алгебраической форме записи кажущейся мощности S сразу определяются активная мощность Р и реактивная мощность Q. В показательной форме записи сопротивлений производится их умножение и деление, необходимое при расчете цепей синусоидального тока при сме­шанном соединении потребителей, и т.д. Необходимость выра­жения комплексов в двух видах следует из примеров, разобран­ных в этой главе.

Активное сопротивление – амплитуда, формула для закона Ома, пример энергия, величина (11 класс)

4.3

Средняя оценка: 4.3

Всего получено оценок: 78.

4.3

Средняя оценка: 4.3

Всего получено оценок: 78.

Цепи переменного тока имеют важное отличие от цепей постоянного тока. Сопротивления в них имеют две составляющих: активную и реактивную. Поговорим о свойствах и особенностях активного сопротивления.

Активное и реактивное сопротивление

В 11 классе известно, что постоянный электрический ток — это направленное движение зарядов по проводнику. Переменный ток — это колебания электрических зарядов вокруг некоторого среднего положения. Двигаясь или колеблясь, заряды совершают работу, которая выделяется на сопротивлении нагрузки.

Рис. 1. Электрический ток.

Сопротивление, на котором энергия электрического тока выделяется в виде тепла, называется активным. В цепи постоянного тока сопротивления бывают только активными. В цепи переменного тока могут быть элементы, которые оказывают сопротивление прохождению тока, но мощность на них не выделяется — такие сопротивления называются реактивными.

Если активное сопротивление преобразует энергию движения электронов в тепло, то реактивное сопротивление часть периода запасает энергию движения электронов (оказывая сопротивление), а часть периода — отдает запасенную энергию электронам.

Активным сопротивлением обладают резисторы, кроме того, любой реальный проводник также обладает некоторым активным сопротивлением. Реактивным сопротивлением обладают конденсаторы и катушки индуктивности.

Рис. 2. Полная цепь переменного тока.

Активное сопротивление в цепи переменного тока

Определим величину тока в цепи переменного тока с чисто активным сопротивлением.

Рис. 3. Схема с чисто активной нагрузкой.

Для переменного тока закон, по которому меняется мгновенное значение напряжения, имеет следующий вид:

$$U=U_m sin(\omega t+\varphi)$$

Мгновенное значение тока через любой элемент находится по закону Ома:

$$I ={U \over R}$$

Подставляя предыдущую формулу в закон Ома, получим:

$$I={U_m sin(\omega t+\varphi)\over R}=I_m sin(\omega t+\varphi)$$

Из этой формулы видно, что колебания силы тока в цепи с чисто активным сопротивлением имеют ту же частоту и фазу, что и колебания напряжения. Ток в цепи в любой момент времени возрастает пропорционально напряжению. 2Rt$$

Указанные соотношения справедливы только для чисто активных сопротивлений. Для сопротивлений, которые имеют реактивную составляющую, к примеру, для катушки индуктивности, зависимость мгновенного значения тока сложнее, и закон Джоуля-Ленца в таком виде использовать нельзя.

Любой реальный проводник обладает некоторой индуктивностью, а между любыми частями реальных проводников и элементов существует некоторая электроемкость. Поэтому чисто активных сопротивлений, строго говоря, не существует. Любое реальное активное сопротивление имеет некоторую реактивную составляющую. На низких частотах она очень мала, и ею пренебрегают. На высоких же частотах ею пренебречь нельзя, и она всегда оказывает заметное влияние на поведение и параметры цепи.

Что мы узнали?

Сопротивление, на котором энергия электрического тока выделяется в виде тепла, называется активным. Оно не обладает инерционностью. Ток, протекающий через активное сопротивление, синфазен с напряжением на нем, и его можно найти по закону Ома для действующих значений.

Мощность, выделяемая на активном сопротивлении, можно найти по закону Джоуля-Ленца для действующих значений.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.3

Средняя оценка: 4.3

Всего получено оценок: 78.

---

А какая ваша оценка?

электрических цепей — Сопротивление или напряжение более эффективно снижают потери мощности?

спросил

2 года 8 месяцев назад

Изменено 1 год, 3 месяца назад

Просмотрено 1к раз

$\begingroup$

Принято считать, что увеличение напряжения источника снижает потери мощности.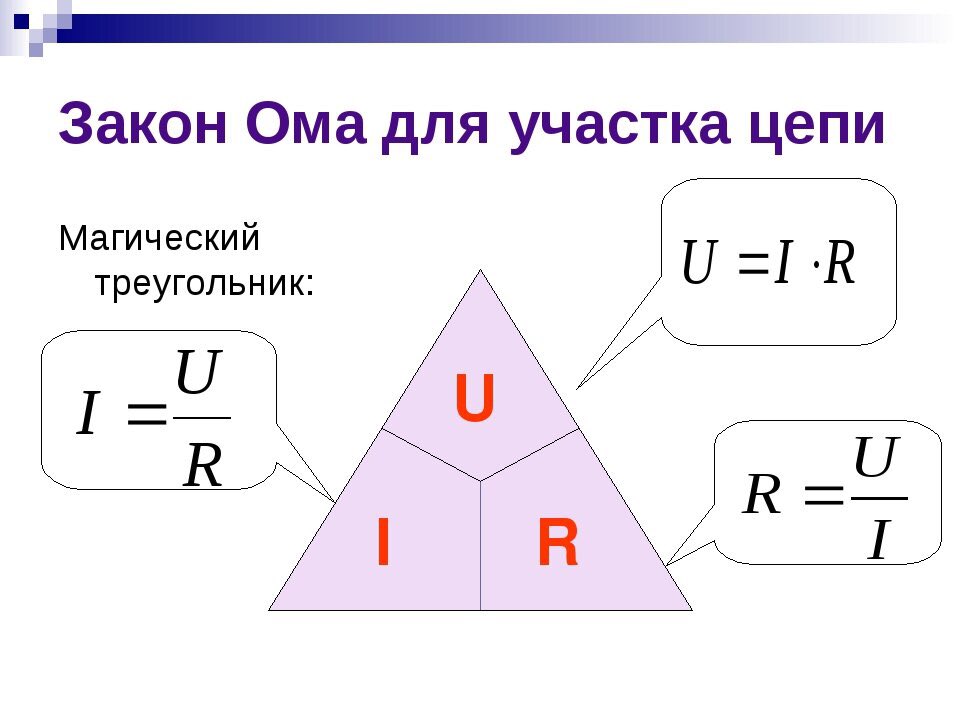 Если напряжение источника увеличивается, ток в цепи увеличивается, что приводит к большим потерям мощности (чем при меньшем напряжении) в компоненте, а также в проводе. 92R$

Чтобы уменьшить потери мощности в проводе, нам нужно меньше тока через него. Если мы увеличим сопротивление компонента, не сможем ли мы эффективно уменьшить потери мощности в проводе? (Поскольку падение мощности на компоненте ниже, чем на проводе)

• электрические цепи
• электрический ток
• электрическое сопротивление
• напряжение
• мощность

$\endgroup$

3

$\begingroup$

Если мы увеличим сопротивление компонента, мы не сможем эффективно уменьшить потери мощности в проводе

Это то же самое, что сказать: спроектировать компонент для работы при низком токе высокого напряжения, что мы и делаем в высоковольтных линиях электропередач.

Однако вы, похоже, запутались в своем вопросе. Вы начинаете путать мощность, подаваемую на нагрузку, с мощностью, растраченной в нагрузке.

Вы также говорите об увеличении сопротивления компонентов после повышения напряжения, чтобы уменьшить потери мощности в проводе из-за увеличения тока из-за более высокого напряжения. Это неправильное мышление. Если у меня есть нагрузка 100 Вт, которая работает при 50 В при 2 А, и я хочу уменьшить потери в проводе, я перепроектирую нагрузку, чтобы она имела более высокое сопротивление, чтобы она могла производить ту же мощность при более низком токе. Это означает, что напряжение должно быть выше. Я увеличил сопротивление, потому что это необходимо для поддержания одинаковой мощности нагрузки при работе от источника более высокого напряжения. 92}{R+r}$ .

Таким образом, при уменьшении разности потенциалов наполовину потеря мощности составит одну четверть. А увеличение внешнего сопротивления приведет к уменьшению тока в цепи, но падение мощности потерь будет меньше, чем в предыдущем случае.

$\endgroup$

2

$\begingroup$

Не совсем понятно, о чем вы спрашиваете. Но если вы спрашиваете, оказывает ли источник напряжения или сопротивление большее влияние на рассеяние мощности, то форма уравнения для мощности, на которую вы должны обратить внимание, будет 92}{R}$$

Предположим, что источником напряжения $V$ является батарея, подключенная к резистору $R$. Далее предположим, что внутреннее сопротивление батареи пренебрежимо мало по сравнению с любым значением R$, которое мы хотим рассмотреть.

Из уравнения видно, что рассеиваемая мощность обратно пропорциональна сопротивлению батареи, а изменяется пропорционально квадрату напряжения на клеммах батареи $V$. Следовательно, уменьшение напряжения приводит к большему снижению рассеиваемой мощности, чем увеличение сопротивления.

Если это не то, что вы хотели знать, дайте мне знать, и я либо удалю свой ответ, либо исправлю его.

Надеюсь, это поможет.

$\endgroup$

$\begingroup$

Если напряжение источника увеличивается, [тогда] ток в цепи увеличивается…

На самом деле у вас все наоборот.

Проблема в том, что вы неправильно понимаете контекст, в котором они «повышают напряжение». Они не говорят о повышении напряжения в какой-то существующей цепи, которая питает, например, какую-то существующую лампочку. Они говорят о настройке проект системы распределения электроэнергии.

Предположим, вы хотите подать 100 Вт на лампочку. Если вы проектируете систему, в которой лампочки рассчитаны на питание 10 В, то вам придется подавать 10 А, чтобы зажечь лампочку. Но если вы проектируете систему для работы при 100 В, вам нужно будет подавать только 1 А. «Увеличение» напряжения конструкции дает вам систему, в которой ток меньше .

Принято считать, что увеличение напряжения источника снижает потери мощности. 92R$ убытков.

$\endgroup$

1

$\begingroup$

Повышение напряжения источника не снижает потери мощности.

Я думаю, вы говорите о передаче электроэнергии по высоким напряжениям. Но этот случай отличается от обычного случая (только резистор). Здесь вы не можете использовать соотношение V = I*R, потому что преобразование низкого напряжения в высокое отличается от увеличения напряжения источника. Увеличение уровня напряжения в повышающем трансформаторе происходит за счет уменьшения тока. Вы должны использовать соотношение постоянной мощности, которое P = I ₁ *V ₁ = I ₂ *V ₂ = константа для расчета тока при повышенном напряжении.

Переходя ко второму вопросу, как вы увеличите сопротивление компонента. Если вы добавите внешний резистор с компонентом последовательно, это определенно уменьшит ток в цепи, но тогда будут дополнительные потери мощности на добавленном резисторе. Также уменьшится падение напряжения на компоненте. Но электрические компоненты требуют определенного уровня напряжения для работы.

Таким образом, мы не можем снизить потери мощности.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.

Молекулярные выражения: электричество и магнетизм

Галерея Информация о лицензии Использование изображения Пользовательские фотографии Партнеры Информация о сайте Свяжитесь с нами Публикации Главная Visit Science, Оптика и вы gif»> Галереи: Фотогалерея Кремниевый зоопарк Фармацевтика Чип-шоты Фитохимикаты Галерея ДНК Микроскейпы Витамины Аминокислоты Камни Религия Коллекция Пестициды пивные шоты Коктейльная коллекция Заставки Выиграть обои Обои для Mac Галерея фильмов

Закон Ома Георг Симон Ом (1787-1854) сформулировал зависимость между напряжением, током и сопротивлением следующим образом: Ток в цепи прямо пропорционален приложенному напряжению и обратно пропорционален сопротивлению цепи. Схема ниже демонстрирует эти отношения. Щелкните ползунок сопротивления, чтобы изменить резисторы. Щелкните ползунок напряжения, чтобы отрегулировать напряжение регулируемого источника питания. Математически закон Ома можно записать как: И = Э/Р , где I — ток в амперах, E — приложенное напряжение в вольтах, а R — сопротивление в омах. Эта схема содержит амперметр, измеряющий ток в миллиамперах. Обратите внимание, что при увеличении напряжения увеличивается ток. По мере увеличения сопротивления ток уменьшается. Важно отметить, что сопротивление нельзя изменить, изменив напряжение или ток. Сопротивление в цепи является физической константой. Сопротивление в цепи можно изменить, только заменив компоненты или резисторы с номиналом больше или меньше Ом. Изменение сопротивления в этой схеме имитирует физическое изменение резисторов с разными номиналами. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника