Чем отличается сила тока от напряжения простыми словами

Физика многим кажется сложной и загадочной. Раздел «Электричество» воспринимается особенно сложно из-за того, что большинство понятий нельзя «потрогать руками». Но мы попробуем объяснить, чем отличается сила тока от напряжения простыми словами.

Содержание

1. В чем разница?
2. Отличия с другими величинами
3. Заключение

В чем разница?

В физике есть фундаментальное понятие заряда. Это такая величина, которая определяет свойство частиц и тел взаимодействовать через электромагнитные силы. Чем он больше, тем сильнее взаимодействие.

Проявление этих сил мы часто видим в жизни. На примере молнии, прилипания кусочков бумаги к наэлектризованной полиэтиленовой пленке, работы электрического чайника. Но не всегда понимаем суть увиденного, и не осознаем, что именно и как воздействовало на конкретный предмет.

Если говорить, очень кратко и утрировано, то ток — это упорядоченное движение заряженных частиц. В металлах это электроны, в электролитах — ионы.

Сила тока — это количество зарядов, которые пройдут через проводник за единицу времени.

Измеряется эта величина в Амперах (в честь одноименного французского физика-математика) и показывает, насколько много энергии протекает за секунду в точке. Например, у молнии — большая сила тока, а у фонарика — маленькая.

Напряжение в цепях электрического тока, если говорить простыми словами — это величина силы, которая заставляет двигаться заряды упорядоченно.

Единицы измерения получили свое названия от итальянского физика и физиолога Алессандро Вольта, который изобрел первую гальваническую батарею.

Простой аналог из жизни — река. Чем больше уклон, тем быстрее она течет. Напряжение — это перепад высот реки, а сила тока — это объем воды, который протекает в конкретном месте.

Теперь становится понятно, в чем отличие тока от напряжения: первый — это движение зарядов, а второе — это то, что их заставляет двигаться.

Отличия с другими величинами

Существует еще ряд величин, которые характеризуют электрические системы: сопротивление, мощность и т.д.

Отличие сопротивления от тока и напряжения, в том, что оно мешает протеканию тока, уменьшая его.

В вышеупомянутой реке, в качестве сопротивления, выступают дно и камни.

Чтобы сохранить ту же силу тока при увеличении сопротивления, надо повышать напряжение.

Для лучшего понимания процесса можно привести еще один пример. Допустим, у нас есть длинный коридор, по которому бежит человек — это и есть сила тока. Чтобы бегун передвигался быстрее, другой человек бьет его палкой — это напряжение. В данном случае сопротивление — это стулья, хаотично расставленные по коридору и мешающие бежать.

По пустому коридору человек передвигается легко, его можно практически не бить, чтоб он быстро бежал. Но чем больше на пути препятствий, тем сильнее должно быть напряжение (удары), чтобы поддерживать тот же темп.

Выражается эта взаимосвязь формулой, описанной в законе Ома (фото ниже).

Еще одна важная величина, участвующая в данном процессе — мощность.

Отличие мощности от напряжения и силы тока, заключается в том, что она показывает величину работы, которую производит наш «бегун» за единицу времени.

В примере с рекой, мощность, это то насколько много намелет муки водяная мельница за день. Чем «мощнее» река, тем больше муки на выходе. Другими словами, это скорость выполнения работы.

Измеряется мощность в Ваттах. Эта единица измерения напрямую зависит от количества выполненной работы, разделенной на время, которое потребовалось на ее выполнение.

Заключение

Чтобы облегчить процесс понимания сложных физических явлений, им нужно найти простые и наглядные аналоги в окружающем мире. Так будет легче найти взаимосвязь между различными величинами и уловить суть. Это касается не только электричества, но и остальных «невидимых» разделов физики (ядерка, термодинамика и т.п.)

Напряжение, сила тока, сопротивление, мощность.

Пусть имеется один пустой бак, который стоит на земле и один полный бак с водой, установленный на некоторой высоте. Между баками есть разность давлений. Если соединить баки шлангом, то по нему потечет вода в бак с меньшим давлением. При этом крыльчатка будет вращаться, совершая работу и создавая некоторое сопротивление движущейся воде. Аналогично соединив проводником две клеммы с напряжением U между ними, потечет электрический ток I. Лампа будет нагреваться от протекающего тока, совершая работу и создавая сопротивление R движущемуся току. Чем больше сопротивление лампы, тем меньше сила протекающего тока.

Сила протекающего тока через электроприемник обратно пропорционально его сопротивлению R и прямо пропорционально напряжению U на нем: .

Мощность, выделяемая в электроприемнике при протекании через него тока: .

Для примера, определим протекающий ток и выделяемую мощность в лампе с сопротивлением 484Ом, подключенную к напряжению 220В:

Протекающий ток , выделяемая мощность

Задание 2.

Электроприемники в однофазной сети.

Электроприемники – лампы освещения, нагревательные элементы, электродвигатели и т.д. При включении в сеть они потребляют электрический ток и совершают определенную работу.

Мощность, которая расходуется на совершение полезной работы, например, нагрев спирали, вращение вала, излучение света и т.п. называется активной мощностью P и измеряется в ваттах (Вт).

Н оминальная активная мощность P и напряжение U указывается в паспорте электроприемника. Например, на лампе указано: , т.е. лампа предназначена для подключения к напряжению 220В и при этом выделяется мощность 100Вт в виде нагрева и излучения света.

При этом лампа накаливания при включении ее на 220В потребляет ток:

Ваттметр предназначен для измерения активной мощности нагрузки в ваттах, и в данном случае покажет 100Вт.

Следует отметить, что при включении лампы на другое напряжение, отличное от номинального 220В, потребляемый ток будет другой, и выделяемая на лампе мощность будет другой, отличной от 100Вт. В этом случае расчет тока правильно делать через сопротивление лампы. Например, определим потребляемый ток при подключении лампы 100Вт, 220В к напряжению 127В.

По паспортным данным сопротивление лампы: . Потребляемый ток: . Мощность лампы при этом: . Лампа будет гореть очень тускло при включении ее на напряжение 127В.

Активно-реактивные электроприемники. Электродвигатели, некоторые светильники потребляют как активную P, так и «бесполезную» реактивную мощность Q в ВАр – вольт амперах реактивных, которая тратится только на образование магнитного поля в обмотках этих электроприемников.

Треугольник мощностей электроприемника P=100Вт, cosφ=0,8

Полная потребляемая мощность S, в ВА, складывается из активной и реактивной мощности согласно треугольнику мощностей следующим образом:

Полная мощность S несколько больше P, что видно из треугольника мощностей. Поэтому, при одинаковой активной мощности по сравнению с активными, активно-реактивные электроприемники потребляют больший ток,:

Соотношение S и P показывает коэффициент активной мощности , и указывается в паспорте электроприемников, например, для светильника: . О пределим полную мощность и потребляемый ток данным светильником:

Видно, что потребляемый ток данным светильником больше, чем ток потребляемый лампой накаливания той же активной мощности 100Вт. При полной мощности в 125ВА ваттметр покажет 100Вт, как и в предыдущем случае.

В ряде задач приведен потребляемый ток и нужно определить полную мощность, которая равна произведению показания амперметра на напряжение сети

Все параметры в треугольнике мощностей связаны законами тригонометрии, например реактивная мощность равна:

Для электродвигателей вместо активной мощности P приводится механическая мощность на валу P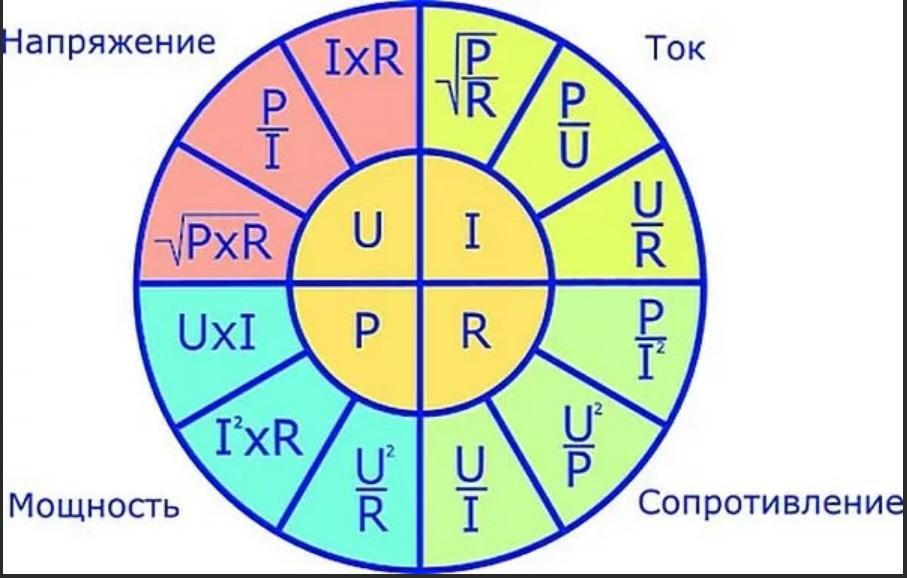

2 и КПД, например: 500Вт, КПД 0,9. Разделив мощность на валу на КПД, получим активную электрическую мощность двигателя 500Вт/0,9=555Вт, причем потери на трение и нагрев обмоток составят 555Вт-500Вт=55Вт.

Параллельное включение электроприемников. На практике электроприемники включаются и работают в сети параллельно.

На примере определим суммарный ток, который будет потреблять из сети нагрузка из нескольких электроприемников, а также активную мощность всей нагрузки. Пусть, к однофазной сети 220В подключены: лампа накаливания, нагревательная спираль, светильник с люминесцентной лампой и однофазный электродвигатель (см. рис. 2.2 а). Для измерения параметров имеется ваттметр W и амперметр А.

Построим треугольник мощностей нагрузки. По горизонтали отложим в масштабе все активные мощности электроприемников (рис. 2.2 б). Сумма активных мощностей электроприемников 1255Вт и будут показаниями ваттметра.

Далее по вертикали откладываются реактивные мощности всех электроприемников, которые определяются дополнительно — светильника 75ВАр, электродвигателя 416ВАр.

Лампа накаливания и нагревательная спираль — не потребляют реактивной мощности.

а) б)

Рис. 2.2 – Электрическая схема (а) и треугольник мощностей (б)

В результате длина вектора полной мощности S составит 1350ВА.

Потребляемый ток нагрузкой от сети:

Итак, в примере показания амперметра РА равны 6,1А.

Можно определить коэффициент активной мощности cosφ нагрузки как отношение прилежащего катета к гипотенузе, т.е. активной (1255Вт) мощности к полной (1350ВА). В приведенном примере cosφ=1255Вт/1350ВА=0,93.

Компенсация реактивной мощности. Нежелательную реактивную мощность нагрузки можно скомпенсировать при помощи конденсаторов и таким образом уменьшить потребляемый нагрузкой ток. Конденсатор, включенный в сеть, потребляет реактивную мощность «другого знака», направленную в противоположную сторону. Подключим параллельно нагрузке конденсатор C емкостью, например 12,5мкФ (см. рис. 2.3 а). Определим его реактивную мощность Q

С по формуле:

(при частоте f=50Гц)

На треугольнике емкостная реактивная мощность откладывается в обратную сторону реактивных мощностей нагрузки (см рис. 2.3 б).

б) а)

Рис. 2.3 – Электрическая схема (а) и треугольник мощностей (б) при компенсации реактивной мощности конденсатором

В результате видно, что полная мощность S уменьшилась (стала 1295ВА, была 1350ВА), снизился и потребляемый от сети ток (стал 5,9А, был 6,1А) при неизменной полезной активной мощности. Также увеличился коэффициент активной мощности cos до 0,97 (был 0,93).

Таким образом, конденсатор позволяет компенсировать реактивную мощность нагрузки, в результате чего уменьшается полная мощность S и потребляемый нагрузкой ток. При этом коэффициент мощности нагрузки cos увеличивается.

Из треугольника мощностей видно, чтобы полностью скомпенсировать реактивную мощность нагрузки необходимо подобрать такую емкость конденсатора, чтобы Q

C=Q. В примере, для полной компенсации реактивной мощности в 491ВАр необходима емкость конденсатора:

После полной компенсации мощность полная мощность S совпадает с активной P, и потребляемый ток равен I=S/U=P/U, а cos=P/S нагрузки равен единице.

Потребляемый ток нагрузкой после компенсации:

На практике компенсация реактивной мощности осуществляется включением специальных батарей конденсаторов нужной емкости параллельно нагрузке и имеет экономическое значение, т.

к. снижается протекающий ток и соответственно потери в сетях.

Критическое значение сопротивления Соотношение между рабочим напряжением и мощностью

6 июня 2016 г. Кори Шредер, директор по маркетингу и разработке продуктов, Stackpole Electronics

Благодаря усовершенствованию технологии производства и материалов производители резисторов смогли увеличить номинальную мощность для данного размера микросхемы. Эти более мощные резисторы могут быть эффективным способом уменьшения размеров или расширения функциональности схемотехники, но понимание взаимосвязи между номинальным рабочим напряжением и номинальной мощностью имеет жизненно важное значение.

«Критическое значение сопротивления» определяется как значение сопротивления, при котором конкретная часть может работать как при полной номинальной мощности, так и при полном номинальном напряжении. Большинство производителей резисторов помимо номинальной мощности указывают максимальное рабочее напряжение. Соотношение между рабочим напряжением и номинальной мощностью значительно влияет на работу резистора в нижней и верхней частях диапазона значений. Это соотношение применимо ко всем резисторам, независимо от технологии или производителя.

На приведенном выше графике показано соотношение между рабочим напряжением, номинальной мощностью и значением сопротивления для чип-резистора размера 0603. При значениях ниже 56,25 кОм количество электроэнергии, которое может выдержать деталь, определяется максимальной номинальной мощностью 0,1 Вт. Если, например, 10-омный 0603 подвергнут максимальному рабочему напряжению 75 вольт, результирующая мощность через деталь будет 562,5 Вт, что намного превышает номинальную мощность детали. И наоборот, для высоких значений сопротивления количество электрической энергии, которую может выдержать резистор 0603, определяется номинальным рабочим напряжением 75 вольт. Если на 10-мегаомный 0603 воздействовать максимальной мощностью 0,1 Вт, подразумеваемое напряжение на детали составит 1000 вольт, что превышает допустимое напряжение детали.

Из этих данных видно, что только при точном сопротивлении 56,25 кОм резистор 0603 может одновременно выдерживать и 75 вольт, и 0,1 Вт. Хотя это представляет некоторый интерес для всех резисторов, это наиболее важно при работе с резисторами с высоким значением и высоким напряжением или резисторами с низким значением, такими как датчики тока и резисторы с проволочной обмоткой.

Токоизмерительные резисторы и проволочные обмотки

Токочувствительные резисторы предназначены для регулирования и контроля мощности от источника до конечного устройства. С быстро развивающимися технологиями проектирования компонентов токоизмерительные резисторы используются для широкого спектра портативных электронных устройств, источников питания всех типов и драйверов светодиодов.

Когда в приложении требуется рассеивание более 5 Вт мощности в течение длительного периода времени, логичным выбором часто являются резисторы с проволочной обмоткой. Эти резисторы известны своей способностью выдерживать большие токи и оставаться стабильными в электрическом и экологическом отношении. Резисторы с проволочной обмоткой имеют несколько регулируемых параметров. Это дает им преимущества перед пленочными резисторами.

В технических описаниях токоизмерительных и проволочных резисторов часто вообще не указано рабочее напряжение. Это в первую очередь связано с тем, что эти серии предлагают только низкие значения сопротивления, когда количество электрической энергии, которую может выдержать деталь, определяется только номинальной мощностью. Например, используя приведенный выше график резисторов микросхемы общего назначения 0603, если бы эта часть была доступна только при значениях сопротивления ниже 50 кОм, то номинальное напряжение 75 вольт было бы бессмысленным; вы никогда не сможете постоянно подавать на деталь 75 вольт, потому что это превысит номинальную мощность.

Для резисторов с проволочной обмоткой одними из самых сложных задач являются те, которые требуют работы с высоким напряжением. Поскольку резисторы с проволочной обмоткой обычно имеют только низкие значения сопротивления, любое приложение, использующее проволочные обмотки, которые должны выдерживать переходные процессы высокого напряжения, требует, чтобы провод элемента был однозначно указан для этой цели.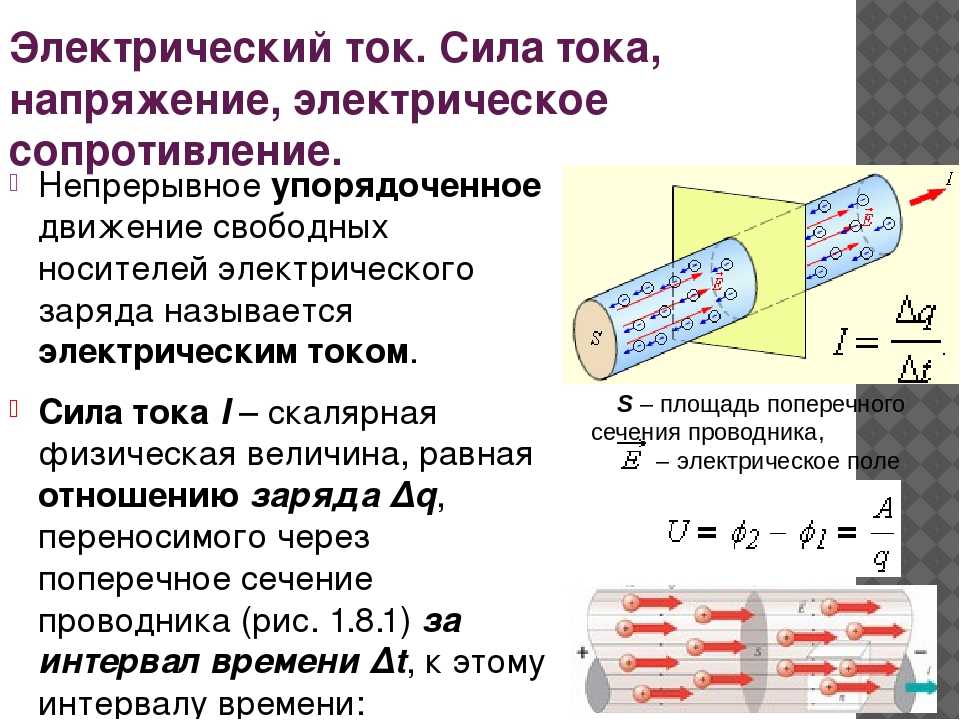

Высоковольтные резисторы

Критическое значение сопротивления чрезвычайно важно для высоковольтных резисторов. Требования к высокому напряжению обычно соответствуют высоким значениям сопротивления и наоборот. Причиной этого является закон Ома и уравнение мощности для напряжения. Проще говоря, высокое напряжение при низком значении сопротивления приведет к генерированию чрезмерного количества энергии. Это, в свою очередь, потребует очень большого резистора для рассеивания энергии и, вероятно, превысит возможности продукта.

Иногда клиенты предполагают, что, поскольку определенный резистор определен и предназначен для высоковольтных приложений, номинальное рабочее напряжение применяется ко всем значениям сопротивления для данного типоразмера. Приведенный выше график показывает, что, хотя цифры значительно изменились по сравнению с общим назначением 0603, соотношение осталось прежним. Поскольку высоковольтный резистор размера 2512 имеет значения сопротивления ниже 4,5 МОм ( — критическое значение сопротивления ), важно понимать, что эти значения сопротивления не будут постоянно работать при полном номинальном рабочем напряжении без нарушения номинальной мощности устройства. Поскольку для многих высоковольтных приложений требуются высокие значения сопротивления, обычно это не проблема.

Рынок резисторов отреагировал технологическими достижениями и улучшениями, чтобы попытаться удовлетворить любые требования, предъявляемые к конструкции энергосистемы. Системы питания продолжают расширять технологические горизонты для более высоких номинальных мощностей, лучшей электрической стабильности, меньших размеров микросхем и, конечно же, более низкой стоимости компонентов. Однако при определении резисторов одним из наиболее важных факторов, который необходимо понимать, являются критические значения сопротивления и их связь с мощностью и напряжением. Короче говоря, количество электроэнергии, которую может выдержать деталь, определяется максимальной номинальной мощностью. Выбор резистора, способного работать с номинальной мощностью без превышения максимального рабочего напряжения, жизненно важен для любой энергосистемы. Выбор резистора без этих данных может привести к деградации резистора и катастрофическому выходу из строя системы питания и электронного устройства.