Примеры решения задач по сопротивлению материалов
Задачи с решениями по сопромату и технической механике с необходимыми пояснениями, графическими построениями и видеоуроками.
- Определение опорных реакций
- Построение эпюр
- Расчеты на прочность
- Расчет балки
- Расчет напряжений
- Проверка на прочность
- Расчет деформаций и перемещений
- Расчеты на жесткость
- Растяжение-сжатие
- Кручение
- Изгиб
- Другие примеры
- Олимпиадные задачи
Помощь с решением задач
Сохранить и поделиться с друзьями
Задачи по условию
Определение опорных реакций
Примеры определения опорных реакций при растяжении-сжатии и плоском поперечном изгибе, определение неизвестного крутящего момента для вала.
Наш короткий видеоурок по расчету реакций опор балки:
Другие видео
Расчеты на прочность
Примеры решения задач по расчету стержней, балок и валов на прочность.
Подбор сечений, проверка на прочность и определение грузоподъемности.
Построение эпюр
Примеры построения эпюр внутренних усилий, напряжений и перемещений при растяжении-сжатии, кручении, изгибе и других видах деформации.
Расчет напряжений
Примеры расчетов нормальных, касательных и главных напряжений при различных видах деформации. Рассмотрены аналитические и графический способ (круг Мора) определения напряжений.
Расчет деформаций и перемещений
Примеры расчетов деформации бруса при различных видах нагружения.
Задачи по видам нагружения
Растяжение-сжатие
Примеры решения задач и расчетно-графических работ по теме растяжение-сжатие стержней и стержневых систем.
Кручение
Примеры решения задач и РГР на тему кручение валов.
Изгиб
Примеры решения задач и РГР по теме плоский поперечный изгиб балок.
Расчет балки
Примеры расчетов двухопорных и консольных балок.
Другие примеры решения задач по сопротивлению материалов представлены в нашей подборке:
Примеры решения задач для олимпиад по сопротивлению материалов.
Другие задачи
- Определение положение центра тяжести сложного сечения
- Определение положения центра тяжести составной фигуры, расчет главных центральных моментов и радиусов инерции, построение эллипса инерции
- Определение реакций в опорах рамы
- Построение эпюр N, Q и M для рамы
- Проверка построенных эпюр в рамах
- Перемещение точки нити перекинутой через блок
Сохранить или поделиться с друзьями
Вы находитесь тут:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Помощь с решением
ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ
- Техническая механика (техмех)
- Теоретическая механика (теормех)
- Сопротивление материалов (сопромат)
- Строительная механика (строймех)
- Теория механизмов и машин (ТММ)
- Детали машин и ОК (ДМ)
Сопротивление материалов | это… Что такое Сопротивление материалов?
Внешние силовые линии увеличиваются около отверстия, в общем случае концентрации напряжений
Сопротивление материалов (в обиходе — сопромат) — часть механики деформируемого твёрдого тела, которая рассматривает методы инженерных расчётов конструкций на прочность, жесткость и устойчивость при одновременном удовлетворении требований надежности, экономичности и долговечности.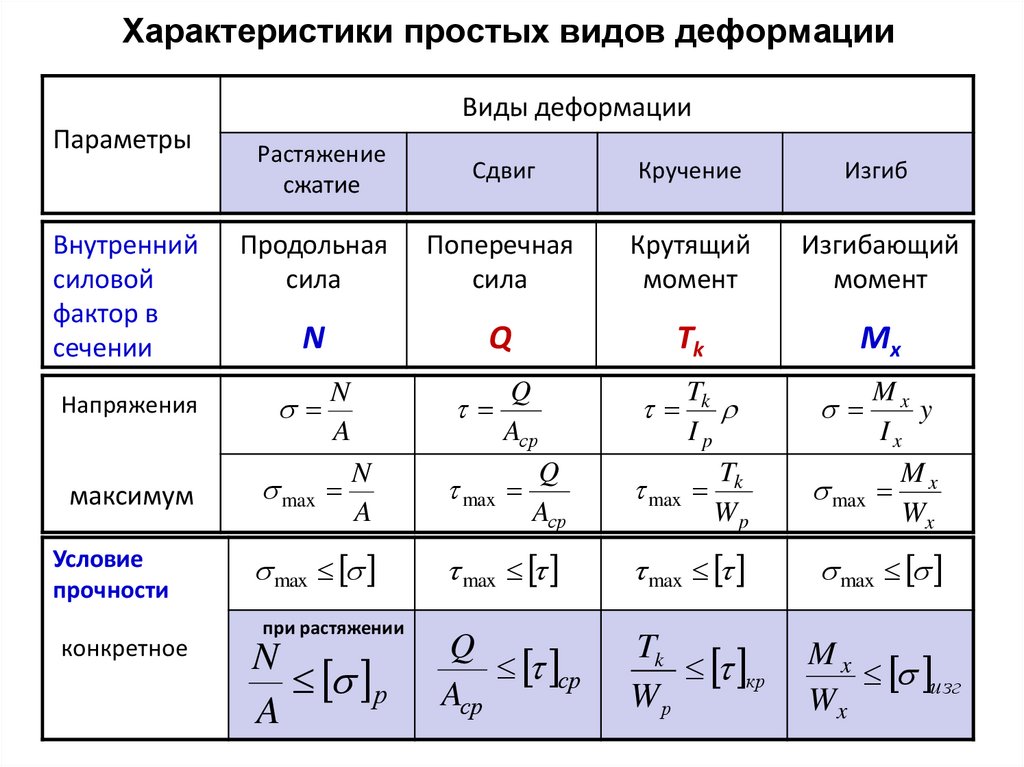
Сопротивление материалов относится к фундаментальным дисциплинам общеинженерной подготовки специалистов с высшим техническим образованием, за исключением специальностей, не связанных с проектированием объектов, для которых прочность является важным показателем.
Содержание
|
Определение
Сопротивление материалов базируется на понятии «прочность», что является способностью материала противостоять приложенным нагрузкам и воздействиям без разрушения. Сопротивление материалов оперирует такими понятиями как: внутренние усилия, напряжения, деформации. Приложенная внешняя нагрузка к некоторому телу порождает внутренние усилия в нём, противодействующие активному действию внешней нагрузки. Внутренние усилия, распределенные по сечениям тела называются напряжениями.
Таким образом, внешняя нагрузка порождает внутреннюю реакцию материала, характеризующуюся напряжениями,которые в свою очередь прямо пропорциональны деформациям тела. Деформации бывают линейные такие как удлинение,укорочение, сдвиг и углы поворота сечений. Основные понятия сопротивления материалов оценивающие способность материала сопротивляться внешним воздействиям являются:
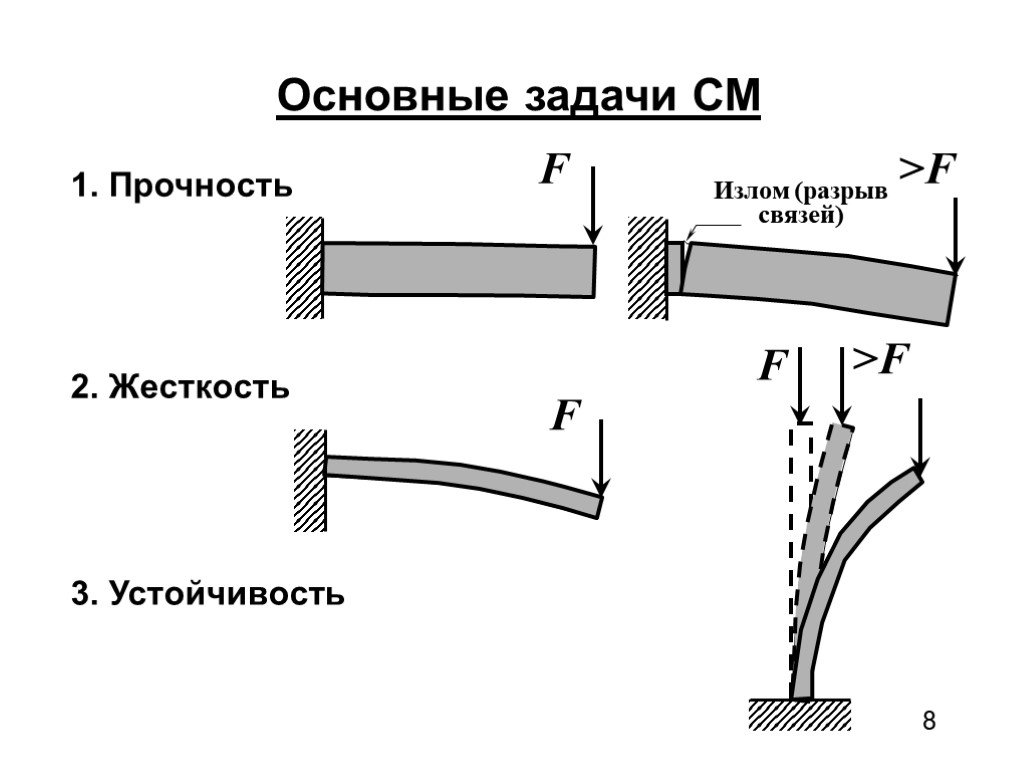
1. Несущая способность — способность материала воспринимать внешнюю нагрузку не разрушаясь;
2. Жесткость — способность материала сохранять свои геометрические параметры в допустимых пределах при внешних воздействиях
3. Устойчивость — способность материала сохранять в стабильности свою форму и положение при внешних воздействиях
Связь с другими науками
В теоретической части сопротивление материалов базируется на математике и теоретической механике, в экспериментальной части — на физике и материаловедении и применяется при проектировании машин, приборов и конструкций. Практически все специальные дисциплины подготовки инженеров по разным специальностям содержат разделы курса сопротивления материалов, так как создание работоспособной новой техники невозможно без анализа и расчета её прочности, жёсткости и надёжности.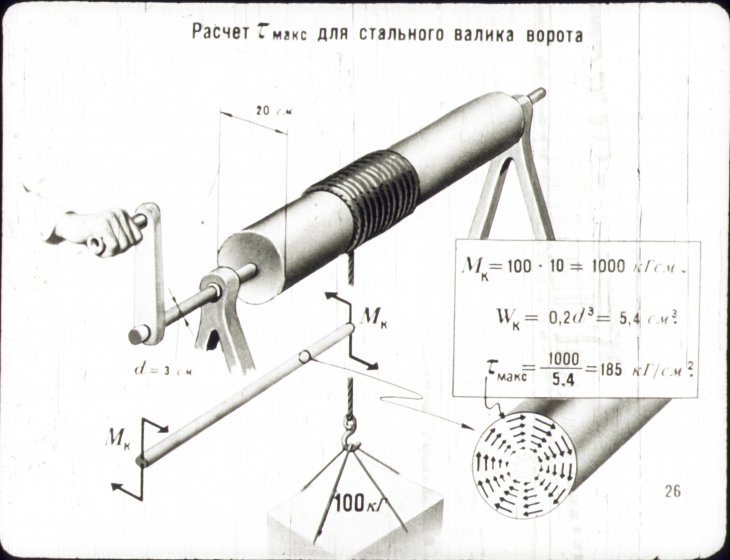
Задачей сопротивления материалов, как одного из разделов механики сплошной среды, является определение деформаций и напряжений в твёрдом упругом теле, которое подвергается силовому или тепловому воздействию.
Эта же задача среди других рассматривается в курсе теории упругости. Однако методы решения этой общей задачи в том и другом курсах существенно отличаются друг от друга. Сопротивление материалов решает её главным образом для бруса, базируясь на ряде гипотез геометрического или физического характера. Такой метод позволяет получить, хотя и не во всех случаях, вполне точные, но достаточно простые формулы для вычисления напряжений. Также поведением деформируемых твёрдых тел под нагрузкой занимается теория пластичности и теория вязкоупругости.
Гипотезы и допущения
Расчет конструкций и их элементов является или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов существует модель идеализированного деформируемого тела.
- Гипотеза сплошности и однородности
- Гипотеза об изотропности материала — физико-механические свойства материала одинаковы по всем направлениям.
- Гипотеза об идеальной упругости материала — тело способно восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию.
- Гипотеза (допущение) о малости деформаций — деформации в точках тела считаются настолько малыми, что не оказывают существенного влияния на взаимное расположение нагрузок, приложенных к телу.
- Допущение о справедливости закона Гука — перемещения точек конструкции в упругой стадии работы материала прямо пропорциональны силам, вызывающим эти перемещения.
- Принцип независимости действия сил — принцип суперпозиции; результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения.
- Гипотеза Бернулли о плоских сечениях — поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.
- Принцип Сен-Венана — в сечениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.
Эти положения ограниченно применимы к решению конкретных закдач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда.
Теории прочности
Прочность конструкций определяется с использованием теории разрушения — науки о прогнозировании условий, при которых твердые материалы разрушаются под действием внешних нагрузок. Материалы, как правило, подразделяются на разрушающиеся хрупко и пластично. В зависимости от условий (например, температура, состояние напряжений, виды нагрузки) большинство материалов может быть отнесено к хрупким или пластичным или обоим видам одновременно.
В математических терминах, теория разрушения выражается в виде различных критериев разрушения, которые справедливы для конкретных материалов. Критерием разрушения является поверхность разрушения, выраженная через напряжения или деформации. Поверхность разрушения разделяет «поврежденное» и «не поврежденное» состояния. Для «поврежденного» состояния трудно дать точное физическое определение. Поэтому это понятие следует рассматривать как рабочее определение, используемое в инженерном сообществе. Термин «поверхность разрушения», используемый в теории прочности, не следует путать с аналогичным термином, который определяет физическую границу между поврежденными и не поврежденными частями тела. Довольно часто феноменологические критерии разрушения одного и того же вида используются для прогнозирования хрупкого и пластичного разрушения.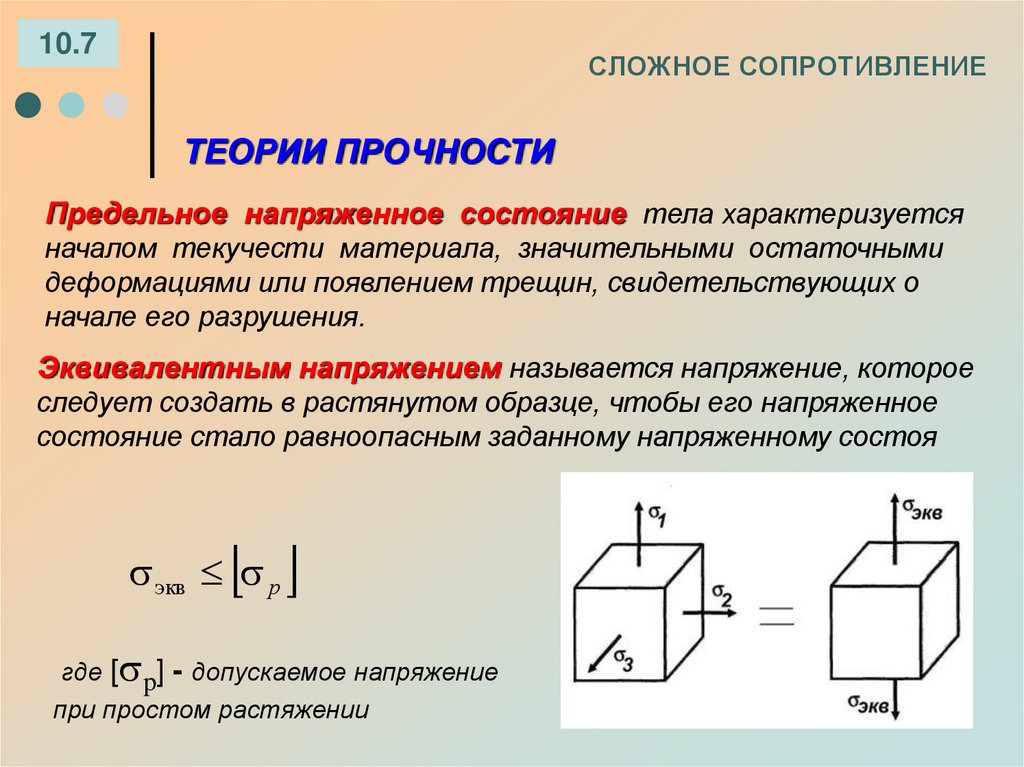
Среди феноменологических теорий прочности наиболее известными являются следующие теории, которые принято называть «классическими» теориями прочности:
1. Теория наибольших нормальных напряжений.
2. Теория наибольших деформаций.
3. Теория наибольших касательных напряжений Треска (Tresca).
4. Теория наибольшей удельной потенциальной энергии формоизменения фон Мизеса (von Mises).
5. Теория Мора (Mohr).
Классические теории прочности имеют существенные ограничения для их применения. Так теории наибольших нормальных напряжений и наибольших деформаций применимы лишь для расчета прочности хрупких материалов, причём только для некоторых определённых условий нагружения. Поэтому эти теории прочности сегодня применяют весьма ограниченно. Из перечисленных теорий наиболее часто используют теорию Мора, которую также называют критерием Мора-Кулона. Кулон (Coulomb) в 1781 г. на основе выполненных им испытаний установил закон сухого трения, который использовал для расчета устойчивости подпорных стенок.
На смену «классическим» теориям прочности в современной практике пришли многочисленные новые новые теории разрушения. Большинство из них используют различные комбинации инвариантов тензора напряжений Коши (Cauchy) Среди них наиболее известны следующие критерии разрушения:
- Друкера-Прагера (Drucker-Prager).
- Бреслера-Пистера (Bresler-Pister) — для бетона.
- Вильяма-Варнке (Willam-Warnke) — для бетона.
- Хенкинсона (Hankinson)- эмпирический критерий, используемый для ортотропных материалов типа древесины.
- Хила (Hill) — для анизотропных тел.
- критерий Tsai-Wu — для анизотропных материалов.
- критерий Hoek-Brown -для скальных массивов.
Перечисленные критерии прочности предназначены для расчета прочности однородных (гомогенных) материалов. Некоторые из них используются для расчёта анизотропных материалов.
Для расчета прочности неоднородных (не гомогенных) материалов используется два подхода, называемые макро-моделированием и микро-моделированием. Оба подхода ориентированы на использование метода конечных элементов и вычислительной техники. При макро-моделировании предварительно выполняется гомогенизация — условная замена неоднородного (гетерогенного) материала на однородный (гомогенный). При микро-моделировании компоненты материала рассматриваются с учётом их физических характеристик.
Микро-моделирование используют в основном в исследовательских целях, так как расчет реальных конструкций требует чрезмерно больших затрат машинного времени. Методы гомогенизации широко используются для расчета прочности каменных конструкций, в первую очередь для расчета стен-диафрагм жесткости зданий. Критерии разрушения каменных конструкций учитывают многообразные формы разрушения каменной кладки. Поэтому поверхность разрушения, как правило. принимается в виде нескольких пересекающихся поверхностей, которые могут иметь разную геометрическую форму.
Применение
Методы сопротивления материалов широко используются при расчете несущих конструкций зданий и сооружений, в дисциплинах связанных с проектированием деталей машин и механизмов.
Как правило, именно из-за оценочного характера результатов, получаемых с помощью математических моделей этой дисциплины, при проектировании реальных конструкций все прочностные характеристики материалов и изделий выбираются с существенным запасом (в несколько раз относительно результата, полученного при расчетах).
Гениев Г.А., Киссюк В.Н., Тюпин Г.А. Теория пластичности бетона и железобетона. — М.: Стройиздат, 1974.
— Bürkert Resistance Таблица химической стойкости
— Bürkert ResistanceAppНекоторые поля отсутствуют
отправить электронное письмо
Bürkert ResistanceApp помогает определить совместимые материалы и собирает для вас информацию о химической стойкости эластомеров, пластмасс и металлов к большому количеству газообразных и жидких сред.
Чтобы обеспечить надежность и долговечность вашей продукции, необходимо проявлять большую осторожность при выборе материалов, которые вступают в контакт с жидкими или газообразными средами, которые вы используете. Особенно это касается агрессивных жидкостей. Наш онлайн-инструмент для проверки сопротивления материалов поможет вам выбрать правильные материалы.
Например, он позволяет оценить химическую стойкость нержавеющей стали, а также пластмасс. Просто попробуйте. Проверьте сопротивление материалов онлайн бесплатно прямо сейчас!
×
База данных также доступна в виде приложения — загрузите Bürkert ResistanceApp
Наш инструмент доступен на нашем веб-сайте на каждой странице с подробным описанием типа, странице с подробным описанием статьи и для загрузки из соответствующих магазинов приложений. С помощью нашего приложения Bürkert ResistanceApp комбинируйте носители и материалы друг с другом, чтобы проверить совместимость ваших материалов.
Скачать бесплатное приложение из магазина приложений
Список материалов
Приложение содержит 454 среды, а также следующие материалы:
|
|
Информация о химической стойкости материалов, не перечисленных здесь, предоставляется по запросу.
Химическая стойкость относится к способности материалов противостоять различным типам химических веществ. Таким образом, он описывает способность материала сопротивляться деструктивным процессам, вызванным реакциями между окружающей средой и поверхностью.
Если материал подвергается воздействию химикатов или если его химическая стойкость недостаточна, это может привести к коррозии и ускорить разрушение материала. Для деталей или машин, изготовленных из этого материала, это отрицательно сказывается на сроке службы или может привести к их выходу из строя.
В этом случае проводится различие между тремя основными категориями:
- Подходит: Химически стойкий (минимальное повреждение материала или его отсутствие)
- Ограниченно подходит: Ограниченная химическая стойкость (коррозия материала от незначительной до средней)
- Не подходит: Не химически стойкий (сильная коррозия до полного разрушения материала)
Или просто скачать PDF-версию базы данных
Вы ищете печатную информацию? Взгляните на нашу таблицу химической стойкости:
{{bar_open.[0]}} ({{products.length}}) {{bar_open.[1]}}Все атрибуты
{{#if product_url}}
{{product_description}} Продолжить покупки
{{/если}}
{{#if product_status}}{{#if product_price}}
{{product_price}}
{{.
./tax_info}} {{/если}}
{{#if product_delivery}}
{{продукт_доставка}}
{{/если}} {{#if product_stock}}
{{product_stock}}
{{/если}} {{#равный product_status 2 }}
{{/равный}} {{#соответствует product_status 1 }} {{/равный}}
{{/если}} {{/каждый}}{{отправить}}
{{copy_link_text}} {{copy_hint}}
{{#каждый атрибут_названия как |ключ значения|}}
{{это}}
{{#каждый .
./продукты}}
{{../../артикул_номер}} {{продукт_артикул}}
{{Описание продукта}}
{{#with (ключ поиска product_attributes) как |attributeObject|}} {{#if attributeObject.text}}
{{attributeObject.text}}
{{/если}} {{#if attributeObject.image}} {{/если}} {{/с}}
{{/каждый}}
{{/каждый}}
Физика для введения в биологию
Когда к объекту прикладывается сила, он деформируется (часто настолько незначительно, что мы не можем увидеть деформацию!).
То, как объект деформируется, очень важно для его функции в организме. Чтобы понять, как свойства материала определяют, почему одни объекты очень устойчивы к деформации, а другие легко деформируются, или почему одни объекты устойчивы к разрушению, а другие легко ломаются, или почему одни структуры повышают эффективность циклических движений, а другие нет , нам нужно отделить эффекты геометрии (в целом размера, но иногда и формы) объекта от материала объекта. Размер объекта стандартизирован путем деления силы (\(F\)) на площадь поперечного сечения (\(A\)) нагруженного объекта и деления изменения длины (\(\ Delta L\), деформация) на начальную длину (\(L_o\)). Это приводит к двум действительно фундаментальным параметрам: 9{-2}\), которые являются единицами давления.
Рисунок 2.6: Несколько идеалистическая кривая напряжения-деформации
Напряжение – это не давление, прикладываемое к конструкции, а нормированная по площади сила реакции материала в ответ на внешнюю нагрузку.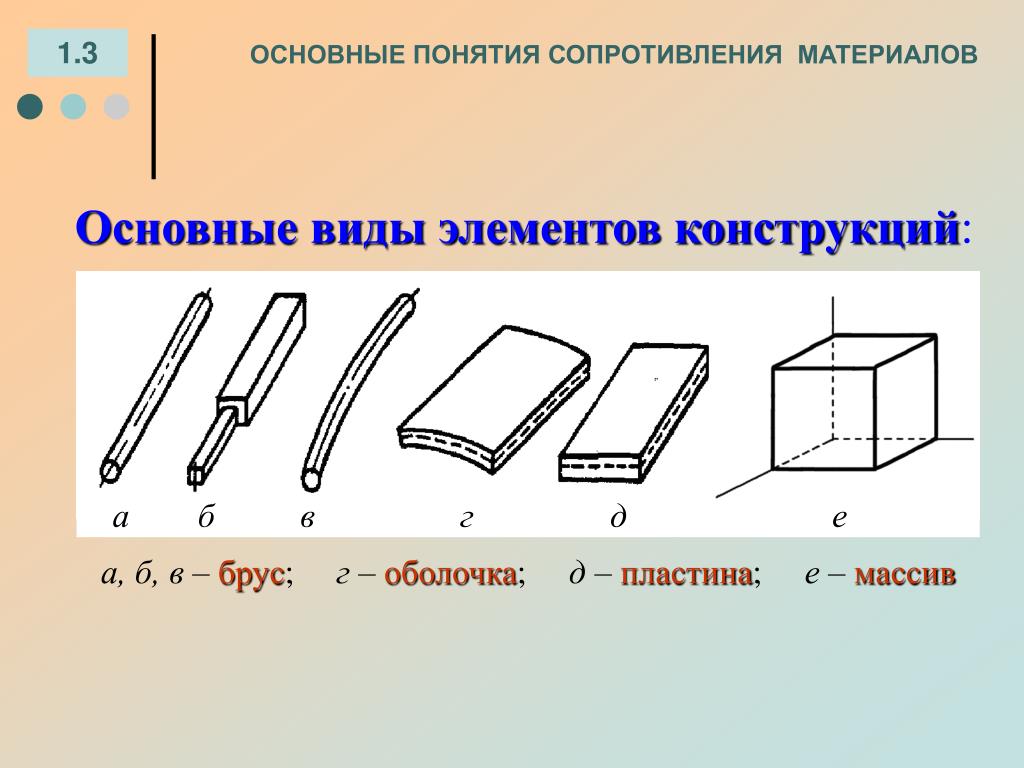
Стресс – это реакция на напряжение. Или стресс — это внутреннее сопротивление деформации. Деформация (деформация) вызывает перегруппировку атомов в материале. Перестроенные атомы притягиваются/отталкиваются друг от друга таким образом, что при удалении внешней нагрузки материал возвращается к исходной длине. Напряжение – это внутренняя стандартизированная сила, возникающая из-за того, что атомы притягиваются/отталкиваются друг от друга. Если с деформированного материала снимается внешняя нагрузка, напряжение все еще остается, и это напряжение присутствует до тех пор, пока добавленная сила притяжения/отталкивания не вернется к исходному значению. Таким образом, в то время как внешняя нагрузка вызывает напряжение, напряжение вызывает стресс! Важно отметить, что все описанные выше условия нагружения могут применяться и к напряжению, поэтому мы используем фразу «напряжение растяжения».
Рисунок 2.7: Кривые относительного напряжения-деформации для гидроксиапатита, коллагена и эластина
Эта способность материала сопротивляться деформации графически показана наклоном кривой напряжения-деформации с напряжением (\(\сигма\)) по оси у и деформацией \(\эпсилон\) по оси х ось.
