Основы электродинамики » ГДЗ (решебник) по физике 7-11 классов
594. Квадратная рамка с током расположена в однородном магнитном поле с индукцией 10 мТл, как показано на рисунке 138. Определите механический вращательный момент, действующий на рамку. Сила тока, идущего по рамке, 10 мА, сторона рамки 20 см.

595. Под каким углом к линиям магнитной индукции надо расположить рамку (см. задачу 594), чтобы вращательный момент, действующий на нее, уменьшился в 2 раза?

596. Стержень массой 0,2 кг лежит на двух горизонтальных рельсах перпендикулярно им (рис. 139). Силы давления стержня на оба рельса равны. Расстояние между рельсами 40 см. Индукция магнитного поля 40 мТл. Линии магнитной индукции направлены вертикально. Коэффициент трения скольжения о рельсы 0,01. Определите минимальную силу тока, который нужно пропустить по стержню, чтобы стержень начал двигаться. Примите g = 9,8 м/с2.

599. Стержень массой 200 г лежит на двух параллельных рельсах перпендикулярно им (рис. 140). Рельсы, расстояние между которыми 60 см, находятся на наклонной плоскости с углом у основания 30°. Линии магнитной индукции поля с индукцией 80 мТл направлены вертикально вверх. Коэффициент трения скольжения равен 0,7. Определите силу тока, идущего по стержню, в двух случаях:
1) стержень начинает подниматься вверх; 2) стержень начинает спускаться с наклонной плоскости.

602. Электрон влетает под углом 30° в область однородного магнитного поля шириной 3 мм (рис. 141), а вылетает под углом 60°. Скорость электрона 106 м/с. Определите индукцию магнитного поля.

606. Электрон влетает в однородное магнитное поле под углом 30° к линиям магнитной индукции со скоростью 104 м/с. Расстояние от начального положения электрона до экрана 40 см. Сколько оборотов сделает электрон, прежде чем он попадет на экран? Индукция магнитного поля

612. Радиус проволочного витка, соединяющего пластины плоского конденсатора емкостью 10 мкФ, равен 20 см. Чему равен заряд на пластинах конденсатора, если виток помещен в однородное магнитное поле (рис. 147), индукция которого изменяется по закону В = В0 + Ы9 где k = 0,005 Тл/с и вектор В направлен под углом 30° к плоскости витка?

615. Мальчик вращает на веревке длиной 20 см в вертикальной плоскости металлический прут длиной 10 см с частотой 2 об/с. Определите максимальную разность потенциалов, которая может возникнуть между концами прута. Горизонтальная составляющая индукции магнитного поля Земли 0,2 мТл.

618. Круговой проволочный контур длиной I находится в однородном магнитном поле, индукция которого равна В. Линии магнитной индукции перпендикулярны плоскости контура. Проводник свернули в виде восьмерки (рис. 152). Удельное сопротивление проволоки р, площадь поперечного сечения S. Определите заряд, прошедший по проводнику.

622. Короткозамкнутая катушка сопротивлением 20 Ом и индуктивностью 0,01 Гн находится в переменном магнитном поле. Когда создаваемый этим полем магнитный поток увеличивается на 10_3 Вб, сила тока в катушке возрастает на 0,05 А. Какой заряд за это время проходит по катушке?

623. В катушке без сердечника за время 0,01 с сила тока увеличивается равномерно от 1 до 2 А. При этом в катушке возникает ЭДС самоиндукции 20 В. Определите индуктивность катушки, а также изменение за указанный промежуток времени магнитного потока.

625. В цепь источника тока с ЭДС, равной 8 В, параллельно подключены катушка индуктивностью 5 • 10“2 Гн и электролампа (рис. 153). Сопротивление электролампы много больше сопротивления катушки, равного 2 Ом. Какое количество теплоты выделится в электролампе при отключении источника?

ЭДС индукции. Примеры решения задач по физике. 10-11 класс
ЭДС индукции. Примеры решения задач по физике. 10-11 класс
Задачи по физике — это просто!
Не забываем
А теперь к задачам!
Элементарные задачи из курса школьной физики на вычисление ЭДС индукции.
Задача 1
За время 5 мс в соленоиде, содержащем 500 витков провода, магнитный поток равномерно убывает от 7 мВб до 3 мВб.
Найдите ЭДС индукции в соленоиде.
Задача 2
Какой магнитный поток пронизывает каждый виток катушки, имеющей 1000 витков, если при равномерном исчезновении магнитного поля в течение 0,1 с в катушке индуцируется ЭДС равная 10 В ?
Задача 3
Виток проводника площадью 2 см2 расположен перпендикулярно вектору магнитной индукции.
Задача 4
В однородном
магнитном поле перпендикулярно к направлению вектора индукции , модуль которого 0,1 Тл, движется провод длиной 2 метра со скоростью 5 м/с, перпендикулярной проводнику.
Какая ЭДС индуцируется в этом проводнике?
Задача 5
Перпендикулярно вектору магнитной индукции перемещается проводник длиной 1,8 метра со скоростью 6 м/c. ЭДС индукции равна 1,44 В.
Найти магнитную индукцию магнитного поля.
Задача 6
Самолет имеет размах крыльев 15 метров. Горизонтальная скорость полета равна720 км/час.
Определить разность потенциалов, возникающих между концами крыльев. Вертикальная составляющая магнитной индукции (перпендикулярно поверхности Земли) равна 50 мкТл.
Задача 7
Магнитный поток через контур проводника сопротивлением 0,03 Ом за 2 секунды изменился на 0,012 Вб.
Найдите силу тока в проводнике если изменение потока происходило равномерно.
Задача 8
В однородном магнитном поле находится плоский виток площадью 10 см2, расположенный перпендикулярно вектору магнитной индукции.
Задача 9
Сопротивление замкнутого контура равно 0,5 Ом. При перемещении кольца в магнитном поле магнитный поток через кольцо изменился на 5×10-3 Вб.
Какой за это время прошел заряд через поперечное сечение проводника?
StudyPort.Ru — Электромагнитная индукция
Страница 1 из 2
175. Соленоид диаметром d = 4 см, имеющий N = 500 витков, помещен в магнитное поле, индукция которого изменяется со скоростью 1 мТл/с. Ось соленоида составляет с вектором магнитной индукции угол а = 45 градусов. Определите ЭДС индукции, возникающую в соленоиде.

176. В магнитное поле, изменяющееся по закону В = В0*cos(ω*t) (B0 = 0,1 Тл, w = 4 c-1), помещена квадратная рамка со стороной a = 50 см, причем нормаль к рамке образует с направлением поля угол α = 45 градусов. Определите ЭДС индукции, возникающую в рамке в момент времени t = 5 с.

177. Кольцо из алюминиевого провод (ρ = 26 нОм*м) помещено в магнитное поле перпендикулярно линиям магнитной индукции. Диаметр кольца D = 30 см, диаметр провода d = 2 мм. Определите скорость изменения магнитного поля, если ток в кольце I = 1 А.

178. Плоскость проволочного витка площадь S = 100 см2 и сопротивлением R = 5 Ом, находящего в однородном магнитном поле напряженность H = 10 кА/м, перпендикулярна линиям магнитной индукции. При повороте витка в магнитном поле отсчет гальванометра, замкнутого на виток, составляет 12,6 мкКл. Определите угол поворота витка.

179. В однородное магнитное поле с индукцией В = 0,3 Тл помещена прямоугольная рамка с подвижной стороной, длина которой l = 15 см. Определите ЭДС индукции, возникающей в рамке, если ее подвижная сторона перемещается перпендикулярно линиями магнитной индукции со скоростью v = 10 м/с.

180. Две гладкие замкнутые металлические шины, расстояние между которыми равно 30 см, со скользящей перемычкой, которая может двигаться без трения, находятся в однородном магнитном поле с индукцией В = 0,1 Тл, перпендикулярном плоскости контура. Перемычка массой m = 5 г скользит вниз с постоянной скоростью v = 0,5 м/с. Определите сопротивление перемычки, пренебрегая самоиндукцией контура и сопротивлением остальной части контура.

181. В катушке длиной l = 0,5 м, диаметром d = 5 см и числом витков N = 1500 ток равномерно увеличивается на 0,2 А за одну секунду. На катушку надето кольцо из медной проволоки (ρ = 17 нОм*м) площадью сечения Sк = 3 мм2. Определите силу тока в кольце.

182. Катушка диаметром d = 2 см, содержащая один слой плотно прилегающих друг к другу N =500 витков алюминиевого провода сечением S = 1 мм2, помещена в магнитное поле. Ось катушки параллельна линиям индукции. Магнитная индукция поля равномерно изменяется со скоростью 1 мТл/с. Определите тепловую мощность, выделяющуюся в катушке, если концы замкнуты накоротко. Удельное сопротивление алюминия ρ = 26 нОм/м.

183. В однородном магнитном поле (B = 0,1 Тл) вращается с постоянной угловой скоростью ω = 50 с-1 вокруг вертикальной оси стер длиной l = 0,4 м. Определите ЭДС индукции, возникающей в стержне, если ось вращения проходит через конец стержня параллельно линиям магнит индукции.

184. В однородном магнитном поле с индукцией В = 0,02 Тл равномерно вращается вокруг вертикальной оси горизонтальный стержень длиной l = 0,5 м. Ось вращения проходит через конец стержня параллельно линиям магнитной индукции. Определите число оборотов в секунду, при котором на концах стержня возникает разность потенциалов U = 0,1 В.

185. В однородном магнитном поле (В = 0,2 Тл) равномерно с частотой n = 600 мин-1 вращается рамка, содержащая N = 1200 витков, плотно прилегающих друг к другу. Площадь рамки S = 100 см2. Ось вращения лежит в плоскости рамки и перпендикулярна линиям магнитной индукции. Определите максимальную ЭДС, индуцируемую в рамке.

186. Магнитная индукция B поля между полюсами двухполюсного генератора равна 1 Тл. Ротор имеет 140 витков (площадь каждого витка S = 500 см2). Определите частоту вращения якоря, если максимальное значение ЭДС индукции равно 220 В.

187. В однородном магнитном поле (B = 0,2 Тл) равномерно вращается прямоугольная рамка, содержащая N = 200 витков, плотно прилегающих друг к другу. Площадь рамки S = 100 см2. Определите частоту вращения рамки, если максимальная ЭДС, индуцируемая в ней, εmax = 12,6 В

188. В однородном магнитном поле равномерно вращается прямоугольная рамка с частотой n = 600 мин-1. Амплитуда индуцируемой ЭДС ε0 = 3 В. Определите максимальный магнитный поток через рамку.

189. Катушка длиной l = 50 см и диаметром d = 5 см содержит N = 200 витков. По катушке течет ток I = 1 А. Определите: 1) индуктивность катушки; 2) магнитный поток, пронизывающий площадь ее поперечного сечения.

190. Длинный соленоид индуктивностью L = 4 мГн содержит N = 600 витков. Площадь поперечного сечения соленоида S = 20 см2. Определите магнитную индукцию поля внутри соленоида, если сила тока, протекающего по его обмотке, равна 6 А.

191. Две длинные катушки намотаны на общий сердечник, причем индуктивности этих катушек L1 = 0,64 Гн и L2 = 0,04 Гн. Определите, во сколько раз число витков первой катушки больше, чем второй.

192. Определите, сколько витков проволоки, вплотную прилегающих друг к другу, диаметром d = 0,5 мм с изоляцией ничтожной толщины надо намотать на картонный цилиндр диаметром D = 1,5 см, чтобы получить однослойную катушку индуктивностью L = 100 мкГн?

193. Определите индуктивность соленоида длиной l и сопротивлением R, если обмоткой соленоида является проволока массой m (принять плотность проволоки и ее удельное сопротивление соответственно за ρи ρ’).

194. Сверхпроводящий соленоид длиной l = 10 см и площадью поперечного сечения S = 3 см2, содержащий N = 1000 витков, может быть подключен к источнику ЭДС ε = 12 В. Определите силу тока через 0,01 с после замыкания ключа.

195. Через катушку, индуктивность L которой равна 200 мГн, проте ток, изменяющийся по закону I = 2cos(3*t). Определите: 1) за изменения ЭДС самоиндукции; 2) максимальное значение ЭДС самоин.

|
Рассмотрим поле, создаваемое током I, текущим по тонкому проводу, имеющему форму окружности радиуса R (рис. 1.7). Рис. 1.7 Определим магнитную индукцию на оси проводника с током на расстоянии х от плоскости кругового тока. Векторы перпендикулярны плоскостям, проходящим через соответствующие и . Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий вектор направлен вдоль оси кругового тока. Каждый из векторов вносит вклад равный , а взаимно уничтожаются. Но , , а т.к. угол между и α – прямой, то тогда получим
Подставив в (1.6.1) и, проинтегрировав по всему контуру , получим выражение для нахождения магнитной индукции кругового тока:
При , получим магнитную индукцию в центре кругового тока:
Заметим, что в числителе (1.6.2) – магнитный момент контура. Тогда, на большом расстоянии от контура, при , магнитную индукцию можно рассчитать по формуле:
Силовые линии магнитного поля кругового тока хорошо видны в опыте с железными опилками (рис. 1.8).
Рис. 1.8 Другие аудио-видео демонстрации по теме или смежным темам:1. Силовые линии магнитов. 2. Линии магнитной индукции. 3. Намагниченность. 4. Электромагниты. 5. Компас. |
4. Основные формулы Электромагнетизм
Связь магнитной индукции
 с напряженностью
с напряженностью магнитного
поля.
магнитного
поля.
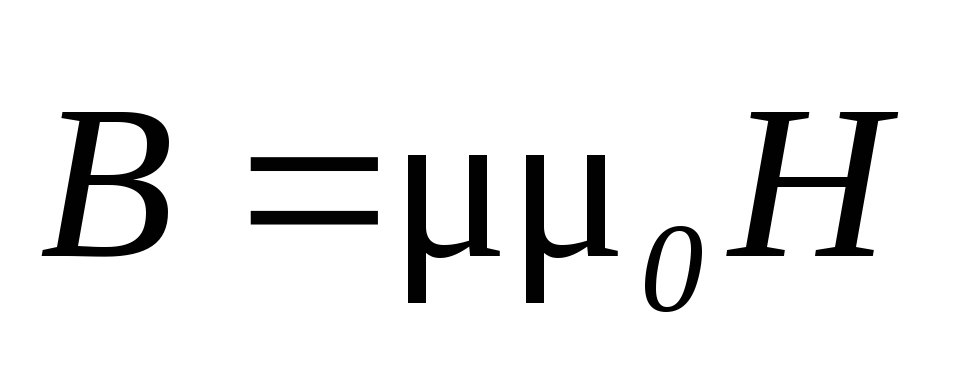 ,
,
где — магнитная проницаемость однородной среды; 0 — магнитная постоянная. В вакууме = 1, и магнитная индукция в вакууме
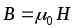 .
.
2. Закон Био-Савара-Лапласа
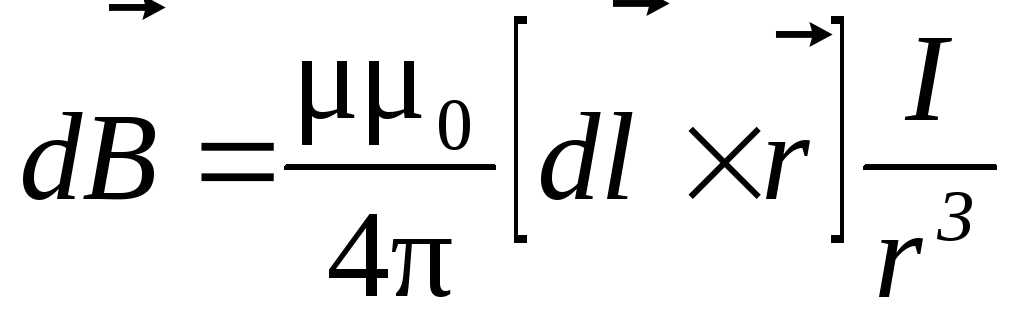 или
или 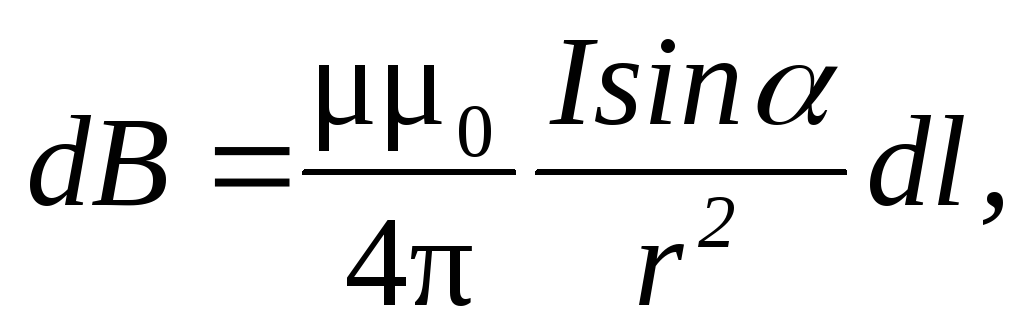
где 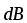 — магнитная индукция поля, создаваемого
элементом провода длиной
— магнитная индукция поля, создаваемого
элементом провода длиной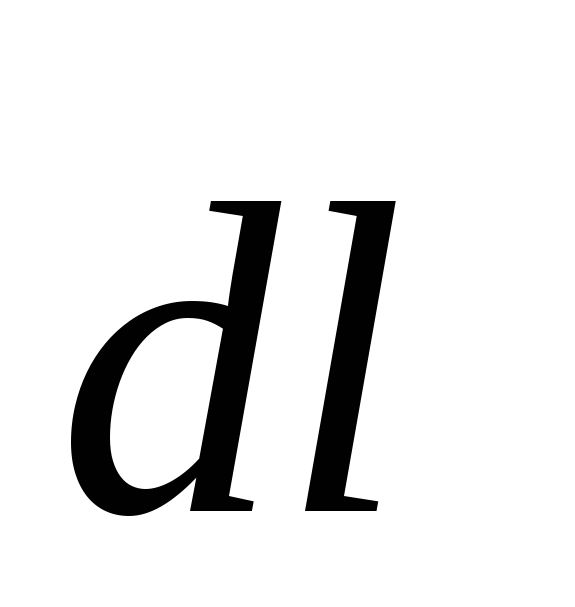 c
током I;
c
током I;  — радиус-вектор, направленный от элемента
проводника к точке, в которой определяется
магнитная индукция; — угол между радиус-вектором и направлением
тока в элементе провода.
— радиус-вектор, направленный от элемента
проводника к точке, в которой определяется
магнитная индукция; — угол между радиус-вектором и направлением
тока в элементе провода.
3. Принцип суперпозиции магнитных полей
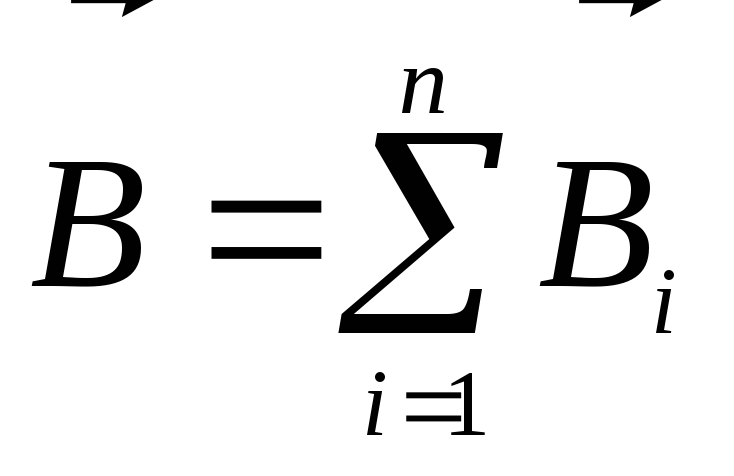 или
или 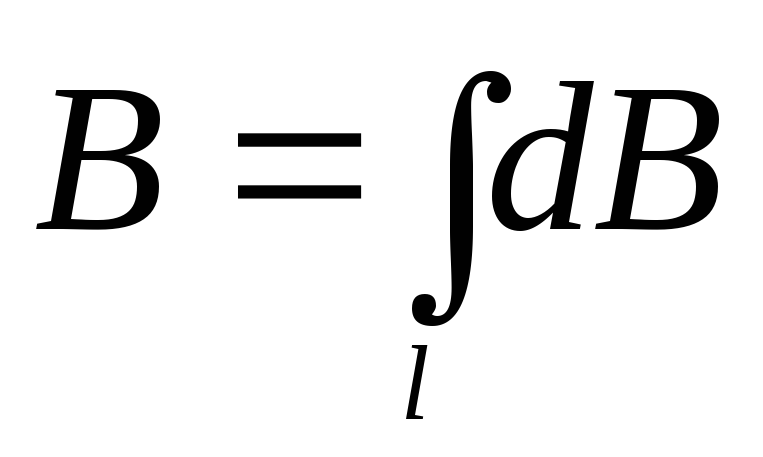
 ,
созданных элементом тока
,
созданных элементом тока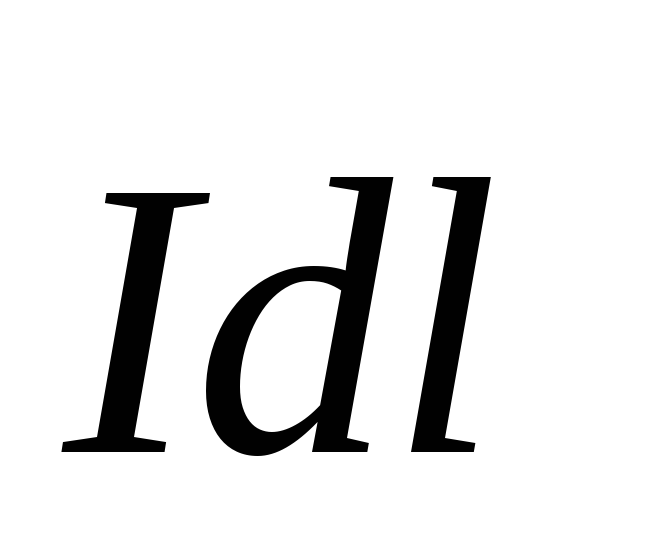 .
. Направление
вектора магнитной индукции 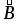 поля, создаваемого прямым током,
определяется по правилу буравчика
(правого винта). Для этого проводим
магнитную силовую линию (штриховая
линия на рис.) и по касательной к ней в
интересующей нас точке проводим вектор
поля, создаваемого прямым током,
определяется по правилу буравчика
(правого винта). Для этого проводим
магнитную силовую линию (штриховая
линия на рис.) и по касательной к ней в
интересующей нас точке проводим вектор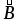 .
Вектор магнитной индукции
.
Вектор магнитной индукции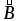 в точкеА направлен перпендикулярно плоскости
чертежа от нас.
в точкеА направлен перпендикулярно плоскости
чертежа от нас.
Рис. 1
4. Магнитная индукция в центре кругового тока
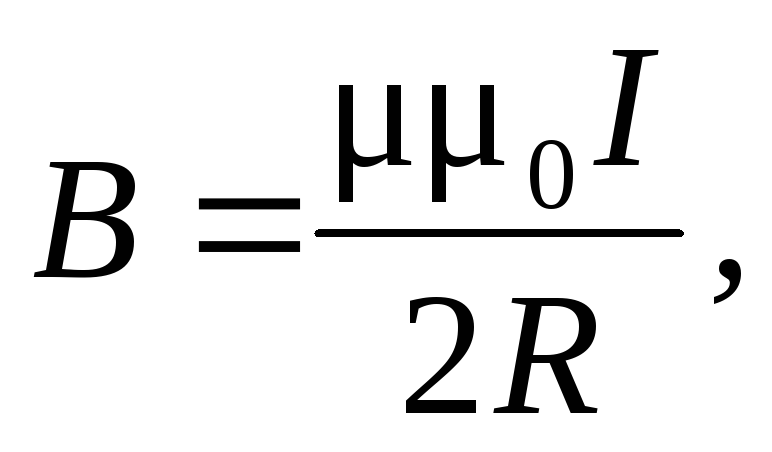
где R — радиус кругового витка.
Магнитная индукция на оси кругового тока

где h — расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком провода с током (вывод этой формулы в примере № 1):
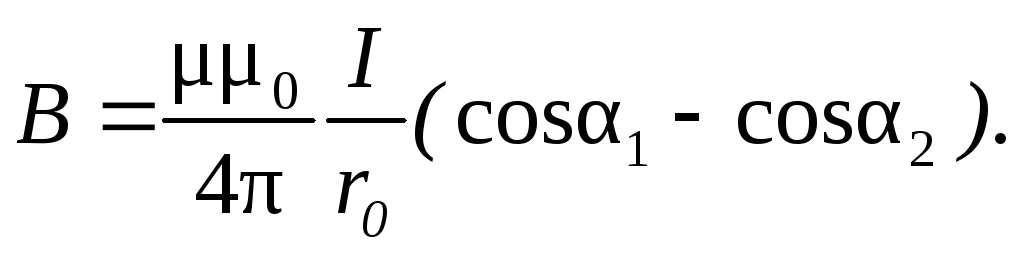
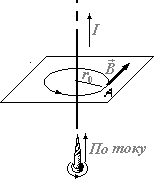
Магнитная индукция поля, создаваемого бесконечно длинным прямолинейным проводником с током:
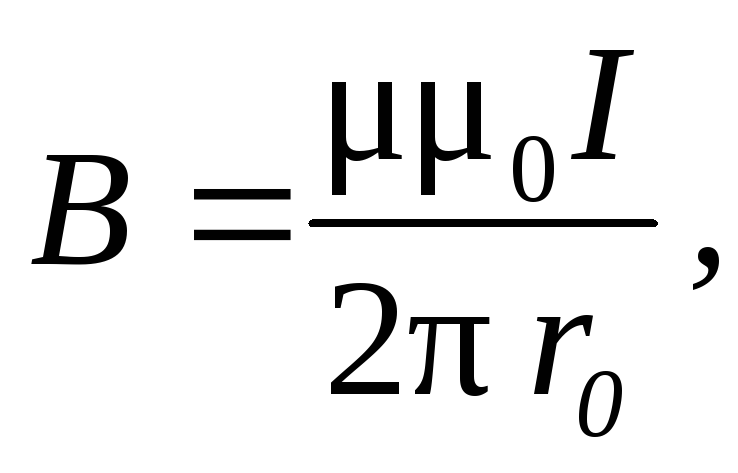
где r0 — расстояние от оси провода до точки, в которой определяется магнитная индукция.
Магнитная индукция поля бесконечно длинного соленоида
B = 0nI,
где n — отношение числа витков соленоида N к его длине l.
5. Сила, действующая на элемент провода с током в магнитном поле (закон Ампера):
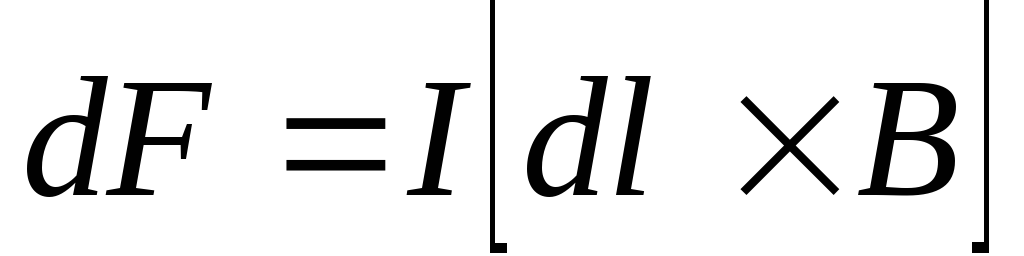 ,
,
где 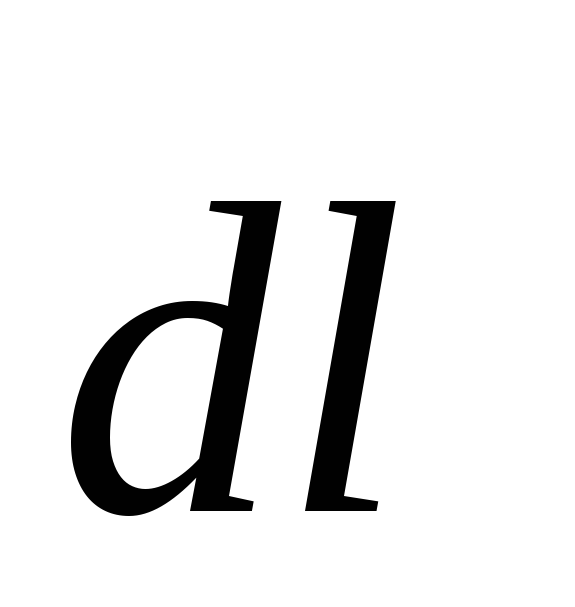 — вектор, равный по модулю длине участка
провода и совпадающий по направлению
с током; — угол между направлением тока в проводе
и вектором магнитной индукции
— вектор, равный по модулю длине участка
провода и совпадающий по направлению
с током; — угол между направлением тока в проводе
и вектором магнитной индукции 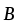 .
.
Для однородного магнитного поля и прямого отрезка провода получим:
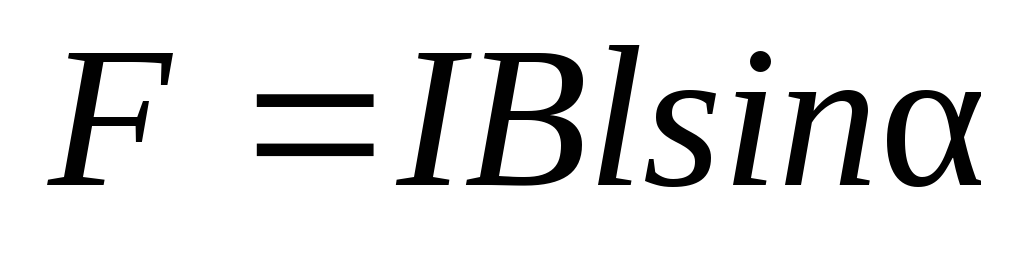 .
.
6. Магнитный момент плоского контура с током
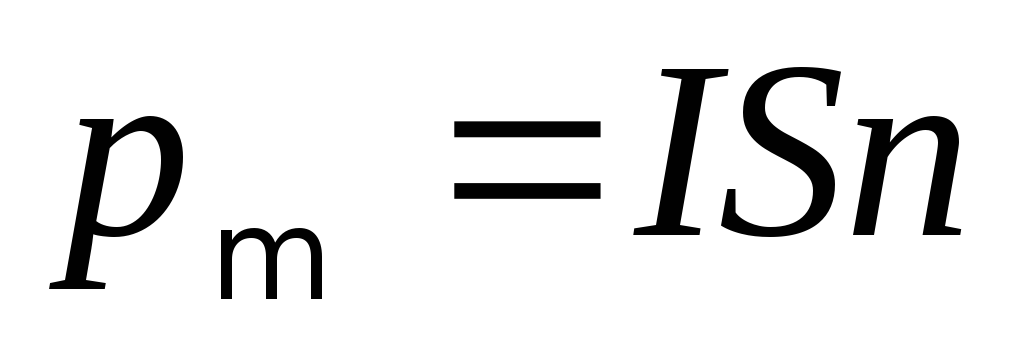 ,
,
где 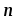 — единичный вектор нормали (положительной)
к плоскости контура;I — сила тока,
протекающего по контуру; S — площадь контура.
— единичный вектор нормали (положительной)
к плоскости контура;I — сила тока,
протекающего по контуру; S — площадь контура.
7. Механический вращающий момент, действующий на контур с током, помещенный в однородное магнитное поле:
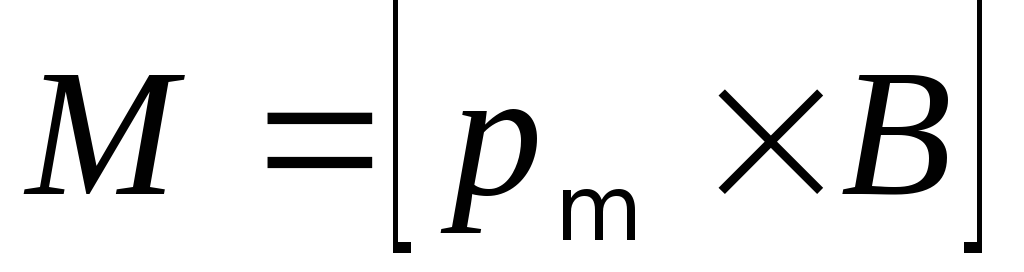 или
или 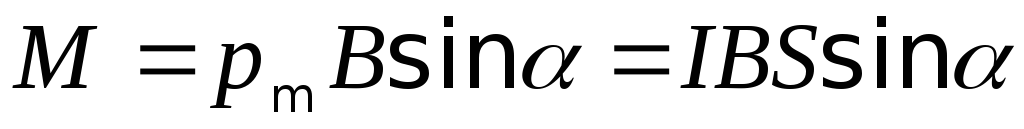 ,
,
где — угол между векторами 
8. Сила Лоренца
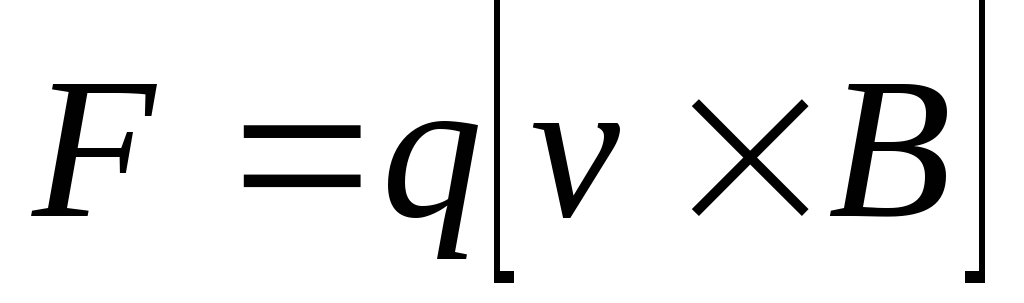 или
или  ,
,
где  — скорость заряженной частицы; — угол между векторами
— скорость заряженной частицы; — угол между векторами  и
и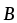 .
.
Если частица находится одновременно в электрическом и магнитном полях, то на нее действует сила
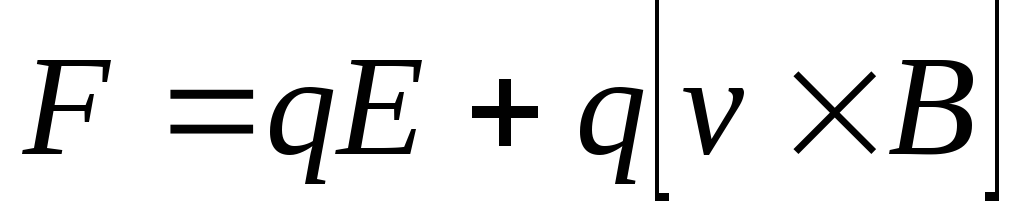 .
.
9. Магнитный поток (через поверхность S):
а) в случае однородного магнитного поля и плоской поверхности
Ф = BScos или Ф = BnS ,
где S — площадь контура; — угол между нормалью к плоскости контура и вектором магнитной индукции;
б) в случае неоднородного поля и произвольной поверхности
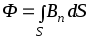
(интегрирование ведется по всей поверхности).
Потокосцепление (полный поток) – = NФ.
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
10. Работа по перемещению замкнутого контура с током в магнитном поле dA=I dФилиА=IФ.
11. Основной закон электромагнитной
индукции (закон Фарадея-Максвелла):  .
.
Разность
потенциалов на концах проводника,
движущегося со скоростью 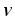 в магнитном поле,U
= Blv·sin,
в магнитном поле,U
= Blv·sin,
где l — длина провода; — угол между векторами 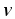 и
и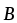 .
.
Заряд, протекающий по замкнутому контуру
при изменении магнитного потока,
пронизывающего этот контур: 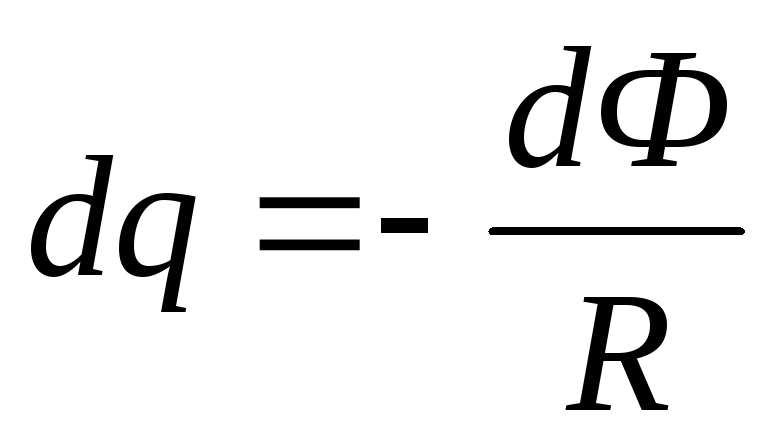 или
или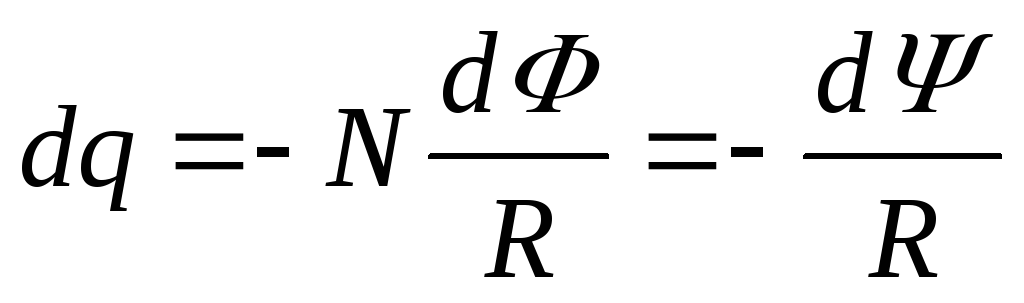 ,
гдеR— сопротивление
контура.
,
гдеR— сопротивление
контура.
12. Индуктивность контура L = Ф/I.
Индуктивность соленоида L = 0n2lS,
где n — отношение числа витков соленоида к его длине; l – длина соленоида, S – площадь его поперечного сечения.
13. Э.д.с. самоиндукции
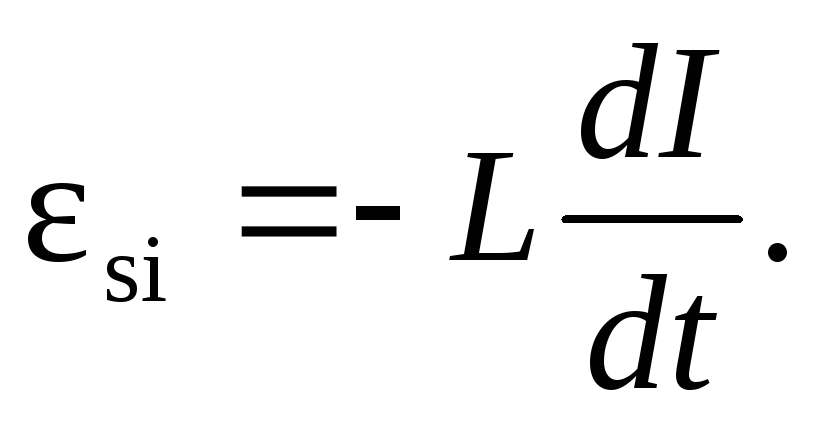
14. Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:
а) 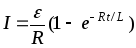 — при замыкании цепи, где -э.д.с. источника тока; t — время, прошедшее после замыкания цепи;
— при замыкании цепи, где -э.д.с. источника тока; t — время, прошедшее после замыкания цепи;
б) 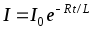 — при размыкании цепи, гдеI0 — сила тока в цепи при t = 0; t — время, прошедшее с момента размыкания
цепи.
— при размыкании цепи, гдеI0 — сила тока в цепи при t = 0; t — время, прошедшее с момента размыкания
цепи.
15.
Энергия магнитного поля соленоида W = 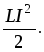
Объемная плотность энергии магнитного поля (отношение энергии поля к его объему)
w = BH/2 = B2/(20) = 0 H2/2.
4. Напряженность магнитного поля кругового тока
Р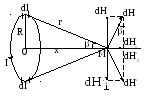 ассмотрим
поле, создаваемое током, текущим по
тонкому проводнику, имеющему форму
окружности радиусом
ассмотрим
поле, создаваемое током, текущим по
тонкому проводнику, имеющему форму
окружности радиусом 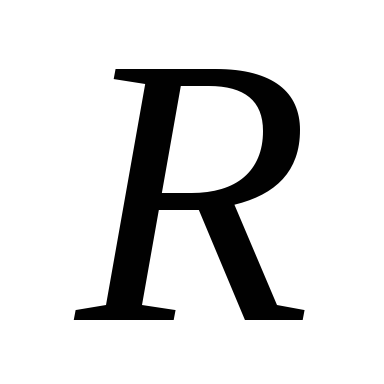 (круговой ток). Найдем напряженность
на оси кругового тока на расстоянии
(круговой ток). Найдем напряженность
на оси кругового тока на расстоянии 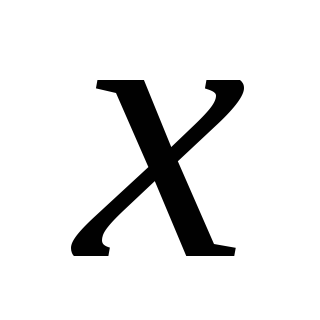 от плоскости, в которой лежит контур.
По закону Био- Савара-Лапласа
напряженность создаваемая элементом
проводника dl равна
от плоскости, в которой лежит контур.
По закону Био- Савара-Лапласа
напряженность создаваемая элементом
проводника dl равна
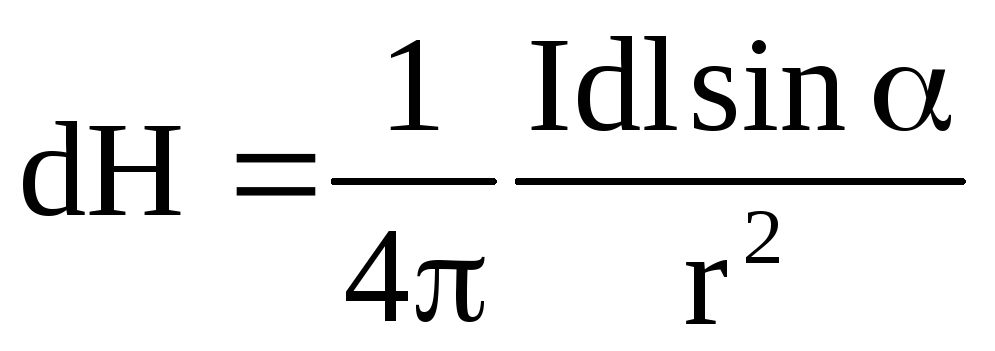
 ,
=90o следовательно,
,
=90o следовательно,
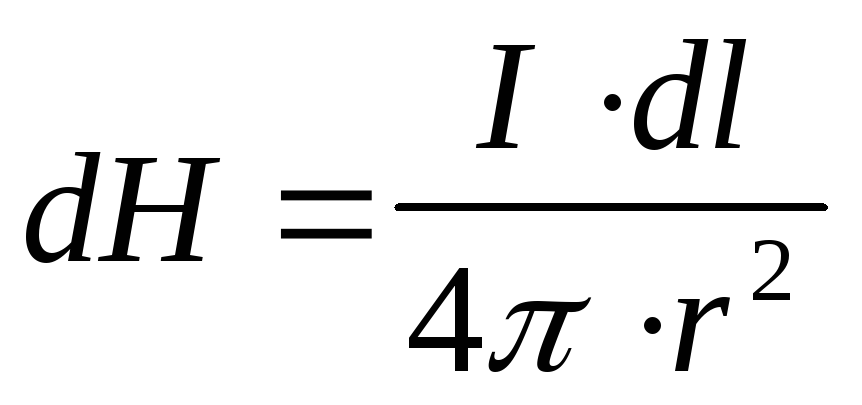 .
.
Вектор  составляет некоторый угол с осью ОМ.
Каждому элементу
составляет некоторый угол с осью ОМ.
Каждому элементу  можно
сопоставить диаметрально противоположный
элемент dl
Для этих элементов перпендикулярные
составляющие
dHи
можно
сопоставить диаметрально противоположный
элемент dl
Для этих элементов перпендикулярные
составляющие
dHи  взаимно
уничтожаются, а параллельные
dHll и dHll составляющие складываются. Следовательно,
результирующее поле будет направлено
по оси ОМ. Зная направление, мы сможем
теперь определить величину
взаимно
уничтожаются, а параллельные
dHll и dHll составляющие складываются. Следовательно,
результирующее поле будет направлено
по оси ОМ. Зная направление, мы сможем
теперь определить величину  ,
сложив составляющие dHll всех элементов контура.
,
сложив составляющие dHll всех элементов контура.
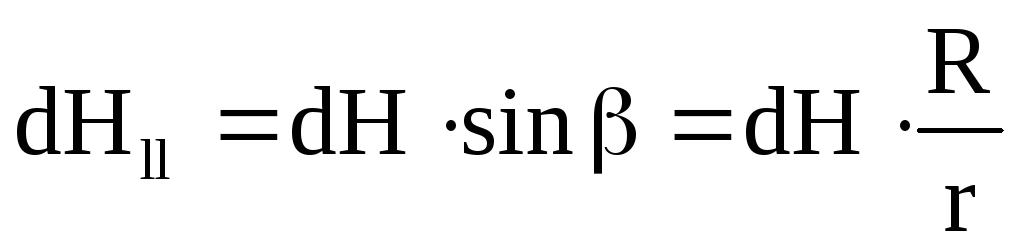
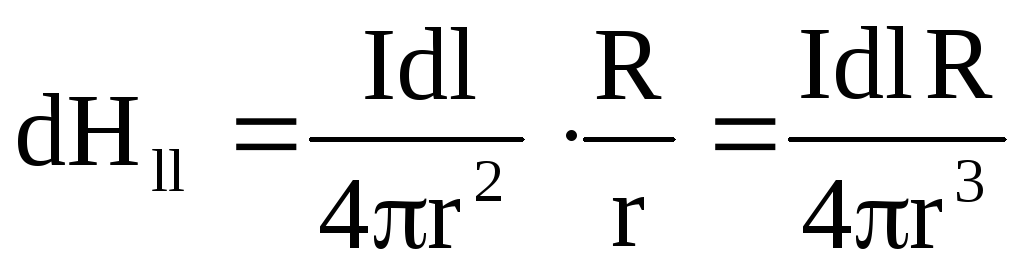
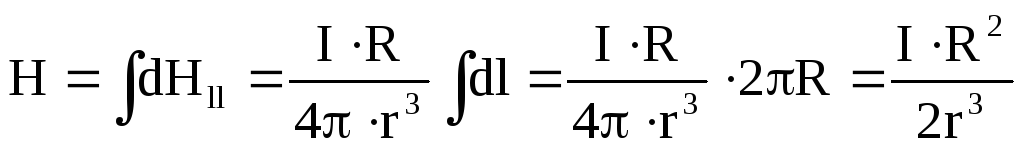
Но 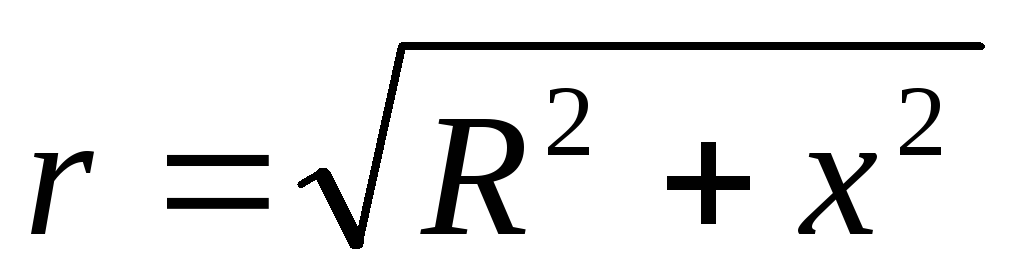 ,
тогда
,
тогда
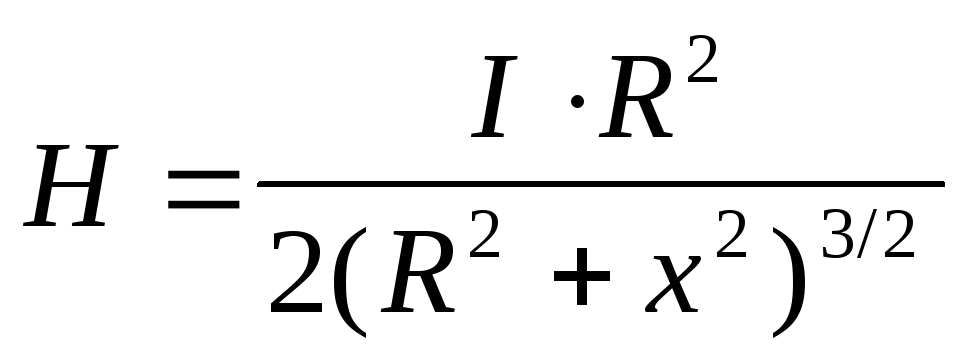 — напряженность магнитного поля на
оси кругового тока
— напряженность магнитного поля на
оси кругового тока
Положив 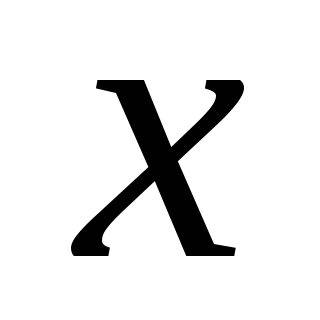 =0,
получим формулу для напряженности поля
в центре кругового витка:
=0,
получим формулу для напряженности поля
в центре кругового витка:
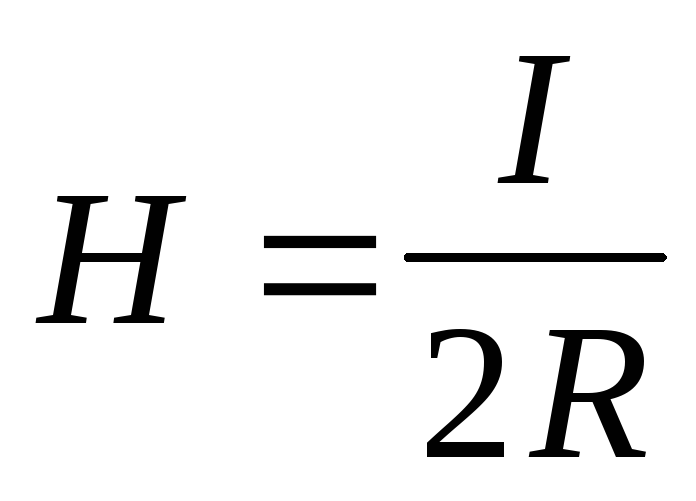
5. Циркуляция вектора .
В электростатике мы ввели понятие циркуляции вектора напряженности как величину равную:
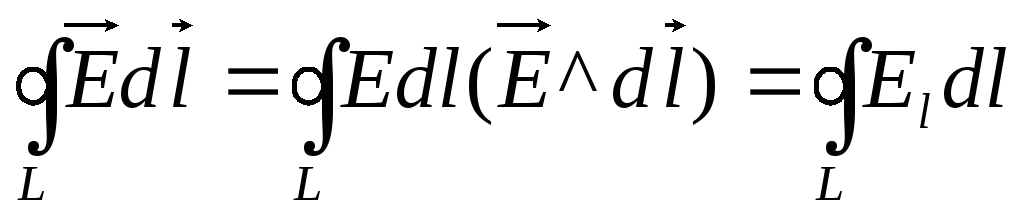
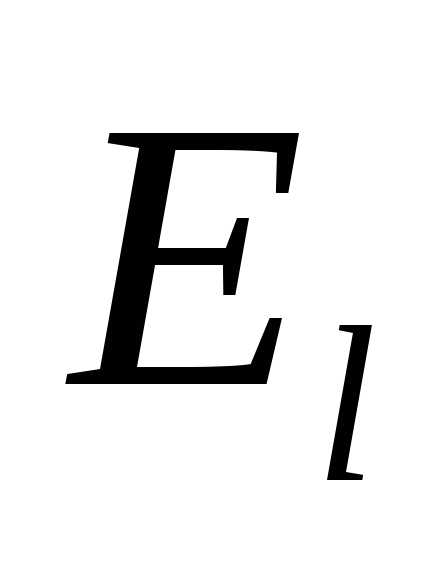 —
проекция E
на направление касательной к контуру
L.
—
проекция E
на направление касательной к контуру
L.
Было показано, что циркуляция вектора Е равна нулю. Физический смысл циркуляции вектора Е — работа по перемещению единичного заряда (F=E при q=1, Edl=A при q=1) по замкнутому контуру. Но в механике было показано, что поле, в котором работа по замкнутому контуру равна нулю, называется потенциальным. Таким образом равенство нулю циркуляции вектора Е говорит о том, что электростатическое поле является потенциальным.
Рассмотрим
теперь, чему равна циркуляция вектора
индукции магнитного поля. Возьмем контур
L, охватывающий
прямой ток и вычислим для него циркуляцию
вектора 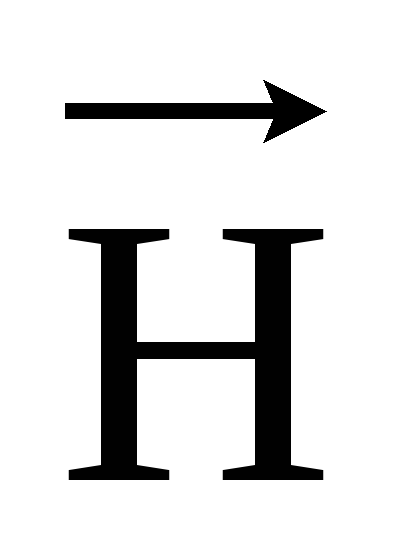 :
:
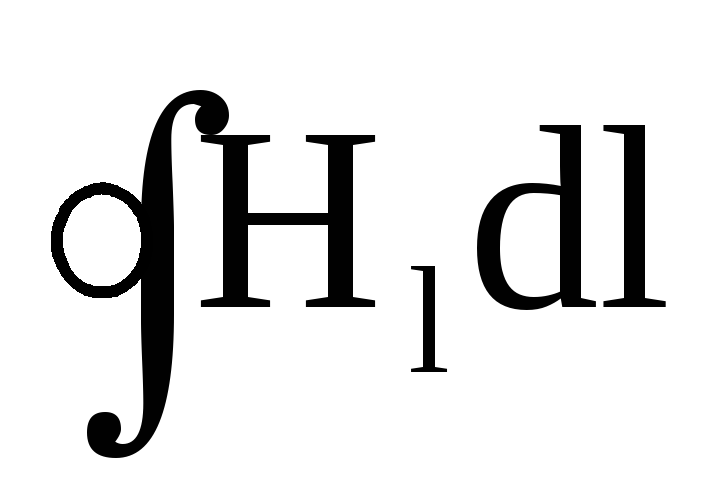
Рассмотрим
случай, когда контур лежит в плоскости
перпендикулярной к току. Пусть ток
перпендикулярен к плоскости чертежа и
направлен за чертеж. Линии напряженности
представляют собой окружности, а вектор 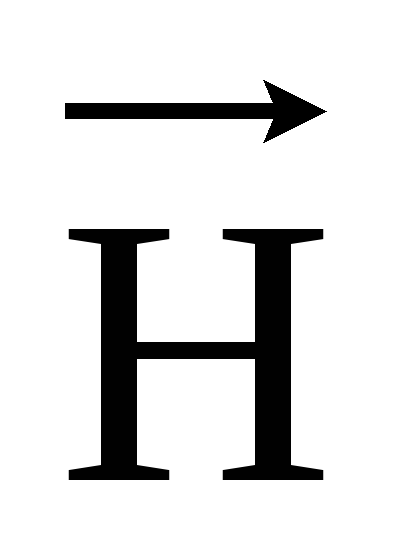 направлен по касательной к окружности.
направлен по касательной к окружности.
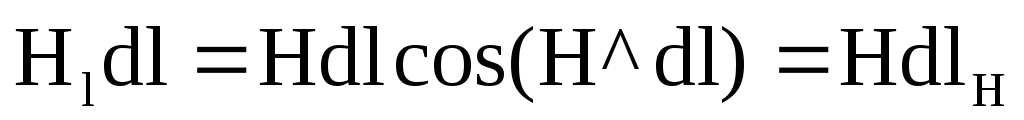
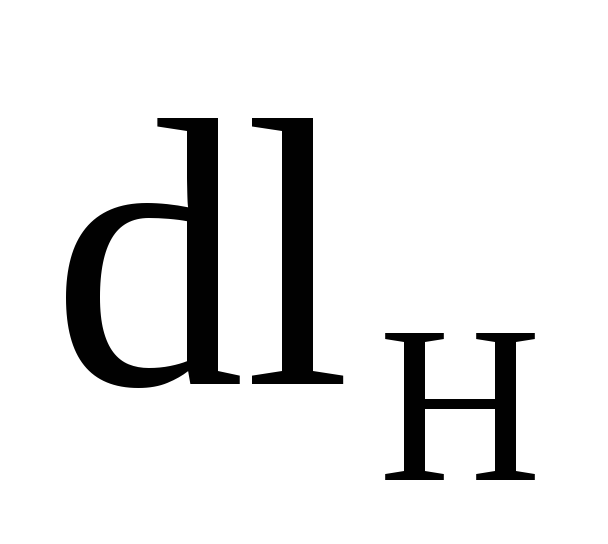 -проекция
вектора
-проекция
вектора 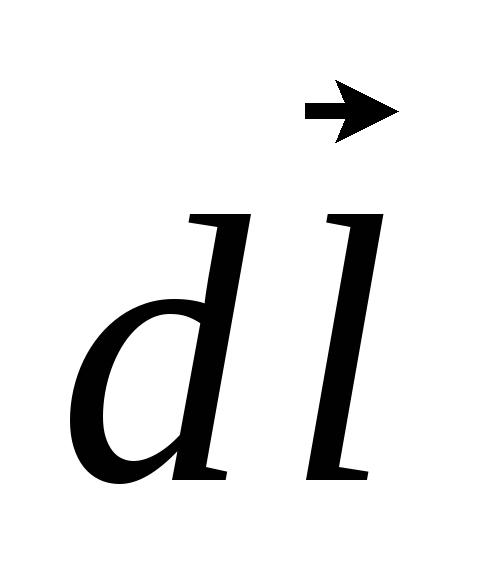 на направление
на направление  .
.
Но 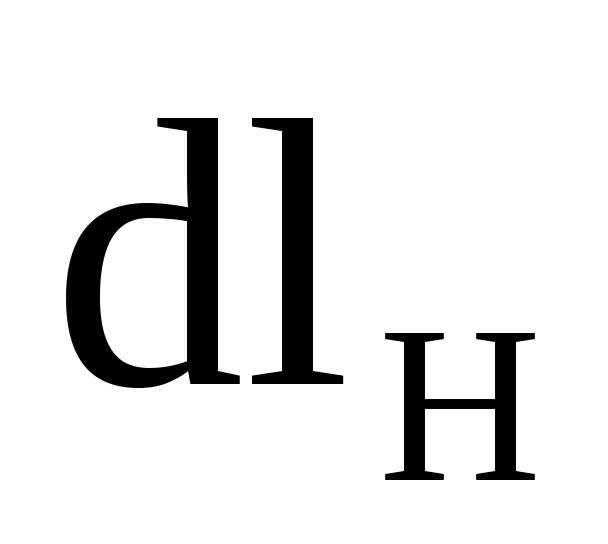 можно представить в виде:
можно представить в виде:
 =
= 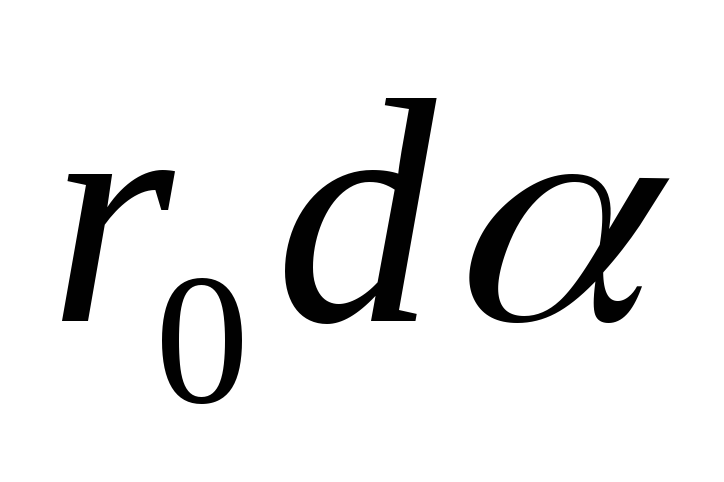 ,
где
,
где 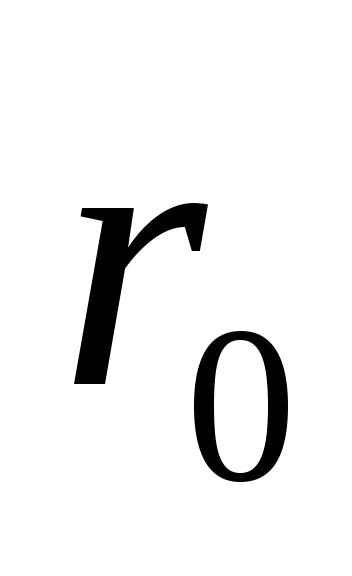 -расстояние
от прямого тока до
-расстояние
от прямого тока до  ,
,  —
угол, под которым виден элемент
—
угол, под которым виден элемент 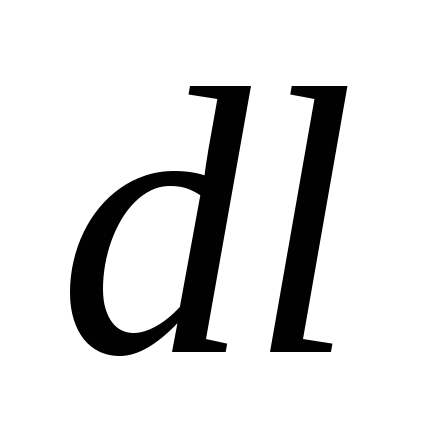 контура
L
из центра
окружности.
контура
L
из центра
окружности.
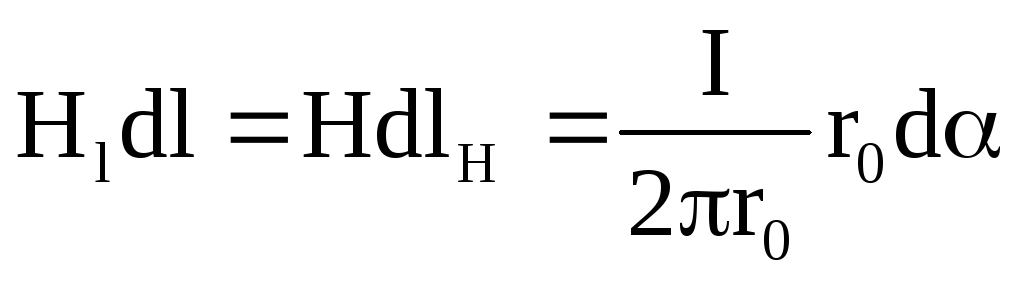
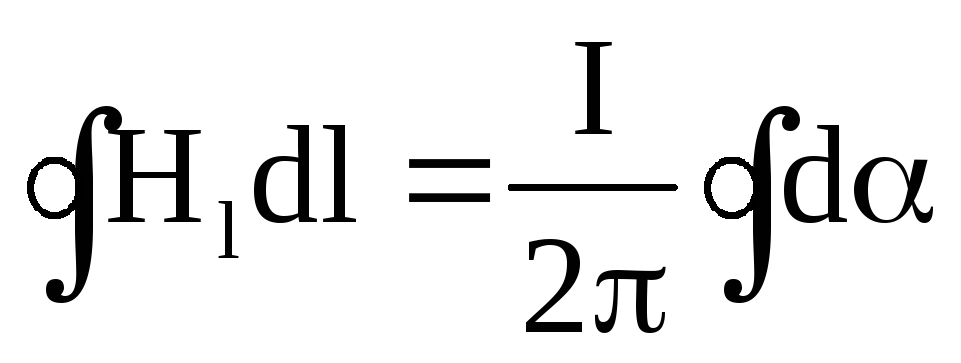
Интегрируя
вдоль всего замкнутого контура
L и учитывая,
что при этом угол  изменяется от нуля до
изменяется от нуля до  ,
получим:
,
получим:
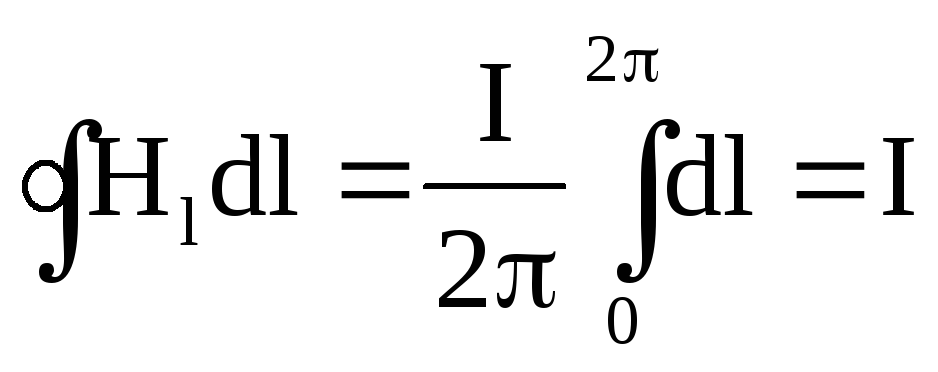
Таким
образом,
циркуляция вектора  магнитного поля прямолинейного бесконечно
длинного проводника с током
магнитного поля прямолинейного бесконечно
длинного проводника с током 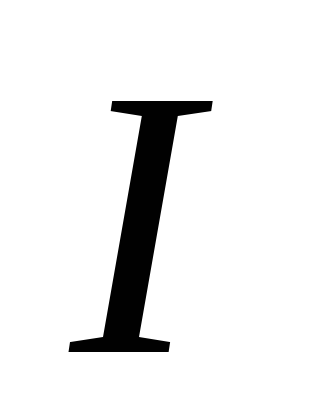 вдоль замкнутого контура, охватывающего
проводник численно равна
вдоль замкнутого контура, охватывающего
проводник численно равна 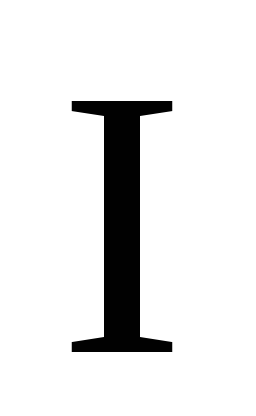 .
.
Если контур не охватывает проводник с током, то:
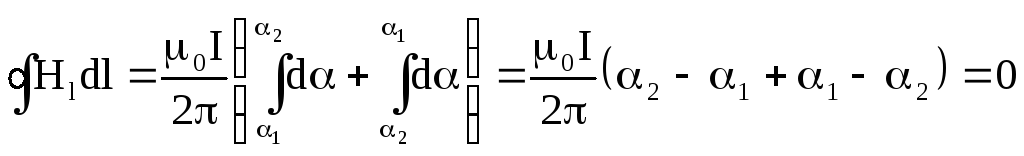

Таким
образом,
если контур тока не охватывает, циркуляция
вектора  равна нулю.
равна нулю.
Мы
рассмотрели циркуляцию вектора  для случая прямого тока. Но можно доказать
что для проводников любой формы и
размеров циркуляция вектора индукции
магнитного поля вдоль любого замкнутого
контура равна силе тока в проводнике,
охватываемом этим контуром.
для случая прямого тока. Но можно доказать
что для проводников любой формы и
размеров циркуляция вектора индукции
магнитного поля вдоль любого замкнутого
контура равна силе тока в проводнике,
охватываемом этим контуром.
Если
контур охватывает несколько токов,
циркуляция  равна их алгебраической сумме.
равна их алгебраической сумме.
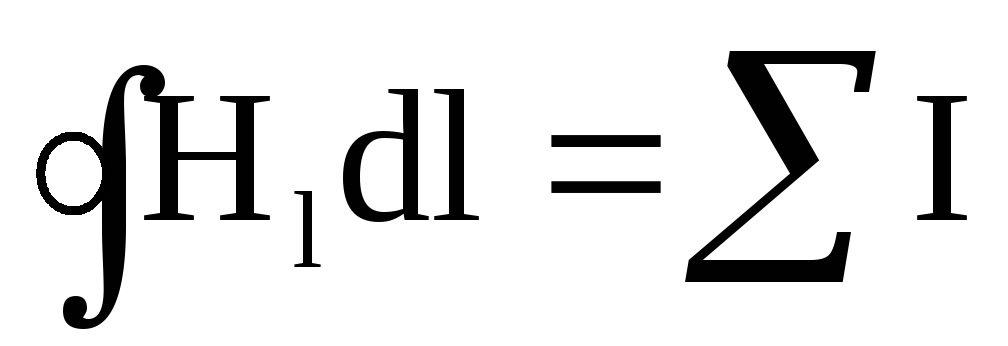 (*)
(*)
Вычисляя сумму токов, положительным нужно считать такой ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления будет отрицательным.
В электротехнике уравнение (*) называется законом полного тока для токов проводимости.
Из
сопоставления выражений для циркуляции
вектора Е электростатического поля и
вектора  магнитного поля следует, что между этими
полями имеется принципиальное различие.
Циркуляция вектора Е равна нулю и
электростатическое поле является
потенциальным. Циркуляция вектора
магнитного поля следует, что между этими
полями имеется принципиальное различие.
Циркуляция вектора Е равна нулю и
электростатическое поле является
потенциальным. Циркуляция вектора  отлична от нуля, если контур по которому
берется циркуляция, охватывает ток.
Поля, обладающие таким свойством,
называют вихревыми (соленоидальными).
Магнитному полю нельзя приписать
потенциал, который был бы связан с
отлична от нуля, если контур по которому
берется циркуляция, охватывает ток.
Поля, обладающие таким свойством,
называют вихревыми (соленоидальными).
Магнитному полю нельзя приписать
потенциал, который был бы связан с  так
же как
так
же как  с Е (Е=-grad
с Е (Е=-grad ).Кроме
того линии напряженности электростатического
поля начинаются и заканчиваются на
зарядах. Линии магнитной индукции всегда
замкнуты, что указывает на отсутствие
в природе магнитных зарядов.
).Кроме
того линии напряженности электростатического
поля начинаются и заканчиваются на
зарядах. Линии магнитной индукции всегда
замкнуты, что указывает на отсутствие
в природе магнитных зарядов.
Закон полного тока имеет для расчета магнитных полей постоянного электрического поля такое же важное значение, как и теорема Гаусса для расчета электростатических полей. В качестве примера рассмотрим применение закона полного тока к расчету магнитного поля соленоида.
Билет №6.
3.На длинный соленоид, имеющий диаметр сечения d=5 см и содержащий n=20 витков на 1 см длины, плотно надет круговой виток из медного провода сечением S=1,0 мм2. Найти ток в витке, если ток в обмотке соленоида увеличивают с постоянной скоростью I = 100 А/С. Магнитным полем индукционного тока пренебречь. Удельное сопротивление меди ρ =16 нОм · м.

4.В модели атома водорода Бора электрон вращается вокруг ядра (протона) по круговой орбите радиусом r. Определите r, зная, что энергия ионизации (т.е. энергия, необходимая для отрыва электрона) по результатам измерения равна Eион=-13,6 эВ.

Билет №7.
3.На дифракционную решетку с периодом 2 мкм падает нормально свет, пропущенный сквозь светофильтр. Фильтр пропускает волны длиной от 500 до 600 нм. Будут ли спектры различных порядков накладываться друг на друга?
Запишем
условие наложения двух соседних спектров kи (k+1) порядков для данных длин
волн λ2и λ1. Они должны быть
видны под одним углом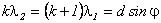 .
Отсюда
.
Отсюда
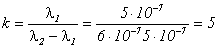 .
.
Спектры данных линий могут перекрываться, начиная с k= 6. Определим максимальный порядокkmax, который дает данная решетка:
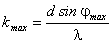 .
.
Для длины волны λ1
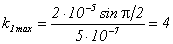 .
.
Для длины волны λ2
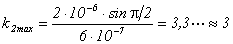 ,
(так как k целое число).
,
(так как k целое число).
Следовательно, спектры длин волн λ1и λ2в данной решетке не перекрываются.
4.Провод с сопротивлением R=1,00 Ом растянули по длине втрое. Чему теперь равно его сопротивление?
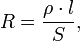
3 l1=l2
R2=3 Ом
Билет №8.
3.Какова линейная дисперсия дифракционной решетки для длины волны 0,589 мкм в спектре 2-го порядка, если постоянная решетки 4 мкм, а фокусное расстояние проецирующей линзы 50 см.
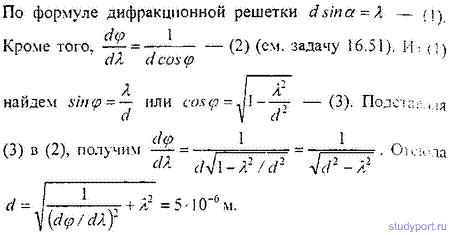
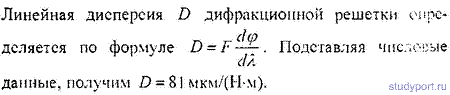
4. На тонкой нити длиной l =8см равномерно распределен заряд Q1=350мкКл действующий силой F=120 мкН на точечный заряд Q2 находящийся на продолжении той же нити на расстоянии r=6см от ее середины. Определить значение точечного заряда Q2, если вся система находится в воздухе.

Билет №9.
3. Расстояние между вторым и четвертым светлыми кольцами Ньютона в отраженном свете равно ∆r=0,9 мм. Определите радиус девятого темного кольца.

4. Определить потенциал электрического поля в центре кольца с внутренним радиусом R1=20,9 см и внешним радиусом R2=40см, если на нем равномерно распределен заряд Q=0,6 мкКл.
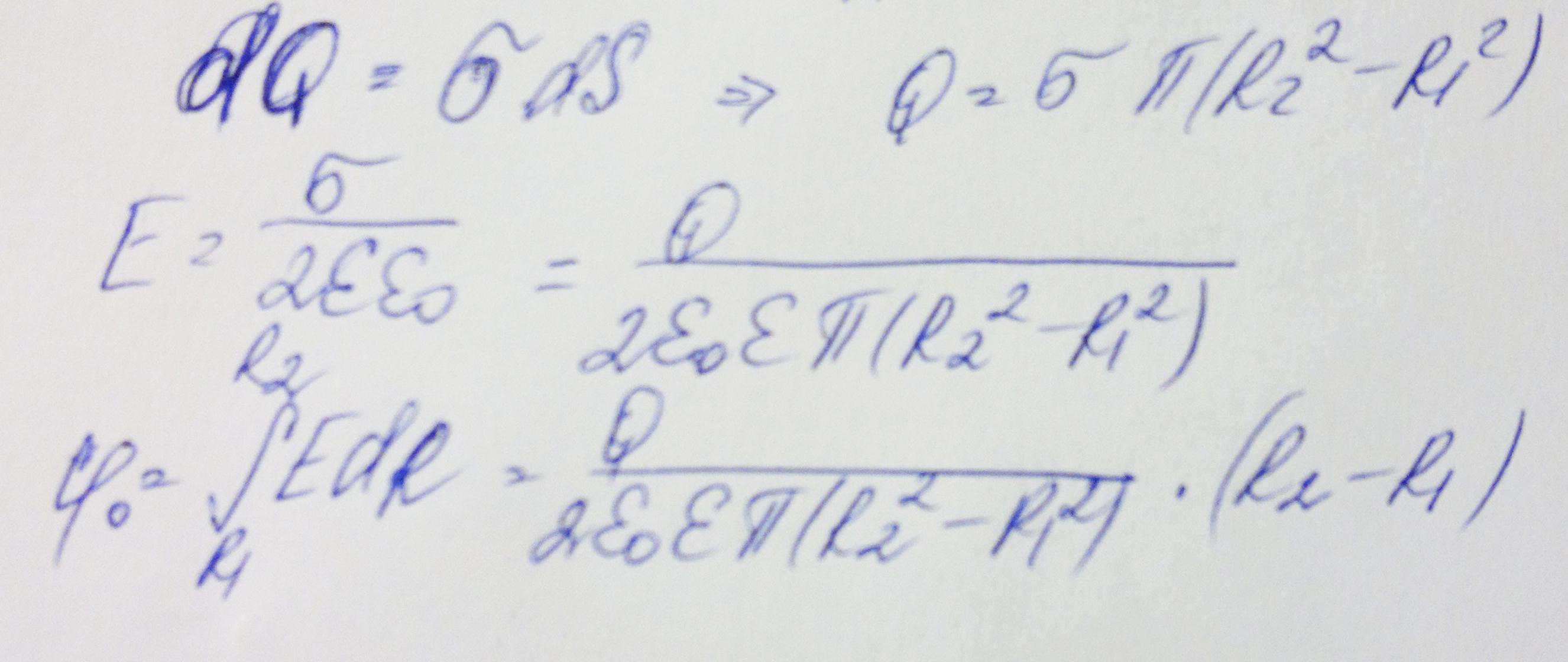
Билет №10.
3.Магнитный поток через неподвижный контур с сопротивлением R изменяется в течение времени τ по закону Ф=αt(t-τ), где α — известная постоянная. Найти количество теплоты, выделившееся в контуре за это время. Магнитным полем индукционного тока пренебречь.

4.Бесконечная плоскость заряжена отрицательно с поверхностной плотностью σ=35,4нКл/м2. По направлению силовой линии поля, созданного плоскостью, летит электрон. Определить минимальное расстояние lmin на которое может подойти к плоскости электрон, если на расстоянии l0=5см он имел кинетическую энергию Т=80 эВ.

Билет №11.
3. Провод, имеющий форму параболы y=кх2, находится в однородном магнитном поле В, перпендикулярном плоскости Оху. Из вершины параболы перемещают поступательно и без начальной скорости проводящую перемычку (параллельную оси (Ох) с постоянным ускорением а. Найти ЭДС индукции в образовавшемся контуре, как функцию у.
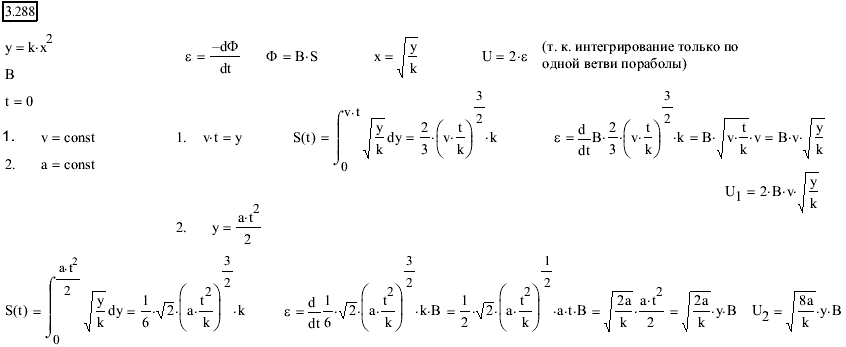

4. Определить заряд Q прошедший по проводу с сопротивлением R=3 Ом при равномерном нарастании напряжения на концах провода от U0=2B до U=4B в течение t=20 с.



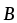 с напряженностью
с напряженностью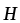 магнитного
поля.
магнитного
поля.