Емкостное сопротивление конденсатора в цепи переменного тока
Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.
Элементы, обладающие реактивным сопротивлением, называют реактивными.
Реактивное сопротивление катушки индуктивности.
При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .
Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:
Реактивное сопротивлениие индуктивностей называют индуктивным.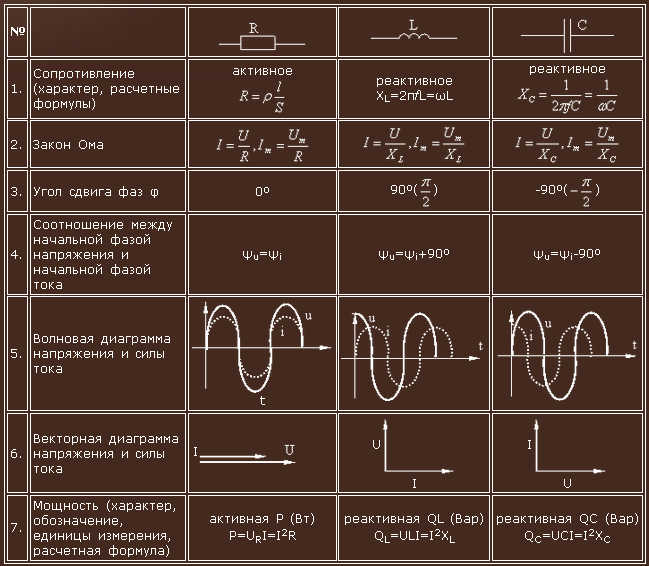
Реактивное сопротивление конденсатора.
Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.
В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = U ampsin(ωt) запишем выражение мгновенного значения тока следующим образом:
Отсюда выразим соотношение среднеквадратичных значений .
Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:
Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.
Онлайн-калькулятор расчёта реактивного сопротивления
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчитать ёмкость или индуктивность для реактивного сопротивления:
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!
Электросопротивление — это параметр в электротехнике, характеризующий возможность вещества препятствовать прохождению электричества. В зависимости от качеств материала, электросопротивляемость может уменьшаться до крайне маленьких величин (микромилиОмы — у проводников, металлов) или повышаться до огромных значений (ГигаОмы — изоляторов, диэлектриков). Величина противоположная сопротивлению — проводимость.
Что такое
Цепь, по которой протекает непостоянный ток, обладает полным сопротивлением. Вычисляется оно по сумме активного и реактивного сопротивлений, возведенных в квадрат.
Графическое изображение этой формулы представляет собой треугольник. Его катеты представлены активным и реактивным сопротивлениями, а гипотенуза полным электросопротивлением.
Емкостное электросопротивление (Xc) является одним из видов реактивного сопротивления. Этот показатель характеризует противодействие электроемкости в цепи электротоку с переменными параметрами. Преобразование электроэнергии в тепловую в момент протекания электричества сквозь емкость не возникает (свойство реактивного сопротивления). Вместо этого осуществляется передача энергии электрического тока электрическому полю и обратно. Потерь энергии при таком обмене не происходит.
Этот показатель характеризует противодействие электроемкости в цепи электротоку с переменными параметрами. Преобразование электроэнергии в тепловую в момент протекания электричества сквозь емкость не возникает (свойство реактивного сопротивления). Вместо этого осуществляется передача энергии электрического тока электрическому полю и обратно. Потерь энергии при таком обмене не происходит.
Емкостное сопротивление конденсатора можно сравнить с кастрюлей, наполняемой жидкостью, при полном заполнении ее объема она переворачивается, выливая содержимое, а затем наполняется заново. После достижения максимального заряда конденсатора происходит разрядка, затем он заряжается вновь.
Дополнительная информация: Конденсатор цепи способен накопить лишь ограниченную величину заряда до перемены полярности напряжения. По данной причине непостоянный ток не падает до нуля, важное отличие от постоянного электричества. Низкие значения частоты тока соответствуют низким показателям заряда, накопленного конденсатором, низким значениям противодействия электричеству, что придает реактивные свойства.
По сути, Xc — это противостояние электродвижущей силы конденсатора, уровню его заряда.
От чего зависит сопротивление конденсаторов цепей переменного тока
Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.
Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.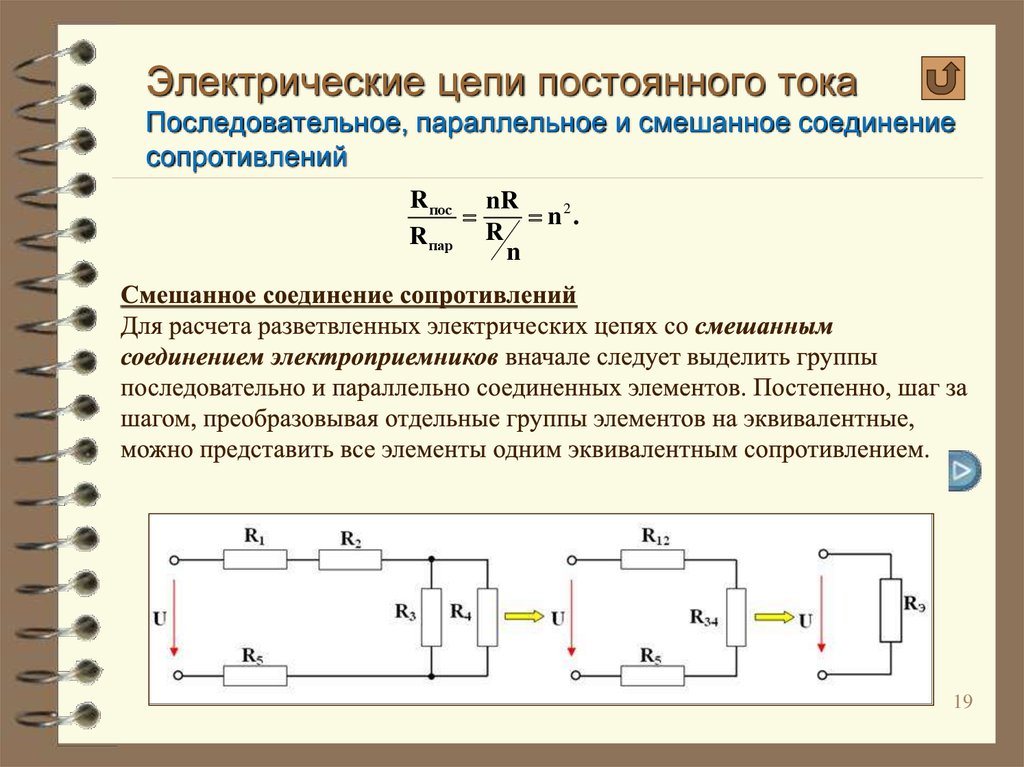
При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.
Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.
При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.
Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку. Его электросопротивляемость является безваттной, реактивной.
Причины ёмкостного сопротивления
Причиной возникновения сопротивления емкостного считается уровень напряжения, возникающий на конденсаторе в процессе его заряда. Вектор его действия встречен вектору напряжения источника электричества, потому создает помеху воспроизведению электротока этим источником.
Как рассчитать Xc
Сила тока цепи с постоянными показателями напряжения в момент работы электроконденсатора равно 0. Ее значения в цепи с переменным напряжением после подключения конденсатора I ? 0. В итоге, цепочке с непостоянным напряжением конденсатор придает Xc меньшее, чем цепочке с неизменным показателем напряжения.
В итоге, цепочке с непостоянным напряжением конденсатор придает Xc меньшее, чем цепочке с неизменным показателем напряжения.
Получается, что изменения напряжения отличаются по фазе от изменений тока на π/2.
По закону, сформулированному Омом, показатели силы электротока находятся в прямой пропорциональной зависимости от величины напряжения цепи. Формула вычисления наибольших величин напряженности и силы тока:
f — показатель частоты непостоянного тока, измеряется в герцах;
ω — показатель угловой частоты тока;
С — размер конденсатора в фарадах.
Важно! Xc не выступает параметром проводника, оно находится в зависимости от такой характеристики электроцепи, как частота электротока.
Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается).
Представим, к цепи подключен конденсатор, емкостью 1 мкФ. Необходимо вычислить, уровень емкостного сопротивления при величине частоты 50 Гц и как изменится емкостное сопротивление цепи переменного тока при частоте 1 кГц.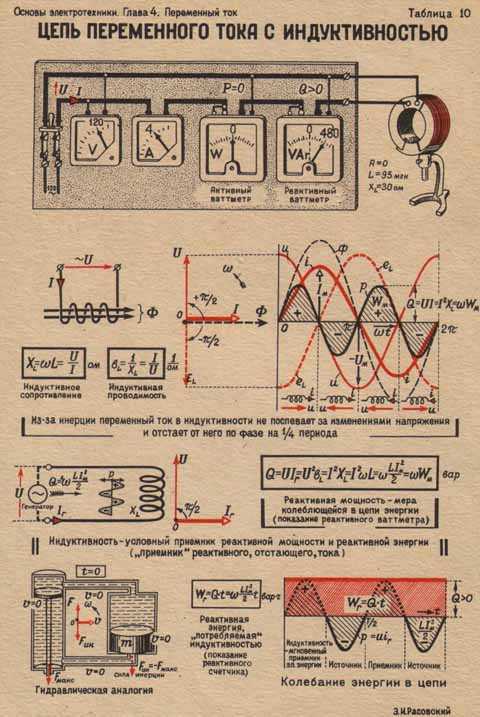 Амплитуда напряжения, подведенного к конденсатору, составляет 50 В.
Амплитуда напряжения, подведенного к конденсатору, составляет 50 В.
После введения данных в формулу, определяющую Xc, и получаются значения:
Емкостное сопротивление приравнивается к соотношению отклонений колебаний напряжения зажимов электрической цепочки с емкостными параметрами (с небольшими индуктивным и активным сопротивлениями) к колебаниям электротока цепочки. Она равнозначна электроконденсатору.
В чем измеряется емкостное электросопротивление
R представлено отношением напряжения к силе тока замкнутой электрической цепи, по закону Ома. Единицы измерения — Ом. Xc, как его разновидность, тоже измеряется в Омах.
Конденсаторы применяются при изготовлении фильтров. При параллельном присоединении к цепи, он способен задерживать высокие частоты, при последовательном удаляет низкие. Также они используются с целью отсечения переменной части от постоянной. Он незаменим в радиотехнике, при производстве датчиков приближения, для контроля процессов производства. Технологии, обладающие выше описанными свойствами, используются во всех областях промышленности.
Технологии, обладающие выше описанными свойствами, используются во всех областях промышленности.
Мы знаем, что конденсатор не пропускает через себя постоянного тока. Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может.
Совершенно иначе ведет себя конденсатор в цепи переменного тока (Рис 1,а).
Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила.
В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i, сила которого будет наибольшей вначале, когда конденсатор не заряжен. По мере приближения заряда к концу сила зарядного тока будет уменьшаться. Заряд конденсатора заканчивается и зарядный ток прекращается в тот момент, когда переменная ЭДС пе-рестает нарастать, достигнув своего амплитудного значения. Этот момент соответствует концу первой четверти периода.
Этот момент соответствует концу первой четверти периода.
После этого переменная ЭДС начинает убывать, одновременно с чем конденсатор начинает разряжаться. Следовательно, в течение второй четверти периода по цепи будет протекать разрядный ток. Так как убывание ЭДС происходит вначале медленно, а затем все быстрее и быстрее, то и сила разрядного тока, имея в начале второй четверти периода небольшую величину, будет постепенно возрастать.
Итак, к концу второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет наибольшего, амплитудного, значения.
С началом третьей четверти периода ЭДС, переменив свое направление, начнет опять возрастать, а конденсатор — снова заряжаться. Заряд конденсатора будет происходить теперь в обратном направлении, соответственно изменившемуся направлению ЭДС. Поэтому направление зарядного тока в течение третьей четверти периода будет совпадать с направлением разрядного тока во второй четверти, т. е. при переходе от второй четверти периода к третьей ток в цепи не изменит своего направления.
Вначале, пока конденсатор не заряжен, сила зарядного тока имеет наибольшее значение. По мере увеличения заряда конденсатора сила зарядного тока будет убывать. Заряд конденсатора закончится и зарядный ток прекратится в конце третьей четверти периода, когда ЭДС достигнет своего амплитудного значения и нарастание ее прекратится.
Итак, к концу третьей четверти периода конденсатор окажется опять заряженным, но уже в обратном направлении, т. е. на той пластине, где был прежде плюс, будет минус, а где был минус, будет плюс. При этом ЭДС достигнет амплитудного значения (противоположного направления), а ток в цепи будет равен нулю.
В течение последней четверти периода ЭДС начинает опять убывать, а конденсатор разряжаться; при этом в цепи появляется постепенно увеличивающийся разрядный ток. Направление этого тока совпадает с направлением тока в первой четверти периода и противоположно направлению тока во второй и третьей четвертях.
Из всего изложенного выше следует, что по цепи с конденсатором проходит переменный ток и что сила этого тока зависит от величины емкости конденсатора и от частоты тока. Кроме того, из рис. 1,а, который мы построили на основании наших рассуждений, видно, что в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°.
Кроме того, из рис. 1,а, который мы построили на основании наших рассуждений, видно, что в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°.
Отметим, что в цепи с индуктивностью ток отставал от напряжения, а в цепи с емкостью ток опережает напряжение. И в том и в другом случае между фазами тока и напряжения имеется сдвиг, но знаки этих сдвигов противоположны
Емкостное сопротивление конденсатора
Мы уже заметили, что ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС
Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.
Рисунок 2. Зависимость емкостного сопротивления конденсатра от частоты.
Для постоянного тока, т. е. когда частота его равна нулю, сопротивление емкости бесконечно велико; поэтому постоянный ток по цепи с емкостью проходить не может.
Величина емкостного сопротивления определяется по следующей формуле:
где Хс — емкостное сопротивление конденсатора в ом;
f—частота переменного тока в гц;
ω — угловая частота переменного тока;
С — емкость конденсатора в ф.
При включении конденсатора в цепь переменного тока, в последнем, как и в индуктивности, не затрачивается мощность, так как фазы тока и напряжения сдвинуты друг относительно друга на 90°. Энергия в течение одной четверти периода— при заряде конденсатора — запасается в электрическом поле конденсатора, а в течение другой четверти периода — при разряде конденсатора — отдается обратно в цепь. Поэтому емкостное сопротивление, как и индуктивное, является реактивным или безваттным.
Нужно, однако, отметить, что практически в каждом конденсаторе при прохождении через него переменного тока затрачивается большая или меньшая активная мощность, обусловленная происходящими изменениями состояния диэлектрика конденсатора. Кроме того, абсолютно совершенной изоляции между пластинами конденсатора никогда не бывает; утечка в изоляции между пластинами приводит к тому, что параллельно конденсатору как бы оказывается включенным некоторое активное сопротивление, по которому течет ток и в котором, следовательно, затрачивается некоторая мощность. И в первом и во втором случае мощность затрачивается совершенно бесполезно на нагревание диэлектрика, поэтому се называют мощностью потерь.
Потери, обусловленные изменениями состояния диэлектрика, называются диэлектрическими, а потери, обусловленные несовершенством изоляции между пластинами, — потерями утечки.
Ранее мы сравнивали электрическую емкость с вместимостью герметически (наглухо) закрытого сосуда или с площадью дна открытого сосуда, имеющего вертикальные стенки.
Конденсатор в цепи переменного тока целесообразно сравнивать с гиб-костью пружины. При этом во избежание возможных недоразумений условимся под гибкостью понимать не упругость («твердость») пружины, а величину, ей обратную, т. е. «мягкость» или «податливость» пружины.
Представим себе, что мы периодически сжимаем и растягиваем спиральную пружину, прикрепленную одним концом наглухо к стене. Время, в течение которого мы будем производить полный цикл сжатия и растяжения пружины, будет соответствовать периоду переменного тока.
Таким образом, мы в течение первой четверти периода будем сжимать пружину, в течение второй четверти периода отпускать ее, в течение третьей четверти периода растягивать и в течение четвертой четверти снова отпускать.
Кроме того, условимся, что наши усилия в течение периода будут неравномерными, а именно: они будут нарастать от нуля до максимума в течение первой и третьей четвертей периода и уменьшаться от максимума до нуля в течение второй и четвертой четвертей.
Сжимая и растягивая пружину таким образом, мы заметим, что в начале первой четверти периода незакрепленный конец пружины будет двигаться довольно быстро при сравнительно малых усилиях с нашей стороны.
В конце первой четверти периода (когда пружина сожмется), наоборот, несмотря на возросшие усилия, незакрепленный конец пружины будет двигаться очень медленно.
В продолжение второй четверти периода, когда мы будем постепенно ослаблять давление на пружину, ее незакрепленный конец будет двигаться по направлению от стены к нам, хотя наши задерживающие усилия направлены по направлению к стене. При этом наши усилия в начале второй четверти периода будут наибольшими, а скорость движения незакрепленного конца пружины наименьшей. В конце же второй четверти периода, когда наши усилия будут наименьшими, скорость движения пружины будет наибольшей и т. д.
Продолжив аналогичные рассуждения для второй половины периода (для третьей и четвертой четвертей) и построив графики (рис. 1,б) изменения наших усилий и скорости движения незакрепленного конца пружины, мы убедимся, что эти графики в точности соответствуют графикам ЭДС и тока в емкостной цепи (рис 1,а), причем график усилий будет соответствовать графику ЭДС , а график скорости — графику силы тока.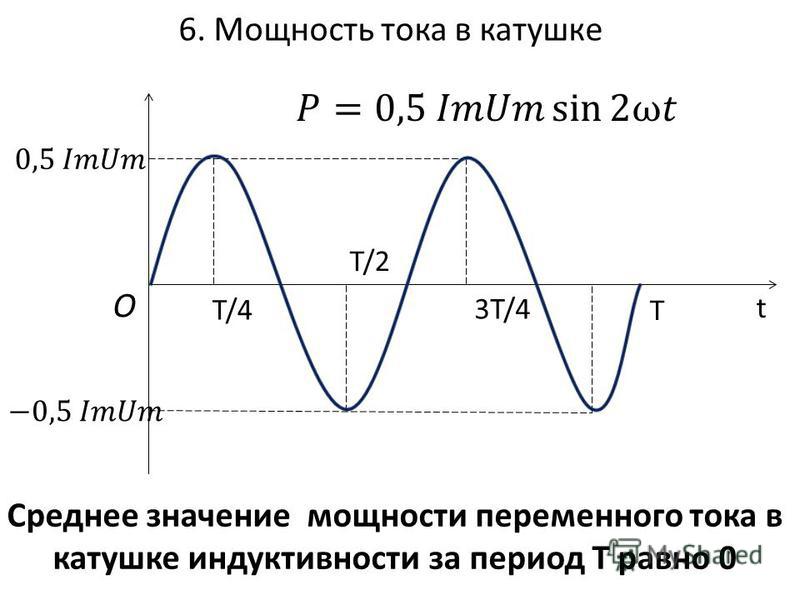
Рисунок 3. а) Процессы в цепи переменного тока с конденсатором и б) сравнение конденсатора с пружиной.
Нетрудно, заметить, что пружина, так же как и конденсатор, в течение одной четверти периода накапливает энергию, а в течение другой четверти периода отдает ее обратно.
Вполне очевидно также, что чем меньше гибкость пружины,- т е. чем она более упруга, тем большее противодействие она будет оказывать нашим усилиям. Точно так же и в электрической цепи: чем меньше емкость, тем больше будет сопротивление цепи при данной частоте.
И наконец, чем медленнее мы будем сжимать и растягивать пружину, тем меньше будет скорость движения ее незакрепленного конца. Аналогично этому, чем меньше частота, тем меньше сила тока при данной ЭДС.
При постоянном давлении пружина только сожмется и на этом прекратит свое движение, так же как при постоянной ЭДС конденсатор только зарядится и на этом прекратится дальнейшее движение электронов в цепи.
А теперь как ведет себя конденсатор в цепи переменного тока вы можете посмотреть в следующем видео:
youtube.com/embed/OwlapldZYYo»>ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Активное и реактивное сопротивление
Активное сопротивление
И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента – резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, “активный – это деятельный, энергичный, проявляющий инициативу”. Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.
То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.
Как смотреть силу тока в цепи через осциллограф
Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается.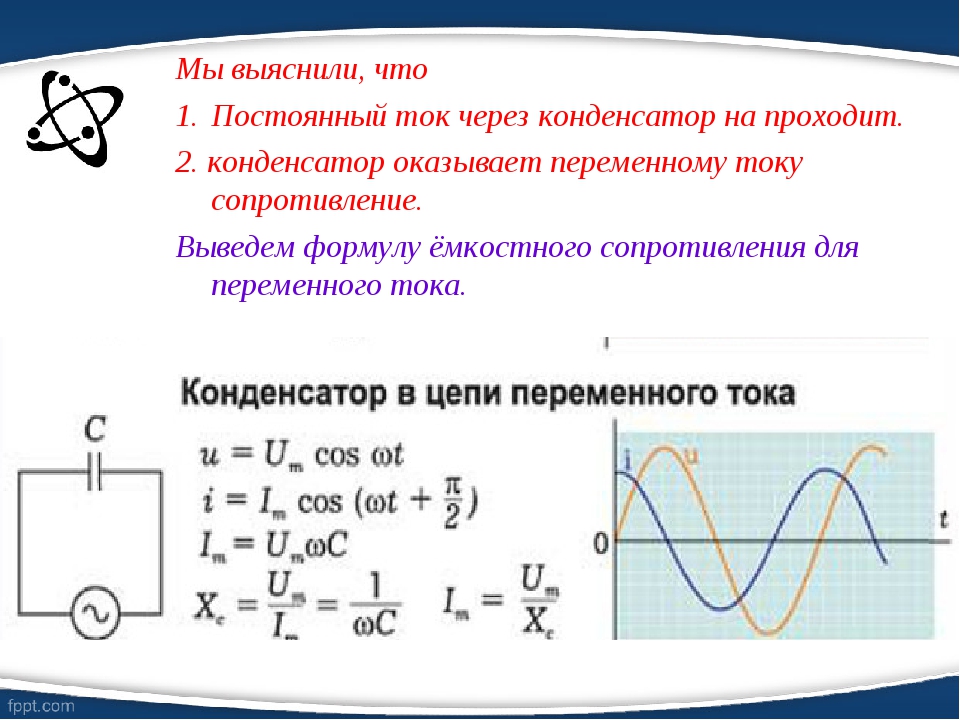 Итак, давайте рассмотрим самую простую схемку во всей электронике:
Итак, давайте рассмотрим самую простую схемку во всей электронике:
На схеме мы видим генератор частоты и резистор.
Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты
А также цифровой осциллограф:
С помощью него мы будем смотреть напряжение и силу тока .
Что?
Силу тока?
Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта.
Кто не помнит – напомню. Имеем обыкновенный резистор:
Что будет, если через него прогнать электрический ток?
На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах
И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока
Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока
Применение
Частотный разделитель ADSL — это фильтр нижних частот и три соединителя в корпусе
Конденсаторы часто используются в различных электрических и электронных устройствах и системах. Вероятно, вы не найдете ни одно электронное устройство, в котором не содержится хотя бы один конденсатор. Конденсаторы используются для хранения энергии, обеспечения импульсов энергии, для фильтрации питающего напряжения, для коррекции коэффициента мощности, для развязки по постоянному току, в электронных частотных фильтрах, для фильтрации шумов, для запуска электродвигателей, для хранения информации, для настройки колебательных контуров, в различных датчиках, в емкостных экранах мобильных телефонов… Этот список можно продолжать до бесконечности.
Резистивно-емкостные (RC) цепи обычно используются в качестве простых фильтров нижних и верхних частот, а также простейших интегрирующих и дифференцирующих цепей.
Осциллограмма силы тока на активном сопротивлении
В данном опыте нам не обязательно знать номинал силы тока в цепи. Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?
Поэтому, наша схема примет вот такой вид:
В этом случае шунтом будет являться резистор сопротивлением в 0,5 Ом. Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.
Осталось снять напряжение с генератора, а также со шунта с помощью осциллографа. Если вы не забыли, со шунта мы снимаем осциллограмму силы тока в цепи. Красная осциллограмма – это напряжение с генератора Uген , а желтая осциллограмма – это напряжение с шунта Uш , в нашем случае – сила тока. Смотрим, что у нас получилось:
Частота 28 Герц:
Частота 285 Герц:
Частота 30 Килогерц:
Как вы видите, с ростом частоты сила тока у нас осталась такой же.
Давайте побалуемся формой сигнала:
Как мы видим, сила тока полностью повторяет форму сигнала напряжения.
Итак, какие можно сделать выводы?
1) Сила тока через активное (омическое) сопротивление имеет такую же форму, как и форма напряжения.
2) Сила тока и напряжение на активном сопротивлении совпадают по фазе, то есть куда напряжение, туда и ток. Они двигаются синфазно, то есть одновременно.
3) С ростом частоты ничего не меняется (если только на очень высоких частотах).
Срезы динамиков конденсатором
Вступление
Покупая динамики и подключая без процессора, либо не имея усилителя не спешите с выбором конденсатора.
Приведем пример:
Возьмем две 4 Ом пищалки и сделаем замер импеданса, скажем на частоте среза 5 кГц, то по факту может получиться что у одной пищалки на этой частоте импеданс 5 Ом а у другой 7 Ом. Согласно таблице ниже, пытаемся их порезать на 5 кГц конденсатором на 8 мкф. В итоге у нас первая порежется на 4 кГц, а вторая с этим же конденсатором порежется на 3 кГц. Итог первая просто будет валить ужасный звук, вторая начнет подгорать.
Итог первая просто будет валить ужасный звук, вторая начнет подгорать.
Таблица срезов динамиков
| Частота среза динамика | Фильтр ВЧ (HPF) | Примечание | |
| 4 Ом | 8 Ом | ||
| 50 Гц | 796.7 мкФ | 398.1 мкФ | — |
| 75 Гц | 530.8 мкФ | 265.4 мкФ | — |
| 100 Гц | 398.1 мкФ | 199 мкФ | — |
| 125 Гц | 318.5 мкФ | 159.2 мкФ | — |
| 150 Гц | 258.4 мкФ | 132.7 мкФ | Минимальное значение для СЧ-динамиков |
| 175 Гц | 227.5 мкФ | 113.7 мкФ | — |
| 200 Гц | 199 мкФ | 99.5 мкФ | — |
| 225 Гц | 176.9 мкФ | 88.5 мкФ | — |
| 250 Гц | 159.2 мкФ | 79.1 мкФ | Минимальное значение для СЧ-динамиков на неодиме |
| 275 Гц | 144.8 мкФ | 72. 4 мкФ 4 мкФ | — |
| 300 Гц | 132.7 мкФ | 66.3 мкФ | — |
| 400 Гц | 99.5 мкФ | 49.8 мкФ | — |
| 500 Гц | 79.6 мкФ | 39.8 мкФ | — |
| 600 Гц | 66.3 мкФ | 33.2 мкФ | — |
| 700 Гц | 56.9 мкФ | 28.4 мкФ | — |
| 900 Гц | 44.2 мкФ | 22.1 мкФ | — |
| 1000 Гц | 39.8 мкФ | 19.9 мкФ | — |
| 1100 Гц | 36.2 мкФ | 18.1 мкФ | — |
| 1200 Гц | 33.2 мкФ | 16.6 мкФ | — |
| 1300 Гц | 30.6 мкФ | 15.3 мкФ | — |
| 1400 Гц | 28.4 мкФ | 14.2 мкФ | — |
| 1500 Гц | 26.5 мкФ | 13.3 мкФ | — |
| 1600 Гц | 24.9 мкФ | 12.4 мкФ | — |
| 1700 Гц | 23.4 мкФ | 11.7 мкФ | — |
| 1800 Гц | 22.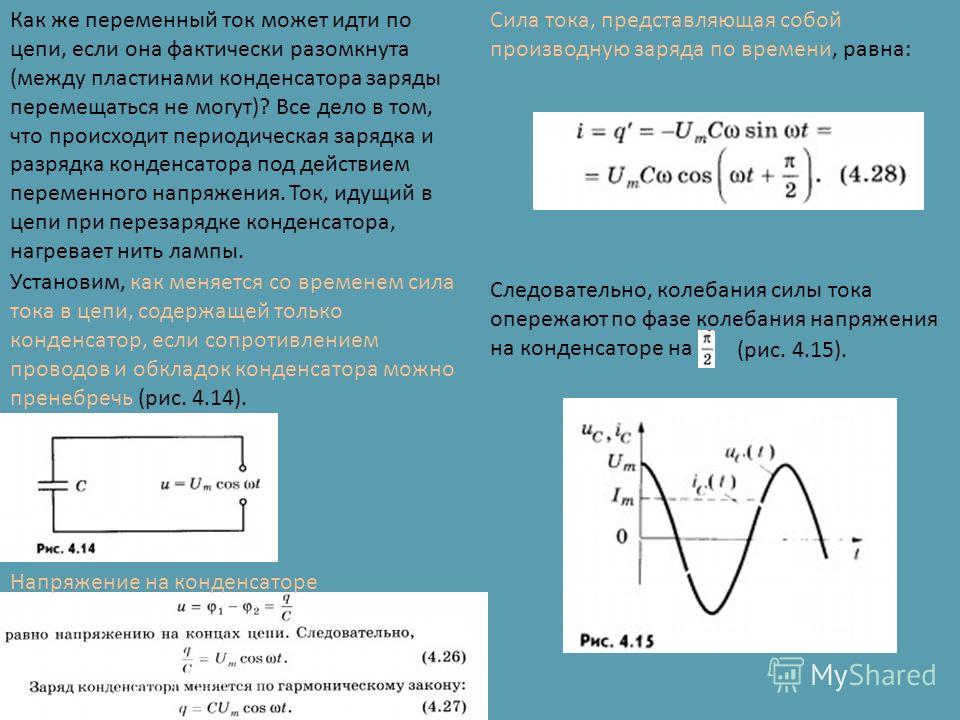 1 мкФ 1 мкФ | 11.1 мкФ | — |
| 1900 Гц | 21 мкФ | 10.5 мкФ | — |
| 2000 Гц | 19.9 мкФ | 9.9 мкФ | — |
| 3000 Гц | 13.3 мкФ | 6.6 мкФ | Минимальное значение для шелковых ВЧ-динамиков |
| 4000 Гц | 10 мкФ | 5 мкФ | — |
| 5000 Гц | 8 мкФ | 4 мкФ | — |
| 6000 Гц | 6.6 мкФ | 3.3 мкФ | Минимальное значение для громких рупорных ВЧ-динамиков |
| 7000 Гц | 5.7 мкФ | 2.8 мкФ | — |
| 8000 Гц | 5 мкФ | 2.5 мкФ | Минимальное значение для громких рупорных ВЧ-динамиков с учетом широкого диапазона СЧ-динамика |
| 9000 Гц | 4.4 мкФ | 2.2 мкФ | — |
| 10000 Гц | 4 мкФ | 2 мкФ | — |
Перед выбором рекомендуем померить мульти-метром импеданс динамиков. Номинал емкость конденсатора указана на его корпусе.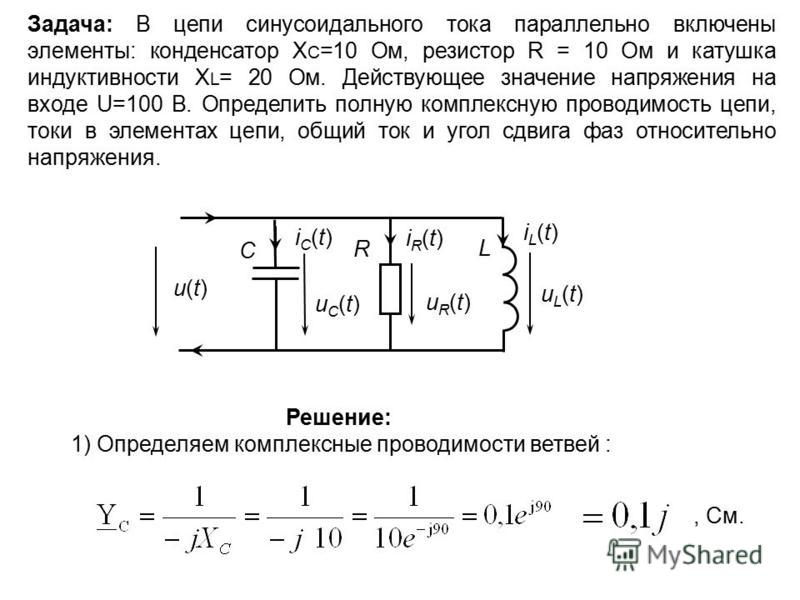 | |||
Заключение
Если делать все по таблицам и верить значениям, не пользуясь головой то получите плохой звук и много спаленных динамиков.
- Ставьте только неполярные конденсаторы.
- Не ставьте электролитические конденсаторы. В большинстве случаем они установлены на дешевых китайских динамиках.
- Купить разной емкости конденсаторы. Чем больше емкость, тем ниже он порежет вашу пищалку.
- Припаивайте конденсатор ближе к клемме. При этом абсолютно не важно на какой из клемм будет висеть конденсатор. Но если начали паять на плюсовую клемму то вешайте на плюсовые на всех остальных пищалках.
ВАЖНО!
Срез динамиков по рекомендации не дает точных значений.
Конденсатор в цепи переменного тока
Ну а теперь давайте вместо резистора поставим конденсатор.
Смотрим осциллограммы:
Как вы видите, конденсатор обладает сопротивлением, так как сила тока в цепи значительно уменьшилась. Но обратите внимание, что произошел сдвиг желтой осциллограммы, то бишь осциллограммы силы тока.
Вспоминаем алгебру старшие классы. Итак, полный период T – это 2П
Теперь давайте прикинем, какой сдвиг фаз у нас получился на графике:
Где-то примерно П/2 или 90 градусов.
Почему так произошло? Во всем виновато физическое свойство конденсатора. В самые первые доли секунд, конденсатор ведет себя как проводник с очень малым сопротивлением, поэтому сила тока в этот момент будет максимальна. В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока
Красная осциллограмма – это напряжение, которое мы подаем на конденсатор, а желтая – это сила тока в цепи конденсатора. По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.
К чему приведет дальнейшее увеличение частоты? Давайте посмотрим:
50 Герц.
100 Герц
200 Герц
Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.
Конвертер величин
Отметим, что величина импеданса идеального конденсатора равна его реактивному сопротивлению. Однако это не идентичные величины, так как между током и напряжением в емкостной цепи существует фазовый сдвиг. Для расчетов используются указанная ниже формула:
Однако это не идентичные величины, так как между током и напряжением в емкостной цепи существует фазовый сдвиг. Для расчетов используются указанная ниже формула:
Здесь
X
C — реактивное сопротивление конденсатора в омах (Ом) ,
Z
LC — импеданс конденсатора в омах (Ом),
ω = 2πf
— угловая частота в рад/с,
j
— мнимая единица.
f
— частота в герцах (Гц),
С
— емкость в фарадах (Ф), и
Для расчета выберите единицы измерения и введите емкость и частоту. Импеданс конденсатора будет показан в омах.
График зависимости реактивного сопротивления конденсатора
X
C и текущего через него тока
I
от частоты
f
для нескольких величин емкости показывает обратную пропорциональную зависимость от частоты реактивного сопротивления
Конденсатор представляет собой пассивный электрический элемент с двумя выводами, состоящий, в основном, из двух электрических проводников, часто в форме тонких металлических пластин, разделенных диэлектриком, например, пластмассовой пленкой, керамикой, бумагой или даже воздухом. Конденсаторы используются для хранения энергии в форме электрического заряда.
Конденсаторы используются для хранения энергии в форме электрического заряда.
Если незаряженный конденсатор подключить к источнику постоянного напряжения, он заряжается до приложенного напряжения и его зарядный ток экспоненциально уменьшается от максимального значения в начальной точке заряда до нуля. В то же время, напряжение на конденсаторе увеличивается до напряжения источника постоянного тока.
Таким образом, когда напряжение на конденсаторе становится максимальным, ток через него достигает минимума. Скорость изменения тока определяется постоянной времени цепи, в которую включен конденсатор. Полностью заряженный конденсатор блокирует ток и действует как временный накопитель энергии.
Идеальный конденсатор поддерживает полный заряд в течение неограниченно долгого времени даже в том случае, если отключить источник постоянного напряжения. Однако в реальной жизни конденсаторы, особенно электролитические, не могут хранить энергию постоянно, так как у них имеется относительно низкое сопротивление утечки и, следовательно, большой ток утечки.
Если к конденсатору приложить синусоидальное напряжение, он заряжается сначала в одном направлении, а затем в противоположном. Полярность его заряда изменяется со скоростью изменения переменного напряжения. Как уже упоминалось выше, когда напряжение достигает максимума, ток становится минимальным и когда напряжение достигает минимума, ток достигает максимума. Ток через конденсатор пропорционален скорости изменения напряжения
, причем ток максимален, когда напряжение изменяется быстрее всего, а это происходит, когда синусоида напряжения пересекает нулевую точку. На рисунке показан график напряжения на конденсаторе, заряда на нем и протекающего через него тока выглядит.
В чисто емкостной цепи величина тока зависит от скорости изменения напряжения. Ток заряжает конденсатор и когда ток медленно понижается до нуля, конденсатор полностью заряжен и напряжение на нем достигает максимума. V
C — напряжение,
Q
C — заряд,
I
C — ток,
φ
= –90° = –
π
/2 — фазовый сдвиг. 1 — конденсатор начинает заряжаться, ток достиг положительного максимума, скорость его изменения нулевая и напряжение на конденсаторе, а также его заряд — нулевые; 2 — конденсатор полностью заряжен, ток через него равен нулю, скорость его изменения в этот момент максимальна, а напряжение на конденсаторе и его заряд в этот момент максимальны и положительны; 3 — конденсатор заряжается в противоположном направлении, ток через него достиг отрицательного максимума, скорость его изменения нулевая, напряжение и заряд конденсатора также нулевые; 4 — конденсатор полностью заряжен, ток через него нулевой, скорость его изменения максимальна, а заряд и напряжение на конденсаторе достигли своих отрицательных максимумов
1 — конденсатор начинает заряжаться, ток достиг положительного максимума, скорость его изменения нулевая и напряжение на конденсаторе, а также его заряд — нулевые; 2 — конденсатор полностью заряжен, ток через него равен нулю, скорость его изменения в этот момент максимальна, а напряжение на конденсаторе и его заряд в этот момент максимальны и положительны; 3 — конденсатор заряжается в противоположном направлении, ток через него достиг отрицательного максимума, скорость его изменения нулевая, напряжение и заряд конденсатора также нулевые; 4 — конденсатор полностью заряжен, ток через него нулевой, скорость его изменения максимальна, а заряд и напряжение на конденсаторе достигли своих отрицательных максимумов
Как мы видим, напряжение на конденсаторе отстает от тока в нем по времени и фазе на 90°, так ток должен течь достаточно долго, чтобы на конденсаторе возник заряд и, соответственно, возросло напряжение. Можно также сказать, что ток опережает напряжение. Величина этого опережения зависит от соотношения величин реактивного сопротивления и активного сопротивления в цепи.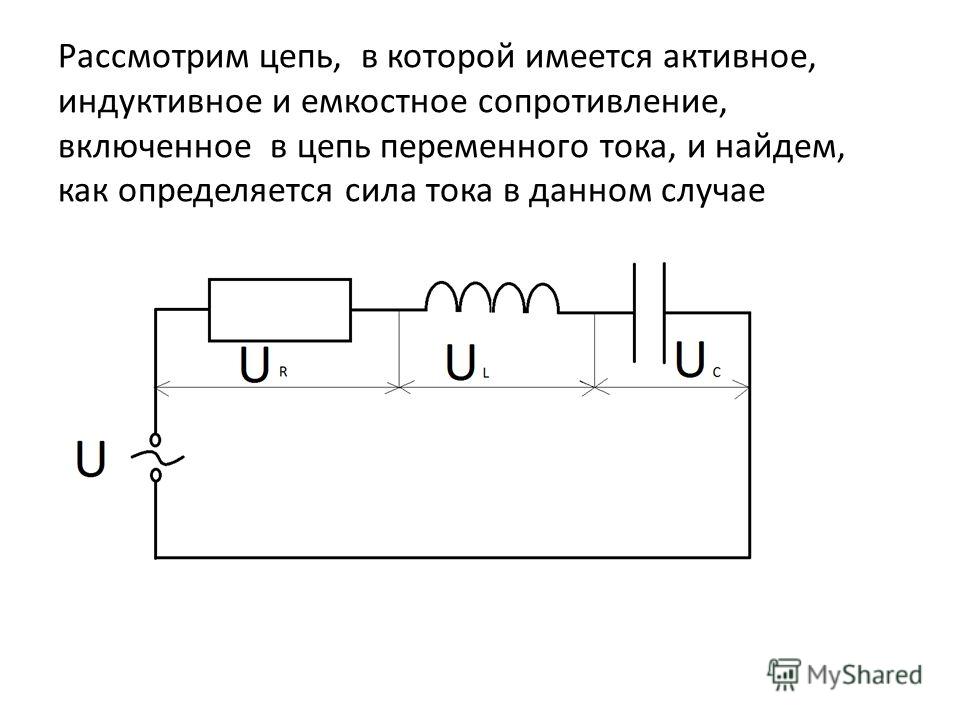 Если сопротивления в цепи нет, то отставание (опережение) будет на 90° (ток нулевой, когда напряжение максимально). Этот угол называется фазовым сдвигом.
Если сопротивления в цепи нет, то отставание (опережение) будет на 90° (ток нулевой, когда напряжение максимально). Этот угол называется фазовым сдвигом.
Аналогичное явление можно наблюдать и в природе. Сравните: Солнце светит сильнее всего в астрономический полдень (солнечный свет — напряжение), однако самая жаркая часть дня обычно бывает через несколько часов после полудня (температура — ток). Или другой пример. День зимнего солнцестояния в северном полушарии (самый короткий день) — в конце декабря, однако самые холодные месяцы еще впереди. В зависимости от того, где вы живете, это будет январь или февраль. Вспомните поговорку «Солнце — на лето, зима — на мороз». Это как раз о поведении емкости, только в природной аналогии. Такой сезонный «сдвиг фаз» или отставание вызван поглощением энергии Солнца огромными массами воды в океанах. Они отдадут эту запасенную энергию, но позже — точно так же, как это делают конденсаторы.
День зимнего солнцестояния
Рассчитанный этим калькулятором импеданс представляет собой меру сопротивления конденсатора пропускаемому через него сигналу на определенной частоте
.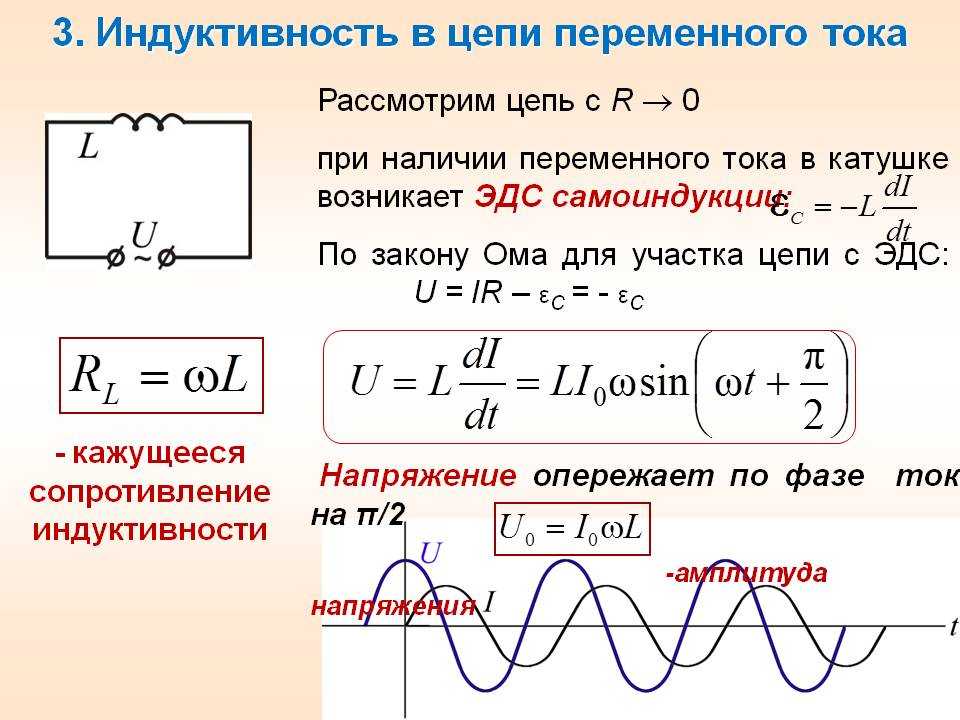 Емкостное реактивное сопротивление обратно пропорционально частоте приложенного переменного напряжения. Приведенные выше формула и график показывают, что реактивное сопротивление конденсатора
Емкостное реактивное сопротивление обратно пропорционально частоте приложенного переменного напряжения. Приведенные выше формула и график показывают, что реактивное сопротивление конденсатора
X
С мало при высоких частотах и велико при низких частотах (катушки индуктивности ведут себя с точностью до наоборот). При нулевой частоте (при постоянном напряжении) емкостное реактивное сопротивление становится бесконечно большим и прерывает протекающий ток. С другой стороны, при очень высоких частотах конденсатор проводит очень хорошо — отсюда правило, которое мы выучили в школе: конденсаторы не пропускают постоянный ток и пропускают переменный. Если частота очень высокая, конденсаторы пропускают сигнал очень хорошо.
Импеданс измеряется в омах, так же, как и сопротивление. Импеданс мешает прохождению электрического тока так же, как и сопротивление, и показывает как сильно конденсатор противодействует прохождению тока через него. Но тогда возникает вопрос: в чем же разница между импедансом и сопротивлением? А разница заключается в зависимости импеданса от частоты приложенного сигнала. Сопротивление от частоты не зависит, а импеданс конденсаторов от частоты зависит. С увеличением частоты импеданс конденсатора уменьшается и наоборот.
Сопротивление от частоты не зависит, а импеданс конденсаторов от частоты зависит. С увеличением частоты импеданс конденсатора уменьшается и наоборот.
Этот калькулятор предназначен для расчета импеданса идеальных конденсаторов. Реальные конденсаторы всегда имеют некоторую индуктивность и сопротивление. Для расчета импеданса реальных конденсаторов пользуйтесь калькулятором импеданса RLС-цепей.
Конденсаторы советского производства, выпущенные в конце 60-х гг. прошлого века
Автор статьи: Анатолий Золотков
Реактивное сопротивление конденсатора
Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть. Но называется оно не просто сопротивлением, а реактивным сопротивлением и вычисляется по формуле:
где
Хс – реактивное сопротивление конденсатора, Ом
П – постоянная и приблизительно равна 3,14
F – частота, Гц
С – емкость конденсатора, Фарад
Реактивное сопротивление катушки индуктивности
Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле
где
ХL – сопротивление катушки, Ом
П – постоянная и равна приблизительно 3,14
F – частота, Гц
L – индуктивность
Подробнее здесь: https://www. ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/
ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/
где
ХL – сопротивление катушки, Ом
П – постоянная и равна приблизительно 3,14
F – частота, Гц
L – индуктивность
Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/
где
ХL – сопротивление катушки, Ом
П – постоянная и равна приблизительно 3,14
F – частота, Гц
L – индуктивность
Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/
где
ХL – реактивное сопротивление катушки, Ом
П – постоянная и равна приблизительно 3,14
Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/
П – постоянная и приблизительно равна 3,14
F – частота, Гц
L – индуктивность, Генри
Преобразователь случайных чисел |
Калькулятор импеданса RC-цепи Этот калькулятор импеданса RC-цепи определяет импеданс и угол разности фаз последовательно соединенных конденсатора и резистора для заданной частоты синусоидальный. Пример: Рассчитайте импеданс конденсатора 500 мкФ и резистора 0,2 Ом на частоте 25 кГц. Вход Сопротивление, R мОм (мОм)Ом (Ом)килоом (кОм)мегом (МОм) Емкость, Кл фарад (Ф)микрофарад (мкФ, мкФ) (пФ) Частота, f герц (Гц) миллигерц (мГц) килогерц (кГц) мегагерц (МГц) гигагерц (ГГц) Доля Выход Угловая частота ω = рад/с Емкостное сопротивление X C = Ом Полное сопротивление RC |Z RC | = Ом Разность фаз φ = ° = рад Введите значения сопротивления, емкости и частоты, выберите единицы измерения и нажмите или коснитесь кнопки Рассчитать . Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы войти в Infinity значение, просто введите inf в поле ввода. Следующие формулы используются для расчета: , где Z RC — RC Circuet в OHM угловая частота в рад/с, f – частота в герцах (Гц), R – сопротивление в омах (Ом), C — емкость в фарадах (Ф), φ — разность фаз между полным напряжением V T и полным током I T в градусах (°) и радианах, а Дж — воображаемая единица. Для расчета введите емкость, сопротивление и частоту, выберите единицы измерения, и результат для импеданса RC будет показан в омах, а для разности фаз — в градусах. Реактивное сопротивление конденсатора также будет рассчитано. График зависимости сопротивления последовательной RC-цепи Z RC от частоты f для заданных емкости и сопротивления обратно пропорционален частоте Векторная диаграмма для последовательной RС-цепи показывает, что полная волна тока опережает полная волна напряжения. Упреждение меньше 90° и больше 0°. При 90° вместо резистора устанавливается перемычка (схема чисто емкостная), а при 0° вместо конденсатора устанавливается перемычка (схема чисто резистивная) Простая последовательная RC-цепь или резисторно-конденсаторная цепь состоит из резистора и конденсатора, соединенных последовательно и управляемых источником напряжения. Ток в конденсаторе и резисторе одинаков, потому что они соединены последовательно. Если вы посмотрите на уравнение для расчета импеданса (выше), вы заметите, что оно похоже на уравнение для расчета гипотенузы прямоугольного треугольника. Это связано с тем, что импеданс RC-цепи в графическом виде выглядит так, как на этом рисунке, где сопротивление R находится на горизонтальной оси, а реактивное сопротивление X C находится на вертикальной оси. Гипотенуза — это импеданс цепи, а фазовый угол — это угол между горизонтальной осью и вектором импеданса. Фазовый угол может составлять от 0° для чисто резистивной цепи до –90° для чисто емкостной цепи. Из треугольника реактивных сопротивлений или с помощью функции арктангенса (арктангенса) В последовательной RC-цепи с источником синусоидального напряжения волна тока опережает волну напряжения с запаздыванием менее 90° (нулевое сопротивление) и более 0° (нулевая емкость). В последовательной RC-цепи один и тот же ток I протекает через конденсатор и резистор. Напряжение конденсатора V C отстает от общего тока на 90°, а напряжение резистора совпадает по фазе с общим током. По закону напряжения Кирхгофа сумма падений напряжения должна равняться общему напряжению V T . Напряжения резистора и конденсатора V R и V C сдвинуты по фазе друг к другу на 90°, поэтому их необходимо суммировать как векторные величины и общее напряжение V T определяется как Обратите внимание, что общее напряжение всегда меньше суммы напряжений на резисторе и конденсаторе — точно так же, как в любом прямоугольном треугольнике, где длина гипотенузы меньше суммы из двух катетов треугольника. Режимы отказаЧто, если что-то пойдет не так в этой цепи? Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных режимах отказа:
Специальные модыClick или Click Or Acplosing Link. Различные режимы постоянного тока Короткое замыкание Обрыв цепи Чисто емкостная цепь Примечания
Эта статья написана Анатолием Золотковым Вас могут заинтересовать другие калькуляторы из группы Калькуляторы для электротехники, ВЧ и электроники:Калькулятор резисторно-конденсаторных (RC) цепей Калькулятор параллельного сопротивления Калькулятор конденсации калькулятор конденсации . Калькулятор импеданса RC-цепи Калькулятор импеданса параллельной LC-цепи Parallel RL Circuit Impedance Calculator Parallel RLC Circuit Impedance Calculator Series LC Circuit Impedance Calculator Series RL Circuit Impedance Calculator Series RLC Circuit Impedance Calculator Battery Energy and Runtime Calculator Drone LiPo Battery Calculator Single -Калькулятор индуктивности многослойной катушки NFC/RFID Калькулятор индуктивности плоской спиральной катушки Калькулятор коаксиального кабеля Калькулятор светодиодов. Расчет токоограничивающих резисторов для одиночного светодиода и светодиодных матриц Калькулятор цветового кода резистора Калькулятор максимальной дальности РЛС Калькулятор максимальной однозначной дальности РЛС и частоты повторения импульсов Калькулятор радиолокационного горизонта и видимости цели Радиолиния прямой видимости Калькулятор расстояния Калькулятор эффективной апертуры антенны Калькулятор дипольной антенны Калькулятор частоты наложения частот DC Power Calculator Калькулятор мощности переменного тока VA к калькулятору ватт Трехфазный калькулятор мощности переменного тока (сбалансированная нагрузка) Обращение фазора: прямоугольный-полосовой Калькулятор времени передачи данных Калькулятор внутреннего сопротивления батареи Калькуляторы Электрические, радиочастотные и электронные калькуляторы | |||||||||
Параллельные резисторно-конденсаторные цепи — электрические…
Используя компоненты одинакового номинала в нашей последовательной примерной схеме, мы соединим их параллельно и посмотрим, что произойдет: (рисунок ниже).
Параллельная резистивно-емкостная цепь.Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и конденсатор имеют одинаковые значения сопротивления и емкости соответственно, они также должны иметь одинаковые значения импеданса. Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:
Поскольку теперь это параллельная цепь, мы знаем, что напряжение распределяется поровну между всеми компонентами, поэтому мы можем поместить цифру общего напряжения (10 вольт ∠ 0 o ) во все столбцы:
/p>
Теперь мы можем применить закон Ома (I=E/Z) по вертикали к двум столбцам таблицы, вычислив ток через резистор и ток через конденсатор:
Как и в цепях постоянного тока, токи ветвей в параллельной цепи переменного тока складываются для формирования полного тока (снова закон тока Кирхгофа):
Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z=E/I) по вертикали в столбце «Общий».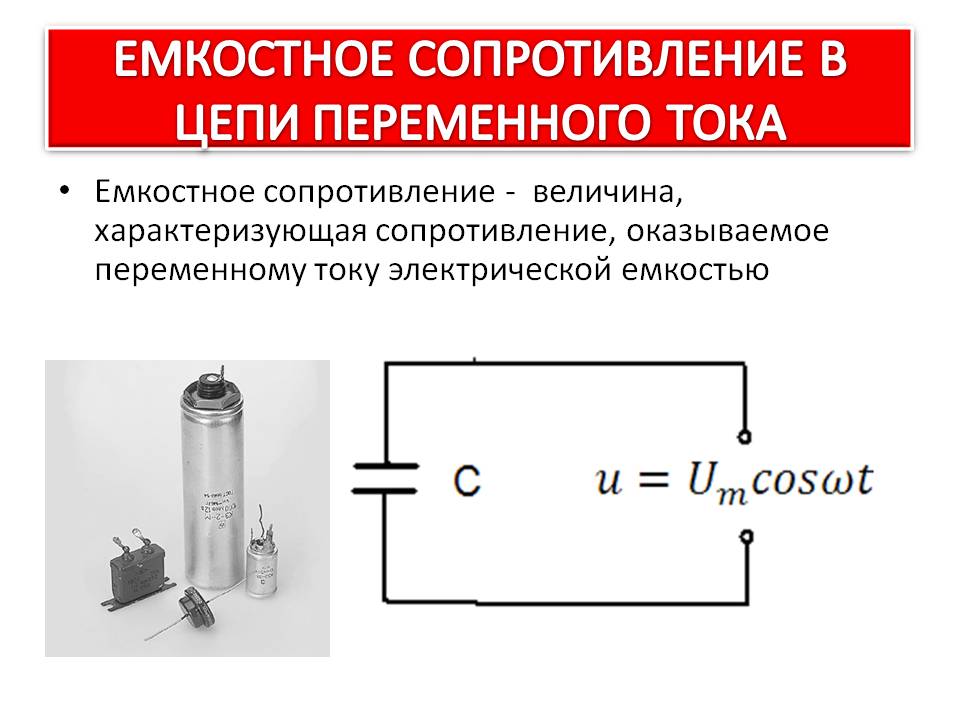 Как мы видели в главе, посвященной индуктивности переменного тока, параллельное сопротивление также можно рассчитать, используя формулу обратной зависимости, идентичную той, что используется при расчете параллельных сопротивлений. Следует отметить, что это правило параллельного импеданса остается верным независимо от типа импеданса, помещенного параллельно. Другими словами, не имеет значения, рассчитываем ли мы цепь, состоящую из параллельных резисторов, параллельных катушек индуктивности, параллельных конденсаторов или какой-либо их комбинации: в форме импедансов (Z) все термины являются общими и могут применяться равномерно по одной и той же формуле. И снова формула параллельного импеданса выглядит так:
Как мы видели в главе, посвященной индуктивности переменного тока, параллельное сопротивление также можно рассчитать, используя формулу обратной зависимости, идентичную той, что используется при расчете параллельных сопротивлений. Следует отметить, что это правило параллельного импеданса остается верным независимо от типа импеданса, помещенного параллельно. Другими словами, не имеет значения, рассчитываем ли мы цепь, состоящую из параллельных резисторов, параллельных катушек индуктивности, параллельных конденсаторов или какой-либо их комбинации: в форме импедансов (Z) все термины являются общими и могут применяться равномерно по одной и той же формуле. И снова формула параллельного импеданса выглядит так:
Единственным недостатком использования этого уравнения является значительный объем работы, необходимый для его расчета, особенно без помощи калькулятора, способного работать со сложными величинами. Независимо от того, как мы рассчитываем полное сопротивление для нашей параллельной цепи (по закону Ома или по формуле обратной связи), мы придем к одной и той же цифре:
- импедансы уменьшаются, чтобы сформировать полный импеданс, используя обратную формулу.



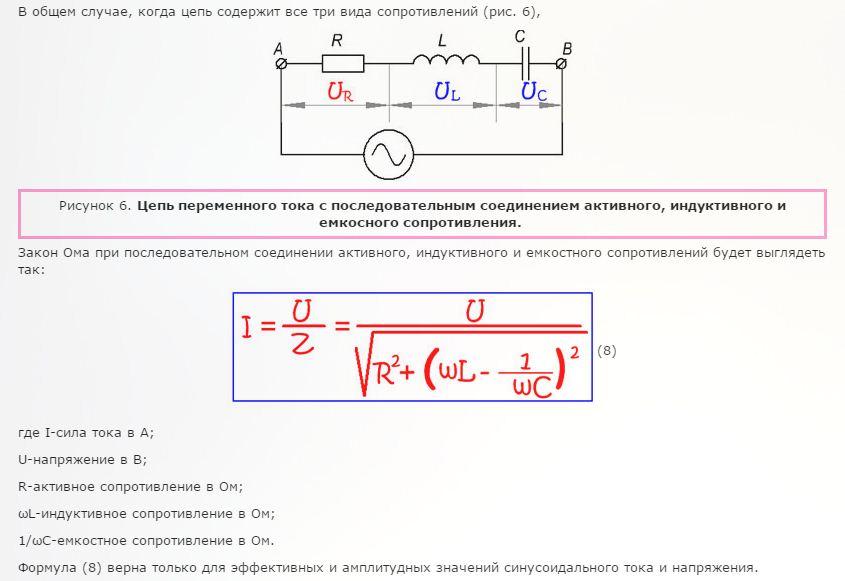
 Напряжения на резисторе V R и конденсаторе V C показаны на схеме под прямым углом друг к другу. Их сумма всегда больше общего напряжения V T .
Напряжения на резисторе V R и конденсаторе V C показаны на схеме под прямым углом друг к другу. Их сумма всегда больше общего напряжения V T . Другими словами, напряжение отстает от тока на φ по фазе; 0° ≤ φ ≤ 90°. Если напряжение В равно В = V м sin(2πft) , то ток I равен I = I м sin(2πft – φ) , где V м и I м — амплитуды напряжения и тока, f — частота (постоянная), φ — фазовый угол (постоянная), t — время (переменное)
Другими словами, напряжение отстает от тока на φ по фазе; 0° ≤ φ ≤ 90°. Если напряжение В равно В = V м sin(2πft) , то ток I равен I = I м sin(2πft – φ) , где V м и I м — амплитуды напряжения и тока, f — частота (постоянная), φ — фазовый угол (постоянная), t — время (переменное)

 и связи между ними.
и связи между ними.  com, были правильными. Однако мы не гарантируем, что наши конвертеры и калькуляторы не содержат ошибок. Весь контент предоставляется «как есть», без каких-либо гарантий. Условия и положения.
com, были правильными. Однако мы не гарантируем, что наши конвертеры и калькуляторы не содержат ошибок. Весь контент предоставляется «как есть», без каких-либо гарантий. Условия и положения.