Полное сопротивление — катушка — индуктивность
Cтраница 1
Полное сопротивление катушки индуктивности: ZK л / К Xl УЗ2 — f 42 5 Ом. [1]
| Блок-схема для измерения частотной характеристики. [2] |
Полное сопротивление катушек индуктивности зависит от паразитной емкости, добротности, тока подмагничивания и других причин. [3]
Для измерения полного сопротивления катушки индуктивности собрана схема, изображенная на рис. 11.9. Показания приборов: 71 5 А, 1 / 220 В. [4]
Для измерения полного сопротивления катушки индуктивности собрана схема, изображенная на рис. 11.11. Показания приборов: 12 А, 6 127 В. [5]
Для измерения полного сопротивления катушки индуктивности собрана схема, изображенная на рис. 11.9. Показания приборов: 71 5 A, t / 220 В. [6]
Для измерения полного сопротивления катушки индуктивности
11.11. Показания приборов: / 2 А, [ 7127 В.
[7]Тангенс угла диэлектрических потерь ферритов определяют расчетом по данным измерения полного сопротивления катушки индуктивности с сердечником при последовательном или параллельном соединении с резистором. [8]
| Потенциометрич. четырехконтактный концентратомер. [9] |
Контролируемый раствор при этом может рассматриваться как корогкозамкнутый вторичный виток. Изменение концентрации электролита ( сопротивления раствора) приводит к изменению полного сопротивления катушки индуктивности
Катушка индуктивности соединена параллельно с конденсатором. Вся система включена под напряжение 120 в. Определить полное сопротивление катушки индуктивности и силу тока в емкости, если сила тока, проходящего через катушку, составляет 5 а, а емкостное сопротивление конденсатора Хс 20 ом.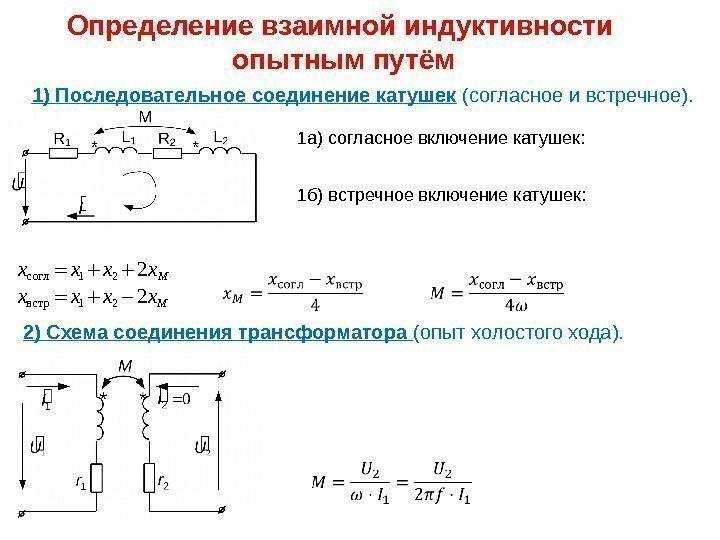
[11]
| Потенциометрич. четырехконтактный концентратомер. [12] |
В первом случае индуктивный датчик Е виде высокочастотной катушки индуктивности либо погружается в раствор, либо надевается на трубку из непроводящего материала, по к-рой протекает раствор. Контролируемый раствор при этом может рассматриваться как короткозамкнутыи вторичный виток. Изменение концентрации электролита ( сопротивления раствора) приводит к изменению полного сопротивления катушки индуктивности за счет привнесенных активного и индуктивного сопротивлений. Величина привнесенных сопротивлений определяется проводимостью раствора, частотой электромагнитного поля катушки и ее геометрич. [13]
На рис. 4 — 2, б показана схема двойного Т — образного моста. Название двойной Т — образный указывает на то, что схема моста состоит из двух Т — образных цепей, соединенных параллельно. На рис. 4 — 2, в показана схема двойного Т — образного моста, применяемая для измерения полного сопротивления катушек индуктивности.
Мост балансируется с помощью двух конденсаторов переменной емкости.
[14]
Страницы: 1
Основы электроники и электротехники — Лабораторная работа №10
ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПЕРЕМЕННОГО ТОКА С
ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
1. Цель работы
Приобретение навыков сборки простых электрических цепей и измерения напряжений на отдельных участках цепи, изучение свойств цепей при последовательном соединении активных и реактивных элементов, знакомство с явлением резонанса напряжений, построение векторных диаграмм.
2. Порядок выполнения работы
2.1. Ознакомиться с лабораторной установкой.
2.2. Собрать электрическую цепь с последовательным соединением резистора R* и конденсатора C* (рис. 1), используя элементы цепи в соответствии с заданным вариантом (табл.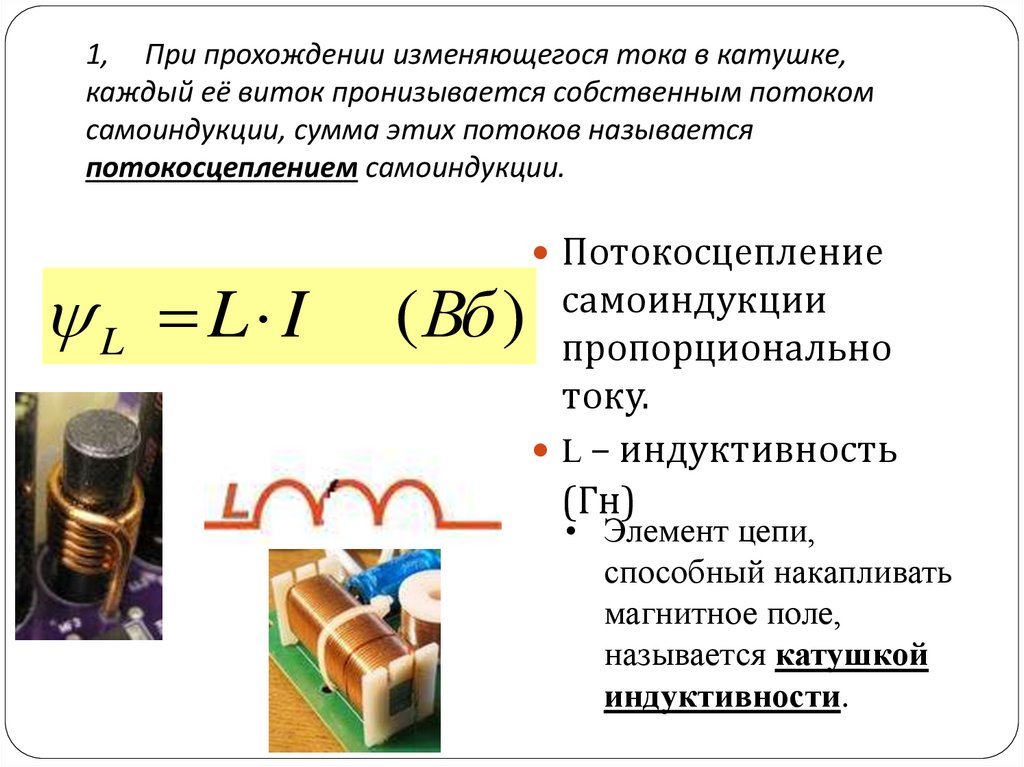
2.3. Включить питание стенда, источник переменного напряжения Е3. Установить на выходе источника питания Е3 напряжение 7 В с частотой 400±10 Гц. Провести измерения указанных в табл. 2 величин. Результаты измерений занести в табл. 2. Выключить источник электропитания Е3.
|
Схема |
U,В |
I,мА |
Ur,В |
Uk,В |
Uc,В |
P,Вт |
|
RC |
|
|
|
——— |
|
|
|
ZkC |
|
|
——- |
|
|
|
2.
4. Собрать электрическую цепь с последовательным соединением реальной катушки индуктивности L* конденсатора C* (рис. 2), используя элементы цепи в соответствии с заданным вариантом (табл. 3). Предъявить схему для проверки преподавателю.
2.5. Включить электропитание, установить на выходе источника питания Е3 напряжение 7 В с частотой ≈ 400±10 Гц. Провести измерения указанных в таблице величин для цепи с последовательным соединением реальной катушки индуктивности L и конденсатора С. Результаты измерений занести в табл. 2. Выключить электропитание.
3.6. Для исследованных цепей по результатам измерений рассчитать:
– полную мощность цепи S,
– реактивную мощность цепи Q,
– коэффициент мощности цепи cosφ и угол сдвига фаз φ между напряжением
на входе цепи и током,
– коэффициент мощности катушки cosφК и угол сдвига фаз φК между
напряжением на катушке и током,
– полные, активные и реактивные сопротивления всей цепи и отдельных
участков (ZК, RК, XK, XC, ZЭ, RЭ, XЭ,).
2) BAp
cosфк
фк.
град
cosф
Ф
град
Zk
Ом
Rk
Ом
Xk
Ом
Xc
Ом
Zэ
Ом
Rэ
Ом
Хэ
Ом
2.
7. По результатам измерений для исследованных цепей построить в масштабе векторные диаграммы, треугольники сопротивлений и мощностей, сделать вывод о характере каждой исследованной цепи.
2.8. Сделать вывод о применении 2-го закона Кирхгофа в цепях переменного тока.
3. Содержание отчета
Отчет по работе должен содержать:
а) наименование работы и цель работы;
б) схему исследуемой цепи;
в) таблицы с результатами опытов и вычислений;
г) расчетные соотношения;
д) векторные диаграммы;
е) выводы по работе.
4. Контрольные вопросы
1. Что такое активная, реактивная и полная мощности в цепи переменного тока?
2. Какая взаимосвязь между полной, активной и реактивной мощностями?
3. Что такое «коэффициент мощности»?
4. Как вычислить полное сопротивление катушки, если известны её активное
сопротивление, индуктивность и частота сети?
5.
Как вычислить полное сопротивление цепи с последовательным соединением резистора, реальной катушки и конденсатора?
6. От чего зависит угол сдвига фаз между напряжением и током на участке электрической цепи переменного тока?
7. Что такое «треугольник сопротивлений»?
8. Чему равны реактивное сопротивление цепи и реактивная мощность цепи при резонансе?
9. В каком случае исследуемая цепь, содержащая катушку индуктивности и конденсатор, будет носить активно-индуктивный характер и в каком случае – активно-емкостной характер?
Преобразователь случайных чисел |
Калькулятор импеданса цепи серии RL Калькулятор полного сопротивления цепи серии RL определяет импеданс и угол разности фаз последовательно соединенных индуктора и резистора для заданной частоты синусоидальный сигнал. Пример: Рассчитайте импеданс катушки индуктивности 500 мГн и резистора 0,2 Ом на частоте 25 кГц. Вход Сопротивление, R мОм (мОм)Ом (Ом)килоом (кОм)мегом (МОм) Индуктивность, л генри (мкнГн)миллигенри (мГн)микрогенри )пикогенри (pH) Частота, f герц (Гц)миллигерц (мГц)килогерц (кГц)мегагерц (МГц)гигагерц (ГГц) Доля Выход Угловая частота ω = рад/с Индуктивное сопротивление X L = Ом Полное сопротивление RL |Z RL | = Ом Разность фаз φ = ° = рад Введите значения сопротивления, индуктивности и частоты, выберите единицы измерения и нажмите или коснитесь кнопки Рассчитать . Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода. The following formulas are used for the calculation: where Z RL is the RL circuit impedance in ohms (Ω), ω = 2πf – угловая частота в рад/с, f – частота в герцах (Гц), R – сопротивление в Ом (Ом), L — индуктивность в генри (Гн), φ — разность фаз между полным напряжением V T и полным током I T в градусах (°) и радианах, а j — воображаемая единица. График сопротивления цепи серии RL Z RL в зависимости от частоты f для заданных индуктивности и сопротивления Для расчета введите индуктивность, сопротивление и частоту, выберите единицы измерения и результат для импеданса RL будет показан в омах, а для разности фаз – в градусах. Также будет рассчитано индуктивное сопротивление в омах. Векторная диаграмма для последовательной RL-цепи показывает, что общая волна тока отстает от полной волны напряжения. Составляется простая серия RL или резистор-индуктор резистор и катушка индуктивности, соединенные последовательно и управляемые источником напряжения. Ток в катушке индуктивности и резисторе одинаков, потому что они соединены последовательно. Напряжения на резисторе V R и дроссель V L показаны на схеме под прямым углом друг к другу. Их сумма всегда больше общего напряжения V T . Если вы посмотрите на уравнение для расчета импеданса (выше), вы заметите, что оно похоже на уравнение для расчета гипотенузы прямоугольного треугольника. Это связано с тем, что импеданс RL-цепи в графическом виде выглядит так, как на этом рисунке, где сопротивление R находится на горизонтальной оси, а реактивное сопротивление X L находится на вертикальной оси. Фазовый угол может составлять от 0° для чисто резистивной цепи до 90° для чисто индуктивной цепи. Из треугольника реактивных сопротивлений или с помощью функции арктангенса (арктангенса) В последовательной RL-цепи с источником синусоидального напряжения волна тока отстает от волны напряжения с запаздыванием менее 90° (нулевое сопротивление) и более 0° (нулевая индуктивность). Другими словами, напряжение опережает ток на φ по фазе; 0° ≤ φ ≤ 90°. Если напряжение В равно В = V м sin(2πft) , то ток I равен I = I м sin(2πft + φ) , где V м и I м — амплитуды напряжения и тока, f — частота (постоянная), φ — фазовый угол (постоянная), t — время (переменная) В последовательной RL-цепи один и тот же ток I протекает и через катушку индуктивности, и через резистор. Обратите внимание, что общее напряжение всегда меньше суммы напряжений на резисторе и катушке индуктивности — точно так же, как в любом прямоугольном треугольнике, где длина гипотенузы меньше суммы из двух катетов треугольника. Учтите также, что напрямую измерить импеданс с помощью обычного мультиметра невозможно — для этого необходимо использовать импедансометр. Пример использования — измерение импеданса нескольких динамиков с трансформаторами, звуковыми катушками и кроссоверами. В отличие от мультиметра, который подает постоянное напряжение на измеряемую цепь, измеритель импеданса подает испытательный сигнал переменного тока на проверяемую цепь. Режимы отказаЧто делать, если что-то пойдет не так в этой цепи? Click or tap a corresponding link to view the calculator in various failure modes:
Специальные режимыЩелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных специальных режимах: Различные режимы постоянного тока Короткое замыкание Разомкнутая цепь Чисто индуктивная цепь Индуктивная цепь Примечания
Эта статья написана Анатолием Золотковым Вас могут заинтересовать другие калькуляторы из группы Калькуляторы электротехники, ВЧ и электроники:Калькулятор резисторно-конденсаторной (RC) цепи Калькулятор параллельного сопротивления Калькулятор параллельной индуктивности 04 Калькулятор конденсаторов серии Калькулятор полного сопротивления конденсатора Калькулятор полного сопротивления катушки индуктивности Калькулятор взаимной индуктивности Калькулятор взаимной индуктивности — параллельные индуктивности Калькулятор взаимной индуктивности — индуктивность в серии Параллельный калькулятор RC -цепи Параллельный схема схемы схемы схемы. Калькулятор Калькулятор импеданса цепи RLC серииКалькулятор энергии и времени работы батареи Калькулятор батареи LiPo для дрона Калькулятор индуктивности однослойной катушки Калькулятор индуктивности плоской спиральной катушки NFC/RFID Калькулятор коаксиального кабеля Калькулятор светодиодов. Калькулятор цветового кода резистора Калькулятор максимальной дальности РЛС Калькулятор максимальной однозначной дальности РЛС и частоты повторения импульсов Калькулятор радиолокационного горизонта и видимости цели Радиолиния видимости Калькулятор расстояний Эффективный калькулятор антенной апертуру Дипольный антенный калькулятор Калькулятор частоты алиаса. –Polar Калькулятор полного гармонического искажения (THD) Калькулятор закона Ома Калькулятор времени передачи данных Калькулятор внутреннего сопротивления батареи Калькуляторы Электрические, радиочастотные и электронные калькуляторы | |||||||||
Также определяется угловая частота.
Отставание меньше 90° и больше 0°. При 90° вместо резистора устанавливается перемычка (схема чисто индуктивная) и при 0° вместо индуктора устанавливается перемычка (схема чисто резистивная)
Гипотенуза — это импеданс цепи, а фазовый угол — это угол между горизонтальной осью и вектором импеданса.
Напряжение катушки индуктивности V L опережает общий ток на 90°, а напряжение резистора находится в фазе с общим током. По закону напряжения Кирхгофа сумма падений напряжения должна равняться общему напряжению V T . Напряжения резистора и катушки индуктивности V R и V L не совпадают по фазе друг с другом на 90°, поэтому их необходимо суммировать как векторные величины и общее напряжение V T определяется как
Если индуктор имеет конечную индуктивность, его реактивное сопротивление при нулевой частоте равно нулю, а для источника постоянного напряжения это представляет собой короткое замыкание.
Расчет токоограничивающих резисторов для одиночного светодиода и светодиодных матриц
com, были правильными. Однако мы не гарантируем, что наши конвертеры и калькуляторы не содержат ошибок. Весь контент предоставляется «как есть», без каких-либо гарантий. Условия и положения.Треугольник импеданса
- Изучив этот раздел, вы сможете описать:
- •Треугольник импеданса.
- •Графическое представление импеданса.
- • Расчет импеданса в индуктивных и емкостных цепях.
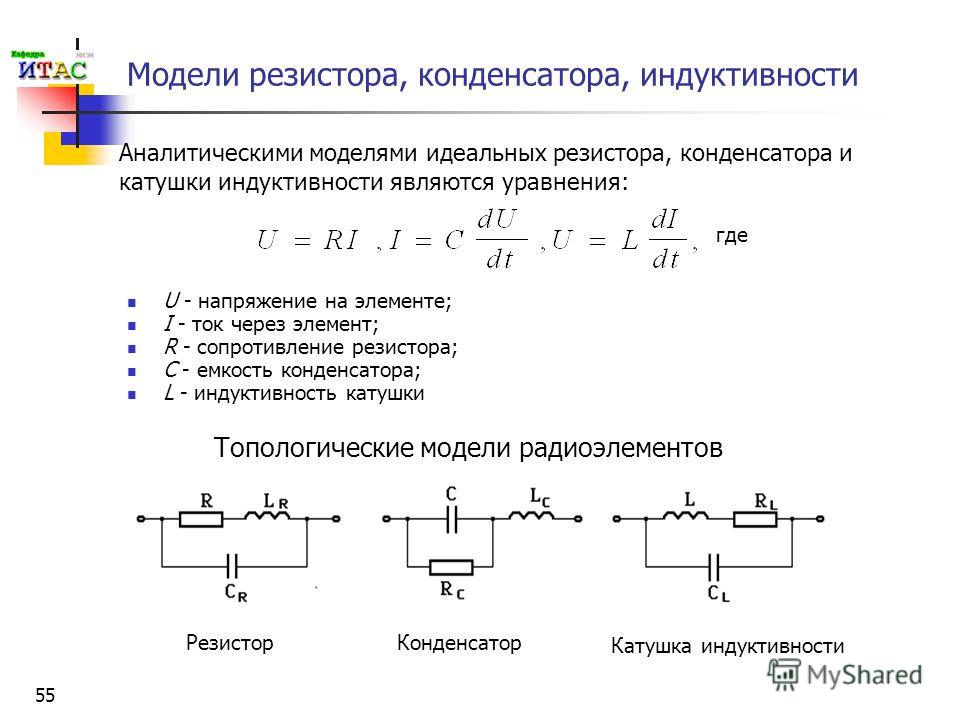
Влияние практического (реального) индуктора на ограничение протекания тока обусловлено не только эффектом противо-ЭДС, который вызывает реактивное сопротивление X L , но также частично обусловлено внутренним сопротивлением индуктор. Поскольку эти две причины, возникающие в одном и том же компоненте, не могут быть физически разделены, часто необходимо учитывать комбинированное влияние как реактивного сопротивления, так и сопротивления на ток через катушку индуктивности.
Имя, используемое для описания этого комбинированного противодействия току, — ИМПЕДАНС, которое измеряется в ОМах, но имеет символ Z.
Рис. 7.1.1 Построение треугольника импеданса
по векторной LR-диаграмме.
Эта комбинация реактивного сопротивления и сопротивления не является простой суммой этих величин. Например, чтобы получить импеданс простой последовательной цепи LR, сначала необходимо рассчитать ФАЗОРНУЮ СУММУ сопротивления и реактивного сопротивления. Причину этого можно понять, изучив рис. 7.1.1, на котором показана векторная диаграмма схемы, нарисованной в виде прямоугольного треугольника. Три стороны треугольника представляют три вектора напряжения в цепи V R V L и V S . Поскольку компоненты схемы соединены последовательно, общий для них общий ток.
Учитывая напряжения V R и V L на рис. умноженное на реактивное сопротивление)
Теперь, поскольку Z — полное сопротивление всей цепи, полное напряжение в цепи, В S = IZ
Поскольку эти вектора теперь образуют прямоугольный треугольник, теорема Пифагора может быть использована для связи всех этих векторов напряжения: L 2
therefore (Because V = IR etc.
)
(IZ) 2 = (IR) 2 + (IX L ) 2 or I 2 Z 2 = I 2 R 2 + I 2 X L 2
Next, dividing throughout by I 2 eliminates I 2 to give Z 2 = R 2 + X L 2
and taking the square root of both sides of это уравнение дает формулу для расчета Z (общее сопротивление цепи LR).
Примечание. При использовании этой формулы на калькуляторе важно не забывать использовать скобки или, в качестве альтернативы, найти сумму R 2 + X L 2 перед использованием ключа квадратного корня.
Рис. 7.1.2 Треугольник импеданса для цепей CR.
Помните, что импедансы, сопротивления и реактивные сопротивления сами по себе не являются векторными величинами. Они влияют на напряжения и токи, заставляя эти величины изменять свое отношение друг к другу, но поскольку Z, R и X сами по себе не меняются со временем, они не являются векторами.
На рис. 7.1.2 показано аналогичное соотношение, существующее в резистивной/емкостной цепи. Диаграмма вектора напряжения для цепей CR может быть преобразована в прямоугольный треугольник и обработана так же, как диаграммы LR на рис. 7.1.1, чтобы получить:
На рис. 7.1.3 показан еще один вариант треугольника импеданса, который можно использовать для расчета импеданса, когда в цепи присутствуют сопротивление (R), индуктивность (L) и емкость (C), а общее реактивное сопротивление ( X) — это разница между индуктивным реактивным сопротивлением (X L ) и емкостным реактивным сопротивлением (X C ). В этом случае формула для Z будет выглядеть так:
Импеданс — это лишь одно из свойств, жизненно важных для понимания цепей переменного тока. Если вы изучили этот модуль и модули 5 (Фаза и фазовращатели) и 6 (Реактивное сопротивление), вы должны начать понимать, как эти свойства работают вместе. Чтобы понять, как импеданс зависит от других свойств цепи, таких как реактивное сопротивление и сопротивление, и увидеть, как импеданс влияет на такие параметры, как ток и напряжение, попробуйте выполнить расчеты с использованием формул из этих модулей модуля 7 «Викторина по импедансу 9».
