Катушка индуктивности в цепи переменного тока кратко – формулы и опредделение (11 класс)
4.2
Средняя оценка: 4.2
Всего получено оценок: 74.
Обновлено 10 Января, 2021
4.2
Средняя оценка: 4.2
Всего получено оценок: 74.
Обновлено 10 Января, 2021
В цепи постоянного тока катушка индуктивности ведет себя так же, как обычный длинный провод. Однако для переменного тока ситуация существенно иная. Поговорим кратко о катушке индуктивности в цепи переменного тока.
Сущность индуктивного сопротивления
Из курса физики в 11 классе известно, что катушке индуктивности присуще явление самоиндукции. Оно состоит в том, что при изменении величины тока, протекающего по катушке, магнитное поле, порожденное этим током, также меняется. Это приводит к изменению магнитного потока через катушку. А по закону электромагнитной индукции изменение магнитного потока вызывает появление в контуре ЭДС. Эта ЭДС по правилу Ленца направлена так, чтобы препятствовать причине, ее порождающей.
Иными словами, при изменении тока в катушке индуктивности в ней возникает некоторая ЭДС, которая препятствует изменению этого тока.
Получается, что катушка «сопротивляется» любым изменениям тока в ней. Если ток возрастает, она не дает ему возрастать. Если ток убывает, она не дает ему убывать. Для переменного тока, который постоянно изменяет свое значение по гармоническому закону, катушка постоянно «сопротивляется». Таким образом, для переменного тока можно говорить об особом, индуктивном, сопротивлении катушки (на постоянном токе это сопротивление равно нулю).
Это сопротивление существенно отличается от сопротивления активного. Если на активном сопротивлении работа тока преобразуется в тепло, то на сопротивлении катушки во время возрастания тока его работа преобразуется в энергию магнитного поля в катушке, а во время убывания она возвращается из магнитного поля в энергию тока. Катушка как бы «имеет реакцию» на изменение тока через нее за счет индуктивности.
Реактивное сопротивление катушки индуктивности
Поскольку в первую половину периода энергия электрического тока запасается в магнитном поле катушки, а во вторую — возвращается в цепь, то в среднем работа электрического тока равна по модулю работе ЭДС самоиндукции, но имеет противоположный знак:
$$e_i =-u$$
Однако амплитудные значения напряжения и тока на катушке индуктивности достигаются неодновременно.
Мгновенное значение тока:
$$i =I_msin \omega t$$
Мгновенное значение напряжения:
$$u =L\omega I_m cos \omega t$$
Учитывая, что максимальная амплитуда напряжения $U_m$ равна $ L\omega I_m $, и приводя к синусу, получаем:
$$u =U_m sin(\omega t+{\pi \over 2})$$
Таким образом, колебания силы тока в катушке индуктивности отстают от колебаний напряжения на четверть периода. В этом важное отличие реактивного сопротивления от активного, где отставания между током и напряжения нет.
Амплитуда силы тока в катушке равна:
$$I_m={U_m\over \omega L}$$
Сравним эту формулу с законом Ома, который используется для определения силы тока в цепи:
$$I={U\over R}$$
Можно видеть, что эти формулы аналогичны, и величина $ \omega L$ играет роль сопротивления. То есть реактивное сопротивление катушки индуктивности (индуктивное сопротивление) равно:
$$X_L= \omega L$$
Отметим, что реактивное сопротивление катушки прямо пропорционально циклической частоте переменного тока. Чем она больше, тем больше сопротивление.
Поскольку любой проводник обладает некоторой индуктивностью, то на очень высоких частотах даже эта малая индуктивность обычных проводников достаточно сильно влияет на сигнал. Поэтому приходится применять специальные меры для ее компенсации. Например, применять вместо проводов волноводы — пустотелые металлические конструкции:
Что мы узнали?
Катушка индуктивности в цепи переменного тока обладает реактивным сопротивлением, пропорциональным частоте.
Первую половину периода она запасает энергию электрического тока в виде магнитного поля, а вторую половину периода возвращает эту энергию электрическому току. При этом колебания силы тока в катушке индуктивности отстают от колебаний напряжения на четверть периода.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 74.
А какая ваша оценка?
Реактивное сопротивление — катушка — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Реактивные сопротивления катушек: XL, и 1 314 — 0 0127 4 ом; XL, XL, 4 ом. [1]
Реактивное сопротивление катушки xL aL пропорционально частоте. [2]
Электрическая дуга. |
Реактивное сопротивление катушки регулируется путем изменения зазора в ее магнитопроводе. Изменяя зазор, можно устанавливать различные токи устойчивого горения дуги при обычных расстояниях между электродами. [4]
Реактивное сопротивление катушек обусловлено возникновением в них электродвижущей силы ( эдс) самоиндукции, которая направлена навстречу приложенному напряжению и создает сопротивление прохождению переменного тока. [5]
Реактивное сопротивление катушки Аь0ю1о314 — 0 0627 19 7 Ом. [6]
Резонансные контуры могут быть последовательными и параллельными. Частота, на которой в них возникает резонанс, определяется величинами индуктивности катушки и емкости конденсатора. Большие индуктивности и емкости создают резонанс на низких, а малые индуктивности и емкости — на высоких частотах.
[7] |
Когда реактивные сопротивления катушки индуктивности
| Эквивалентная собственные индуктивность и ем. [9] |
Уменьшение реактивного сопротивления катушки х достигается применением специальных способов намотки катушек. [10]
| Последовательное соединение двух катушек ( / d и Кг индуктивности.| Катушка и конденсатор соединены параллельно. [11] |
Наконец, реактивное сопротивление катушек найдем, применив теорему Пифагора к треугольнику сопротивлений.
[12]
Наконец, реактивное сопротивление катушек найдем, применив теорему Пифагора к треугольнику сопротивлений ( стр. [13]
Как изменится реактивное сопротивление катушки индуктивности при введении в нее стержня, изготовленного из: а) электротехнического железа; б) алюминия; в) меди. [14]
Как изменится реактивное сопротивление катушки индуктивности
Страницы: 1 2 3 4 5
электрических цепей — Эффективное сопротивление катушки индуктивности
спросил
Изменено 9 лет, 10 месяцев назад
Просмотрено 10 тысяч раз
$\begingroup$
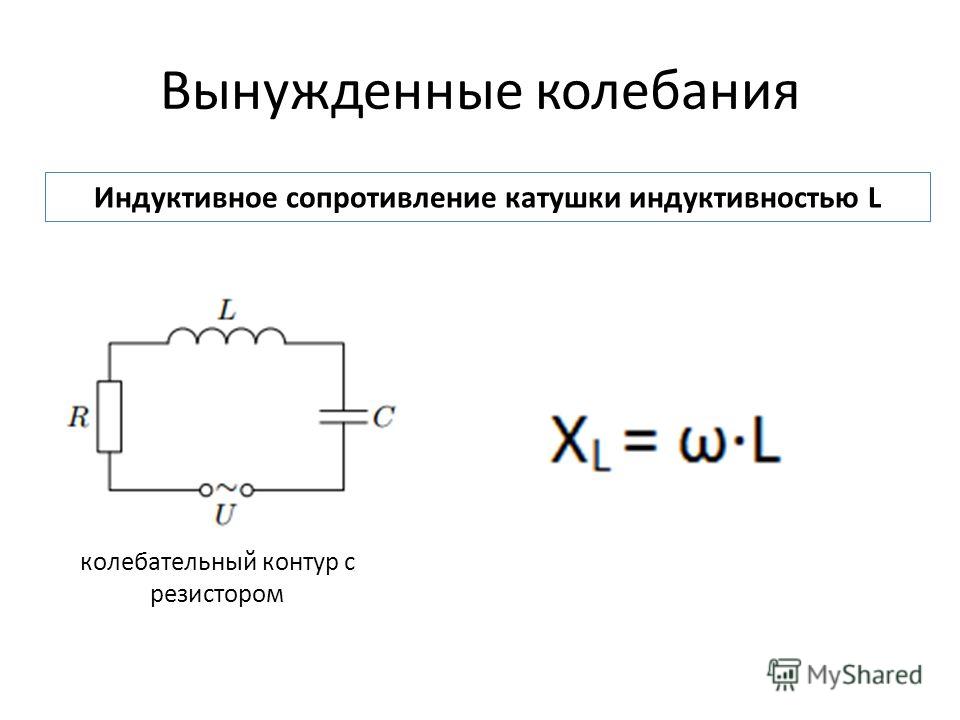
В лабораторном эксперименте мы подключили простую схему: источник переменного напряжения, соединенный (последовательно) с переменным резистором и катушкой индуктивности.
Что мы не поняли?
- электрические цепи
- электрическое сопротивление
- индуктивность
$\endgroup$
2
$\begingroup$
Здесь может быть задействовано несколько нелинейных эффектов магнитного материала, хотя этот ответ следует охарактеризовать как спекуляцию без дополнительных подробностей. Оба эффекта более выражены, если ваш индуктор не закрыт.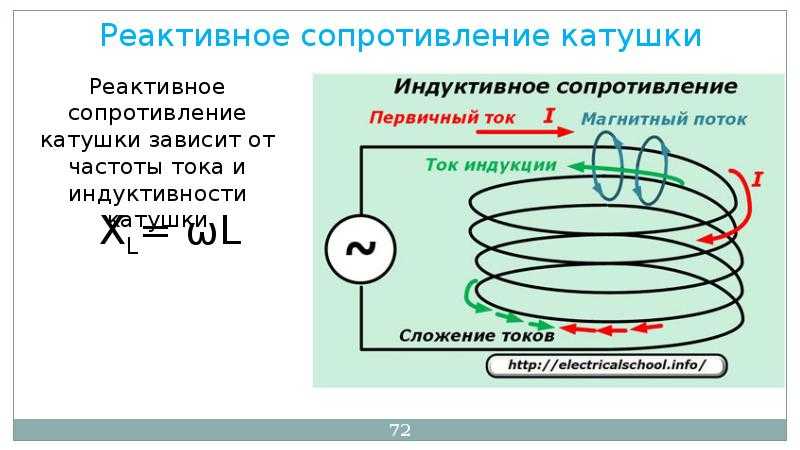
1) При очень низких уровнях тока (соответствующих очень низким уровням магнитного поля H) индуктивность может быть ниже номинальной. (Характеристика B-H материала магнитного сердечника имеет меньший наклон прямо в начале координат.) По мере увеличения тока от этих низких уровней расчетное полное сопротивление катушки индуктивности $Z_L =2 \pi f L$ будет увеличиваться, а затем стабилизируется на номинальном уровне. ценность.
2) Поскольку ток продолжает увеличиваться, катушка индуктивности в конце концов начинает насыщаться. (Характеристика BH выравнивается при высоких полях.) Затем индуктивность становится убывающей функцией тока, поэтому расчетное полное сопротивление катушки индуктивности будет уменьшаться.
Вы можете увидеть некоторые кривые B-H, иллюстрирующие эти эффекты, в статье Википедии «Насыщение (магнитное)».
Наличие зазора в магнитопроводе снижает индуктивность компонента, но стабилизирует его против этих эффектов.
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Электрическое сопротивление— Вопрос о катушке индуктивности и резисторе в цепях
спросил
Изменено 1 год, 11 месяцев назад
Просмотрено 111 раз
$\begingroup$
Когда чистый источник постоянного тока соединяется с чистым индуктором, изменение тока в индукторе линейно по индуктору относительно времени Circuit) с ним получаем экспоненциальное изменение тока в той (RL) цепи.
Мой вопрос заключается в том, почему добавление сопротивления последовательно с катушкой индуктивности и источником постоянного тока делает изменение тока экспоненциальным, хотя мы получаем линейное изменение тока, когда соединяем источник постоянного тока с чистой катушкой индуктивности.
Что находится в резисторе, который делает изменение тока экспоненциальным, когда к сопротивлению добавляется чистая катушка индуктивности последовательно с источником постоянного тока?
- электрические цепи
- электрические сопротивления
- индуктивности
$\endgroup$
$\begingroup$
Ну, только для катушки индуктивности, подключенной к источнику постоянного напряжения: $$V = L\frac{dI}{dt},$$, поэтому $$I=\frac{V}{L}t.$$ С резисторе, напряжение на катушке индуктивности уменьшается на величину, пропорциональную току: \начать{выравнивать} V_{DC}&=V_R+V_L,\\ V_R&=ИК,\\ V_L&=L\frac{dI}{dt},\\ \frac{V_{DC}-IR}{L}&=\frac{dI}{dt} \end{выравнивание}
Резистор представлен дополнительным членом $IR$ в окончательном уравнении, которого раньше не было. Он вводит в схему обратную связь: увеличение тока происходит из-за напряжения на катушке индуктивности, но резистор делает так, что это напряжение (и, следовательно, увеличение тока) становится меньше по мере увеличения тока.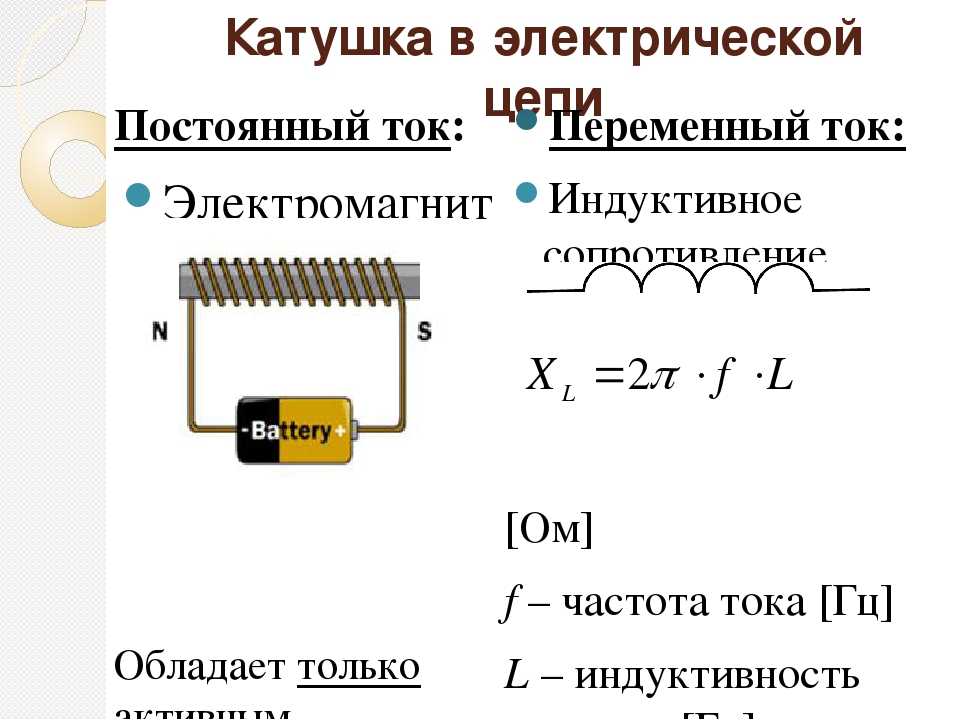
Таким образом, кривая $I-t$ с течением времени все больше и больше отклоняется от линии, образуя экспоненциальную кривую. $$I=\frac{V_{DC}}{R}\left(1-\exp\left(-\frac{R}{L}t\right)\right).$$ На достаточно короткое время вправо когда вы включаете схему, кривая $I-t$ выглядит линейной, как если бы резистора не было (поскольку ток через/напряжение на резисторе еще не сильно вырос). Через достаточно долгое время после включения цепи кривая $I-t$ выглядит постоянной, как если бы катушки индуктивности не было (поскольку напряжение на катушке индуктивности упало практически до нуля).
$\endgroup$
1
$\begingroup$
В подобных случаях полезно помнить аналогии механика х электричество, потому что они более наглядны и в то же время строги, так как основаны на тех же дифференциальных уравнениях:
Катушка индуктивности – это масса, Напряжение – это сила, ток скорость и сопротивление есть трение.
