Определение индуктивности, активного сопротивления катушки.
⇐ ПредыдущаяСтр 9 из 10Следующая ⇒Для колебательного контура рекомендуется выбрать катушку 220/127 от школьного трансформатора, магазин конденсаторов Р544, выставив емкость порядка 0,5 мкФ, и магазин сопротивлений Р33.
 Определить индуктивность и активное сопротивление катушки методом амперметра и вольтметра. Для этого собрать схему, указанную на (Рис. 4). При подключении в качестве источника тока постоянного выхода ВС-24 сопротивление rL равно
Определить индуктивность и активное сопротивление катушки методом амперметра и вольтметра. Для этого собрать схему, указанную на (Рис. 4). При подключении в качестве источника тока постоянного выхода ВС-24 сопротивление rL равно
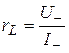 ,
,
а при подключении переменного выхода – сопротивление Z равно:
 ,
,

Расчет параметров колебательного контура и экспериментальное получение затухающих колебаний.
Задав емкость конденсатора порядка 0,1 мкФ и активное сопротивление R равное нулю, рассчитать параметры получившегося колебательного контура: частоту n (или w), коэффициент затухания b, период затухающих колебаний Т, логарифмический декремент затухания d, добротность колебательного контура Q, критическое сопротивление Rкр.
Собрать схему (Рис. 5), выставив на магазине емкостей 0,1 мкФ, на магазине сопротивлений – 0 Ом. Для того, чтобы картина затухающих колебаний была постоянно видна на экране осциллографа, необходимо периодически добавлять энергию в колебательный контур подзаряжая конденсатор. В качестве периодического источника энергии используется выход пилообразного 
Конденсатор Сдиф и входное сопротивление осциллографа Rвх представляют из себя дифференцирующую цепь, превращающую пилообразный сигнал в импульсный (Рис. 6). При плавном нарастании напряжения конденсатор успевает заряжаться, напряжение на нем в каждый момент времени практически равно напряжению источника пилообразного сигнала, и ток в цепи отсутствует. При резком уменьшении напряжения в цепи наблюдается импульс тока разрядки конденсатора. Выходное напряжение является дифференциалом входного напряжения по времени. Подобрать
По полученной картине определить параметры колебательного контура и сравнить их с рассчитанными ранее. Меняя индуктивность катушки, вводя в нее сердечник, и емкость конденсатора, пронаблюдать и объяснить изменение картины затухающих колебаний.
Пронаблюдать изменение картины при увеличении активного сопротивления R. Выставить на магазине сопротивлений такое R, чтобы выполнялось условие:
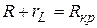 ,
,
и убедиться, что колебания в контуре отсутствуют.
Вопросы к зачету по работе.
– Объяснить физический механизм электромагнитных колебаний в колебательном контуре.
– Как преобразуется энергия при электромагнитных колебаниях и чему равна полная энергия?
– Как влияет наличие активного сопротивления колебательного контура на электромагнитные колебания? Что такое затухающие электромагнитные колебания?
– Какие параметры контура определяют характер электромагнитных колебаний в контуре?
– Объяснить, почему наличие критического сопротивления в цепи препятствует возникновению электромагнитных колебаний в контуре.
Лабораторная работа № 10
Явления в цепях переменного тока
Цель работы.
Изучить закономерности явлений, наблюдаемых в цепях переменного тока.
Знания, необходимые для допуска к работе.
– Индуктивность и емкость в цепях переменного тока;
– Закон Ома для переменного тока;
– Резонансные явления в цепях переменного тока.
Краткие сведения из теории.
Переменным током называется любой ток, величина которого периодически меняется со временем. Но чаще всего под переменным током подразумевается ток, меняющийся по закону синуса (или косинуса):
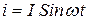 ,
,
где I – амплитуда тока,  – циклическая частота, а
– циклическая частота, а 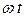
 Рассмотрим электрическую цепь, содержащую последовательно соединенные резистор, конденсатор и катушку индуктивности, подключенную к источнику переменного напряжения (Рис. 1). По этой цепи протекает ток, меняющийся по синусоидальному закону
Рассмотрим электрическую цепь, содержащую последовательно соединенные резистор, конденсатор и катушку индуктивности, подключенную к источнику переменного напряжения (Рис. 1). По этой цепи протекает ток, меняющийся по синусоидальному закону
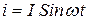 .
.
 ,
,
но при переменном токе в цепи, содержащей емкость и индуктивность, есть некоторые отличия.
Падение напряжения на резисторе колеблется по такому же закону, как и ток
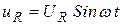 ,
,
и их фазы колебаний совпадают.
Напряжение на обкладках конденсатора пропорционально заряду на них в каждый момент времени
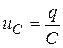
а заряд можно определить как интеграл тока по времени
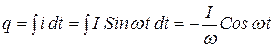 .
.
Тогда
 .
.
Из этого выражения следуют два вывода: во-первых, колебания напряжения на конденсаторе отстают от колебаний тока на 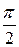 , а во-вторых, амплитудное значение напряжение связано с амплитудным значением тока соотношением:
, а во-вторых, амплитудное значение напряжение связано с амплитудным значением тока соотношением:

где  называется емкостным сопротивлением.
называется емкостным сопротивлением.
 .
.
В этом случае для участка цепи, содержащего катушку (т.е. источник ЭДС, включенный навстречу току) падение напряжения равно
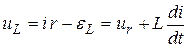 ,
,
так как помимо ЭДС самоиндукции происходит падение напряжения на сопротивлении провода
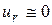 и
и
 .
.
Очевидно, что колебания напряжения на катушке опережают колебания тока на 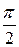 , а их амплитуды связаны соотношением
, а их амплитуды связаны соотношением
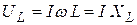 ,
,
где 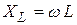
Сопротивления R, r называются активными (или омическими), а сопротивления XL и XC – реактивными.
 Соотношения фаз колебаний напряжений на активных и реактивных сопротивлениях можно проиллюстрировать на векторной диаграмме (Рис. 2). За основное направление надо взять силу тока, так как он является общим для последовательно соединенных элементов схемы. Величину амплитуды выходного напряжения можно определить, используя закон сложения векторов:
Соотношения фаз колебаний напряжений на активных и реактивных сопротивлениях можно проиллюстрировать на векторной диаграмме (Рис. 2). За основное направление надо взять силу тока, так как он является общим для последовательно соединенных элементов схемы. Величину амплитуды выходного напряжения можно определить, используя закон сложения векторов:
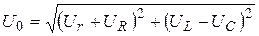
Видно, что колебания напряжения и тока сдвинуты по фазе друг относительно друга на j. Вынеся общий множитель – силу тока – из-под корня, получаем выражение:
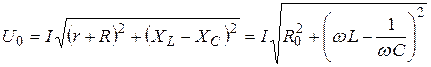 ,
,
где R0 – все активное сопротивление электрической цепи. Это выражение является математической формулировкой закона Ома для переменной цепи. Общее сопротивление цепи Z и тангенс сдвига фаз между колебаниями тока и напряжения tgj определяется по формулам:
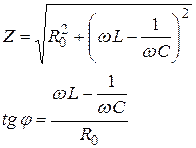 .
.
Как видно из этих формул, полное сопротивление цепи переменного тока зависит не только от величин активного сопротивления, индуктивности и емкости, но и от частоты переменного тока. При частоте близкой к нулю полное сопротивление цепи определяется емкостным сопротивлением 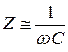 и стремится к бесконечности, а сдвиг фаз
и стремится к бесконечности, а сдвиг фаз 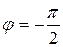 . При высокой частоте переменного тока соответственно
. При высокой частоте переменного тока соответственно 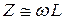 и
и 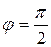 .
.
Интересная ситуация наблюдается, когда частота переменного тока удовлетворяет условию:
 .
.
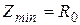 , а сдвиг фаз – нулю. Ток в этом случае приобретает максимальное значение
, а сдвиг фаз – нулю. Ток в этом случае приобретает максимальное значение  . Такое состояние цепи переменного тока называется резонансом напряжений, а частота – резонансной частотой wрез.
. Такое состояние цепи переменного тока называется резонансом напряжений, а частота – резонансной частотой wрез.
Интересен также факт превышения напряжения на реактивных элементах схемы выходного напряжения источника тока. Если в момент резонанса индуктивное и емкостное сопротивления больше активного сопротивления цепи 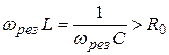 , то напряжения на них
, то напряжения на них 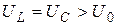 .
.
Практические задания
что это такое и от чего зависит
В радиотехнике часто приходится сталкиваться с индуктивным сопротивлением. Его источником являются катушки. Они представляют собой двухполюсник, намотанный медным эмалированным проводом (обычно это ПЭТВ) на ферритовый или железный сердечник. Подобные детали встречаются в широком перечне оборудования: от древних советских радиоприёмников до материнских плат ПК последних моделей.

Катушки индуктивности
Формулы, зависимости и виды индуктивности
Электрическая индуктивность L – это величина, равная коэффициенту пропорциональности между током I, протекающим в замкнутом контуре, и создаваемым им магнитным потоком, иначе называемым потокосцеплением Y:
Y = LI.
Если к выводам катушки на некоторое время приложить напряжение, то в ней начнёт протекать ток I и формироваться магнитное поле. Чем меньше индуктивность L, тем быстрее протекает данный процесс. В итоге рассматриваемый двухполюсник накопит некоторое количество потенциальной энергии. При отключении питания он будет стремиться её вернуть. В результате на выводах катушки образуется ЭДС самоиндукции E, которая многократно превышает изначально приложенное напряжение. Подобная технология ранее использовалась в магнето систем зажигания ДВС, а сейчас широко встречается в повышающих DC-DC преобразователях.
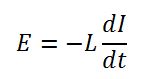
Формула ЭДС самоиндукции, здесь t – это время, в течение которого ток I уменьшится до нуля
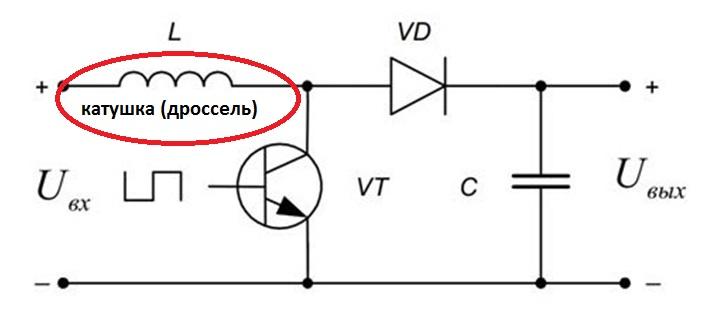
Простой DC-DC повышающий преобразователь
Катушка (она же – дроссель) – это радиодеталь с ярко выраженной индуктивностью, ведь именно для этого её и создавали. Однако подобным свойством обладают в принципе все элементы. Например, конденсатор, резистор, кабель, просто кусок провода и даже тело человек также имеют некоторую индуктивность. В расчетах ВЧ схем это обязательно принимается во внимание.
Важно! Проводя измерение индуктивности специализированным прибором, стоит помнить, что нельзя держаться руками за оба его вывода. В противном случае показания могут измениться и будут неверными. Вызвано это включением в измеряемую цепь тела человека с его собственной индуктивностью.
Сопротивление катушки переменному току
Гораздо интереснее дела обстоят с индуктивностью в контуре переменного тока. Любая катушка содержит в себе две составляющие сопротивления:
- Активную;
- Индуктивную.
При постоянном токе учитывается только первый фактор, а при переменном – оба. Формула индуктивного сопротивления XL катушки имеет следующий вид:
XL = 2pfL,
где:
- p = 3.14;
- f – частота переменного тока, Гц;
- L – индуктивность катушки, Гн.
Полное сопротивление катушки Z, называемое импедансом, определяется, исходя из активной R и индуктивной XL составляющих.
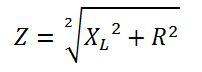
Импеданс катушки
Важно! Если катушка установлена в печатную плату, то для проверки её следует отпаять. В таком случае индуктивность будет измеряться независимо от других компонентов, что существенно повысит точность показаний прибора.
Расчёт индуктивного сопротивления катушки
Любая индуктивность, в т.ч. катушка, оказывает переменному току некоторое сопротивление. Как его рассчитать, было описано выше. Из формулы XL=2pfL видно, что сопротивление дросселя в первую очередь зависит от частоты протекающего по нему тока и его индуктивности. При этом с обоими параметрами связь прямо пропорциональная.
Частота – это характеристика внешней среды, индуктивность катушки зависит от ряда её геометрических свойств:
L=u0urN2S/l,
где:
- u0 – магнитная проницаемость вакуума – 4p*10-7 Гн/м;
- ur – относительная проницаемость сердечника;
- N – количество витков дросселя;
- S – его поперечное сечение в м2;
- l – длина катушки в метрах.
Располагая вышеописанными формулами и информацией о материале и размерах катушки, можно достаточно точно прикинуть её индуктивное сопротивление без каких-либо измерительных приборов.
Дополнительная информация. Некоторые цифровые мультиметры имеют режим замера индуктивности. Подобная функция встречается редко, однако иногда оказывается очень полезной. Поэтому при выборе прибора стоит обратить внимание на то, способен ли он измерять индуктивность.
Где применяется катушка (дроссель, индуктивность)
Дроссели имеют примитивную конструкцию: просто намотанный витками на каком-либо сердечнике проводник. В то же время в таком приборе нечему ломаться. Также у дросселей широчайший функционал и десятки применений. Из всего этого следует, что в какой бы точке города ни находился человек, в радиусе 1 км от него всегда будут тысячи катушек индуктивности, настолько они распространены.
Катушка как электромагнит
Самое простое применение катушки – это электромагнит. С подобным применением каждый сталкивается, заходя в подъезд. Сила, удерживающая дверь на месте и препятствующая несанкционированному доступу чужака, берётся из электромагнита. Он находится сверху.
Электрический ток, проходя по виткам катушки, создаёт вокруг неё переменное электромагнитное поле. Оно возбуждает в металлическом «бруске», расположенном на двери, вихревые токи, которые так же создают магнитное поле. В результате получаются два управляемых магнита. Они притягиваются друг к другу. Тем самым дверь надёжно удерживается на месте.
Другое применение электромагнитов в быту – индукционные плиты. Катушка наводит в металлической посуде переменный высокочастотный ток. Он, в свою очередь, своим тепловым действием разогревает кастрюлю. В промышленности нечто подобное используется для разогрева и плавки металлов. Только в таком случае применяются на порядки более высокие мощности и другие частоты тока.

Индукционный нагрев металла
Индуктивность как фильтр
Импульсные блоки питания, электрические двигатели и диммеры для регулировки яркости ламп накаливания выбрасывают в сеть большое количество искажений и помех. Вызвано это неравномерностью потребляемого тока. Для борьбы с подобными сетевыми шумами применяются специальные фильтры на основе конденсаторов и дросселей.
Данный узел представляет собой небольшую катушку из медного эмалированного провода диаметром 0,2-2 мм. Обмотка наматывается на ферритовый сердечник. Чаще всего он изготовлен в форме кольца, немного реже встречаются так называемые «гантельки».
Подобные фильтры имеются в компьютерных блоках питания, компактных люминесцентных лампах (иногда не ставят, экономят), на выходах сварочных инверторов.
Также фильтр может быть звуковым. Его задача – срезать определённый диапазон частот. Индуктивные свойства этого прибора таковы, что он хорошо проводит низкие частоты, а высокие – приглушает. Поэтому дроссели используют для того, чтобы до динамиков дошёл только бас. По факту ослаблено будут слышны и другие частоты. Для более эффективной работы фильтра нужны дополнительные детали: конденсаторы и операционные усилители.

Самодельный звуковой фильтр
Катушка как источник ЭДС
Китайская промышленность удивила школьников 2000-х новой игрушкой – вечным фонариком. Его не нужно было заряжать. Фонарик работал от катушки индуктивности, около которой под действием движения рук перемещался магнит. Он наводил в обмотке переменную ЭДС, которая питала осветительный прибор.
Подобное явление объясняется законом электромагнитной индукции. Если проводник (рамка) находится в переменном электромагнитном поле, то в нём начинает наводиться электродвижущая сила. Иными словами, появляется напряжение.
Закон этот совсем неигрушечный, ведь он используется в работе генераторов на подавляющем большинстве электростанций, в том числе любые ТЭЦ, ГЭС, АЭС и ветряки. По подобному принципу работают динамомашины, питающие фары велотранспорта.
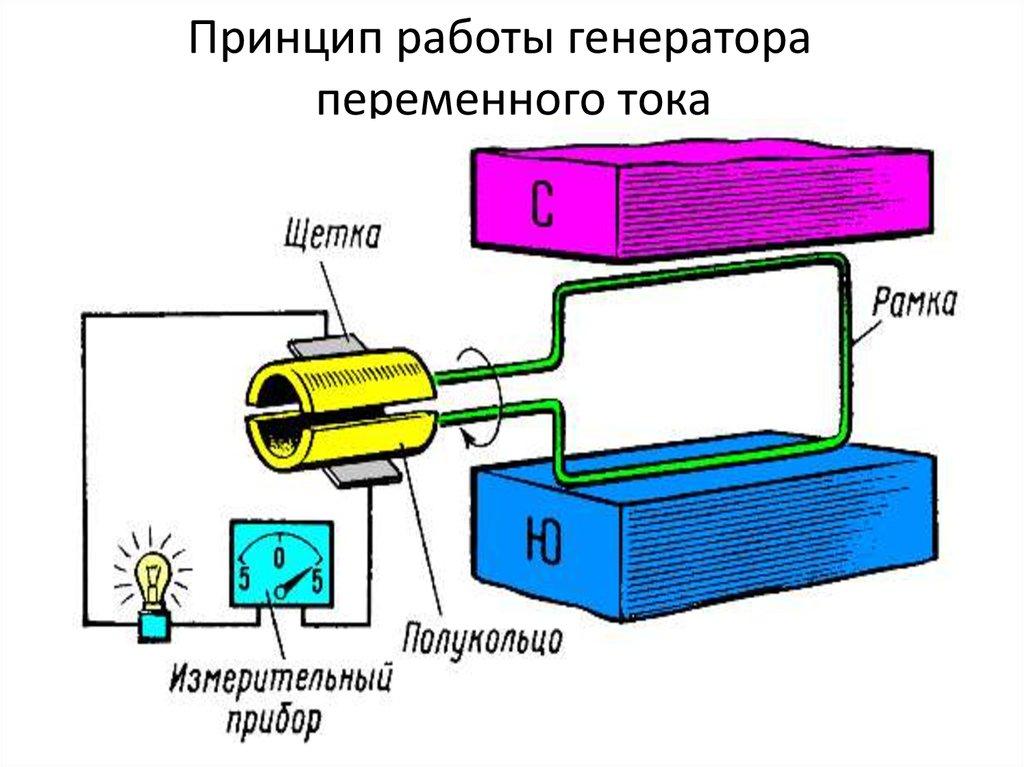
Принцип работы генератора
Две катушки – трансформатор
Ещё одно распространённое применение – это электрический трансформатор. Конструктивно он состоит из двух и более катушек, расположенных на одном железном или ферритовом сердечнике. Подобный агрегат работает только с переменным напряжением. Если на первичную обмотку подать ток, то он создаст в сердечнике магнитный поток. Он, в свою очередь, наведёт ЭДС во вторичной обмотке. Напряжения во входной и выходной катушках прямо зависят от количества их витков.
Таким образом, можно трансформировать 220 В из розетки в 12 В, необходимых для питания небольшой стереосистемы, или преобразовать 10 000 вольт в 220 для передачи от подстанции к жилым домам. Подобным методом можно добиться и повышения напряжения, т.е. превратить 12 В обратно в 220.
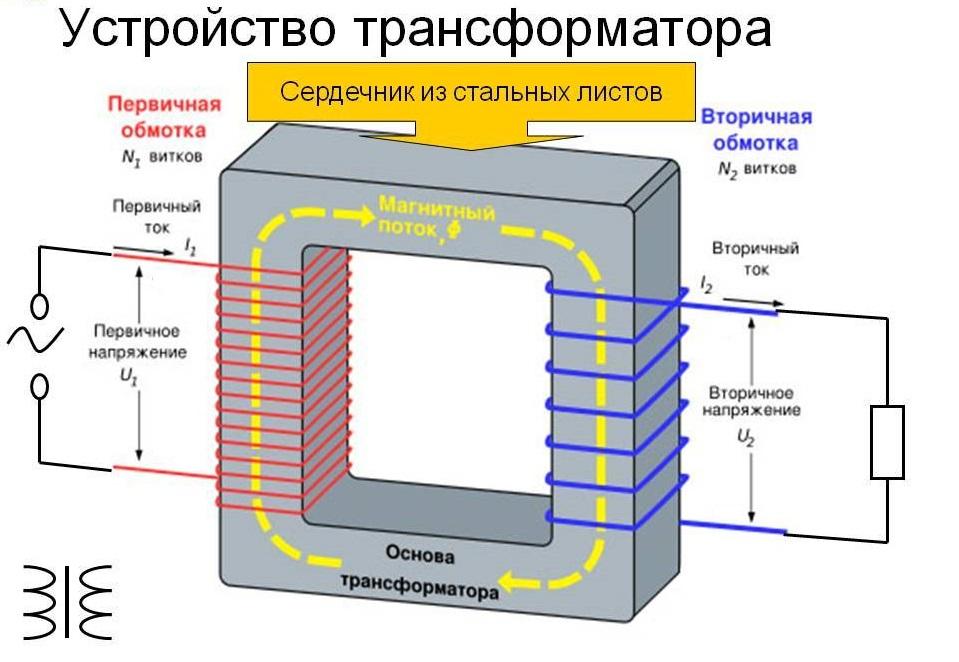
Устройство трансформатора
Катушка индуктивности — элемент колебательного контура
Сейчас это уже редкость, но раньше для подстройки нужной радиостанции использовали колебательный контур. Он состоит из двух элементов, включенных параллельно: катушки индуктивности и переменного конденсатора. Работая в паре, они способны выделить из множества окружающих сигналов именно тот, который требуется. При попадании на антенну приёмника нужной частоты электромагнитных волн колебательный контур входит в резонанс. Процесс сопровождается лавинообразным увеличением ЭДС. Частота, на которой это происходит, зависит от индуктивности катушки и ёмкости конденсатора.
Катушка индуктивности – дроссель ДРЛ ламп
Несмотря на то, что освещение улиц и промышленных предприятий стремительно переходит на LED светильники, по СНГ всё ещё осталось огромное количество мест, где используются устаревшие дуговые ртутные люминесцентные лампы типа ДРЛ. Более всего они распространены в мелких городах и на второстепенных улицах. Их можно узнать по характерному холодно-белому свету и долгому розжигу.
ДРЛ лампы не способны работать без пускорегулирующего дросселя. Он обладает высоким индуктивным сопротивлением и призван ограничить пусковой ток осветительного прибора. Дроссели для ламп подбираются, исходя из их мощности. Наиболее распространённые номиналы – 250, 400 и 1000 Вт. Информация о мощности указывается на самом дросселе. Там же можно найти схемы включения.
Из вышесказанного можно подчеркнуть, что катушка индуктивности является консервативным и давно освоенным на практике электронным компонентом. Однако спрос на его применение по-прежнему не спадает. Поэтому знания, необходимые для расчета катушек и их правильного включения, необходимы каждому специалисту, имеющему дело с электроникой.
Видео
Катушка индуктивности
Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Такая система способна накапливать магнитную энергию при протекании электрического тока.
Устройство
Устройство обычно представляет собой винтовую, спиральную или винтоспиральную катушку из одножильного или многожильного изолированного провода, намотанного на цилиндрический, тороидальный или прямоугольный каркас из диэлектрика или плоскую спираль, волну или полоску печатного или другого проводника. Также бывают и бескаркасные катушки. Намотка может быть как однослойной (рядовая и с шагом), так и многослойная (рядовая, внавал, «универсал»). Намотка «универсал» имеет меньшую паразитную ёмкость.
Для увеличения индуктивности применяют сердечники из ферромагнитных материалов: электротехнической стали, пермаллоя, карбонильного железа, ферритов. Также сердечники используют для изменения индуктивности катушек в небольших пределах.
Свойства катушки индуктивности
Катушка индуктивности в электрической цепи хорошо проводит постоянный ток и в то же время оказывает сопротивление переменному току, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению.
Катушка индуктивности
обладает реактивным
сопротивлением величина которого равна: 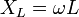 ,
где
,
где 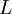 —
индуктивность катушки,
—
индуктивность катушки,  — циклическая
частота протекающего тока. Соответственно, чем
больше частота тока, протекающего через
катушку, тем больше её сопротивление.
— циклическая
частота протекающего тока. Соответственно, чем
больше частота тока, протекающего через
катушку, тем больше её сопротивление.
При протекании тока катушка запасает
энергию, равную работе, которую необходимо
совершить для установления текущего
тока 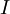 .
Величина этой энергии равна
.
Величина этой энергии равна

При изменении тока в катушке возникает ЭДС самоиндукции, значение которой
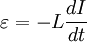
Характеристики катушки индуктивности
] Индуктивность
Основным параметром катушки индуктивности является её индуктивность, которая определяет, какой поток магнитного поля создаст катушка при протекании через неё тока силой 1 ампер. Типичные значения индуктивностей катушек от десятых долей мкГн до десятков Гн.
Индуктивность соленоида

Индуктивность торойда
Индуктивность катушки пропорциональна линейным размерам катушки, магнитной проницаемости сердечника и квадрату числа витков намотки. Индуктивность катушки, намотанной на тороидальном сердечнике
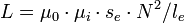
где:
μ0 — магнитная постоянная
μi — магнитная проницаемость материала сердечника (зависит от частоты)
se — площадь сечения сердечника
le — длина средней линии сердечника
N — число витков
При последовательном соединении катушек общая индуктивность равна сумме индуктивностей всех соединённых катушек.

При параллельном соединении катушек общая индуктивность равна

Сопротивление потерь
В катушках индуктивности помимо основного
эффекта взаимодействия тока и магнитного
поля наблюдаются паразитные эффекты,
вследствие которых сопротивление
катушки не является чисто реактивным.
Наличие паразитных эффектов ведёт к
появлению потерь в катушке, оцениваемых
сопротивлением потерь  .
Потери складываются из потерь в проводах,
диэлектрике, сердечнике и экране.
.
Потери складываются из потерь в проводах,
диэлектрике, сердечнике и экране.
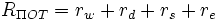
Потери в проводах
Потери в проводах вызваны тремя причинами:
Во-первых, провода обмотки обладают омическим (активным) сопротивлением.
Во-вторых, сопротивление провода обмотки переменному току возрастает с ростом частоты, что обусловлено скин-эффектом, суть которого состоит в том, что ток протекает не по всему сечению проводника, а по кольцевой части поперечного сечения.
В третьих, в проводах обмотки, свитой в спираль, проявляется эффект близости, суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля к периферии провода, прилегающей к каркасу, в результате чего сечение, по которому протекает ток, принимает серповидный характер, что ведёт к дополнительному возрастанию сопротивления провода.
Потери в диэлектрике
Потери в диэлектрике обусловлены тем, что между соседними витками катушки существует паразитная ёмкость, что приводит к утечкам переменного тока между витками.
Потери в сердечнике
Потери в сердечнике складываются из потерь на вихревые токи, потерь на гистерезис и начальных потерь.
Потери в экране
Потери в экране обусловлены тем, что ток, протекающий по катушке, индуцирует ток в экране.
Добротность
С сопротивлениями потерь тесно связана другая характеристика — добротность. Добротность катушки индуктивности определяет отношение между активным и реактивным сопротивлениями катушки. Добротность равна
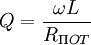
Практически величина добротности лежит в пределах от 30 до 200. Повышение добротности достигается оптимальным выбором диаметра провода, увеличением размеров катушки индуктивности и применением сердечников с высокой магнитной проницаемостью и малыми потерями, намоткой вида «универсаль», применением посеребрёного провода, применением многожильного провода вида «литцендрат».
Температурный коэффициент индуктивности (ТКИ)
ТКИ — это параметр, характеризующий зависимость индуктивности катушки от температуры.
Температурная нестабильность индуктивности обусловлена целым рядом факторов: при нагреве увеличивается длина и диаметр провода обмотки, увеличивается длина и диаметр каркаса, в результате чего изменяются шаг и диаметр витков; кроме того при изменении температуры изменяются диэлектрическая проницаемость материала каркаса, что ведёт к изменению собственной ёмкости катушки.
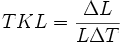
Разновидности катушек индуктивности
Контурные катушки индуктивности
Эти катушки используются совместно с конденсаторами для получения резонансных контуров. Они должны иметь высокую стабильность, точность и добротность.
Катушки связи
Такие катушки применяются для обеспечения индуктивной связи между отдельными цепями и каскадами. Такая связь позволяет разделить по постоянному току цепи базы и коллектора и т. д. К таким катушкам не предъявляются жёсткие требования на добротность и точность, поэтому они выполняются из тонкого провода в виде двух обмоток небольших габаритов. Основными параметрами этих катушек являются индуктивность и коэффициент связи.
Вариометры
Это катушки, индуктивность которых можно изменять в процессе эксплуатации для перестройки колебательных контуров. Они состоят из двух катушек, соединённых последовательно. Одна из катушек неподвижная (статор), другая располагается внутри первой и вращается (ротор). При изменении положения ротора относительно статора изменяется величина взаимоиндукции, а следовательно, индуктивность вариометра. Такая система позволяет изменять индуктивность в 4 − 5 раз. В ферровариометрах индуктивность изменяется перемещением ферромагнитного сердечника.
Дроссели
Это катушки индуктивности, обладающие высоким сопротивлением переменному току и малым сопротивлением постоянному. Обычно включаются в цепях питания усилительных устройств. Предназначены для защиты источников питания от попадания в них высокочастотных сигналов. На низких частотах они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники.
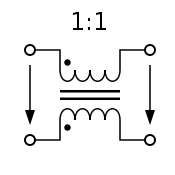
Сдвоенный дроссель
Сдвоенные дроссели
две намотанных встречно катушки индуктивности, используются в фильтрах питания. За счёт встречной намотки и взаимной индукции более эффективны при тех же габаритных размерах. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания; в дифференциальных сигнальных фильтрах цифровых линий, а также в звуковой технике.
Применение катушек индуктивности
Катушки индуктивности (совместно с конденсаторами и/или резисторами) используются для построения различных цепей с частотно-зависимыми свойствами, в частности, фильтров, цепей обратной связи, колебательных контуров и т. п..
Катушки индуктивности используются в импульсных стабилизаторах как элемент, накапливающий энергию и преобразующий уровни напряжения.
Две и более индуктивно связанные катушки образуют трансформатор.
Катушка индуктивности, питаемая импульсным током от транзисторного ключа, иногда применяется в качестве источника высокого напряжения небольшой мощности в слаботочных схемах, когда создание отдельного высокого питающего напряжения в блоке питания невозможно или экономически нецелесообразно. В этом случае на катушке из-за самоиндукции возникают выбросы высокого напряжения, которые можно использовать в схеме, например, выпрямив и сгладив.
Катушки используются также в качестве электромагнитов.
Катушки применяются в качестве источника энергии для возбуждения индуктивно-связанной плазмы.
Для радиосвязи — излучение и приём электромагнитных волн (магнитная антенна, кольцевая антенна).
Для разогрева электропроводящих материалов в индукционных печах.
Как датчик перемещения: изменение индуктивности катушки может изменяться в широких пределах перемещением (вытаскиванием) сердечника.
Катушка индуктивности используется в индукционных датчиках магнитного поля. Индукционные магнитометры были разработаны и широко использовались во времена Второй мировой войны.[3]
Активное сопротивление, индуктивность, емкость
а) Активное сопротивление R, r – это идеализированный элемент цепи, в котором происходят необратимые превращения электрической энергии в тепловую:
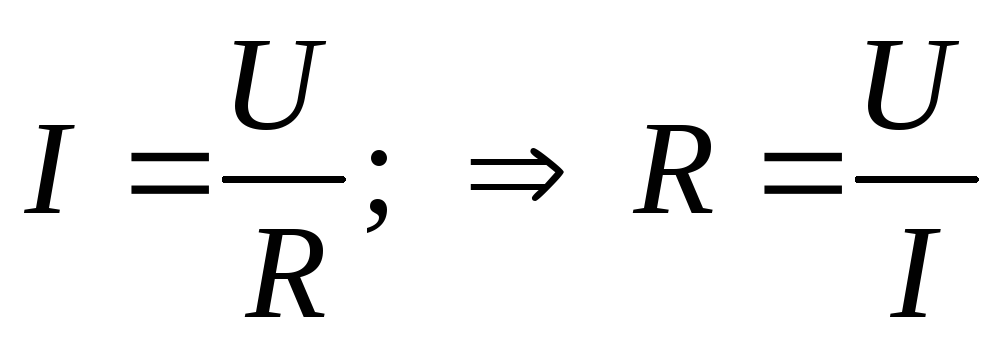 ,
(3.5)
,
(3.5)
 А.
А.
б) Индуктивность L – идеализированный элемент цепи, который характеризуется способностью накапливать энергию магнитного поля. Индуктивность численно равна отношению потокосцепления к току, которым это потокосцепление обусловлено:
 ,
(3.6)
,
(3.6)
где 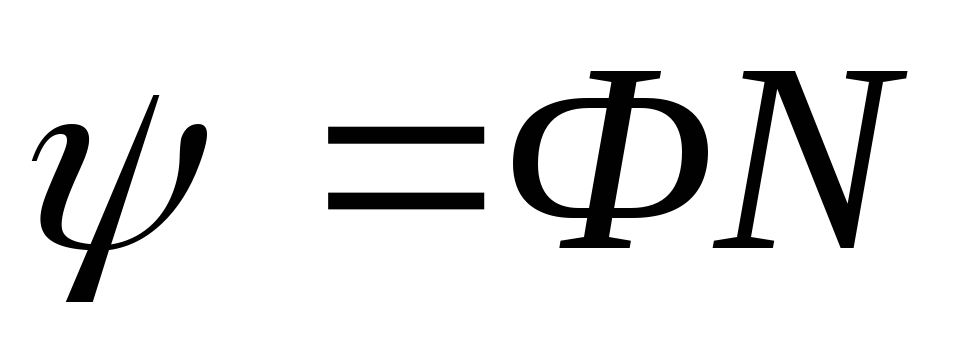 — поток сцепления катушки индуктивности,
— поток сцепления катушки индуктивности,
N –число витков катушки,
Ф– магнитныйпоток.
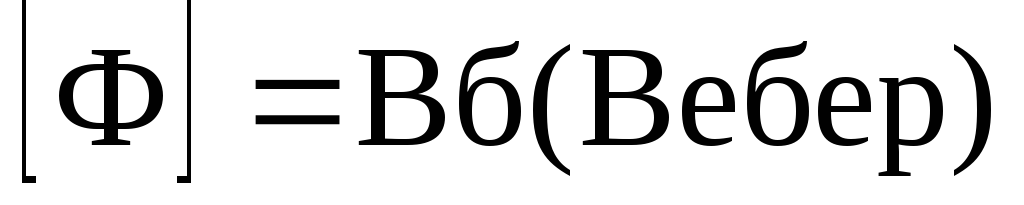 .
.
в) Емкость C– идеализированный элемент электрической цепи, который характеризуетсяспособностью накапливать энергию электрического поля.
 ,
(3.7)
,
(3.7)
где 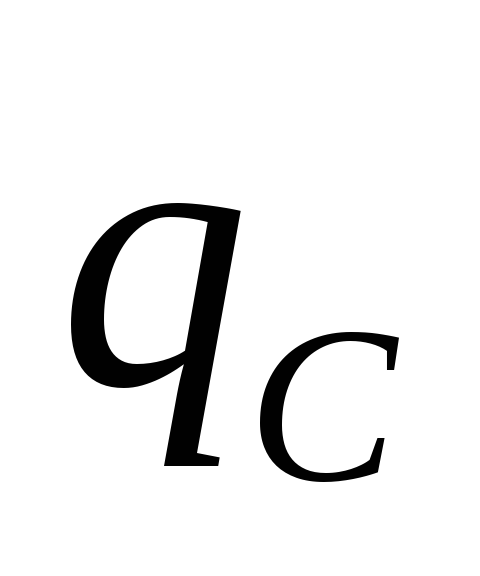 –
заряд на обкладках или пластинах
конденсатора,
–
заряд на обкладках или пластинах
конденсатора,
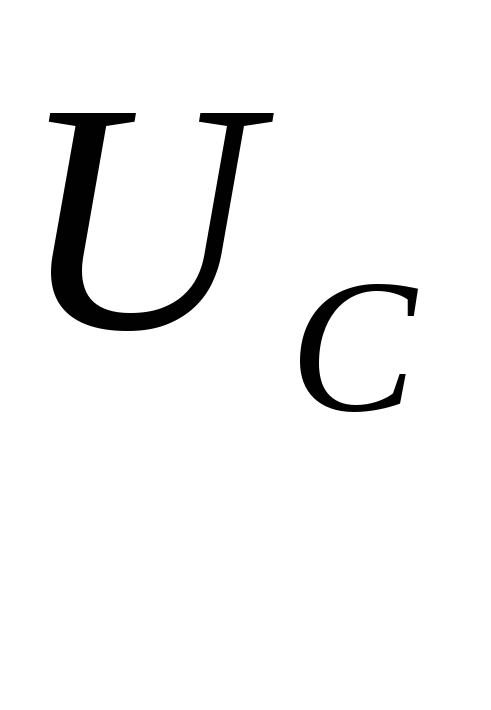 – разность потенциалов между пластинами
конденсатора.
– разность потенциалов между пластинами
конденсатора.
Емкость
С – не зависит от 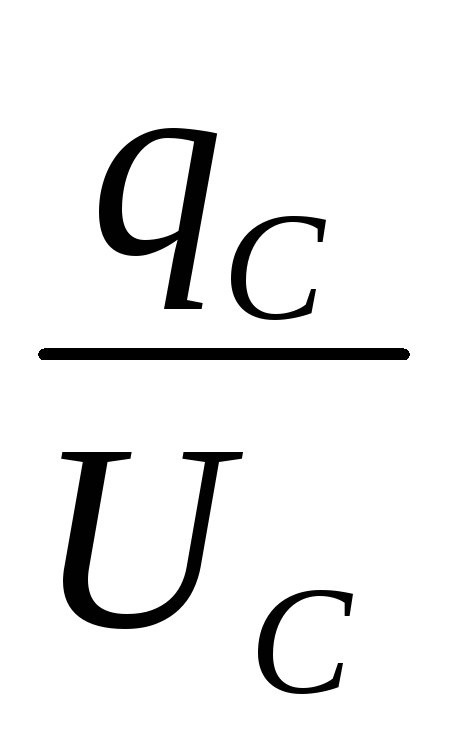 ,
а определяется размерами, формой
конденсатора, а также диэлектрическими
свойствами среды, находящейся между
обкладками конденсатора.
,
а определяется размерами, формой
конденсатора, а также диэлектрическими
свойствами среды, находящейся между
обкладками конденсатора.
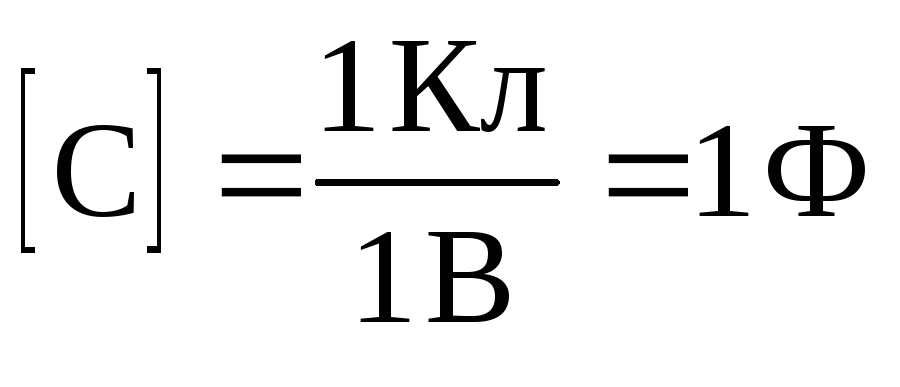 .
.
Действующее значение переменного тока
Колебания, возникающие под воздействием внешней периодически изменяющейся ЭДС, называются вынужденными электромагнитными колебаниями. Установившиеся вынужденные электромагнитные колебания можно рассматривать как протекание переменного тока в цепи, содержащей резистор, катушку индуктивности и конденсатор.
На рис. 3.5 представлен график переменного синусоидального тока.
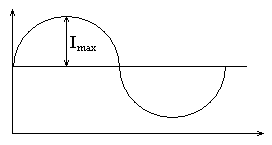
Рис. 3.5. График переменного тока
Действующее значение переменного тока равно такому значению постоянного тока, которое за время, равное периоду переменного тока, выделяет в том же сопротивлении такое же количество теплоты, что и данный ток. Определяется по формуле 3.8.
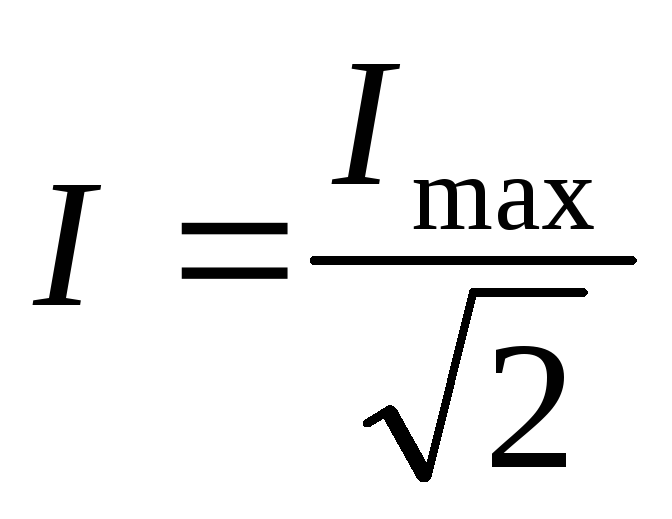 . (3.8)
. (3.8)
Активное, реактивное и полное сопротивление в цепях переменного тока
Ток в активном сопротивлении
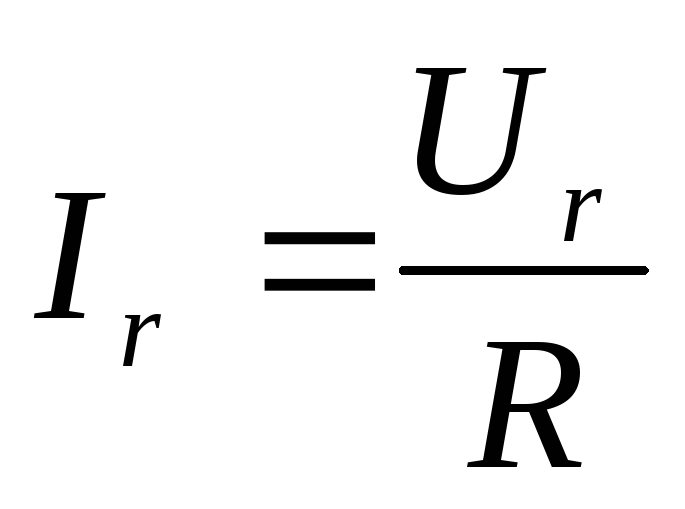 ,
(3.9)
,
(3.9)
где Ir, Ur — действующие значения тока и напряжения на активном сопротивлении R.
Сдвиг фаз между током и напряжением на резисторе равен нулю (см. рис. 3.6).
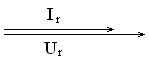
Рис. 3.6. Векторная диаграмма тока и напряжения на резисторе
Ток в индуктивности
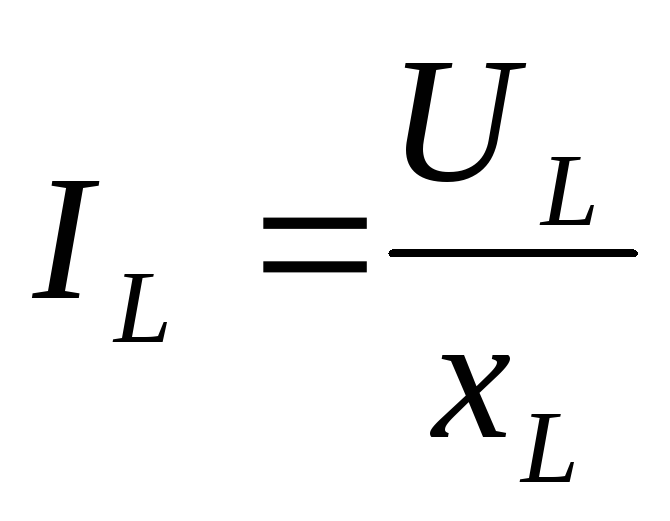 ,
(3.10)
,
(3.10)
где IL, UL — действующие значения тока и напряжения на индуктивном сопротивлении хL.
 ,
(3.11)
,
(3.11)
где ω – циклическая частота, равна нуль, поэтому при постоянном токе катушка индуктивности не имеет сопротивления.
В индуктивном сопротивлении ток отстает от напряжения на угол 90° (рис. 3.7).
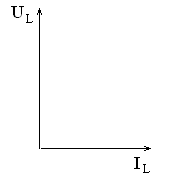
Рис. 3.7. Векторная диаграмма тока и напряжения на индуктивности
Величина хC называется реактивным емкостным сопротивлением.
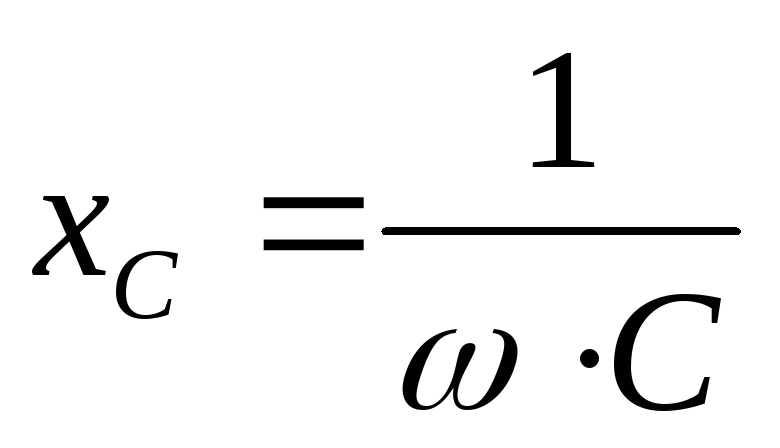 .
(3.12)
.
(3.12)
При емкостном сопротивлении напряжение отстает от тока на угол 90° (рис. 3.8).
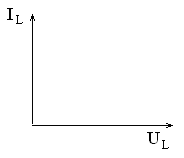
Рис. 3.8. Векторная диаграмма тока и напряжения на емкости
Для постоянного тока ω равна нулю и хC=∞, т.е. постоянный ток через конденсатор течь не может.
 ,
(3.13)
,
(3.13)
где Z – полное сопротивление цепи,
х – реактивное сопротивление:  .
.
Индуктивное сопротивление: обозначение, сопротивление катушки формула
Когда в цепи нарастает или уменьшается ток, электромагнитное поле создает противодействующую электродвижущую силу. Это явление порождается индуктивностью катушки. Индуктивное сопротивление воздействует только на переменный ток, быстрые изменения которого порождают противодействующую силу. В статье будет более подробно рассказано о природе этого явления.
Что зовется индуктивным сопротивлением
Когда на катушку подают переменное напряжение, ток, проходящий по ней, меняется согласно поданному напряжению. Это служит причиной изменения магнитного поля, создающего электродвижущую силу, препятствующую происходящему.

Схема для измерения
В такой цепи имеется зависимость электрических параметров от двух видов: обычного и индуктивного. Они обозначаются, соответственно, как R и XL.
На обычном происходит выделение мощности. Однако на реактивных элементах она является нулевой. Это связано с постоянным изменением направления переменного тока.
В течение одного периода колебаний энергия дважды закачивается в катушку и столько же раз возвращается в источник.

Определение индуктивности
От каких факторов зависит сопротивление
Изменение силы тока создает электромагнитное поле переменной интенсивности. Результатом его воздействия на проводник является противодействие происходящему изменению тока.
Это противодействие называется реактивным сопротивлением. Существуют две его разновидности: индуктивная и емкостная. Первая создается при наличии в схеме индуктивного элемента, вторая — конденсатора.
В ситуации, когда в цепи присутствует катушка, ее реакция усиливается по мере увеличения частоты.

Цепь, в которой возникает индукция
В случае, когда ее индуктивность уменьшается, то противодействующая сила также становится меньше. При увеличении она возрастает.
Индуктивное сопротивление существенно связано с тем, какую форму принимает проводник. Оно имеется также и у отдельного провода, лежащего прямо. Однако если рядом будет еще один, то он будет оказывать воздействие дополнительно, что повлияет на рассматриваемую величину.
Рассматриваемую характеристику отдельного провода можно определять в зависимости от его толщины, но оно никак не связано с его сечением.

Принцип действия электродвижущей силы
Катушка индуктивности
Он представляет собой изолированный провод, многократно намотанный вокруг сердечника.
Обычно каркас имеет цилиндрическую или тороидальную форму.
Индуктивность рассматривается в качестве основной характеристики катушки. Это качество выражает способность элемента осуществлять преобразование переменного тока в магнитное поле.
Важно! Магнитные свойства существуют даже у одиночного провода, при условии, что изменяется проходящий через него ток. Воздействие поля направлено так, чтобы противодействовать его изменению. Если он будет увеличиться, поле будет его тормозить, а если ослабевать — усиливать.

Катушки индуктивности
Определение направления силовых линий подчиняется «правилу большого пальца»: если у сжатой в кулак руки большой палец указывает в направлении изменения силы тока, то сомкнутые пальцы подсказывают направление силовых линий поля.
Таким образом в том случае, если провод многократно намотан на цилиндрическое основание, то силовые линии от разных витков складываются и проходят через ось.
Для того, чтобы многократно увеличить индуктивность, в центр цилиндра помещают сердечник из ферромагнитного материала.
Индуктивное сопротивление – единицы измерения
Измерение этой величины производится в омах. Здесь используются такая же единица измерения, как и для резистора, несмотря на то, что у них различная природа. Рассматриваемая величина порождается электродвижущей силой, противодействующей происходящему изменению. Обычное возникает в связи с рассеиванием энергии при прохождении электронов по проводнику.

Магнитное поле индуктивного элемента
Индуктивное сопротивление – как его найти
Реальная катушка имеет не только реактивное, но и обычное сопротивление. Индуктивное сопротивление определяется по формуле:
XL=2*П*v*L
Здесь употреблены следующие обозначения:
- XL – рассматриваемая величина.
- Символом «П» обозначено число Пи.
- V представляет собой частоту.
- L — это обозначение величины индуктивности.
Надо отметить, что величина (2*П*v) представляют собой круговую частоту, которую обозначают греческим символом «омега».

Катушки с различными сердечниками
Рассматриваемая величина подчиняется закону Ома. Формула выглядит так:
I = U / XL
I, U представляют собой ток и напряжение, XL – это индуктивное сопротивление.

Конфигурация магнитного поля катушки
Для определения искомой величины можно воспользоваться приведенными формулами. При этом можно воспользоваться амперметром и вольтметром. Первый из них надо включить последовательно, второй — параллельно.
При этом необходимо учитывать следующее. На самом деле, в цепи, в которую включена индуктивность, действует два вида сопротивления: активное и реактивное. Измерив ток и напряжение, можно определить их результирующую величину. Нужно помнить, что она не является их простой суммой.
Дело в том, что в переменной цепи, где имеется только катушка и нет конденсатора, напряжение находится впереди тока на четверть периода колебания. Эта величина равна 90 градусам.
Полное сопротивление определяется следующим образом. Для этого необходимо нарисовать соответствующую диаграмму. Если по горизонтали отложить величину обычного, а по вертикали — реактивного, а затем по этим векторам построить прямоугольник, то длина его диагонали будет равна полному значению.

Магнитное поле провода
К примеру, если подобрать элементы цепи таким образом, чтобы по абсолютной величине обе этих величины были равны, то искомая часть определится как их полное значение, умноженное на квадратный корень из двух.
Для того, чтобы получить информацию о зависимости индуктивного сопротивления от частоты, возможно воспользоваться осциллографом.
При использовании переменного тока необходимо учитывать не только обычное, но и индуктивное сопротивление. Оно возникает в том случае, если в электрической цепи присутствует катушка.
Реальная катушка в цепи переменного тока


Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью Q.
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.
Схема замещения катушки с последовательным соединением элементов
В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.
Активное сопротивление определяется величиной мощности потерь
R = P/I2


а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением i = Imsinωt. Требуется определить напряжение в цепи и мощность.
При переменном токе в катушке возникает э. д. с. самоиндукции eL поэтому ток зависит от действия приложенного напряжения и эдс eL. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид:

Приложенное к катушке напряжение состоит из двух слагаемых,одно из которых uR равно падению напряжения в активном сопротивлении, а другое uL уравновешивает эдс самоиндукции.


В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б).
Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам полученных в этих предыдущих двух (первая, вторая) статьях получим — uR совпадает по фазе с током, UL опережает ток на 90°.
Поэтому:
u = R*Imsinωt + ωLImsin(ωt+π/2).
Векторная диаграмма реальной катушки и полное её сопротивление
Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения
UmR = RIm; UmL = ωLIm ,
а действующие величины
UR = RI; UL = XLI .
Вектор общего напряжения
U = UR + UL
Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Mi и напряжения Мu.
За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока Ψi =0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.
Вектор UR по направлению совпадает с вектором тока I, а вектор UL направлен перпендикулярно вектору I с положительным углом.
Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ>0, но φ<90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях UR и UL :
UR = Ucosφ


Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Для катушки по схеме рис. 13.9 при Ua = UR
U = Usinφ (13.14)
Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается Up. Для катушки Up = UL


При токе i = Imsinωt уравнение напряжения можно записать на основании векторной диаграммы в виде
U = Umsin(ωt+φ)
Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное R = UR/I и индуктивное XL = UL/I, сопротивления, а гипотенузой величина Z = U/I.
Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи.
Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени.
Из треугольника сопротивлений следует


Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома:


Из треугольников сопротивления и напряжения определяются
cosφ = UR/U = R/Z; sinφ = UL/U = XL/Z; tgφ = UL/UR = XL/R. (13.18)
Мощность реальной катушки


Мгновенная мощность катушки
p = ui = Umsin(ωt+φ) * Imsinωt
Из графика мгновенной мощности (рис. 13.11) видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется. Относительно некоторой оси t’, сдвинутой параллельно оси t на величину Р, график мгновенно мощности является синусоидальной функцией двойной частоты.
При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).
Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).
Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.
Согласно выводам полученных в этих предыдущих (первая, вторая) статьях — в активном сопротивлении P = URI Q = 0; а в индуктивном Р = 0; Q = ULI.
Активная мощность всей цепи равна активной мощности в сопротивлении R, а реактивная — реактивной мощности в индуктивном сопротивлении XL. Подставляя значения UR = Ucosφ и UL = Usinφ, определяемые из треугольника напряжений по формулам (13.18), получим:
P = UIcosφ (13.19)
Q = UIsinφ (13.20)
Кроме активной и реактивной мощностей пользуются понятием полной мощности S, которая определяется произведением действующих величин напряжения и тока цепи;
S = UI = I2Z (13.21)
Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):

 (13.22)
(13.22)
Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток. Из треугольника мощностей можно определить
cosφ = P/S; sinφ = Q/S; tgφ = Q/P. (13.23)
Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В · А).
Активная мощность Р меньше или равна полной мощности цепи.
Отношение активной мощности цепи к ее полной мощности P/S =
= cosφ называют коэффициентом мощности.
Назначение приемников электрической энергии — преобразование
ее в другие виды энергии. Поэтому колебания энергии в цепи не только
бесполезны, но и вредны, так как при этом в приемнике не совершается
полного преобразования электрической энергии в работу или тепло,
а в соединительных проводах она теряется.
Схема замещения реальной катушки в с параллельным соединением элементов


Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной BL проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее.
Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.
Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством
I = IG + IL (13.24)
Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: IG —ток в ветви с активной проводимостью, по фазе совпадает с напряжением; IL — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.
Вектор тока I и его составляющие IG и IL образуют прямоугольный треугольник, поэтому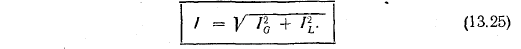
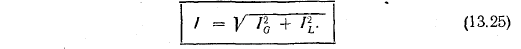
Составляющая тока в активном элементе
IG = Icosφ
Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается Iа. Для катушки по схеме на рис. 13.12, б Ia = IG.
Составляющая тока в реактивном элементе
IL = Isinφ
Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки Iр = IL .
Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная G = IG/U и индуктивная ВL = IL/U проводимости, а гипотенузой — величина Y = I/U, называемая полной проводимостью цепи.
Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим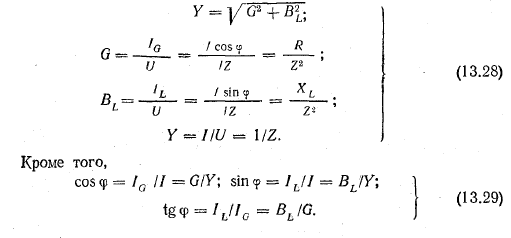
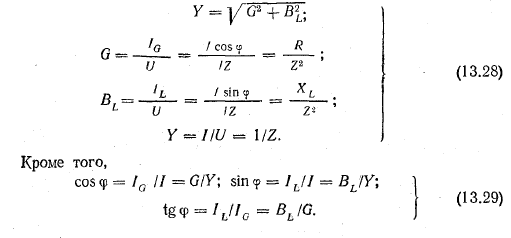
5.1 Расчет цепи с активным сопротивлением и индуктивностью
5.1.1 Рекомендации для студента
Реальные электрические цепи не могут состоять из идеальных реактивных сопротивлений, в них присутствует активное сопротивление. В цепи, с последовательно соединенными активным сопротивлением и индуктивностью (рисунок 5.1), активное напряжение совпадает по фазе с током, индуктивное напряжение опережает ток по фазе на угол 900.

При протекании тока  в электрической цепи с активным
сопротивлением и индуктивностью
справедливы следующие соотношения:
в электрической цепи с активным
сопротивлением и индуктивностью
справедливы следующие соотношения:
Треугольники напряжений, сопротивлений, мощностей.
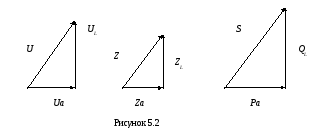
5.1.2 Примеры решения задач
Задача№ 5.1
К сети переменного напряжения 220В подключена катушка с активным сопротивлением 6 Ом и индуктивностью 50 мГн (рисунок 5.3) . Определить действующее значение тока, полную, активную и реактивную мощности.
Дано: U=220В
f =50Гц
L=50мГн
R = 6Ом
—————————
Определить: I, P, Q, S
Решение задачи
Индуктивное сопротивление катушки:
ХL=ω*L=2π*f*L;
ХL=2*π*50*10-3=15,7Ом;
Полное сопротивление цепи:
 ;
;
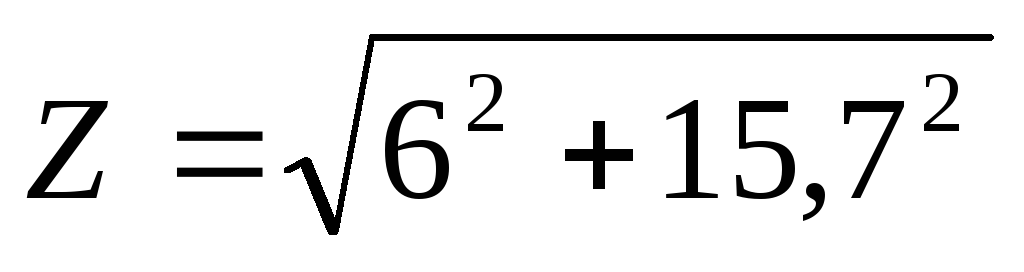 =16,8Ом;
=16,8Ом;
Ток в цепи равен:
I=U/Z;
I=220\16,8=13,1А;
Полная мощность цепи:
S=U*I;
S=220*13,1=2882ВА;
cos φ=R/Z;
cos φ =6/16,8=0,38;
sin φ=XL/Z;
sin φ= 15,7/16,8=0,93;
Активная мощность:
P=S*cosφ;
P=2882*0,38=1095,16Вт;
Реактивная мощность:
Q=S*sinφ;
Q=2882*0,93=2680 вар.
5.2 Цепь с активным сопротивлением и емкостью
5.2.1 Рекомендации для студента
В цепи (рисунок 5.4) с активным сопротивлением и емкостью напряжение на реактивном сопротивлении отстает от тока по фазе на 900.
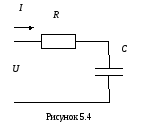
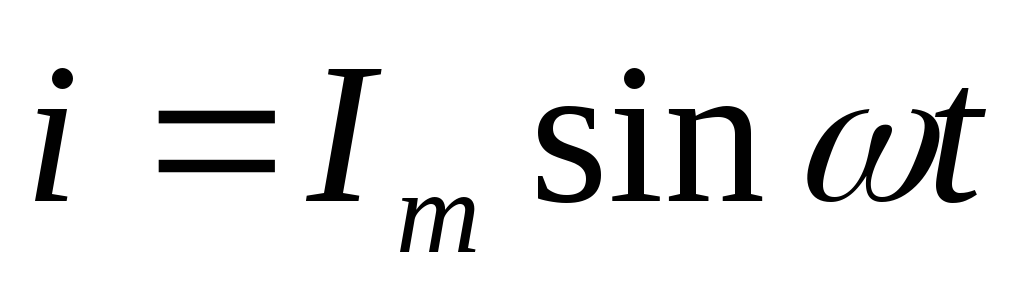 —
ток в цепи;
—
ток в цепи;
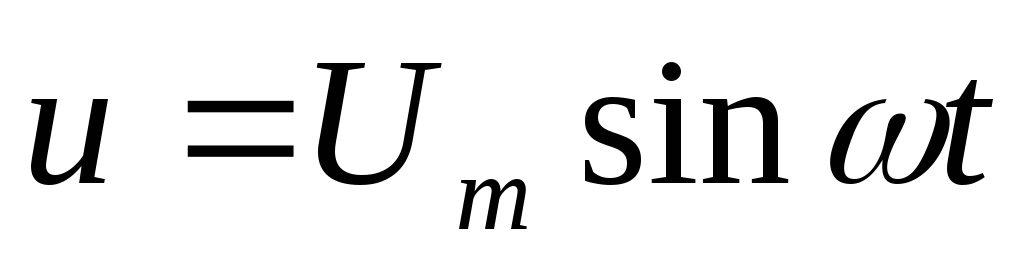 -напряжение на активном сопротивлении;
-напряжение на активном сопротивлении;
 — напряжение на емкостном сопротивлении;
— напряжение на емкостном сопротивлении;
— напряжение цепи;
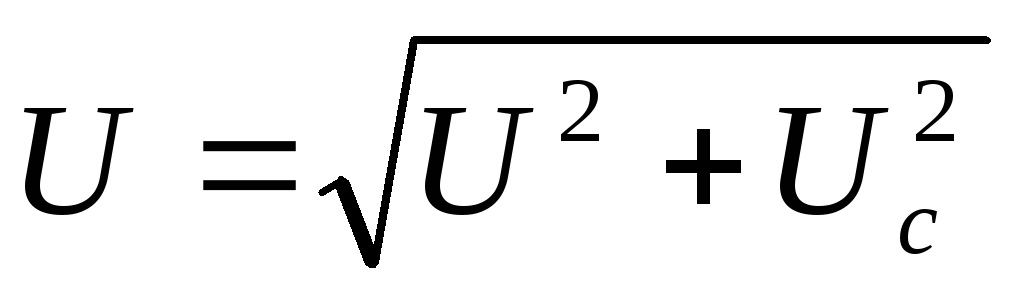 =
=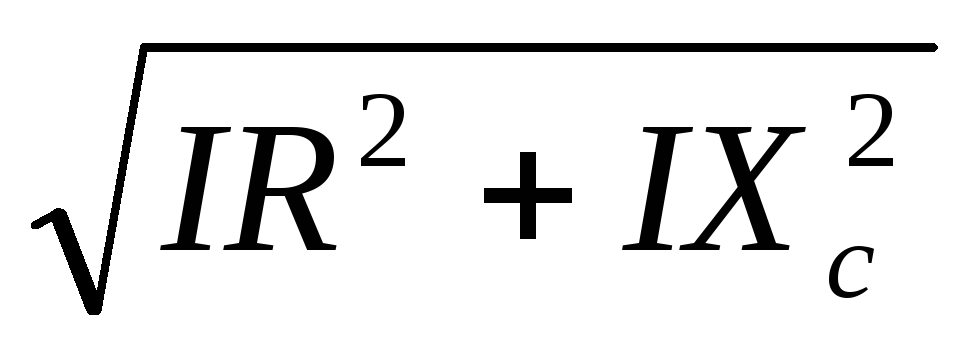 =
=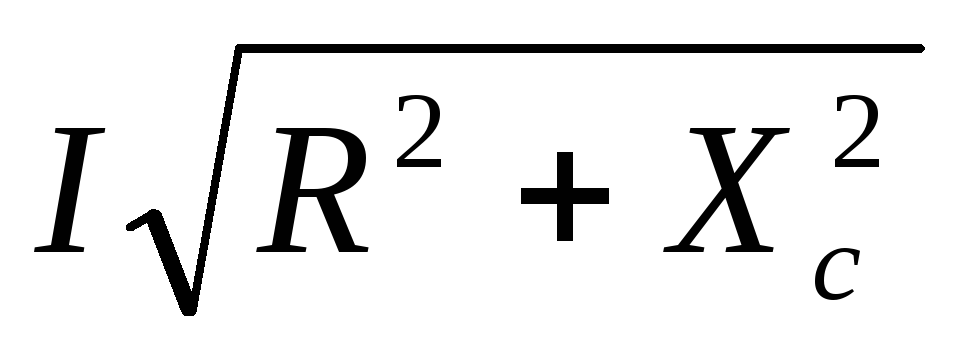 — действующее напряжение в цепи;
— действующее напряжение в цепи;
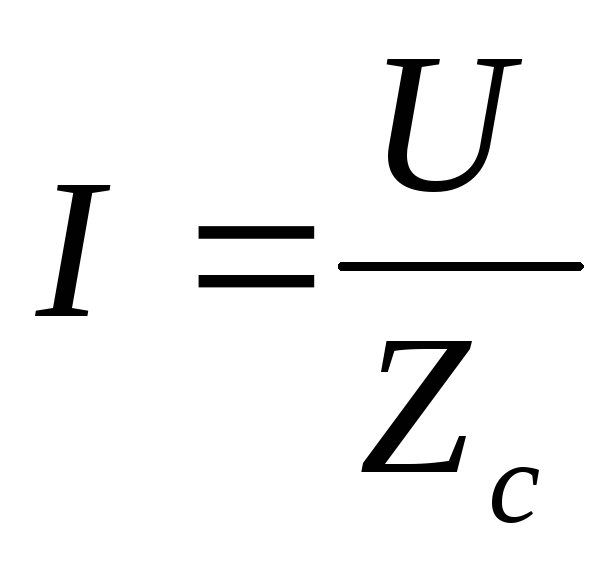 — ток в этой цепи определяется по закону
Ома;
— ток в этой цепи определяется по закону
Ома;
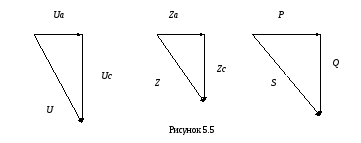
5.2.2 Примеры решения задач
Задача№5.2
В цепи переменного тока с активным сопротивлением и емкостью при частоте 100Гц измерительные приборы показывают: амперметр – 6А, вольтметр – 180В, ваттметр – 360 Вт. Определить параметры схемы замещения (рисунок 5.6) с последовательным соединением элементов, реактивную и полную мощности цепи.
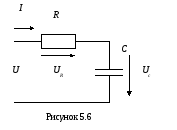
Дано: I=6А;
U=180В;
Р=360Вт;
———————-
Определить: R, Xc, Z, S, Q
Решение задачи
Определим полное сопротивление: 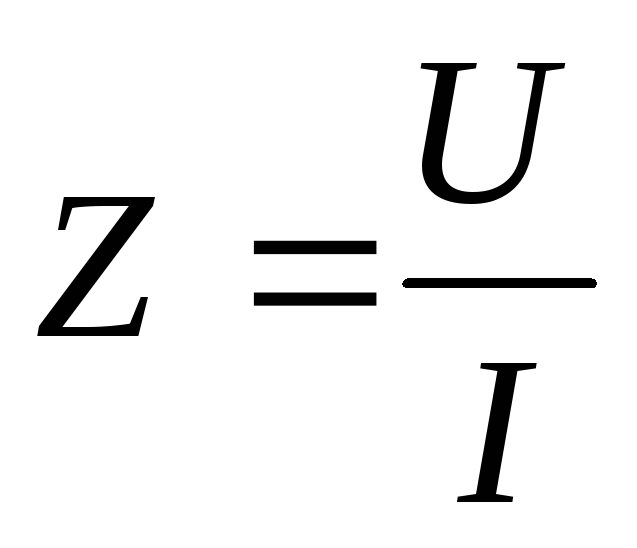
Z=180/6=30 Ом;
Активное сопротивление: R=P/I
R=360/36=10 Ом;
Емкостное сопротивление: 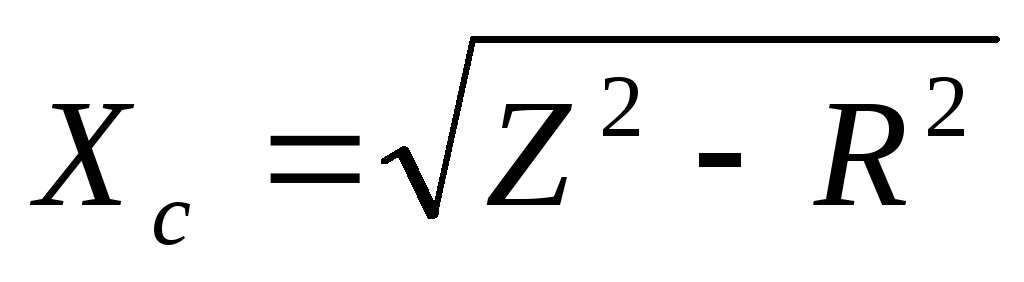 ;
;
Xc= =
28 Ом;
=
28 Ом;
Полная мощность: 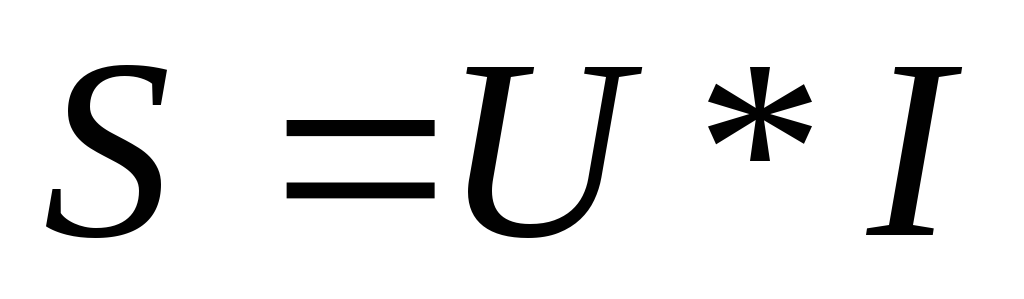 ;
;
S=180*6=1080ВА;
Реактивная мощность:  ;
;
Q= 1018
вар.
1018
вар.
Задача№5.3
В сеть переменного синусоидального тока напряжениемU=220В необходимо включить электрическую лампу напряжениемUл=127В и мощностьюРл=100Вт. Определить емкость конденсатораС, который необходимо включить последовательно с лампой, чтобы напряжение на лампе не превышало номинальногоUн=127В. На какое напряжение должен быть рассчитан конденсатор (рабочее напряжение), чтобы иметь четырехкратный запас прочности? Частота тока сетиf=50 Гц.
Дано: U=220В;
Uл=127 В;
Рл=100Вт;
f=50 Гц;
—————————
Определить: С, Uс
Решение задачи
Номинальный ток электрической лампы:
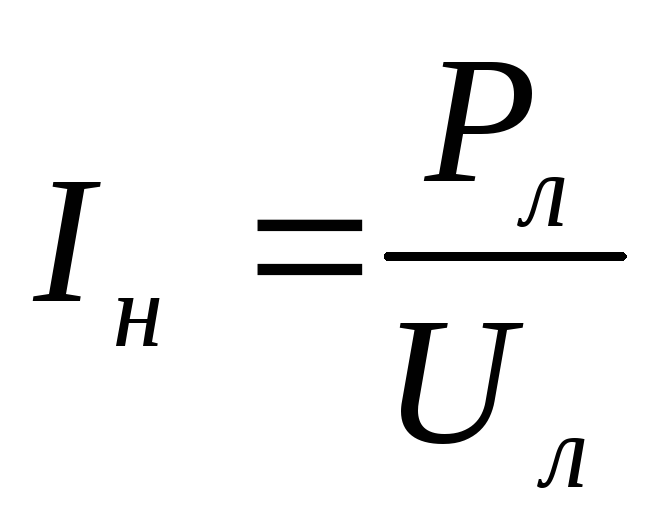 ;
;
Iн= 100/127=0,79А;
Напряжение, которое компенсируется конденсатором:
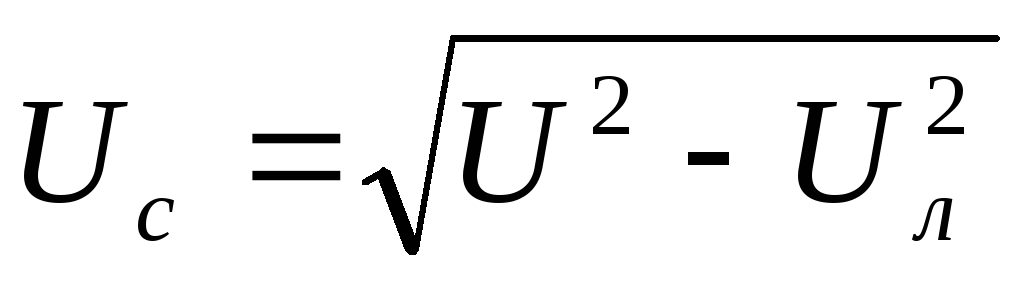 ;
;
Uc= B;
B;
Umc=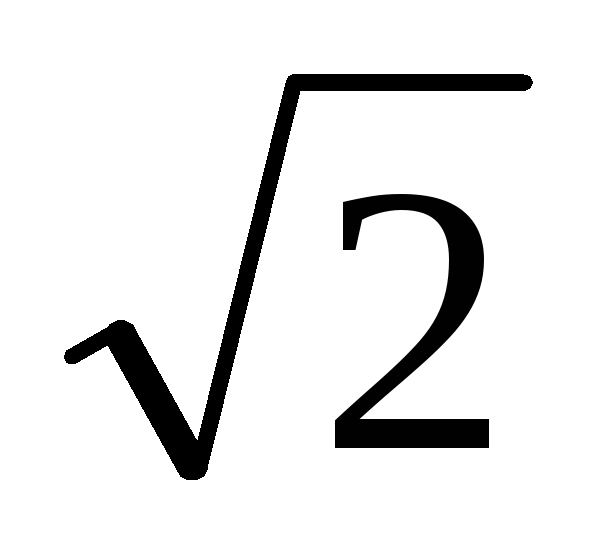 Uc;
Uc;
Umc= 1,41*180=254В;
Сопротивление конденсатора:
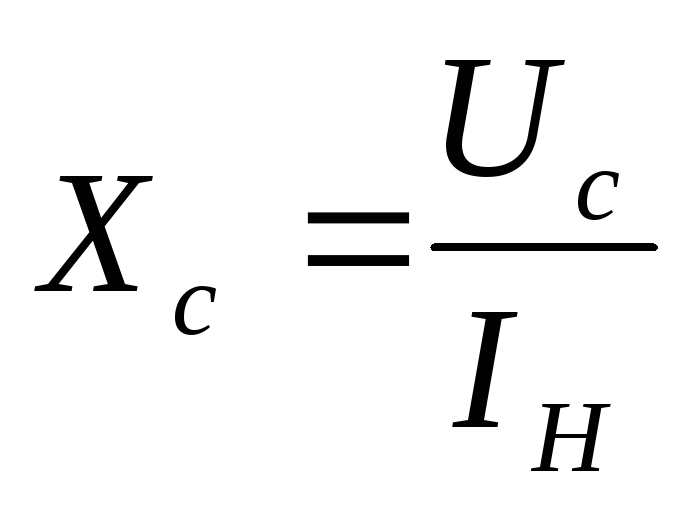 ;
;
Хс=180/0,79=227,8Ом;
Емкость такого конденсатора:
 ;
;
Обеспечение четырехкратного запаса прочности:
UР=4Umс;
Uр=4*254=1064В.
Конденсатор рассчитан на рабочее напряжение 1000 В.

