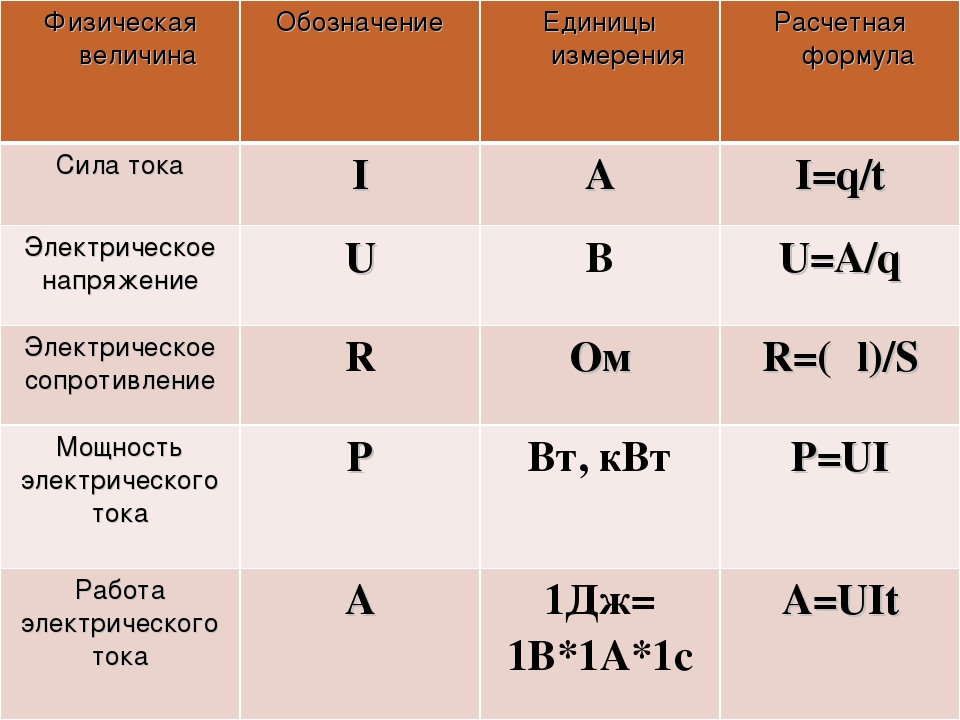
Основные физические понятия
Удельное электрическое сопротивление, или просто удельное сопротивление вещества характеризует его способность проводить электрический ток.
Единица измерения удельного сопротивления в СИ — Ом·м; также измеряется в Ом·см и Ом·мм²/м. Физический смысл удельного сопротивления в СИ: сопротивление однородного куска проводника длиной 1 м и площадью токоведущего сечения 1 м².
В технике часто применяется в миллион раз меньшая производная единица: Ом·мм²/м, равная 10-6 от 1 Ом·м: 1 Ом·м = 1*106 Ом·мм²/м. Физический смысл удельного сопротивления в технике: сопротивление однородного куска проводника длиной 1 м и площадью токоведущего сечения 1 кв.мм.
Величина удельного сопротивления обозначается символом ρ (ро). Более подробную информацию Вы сможете получить по этой ссылке в Википедии.
Временное сопротивление или предел прочности — механическое напряжение σ0(в), выше которого происходит разрушение материала. Поскольку при оценке прочности время нагружения образцов часто не превышает нескольких секунд от начала нагружения до момента разрушения, то его также называют условно-мгновенным пределом прочности, или хрупко-кратковременным пределом прочности. Более подробную информацию Вы сможете получить по этой ссылке в Википедии.
Поскольку при оценке прочности время нагружения образцов часто не превышает нескольких секунд от начала нагружения до момента разрушения, то его также называют условно-мгновенным пределом прочности, или хрупко-кратковременным пределом прочности. Более подробную информацию Вы сможете получить по этой ссылке в Википедии.
Предел текучести — механическое напряжение σт, дальше которого упругая деформация тела (исчезающая после снятия напряжения) переходит в пластическую (необратимую, когда геометрия тела не восстанавливается после снятия деформирующего напряжения).
Предел текучести соответствует площадке текучести диаграммы деформирования материала. В случае, если такая площадка отсутствует, вместо σт используется напряжение σ0,2 (читается: сигма ноль-два), которое соответствует напряжению, при котором остаточные деформации конструкции (пластические деформации) составляют 0,2 % от длины испытываемого образца. Более подробную информацию Вы сможете получить по этой ссылке в Википедии.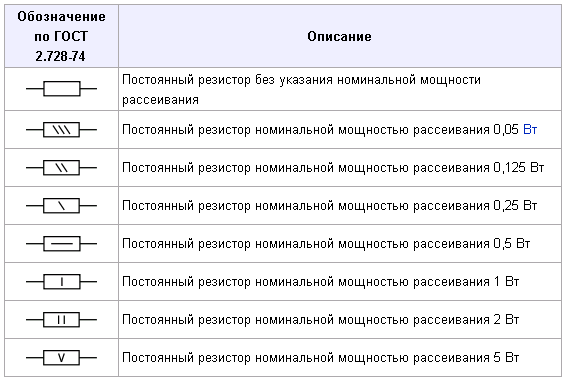
Относительное удлинение — отношение абсолютного удлинения или уменьшения, т. е. приращения длины линейного элемента или образца или части их при растяжении, к их первоначальной длине. Измеряют в долях (в процентах).
Твёрдость — свойство материала сопротивляться проникновению в него другого, более твёрдого тела, а также свойство более твёрдого тела проникать в другие материалы. Твёрдость определяется как величина нагрузки необходимой для начала разрушения материала. Различают относительную и абсолютную твёрдость. Относительная — твёрдость одного минерала относительно другого. Является важнейшим диагностическим свойством. Абсолютная, она же инструментальная — измеряется методами вдавливания. Твердость определяют различными методами: по Виккерсу, по Бринеллю, по Роквеллу и т.д. Более подробную информацию Вы сможете получить по этой ссылке в Википедии.
чем это может быть полезно?
1) Сопротивление катушки постоянному току обозначается буквой R.
Re — фактическое сопротивление катушки постоянному току. Именно это сопротивление увидит усилитель в двух случаях: когда катушка вне магнитного поля, когда катушка в состоянии покоя(не подведен ток, заклинила и т.п.). То есть, знать Re нужно только для этих вот случаев.
Измерить можно обычным мультиметром, но хороших их мало, а значит измерение в большинстве случаев будет совсем не точным. Правильно взять батарейку, на короткое время подключить к ней катушку и измерить силу тока+напряжение, а затем рассчитать Re как U/I.
Rnom — номинальное сопротивление катушки постоянному току.
Когда в любой заявке, будь то сопротивление, или мощность, или давление, или что-угодно еще, вы видите слово «номинальное» — знайте, это НЕ измеренный параметр, а приведенный, назначенный. Так, Rnom — часто это банально округленный в бОльшую сторону Re. То есть, заявка Rnom 2+2Ом на деле может означать и 1.1+1.1, и 1.9+1.9, и 1.1+1.9 Ом.
В хороших случаях, не лишенных смысла, и редких, Rnom = Zmin.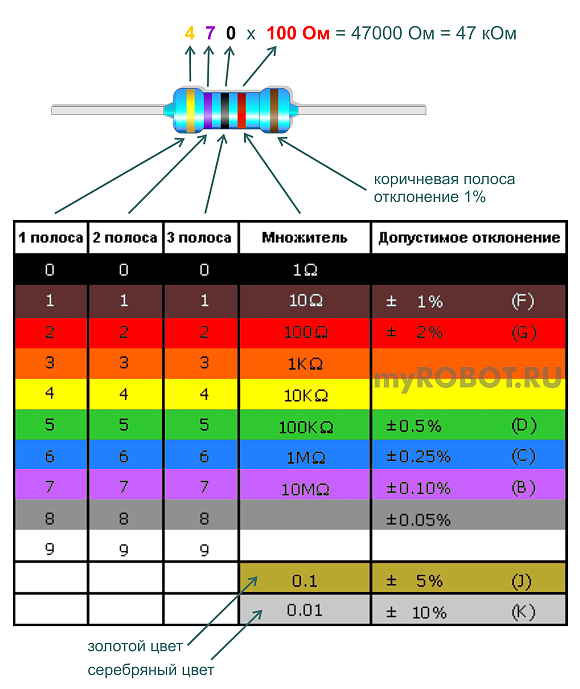 Как вы понимаете, в остальных случаях знание Re или Rnom для не профессионала, в общем-то, бесполезно. Заявляя Rnom, подавляющее большинство производителей, с одной стороны, бережет вас от поломок, а с другой — вынуждает приобретать более дорогие усилители.
Как вы понимаете, в остальных случаях знание Re или Rnom для не профессионала, в общем-то, бесполезно. Заявляя Rnom, подавляющее большинство производителей, с одной стороны, бережет вас от поломок, а с другой — вынуждает приобретать более дорогие усилители.
2) Индуктивное сопротивление обозначается буквой Z. В народе такое сопротивление называют «импеданс» («импеданс» в переводе с англ и значит «сопротивление»).
Во всех прочих случаях, кроме описанных выше, усилитель видит Z, а не R. Z — гораздо более сложный, комплексный параметр, который изменяется в зависимости от многих факторов. Однако, Z не бывает ниже Re, а выше — бывает почти всегда.
Zmin и Zmax — минимальное и максимальное сопротивление, которое увидит усилитель. Оба прямо или косвенно зависят от частоты, от хода, от мощности, от характера акустической нагрузки(и корпуса, и салона), от температуры, от конструкции динамика…
Имеет смысл измерять Z как для динамика вне оформления, так и в полностью готовой, законченной системе. Измерения проще всего выполнить путем измерения силы тока и напряжения, а затем вычислить Z через U\I.
Измерения проще всего выполнить путем измерения силы тока и напряжения, а затем вычислить Z через U\I.
Оформление не может сделать Zmin ниже, чем то, что измерено на динамике вне оформления.
В ситуации, когда катушка стремится покинуть зазор, оба эти сопротивления устремляются к Re. Зная это, возможно определять и так контролировать величину хода, что полезно во множестве случаев.
Нет никаких вариантов «предположить» Z без фактических измерений — импеданс от системы к системе сильно отличается. Вопрос «а можно ли подключать пару DD812 в 0.25» звучит глупо и без измерений не имеет ответа.
Znom или номинальный импеданс — это очередная «заявка», сделанная с теми или иными целями. Иногда Znom=Zmin*1,15, в других случаях Znom=Zmin*1,3, ну а во многих случаях — от балды.
Z-характеристика.
Если измерить импеданс на каждой частоте, то на выходе получим «Z-характеристику динамика» или «Z-кривую» или «импедансную кривую». Зная Z-кривую, можно выяснить множество моментов, полезных для проектирования системы, от подбора усилителей и до проектирования корпуса. Дайте знать если вам интересно — сделаем отдельный пост.
Дайте знать если вам интересно — сделаем отдельный пост.
Обратите внимание на комментарии к иллюстрациям.
3) Z и усилитель.
Взяли вы в руки динамик, измерили Zmin, и теперь подбираете к нему усилитель.
Мощность, как известно, является произведением силы тока на напряжение. Напряжение ведет к клипу, а ток ведет к перегреву — и то, и другое в перспективе плохо.
Т.к. напряжение и сила тока — оба описывают один и тот же процесс и не существуют друг без друга, то выбор усилителя достаточно прост. За одни и те же деньги вы выберете или надежность+меньшую мощность, или риск+большую мощность. Тут нет никаких иных вариантов, никаких чудодейственных иноземных рецептов.
Имея некий Z на частоте настройки ФИ, мы видим огромный рост ниже и выше, за которыми следуют глубокие спады. Кроссоверы сверх-высоких порядков что-то обрежут, а 1-4 порядки — нет. Поэтому, бюджетные усилители следует подбирать, ориентируясь на Zmin динамика вне оформления, а топовые модели с большим запасом в БП — ориентируясь на Z, найденный на частоте настройки.
Как мы можем менять Z? С одной стороны, можем выбирать сопротивление катушек, для того они и сделаны разными, с другой стороны — использовать один мощный или мост более слабых усилителей (в т.ч. «бразилию»).
Измерение Re — только 2 из 5 моих мультиметров показывают более-менее верное значение. Оба они стоят не 100р, да и то измеряют не сразу — приходится некоторое время ждать.
0.387/0.78 = 0.496 Ом. Вот так гораздо лучше. Для замера сгодится и пара мультиков за 100р каждый — дешево и сердито. Ну и попутно выяснили, что заявка катушек(Rnom) 1+1Ом — это именно Re. Честный Re, и, тем не менее, не Zmin.
Re этого динамика равен 0.5Ом. Посмотрите, как растет и как меняется импеданс на разной подведенной мощности на одной и той же частоте — от 2.8 и до 1.8Ом. И это не предел, тк динамик вытерпит гораздо больше.
Этот же разброс увидит и ваш усилитель. То есть, ориентироваться на маломощные измерения (а именно такие регламентированы большинством стандартов), определенно, не следует.
Современные теории, учитывающие реальную картину, сложны и не популярны, понятны лишь узкому кругу специалистов, как правило, занятых профессиональной разработкой АС. Если вы не один из них — проще измерьте Z-кривую своей системы сразу на максимальном используемом ходе\мощности и по полученным цифрам делайте выводы.
А это замер Z-кривой динамика в реальном оформлении. Тут, как видим, Z на частоте настройки(33Гц) равен 2.7Ом, а Zmin приходится на 63Гц и равен 2.1Ом.
Если выбирать усилитель в эту систему, то в случае с DD DM серией ориентироваться следует на Z@63Гц, а в случае с DD M — на Z@33Гц. То есть, с выбором в пользу DD M, получим либо серьезный запас в надежности, либо существенно больше мощности при равной надежности — и то, и другое очень неплохо! Ну а с выбором DD DM — неплохо сэкономим!
Если рассматриваете другие усилители, не DD, то картина в целом будет такой же — усилитель, который не боится больших токов, всегда надежнее. Усилитель с минимальной заявкой 2 Ом сработает тут на пределе своих возможностей, тогда как усилитель с заявкой 1Ом покажет очень большой запас.
К тому же, если фильтрами высоких порядков обрезать диапазон, к примеру, 30-50Гц, то и динамику, и усилителю будет работать гораздо проще, а значит и нагрузить оба можно больше при необходимости. От ящика к ящику такой диапазон будет меняться.
Пример Z-кривой для динамика вне оформления. Zmin — сопротивление, ниже которого усилитель видеть не будет.
То есть, пара таких динамиков и один усилитель, либо мост усилителей на один динамик — прям то, что доктор прописал))
И соответствующим образом планируем настройку оформления + фильтров. Zmax — на этой частоте ход максимален и получится ранний клип, Zmin — там катушка получит максимум тепла. Хорошо бы если оформление превратит слабые стороны в сильные 😉
резисторов
резисторовРезисторы последовательно и параллельно, правила Кирхгофа
Резисторы, включенные последовательно и параллельно
Проблема:
Четыре одинаковые лампочки сопротивлением R являются
подключен, как показано на рисунке.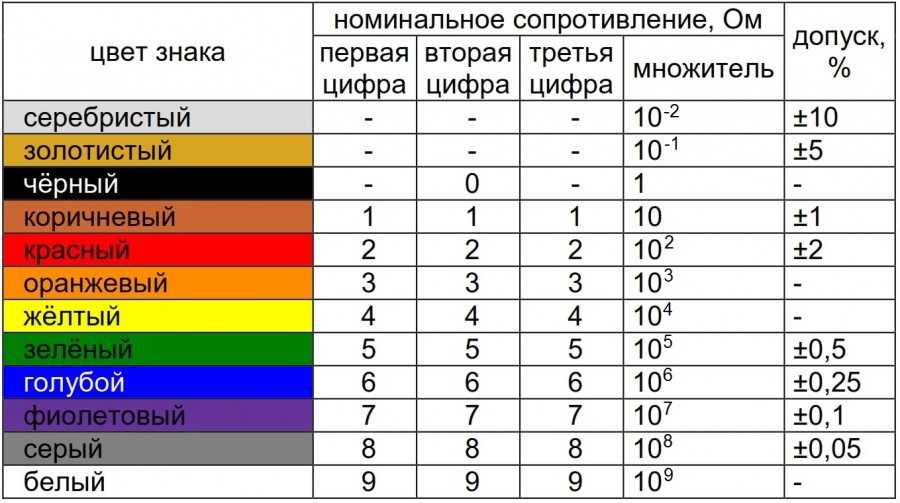
Батарея обеспечивает разность потенциалов В 0 .
Переключатели S 1 и S 2 могут быть разомкнуты и/или
закрыто в четырех различных комбинациях: открыто-открыто, закрыто-закрыто, открыто-закрыто,
закрыто-открыто.
(a) Рассмотрите лампочку A: определите, какая
комбинации переключателей дадут самый яркий и самый тусклый свет в лампе A.
(b) Рассмотрите лампочку B: определите, какая
комбинации переключателей будут давать самый яркий и самый тусклый свет в лампе B.
Решение:
- Концепты:
Резисторы последовательно и параллельно - Рассуждение:
Проанализируйте простую схему. - Детали расчета:
(a) самый яркий: S 1 закрытый, S 2 разомкнут, I A = 2В/(5R).
самый тусклый: S 2 закрытый, I A = 0,
(b) самый яркий: S 2 закрытый, S 1 открытый, I B = V/(2R).
самый тусклый: S 1 закрытый, S 2 открытый, I B = V/(5R).
Проблема:
схема, показанная на схеме, содержит идеальную батарею и два резистора R 1 и R 2 .
Вольтметром измеряют напряжение на R 1
Его показания соответственно 2,0 В; 3,0 В; 6,0 В.
Каковы фактические напряжения на резисторах?
Решение:
- Концепты:
Резисторы последовательно и параллельно - Рассуждение:
Вольтметр так же имеет шунтирующее сопротивление R. Он считывает напряжение на это сопротивление. При размещении в цепи он правильно считывает напряжение батареи, а не напряжения на резисторах невозмущенного схема.
Напряжение батареи V = 6 В.
Напряжения на R 1 и R 2 (без вольтметра в схеме)
V 1 = 6V R 1 /(R 1 + R 2 ) и V
В 1 = 6В /(1 + R 2 /R 1 ), В 2 = 6В /(1 + R 1 /R 2 ).
Нам нужно найти соотношение R 1 /R 2 . - Детали расчета:
С вольтметром в схеме имеем:
2В = 6В [R 1 R/(R 1 + R)]/[ (R 1 R/(R 1 + R)) + R 2 ] или 2 В = 6 В/[1 + R 2 (R 1 + R)/(R 1 R)]
3В = 6В [R 2 R/(R
[1 + R 2 (R 1 + R)/(R 1 R)] = 3, R 2 (R 1 + R)/(R 1 R) = 2, R 2 /R + R 2 /R 1 = 2, 1/R = 2/R 2 — 1/R 1
[1 + R 1 (R 2 + R)/(R 2 R)] = 2, R 1 (R 2 + R)/(R 2 R) = 1, R 1 /R + R 1 /R 2 = 1.
Следовательно, 3/R 2 = 2/R 1 , R 1 /R 2 = (2/3).
В 1 = 6 В * 2/5 = 2,4 В, В 2 = 6 В * 3/5 = 3,6 В.
Проблема:
Что сопротивление следующей сети? Каждый омический резистор имеет сопротивление R
.Решение:
- Концепты:
Резисторы последовательно и параллельно - Рассуждение:
Схема имеет достаточную симметрию, чтобы мы могли анализировать ее как простую схему. схема с резисторами последовательно и параллельно. - Детали расчета:
р всего
Проблема:
(a) Четыре конденсатора подключены, как показано на рисунке.
С 1 = С 2 = С 3 = С 4 = 1
мкФ.
Чему равна общая емкость между точками А и В?
(b) Пять одинаковых резисторов сопротивлением 1 Ом соединены и образуют четыре стороны квадрата. и его диагонали. Чему равно сопротивление между точками А и В?
и его диагонали. Чему равно сопротивление между точками А и В?
Решение:
- Концепты:
Конденсаторы и резисторы последовательно и параллельно - Рассуждение:
Нас просят найти эффективную емкость и сопротивление данного конфигурации. - Детали расчета:
(a) Обратная эквивалентная емкость для подсхема с двумя конденсаторами C 3 и C 4 —
1/C eq = 1/1 + 1/1 = 2, таким образом, C eq = ½. Сейчас эквивалентная емкость для подсхемы с C 2 , C 3 , и C 4 представляет собой C eq ‘= C + C eq = 1 + ½ = 3/2. Наконец, эквивалентная емкость для всей цепи составляет 1/C экв. » = 1/C 1 + 1/C eq ‘ = 1 + (2/3) = 5/3, таким образом, C eq »= 3/5. Суммарная емкость 0,6 мкФ.(b) Эквивалентное сопротивление подцепи с R
 Эквивалентное сопротивление подцепи с R 3 ,
R 4 и R 5 равны 1/R экв. =1/1 + ½ = 3/2, таким образом, R экв. = (2/3). Эквивалентное сопротивление подцепи с R 2 , Р 3 ,
R 4 и R 5 равно R eq ‘ = R 2 + Re q = 1 + (2/3) = 5/3. Наконец, эквивалентное сопротивление всей цепи равно 1/R eq »=
1/1 + 3/5 = 8/5, таким образом, R eq »= 5/8. Сопротивление между точками А
и B составляет 5/8 Ом.
Эквивалентное сопротивление подцепи с R 3 ,
R 4 и R 5 равны 1/R экв. =1/1 + ½ = 3/2, таким образом, R экв. = (2/3). Эквивалентное сопротивление подцепи с R 2 , Р 3 ,
R 4 и R 5 равно R eq ‘ = R 2 + Re q = 1 + (2/3) = 5/3. Наконец, эквивалентное сопротивление всей цепи равно 1/R eq »=
1/1 + 3/5 = 8/5, таким образом, R eq »= 5/8. Сопротивление между точками А
и B составляет 5/8 Ом.
Проблема:
Найдите максимальную мощность
нагревательный элемент , который можно сконструировать из куска проволоки с сопротивлением 536 Ом. Элемент должен быть запитан
постоянным напряжением V = 110В. Ток по проводу
не может превышать 2,0 А.
(а) Предположим, что вы
допускается выбраковка отрезка провода,
(б) Предположим, что вам НЕ разрешено выбрасывать часть провода,

Решение:
- Концепты:
Закон Ома, I = V/R, мощность P = IV, резисторы в последовательно и параллельно - Рассуждение:
Мы можем разрезать провод на N кусков и соединить эти куски параллельно источник питания. - Детали расчета:
Поскольку V постоянно, мы должны максимизировать I, чтобы максимизировать P.
На каждый из отрезков провода, соединенных параллельно, имеем
I = V/R, I макс. = 2 A = 110 В/R мин. , R мин. = 55 Ом.
(a) Мы можем отрезать 9 кусков по 55 Ом и выбросить один кусок по 41 Ом.
Тогда общий ток равен 9*2 А, а рассеиваемая мощность 1980 Вт.
(b) Мы можем отрезать 8 кусков по 55 Ом и 1 кусок по 96 Ом. Суммарный ток их
I всего = 8*110 В/(55 Ом) + 110 В/(96 Ом). Мощность P = VI всего = 1886 Вт.
I = V/R, dI = -(V/R 2 )dR
Суммарное изменение тока по проводам в них равно dI = -(V/R 2 55 Ом )dR + (V/R 2 96 Ом )dR.
dI отрицателен, ток меньше, меньше мощность рассеивается при нагреве. элемент. Максимальная мощность, рассеиваемая при обогреве элемент 1886Вт.
Проблема:
В
бесконечная цепь, показанная на схеме, каждая батарея имеет ЭДС ε и внутреннюю
сопротивление р. Каждый резистор имеет сопротивление 2r. Найдите ЭДС и внутреннюю
сопротивление эквивалентной батареи.
Решение:
- Концепты:
Ан бесконечная лестничная сеть - Рассуждение:
Поскольку лестница бесконечна, ток через эквивалентную ЭДС и внутреннее сопротивление не будет изменить, если к передней части лестницы добавляется дополнительная секция. - Детали расчета:
Любая комбинация батарей и сопротивлений с двумя клеммами может быть заменены одним источником напряжения V и одним последовательным резистором R. Напряжение V является идеальным источником напряжения, равным разомкнутой цепи. напряжение на клеммах. Сопротивление Thevenin R — это сопротивление измеряется на клеммах со всеми источниками напряжения, замененными короткозамкнутыми цепи и все источники тока заменены разомкнутыми цепями.
Сеть состоит из бесконечного числа секций.
Давайте построим новую двухполюсную сеть, добавив еще один участок в сеть. перед старой двухтерминальной сетью.Пусть напряжение Thevenin новой сети равно V’ и пусть Thevenin сопротивление R’.
У нас есть
V’ = ε + V2r/(2r + R), R’ = 2rR/(R + 2r) + r = (3rR + 2r 2 )/(R + 2р).
Полагая R’ = R, V’ = V, получаем
R 2 — rR — 2r 2 = 0, R = r/2 + ((r/2) 2 + 2r 2 ) ½ = 2р.
V = (2r + R)ε/R = 2ε.
ЭДС эквивалентной батареи равна 2ε, а внутреннее сопротивление равно 2r.
Проблема:
(a) Рассчитайте сопротивление между двумя точками A
и B бесконечной системы резисторов.
(b) Рассчитайте сопротивление между точками A и
B куба из одинаковых резисторов r.
Решение:
Проблема:
Какое эквивалентное сопротивление показанной сети? Каждый резистор имеет сопротивление R.
Решение:
- Концепции:
Резисторы последовательно и параллельно - Обоснование:
Через центральный резистор не протекает ток. Его можно игнорировать. Затем схема имеет достаточную симметрию, чтобы мы могли анализировать ее как простую схему с двумя пары резисторов последовательно. Пары параллельны друг другу. - Детали расчета:
Для двух последовательно соединенных резисторов: R эфф = R 1 + R 2 .
Для двух резисторов, включенных параллельно: 1/R эфф = 1/R 1 + 1/R 2 .
Каждый резистор имеет сопротивление R, эквивалентное сопротивление равно R.
Правила Кирхгофа
Проблема:
Найдите эквивалентное сопротивление между точками А и В цепи показано на рисунке ниже.
Решение:
- Концепты:
Правила Кирхгофа - Рассуждение:
Мы можем найти эквивалентное сопротивление, используя правила Кирхгофа. Правило соединения гласит, что сумма токов, входящих в соединение, должна
равна сумме токов, выходящих из этого соединения. Правило цикла гласит
что сумма разностей потенциалов вокруг любой замкнутой цепи должна
быть нулем.
Правило соединения гласит, что сумма токов, входящих в соединение, должна
равна сумме токов, выходящих из этого соединения. Правило цикла гласит
что сумма разностей потенциалов вокруг любой замкнутой цепи должна
быть нулем.
Предположим, что ток, протекающий в каждой части цепи, имеет некоторое направление.Если резистор перемещается в направлении тока, изменение потенциала на резисторе равно -IR.
Если резистор перемещается в направлении, противоположном этому тока изменение потенциала на резисторе равно +IR.
Если источник напряжения пересекается в направлении от — до +, изменение потенциала равно +V.
Если источник напряжения перемещается в направлении от + к -, изменение потенциала равно -V.
Мы можем использовать правило соединения столько раз, сколько возможно включить в него ток, который не использовался в предыдущем правиле соединения уравнение.
 Количество уравнений должно быть равно количеству неизвестных.
Количество уравнений должно быть равно количеству неизвестных. - Детали расчета:
Предположим, вы подключили батарею между A и B, так что A находится под некоторым напряжением V. и B находится на земле. Ток I начнет течь по цепи от A к B. V = IR, R = V/I. Если ты знаешь меня, то ты знаешь Р.Чтобы найти R для цепи, нам нужно знать токи, протекающие через 6 резисторы. Пусть I(1) обозначает ток, протекающий через резистор 1 Ом, I(2) обозначает ток через резистор 2 Ом и так далее. Общая текущая точка выхода A обозначается I. Нам нужно использовать правила Кирхгофа, чтобы найти 7 уравнений для семи токов, а затем использовать алгебру, чтобы решить эти семь уравнений одновременно.
(1) Для соединения с номером J1 имеем I(1) + I(2) + I(5) — I = 0,
(2) Для соединения с номером J2 имеем I(2) — I(7) — I(9) = 0
(3) Для соединения с номером J3 имеем I(13) — I(7) — I(5) = 0
(4) Для петли 1 имеем V — 1*I(1) = 0
(5) Для цикла 2 имеем 1*(I1) — 2*I(2) — 9*I(9) = 0
(6) Для цикла 3 имеем 9*I(9) — 7*I(7) — 13*I(13) = 0
(7) Для контура 4 имеем 2*I(2) + 7*I(7) — 5*I(5) = 0Теперь воспользуемся уравнением 4, чтобы исключить I(1) из других уравнений.

I(1) = V. Теперь у нас есть шесть уравнений.
(1) Для соединения с номером J1 имеем V + I(2) + I(5) — I = 0,
(2) Для соединения с номером J2 имеем I(2) — I(7) — I(9) = 0
(3) Для соединения с номером J3 имеем I(13) — I(7) — I(5) = 0
(5) Для петли 2 имеем V — 2*I(2) — 9*I(9) = 0
(6) Для цикла 3 имеем 9*I(9) — 7*I(7) — 13*I(13) = 0
(7) Для контура 4 имеем 2*I(2) + 7*I(7) — 5*I(5) = 0Теперь воспользуемся уравнением 2, чтобы исключить I(2) из других уравнений.
Я(2) = Я(7)+Я(9). Теперь у нас есть пять уравнений.
(1) Для соединения с номером J1 имеем V + I(7) + I(9) + I(5) — I = 0,
(3) Для соединения с номером J3 имеем I(13) — I(7) — I(5) = 0
(5) Для петли 2 имеем V — 2*I(7) — 11*I(9) = 0
(6) Для цикла 3 имеем 9*I(9) — 7*I(7) — 13*I(13) = 0
(7) Для контура 4 имеем 9*I(7) + 2*I(9) — 5*I(5) = 0Теперь воспользуемся уравнением 3, чтобы исключить I(5) из других уравнений.

I(5) = I(13)-I(7). Теперь у нас есть 4 уравнения.
(1) Для соединения с номером J1 имеем V + I(9) + I(13) — I = 0,
(5) Для петли 2 имеем V — 2*I(7) — 11*I(9) = 0
(6) Для цикла 3 имеем 9*I(9) — 7*I(7) — 13*I(13) = 0
(7) Для контура 4 имеем 14*I(7) + 2*I(9) — 5*I(13) = 0Теперь воспользуемся уравнением 5, чтобы исключить I(7) из других уравнений.
2*I(7) = V-11*I(9). Теперь у нас есть три уравнения.
(1) Для соединения с номером J1 имеем V + I(9) + I(13) — I = 0,
(6) Для цикла 3 имеем -7*V + 95*I(9) — 26*I(13) = 0
(7) Для контура 4 имеем 7*V — 75*I(9) — 5*I(13) = 0Теперь воспользуемся уравнением 7, чтобы исключить I(9) из других уравнений.
75*I(9) = 7*V — 5*I(13). Теперь у нас есть 2 уравнения.
(1) Для соединения J1 имеем 82*V + 70*I(13) — 75*I = 0,
. (6) Для контура 3 имеем 140*V — 2425*I(13) = 0Теперь воспользуемся уравнением 6, чтобы исключить I(13) из других уравнений.

485*I(13) = 28*V. Теперь у нас есть 1 уравнение.
(1) Для соединения J1 имеем 41730*V — 36375*I = 0,I = (41730/36375)*V = 1,147*V
R = V/I = 0,87 ОмСопротивление 0,87 Ом.
Проблема:
В приведенной выше схеме выразите ток в резисторе 3R через V и R.
Решение:
- Концепты:
Правила Кирхгофа - Рассуждение:
Мы можем найти токи I 1 , I 2 и I 3 используя правила Кирхгофа. Правило соединения гласит, что сумма токи, входящие в соединение, должны быть равны сумме токов, выходящих из этого соединения. узел. Правило петли гласит, что сумма разностей потенциалов вокруг любого замкнутого контура должно быть равно нулю.
- Детали расчета:
Я 1 + Я 2 = Я 3 , Я 1 = Я 2 , В — 3РИ 3 — РИ 2 = 0. И 3 = 2В/(7R).
Сопротивление: определение, формула и символ
Сопротивление: определение, формула и символ | StudySmarterВыберите ваш язык
Предлагаемые вам языки:
Немецкий (DE)
Дойч (Великобритания)
Европа
- английский (DE)
- английский (Великобритания)
StudySmarter — универсальное учебное приложение.
4.8 • Рейтинг +11k
Более 3 миллионов загрузок
Бесплатно
Сопротивление
СОДЕРЖАНИЕ :
ОГЛАВЛЕНИЕ
Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken
Jetzt kostenlos anmelden
Nie wieder prokastinieren mit unseren Lernerinnerungen.
Jetzt kostenlos anmelden
Электричество является жизненно важной частью современного общества. Мы полагаемся на электричество для производства, отопления, освещения и многих других повседневных потребностей. По сути, электричество можно объяснить, используя три его основных свойства: ток, напряжение и сопротивление, которые в совокупности образуют один из важнейших законов физики — закон Ома. Об этом объявил в 1827 году немецкий физик Георг Симон Ом, который первым описал электричество таким образом. Он провел эксперимент, используя металлическую проволоку и компас, чтобы определить соотношение между напряжением и током, и пришел к выводу, что их отношение равно свойству, которое мы теперь называем электрическим сопротивлением. В результате этого открытия единицы измерения сопротивления были названы в честь Ома. В этой статье мы объясним, что такое электрическое сопротивление и как оно рассчитывается.
Об этом объявил в 1827 году немецкий физик Георг Симон Ом, который первым описал электричество таким образом. Он провел эксперимент, используя металлическую проволоку и компас, чтобы определить соотношение между напряжением и током, и пришел к выводу, что их отношение равно свойству, которое мы теперь называем электрическим сопротивлением. В результате этого открытия единицы измерения сопротивления были названы в честь Ома. В этой статье мы объясним, что такое электрическое сопротивление и как оно рассчитывается.
Определение сопротивления
Для начала давайте определим, что такое электрическое сопротивление .
Сопротивление — это мера степени сопротивления объекта движению электрических зарядов.
В электрических системах и электронных устройствах, таких как утюги, электронные часы или мобильные телефоны, всегда требуются элементы с постоянным или переменным электрическим сопротивлением. Независимо от их конкретной конструкции, все эти элементы считаются резисторы .
Резистор — элемент электрической цепи, ограничивающий поток электрических зарядов.
Резисторы могут преобразовывать электрическую энергию в тепловую энергию, что может изменять температуру резистора и окружающей его среды.
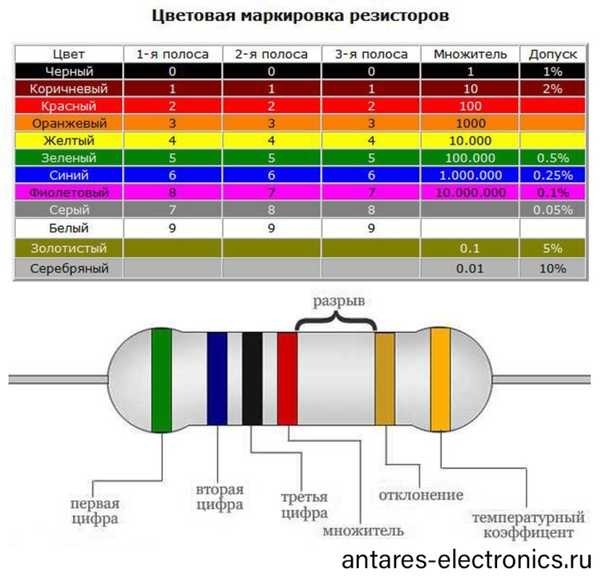
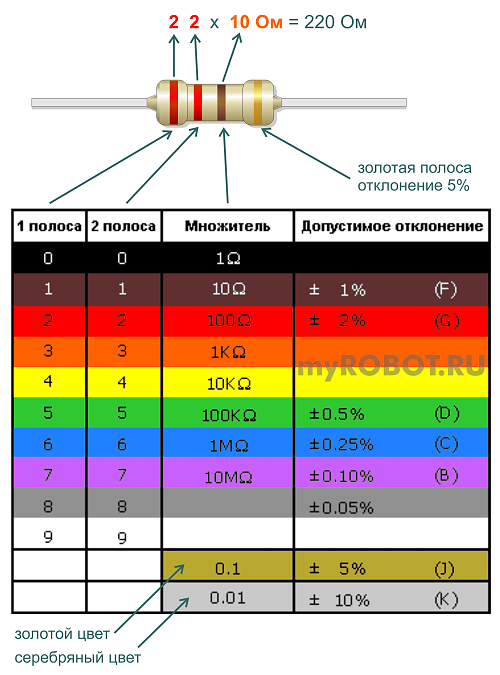
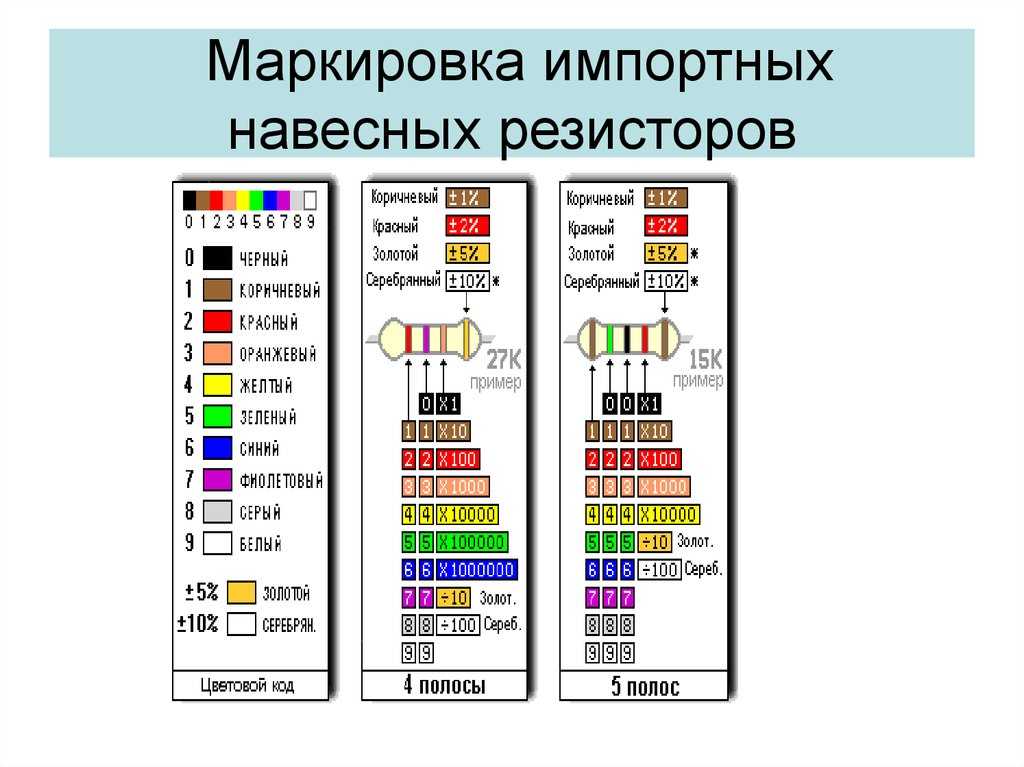
Рис. 1. Каждая цветовая полоса на резисторе дает нам полезную информацию о конкретном резисторе.
Они очень разнообразны как по диапазону сопротивления, так и по конструкции. Как правило, резисторы имеют от трех до шести полос разных цветов, как показано на рисунке 1 выше. Каждый цвет и расположение указывают на другое значение сопротивления или свойство.
Цветовой код резистора
Наиболее часто используемый тип резистора состоит из четырех полос, поэтому давайте объясним значение каждой из этих полос. Чтобы определить свойства резистора, мы должны читать его слева направо. Первые две полосы соответствуют первым двум цифрам. Третья полоса — это множитель , который просто указывает, сколько нулей мы должны добавить к первым двум цифрам.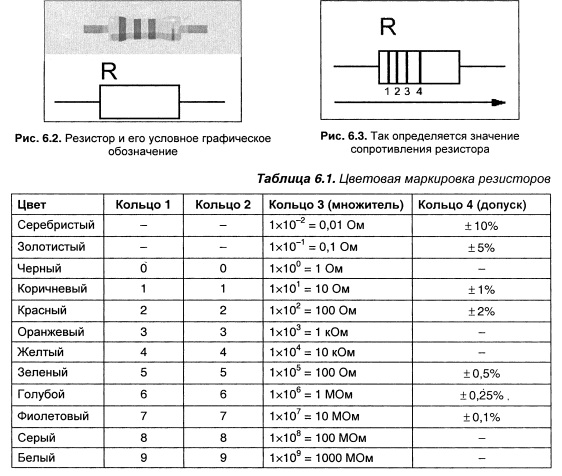 Наконец, четвертая полоса — это допуск или погрешность резистора. Каждому цвету соответствует номер, который указан в Таблице 1 ниже. 9{-2}\)
Наконец, четвертая полоса — это допуск или погрешность резистора. Каждому цвету соответствует номер, который указан в Таблице 1 ниже. 9{-2}\)
Чтобы понять применение Чтобы лучше понять эти значения, давайте проанализируем резистор в крайней правой части рисунка 1.
Определите номинал четырехполосного резистора со следующими цветами полос: желтой, фиолетовой, оранжевой и золотой.
Ответ:
В данном случае желтый и фиолетовый — это первые две цифры, оранжевый соответствует множителю, а золотой подскажет нам допуск. 93\,\Omega \pm5\%\) или \(47\,\mathrm{k}\Omega \pm 5\%\).
- Трехполосные резисторы состоят из двух цифр и множителя, так как полоса допуска всегда «бесцветная».
- Пятиполосные резисторы аналогичны четырехполосным резисторам, только с тремя цифрами, а не с двумя.
- Шестиполосные резисторы аналогичны пятиполосным резисторам, только имеют дополнительную полосу, обозначающую температурный коэффициент.

Символ сопротивления
В уравнениях сопротивление обозначается буквой «R», что довольно просто. Это становится немного сложнее, когда нам нужно включить резисторы в электрическую цепь, где, как и у любого другого компонента, у них есть свой собственный символ. В зависимости от источника и страны происхождения постоянный резистор может быть представлен либо в виде зигзагообразной линии (американский стиль), либо в виде прямоугольного прямоугольника (международный стиль), как показано на рисунке 2 ниже. Простой способ связать зигзагообразную линию с сопротивлением — представить ток, проходящий по прямой линии, а не такой быстро меняющийся путь — очевидно, что электрическому заряду будет намного труднее пройти через нее.
Рис. 2 — Символы резисторов, прямоугольная рамка — международная версия, зигзаг — американская версия.
Во всех наших примерах мы будем использовать зигзагообразную линию для обозначения резистора; однако полезно также ознакомиться с международно признанной версией.
Постоянный резистор просто означает, что его сопротивление остается постоянным и не может быть отрегулировано. Иногда вокруг этих символов нарисованы дополнительные линии и стрелки. Это указывает на очень специфический тип резистора с особыми функциями, которые мы не будем рассматривать в этом курсе.
Сопротивление и удельное сопротивление
Сопротивление и удельное сопротивление часто считают одним и тем же, что определенно не так. Эти две концепции переплетены, но сопротивление описывает противодействие тока из-за материи, в то время как удельное сопротивление количественно определяет структурные свойства материи.
Удельное сопротивление — это фундаментальное свойство материала, которое количественно определяет, насколько сильно материал сопротивляется движению электрического заряда.
9{17}\)Формула сопротивления
Основными факторами, влияющими на сопротивление объекта, являются его форма и материал, из которого он изготовлен. Мы можем легко получить выражение для сопротивления, рассматривая цилиндр, подобный показанному на рис. 3.
Мы можем легко получить выражение для сопротивления, рассматривая цилиндр, подобный показанному на рис. 3.
Рис. 3. Сопротивление цилиндра прямо пропорционально его длине и удельному сопротивлению и обратно пропорционально площади его поперечного сечения.
Математически выражение сопротивления равно 92}\right)\), а \(\rho\) — удельное сопротивление материала, измеренное в ом-метрах \(\left(\Omega\,\mathrm{m}\right)\). Это уравнение можно применить к другим, более сложным формам.
По сути, сопротивление объясняет, насколько легко электрические заряды проходят через этот цилиндр. Увеличение его длины увеличит общее количество столкновений между атомами в материале и электрическими зарядами, поскольку они будут перемещаться на большее расстояние. Точно так же, если мы увеличим диаметр цилиндра, току будет легче проходить через него, поэтому он будет испытывать меньшее сопротивление. Наконец, если удельное сопротивление материала выше, это означает, что материал может сильнее сопротивляться электрическому току, поэтому сопротивление всего цилиндра будет выше. {-8} \, \ Омега \, \mathrm{m}\)). 9{-4} \, \mathrm{м}. \end{align}$$
{-8} \, \ Омега \, \mathrm{m}\)). 9{-4} \, \mathrm{м}. \end{align}$$
Диаметр просто в два раза больше радиуса окружности, поэтому диаметр этого медного провода равен
$$ D=1,79\,\mathrm{мм}. $$
Электрическое сопротивление и проводимость
При работе с электрическими цепями электрическое сопротивление и проводимость являются важными характеристиками, описывающими их поведение. Оба этих свойства тесно связаны с электрическим током и способностью компонента проходить через него. Давайте рассмотрим каждый из них отдельно.
Сопротивление
Сопротивление можно измерить с помощью омметра или рассчитать по закону Ома :
\[R=\frac{\Delta V}{I},\]
где \(R\) сопротивление в омах (\(\Omega\)), \(V\) — напряжение в вольтах (\(\mathrm{V}\)), а \(I\) — ток в амперах (\(\ матрм{А}\)).
Если мы знаем тип цепи и индивидуальное сопротивление каждого резистора, мы можем найти общее сопротивление электрической системы, используя следующие соотношения:
Если резисторы находятся в серии (т.
 е. рядом друг с другом), вы складываете значение каждого резистора вместе: \[R_\mathrm{series}=\sum_{n}R_n=R_1+R_2+ \cdots ,\]
е. рядом друг с другом), вы складываете значение каждого резистора вместе: \[R_\mathrm{series}=\sum_{n}R_n=R_1+R_2+ \cdots ,\]Если резисторы параллельны , правило нахождения общего сопротивления будет следующим: \[\frac{1}{R_\mathrm{parallel}}=\sum_{n}\frac {1}{R_n} =\frac{1}{R_1}+\frac{1}{R_2}+\cdots.\]
Проводимость
Проводимость — это свойство, прямо противоположное сопротивлению. Если сопротивление говорит нам о том, насколько компонент сопротивляется току, проводимость объясняет, насколько легко ток может течь через указанный компонент.
Проводимость — это способность определенного компонента проводить электричество.
Учитывая обратную величину сопротивления, математически проводимость \(G\) может быть выражена как
\[G=\frac{1}{R}=\frac{I}{\Delta V}.\]
Он измеряется в единицах сименса (\(\mathrm{S}\)), которые являются обратными омам: \(1\,\mathrm{S}=1\,\frac{1}{\Omega} .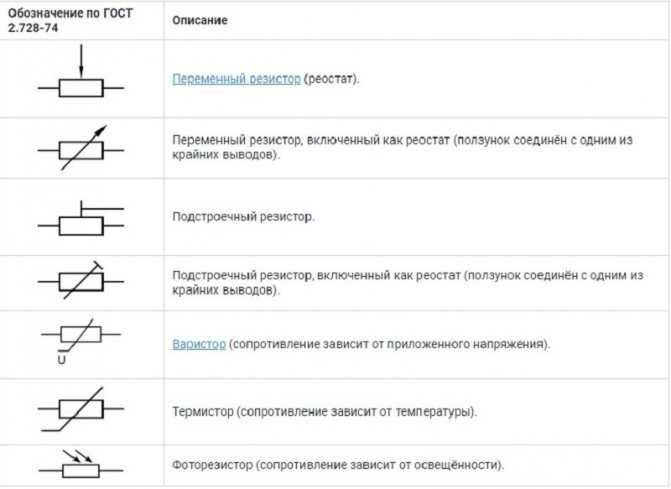 \)
\)
Не путать с проводимостью \(\сигма\) , , которая является неотъемлемым свойством материала, как и удельное сопротивление.
Сопротивление — основные выводы
- Сопротивление — это мера степени сопротивления объекта движению электрических зарядов.
- Резистор — элемент электрической цепи, ограничивающий поток электрических зарядов.
- Сопротивление обозначается буквой «R», а сопротивление в электрической цепи обозначается зигзагообразной линией.
- Удельное сопротивление — это фундаментальное свойство материала, которое количественно определяет, насколько сильно материал сопротивляется движению электрического заряда.
- Удельное сопротивление обозначается символом \(\rho\) и зависит от атомной структуры и температуры материала.
- Математически выражение для сопротивления равно \( R=\frac{\rho \ell}{A}.\)
- Сопротивление является одним из основных свойств электрической цепи, где его можно рассчитать с помощью закона Ома \ (R=\frac{\Delta V}{I}.
 \)
\) - Проводимость — это способность определенного компонента проводить электричество.
Каталожные номера
- Рис. 1 — Массив электронных осевых выводов-резисторов (https://commons.wikimedia.org/wiki/File:Electronic-Axial-Lead-Resistors-Array.jpg), Эван-Амос (https ://commons.wikimedia.org/wiki/User:Evan-Amos) находится под лицензией Public Domain.
- Рис. 2 — Символы резисторов, StudySmarter Originals.
- Таблица 2 – Удельное сопротивление материалов, Douglas C. Giancoli, Physics, 4th Ed, Prentice Hall, 1995.
- Рис. 3 – Сопротивление цилиндра, StudySmarter Originals.
Часто задаваемые вопросы о сопротивлении
Сопротивление — это мера степени сопротивления объекта движению электрических зарядов.
Сопротивление описывает противодействие тока материи и математически может быть выражено как R=ρl/A.
Примером сопротивления является ток, протекающий по длинному цилиндрическому металлическому проводу, в котором атомная структура материала сопротивляется потоку заряда.
Сопротивление вызвано потоком электронов, взаимодействующих с ионами, присутствующими в среде.
Сопротивление в цепи является мерой противодействия электрического заряда, протекающего через электрическую цепь.
Заключительный тест на сопротивление
Вопрос
Что такое определение сопротивления?
Показать ответ
Ответ
Сопротивление – это мера степени сопротивления объекта движению электрических зарядов.
Показать вопрос
Вопрос
Верно/неверно: Резисторы могут преобразовывать электрическую энергию в тепловую, что может изменить температуру резистора и окружающей его среды.
Показать ответ
Ответ
Показать вопрос
Вопрос
Верно/неверно: проводимость и сопротивление прямо пропорциональны .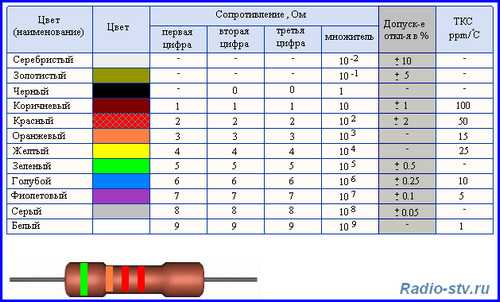
Показать ответ
Ответ
Неверно.
Показать вопрос
Вопрос
Какое математическое выражение используется для расчета сопротивления \(R\) провода? Здесь \(\rho\) — удельное сопротивление материала провода, \(\ell\) — длина провода, а \(A\) — площадь поперечного сечения провода.
Показать ответ
Ответ
\(R=\frac{\rho \ell}{A}\).
Показать вопрос
Вопрос
Какое выражение используется для расчета проводимости \(G\). Здесь \(V\) — напряжение, а \(I\) — ток.
Показать ответ
Ответ
\(G=\frac{I}{\Delta V}\).
Показать вопрос
Вопрос
Каковы единицы проводимости?
Показать ответ
Ответ
Сименс (\(\mathrm{S}\)).
Показать вопрос
Вопрос
Какие факторы не влияют на удельное сопротивление материала?
Показать ответ
Ответ
Строение атома.
Показать вопрос
Вопрос
Как математически выражается закон Ома? Здесь \(R\) – сопротивление, \(V\) – напряжение, а \(I\) – сила тока.
Показать ответ
Ответ
\(R=\frac{\Delta V}{I}\).
Показать вопрос
Вопрос
Каково назначение резистора в электрической цепи?
Показать ответ
Ответ
Чтобы ограничить поток электрических зарядов.
Показать вопрос
Вопрос
Какой символ используется для обозначения резистора в электрической цепи?
Показать ответ
Ответ
Зигзагообразная линия.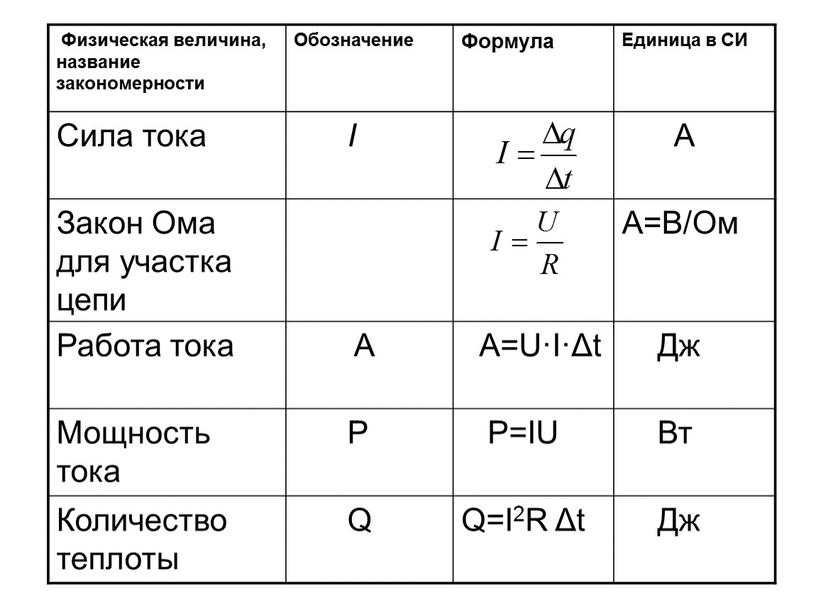
Показать вопрос
Вопрос
Какое из следующих уравнений можно использовать для нахождения сопротивления \(R\) в параллельной цепи ?
Показать ответ
Ответ
\(R_\mathrm{parallel}=\sum_{n}R_n=R_1+R_2+ \cdots.\)
Показать вопрос
Вопрос
Верно/Неверно: проводимость и проводимость — это одно и то же.
Показать ответ
Ответ
Неверно.
Показать вопрос
Вопрос
Ток течет по длинному цилиндрическому проводу. Если длину этого провода увеличить, что произойдет с сопротивлением?
Показать ответ
Ответ
Сопротивление увеличится.
Показать вопрос
Вопрос
Верно/неверно: вокруг всех резисторов расположены четыре полосы разных цветов.
Показать ответ
Ответ
Неверно.
Показать вопрос
Вопрос
Какой инструмент можно использовать для измерения сопротивления?
Показать ответ
Ответ
Омметр.
Показать вопрос
Подробнее о Сопротивлении
Откройте для себя подходящий контент для ваших тем
Не нужно обманывать, если у вас есть все необходимое для успеха! Упаковано в одно приложение!
Учебный план
Будьте идеально подготовлены вовремя с индивидуальным планом.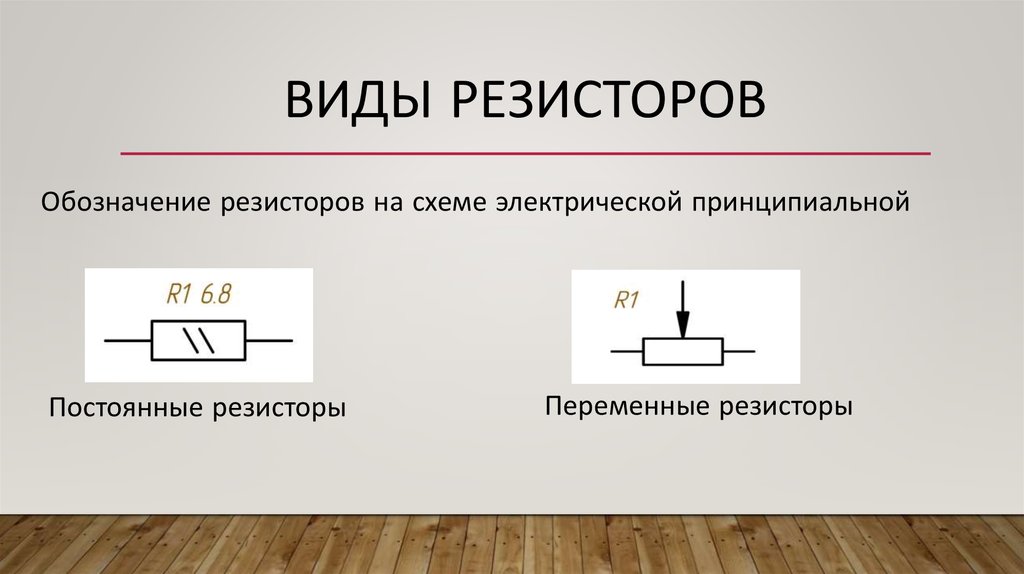
Тесты
Проверьте свои знания с помощью игровых тестов.
Карточки
Создавайте и находите карточки в рекордно короткие сроки.
Заметки
Создавайте красивые заметки быстрее, чем когда-либо прежде.
Учебные наборы
Все учебные материалы в одном месте.
Документы
Загружайте неограниченное количество документов и сохраняйте их в Интернете.
Study Analytics
Определите сильные и слабые стороны вашего исследования.
Еженедельные цели
Ставьте индивидуальные учебные цели и зарабатывайте баллы за их достижение.
Умные напоминания
Хватит откладывать на потом наши напоминания об учебе.
Награды
Зарабатывайте очки, открывайте значки и повышайте уровень во время учебы.
Волшебный маркер
Создавайте карточки в заметках полностью автоматически.
Интеллектуальное форматирование
Создавайте самые красивые учебные материалы, используя наши шаблоны.





 Эквивалентное сопротивление подцепи с R 3 ,
R 4 и R 5 равны 1/R экв. =1/1 + ½ = 3/2, таким образом, R экв. = (2/3). Эквивалентное сопротивление подцепи с R 2 , Р 3 ,
R 4 и R 5 равно R eq ‘ = R 2 + Re q = 1 + (2/3) = 5/3. Наконец, эквивалентное сопротивление всей цепи равно 1/R eq »=
1/1 + 3/5 = 8/5, таким образом, R eq »= 5/8. Сопротивление между точками А
и B составляет 5/8 Ом.
Эквивалентное сопротивление подцепи с R 3 ,
R 4 и R 5 равны 1/R экв. =1/1 + ½ = 3/2, таким образом, R экв. = (2/3). Эквивалентное сопротивление подцепи с R 2 , Р 3 ,
R 4 и R 5 равно R eq ‘ = R 2 + Re q = 1 + (2/3) = 5/3. Наконец, эквивалентное сопротивление всей цепи равно 1/R eq »=
1/1 + 3/5 = 8/5, таким образом, R eq »= 5/8. Сопротивление между точками А
и B составляет 5/8 Ом.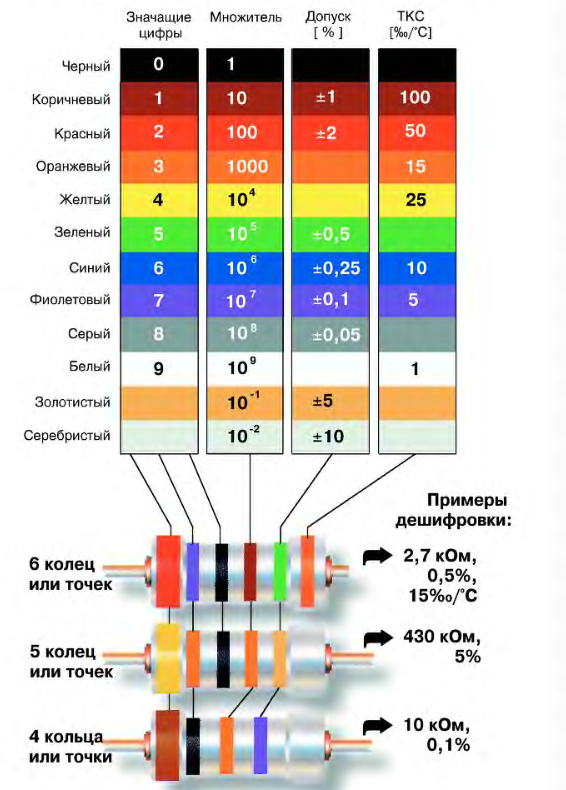
 Правило соединения гласит, что сумма токов, входящих в соединение, должна
равна сумме токов, выходящих из этого соединения. Правило цикла гласит
что сумма разностей потенциалов вокруг любой замкнутой цепи должна
быть нулем.
Правило соединения гласит, что сумма токов, входящих в соединение, должна
равна сумме токов, выходящих из этого соединения. Правило цикла гласит
что сумма разностей потенциалов вокруг любой замкнутой цепи должна
быть нулем.  Количество уравнений должно быть равно количеству неизвестных.
Количество уравнений должно быть равно количеству неизвестных.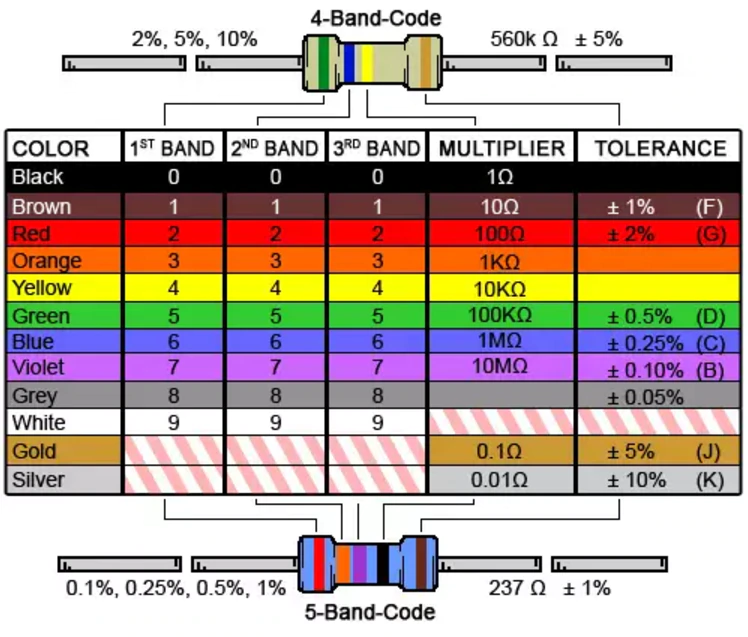

 е. рядом друг с другом), вы складываете значение каждого резистора вместе: \[R_\mathrm{series}=\sum_{n}R_n=R_1+R_2+ \cdots ,\]
е. рядом друг с другом), вы складываете значение каждого резистора вместе: \[R_\mathrm{series}=\sum_{n}R_n=R_1+R_2+ \cdots ,\]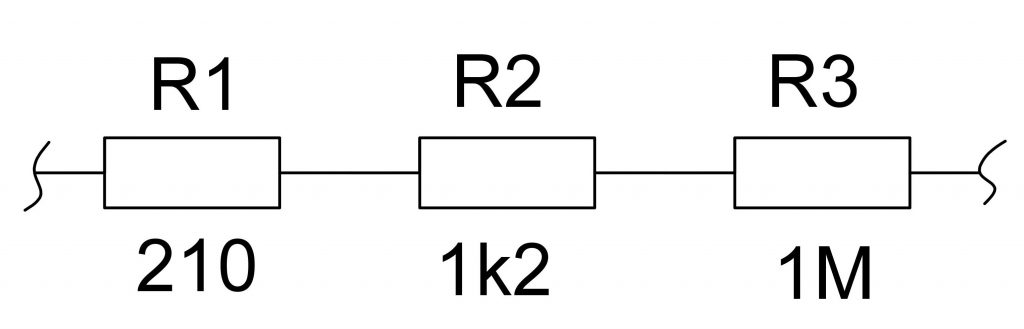 \)
\)