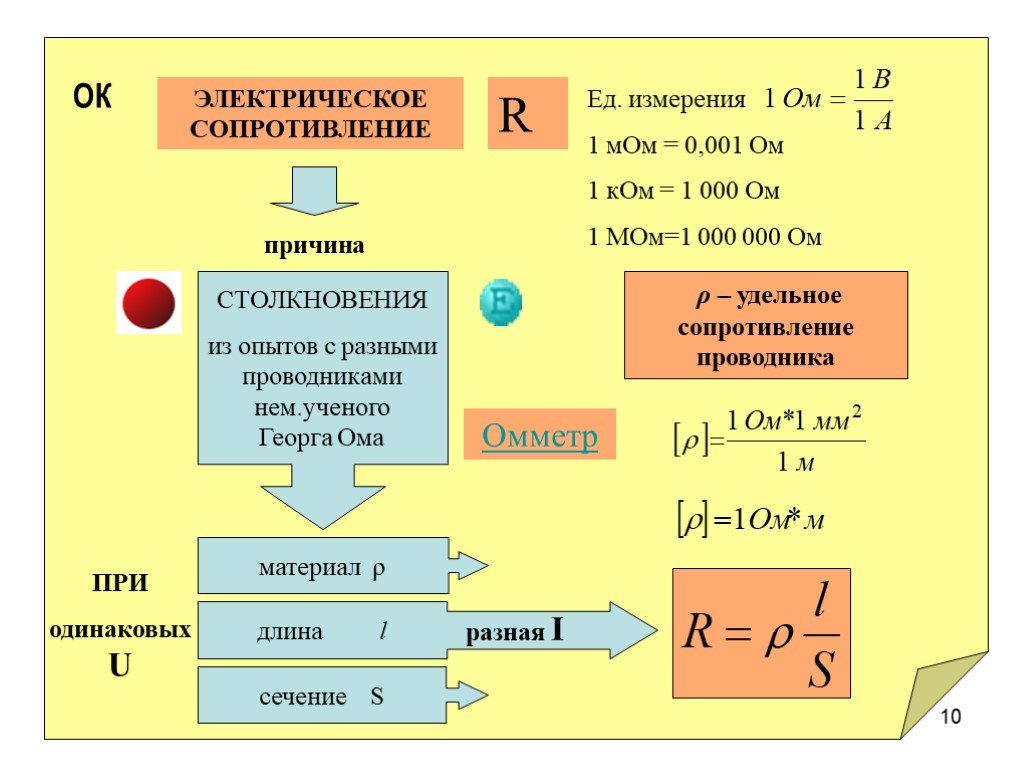
Физика — 8

• Сопротивление проводника обратно пропорционально площади его поперечного сечения.

3. Сила тока, проходящего через железный проводник, подключенный к источнику постоянного тока (U=const), в 10 раз превышает силу тока, проходящего через нихромовый проводник, а сопротивление его в 10 раз меньше.

• Сопротивление проводника зависит от вещества, из которого он изготовлен.

Таким образом, формула зависимости сопротивления проводника имеет вид:

R = ρl
S

Здесь R — сопротивление проводника, l — длина проводника,

S — площадь поперечного сечения проводника, ρ — удельное сопротивление проводника. Удельное сопротивление — это физическая величина, зависящая от вещества, из которого изготовлен проводник. В таблице 6.2. показаны удельные сопротивления некоторых веществ, полученные опытным путем. При длине проводника l = 1 м и площади поперечного сечения S = 1 м² из формулы

ρ = RS
l

получим, что удельное сопротивление численно равно ρ = R.

• Удельное сопротивление — это сопротивление проводника длиной 1 м и площадью поперечного сечения 1 м
  2. Единицей удельного сопротивления в системе СИ является ом·метр · (1 Ом·м):

[ρ] = [R] · [S]
[l] = 10м · 1м²
1м = 10м · м.

Площадь поперечнего сечения проводника небольшая и измеряется в мм².
Поэтому единицу удельного сопротивления можно записать и так:

[ρ] = 1Oм · мм²
м

Таблица 6.2. Удельное сопротивление некоторых веществ (t = 20°С).

Вещество	ρ,Oм · мм2 м	Вещество	ρ,Oм · мм2 м
Серебро	0,016	Манганин (сплав)	0,43
Медь	0,017	Константан (сплав)	0,5
Золото	0,024	Ртуть	0,96
Алюминий	0,028	Нихром (сплав)	1,1
Вольфрам	0,055	Фехраль (сплав)	1,3
Железо	0,1	Графит	13
Свинец	0,21	Керамика	1019
Никелин (сплав)	0,4	Эбонит	1020

формула удельного сопротивления и закон Ома

Закон Ома является основным законом электрических цепей.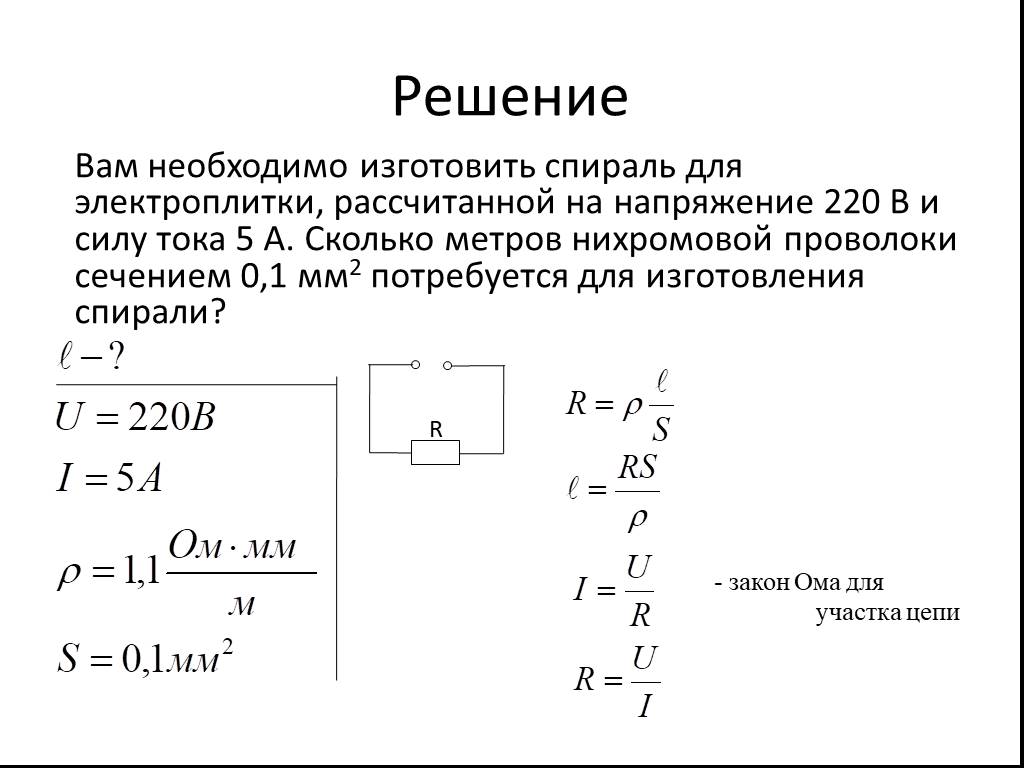 При этом он позволяет объяснять многие явления природы. Например, можно понять, почему электричество не «бьет» птиц, которые сидят на проводах. Для физики закон Ома является крайне значимым. Без его знания невозможно было бы создавать стабильно работающие электрические цепи или вовсе не было бы электроники.

Зависимость I = I(U) и ее значение

История открытия сопротивления материалов напрямую связана с вольт-амперной характеристикой. Что это такое? Возьмем цепь с постоянным электрическим током и рассмотрим любой ее элемент: лампу, газовую трубку, металлический проводник, колбу электролита и т. д.

Меняя напряжение U (часто обозначается как V), подаваемое на рассматриваемый элемент, будем отслеживать изменение силы тока (I), проходящего через него. Как итог, мы получим зависимость вида I = I (U), которая носит название «вольт-амперная характеристика элемента» и является прямым показателем его электрических свойств.

Вольт-амперная характеристика может выглядеть по-разному для различных элементов. Самый простой ее вид получается при рассмотрении металлического проводника, что и сделал Георг Ом(1789 — 1854).

Вольт-амперная характеристика — это линейная зависимость. Поэтому ее графиком служит прямая линия.

Закон в простой форме

Исследования Ома по изучению вольт-амперных характеристик проводников показали, что сила тока внутри металлического проводника пропорциональна разности потенциалов на его концах (I ~ U) и обратно пропорциональна некоему коэффициенту, то есть I ~ 1/R. Этот коэффициент стал называться «сопротивление проводника», а единица измерения электрического сопротивления — Ом или В/А.

Стоит отметить еще вот что. Закон Ома часто используется для расчета сопротивления в цепях.

Формулировка закона

Закон Ома говорит, что сила тока (I) отдельно взятого участка цепи пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.

Следует заметить, что в таком виде закон остается верным только для однородного участка цепи. Однородной называется та часть электрической цепи, которая не содержит источника тока. Как пользоваться законом Ома в неоднородной цепи, будет рассмотрено ниже.

Позже опытным путем было установлено, что закон остается справедливым и для растворов электролитов в электрической цепи.

Физический смысл сопротивления

Сопротивление — это свойство материалов, веществ или сред препятствовать прохождению электрического тока. Количественно сопротивление в 1 Ом означает, что в проводнике при напряжении 1 В на его концах способен проходить электрический ток силой 1 А.

Удельное электрическое сопротивление

Экспериментальным методом было установлено, что сопротивление электрического тока проводника зависит от его размеров: длина, ширина, высота. А также от его формы (сфера, цилиндр) и материала, из которого он сделан. Таким образом, формула удельного сопротивления, например, однородного цилиндрического проводника будет: R = р*l/S.

Если в этой формуле положить s = 1 м² и l = 1 м, то R численно будет равен р.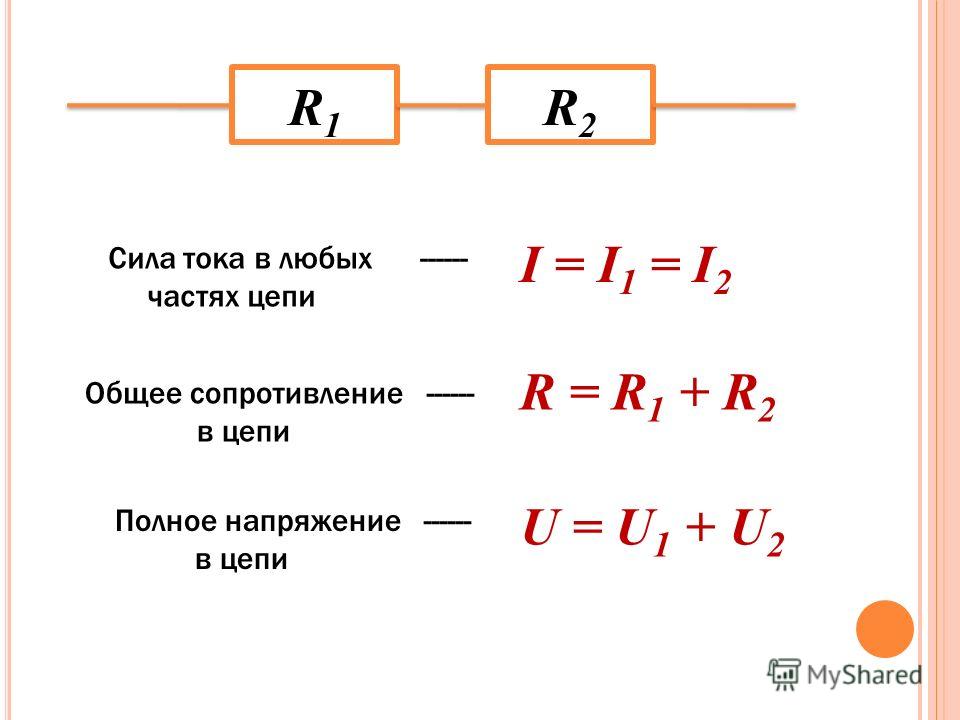 Отсюда вычисляется единица измерения для коэффициента удельного сопротивления проводника в СИ — это Ом*м.

В формуле удельного сопротивления р — это коэффициент сопротивления, определяемый химическими свойствами материала, из которого изготовлен проводник.

Для рассмотрения дифференциальной формы закона Ома, необходимо рассмотреть еще несколько понятий.

Плотность тока

Как известно, электрический ток — это строго упорядоченное движение любых заряженных частиц. Например, в металлах носителями тока выступают электроны, а в проводящих газах — ионы.

Возьмем тривиальный случай, когда все носители тока однородны — металлический проводник. Мысленно выделим в этом проводнике бесконечно малый объем и обозначим через u среднюю (дрейфовую, упорядоченную) скорость электронов во взятом объеме. Далее пусть n обозначает концентрацию носителей тока в единице объема.

Теперь проведем бесконечно малую площадь dS перпендикулярно вектору u и построим вдоль скорости бесконечно малый цилиндр с высотой u*dt, где dt — обозначает время, за которое все носители скорости тока, содержавшиеся в рассматриваемом объеме, пройдут сквозь площадку dS.

При этом электронами сквозь площадку будет перенесен заряд, равный q = n*e*u*dS*dt, где e — заряд электрона. Таким образом, плотность электрического тока — это вектор j = n*e*u, обозначающий количество заряда, переносимого в единицу времени через единицу площади.

Один из плюсов дифференциального определения закона Ома заключается в том, что часто можно обойтись без расчета сопротивления.

Электрический заряд. Напряженность электрического поля

Напряженность поля наряду с электрическим зарядом является фундаментальным параметром в теории электричества. При этом количественное представление о них можно получить из простых опытов, доступных школьникам.

Для простоты рассуждений будем рассматривать электростатическое поле. Это электрическое поле, которое не изменяется со временем. Такое поле может быть создано неподвижными электрическими зарядами.

Также для наших целей необходим пробный заряд. В его качестве будем использовать заряженное тело — настолько малое, что оно не способно вызывать какие-либо возмущения (перераспределение зарядов) в окружающих объектах.

Рассмотрим поочередно два взятых пробных заряда, последовательно помещенных в одну точку пространства, находящуюся под воздействием электростатического поля. Получается, что заряды будут подвергаться неизменному во времени воздействию с его стороны. Пусть F₁ и F₂ — это силы, воздействующие на заряды.

В результате обобщения опытных данных было установлено, что силы F₁ и F₂ направлены либо в одну, либо в противоположные стороны, а их отношение F₁/F₂ является независимым от точки пространства, куда были поочередно помещены пробные заряды. Следовательно, отношение F₁/F₂ является характеристикой исключительно самих зарядов, и никак не зависит от поля.

Открытие данного факта позволило охарактеризовать электризацию тел и в дальнейшем было названо электрическим зарядом. Таким образом, по определению получается q₁/q₂ = F₁/F₂, где q₁ и q₂ — величина зарядов, помещаемых в одну точку поля, а F₁ и F₂ — силы, действующие на заряды со стороны поля.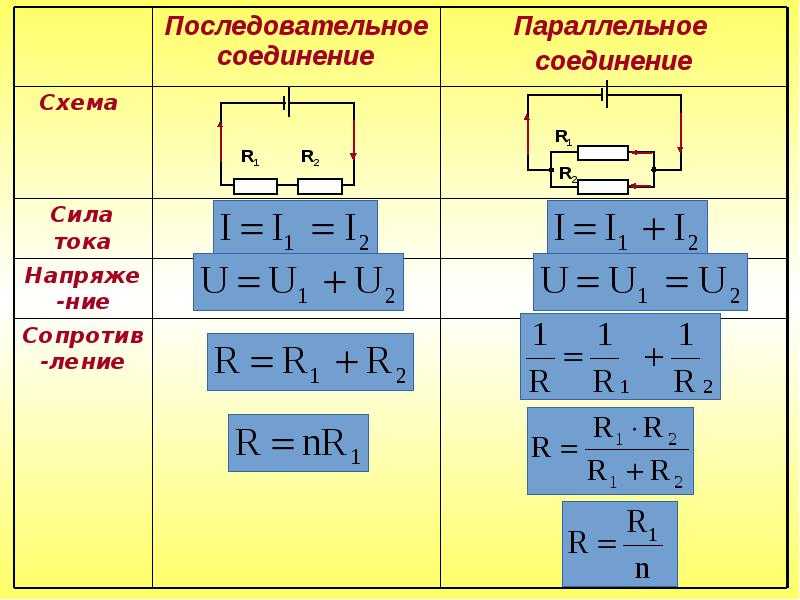

Из подобных соображений были экспериментально установлены величины зарядов различных частиц. Условно положив в соотношение один из пробных зарядов равным единице, можно вычислить величину другого заряда, измерив соотношение F₁/F₂.

Через известный заряд можно охарактеризовать любое электрическое поле. Таким образом, сила, действующая на единичный пробный заряд, находящийся в состоянии покоя, называется напряженностью электрического поля и обозначается E. Из определения заряда получаем, что вектор напряженности имеет следующий вид: E = F/q.

Связь векторов j и E. Другая форма закона Ома

В однородном проводнике упорядоченное движение заряженных частиц будет происходить по направлению вектора E. А это значит, что векторы j и E будут сонаправлены. Как и при определении плотности тока, выделим в проводнике бесконечно малый цилиндрический объем. Тогда через поперечное сечение этого цилиндра будет проходить ток, равный j*dS, а напряжение, приложенное к цилиндру, будет равно E*dl.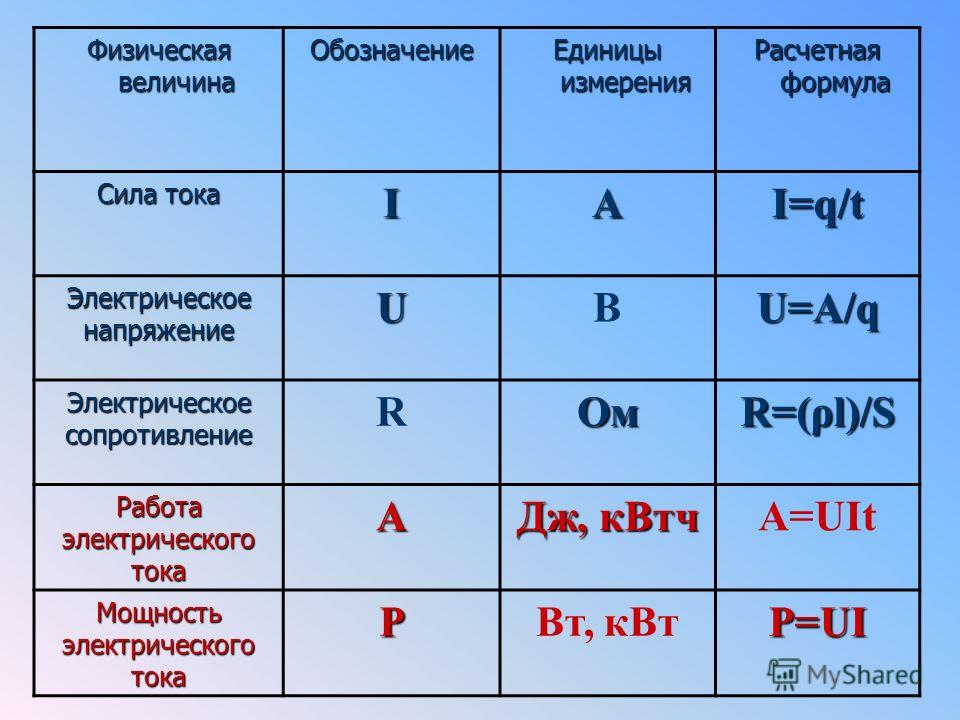 Также известна формула удельного сопротивления цилиндра.

Тогда, записав формулу силы тока двумя способами, получим: j = E/р, где величина 1/р носит название удельной электрической проводимости и является обратной к удельному электрическому сопротивлению. Ее принято обозначать σ (сигма) или λ (лямбда). Единицей измерения проводимости является См/м, где См — это Сименс. Единица, обратная Ом.

Таким образом, можно ответить на вопрос, поставленный выше, о законе Ома для неоднородной цепи. В таком случае на носителей тока будет действовать сила со стороны электростатического поля, которая характеризуется напряженностью E₁, и другие силы, воздействующие на них со стороны другого источника тока, которые можно обозначить E₂. Тогда Закон Ома применительно к неоднородному участку цепи будет иметь вид: j = λ(E₁ + E₂).

Подробнее о проводимости и сопротивлении

Способность проводника проводить электрический ток характеризуется его удельным сопротивлением, которое можно найти через формулу удельного сопротивления, или удельной проводимостью, рассчитывающейся как обратное проводимости. Величина данных параметров определяется как химическими свойствами материала проводника, так и внешними условиями. В частности температурой окружающей среды.

Для большинства металлов удельное сопротивление при нормальной температуре пропорционально ей, то есть р ~ T. Однако при низких температурах наблюдаются отклонения. У большого ряда металлов и сплавов при температурах, близких к 0°К, расчет сопротивления показывал нулевые значения. Это явление получило название сверхпроводимости. Таким свойством обладают, например, ртуть, олово, свинец, алюминий и др. Для каждого металла существует свое критическое значение температуры T_k, при которой наблюдается явление сверхпроводимости.

Также отметим, что определение удельного сопротивления цилиндра можно обобщить для проводов, состоящих из одного материала. В таком случае площадь поперечного сечения из формулы удельного сопротивления будет равна сечению провода, а l — его длине.

Сопротивление воздуха: определение, формула и пример

У вас когда-нибудь возникало ощущение, что что-то пытается замедлить вас, когда вы едете на велосипеде? Когда вы движетесь вперед, сила трения воздуха снижает вашу скорость.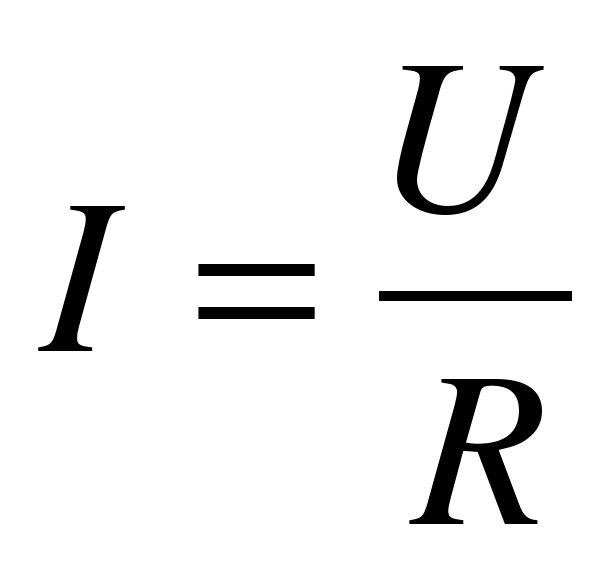 Сила трения действует на ваше лицо и тело в направлении, противоположном движению велосипеда. Сила сопротивления воздуха увеличивается пропорционально скорости. Приседание на велосипеде позволяет уменьшить влияние силы сопротивления воздуха и двигаться быстрее.

Сейчас вы можете думать о силе сопротивления воздуха как о чем-то негативном и препятствующем движению, но на самом деле она оказывается весьма полезной в нашей повседневной жизни. Например, когда парашютист выпрыгивает из самолета и раскрывает парашют, воздух замедляет падение. Скорость парашютиста уменьшается по мере приближения к земле из-за сопротивления воздуха. В результате человек благополучно и плавно достигает земли — все из-за силы сопротивления. В этой статье мы более подробно обсудим науку о сопротивлении воздуха.

Определение сопротивления воздуха

До сих пор в большинстве физических задач, связанных с движением, прямо указывалось, что сопротивлением воздуха можно пренебречь. В реальной жизни это не так, поскольку все объекты испытывают определенный уровень сопротивления при прохождении через воздух.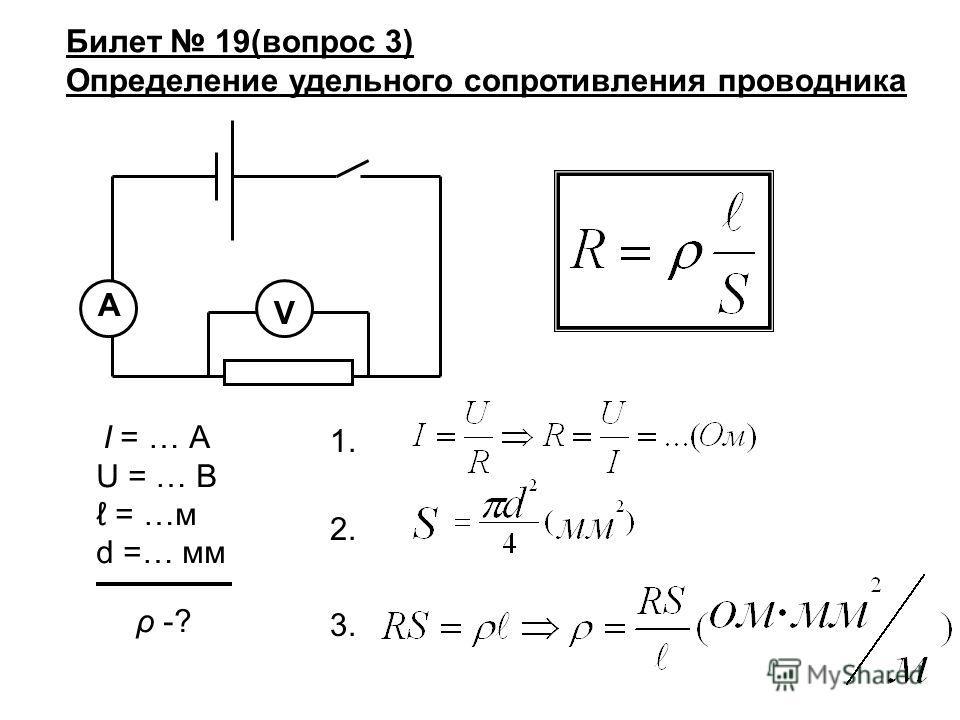

Сопротивление воздуха или Сопротивление Сила Тип трения, возникающего между объектом и окружающим его воздухом.

Эти силы сопротивления заставляют объект двигаться медленнее, действуя в направлении входящего потока и пропорциональны скорости. Это тип неконсервативных сил, поскольку он заставляет энергию рассеиваться.

Допустим, у нас есть мяч массой \(m\). Мы бросаем его, и когда он падает, на него действует сила сопротивления. Сила сопротивления математически равна

$$ \vec{F}_{\mathrm{r}} = — k \vec{v} $$

, где \(k\) — положительная постоянная, а \( v\) — скорость тела относительно среды. Знак минус указывает на то, что сила сопротивления направлена ​​против скорости.

На данном этапе вашего обучения достаточно знать эту версию уравнения силы сопротивления, однако более точное и реалистичное представление сопротивления воздуха будет дано выражением \(\vec{F}_{\mathrm{r}} = — k \vec{v}^2\).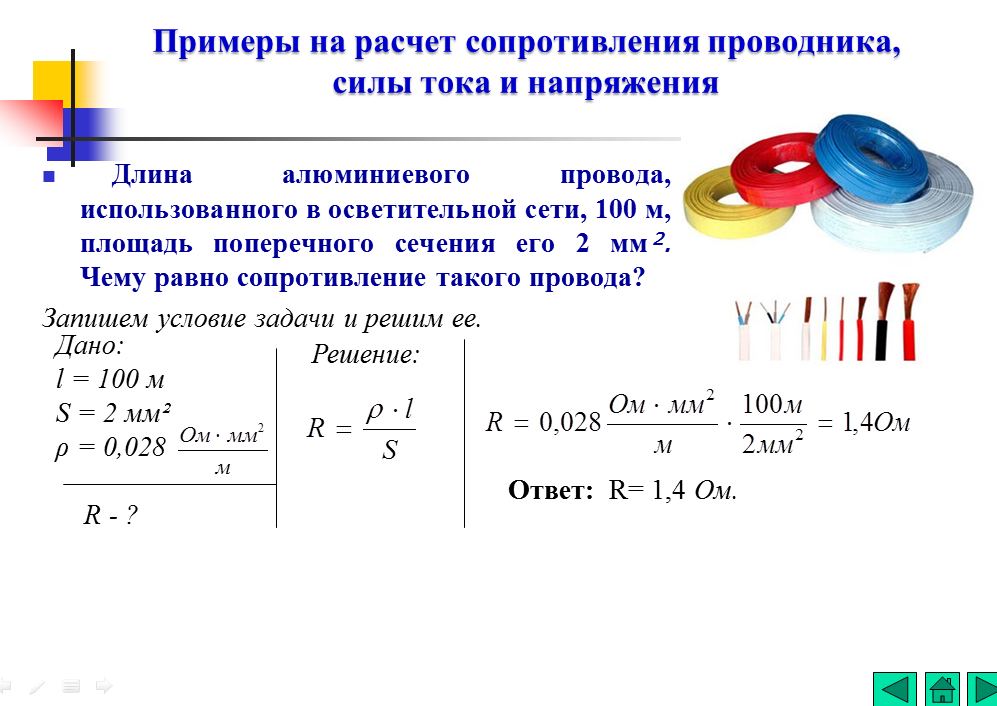 Подробнее об этом читайте в глубоком погружении! 92\). К сожалению, такой глубокий анализ сопротивления воздуха выходит за рамки уровня AP Physics, поэтому мы будем рассматривать сопротивление воздуха, линейное по скорости воздуха.

Коэффициент сопротивления воздуха

Как обсуждалось ранее, \(k\) является константой пропорциональности. Его значение определяется свойствами среды и уникальными характеристиками объекта. Основными факторами, влияющими на это, являются плотность среды, площадь поверхности объекта и безразмерная величина, известная как коэффициент сопротивления. В реальном примере с парашютистом средой будет воздух, а площадь поверхности будет относиться либо к парашютисту, либо к парашюту. 92$$

где \(D\) — коэффициент сопротивления, \(\rho\) — плотность среды, \(A\) — площадь поверхности объекта, \(\vec{v} \) — скорость.

Давайте посмотрим на диаграмму свободного тела, чтобы лучше понять его движение.

Диаграмма сопротивления воздуха в свободном состоянии

Что происходит с объектом, когда он падает и падает? На него действует нисходящая сила в виде веса и сила сопротивления в направлении, противоположном движению, из-за сопротивления воздуха, оба из которых визуализируются на диаграмме свободного тела, видимой ниже.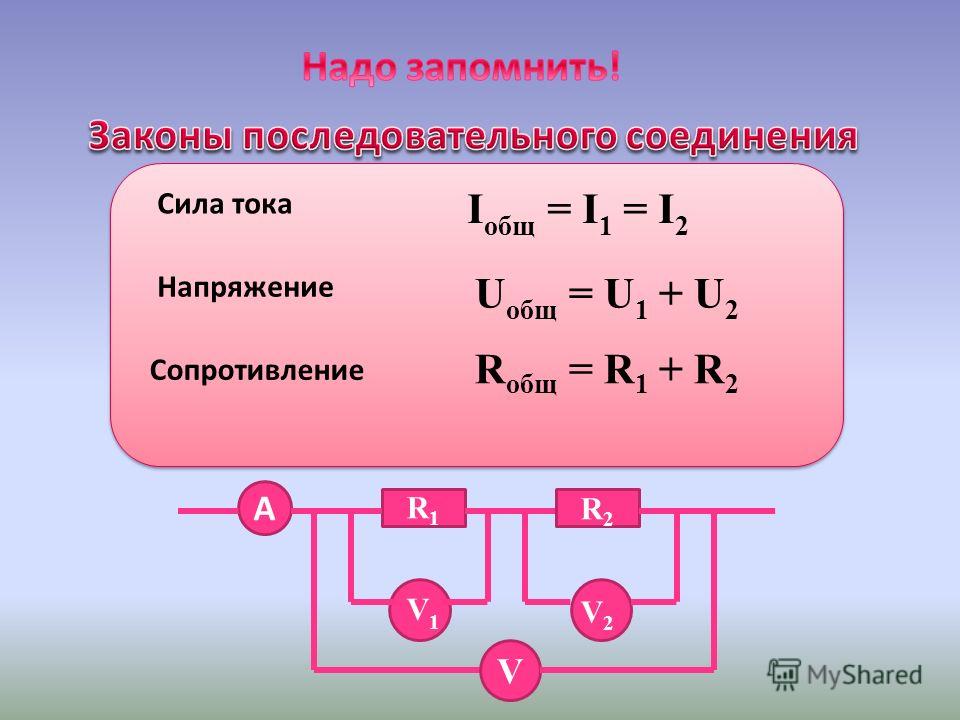

Рис. 1 — Когда объект падает, сила сопротивления действует на него вверх, в то время как вес тянет его вниз.

Согласно второму закону Ньютона, результирующая сила, действующая на объект \(\vec{F}_{\mathrm{net}}\), равна массе \(m\) объекта, умноженной на его ускорение \( \vec{а}\). Итак, зная все это, мы можем получить следующее выражение

$$ m\vec{g} — k\vec{v} = m\vec{a}.$$

0\), его начальная скорость равна \(\vec{v}_0=0\), следовательно, начальная сила сопротивления воздуха также равна нулю. По прошествии времени, когда объект начинает двигаться, в конце концов он достигает постоянной скорости, которая называется конечной скоростью \(\vec{v}_\mathrm{T}\). Поскольку скорость постоянна, ускорение будет равно нулю. Правая часть выражения становится равной нулю, и мы можем переставить оставшиеся члены

$$ m\vec{g} = k\vec{v}_\mathrm{T} $$

найти уравнение для конечной скорости

$$ \vec{v}_\mathrm{T}= \frac{m\vec{g}}{k}. $$

Конечная скорость – это максимальная скорость, достигаемая объектом, движущимся под действием постоянной силы и силы сопротивления, действующих на объект в противоположных направлениях.

Конечная скорость достигается, когда к объекту не прилагается результирующая сила, что означает, что ускорение равно нулю. Давайте рассмотрим пример задачи, связанной с предельной скоростью.

Формула сопротивления воздуха

Теперь найдем скорость как функцию времени. Для этого нам нужно преобразовать второй закон Ньютона в дифференциальное уравнение. Ускорение является первой производной скорости, поэтому \(\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\). Тогда мы можем написать

$$ m\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=m\vec{g}-k\vec{v}. $$

Разделим наши переменные:

$$ \frac{\mathrm{d}v}{mg- kv}=\frac{\mathrm{d}t}{m}.$$

Чтобы выполнить все необходимые математические операции, мы пока рассмотрим только одно измерение и будем рассматривать векторные величины как скаляры.

Здесь важно установить пределы интегрирования. Время идет от нуля до времени \(t_{\mathrm{f}}\). Когда время равно нулю, наша начальная скорость также равна нулю, а по мере того, как время приближается к \(t_{\mathrm{f}}\), наша скорость становится скоростью \(v_{\mathrm{f}}\).

Причина, по которой мы не устанавливаем верхний предел конечной скорости, заключается в том, что мы пытаемся найти скорость как функцию времени! 9{-\frac{t_{\mathrm{f}}}{T}}) $$

, где \(T\) — постоянная времени и равна \(\frac{m}{k}\) .

Вот как мы получаем выражение скорости как функцию времени! Окончательное уравнение подтверждает наши предыдущие выводы о конечной скорости. Если значение \(t_{\mathrm{f}}\) установлено равным нулю, \(\vec{v_{\mathrm{f}}}\) также будет равно нулю, между тем, если \(t_{\mathrm {f}}\) установлен на что-то огромное, скажем, бесконечность, у нас останется \(\vec{v_{\mathrm{f}}} = \vec{v_\mathrm{T}}\).

Что же произошло бы, если бы начальная скорость была не нулевой?

Допустим, у нас есть автомобиль с начальной скоростью \(\vec{v}_0\) против некоторой силы сопротивления \(\vec{F}_\mathrm{r}\), которая снова равна \(-k \vec{v}\). Когда мы рисуем диаграмму свободного тела автомобиля, вес направлен вниз, нормальная сила направлена ​​вверх, а сила сопротивления воздуха направлена ​​в направлении, противоположном движению.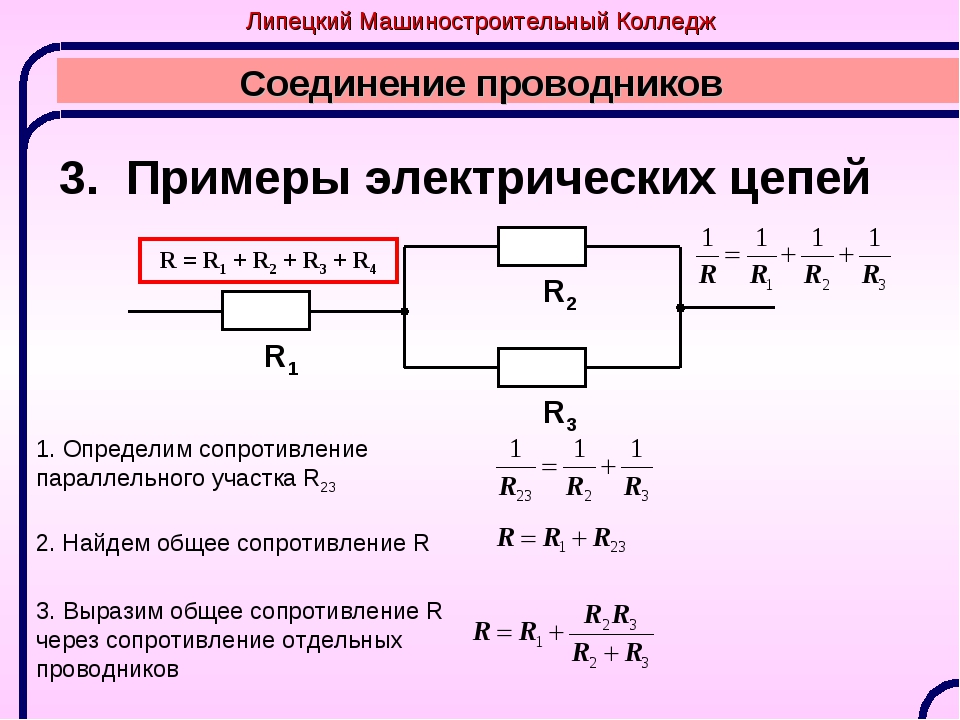

В этом случае конечная скорость будет равна нулю, и машина остановится. Единственная сила, действующая на объект в направлении движения, — это сила сопротивления, поэтому это будет наша результирующая сила. Тогда мы можем написать

$$ m\vec{a} = -k\vec{v}.$$

Мы собираемся повторить ту же процедуру, что и ранее, поскольку это становится дифференциальным уравнением, когда мы записываем ускорение как \(\vec{a }=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\) и получить

$$ \begin{align} m \frac{\mathrm{d}\vec{v }}{\mathrm{d}t} & = — k\vec{v} \\ \frac{\mathrm{d}v}{v} & =\frac{-k}{m} \mathrm{d} т. \end{align}$$

Еще раз для расчетов рассмотрим скалярную версию уравнения. Здесь мы должны взять интегралы от обеих сторон, но сначала нам нужно определиться с пределами. Время снова идет от нуля до \(t\). Однако теперь у нас есть начальная скорость, поэтому наш предел скорости от \(v_0\) до \(v\) 9{\frac{-kt_{\mathrm{f}}}{m}}.$$

Пример сопротивления воздуха

Давайте рассмотрим пример задачи с тем же парашютистом, о котором упоминалось ранее, чтобы проверить наши знания!

Парашютист падает с начальной скоростью \(\vec{v}_0\) по воздуху. В этот момент (\(t = 0\)) они раскрывают парашют и испытывают силу сопротивления воздуха, величина которой определяется уравнением \(\vec{F} = -k\vec{v}\), где переменные такие же, как определены ранее. Суммарная масса парашютиста и снаряжения равна \(m\).

Определите выражение для ускорения парашютиста, конечной скорости и постройте график зависимости скорости от времени.

Решение

Мы знаем, что

$$ \vec{F}_{\mathrm{net}} = \vec{F}_\mathrm{g} — \vec{F}_\mathrm{r } $$

поэтому, рассматривая диаграмму свободного тела, описанную ранее, мы можем найти выражение для ускорения

$$ \begin{align} m\vec{a} & = m\vec{g} — k\vec{ v}, \\ \vec{a} & = \frac{m\vec{g} — k\vec{v}}{m}.\end{align}$$

Основываясь на предыдущем определении, парашютист достигнет своей конечной скорости, когда скорость постоянна (\(\vec{v} = \vec{v}_\mathrm{T}\)). Это означает, что ускорение становится равным нулю. \vec{v}_\mathrm{T} = \frac{m\vec{g}}{k}. $$

Теперь воспользуемся этим выражением для построения графика зависимости скорости от времени.

Рис. 3. Изменения скорости от начального спуска парашютиста до момента, когда они приближаются к конечной скорости с течением времени. Градиент этого графика представляет собой ускорение парашютиста.

Первоначально парашютист спускается со скоростью \(\vec{v}_0\) и ускоряется примерно с ускорением свободного падения \(\vec{g}\). При раскрытии парашюта на парашютиста действует значительная сила сопротивления — сопротивление воздуха. Ускорение от силы сопротивления приводит к восходящему ускорению, поэтому нисходящая скорость уменьшается. Градиент нашего графика зависимости скорости от времени представляет собой ускорение. Основываясь на предыдущих наблюдениях, она не будет постоянной, а скорее будет приближаться к нулю, когда скорость достигает конечной скорости \(\vec{v}_\mathrm{T}\). В результате сюжет нелинейный.

Некоторые другие примеры сопротивления воздуха в нашей повседневной жизни:

1. Прогулка в шторм довольно часто затрудняет ходьбу. Человек, идущий против ветра, испытывает значительное сопротивление, что затрудняет продвижение вперед. По той же причине сложно держать зонт в руке при сильном ветре.

2. Перо, падающее на землю , имеет тенденцию плавать и двигаться медленно, а не падать в течение нескольких секунд, как другие объекты, немного большей массы. Сила гравитации притягивает перо к земле; однако сила сопротивления воздуха предотвращает падение или движение пера во время движения.

3. Бумажные самолетики , если они собраны правильно, легко летают в воздухе. Для этого переднюю поверхность бумажного самолета затачивают. В результате бумажный самолет рассекает воздух и избегает силы сопротивления воздуха ровно настолько, чтобы дольше оставаться в воздухе.

4. Двигатель настоящего самолета , крылья и пропеллеры созданы для обеспечения достаточной тяги, чтобы помочь самолету преодолеть силу сопротивления воздуха. Турбулентность также вызвана трением, которое создает воздух. Однако космические корабли должны беспокоиться только о сопротивлении воздуха при запуске и посадке, поскольку в космосе воздуха нет.

Сопротивление воздуха — основные выводы

• Силы, препятствующие относительному движению объекта при его движении в воздухе, называются сопротивлением воздуха.
• Эти силы сопротивления заставляют объект двигаться медленнее, действуя в направлении набегающего потока и пропорциональны скорости.
• Математическое выражение для сопротивления воздуха: \( \vec{F}_\mathrm{r} = — k \vec{v}\), где отрицательный знак указывает на противоположное направление движения.
• Конечная скорость определяется как максимальная скорость, достигаемая объектом, движущимся под действием постоянной силы и силы сопротивления, действующих на объект в противоположных направлениях.
• Когда к объекту не прилагается результирующая сила, что означает, что ускорение равно нулю, достигается конечное состояние.
• Некоторые примеры сопротивления воздуха включают ходьбу во время шторма, падение пера на землю, бумажный самолетик, самолет, парашютиста с парашютом и езду на велосипеде.

Схема — Схемы — Физика 106

Схема — схемы Электрические цепи. Определение терминов Электрический ток I равен скорости протекания тока. Для постоянного тока I = q/t. Для переменного тока I = dq/dt. На рис. 1 выше электрон движется в проводнике с эквивалент постоянной скорости дрейфа v d в постоянное электрическое поле E. В действительности электрон испытывает серия ускорений в электрическом поле после столкновений с ядрами и внутренними электронами атомов, составляющих материал. Пусть n = число электронов/объем, e заряд электрона, A площадь поперечного сечения проводника, а L его длина = v д т, где t — время, за которое электрон проходит длину проводника. Тогда суммарный заряд в движении равен q = neAv d t а ток I = q/t = neAv d . Пример задачи в 106 Набор задач для цепей : 1. Сопротивления Сопротивление R проводника прямо пропорционально к его длине L, обратно пропорционально его поперечному сечению области A и зависит от сопротивления материала r. R = rL/А. Закон Ома. Разность потенциалов V ab через сопротивление R от a до b с током I от a до b определяется законом Ома, эмпирическим законом, В аб = ИК. Комбинации резисторов Резисторы в серии Ток I одинаков в каждом резисторе Разность потенциалов на всех резисторах равна сумме индивидуальных разностей потенциалов: В аб = В ac + В кд + В дБ R экв. = В аб /I = В ac /I + V кд /I + V db /I = R 1 + R 2 + R 3 (рис. 2а ниже) Резисторы параллельно Разность потенциалов В аб между все резисторы одинаковые. Суммарный ток I равен сумме токов в каждом из резисторов:   I = I 1 + Я 2 + Я 3 I/V ab = I 1 /V ab + I 2 /V аб + I 3 /V аб 1/R экв. = 1/R 1 + 1/R 2 + 1/R 3  (рис. 2b ниже) Примеры задач в 106 Набор задач для цепей : 2, 3, 7. Мощность Мощность = P = (U a — U b )/t = q(V a — V b )/t = (q/t)(V a — V b ) = IV ab Приведенное выше утверждение всегда верно. Если элемент цепи между a и b является омическим резистор, для которого V ab = IR, тогда P = I(V ab ) может можно записать как P = I(IR) = I 2 R   или P = (I)V ab  можно записать как P = (V ab /R)V ab = (V аб ) 2 /R. Пример задачи в 106 Набор задач для цепей : 4. Электродвижущая сила e Электродвижущая сила e = энергия/заряд = U/q или qe = U и мощность = P = U/t = (q/t)e = Ie. Для схемы, показанной на рис. 3 выше, r — внутреннее сопротивление. аккумулятора. Для этой цепи: Потребляемая мощность = выходная мощность Химическая энергия в электрическую = электрическая энергия в тепло Ie = I 2 R + I 2 r         (уравнение 1) Из уравнения. 1, I = e/(R + r) е — Ир = ИК = В аб Напряжение на клеммах аккумулятора В аб = е-Ир Примеры задач в 106 Проблема Набор для цепей : 5, 8. Правила Кирхгофа Правило соединения. Сумма токов, входящих в любой переход равна сумме токов, выходящих из этого соединения. Этот это просто утверждение о сохранении заряда. Правило цикла. Сумма разностей потенциалов по каждому элемент вокруг любой замкнутой цепи равен нулю. Это только заявление о сохранении энергии. Если перейти от минуса к плюсу батареи, химическая энергия превращается в электрическую и вы собираете энергию, поэтому знак плюс. 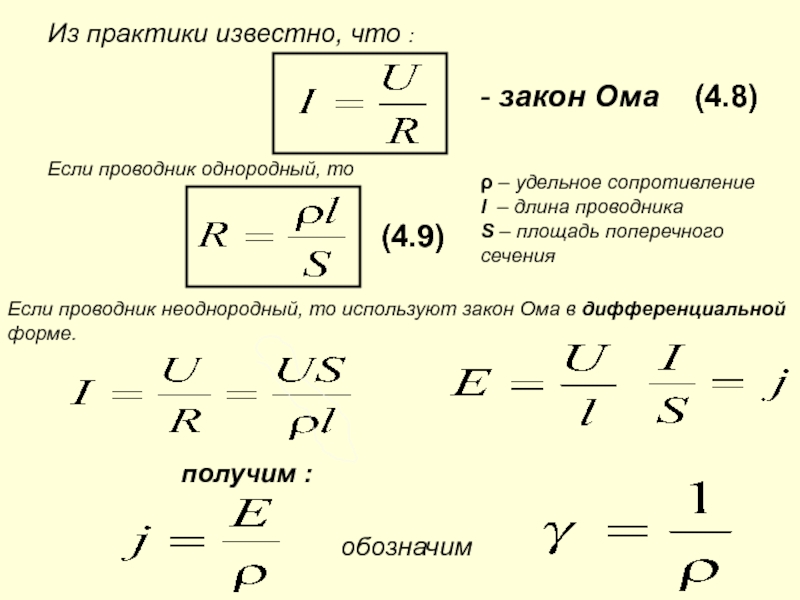Если перейти от плюса батареи к минусу знак, знак отрицательный. Если обойти петлю в том же направлении, что и ток, электрическая энергия превращается в тепло, и вы теряете энергию поэтому этот IR отрицателен. Если пройти по петле напротив к направлению течения, вы идете от более низкий потенциал к более высокому потенциалу, поэтому этот IR положительный. Общий комментарий. Как только вы выбираете направления токов, и обходя петлю по часовой стрелке или против часовой стрелки, оставайтесь с ним. Вы можете изменить направление движения вокруг петли для второй петли, но не меняйте направления течений. Пример задачи в 106 Набор задач для цепей:  9. RC-цепи Разность потенциалов на омическом резисторе = IR и на конденсаторе = q/C Когда переключатель S переведен в положение зарядки Используя правило цикла, находим е = ИК + к/с. Поскольку I = dq/dt, мы можем записать это как е = dq/dt R + q/C             (Уравнение 2) Арифметика дает нам (dq/dt)RC = -(q — eC)          (Уравнение 3) Разделение переменных: dq/(q — EC) = -1/RC dt              (Уравнение 4) Интеграция с обеих сторон: или ln [(q-eC)/-eC} = -t/RC              (Уравнение 5) Взяв антилогарифм обеих частей уравнения. 5: (q-eC)/-eC = е -t/RC q — eC = -eC(e -t/RC ) или наконец, q(t) = eC(1 — e -t/RC ) (Уравнение 6) Разность потенциалов на конденсаторе для зарядки конденсатор V cb иногда называют В С = q/C = e(1 — e -t/RC  ). (Уравнение 7) Текущий I = dq/dt = e/R( е -т/RC  ) (Уравнение 8) Разность потенциалов на резисторе для зарядки конденсатор В ac  иногда называется В Р = ИК = е( e -t/RC  )               (Уравнение 9) Для рисунков 4 (вверху) и 5 ​​(внизу) я выбрал e = 1,0 В, R = 10 6 Вт = 10 6 В/А, и C = 5 x 10 -6 F = 5 х 10 -6 К/В. Постоянная времени = RC =10 6 В/А x 5 x 10 -6 В/В = 5 В/А = 5 Кл/(Кл/с) = 5 с. Для накопления заряда,  В C (t) = e(1 — e -t/RC ). Когда t = RC = 5 с, В C (RC) = 1,0 В (1 — e -RC/RC ) = 1,0 V(1 — e -1 ) = 1,0 В(0,632) = 0,632 В, как показано ниже. Для накопления заряда  V R (t) = ee -t/RC . Когда t = RC = 5 с, В C (RC) = 1,0 В ( e -RC/RC ) = 1,0 V(e -1 ) = 1,0 В (0,368) = 0,368 В, как показано выше. При переводе переключателя в нижнее положение батарея больше не в цепи и конденсатор разряжается. В аб = 0 = IR + q/C = dq/dt R + q/C              (уравнение 10) Преобразование уравнения: dq/q = -dt/RC Пределы теперь от максимального заряда Q = eC к q, когда t изменяется от 0 до t. Конденсатор разряжается а я в противоположном направлении. ln q/eC = — t/RC или q(t) = Qe -t/RC = eCe -t/RC                   (Уравнение 11) I(t) = dq/dt = -(eC/RC)e -t/RC = — (e/R)e -t/RC V cb = V C = q/C = ee -t/RC и    V ac = ИК = -ee -т/RC Ссылаясь на рис. 5b ниже, Для распада заряда, В C (t) = e е -т/RC . Когда t = RC = 5 с, В C (RC) = 1,0 В (e -RC/RC ) = 1,0 В ( e -1 ) = 1,0 В (0,368) = 0,368 В. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника