СУНЦ УрФУ
Расписание
Электронный журнал
Поступающим
Олимпиады, турниры, конкурсы
Планы работы
Подготовительные курсы
Новости:
24.10.2022
СУНЦ на конкурсе «Университетская книга»
Издания СУНЦ УрФУ получили высокую оценку на межрегиональном конкурсе.
20.10.2022
УрКОП: шаг вперёд сделан!
Учащийся СУНЦ в составе команды стал победителем командной олимпиады по программированию.
19.10.2022
«Любите общагу!»
Лицеисты, живущие в интернате, поздравили воспитателей.
14.10.2022
СУНЦ как кузница ученых будущего
Лицеист СУНЦ стал победителем международного конкурса в номинации «Математика».
07.10.2022
Все учителя СУНЦ — бриллианты!
Под этим девизом пятого октября в СУНЦ прошел концерт в честь Дня учителя.
29.09.2022
Лицеисты СУНЦ покорили хребет Зюраткуль!
В последние выходные сентября учащиеся СУНЦ побывали в национальном парке «Зюраткуль».
Больше новостей
Видеогалерея:
Концерт к Дню учителя (2022)
Репортаж ТРК «Вести-Урал» о гаджетах у школьника (2022)
Концерт, посвященный Дню Победы (5 мая 2022 года)
Больше видео
О нас:
Специализированный учебно-научный центр (СУНЦ) — структурное подразделение ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина», созданное в 1990 году как нетиповое структурное подразделение вуза, осуществляющее углубленное дифференцированное обучение по программам основного общего и среднего общего образования. Всего в России 10 СУНЦев. До мая 2011 года СУНЦ работал в составе Уральского государственного университета имени А. М. Горького (УрГУ).
В настоящее время СУНЦ имеет в своем составе 8 кафедр, укомплектованных профессорско-преподавательским составом УрФУ и учителями. Обучение производится по авторским программам, разработанным в соответствии с федеральными государственными образовательными стандартами; в составе СУНЦ — 8–11 классы различных профилей.
Иногородние обучающиеся проживают в уютном общежитии.
Прием производится в 8, 9 и 10 классы. Работают подготовительные курсы.
Подробнее о правилах приема в СУНЦ можно узнать в отделе конкурсного отбора
Как нас найти:
Данилы Зверева ул., 30, Екатеринбург. N56°52´4˝ E60°39´16˝
Проезд:
- автобусами № 48, 52, 81 до остановки «Фирма Авангард»;
- автобусами № 28, 58 до остановки «Данилы Зверева», далее 7 минут пешком по улице Данилы Зверева;
- троллейбусом № 18 до остановки «Данилы Зверева», далее 14 минут пешком по улицам Сулимова, Данилы Зверева;
- троллейбусами № 4 до остановки «Сулимова», № 12, 19 до остановки «Боровая», далее 15 минут пешком по улицам Боровая, Вилонова, Данилы Зверева.
Эквивалентное сопротивление что это? — Электрика от А до Я
Содержание
- 2 Как найти R эквивалентное формула?
- 3 Как найти общее сопротивление в треугольнике?
- 4 Как найти сопротивление по схеме?
- 5 Как найти эквивалентное сопротивление в цепи?
- 6 Чему равно эквивалентное сопротивление?
- 7 Как найти R в параллельном соединении?
- 8 Как найти напряжение?
- 9 Как найти r2 при параллельном соединении?
- 10 Как найти общее сопротивление в электрической цепи?
- 11 Как определить общее сопротивление сложной цепи?
- 12 В чем разница между соединением звездой и треугольником?
- 13 Как рассчитать сопротивление динамика?
- 14 Как рассчитать сопротивление на участке цепи?
Что такое эквивалентное сопротивление?
эквивалентное сопротивление импульсного трансформатора — Электрическое сопротивление, равное отношению произведения внутреннего сопротивления генератора и приведенного сопротивления нагрузки по эквивалентной схеме импульсного трансформатора к их сумме [ГОСТ 20938 75] Тематики трансформатор… …
Как найти R эквивалентное формула?
е.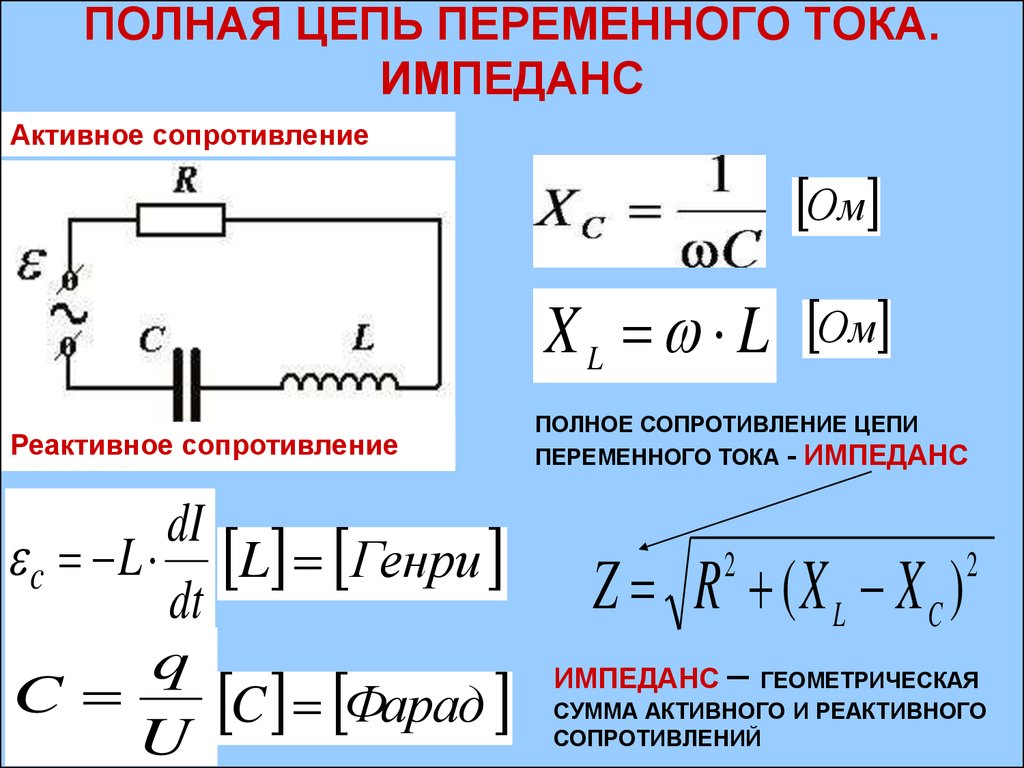 эквивалентное сопротивление. Точно так же для каждой ветви I1 = U1 / R1, I2 = U2 / R2, где I1 и I2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.
эквивалентное сопротивление. Точно так же для каждой ветви I1 = U1 / R1, I2 = U2 / R2, где I1 и I2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.
Как найти общее сопротивление в треугольнике?
Расчет сопротивления схемы с преобразованием треугольник-звезда. Сопротивления R12, R13, R23 найдены по формулам 1-3: Чтобы найти сопротивление луча звезды надо произведение сопротивлений прилегающих к нему сторон треугольника разделить на сумму сопротивлений всех сторон треугольника.
Как найти сопротивление по схеме?
Как найти эквивалентное сопротивление в цепи?
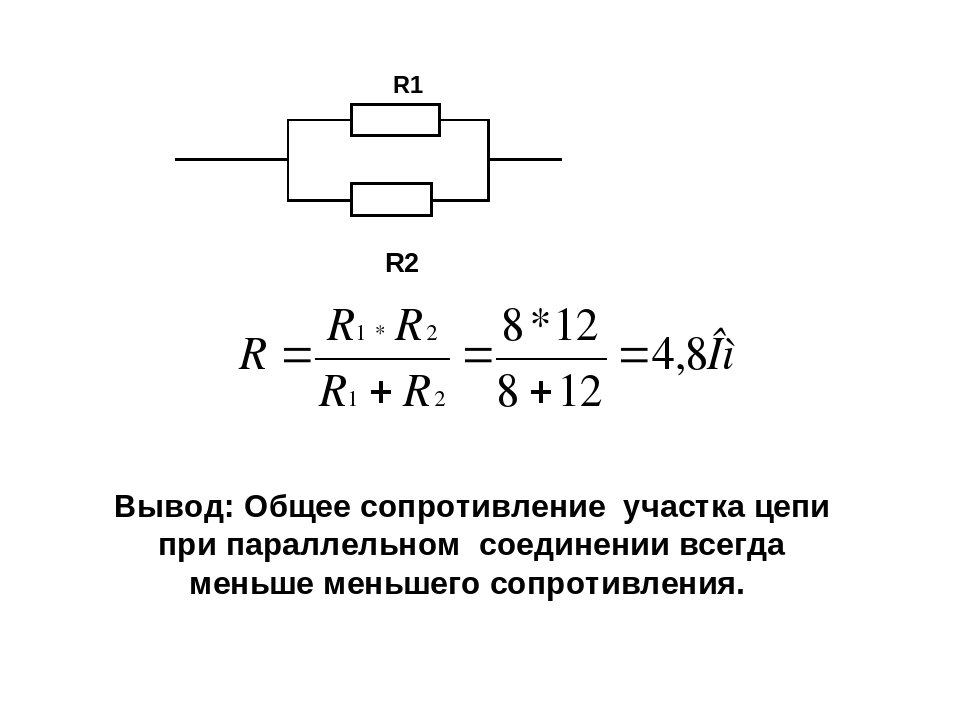
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв.
 = R1+R2.
= R1+R2.
Чему равно эквивалентное сопротивление?
Резисторы соединены последовательно, если по ним течет один и тот же ток. Эквивалентное сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме их сопротивлений: .
Как найти R в параллельном соединении?
Общее сопротивление цепи при параллельном соединении проводников определяется по формуле: 1 R = 1 R 1 + 1 R 2 . Обратное значение общего сопротивления равно сумме обратных значений сопротивлений отдельных проводников. Для проверки формулы можно использовать омметр.
Как найти напряжение?
Как найти r2 при параллельном соединении?
Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + … + (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ.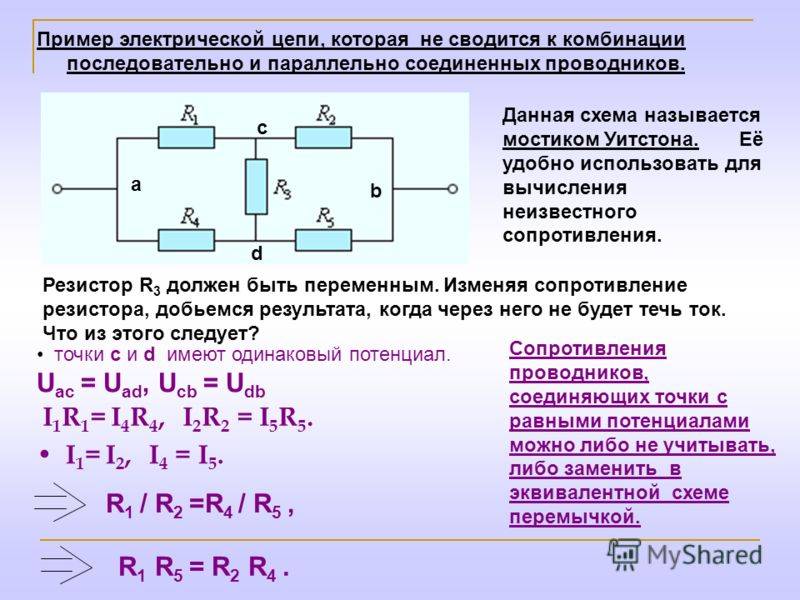
Как найти общее сопротивление в электрической цепи?
Формула для вычисления общего сопротивления последовательной цепи: Req = R1 + R2 + …. Rn где n — общее количество резисторов в цепи, соединенных последовательно. Таким образом, сопротивления всех резисторов просто суммируются. Например, найдем сопротивление цепи, показанной на рисунке.
Как определить общее сопротивление сложной цепи?
R = R1 + R2. При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников. Этот результат справедлив для любого числа последовательно соединенных проводников. При параллельном соединении (рис.
В чем разница между соединением звездой и треугольником?
В схеме соединения треугольник конец одной обмотки монтируется с началом следующей обмотки. Электродвигатель с обмотками, соединенными звездой работает более плавно, чем двигатель с соединением в треугольник. … При соединении в треугольник мощность двигателя почти в полтора раза выше, чем при соединении в звезду.
Как рассчитать сопротивление динамика?
При последовательном соединении сопротивление динамиков рассчитывается по формуле: R = R1 + R2, где R — сопротивление, которое мы получим в результате такого соединения, а R1 и R2 — сопротивление динамиков 1 и 2. Сопротивление большего количества динамиков рассчитывается аналогично: R = R1 + R2 + R3 + …
Как рассчитать сопротивление на участке цепи?
Сопротивление на участке цепи рассчитывается по классической формуле R = U I . Для этого необходимо установить значения напряжения и тока. Сопротивление – отношение напряжения к току.
Как измерить сопротивление | Hioki
Хотите узнать об измерении сопротивления? Основные методы измерения сопротивления, меры предосторожности и сопутствующая информация
Обзор
Электрическое сопротивление играет чрезвычайно важную роль в схемах электронных устройств. Такие устройства могут выйти из строя, если сопротивление в их цепях отклоняется от должного уровня. Однако электричества не видно. Для проверки правильности сопротивления цепи необходим специальный измерительный прибор.
Такие устройства могут выйти из строя, если сопротивление в их цепях отклоняется от должного уровня. Однако электричества не видно. Для проверки правильности сопротивления цепи необходим специальный измерительный прибор.
Для измерения сопротивления необходим такой прибор, как тестер, но как выполняется такое измерение? На этой странице подробно описано, как можно использовать тестер или мультиметр для измерения сопротивления.
Как измеряется сопротивление?
Сопротивление измеряется с помощью такого прибора, как аналоговый или цифровой мультиметр. Оба типа приборов могут измерять не только сопротивление, но и ток, напряжение и другие параметры, поэтому их можно использовать в самых разных ситуациях.
Однако измерение сопротивления не включает измерение самого значения сопротивления цепи. Вместо этого сопротивление рассчитывается путем измерения тока и напряжения, приложенных к цепи. Когда ток подается на измеряемую цепь, в цепи (сопротивлении) появляется напряжение (точнее, падение напряжения). Сопротивление можно рассчитать, измерив ток и напряжение по закону Ома.
Сопротивление можно рассчитать, измерив ток и напряжение по закону Ома.
В результате можно определить значение сопротивления цепи, если известны измеренные значения тока и напряжения. Аналоговые мультиметры и цифровые мультиметры используют принцип измерения закона Ома для измерения сопротивления.
Измерение сопротивления аналоговым тестером
При измерении сопротивления аналоговым мультиметром отключите питание измеряемой цепи. Подключите красный щуп к положительному входному разъему с отметкой «+», а черный щуп — к входному разъему COM. Переключите прибор в режим Ω и установите кнопку диапазона в соответствии с ожидаемым сопротивлением цепи.
Закоротите черный и красный контрольные контакты и установите стрелку на 0 Ом с помощью ручки регулировки 0 Ом. Затем поместите красный и черный контрольные штырьки в контакт с обоими концами измеряемой цепи и считайте значение, показанное измерителем.
Имейте в виду, что подача напряжения на измерительные провода, когда прибор находится в режиме сопротивления, может повредить тестер.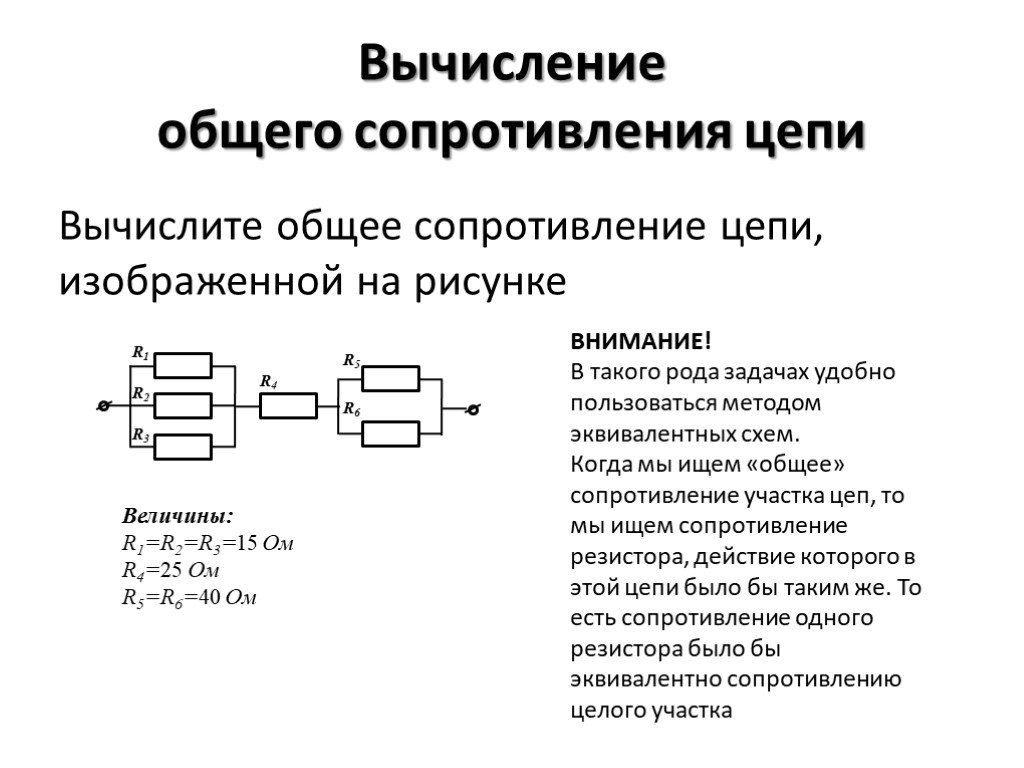
Всегда выполняйте настройку нуля при измерении сопротивления.
(механическая и электрическая установка нуля)
Ситуации, в которых подается напряжение, опасны, поэтому разделение имеет решающее значение.
Измерение сопротивления цифровым мультиметром
В целом сопротивление измеряется цифровым мультиметром так же, как и аналоговым мультиметром, и это очень простой процесс. Единственное отличие состоит в том, что значение указывается в цифровом виде, а не аналоговой стрелкой; в остальном основной метод в основном такой же. Однако цифровые мультиметры поддерживают два метода измерения:
В большинстве случаев при измерении сопротивления цифровым мультиметром используется метод измерения с двумя клеммами. В этом методе применяется постоянный ток и измеряется значение сопротивления с помощью вольтметра прибора. Этот метод такой же, как и в аналоговых мультиметрах. Однако недостатком двухполюсного измерения является получение значений сопротивления, которые включают проводку между прибором и измеряемой цепью.
Этот метод такой же, как и в аналоговых мультиметрах. Однако недостатком двухполюсного измерения является получение значений сопротивления, которые включают проводку между прибором и измеряемой цепью.
Чтобы свести к минимуму влияние этого дополнительного сопротивления, измерительные провода закорачивают перед измерением, чтобы скорректировать значение сопротивления до нуля. Однако этот метод не может полностью устранить последствия. Для устранения этого недостатка было создано четырехтерминальное измерение. Четырехконтактное измерение использует четыре измерительных провода и отдельные цепи вольтметра и амперметра.
Существуют различные типы сопротивления, включая сопротивление проводов, реле и разъемов, а также внутреннее сопротивление батарей, поэтому важно использовать правильный прибор для выполнения поставленной задачи измерения. Покупая инструмент, выберите тот, который подходит для ваших целей.
Источники погрешности при измерении сопротивления
Сопротивление проводки измерительных проводов не является единственным фактором, влияющим на результаты измерения значения сопротивления.
- Электродвижущая сила
- Тепловой шум
- Ток утечки
- Диэлектрическая абсорбция
- Шум трения
- Внешний шум
- Измерители температуры, влажности и ветра
- снижают функциональность влияние температуры и других факторов, например, путем считывания разницы между температурным датчиком, подключенным к измерителю, и эталонной температурой и соответствующей корректировки значений сопротивления. Если измеренные значения сопротивления демонстрируют нестабильность, вам необходимо оценить, какие факторы влияют на измерение, и принять меры для их устранения.
- Resistance Meter RM3544
- Resistance Meter RM3548
- Resistance Meter RM3545
- HiTester 3030-10
- Battery HiTester BT3562A
- Какова общая сила тока в показанной цепи? Дайте свой ответ на
один десятичный знак.

- Какова общая мощность, рассеиваемая цепью? Дай свой ответ до одного десятичного знака.
- Какие показания будут на амперметре? Дай свой ответ
до одного десятичного знака.

- Какими были бы показания амперметра, если бы он был подключен к параллельно Резистор 3,5 Ом? Отдай свое ответ до одного десятичного знака.
- Какой ток через Резистор 20 Ом?
- Какой ток на минусовой клемме Батарея 5,0 В?
- Какой ток на отрицательной клемме Аккумулятор 10,0 В?
- Найти текущий 𝐼. Отдай свое ответ до двух знаков после запятой.
- Найти текущий 𝐼. Дайте ответ на два десятичные разряды.
- Найдите разность потенциалов на неизвестном резисторе.
 Дайте свой ответ на
Ближайшая
вольт.
Дайте свой ответ на
Ближайшая
вольт.
Rt = Rt0 × { 1 + αt0 × (t — t0) }
Rt:Фактически протестированное сопротивление [Ом]
Rt0:Компенсированное сопротивление [Ом]
t0:Опорная температура [°C]
t:Текущая температура окружающей среды [°C]
αt0:Температурный коэффициент при t0
Используя измеритель сопротивления с температурной компенсацией, вы можете автоматически фиксировать значение сопротивления, преобразованное в температуру.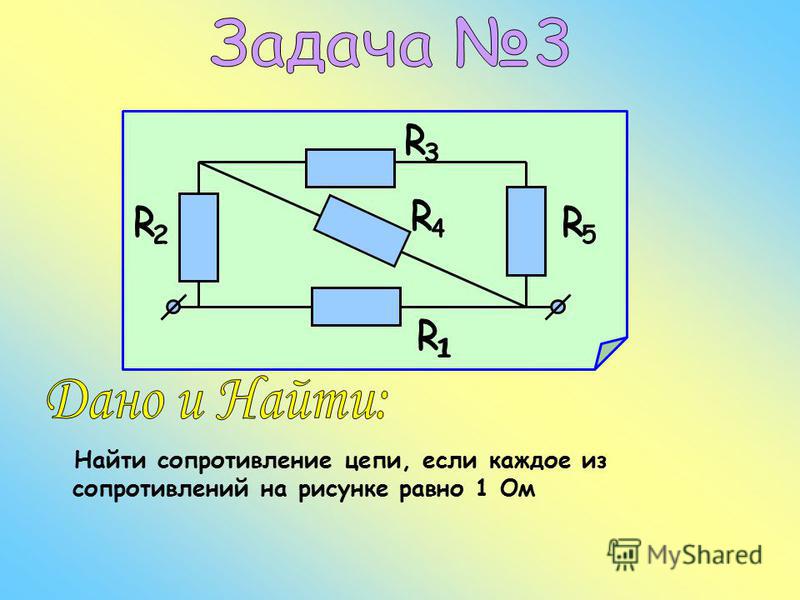
Используйте четырехконтактный измеритель сопротивления для более точного измерения низкого сопротивления.
Аналоговые мультиметры и цифровые мультиметры используют закон Ома для расчета сопротивления на основе тока и напряжения, а не измерения самого сопротивления. Оба типа инструментов используются одинаково. Цифровые приборы обеспечивают такие функции, как измерение с четырьмя клеммами для большей точности.
На значения сопротивления влияют различные внешние воздействия. Если результаты измерения демонстрируют нестабильность, необходимо определить причину и принять меры для ее устранения.
Applications
How to Use
Related Products
Lesson Explainer: Analyzing Combination Circuits
В этом объяснителе мы научимся определять токи через и
напряжения на участках цепей, содержащих резисторы как последовательно, так и
параллельно.
Напомним, что последовательно соединенные резисторы соединяются в один проводящий путь. На приведенной ниже схеме показаны три последовательно соединенных резистора.
В показанном выше примере полное сопротивление цепи, 𝑅, это 𝑅=𝑅+𝑅+𝑅.
Это распространяется на любое количество последовательно соединенных резисторов: 𝑅=𝑅+𝑅+⋯+𝑅.
токопроводящие пути. На приведенной ниже схеме показаны три резистора, соединенные последовательно. параллельно.
В показанном выше примере полное сопротивление цепи, 𝑅, это 𝑅=1𝑅+1𝑅+1𝑅.
Это распространяется на любое количество резисторов, включенных параллельно: 𝑅=1𝑅+1𝑅+⋯+1𝑅.
Комбинированная схема содержит секции резисторов, соединенных последовательно и параллельно. На приведенной ниже схеме показаны два резистора, соединенные последовательно с двумя резисторы параллельно.
В приведенном выше примере участок цепи, содержащий
𝑅 и 𝑅 последовательно, а участок цепи, содержащий
𝑅 и 𝑅 параллельны.
Для анализа этой схемы каждый набор резисторов можно преобразовать в их эквивалентный резистор. На приведенной ниже диаграмме показано, как последовательно подключить два резистора. и два резистора параллельно могут быть преобразованы в один эквивалентный резисторы, которые затем могут быть преобразованы в окончательный эквивалентный резистор для вся схема.
Раздел серии, содержащий 𝑅 и 𝑅 можно преобразовать в его эквивалентный резистор, 𝑅: 𝑅=𝑅+𝑅.
Параллельная секция, содержащая 𝑅 и 𝑅 можно преобразовать в эквивалентный ему резистор, 𝑅: 𝑅=1𝑅+1𝑅.
Затем, наконец, эквивалентное сопротивление всей цепи, 𝑅, это 𝑅=𝑅+𝑅.
Давайте рассмотрим пример этого вопроса.
Пример 1: Определение эквивалентного сопротивления комбинированной цепи
Показанная схема содержит как последовательные, так и параллельные комбинации резисторов.
Ответ
Часть 1
В первой части этого вопроса мы должны рассчитать общий ток в схема. Для этого необходимо найти эквивалентное сопротивление схема.
Мы начнем с обозначения компонентов на принципиальной схеме.
Первый шаг в расчете эквивалентного сопротивления цепи: найти эквивалентное сопротивление параллельного участка, состоящего из 𝑅 и 𝑅. Обозначим эквивалентное сопротивление этого параллельного участка на 𝑅: 𝑅=1𝑅+1𝑅.
Подстановка известных значений для 𝑅=2,5Ом и 𝑅=3,2Ω дает нам 𝑅=12,5+13,2𝑅=1,40.ΩΩΩΩ
Теперь мы можем рассчитать эквивалентное сопротивление всей цепи, 𝑅: 𝑅=𝑅+𝑅+𝑅.
Подставляя известные значения для
𝑅=1,6Ω и
𝑅=1,5Ом
и значение 𝑅, которое мы рассчитали как
1,40 Ом дает нам
𝑅=1,6+1,5+1,4𝑅=4,5.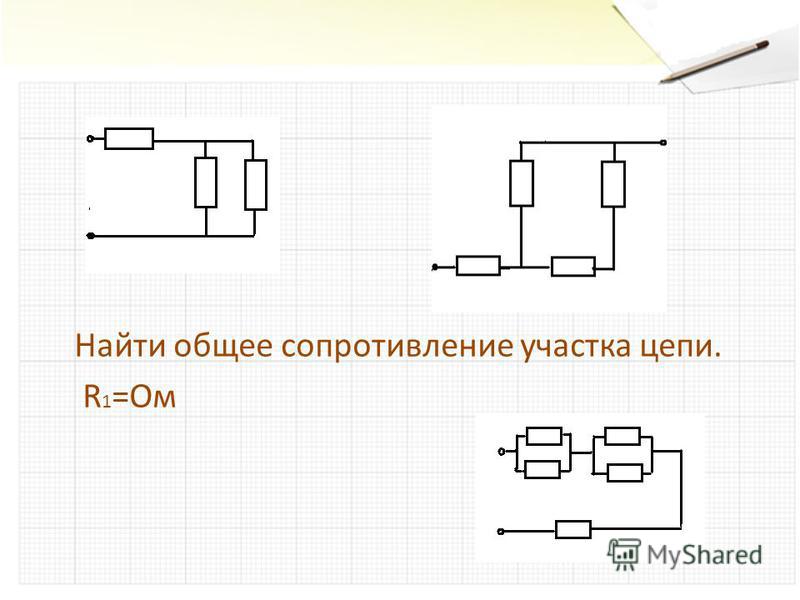 ΩΩΩΩΩ
ΩΩΩΩΩ
Тогда мы можем использовать закон Ома для расчета полного тока в цепи, при 𝑉=5,5 В: 𝐼=𝑉𝑅𝐼=5,54,5.ВОм
Суммарный ток в цепи с точностью до одного десятичного знака составляет 𝐼=1.2.A
Часть 2
Полная мощность, рассеиваемая в цепи, может быть рассчитана путем умножения ток в цепи на полное падение потенциала на схема: 𝑃=𝐼𝑉𝑃=1,2×5,5.AV
Полная мощность, рассеиваемая в цепи, с точностью до одного десятичного знака равна 𝑃=6.7.W
Эти методы анализа комбинированных цепей также можно использовать для анализировать схемы, содержащие компоненты, отличные от резисторов. Мы сейчас проработайте пример вопроса об этом.
Пример 2. Анализ цепей, содержащих компоненты, отличные от Резисторы
Ток измеряется амперметром в цепи, показанной на схеме. Амперметр имеет сопротивление 2,5 мкОм.
Ответ
Часть 1
В первой части вопроса нам предлагается рассчитать сумму текущего через цепь. Для этой цели мы можем заменить амперметр на резистор эквивалентного сопротивления.
Мы можем обобщить это на диаграмме, где каждый резистор помечен. 𝑅 — эквивалентное сопротивление для амперметра.
Общее сопротивление цепи равно 𝑅=𝑅+𝑅+𝑅𝑅=2,5+3,5+2,5×10𝑅=6,0000025.ΩΩΩΩΩ
Ток в цепи можно рассчитать по закону Ома: 𝐼=126,0000025𝐼=1,9999991.VΩA
Амперметр будет показывать до одного десятичного знака 2,0 А. Давайте сравните это с идеальным амперметром, который имеет нулевое внутреннее сопротивление.
Общее сопротивление цепи будет точно равно сумме
из двух резисторов:
𝑅=2,5+3,5𝑅=6,0. ΩΩΩΩ
ΩΩΩΩ
Это означает, что ток в цепи равен 𝐼=126.0𝐼=2.0.VΩA
Таким образом, амперметр покажет точно 2,0 А. Это подчеркивает, насколько важно иметь амперметр с очень низким внутреннее сопротивление. Если внутреннее сопротивление достаточно низкое, т. в данном примере, им можно пренебречь при расчетах.
Часть 2
Во второй части вопроса нам предлагается рассмотреть, что произойдет, если амперметр будет подключен параллельно Резистор 3,5 Ом.
Заменив амперметр его эквивалентным резистором, мы можем нарисуй на схеме.
Теперь мы должны рассчитать эквивалентное сопротивление, 𝑅, параллельного участка цепи: 𝑅=13,5+12,5×10𝑅=(0,28+400000)𝑅=400000,28𝑅=2,499998×10,ΩΩΩ
7 Здесь сопротивление
7 амперметр такой низкий по сравнению
до 3,5 Ом
резистора, что он полностью доминирует над эквивалентным сопротивлением
два.
Тогда общее сопротивление цепи равно 𝑅=2,5+2,499998×10𝑅=2,5000025, Ом
Ток в цепи можно рассчитать по закону Ома: 𝐼=122,5000025𝐼=4,799995.VΩA
Итак, с точностью до одного десятичного знака амперметр показывает 4,8 А.
Рассчитаем показание тока, если эквивалентное сопротивление параллельным сечением в расчете пренебрегают: 𝐼=122,5𝐼=4,8.VΩA
Как видно, внутреннее сопротивление амперметра настолько мало, что эквивалентным сопротивлением параллельного участка можно пренебречь.
В то время как эквивалентное сопротивление позволяет нам анализировать многие комбинированные схемы, есть некоторые, которые нельзя решить, используя только эквивалентное сопротивление.
Цепь, показанная на следующей принципиальной схеме, не может быть проанализирована с помощью только эквивалентное сопротивление.
Поскольку есть две батареи, мы не можем рассчитать эквивалентное сопротивление
из 𝑅 и 𝑅.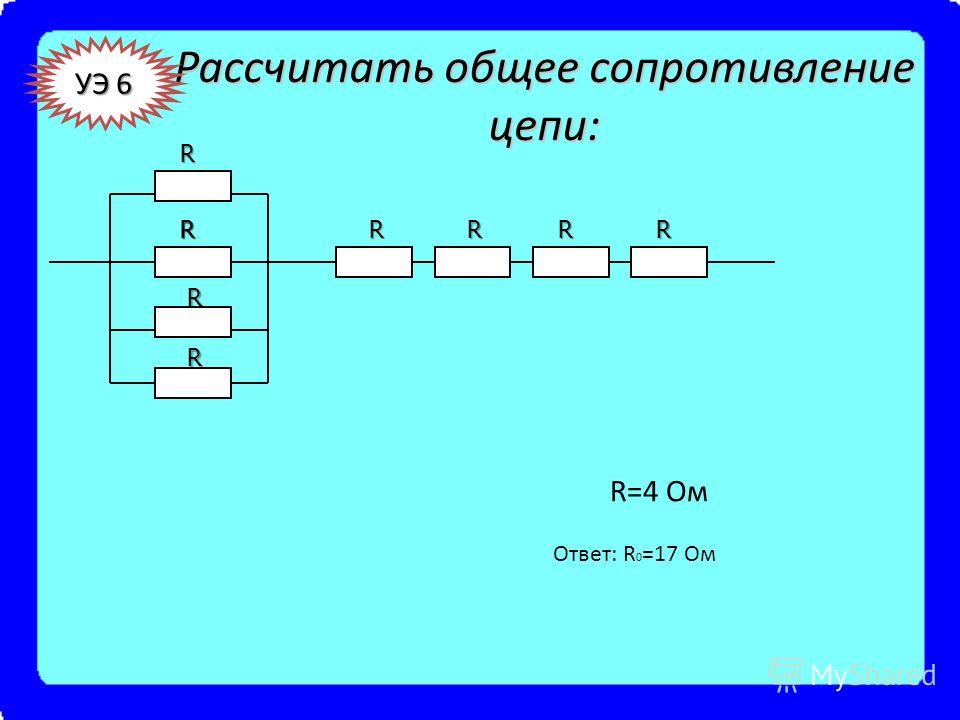
Для анализа таких цепей мы можем использовать законы Кирхгофа.
Первый закон Кирхгофа гласит, что ток в переходе или узле в цепь должна быть такой же, как и ток, выходящий из перехода или узла.
Определение: Первый закон Кирхгофа
Первый закон Кирхгофа утверждает, что сумма токов в соединение/узел в цепи, 𝐼+𝐼+⋯()()inin, должно быть таким же, как сумма токов из узла/узла, 𝐼+𝐼+⋯()()outout: 𝐼+𝐼+⋯=𝐼+𝐼+⋯.()()()()ininoutout
Например, предположим, что в следующем соединении цепи есть токи 𝐼 и 𝐼 на перекрестке и 𝐼 с перекрестка.
Первый закон Кирхгофа гласит, что сумма токов в переходе, 𝐼+𝐼, должны равняться сумме токов из перекресток, 𝐼: 𝐼+𝐼=𝐼.
Второй закон Кирхгофа позволяет нам анализировать разность потенциалов на различных точках комбинационной цепи.
Второй закон Кирхгофа гласит, что сумма всех разностей потенциалов
между компонентами в цикле должны быть равны нулю.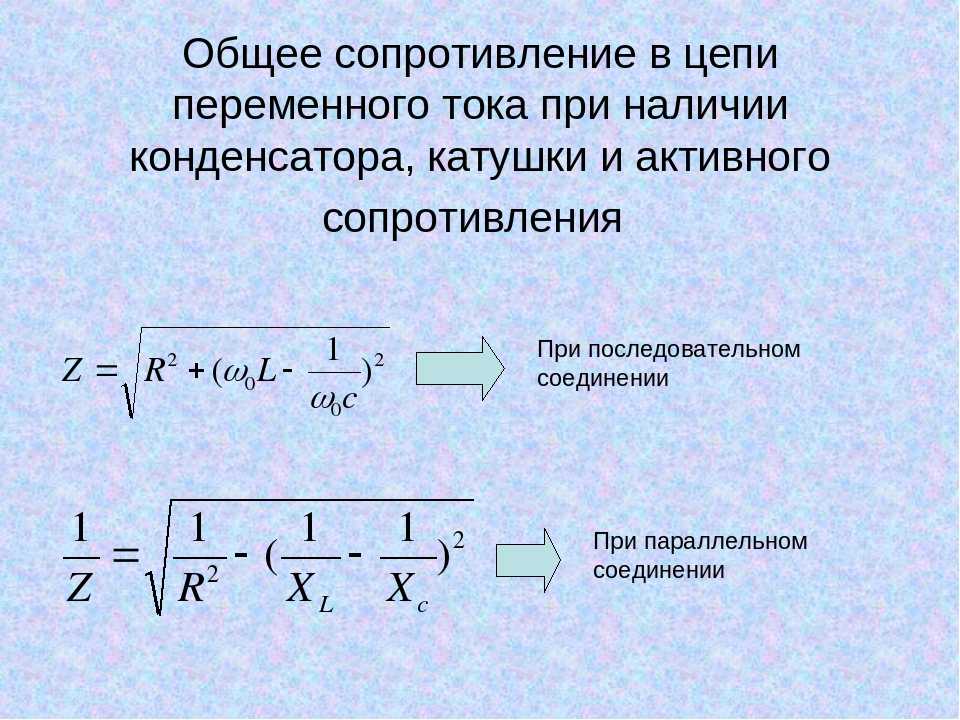
На следующей принципиальной схеме показано последовательное подключение трех резисторов к батарее.
Определение: второй закон Кирхгофа
Сумма разностей потенциалов на каждом компоненте контура равна нуль: 𝑉+𝑉+⋯+𝑉=0,
В схеме примера разность потенциалов на ячейке равна 𝑉, а на трех резисторах разность потенциалов равна 𝑉, 𝑉 и 𝑉 соответственно.
Закон Кирхгофа гласит, что сумма разностей потенциалов по всем компоненты в цикле равны нулю. То есть, 𝑉+𝑉+𝑉+𝑉=0,
В этом случае разность потенциалов на ячейке положительна и равна по модулю равна полной разности потенциалов на трех резисторы.
Законы Кирхгофа можно использовать для сравнения цепей. Мы будем работать через пример вопрос об этом сейчас.
Пример 3. Анализ нескольких похожих цепей
Схемы (a) и (b) кажутся очень похожими, но немного отличаются друг от друга.
Другой. Какова разница в полном токе между цепью, показанной на рис.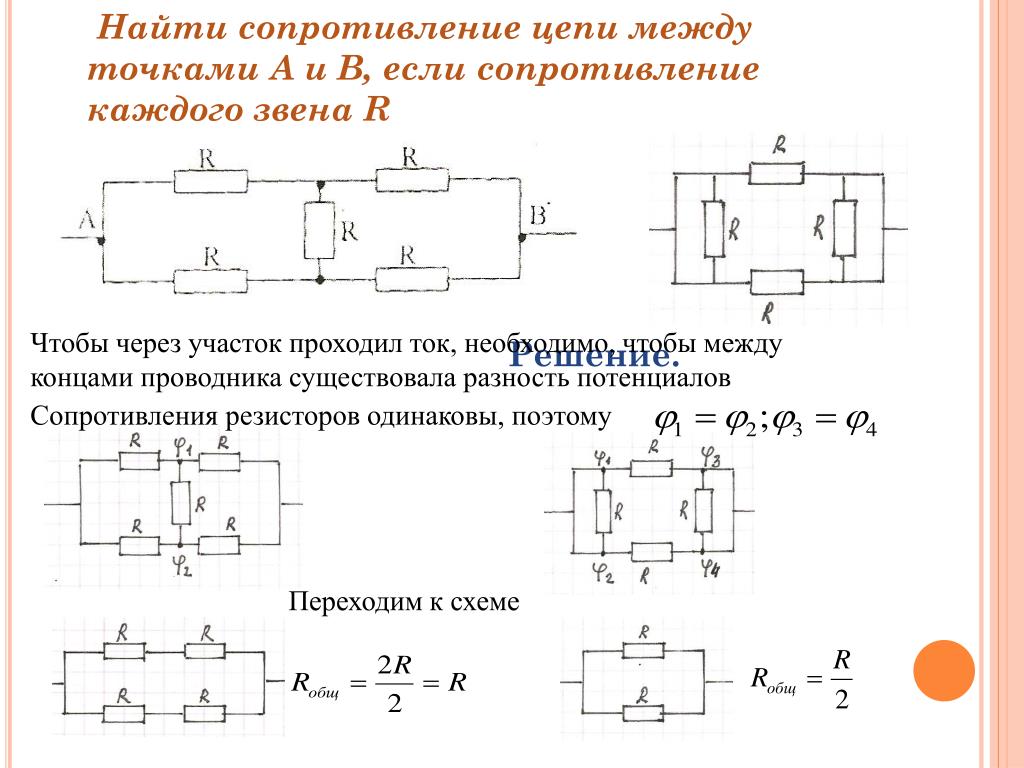 схеме (а) и цепи, показанной на схеме (б)? Дайте ответ с точностью до одного десятичного знака.
схеме (а) и цепи, показанной на схеме (б)? Дайте ответ с точностью до одного десятичного знака.
Ответ
Начнем с анализа схемы (б).
Мы можем использовать второй закон Кирхгофа для петли, образованной цепью. Отзывать что второй закон Кирхгофа гласит, что сумма разностей потенциалов по каждому компоненту в цикле должен равняться нулю.
Обозначим разность потенциалов на 800 мОм резистор как 𝑉 и разность потенциалов на Резистор 960 мОм как 𝑉.
Два резистора можно преобразовать в один эквивалентный резистор, который мы будет коллировать 𝑅 со следующим сопротивлением: 𝑅=880+960𝑅=1840.мОммОммОм
Разность потенциалов на этом эквивалентном резисторе равна 𝑉 и равно 𝑉=𝑉+𝑉.
Сумма разности потенциалов на каждом компоненте цепи (b)
можно записать как
2,5+1,4−𝑉−𝑉=0,ВВВ
или, учитывая эквивалентный резистор, 𝑅, это можно записать как
2,5+1,4−𝑉=0𝑉=3,9. VVVV
VVVV
Итак, разность потенциалов на этом эквивалентном резисторе равна 3,9 В.
Ток в цепи (b), 𝐼, можно рассчитать, используя Закон Ома, сначала преобразуя сопротивление из миллиомы в Ом: 𝐼=𝑉𝑅𝐼=3,91,84𝐼=2,12.VΩA
Теперь проанализируем схему (а).
Схема (а) почти идентична схеме (б), за исключением того, что Батарея 1,4 В есть перевернулся. Когда мы на этот раз применим второй закон Кирхгофа, эта батарея вносит в уравнение отрицательную разность потенциалов.
Объединение резисторов в эквивалентный резистор, как мы это делали ранее, мы можем написать 2,5−1,4−𝑉=0𝑉=1.1.VVVV
Итак, разность потенциалов на этом эквивалентном резисторе равна 1,1 В.
Ток в цепи (a), 𝐼, можно рассчитать, используя Закон Ома, сначала преобразуя сопротивление из миллиомы в Ом: 𝐼=𝑉𝑅𝐼=1,11,84𝐼=0,60.VΩA
Тогда разница токов между двумя цепями равна
𝐼−𝐼=2,12−0,06𝐼−𝐼=1,52. AAA
AAA
Разница в общем токе между цепью, показанной на схеме (а) и схема, показанная на диаграмме (б), поэтому 1,5 А до одного десятичного знака.
Законы Кирхгофа также можно использовать для анализа комбинационных цепей. Когда мы учитывая комбинированную схему, мы должны идентифицировать петли и соединения/узлы.
Например, следующая принципиальная схема содержит несколько резисторов и аккумуляторы в разных цепях цепи.
Мы можем идентифицировать два узла в этой цепи и три петли. Это проиллюстрировано на следующей диаграмме.
Теперь мы поработаем с примером вопроса, где мы должны использовать метод Кирхгофа. законы для анализа комбинационной цепи.
Пример 4. Использование законов Кирхгофа для анализа комбинационных цепей
На схеме показана схема, содержащая несколько ячеек.
Ответ
Часть 1
Начнем с обозначения принципиальной схемы.
Токи в каждой ветви цепи маркируются в соответствии с узел в нижней части цепи. Ток от Ячейка 10,0 В к узлу помечен 𝐼 и считается током в узел. Ток от узла к 20 Ом помечено 𝐼 и считается вне узла. Электрический ток от узла к Ячейка 5,0 В помечена 𝐼 и считается вне узла.
Мы можем применить второй закон Кирхгофа к каждому контуру цепи, чтобы найти разность потенциалов на каждом резисторе.
Начиная с цикла, содержащего 𝑉 и 𝑅, имеем 𝑉−𝑉=0,В поэтому разность потенциалов на 𝑅 равна 𝑉=10,0.V
Используя закон Ома, мы можем рассчитать ток через 𝑅: 𝐼=𝑉𝑅𝐼=10,020𝐼=0,5.VΩA
Это равно 𝐼. Ток через Резистор 20 Ом 𝐼 и, следовательно, равно 0,5 А.
Часть 2
Далее мы можем посмотреть на цикл, содержащий 𝑉, 𝑉 и 𝑅: 𝑉+𝑉−𝑉=05,0+10,0−𝑉=0,VVVV
Итак, разность потенциалов на 𝑅 равна
𝑉=15,0. V
V
Из закона Ома мы можем рассчитать ток через 𝑅: 𝐼=𝑉𝑅𝐼=15,015𝐼=1,0.VΩA
Это равно 𝐼. Ток на минусе терминал 5,0 А аккумулятор 𝐼 и, следовательно, равно 1,0 А.
Часть 3
Используя первый закон Кирхгофа, мы можем вычислить 𝐼 из узел в нижней части схемы: 𝐼=𝐼+𝐼𝐼=1.0+0.5=1.5.A
Ток на минусовой клемме Батарея 10,0 В есть 𝐼 и поэтому равно 1,5 А.
Пример 5. Использование законов Кирхгофа для анализа комбинационных цепей с Неизвестные компоненты
В показанной цепи сопротивление одного из резисторов неизвестно. Общая ток в цепи есть 0,25 А.
Ответ
Часть 1
Начнем с маркировки компонентов схемы.
В первой части вопроса нам предлагается найти 𝐼, ток через 𝑅. Для этого нам нужно найти разность потенциалов на параллельном участке цепи.
Мы можем преобразовать параллельный участок цепи в эквивалентный резистора по следующей формуле: 𝑅=1𝑅+1𝑅.
Вставка значений 𝑅=2,5Ом и 𝑅=3,2Ω дает нам 𝑅=12,5+13,2𝑅=1,40.ΩΩΩ
Зная, что ток в цепи 0,25 А, потенциал разницу между эквивалентным резистором можно рассчитать, используя сопротивление Ом. закон: 𝑉=𝐼𝑅𝑉=0,25×1,40𝑉=0,35.AΩV
Эта разность потенциалов одинакова на обеих ветвях параллельного участок цепи. Тогда ток 𝐼 может быть рассчитывается по закону Ома: 𝐼=𝑉𝑅𝐼=0,352,5𝐼=0,14.VΩA
Часть 2
Во второй части вопроса нам предлагается рассчитать текущий
𝐼.
Мы уже рассчитали разность потенциалов на параллели участок цепи, поэтому мы можем применить закон Ома к 𝑅: 𝐼=𝑉𝑅𝐼=0,353,2𝐼=0,11.VΩA
Часть 3
В третьей части этого вопроса нам предлагается рассчитать потенциал разница на неизвестном резисторе.
Мы можем использовать второй закон Кирхгофа, чтобы решить эту задачу. Кирхгофа Второй закон гласит, что сумма разностей потенциалов на каждом отдельная компонента в цикле равна нулю. Для этой схемы мы запишет разность потенциалов через 𝑅 как 𝑉, по параллельному сечению как 𝑉, а поперек 𝑅 как 𝑉: 12−𝑉−𝑉−𝑉=0,V
Мы уже рассчитали 𝑉=0,35В. 𝑉 можно рассчитать по закону Ома: 𝑉=𝐼𝑅𝑉=0,25×2,2𝑉=0,55.AΩV
Мы можем подставить их в уравнение для второго закона Кирхгофа, помня, что это уменьшение потенциала, поэтому они отрицательны: 12−𝑉−0,55−0,35=0,VVV
Затем мы можем изменить это, чтобы получить значение разности потенциалов
через 𝑅 неизвестный резистор:
𝑉=11,1.


 = R1+R2.
= R1+R2.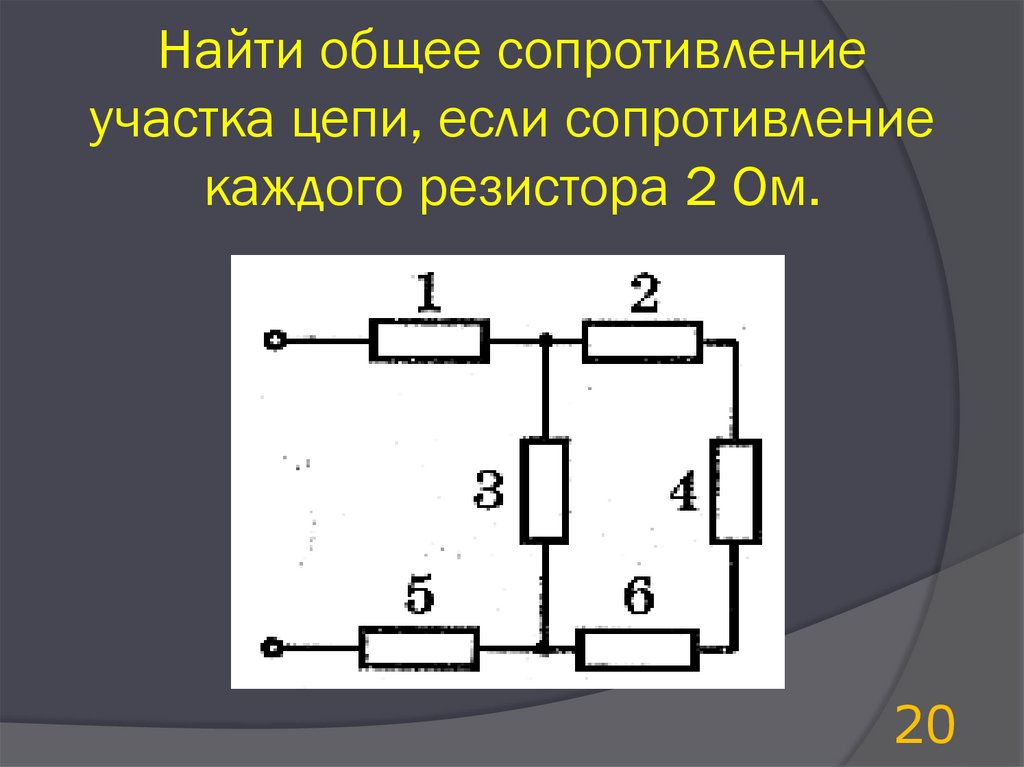

 Дайте свой ответ на
Ближайшая
вольт.
Дайте свой ответ на
Ближайшая
вольт.