Текущая плотность с учетом удельного сопротивления Калькулятор
| Search | ||
| Дом | физика ↺ | |
| физика | Текущее электричество ↺ | |
✖Электрическое поле определяется как электрическая сила на единицу заряда.ⓘ Электрическое поле [E] | Abvolt / СантиметрКиловольт / СантиметрКиловольт / дюймКиловольт на метрКиловольт на микрометрКиловольт на миллиметрКиловольт на нанометрМегавольт на сантиметрМегавольт на дюймМегавольт на метрМегавольт на микрометрМегавольт на миллиметрМегавольт на нанометрМикровольт на сантиметрМикровольт на дюймМикровольт на метрМикровольт на микрометрМикровольт на миллиметрМикровольт на нанометрМилливольт на сантиметрМилливольт на дюймМилливольт на метрМилливольт на микрометрМилливольт на миллиметрМилливольт на нанометрНьютон / КулонаStatvolt / СантиметрStatvolt / дюймВольт на сантиметрВольт / дюймВольт на метрВольт на микрометрВольт / милвольт на миллиметрВольт на нанометр | +10% -10% | |
✖Удельное сопротивление — это мера того, насколько сильно материал сопротивляется протеканию через него тока. | Abohm Сантиметрциркулярный мил Ом / Футкилоом сантиметркилометркилоом микрометркилоом миллиметркилоом нанометрМегом СантиметрМегаомметрМегаом микрометрМегом МиллиметрМегаом-нанометрмикроом Сантиметрмикроом дюймМикроомметрмикроом микрометрмикроом миллиметрмикроом нанометрМиллиом СантиметрМиллиомметрМиллиом микрометрМиллиом МиллиметрМиллиом Нанометрнаноом MeterОм СантиметрОм-дюймОм метрОм МикрометрОм МиллиметрОм НанометрStatohm СантиметрСтаомметрСтатом-микрометрСтатом МиллиметрСтатом Нанометр | +10% -10% |
|
✖Плотность электрического тока — это количество заряда в единицу времени, которое проходит через единицу площади выбранного поперечного сечения.ⓘ Текущая плотность с учетом удельного сопротивления [J] |
|
⎘ копия |
👎
Формула
сбросить
👍
Текущая плотность с учетом удельного сопротивления Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Электрическое поле: 600 Вольт на метр —> 600 Вольт на метр Конверсия не требуется
Удельное сопротивление: 1.7E-05 Ом метр —> 1.7E-05 Ом метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
35294117.6470588 Ампер на квадратный метр —> Конверсия не требуется
< 20 Текущее электричество Калькуляторы
Потенциальная разница через вольтметр
Идти Разность электрических потенциалов = (Электрический ток через гальванометр*Сопротивление)+(Электрический ток через гальванометр*Сопротивление через гальванометр)
Электрический ток при заданной скорости дрейфа
Идти Электрический ток = Количество 1 свободных заряженных частиц на единицу объема*[Charge-e]*Площадь поперечного сечения*Скорость дрейфа
Шунт в амперметре
Идти Шунт = Электрический ток через гальванометр*Сопротивление через гальванометр/(Электрический ток-Электрический ток через гальванометр)
Скорость дрейфа с учетом площади поперечного сечения
Идти Скорость дрейфа = Электрический ток/(Количество электронов*[Charge-e]*Площадь поперечного сечения)
Температурная зависимость сопротивления
Идти Сопротивление = Сопротивление при эталонной температуре*(1+Температурный коэффициент сопротивления*Изменение температуры)
Скорость дрейфа
Идти Скорость дрейфа = ((1/2)*[Charge-e]*Электрическое поле*Время отдыха)/[Mass-e]
Тепловая энергия с учетом разности электрических потенциалов, электрического тока и затраченного времени
Идти Тепловая скорость = Разность электрических потенциалов*Электрический ток*Общее затраченное время
Тепловая энергия при заданной разности электрических потенциалов и сопротивлении
Идти Тепловая скорость = Разность электрических потенциалов^2*Общее затраченное время/Сопротивление
Тепло, выделяемое сопротивлением
Идти Тепловая скорость = Электрический ток^2*Сопротивление*Общее затраченное время
Электродвижущая сила при разрядке аккумулятора
Идти Напряжение = (Электродвижущая сила)-(Электрический ток*Сопротивление)
Электродвижущая сила при зарядке аккумулятора
Идти Напряжение = (Электродвижущая сила)+(Электрический ток*Сопротивление)
Метр Мост
Идти Окончательное сопротивление = (100-Длина)/Длина*Сопротивление
Текущая плотность с учетом удельного сопротивления
Идти Плотность электрического тока = Электрическое поле/Удельное сопротивление
Электрическое поле
Идти Электрическое поле = Разность электрических потенциалов/Длина проводника
Плотность тока с учетом электрического тока и площади
Идти Плотность электрического тока = Электрический ток/Площадь проводника
Мощность, заданная разностью электрических потенциалов и электрическим током
Идти Сила = Разность электрических потенциалов*Электрический ток
Приведенная мощность Разность электрических потенциалов и сопротивление
Идти Сила = (Разность электрических потенциалов^2)/Сопротивление
Электрический ток с данным зарядом и временем
Идти Электрический ток = Обвинение/Общее затраченное время
Мощность при заданном электрическом токе и сопротивлении
Идти Сила = ((Электрический ток)^2)*Сопротивление
Закон Ома
Идти Напряжение = Электрический ток*Сопротивление
< 19 Конденсатор Калькуляторы
Емкость сферического конденсатора
Идти Емкость = (Диэлектрическая постоянная*Радиус сферы*Радиус оболочки)/([Coulomb]*(Радиус оболочки-Радиус сферы))
Емкость цилиндрического конденсатора
Идти Емкость = (Диэлектрическая постоянная*Длина цилиндра)/(2*[Coulomb]*(Внешний радиус цилиндра-Внутренний радиус цилиндра))
Емкость конденсатора с параллельными пластинами
Идти Емкость параллельных пластин = Диэлектрическая постоянная*[Permitivity-vacuum]*Площадь плит/Расстояние между двумя массами
Емкость параллельных пластинчатых конденсаторов с диэлектриком между ними
Идти Емкость = Разрешающая способность*Диэлектрическая постоянная*Площадь плит/Расстояние между отклоняющими пластинами
Эквивалентная емкость для двух последовательно соединенных конденсаторов
Идти Емкость = (Емкость конденсатора 1*Емкость конденсатора 2)/(Емкость конденсатора 1+Емкость конденсатора 2)
Конденсатор с диэлектриком
Идти Емкость = Разрешающая способность*Константа а*Площадь плит/Расстояние между отклоняющими пластинами
Сила между конденсаторами с параллельными пластинами
Идти Сила = (Обвинение^2)/(2*Емкость параллельных пластин*Расстояние между двумя массами)
Плотность энергии в электрическом поле
Идти
Плотность энергии = 0. 5*[Permitivity-vacuum]*Электрическое поле*Электрическое поле
5*[Permitivity-vacuum]*Электрическое поле*Электрическое поле
Емкость
Идти Емкость = Диэлектрическая постоянная*Обвинение/вольтаж
Текущая плотность с учетом удельного сопротивления
Идти Плотность электрического тока = Электрическое поле/Удельное сопротивление
Плотность энергии в электрическом поле с учетом проницаемости свободного пространства
Идти Плотность энергии = 1/(2*Разрешающая способность*(Электрическое поле)^2)
Плотность энергии с учетом электрического поля
Идти Плотность энергии = 1/(2*Разрешающая способность*(Электрическое поле)^2)
Эквивалентное сопротивление в серии
Идти Эквивалентное сопротивление = Сопротивление+Окончательное сопротивление
Энергия, запасенная в конденсаторе, при заданной емкости и напряжении
Идти Электростатическая потенциальная энергия = (1/2)*(Емкость*вольтаж^2)
Энергия, запасенная в конденсаторе, при заданном заряде и напряжении
Идти Электростатическая потенциальная энергия = (1/2)*(Обвинение*вольтаж)
Энергия, запасенная в конденсаторе, с учетом заряда и емкости
Идти Электростатическая потенциальная энергия = (Обвинение^2)/(2*Емкость)
Плотность тока с учетом электрического тока и площади
Идти Плотность электрического тока = Электрический ток/Площадь проводника
Плотность тока с учетом проводимости
Идти Плотность электрического тока = Электрическое поле*Проводимость
Эквивалентная емкость для двух конденсаторов, включенных параллельно
Идти Емкость = Емкость конденсатора 1+Емкость конденсатора 2
Текущая плотность с учетом удельного сопротивления формула
Плотность электрического тока = Электрическое поле/Удельное сопротивление
J = E/ρ
Как рассчитывается плотность тока?
Плотность тока, вектор, в точке имеет величину, равную току на единицу нормальной площади в этой точке, а направление — вдоль направления тока в этой точке J = E / ρ. Где J — плотность тока, единица измерения ампер-квадратный метр, E — электрическое поле, единица измерения которого — ньютон / кулон, ρ — удельное сопротивление, единица измерения которого — омметр.
Где J — плотность тока, единица измерения ампер-квадратный метр, E — электрическое поле, единица измерения которого — ньютон / кулон, ρ — удельное сопротивление, единица измерения которого — омметр.
Share
Copied!
Странные результаты для сопротивления P2P и плотности тока при моделировании сети электростатического разряда на кристалле (100-кратное отклонение) — почему?
Перейти к основному содержанию
Abstract Проверка сопротивления между диодными ячейками ESD и контактными площадками или силовыми зажимами, а также анализ плотности тока для таких токов обычно используются для проверки сетей ESD [1]. Когда в таких симуляциях используются стандартные списки соединений после компоновки, созданные инструментами паразитного извлечения, расчетные сопротивления могут быть значительно выше или ниже реальных значений в 100 раз, что очень много. Плотность тока также может значительно отличаться. Использование таких симуляций приводит либо к упущенным проблемам электростатического разряда, либо к потере времени на попытки исправить искусственные ошибки на хорошей схеме. Корневыми причинами таких ошибок являются артефакты паразитного извлечения, в том числе неправильное обращение с распределенным ЭСР-диодом как с ячейкой с одним выводом экземпляра или соединение ЭСР-диода с портом небольшим (1 мОм) резистором. В этом документе обсуждается, как обнаружить, идентифицировать и обойти эти артефакты.
Плотность тока также может значительно отличаться. Использование таких симуляций приводит либо к упущенным проблемам электростатического разряда, либо к потере времени на попытки исправить искусственные ошибки на хорошей схеме. Корневыми причинами таких ошибок являются артефакты паразитного извлечения, в том числе неправильное обращение с распределенным ЭСР-диодом как с ячейкой с одним выводом экземпляра или соединение ЭСР-диода с портом небольшим (1 мОм) резистором. В этом документе обсуждается, как обнаружить, идентифицировать и обойти эти артефакты.
Проверки сопротивления и проверки плотности тока часто выполняются в списках соединений после компоновки для проверки сетей защиты от электростатического разряда [1] – см. рис.1. Сопротивление точка-точка (P2P) используется в качестве косвенного показателя или показателя качества металлизации, а также в качестве косвенного показателя стрессового напряжения электростатического разряда. Высокие значения сопротивления P2P (например, выше 1 Ом) указывают на некоторые проблемы с металлизацией и должны быть устранены и улучшены.
Высокие значения сопротивления P2P (например, выше 1 Ом) указывают на некоторые проблемы с металлизацией и должны быть устранены и улучшены.
В последние годы многие компании, разрабатывающие полупроводники, не имеющие производственных мощностей, сообщали о загадочных проблемах с моделированием устойчивости к электростатическому разряду и плотности тока, когда используются списки соединений после компоновки, созданные стандартными инструментами паразитного извлечения. К этим проблемам относятся неоправданно большие или низкие (примерно в 100 раз) сопротивления между диодами ESD и контактными площадками или зажимами питания, а также нефизическая плотность тока в межсоединениях. Эти проблемы стали особенно серьезными в новейших, менее 10-нм технологиях, узлах с высоким сопротивлением межсоединений.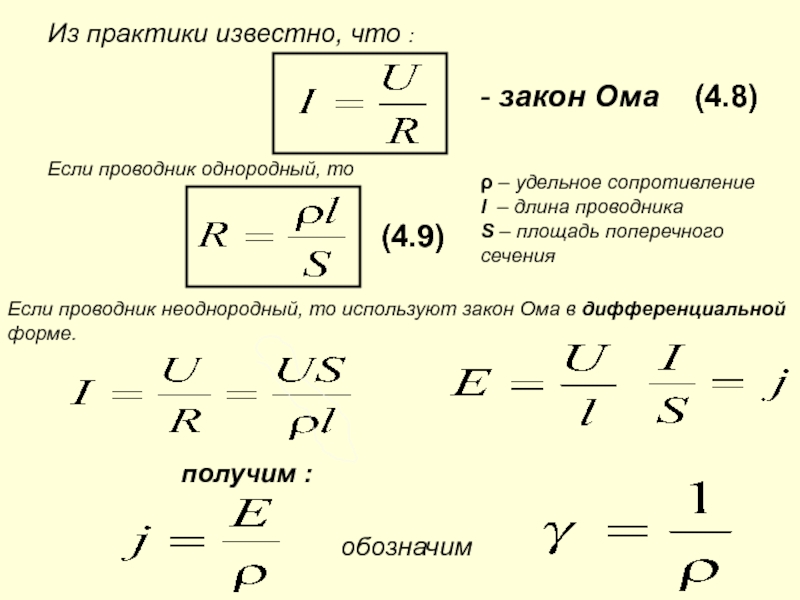
Эти проблемы обычно возникают, когда компании, не использующие фабрики, используют p-ячейки с диодами ESD, поставляемые производителями. Ячейки спроектированы, проверены и квалифицированы литейными заводами и должны быть качественными. Однако качество соединений этих ячеек ЭСР с сетями питания и с сетями ввода-вывода может быть низким. Такие плохие соединения могут привести к высокому сопротивлению и плотности тока, а также к большим проблемам с электростатическим разрядом. Вот почему, даже если сами элементы ESD имеют высокое качество, требуются проверки сопротивления и плотности тока во всей сети ESD.
Корпус с искусственным высоким сопротивлением В PDK, поставляемых литейным производством, диоды ESD часто представляются в виде p-ячеек (параметризованных ячеек) с одним выводом экземпляра для каждой из клемм, анода и катода. Это отличается от того, как обычно обрабатываются полевые МОП-транзисторы с ограничением мощности в PDK, где каждый отдельный палец многопальцевого устройства представлен как отдельный экземпляр устройства с собственными выводами экземпляра для клемм.
Эти выводы экземпляра обычно используются в качестве начальной или конечной точки для моделирования сопротивления P2P. В результате, в случае имитации p-ячейки диода ESD, ток течет в дискретную точку, создавая искусственное скопление тока, высокие значения плотности тока и высокое сопротивление растеканию — см. рис.2.
Рис. 2. Вертикальное сечение диода ESD, показывающее схему протекания тока для моделирования с использованием (а) единственного экземпляра вывода, (б) реалистичного распределения тока по площади диода. Это артефакт симуляции, вызванный артефактами представления большого распределенного устройства одним выводом дискретного экземпляра. В реальной работе, в реальной жизни, ЭСР-диоды будут проводить ток всеми пальцами, а суммарный ток ЭСР будет распределяться по большой площади, более или менее равномерно, на множество пальцев. В многослойных узлах с передовыми технологиями нижние металлические слои имеют высокое удельное сопротивление листа, они используются для вертикальной проводки тока и мало влияют на общее сопротивление. Все контакты и переходные отверстия над активным устройством проводят вертикальный ток параллельно, в идеале — равномерно. Ток распределяется между многими контактами и переходными отверстиями, что приводит к низкому общему сопротивлению.
Все контакты и переходные отверстия над активным устройством проводят вертикальный ток параллельно, в идеале — равномерно. Ток распределяется между многими контактами и переходными отверстиями, что приводит к низкому общему сопротивлению.
Наоборот, при моделировании с использованием одного штифта экземпляра в качестве начальной или конечной точки ток становится концентрированным и сгущается возле этого штыря экземпляра. Он создает искусственные, нереалистичные схемы протекания тока, такие как поперечный ток в нижних слоях металла (M0, M1, M2, …), сильно неравномерный ток в переходных отверстиях, с высокой плотностью тока в переходных отверстиях вблизи вывода экземпляра и т. д. .
Это приводит к искусственно завышенному сопротивлению растеканию. На рис. 3 сравниваются результаты моделирования для стандартного диода ESD для 5-нм технологии. Сопротивление, рассчитанное с использованием одного вывода экземпляра, составляет ~ 7,65 Ом. Сопротивление, смоделированное с использованием условий, обеспечивающих реалистичное (распределенное) распределение тока по площади устройства, равно 0,069. Ом – более чем в 100 раз ниже!
Ом – более чем в 100 раз ниже!
Кроме того, уровни показывают очень разные рейтинги в их вкладе в общее сопротивление P2P для этих двух условий моделирования. Моделирование с выводами дискретных экземпляров может привести к совершенно неправильной стратегии оптимизации слоев, фокусируясь на неправильных слоях.
Рис. 3. Сопротивление P2P от диода ESD к заземляющему сетевому порту и вклад сопротивления по слоям для (а) корпуса с одним выводом и (б) распределенных условий моделирования.Распределение плотности тока в нижних слоях показывает сильное скопление тока вблизи единичного вывода – см. рис. 4. В случае распределенного протекания тока плотность тока более или менее однородна, и ее пиковое значение в ~63 раза ниже, чем в футляр для булавки в единственном экземпляре.
Рис. 4. Распределение плотности тока в (а) одиночном выводе и (б) распределенных условиях моделирования. Пиковая плотность тока для случая (а) в 63 раза выше, чем для случая (б). Корпус с искусственно низким сопротивлением В некоторых случаях вывод экземпляра ESD-диода подключается не к низкоуровневым слоям (таким как диффузия или контакты), а непосредственно к порту (выводу) силовой цепи, расположенному на верхнем металлическом слое. Сопротивление этого разъема очень низкое, например 1 мОм. Почему это происходит? Я могу предположить, что клемма диода ESD отображается на лунку или слой подложки, который не извлекается для сопротивления. В результате инструмент извлечения паразитов подключает его к сети R сети в довольно произвольной точке, которая оказывается портом, с помощью соединительного резистора. Это похоже на то, как клеммы MOSFET обычно подключаются к порту (поскольку лунки и подложки не извлекаются для сопротивления).
Сопротивление этого разъема очень низкое, например 1 мОм. Почему это происходит? Я могу предположить, что клемма диода ESD отображается на лунку или слой подложки, который не извлекается для сопротивления. В результате инструмент извлечения паразитов подключает его к сети R сети в довольно произвольной точке, которая оказывается портом, с помощью соединительного резистора. Это похоже на то, как клеммы MOSFET обычно подключаются к порту (поскольку лунки и подложки не извлекаются для сопротивления).
Визуализация паразитных помех и их зондирования позволяет инженерам идентифицировать такие детали извлечения и понять, что происходит при извлечении паразитных частиц и электрическом анализе, как показано на рис. 5.
резисторы нефизических разъемов и паразитные датчики. Таким образом, неправильное подключение диода ESD к сети питания. Сопротивление от диода ESD до порта силовой сети очень низкое (1 мОм) из-за того, что этот соединительный резистор пропускает реальный путь тока через межсоединения.
Чтобы правильно смоделировать сопротивление и ток для этого случая, сопротивление разъема должно быть удалено, а вывод экземпляра диода должен быть подключен к нижнему слою распределенным образом. Было бы идеально, если бы это делал инструмент паразитного извлечения.
Соединительные резисторы Соединительные резисторы — это полускрытая функция в инструментах для извлечения паразитов. Это нефизические резисторы, т. е. они не генерируются формой компоновки и их удельным сопротивлением. Эти резисторы не контролируются пользователями. Поставщики средств извлечения не сообщают полупроводниковым компаниям об этой функции, вероятно, потому, что она считается внутренней деталью реализации.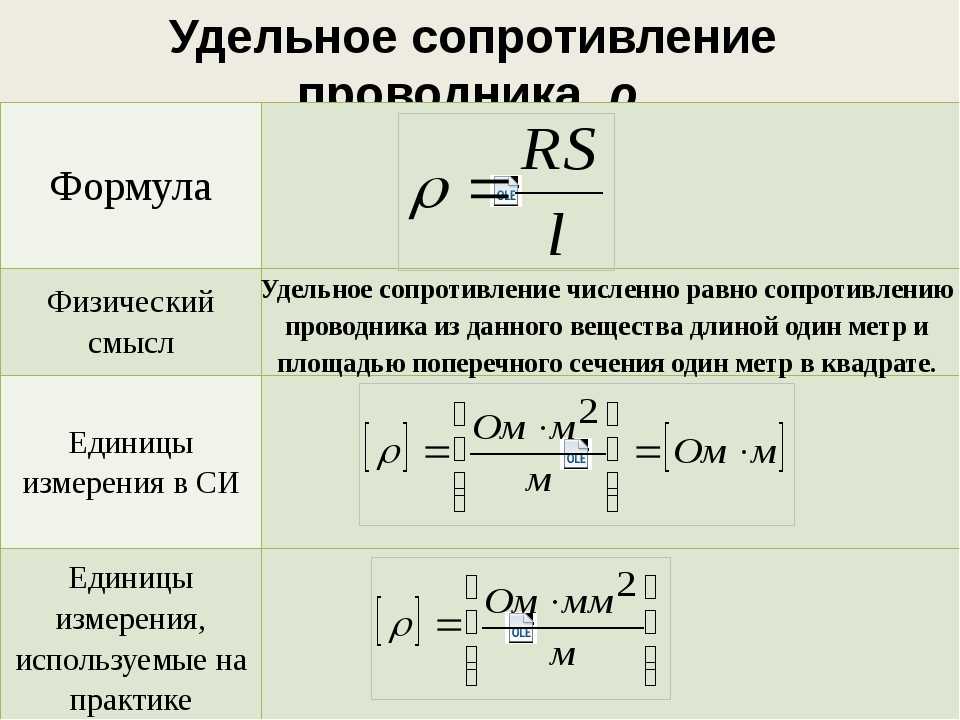
Соединительные резисторы используются для различных целей подключения, например, для соединения выводов экземпляров устройств с резистивной сетью или к другим выводам экземпляра, для соединения разъединенных («размыкающих») частей сети, к «коротким» портам и для многие другие цели. Их значение обычно очень низкое — например, 0,1, 1, 10 или 100 мОм. В большинстве случаев они не оказывают вредного влияния на результаты электрического моделирования. Однако иногда, как обсуждалось в предыдущем разделе, они могут иметь странный или очень плохой эффект — например, закорачивание конечного сопротивления межсоединений или добавление сопротивления 0,1 Ом к системе, которая имеет гораздо более низкое сопротивление (например, силовой полевой транзистор). иметь значения сопротивления межсоединений в диапазоне мОм).
Умение «понимать», идентифицировать и визуализировать соединительные резисторы на схеме (как показано на рис. 5), а также просто знать об их наличии и потенциальном влиянии очень важно для хорошего понимания структуры, возможность подключения и потенциальные ловушки в списке соединений после макета.
Проверки сопротивления и плотности тока являются полезными и необходимыми шагами для проверки электростатического разряда, но при настройке моделирования необходимо соблюдать осторожность. Условия моделирования должны имитировать и воспроизводить реалистичный ток, протекающий над устройствами и рядом с ними, чтобы избежать паразитного извлечения и артефактов моделирования.
Все модели и визуализации, представленные в этой статье, были выполнены с использованием ParagonX [2].
Ссылки1. «Проверки автоматизации проектирования электроники ESD», Технический отчет, Ассоциация ESD, 2014 г. Бесплатная загрузка: https://www.esda.org/zh_CN/store/standards/product/4/esd- tr18-0-01-14 (ищите кнопку «Бесплатная загрузка»).
2. Руководство пользователя ParagonX, Diakopto Inc., 2022.
Сопротивление затвора в потоке проектирования ИС
1 мая 2023 г.

Ваши симметричные макеты показывают несоответствия в симуляциях SPICE. Что происходит?
1 ноября 2022 г.
Моделирование цепей и паразиты: нам нужно больше скорости или больше понимания (или и то, и другое)?
26 окт. 2020 г.
Что такое Guardbands и Guardbanding? (в машиностроении)
14 июля 2017 г.

Другие также смотрели
Закон Ома, вид под микроскопом
В качестве примера микроскопического представления закона Ома будут рассмотрены параметры меди. С одним свободным электроном на атом в его металлическом состоянии электронная плотность меди может быть рассчитана из ее объемной плотности и ее атомной массы.
Энергия Ферми для меди составляет около 7 эВ, поэтому скорость Ферми равна
.Измеренная электропроводность меди при 20°C составляет
Длина свободного пробега электрона в меди в этих условиях может быть рассчитана из
Скорость дрейфа зависит от приложенного электрического поля. Например, медный провод диаметром 1 мм и длиной 1 метр, к которому приложено 1 вольт, дает следующие результаты.
На 1 приложенный вольт это дает силу тока 46,3 ампера и плотность тока
Это соответствует скорости дрейфа всего в миллиметрах в секунду, в отличие от высокой фермиевской скорости электронов.
Внимание! Не пытайтесь повторить это дома! Доктор Бейхай Ма из Аргоннской национальной лаборатории указал, что плотность тока 5900 А/см 2 в этом примере более чем в десять раз превышает плотность тока 500 А/см 2 медь обычно выдерживает температуру 40°F. Так что делать это в лаборатории может быть слишком увлекательно. Спасибо за проверку вменяемости, доктор Ма.
(Если вы уменьшите приложенное напряжение так, чтобы ток составлял всего 3 ампера, плотность тока 382 А/см 2 , так что медный провод останется неповрежденным, расчетная скорость дрейфа составит всего 0,00028 м/с. Это будет быть более типичным для условий работы в этом проводе.)
Как насчет квантовых эффектов и статистики Ферми-Дирака?
Обработка микроскопического Закона Ома и скорости дрейфа, описанная выше, в основном является классической обработкой. Но мы знаем, что электроны в металле подчиняются статистике Ферми-Дирака и что при низких температурах все доступные энергетические уровни электронов заполняются до уровня Ферми. Мы также знаем, что этот уровень Ферми (около 7 эВ в меди) очень высок по сравнению с тепловой энергией при комнатной температуре. Тогда как мы можем оправдать использование всей популяции свободных электронов выше в расчете дрейфовой скорости, когда для тепловых взаимодействий доступны для взаимодействия только те электроны, которые находятся в пределах примерно kT от уровня Ферми?
Но мы знаем, что электроны в металле подчиняются статистике Ферми-Дирака и что при низких температурах все доступные энергетические уровни электронов заполняются до уровня Ферми. Мы также знаем, что этот уровень Ферми (около 7 эВ в меди) очень высок по сравнению с тепловой энергией при комнатной температуре. Тогда как мы можем оправдать использование всей популяции свободных электронов выше в расчете дрейфовой скорости, когда для тепловых взаимодействий доступны для взаимодействия только те электроны, которые находятся в пределах примерно kT от уровня Ферми?
Одно место, где эта ситуация обсуждается, находится в классической книге «Физика твердого тела» Чарльза Киттеля. Он указывает, что из-за полной заселенности электронами проводимости до уровня Ферми эти электроны в медной проволоке имеют очень большую скорость, порядка 1,6·10 6 см/сек для меди. Внешнее электрическое поле в медной проволоке будет оказывать постоянную силу на электроны и будет продолжать их ускорять, если это ускорение не будет случайным из-за множественных столкновений и взаимодействия с решеткой. Соблюдение закона Ома экспериментально показывает нам, что достигается равновесный ток, и что предположение, что все электроны проводимости участвуют, позволяет нам спроектировать эффективную скорость дрейфа для этих электронов под влиянием приложенного электрического поля. Отмечается, что это совершенно классическая презумпция.
Соблюдение закона Ома экспериментально показывает нам, что достигается равновесный ток, и что предположение, что все электроны проводимости участвуют, позволяет нам спроектировать эффективную скорость дрейфа для этих электронов под влиянием приложенного электрического поля. Отмечается, что это совершенно классическая презумпция.
Продолжая исследовать электропроводность с точки зрения статистики Ферми-Дирака, Киттель делает следующее замечание: «Это несколько удивительный факт, что введение распределения Ферми-Дирака вместо классического распределения Максвелла-Больцмана обычно мало влияет на электропроводность, часто изменяя только тип среднего значения, используемого при спецификации времени релаксации. На первый взгляд можно было ожидать более резкого изменения, потому что с распределением Ферми-Дирака только те электроны, которые находятся вблизи Поверхность Ферми может участвовать в столкновительных процессах».
Киттель утверждает, что принцип исключения не препятствует вмешательству электрического поля, поскольку оно воздействует на каждый электрон в распределении, вызывая одинаковое изменение скорости.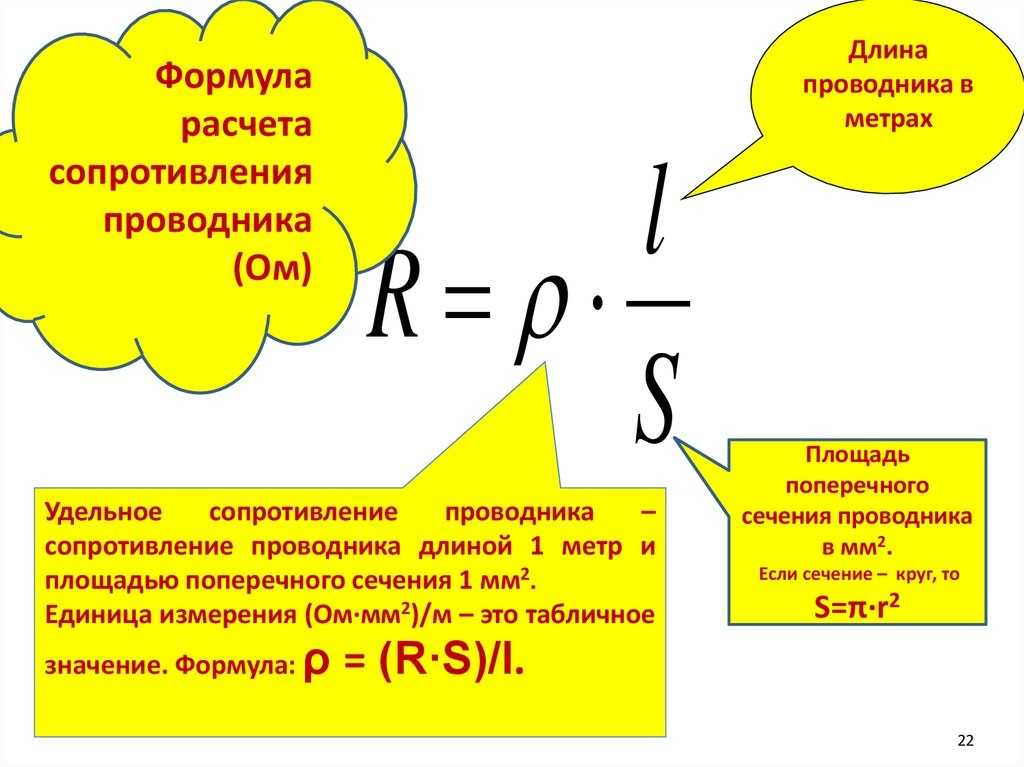


 ⓘ Удельное сопротивление [ρ]
ⓘ Удельное сопротивление [ρ]