Соленоидальное векторное поле — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016; проверки требуют 2 правки.Векторное поле называется соленоидальным или вихревым[источник не указан 499 дней], если через любую замкнутую поверхность S его поток равен нулю:
- ∫Sa→⋅ds→=0{\displaystyle \int \limits _{S}{\vec {a}}\cdot {\vec {ds}}=0}.
Другое определение соленоидального поля: Векторное поле a→{\displaystyle {\vec {a}}}называют соленоидальным, если оно является вихрем некоторого поля b→{\displaystyle {\vec {b}}},a→=rotb→{\displaystyle {\vec {a}}=rot{\vec {b}}}. При этом векторное поле b→{\displaystyle {\vec {b}}} называют векторным потенциалом поля a→{\displaystyle {\vec {a}}}
Если это условие выполняется для любых замкнутых S в некоторой области (по умолчанию — всюду), то это условие равносильно тому, что равна нулю дивергенция векторного поля a→{\displaystyle {\vec {a}}}:
- diva→≡∇⋅a→=0{\displaystyle \mathrm {div} \,{\vec {a}}\equiv \nabla \cdot {\vec {a}}=0}
всюду на этой области (подразумевается, что дивергенция всюду на этой области существует). Поэтому соленоидальные поля называют также бездивергентными.
Для широкого класса областей это условие выполняется тогда и только тогда, когда a→{\displaystyle {\vec {a}}} имеет векторный потенциал, то есть существует некое такое векторное поле A→{\displaystyle {\vec {A}}} (векторный потенциал), что a→{\displaystyle {\vec {a}}} может быть выражено как его ротор:
- a→=∇×A→≡rotA→.{\displaystyle {\vec {a}}=\nabla \times {\vec {A}}\equiv \mathrm {rot} \,{\vec {A}}.}
Иначе говоря, поле является вихревым, если оно не имеет источников. Силовые линии такого поля не имеют ни начала, ни конца, и являются замкнутыми. Вихревое поле порождается не покоящимися зарядами (источниками), а изменением связанного с ним поля (например, для электрического поля порождается изменением магнитного). Поскольку в природе не существует магнитных зарядов, то магнитное поле всегда является вихревым, и его силовые линии всегда замкнуты. Силовые линии постоянного магнита, несмотря на то, что выходят из его полюсов (словно имеют источники внутри), на самом деле замыкаются внутри магнита. Поэтому, разрезав магнит надвое, не удастся получить два отдельных магнитных полюса.
Слово соленоидальное происходит от греческого соленоид (σωληνοειδές, sōlēnoeidēs), означающее «трубообразно» или «как в трубе», содержащего слово σωλην (Solen) — труба. В данном контексте это означает фиксацию объема для модели текущей жидкости, отсутствие источников и стоков (как при течении в трубе, где новая жидкость не появляется и не пропадает).[источник не указан 499 дней]
- ↑ А.Н. Канатников. Курс лекций
Соленоидальное векторное поле — Википедия
Материал из Википедии — свободной энциклопедии
Определение
Векторное поле называется соленоидальным или вихревым[источник не указан 409 дней], если через любую замкнутую поверхность S его поток равен нулю:
- ∫Sa→⋅ds→=0{\displaystyle \int \limits _{S}{\vec {a}}\cdot {\vec {ds}}=0}.
Другое определение соленоидального поля: Векторное поле a→{\displaystyle {\vec {a}}}называют соленоидальным, если оно является вихрем некоторого поля b→{\displaystyle {\vec {b}}},a→=rotb→{\displaystyle {\vec {a}}=rot{\vec {b}}}. При этом векторное поле b→{\displaystyle {\vec {b}}} называют
Если это условие выполняется для любых замкнутых S в некоторой области (по умолчанию — всюду), то это условие равносильно тому, что равна нулю дивергенция векторного поля a→{\displaystyle {\vec {a}}}:
- diva→≡∇⋅a→=0{\displaystyle \mathrm {div} \,{\vec {a}}\equiv \nabla \cdot {\vec {a}}=0}
всюду на этой области (подразумевается, что дивергенция всюду на этой области существует). Поэтому соленоидальные поля называют также бездивергентными.
Для широкого класса областей это условие выполняется тогда и только тогда, когда a→{\displaystyle {\vec {a}}} имеет векторный потенциал, то есть существует некое такое векторное поле A→{\displaystyle {\vec {A}}} (векторный потенциал), что a→{\displaystyle {\vec {a}}} может быть выражено как его ротор:
- a→=∇×A→≡rotA→.{\displaystyle {\vec {a}}=\nabla \times {\vec {A}}\equiv \mathrm {rot} \,{\vec {A}}.}
Иначе говоря, поле является вихревым, если оно не имеет источников. Силовые линии такого поля не имеют ни начала, ни конца, и являются замкнутыми. Вихревое поле порождается не покоящимися зарядами (источниками), а изменением связанного с ним поля (например, для электрического поля порождается изменением магнитного). Поскольку в природе не существует магнитных зарядов, то магнитное поле всегда является вихревым, и его силовые линии всегда замкнуты. Силовые линии постоянного магнита, несмотря на то, что выходят из его полюсов (словно имеют источники внутри), на самом деле замыкаются внутри магнита. Поэтому, разрезав магнит надвое, не удастся получить два отдельных магнитных полюса.
Примеры
Этимология
Слово соленоидальное происходит от греческого соленоид (σωληνοειδές, sōlēnoeidēs), означающее «трубообразно» или «как в трубе», содержащего слово σωλην (Solen) — труба. В данном контексте это означает фиксацию объема для модели текущей жидкости, отсутствие источников и стоков (как при течении в трубе, где новая жидкость не появляется и не пропадает).[источник не указан 409 дней
См. также
- ↑ А.Н. Канатников. Курс лекций (неопр.). МГТУ им. Н.Э.Баумана. Дата обращения 8 января 2019.
15.2.2. Соленоидальное векторное поле
Определение. Векторное поле  называется соленоидальным (трубчатым)
полем, если дивергенция его равна нулю:
называется соленоидальным (трубчатым)
полем, если дивергенция его равна нулю:
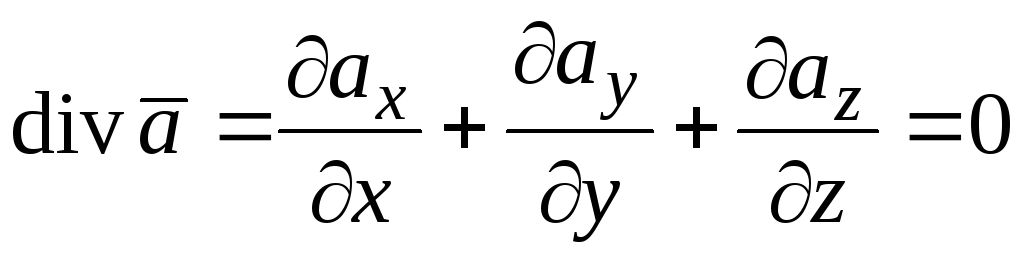
(то есть это поле без источников и стоков). Из теоремы (1.11) следует, что в соленоидальном поле поток
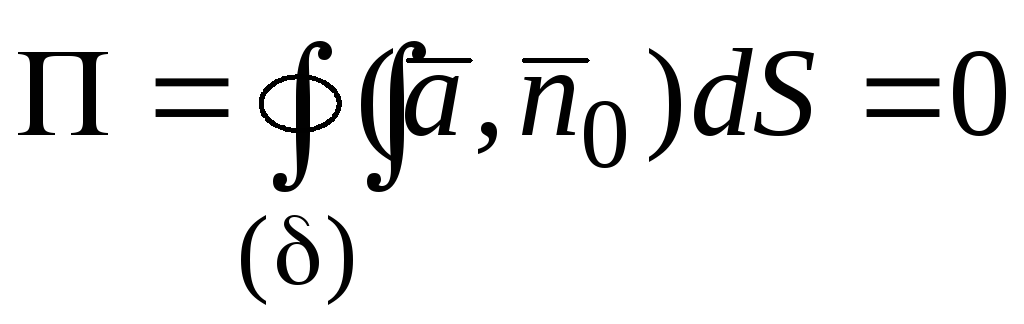 (2.8)
(2.8)
через любую замкнутую поверхность, лежащую в этом поле.
Пример.Какие из нижеследующих полей являются соленоидальными (в естественной области определения):
1) 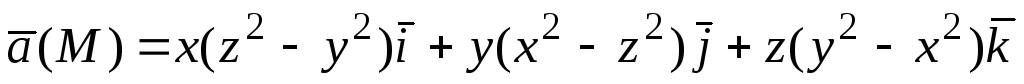 ;
;
2) 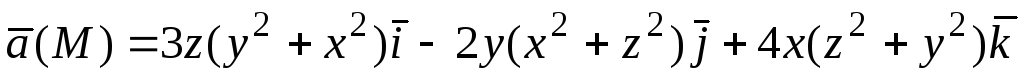
Решение.
1) вычислим критерий (2.7): 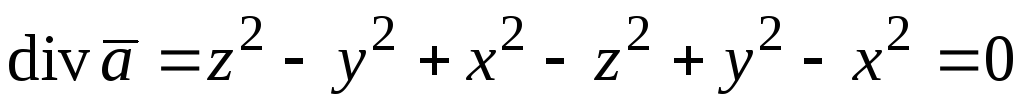 —
— поле вектора
—
— поле вектора  соленоидально; 2)
соленоидально; 2)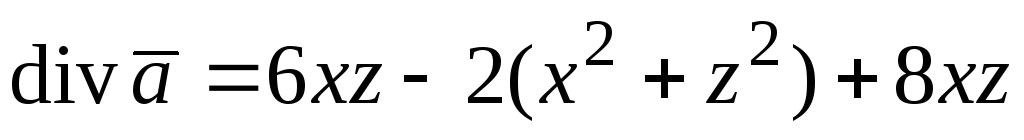 — поле не соленоидально.
— поле не соленоидально.
15.2.3. Дифференциальные операции второго порядка.
Лапласово (гармоническое) векторное поле
Дифференциальные
операции второго порядка – это повторно
примененные операции grad,
div и rot
к скалярным и векторным полям, полученным
в результате применения этих же операций
к скалярным 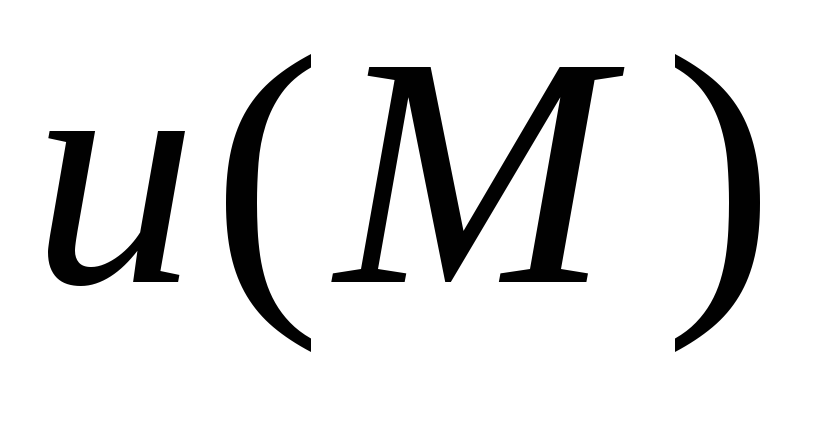
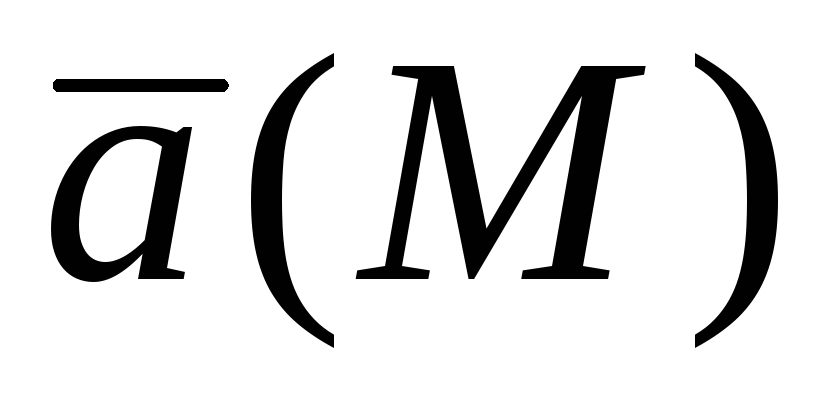 полям. Возможны лишь следующие повторные
операции:
полям. Возможны лишь следующие повторные
операции: 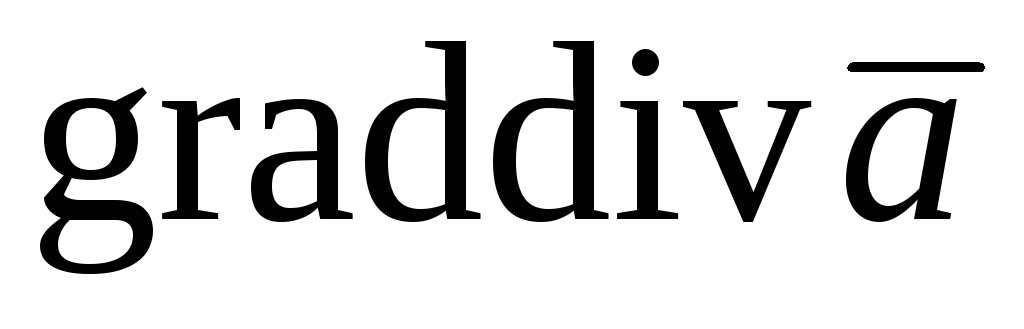 ;
; 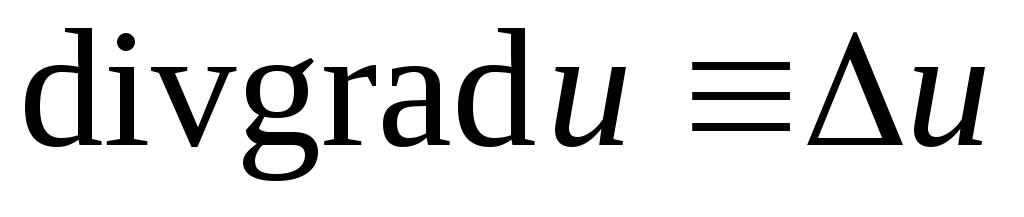 , где
, где 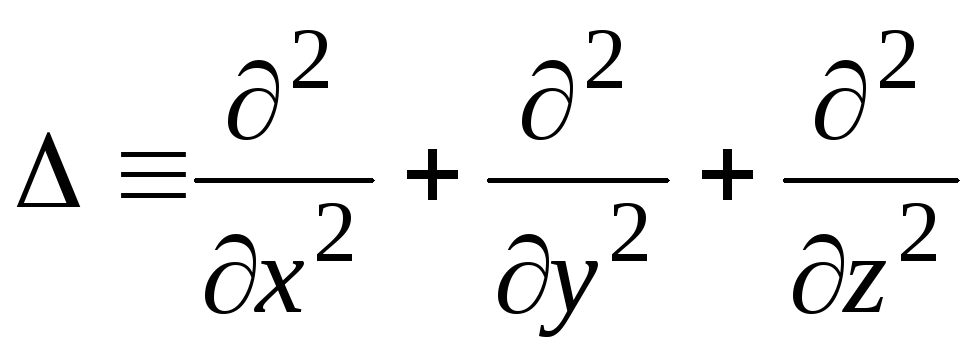 -лапласиан;
-лапласиан;  ;
; 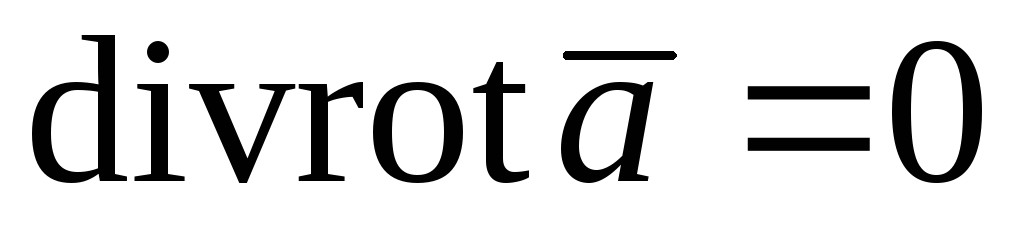 ;
; 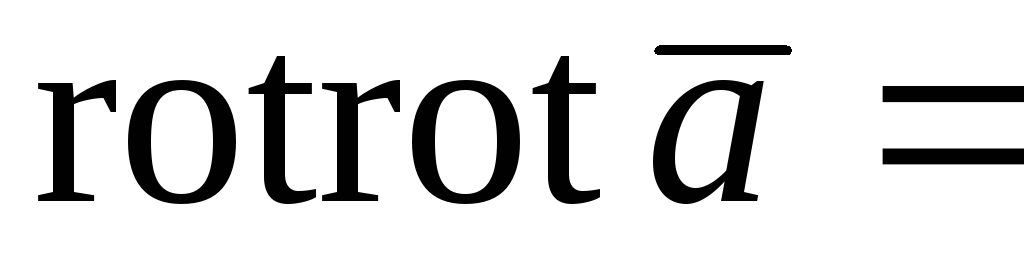
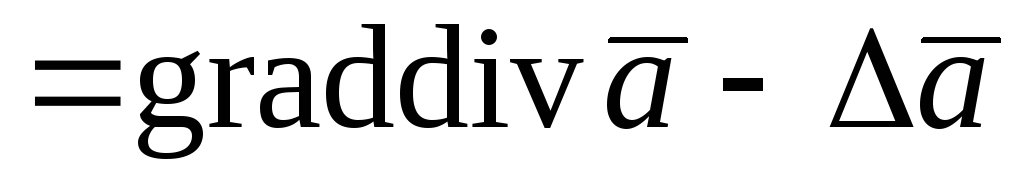 .
. Операции
первого и второго порядков удобно
записывать (и вычислять, доказывать) с
помощью специального символического
оператора  (читается “набла”):
(читается “набла”):
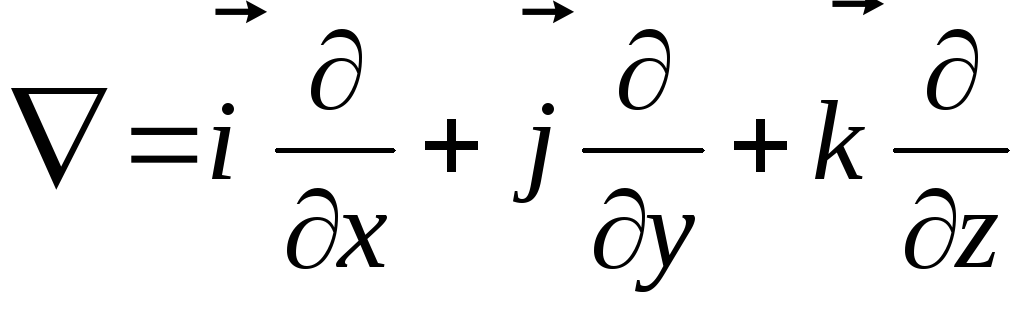 .
(2.9)
.
(2.9)
Для дифференциальных операций первого порядка имеем
; 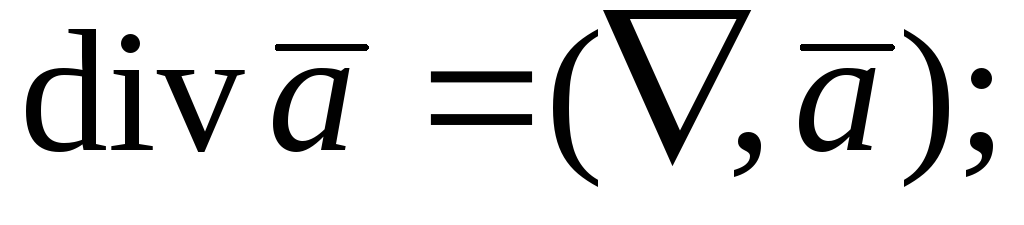
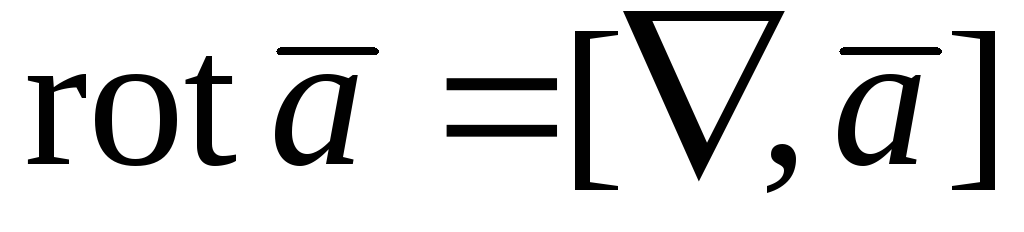 .
(2.10)
.
(2.10)Операции второго порядка:
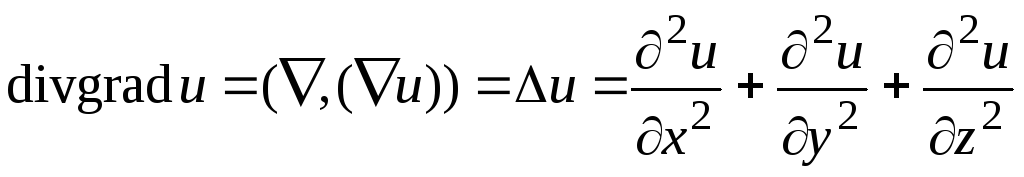 ;
;
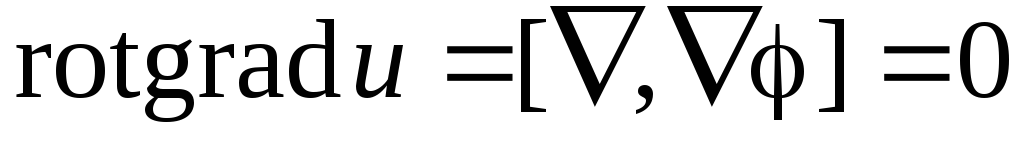 ;
;
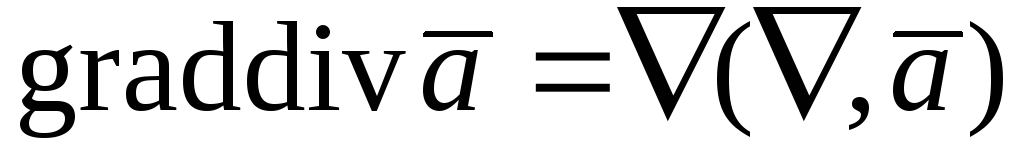 ;
;
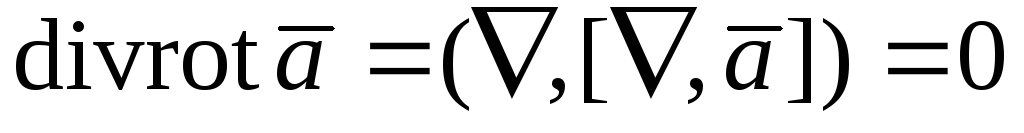 ;
;
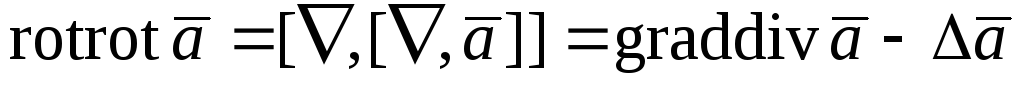 .
.
При
применении оператора “набла”
руководствуются следующим правилом:
при применении оператора  к произведениям скалярных
к произведениям скалярных ,
, )
и векторных
)
и векторных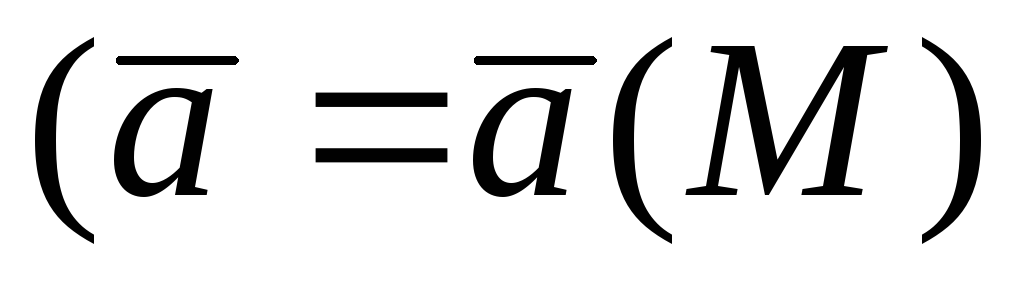 ,
,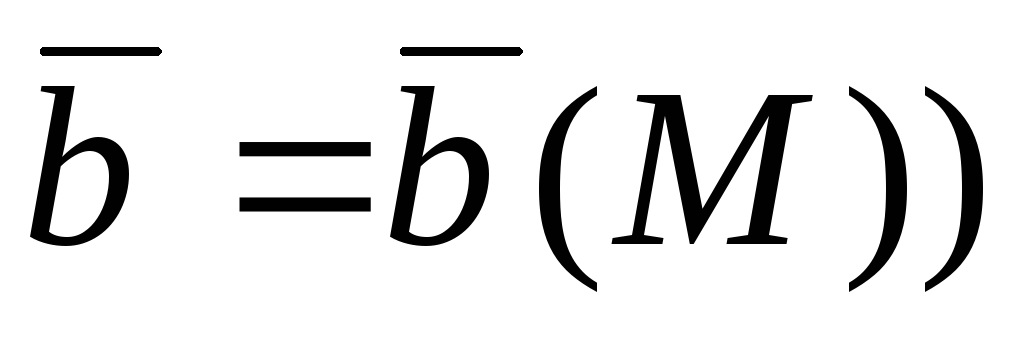 полей:
полей: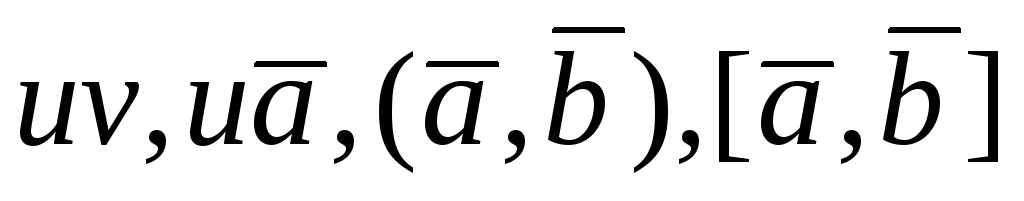 можно поступать так: применить оператор
можно поступать так: применить оператор к каждому из сомножителей отдельно,
считая другой постоянным (их обозначаем
к каждому из сомножителей отдельно,
считая другой постоянным (их обозначаем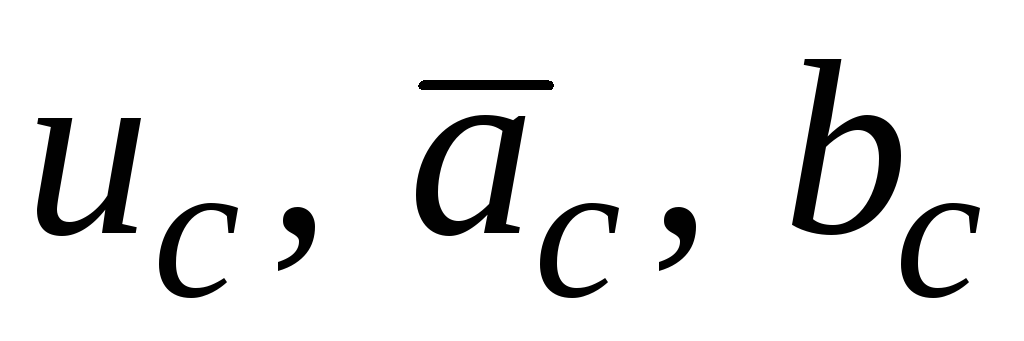 ),
и результаты сложить; затем каждоеслагаемое
преобразовать по правилам векторной
алгебра так, чтобы оператор
),
и результаты сложить; затем каждоеслагаемое
преобразовать по правилам векторной
алгебра так, чтобы оператор стоял на предпоследнем месте перед
переменным множителем.
стоял на предпоследнем месте перед
переменным множителем.
Пример. Показать, что 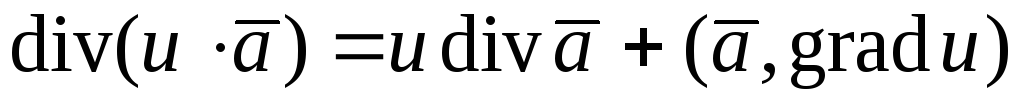 .
.
Решение.
В символической форме записи 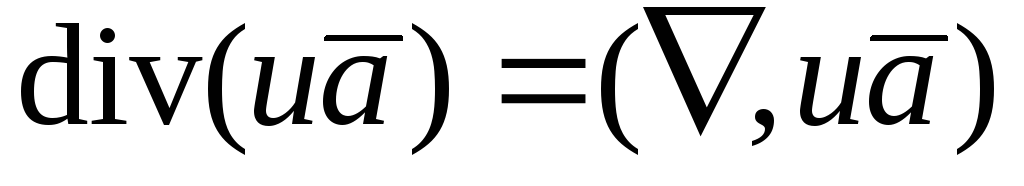 .
Учитывая сначала дифференциальный
характер
.
Учитывая сначала дифференциальный
характер ,
мы должны написать
,
мы должны написать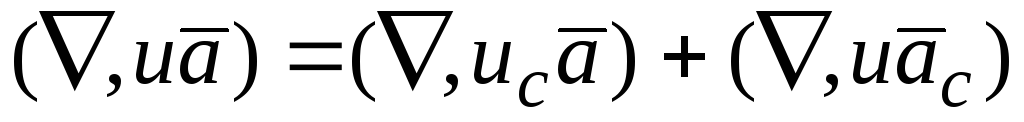 .
Рассматривая выражение
.
Рассматривая выражение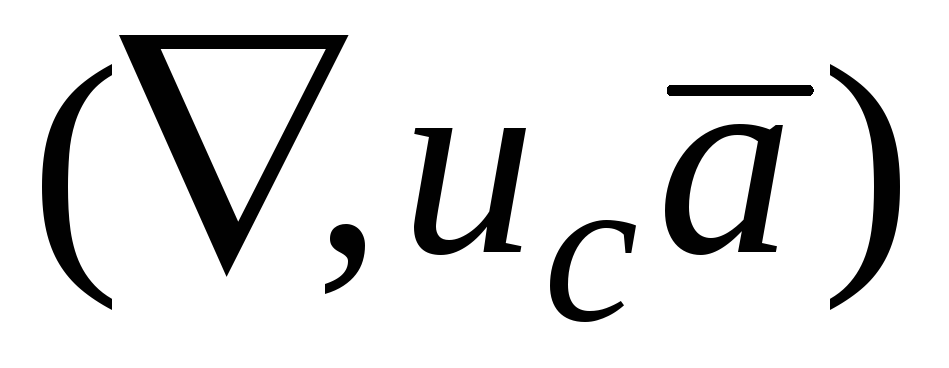 мы можем постоянный множитель
мы можем постоянный множитель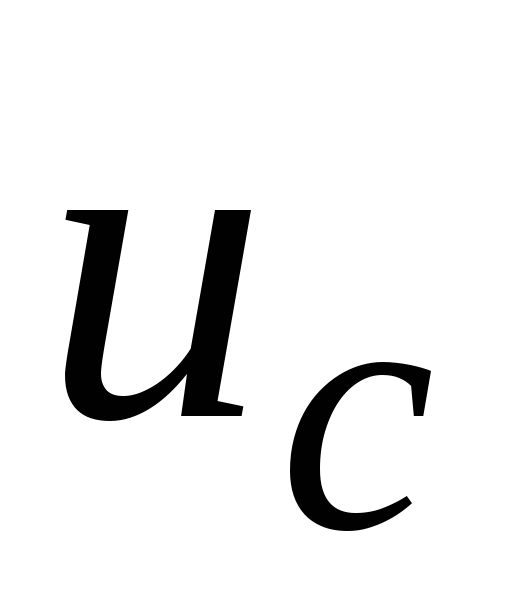 вынести за знак “набла” и, как скаляр,
за знак скалярного
произведения, что
дает
вынести за знак “набла” и, как скаляр,
за знак скалярного
произведения, что
дает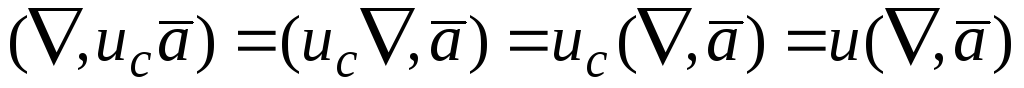 (на последнем шаге мы опустили индекс
“c”).
(на последнем шаге мы опустили индекс
“c”).
В
выражении 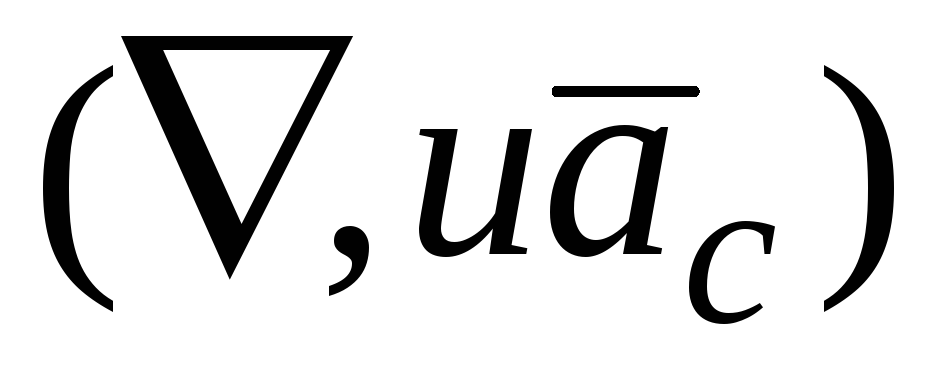 оператор
оператор действует только на скалярную функциюu;
поэтому мы можем написать, что
действует только на скалярную функциюu;
поэтому мы можем написать, что 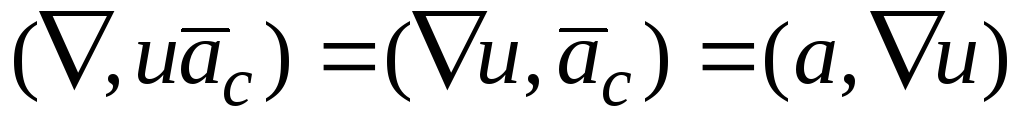 .
В результате получаем формулу
.
В результате получаем формулу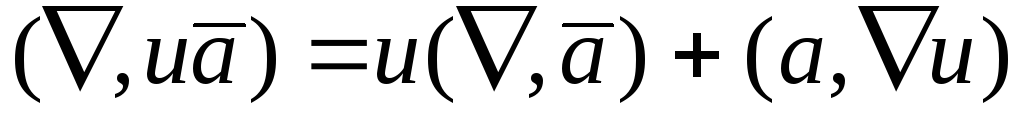 или
или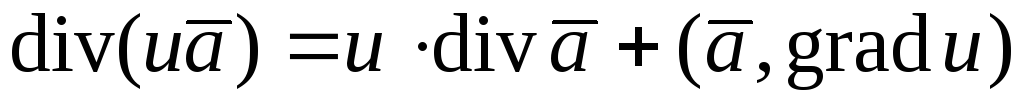 .
.
Задачи для самостоятельного решения
Найти потенциалы следующих плоских и трехмерных полей:
91. 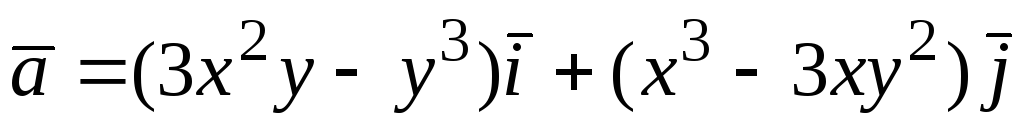 ;92.
;92. 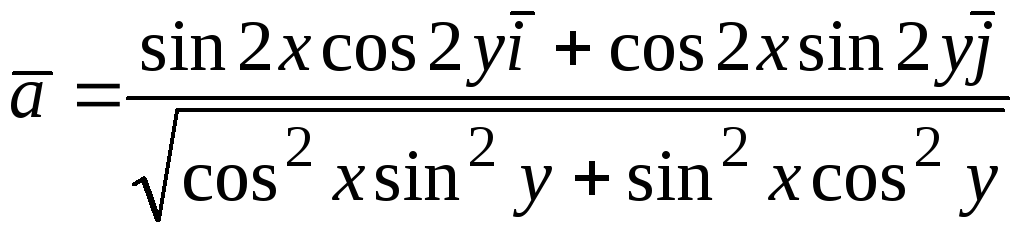 ;
;
93. 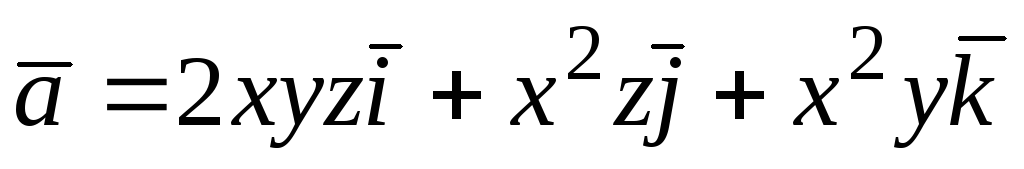 ; 94.
; 94. 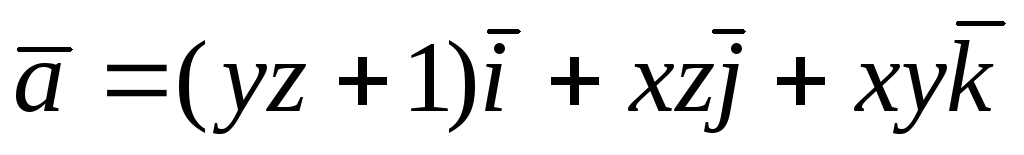 ;
;
95. 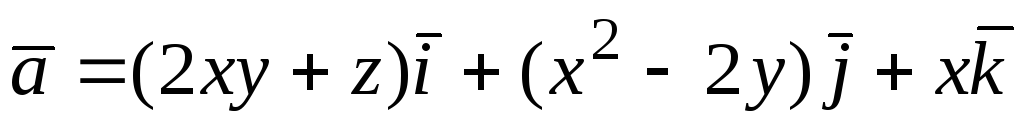 ;
96.
;
96. 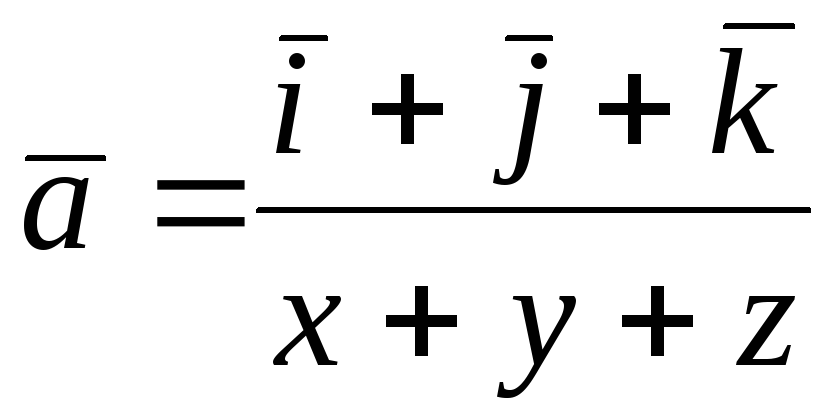 ;
97.
;
97. 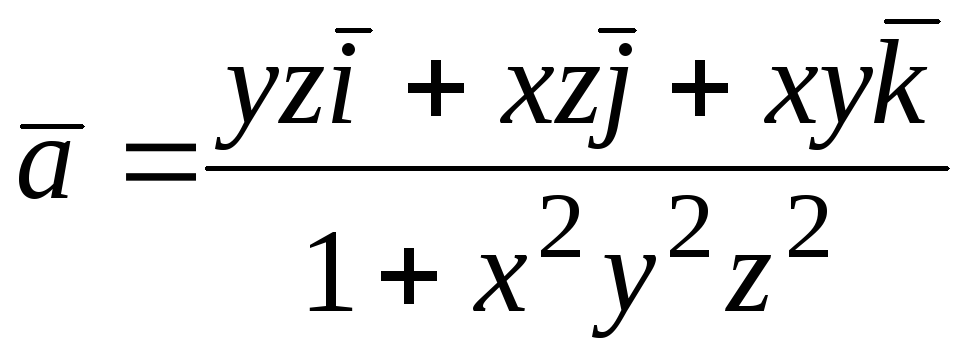 ;
;
98. 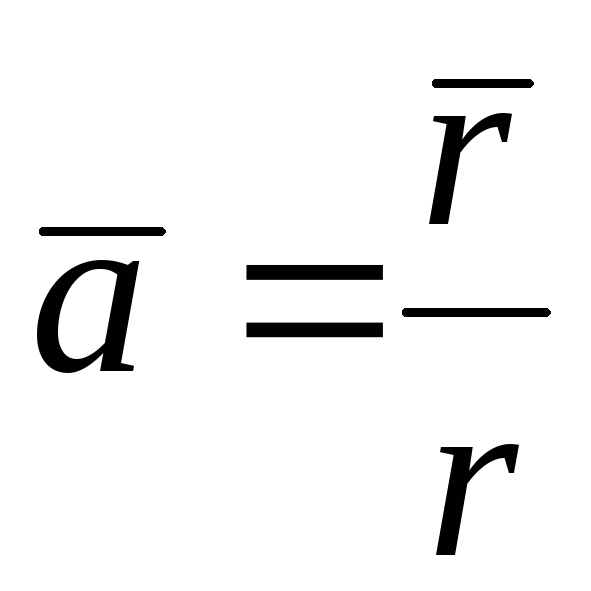 ;
99.
;
99. 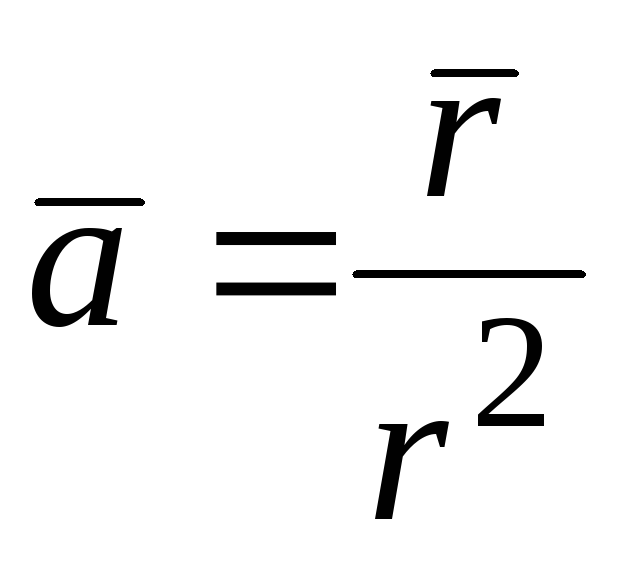 ;
100.
;
100. 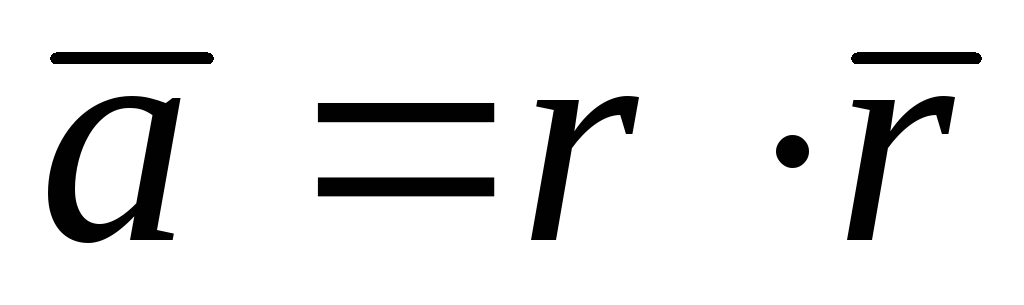 ;
;
101. 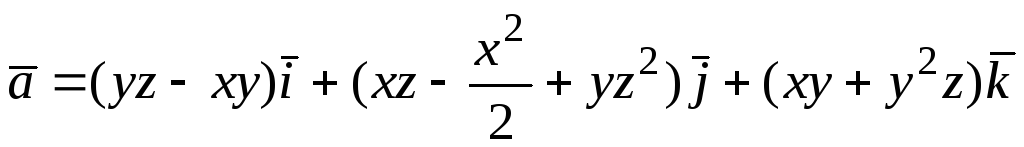 ;
;
102. 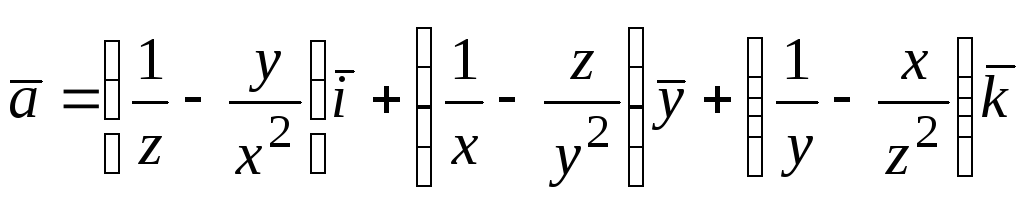 ;
;
103.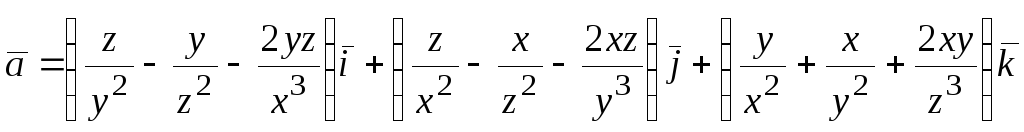 .
.
104. Доказать, что поле вихрей соленоидально: 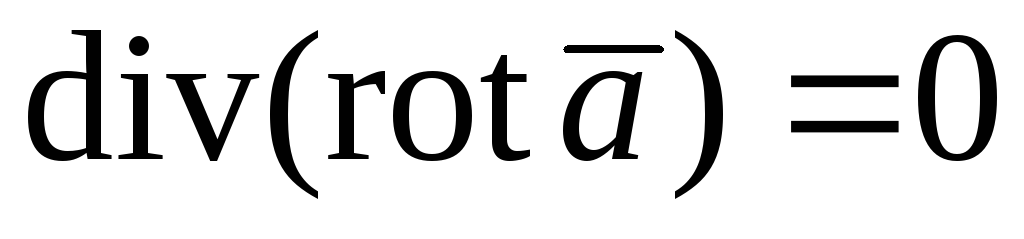 .
.
105. Доказать, что в соленоидальном поле поток вектора через замкнутую поверхность, не содержащую внутри особых точек, равен нулю.
В задачах 106 – 109 проверить соленоидальность заданных полей:
106. 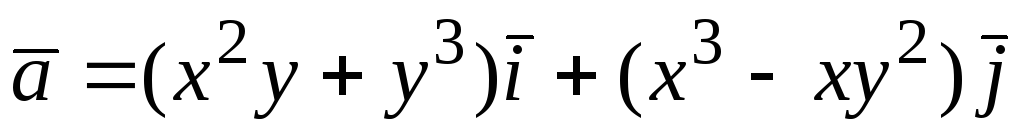 ;107.
;107. 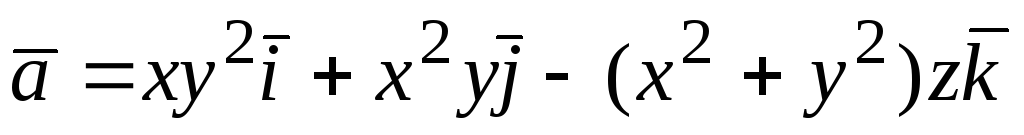 ;
;
108. 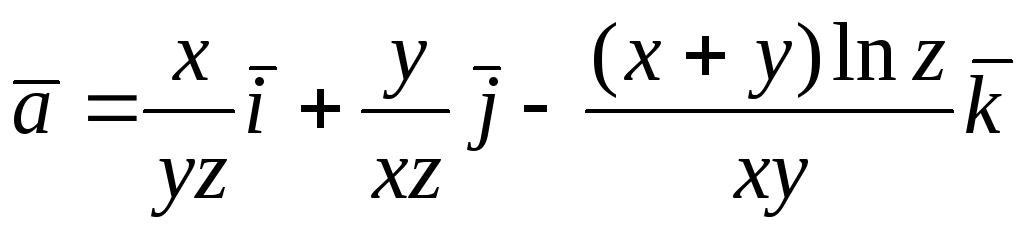 ; 109.
; 109. 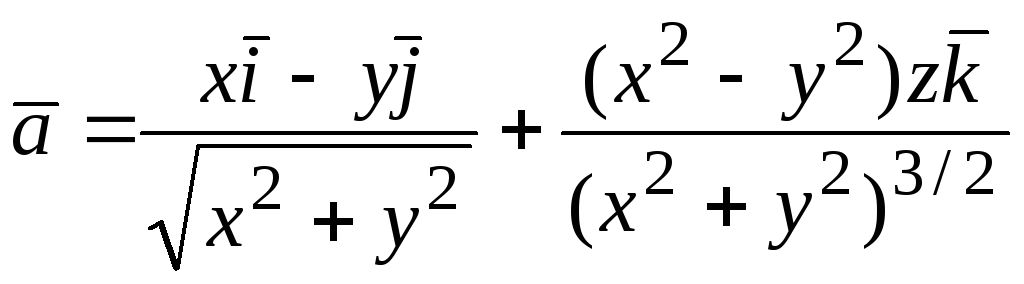 .
.
110. Доказать, что в соленоидальном поле поток вектора поля через поперечное сечение любой векторной трубки (определенный в одном и том же направлении) сохраняет постоянное значение.
111. Показать, что поле вектора 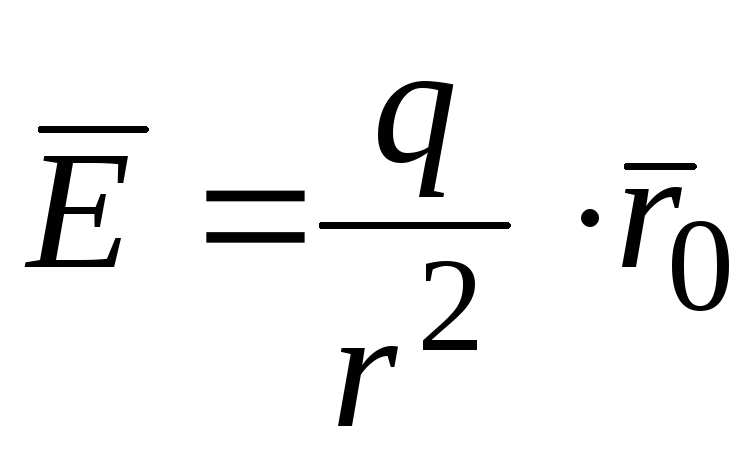 соленоидально во всякой области, не
содержащей начало координатO(0,0,0).
соленоидально во всякой области, не
содержащей начало координатO(0,0,0).
112. Найти условие соленоидальности поля 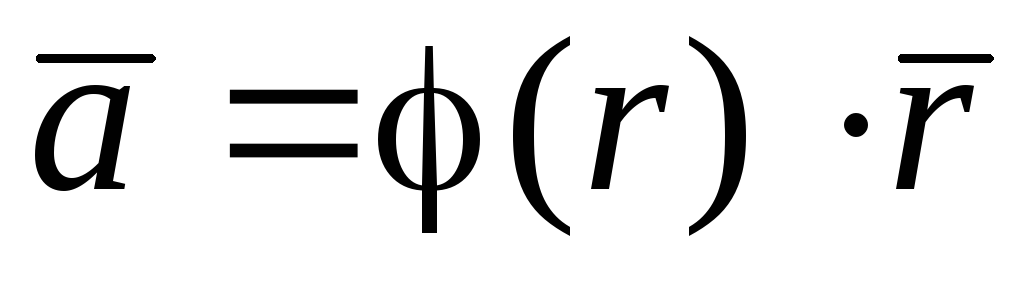 .
.
113. Показать, что в соленоидальном поле
поток вектора 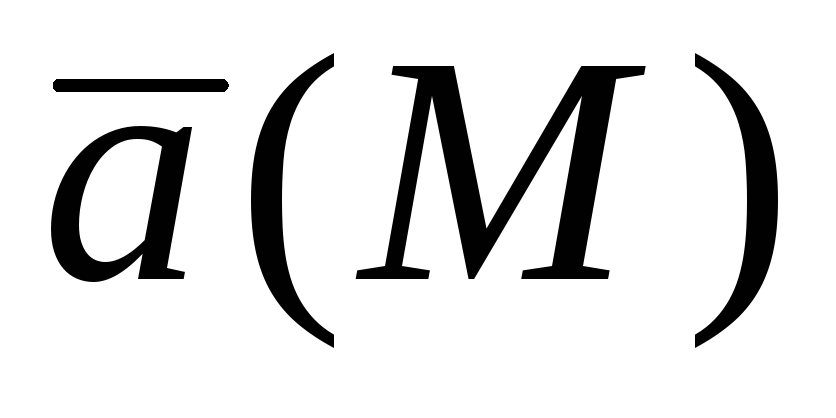 не зависит от вида поверхности (S),
натянутой на данный контур (L),
а зависит только от самого контура.
не зависит от вида поверхности (S),
натянутой на данный контур (L),
а зависит только от самого контура.
114.Показать,
что векторное поле 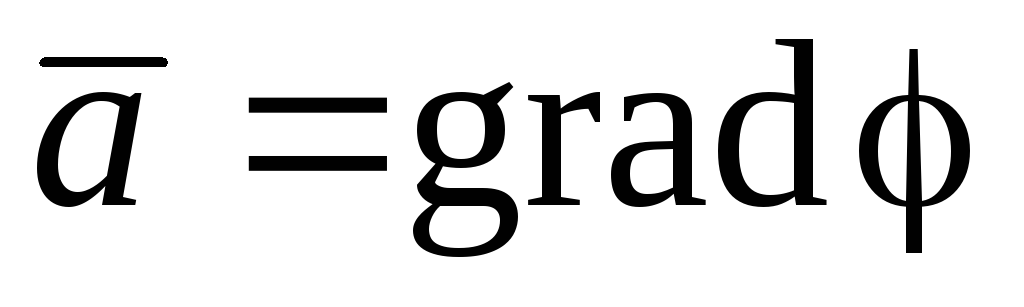 — соленоидальное и безвихревое.
— соленоидальное и безвихревое.
Используя
правило применения оператора  к произведениям скалярных и векторных
полей, доказать справедливость следующих
формул:
к произведениям скалярных и векторных
полей, доказать справедливость следующих
формул:
115. 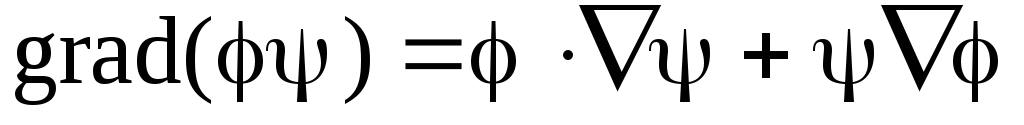 ;116.
;116. 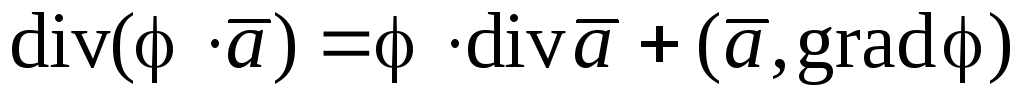 ;
;
117.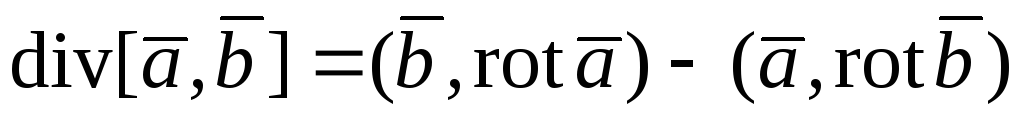 ; 118.
; 118.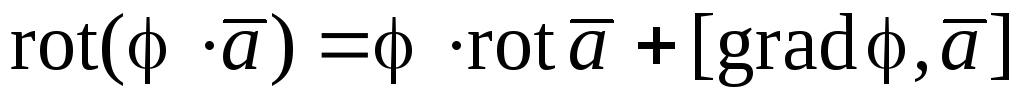 ;
;
119. 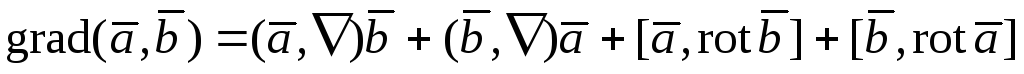 ;
;
120. 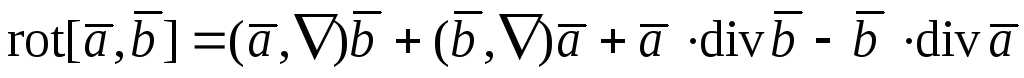 ;
;
121. 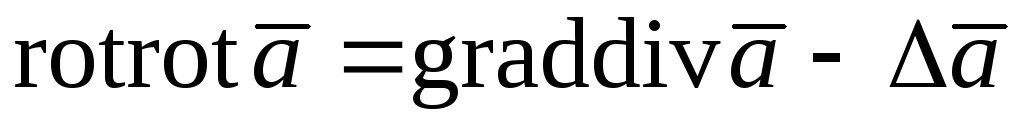 .
.
122. Найти  .
В каком случае
.
В каком случае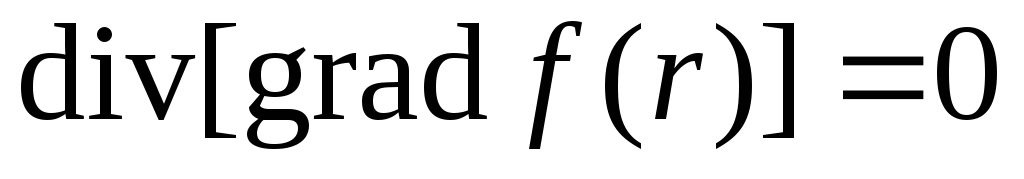 ?
?
123. Показать, что скалярное поле 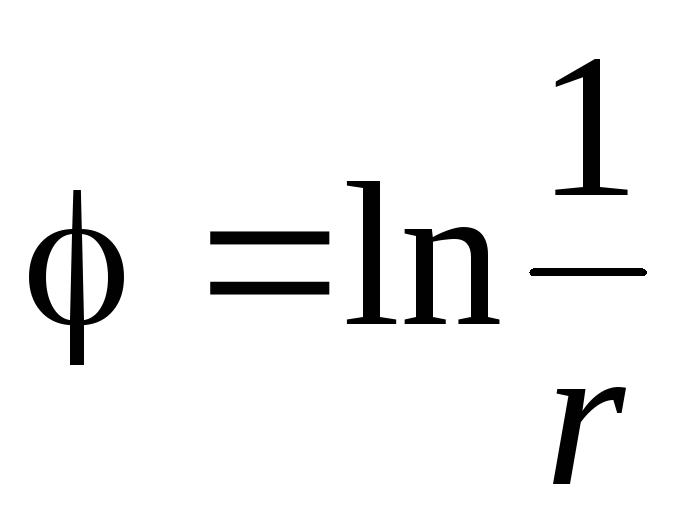 ,
,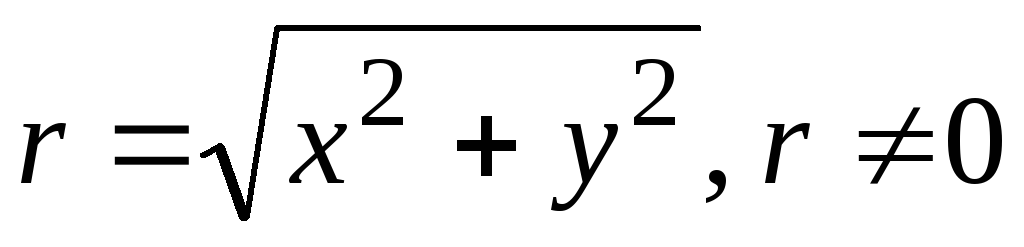 ,
является гармоническим
,
является гармоническим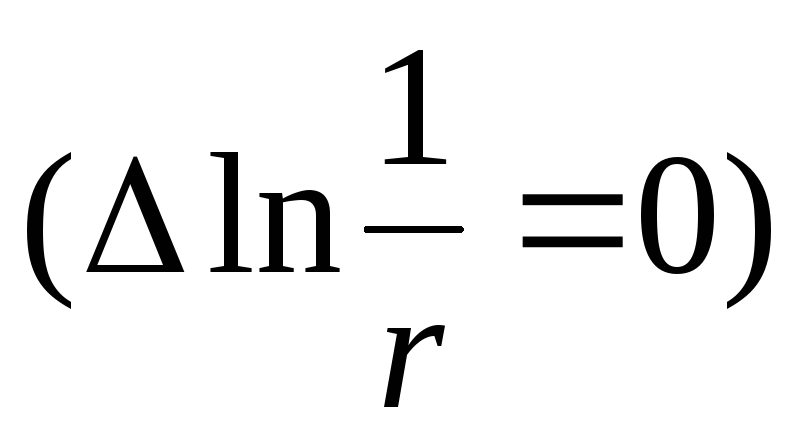 .
.
В задачах 124 – 131 выяснить, какие поля – гармонические, какие – нет:
Соленоидальное векторное поле — Википедия
Материал из Википедии — свободной энциклопедии
Определение
Векторное поле называется соленоидальным или вихревым[источник не указан 34 дня], если через любую замкнутую поверхность S его поток равен нулю:
- ∫Sa→⋅ds→=0{\displaystyle \int \limits _{S}{\vec {a}}\cdot {\vec {ds}}=0}.
Если это условие выполняется для любых замкнутых S в некоторой области (по умолчанию — всюду), то это условие равносильно тому, что равна нулю дивергенция векторного поля a→{\displaystyle {\vec {a}}}:
- diva→≡∇⋅a→=0{\displaystyle \mathrm {div} \,{\vec {a}}\equiv \nabla \cdot {\vec {a}}=0}
всюду на этой области (подразумевается, что дивергенция всюду на этой области существует). Поэтому соленоидальные поля называют также бездивергентными.
Для широкого класса областей это условие выполняется тогда и только тогда, когда a→{\displaystyle {\vec {a}}} имеет векторный потенциал, то есть существует некое такое векторное поле A→{\displaystyle {\vec {A}}} (векторный потенциал), что a→{\displaystyle {\vec {a}}} может быть выражено как его ротор:
- a→=∇×A→≡rotA→.{\displaystyle {\vec {a}}=\nabla \times {\vec {A}}\equiv \mathrm {rot} \,{\vec {A}}.}
Иначе говоря, поле является вихревым, если оно не имеет источников. Силовые линии такого поля не имеют ни начала, ни конца, и являются замкнутыми. Вихревое поле порождается не покоящимися зарядами (источниками), а изменением связанного с ним поля (например, для электрического поля порождается изменением магнитного). Поскольку в природе не существует магнитных зарядов, то магнитное поле всегда является вихревым, и его силовые линии всегда замкнуты. Силовые линии постоянного магнита, несмотря на то, что выходят из его полюсов (словно имеют источники внутри), на самом деле замыкаются внутри магнита. Поэтому, разрезав магнит надвое, не удастся получить два отдельных магнитных полюса.
Примеры
Этимология
Слово соленоидальное происходит от греческого соленоид (σωληνοειδές, sōlēnoeidēs), означающее «трубообразно» или «как в трубе», содержащего слово σωλην (Solen) — труба. В данном контексте это означает фиксацию объема для модели текущей жидкости, отсутствие источников и стоков (как при течении в трубе, где новая жидкость не появляется и не пропадает).[источник не указан 34 дня]
См. также
Соленоидальное векторное поле / Теория поля / 3dstroyproekt.ru
Определение соленоидального поля
Векторное поле $\bar { a } (\mathbf { \textit { M } } )$ называется соленоидальным в области $\mathbf { \textit { V } } $, если во всех точках этой области $div\bar { a } (M)=0$.
Согласно этому определению, поле не может иметь в области $\mathbf { \textit { V } } $ источников и стоков, таким свойством обладает магнитное поле соленоида, что и объясняет происхождение термина.
Соленоидально поле ротора любого достаточно гладкого поля: $div\,rot\bar { a } (M)=\nabla \cdot \left[ { \nabla \times \bar { a } }\right]=0$.
Самостоятельно доказать это свойство в координатной форме.
Свойства соленоидального поля
- Поток соленоидального векторного поля через поверхность $\sigma $, ограничивающую область $V_\sigma \in V$, равен нулю. Это прямое следствие формулы Остроградского.
- Верно и обратное утверждение: равенство нулю потока через любую замкнутую поверхность $\sigma $ достаточно для соленоидальности поля $\bar { a } (\mathbf { \textit { M } } )$. Действительно, в разделе Инвариантное определение дивергенции мы доказали, что $div\bar { a } (M)=\mathop { \lim } \limits_ { \sigma \to M } \frac { \Pi } { V } =\mathop { \lim } \limits_ { \sigma \to M } \frac { \mathop { { \iint } } \limits_\sigma { \bar { a } \bar { n } d\sigma } } { V } \mathbf { , } $ и, так как $\mathop { { \iint } } \limits_\sigma { \bar { a } \bar { n } d\sigma } =0$, то $div\bar { a } (M)=0$.
- Пусть в $\mathbf { \textit { V } } $ имеется изолированный источник { или сток } поля. Если поле $\bar { a } (\mathbf { \textit { M } } )$ соленоидально, то его поток через любую замкнутую поверхность $\sigma $, содержащую этот источник имеет одно и то же значение. Фраза «в $\mathbf { \textit { V } } $ имеется изолированный источник { или сток } поля» означает, что область $\mathbf { \textit { V } } $, в которой поле соленоидально, неодносвязна из $\mathbf { \textit { V } } $ выколота точка, в которой находится источник. Так, поле электрической напряжённости, создаваемое зарядом $\mathbf { \textit { q } } , \bar { E } =\frac { q } { r^3 } \bar { r } $, соленоидально всюду, кроме точки $r=0$, в которой расположен источник.
- Поток соленоидального векторного поля через любое поперечное сечение векторной трубки один и тот же. Это следует из того, что поток через боковую поверхность трубки равен нулю.
Соленоидальное векторное поле Википедия
Содержание
- 1 Определение
- 2 Примеры
- 3 Этимология
- 4 См. также
Определение[ | ]
Векторное поле называется соленоидальным или вихревым[источник не указан 499 дней], если через любую замкнутую поверхность S его поток равен нулю:
- ∫Sa→⋅ds→=0{\displaystyle \int \limits _{S}{\vec {a}}\cdot {\vec {ds}}=0}.
Другое определение соленоидального поля: Векторное поле a→{\displaystyle {\vec {a}}}называют соленоидальным, если оно является вихрем некоторого поля b→{\displaystyle {\vec {b}}},a→=rotb→{\displaystyle {\vec {a}}=rot{\vec {b}}}. При этом векторное поле b→{\displaystyle {\vec {b}}} называют векторным потенциалом поля a→{\displaystyle {\vec {a}}}.[1]
Если это условие выполняется для любых замкнутых S в некоторой области (по умолчанию — всюду), то это условие равносильно тому, что равна нулю дивергенция векторного поля a→{\displaystyle {\vec {a}}}:
- diva→≡∇⋅a→=0{\displaystyle \mathrm {div} \,{\vec {a}}\equiv \nabla \cdot {\vec {a}}=0}
всюду на этой области (подразумевается, что дивергенция всюду на этой области существует). Поэтому соленоидальные поля называют также бездивергентными.
Для широкого класса областей это условие выполняется
тогда и только тогда, когда a→{\displaystyle {\vec {a}}} имеет векторный потенциал, то есть существует некое такое векторное поле A→{\displaystyle {\vec {A}}}
Соленоидальное векторное поле — это… Что такое Соленоидальное векторное поле?
Определение
Векторное поле называется соленоидальным или вихревым, если через любую замкнутую поверхность S его поток равен нулю:
- .
Если это условие выполняется для любых замкнутых S в некоторой области (по умолчанию — всюду), то это условие равносильно тому, что равна нулю дивергенция векторного поля :
всюду на этой области (подразумевается, что дивергенция всюду на этой области существует). Поэтому соленоидальные поля называют также бездивергентными.
Для широкого класса областей это условие выполняется тогда и только тогда, когда имеет векторный потенциал, то есть существует некое такое векторное поле (векторный потенциал), что может быть выражено как его ротор:
Проще говоря, поле является вихревым, если оно не имеет источников. Силовые линии такого поля не имеют ни начала, ни конца, и являются замкнутыми. Вихревое поле порождается не покоящимися зарядами (источниками), а изменением связанного с ним поля (например, для электрического поля порождается изменением магнитного). Поскольку в природе не существует магнитных зарядов, то магнитное поле всегда является вихревым, и его силовые линии всегда замкнуты. Силовые линии постоянного магнита, несмотря на то, что выходят из его полюсов (словно имеют источники внутри), на самом деле замыкаются внутри магнита. Поэтому, разрезав магнит надвое, не удастся получить два отдельных магнитных полюса.
Примеры
Этимология
Слово cоленоидальное происходит от греческого соленоид (σωληνοειδές, sōlēnoeidēs), означающее «трубообразно» или «как в трубе», содержащего слово σωλην (Solen) — труба. В данном контексте это означает фиксацию объема для модели текущей жидкости, отсутствие источников и стоков (как при течении в трубе, где новая жидкость не появляется и не пропадает).

