Определение собственной частоты колебаний упругой оболочки и ее присоединенной массы
Введение. При решении задач динамики, часто возникает необходимость экспериментального определения параметров, входящих в дифференциальные уравнения, которые описывают какую-либо технологическую систему или процесс.
Например, сейчас в России производятся установки для утилизации изношенных покрышек фрезерованием крупногабаритной цилиндрической фрезой [1, 2]. Для одной из таких установок [2] была составлена и опубликована [3] математическая модель, которая в перспективе должна позволить снизить затраты на натурные испытания и доработку. Модель содержит ряд неизвестных параметров, относящихся к обрабатываемому объекту – автомобильной покрышке. Результаты экспериментального определение радиальной и тангенциальной жесткости покрышки ранее уже были опубликованы [4]. В данной статье приводятся результаты экспериментального определения собственной частоты колебаний автомобильной покрышки и ее присоединенной массы, которые могут быть применимы и к другим аналогичным задачам.
Постановка задачи. В случае вынужденных или свободных колебаний упругой оболочки, колебания совершает не вся оболочка, а лишь некоторая ее часть. Массу этой части оболочки далее будем называть присоединенной.
Значение присоединенной массы можно выразить из формулы определения собственной частоты колебаний тела [5, с.79], [6, с.11], [7, с.62]. Получим:
где m – присоединенная масса, кг; c – жесткость, Н/м; ω0 – собственная круговая частота колебаний, рад/с.
Чтобы воспользоваться этой формулой, необходимо знать собственную частоту колебаний оболочки. При отсутствии внутреннего трения собственная частота совпадает с резонансной. В случае вынужденных гармонических колебаний при наличии трения, резонансную частоту колебаний можно вычислить по формуле [5, с. 101]:
,
где ω – резонансная частота колебаний, рад/с; λ – коэффициент затухания, с-1.
При этом, если λ <<ω0, разница между резонансной частотой и собственной будет второго порядка малости [5, с. 101] и ей можно пренебречь. В этом случае ω=ω0.
101] и ей можно пренебречь. В этом случае ω=ω0.
Известно, что явление резонанса, сопровождается значительным ростом амплитуды колебаний. В случае вынужденных колебаний при наличии вязкого трения, величина амплитуды колебаний при резонансе зависит от коэффициента затухания λ [5, с. 105], [6, с.23] и вычисляется по формуле:
,
где b – амплитуда колебаний, м; ω0 – собственная круговая частота колебаний, рад/с; γ – частота воздействия вынуждающей силы, рад/с; λ – коэффициент затухания, с-1; f – амплитуда вынуждающей силы, Н; m – масса, кг.
При достаточно большом значении коэффициента затухания, резонанс может вообще не сопровождаться ростом амплитуды (рис. 1). Также с ростом коэффициента затухания, границы области резонанса становятся более размытыми, а максимум амплитуды сдвигается в область меньшей частоты, относительно собственной. В результате определение области резонанса по амплитуде колебаний для материалов с высоким значением коэффициентом демпфирования, каковым, например, является резина, затруднительно, либо вовсе невозможно.
Рис. 1. Графики зависимости амплитуды колебаний b и фазового сдвига ψ от λ и отношения частоты вынуждающей γ к собственной частоте колебаний ω0. Для верхней линии λ=0,1ω0, для нижней λ=1ω0, шаг промежуточных линий 0,1ω0
Известна другая характерная особенность вынужденных колебаний – разность фаз ψ между перемещением колеблющегося тела и вынуждающей силой при совпадении частот равна [5, с. 104], [6, с.21] и не зависит от значения коэффициента демпфирования (рис. 1). Таким образом, зная фазовый сдвиг ψ между вынуждающей силой и смещением поверхности оболочки в точке приложения этой силы при изменении частоты колебаний, можно достаточно точно определить собственную частоту колебаний.
Для экспериментального определения частоты собственных колебаний автомобильной покрышки этим методом, была сконструирована специальная установка, показанная на рис. 2.
Рис. 2. Установка определения резонансной частоты колебаний покрышки
На массивном металлическом столе надежно закреплена покрышка. Рядом с покрышкой на стол устанавливается вибратор. Вибратор воздействует на протектор покрышки через толкатель 6, к которому жестко присоединен высокоточный тензометрический датчик давления с линейной зависимостью. Толкатель 6 соединен с электромотором 1 через кривошипно-шатунный механизм 4 и ременную передачу 2. Электромотор 1 представляет собой асинхронный трехфазный двигатель АПН 011/4, с частотой вращения вала n
Рядом с покрышкой на стол устанавливается вибратор. Вибратор воздействует на протектор покрышки через толкатель 6, к которому жестко присоединен высокоточный тензометрический датчик давления с линейной зависимостью. Толкатель 6 соединен с электромотором 1 через кривошипно-шатунный механизм 4 и ременную передачу 2. Электромотор 1 представляет собой асинхронный трехфазный двигатель АПН 011/4, с частотой вращения вала n
Для проведения эксперимента использовалось следующее измерительное оборудование: сейсмический вибродатчик измерения вибросторости СГ-10, осциллограф С1-93, низкочастотный звуковой генератор ГЗ-102, оптопара, высокоточный керамический тензодатчик давления, легковая покрышка MATADOR-OMSKSHINA MP-50 Sibir массой 6,9 кг.
В ходе эксперимента, на осциллограф С1-93 подавались сигналы: на ось Oy с вибродатчика виброскорости СГ-10, на ось Ox со звукового генератора ГЗ-102. Вибродатчик виброскорости СГ-10 плотно прижимался к протектору колеблющейся покрышки. Далее выполнялось изменение частоты сигнала звукового генератора до появления на экране осциллографа фигур Лиссажу. Таким образом, по частоте звукового генератора определялась текущая частота колебаний покрышки.
Максимальная частота колебаний, достигнутая с использованием данной установки, составила ξmax Гц. Звуковой генератор ГЗ-102 выдает частоты от 17,7 до 210 Гц, без использования множителя. Таким образом, диапазон частот, которые можно точно определить и зафиксировать с использованием звукового генератора и данной установки составляет 17,7÷46 Гц.
В результате выполнения эксперимента по определению собственной частоты колебаний покрышки с использованием виброустановки были получен ряд графиков, показанных на рис. 3 и 4.
Рис. 3. Фазовый сдвиг между вынуждающей силой и перемещением
Рис. 4. Фазовый сдвиг между вынуждающей силой и перемещением
Длинная вертикальная линия показывает фазовый сдвиг «нулевой» точки относительно вынуждающей силы. Значение фазового сдвига при этом составило приблизительно 67°. Видно, что независимо от частоты колебаний эта линия остается почти неподвижной. Такой результат является довольно странным, поскольку с ростом частоты она должна приближаться к линии Pi/2. Поэтому был выполнен еще ряд экспериментов.
Для приближенного определения форм и частот собственных колебаний шины, была построена упрощенная трехмерная модель шины в программе SolidWorks. Материал шины – резина, со следующими характеристиками: модуль Юнга E=15 МПа, модуль упругости при сдвиге G=3 МПа, коэффициент Пуассона μ=0,49, плотность ρ=1100 кг/м3. Наличие корда в шине не учитывалось.
Наличие корда в шине не учитывалось.
Далее, в SolidWorks Simulation были определены собственные формы и частоты свободных колебаний этой модели шины. В результате были получены 5 форм (табл.) и собственных частот колебаний. Однако две из пяти формы колебаний являются ортогональными двум другим (частоты колебаний идентичны). Таким образом, были получены лишь 3 действительно отличных друг от друга формы и частоты колебаний. Модель шины была жестко зафиксирована за бортовые кольца.
Таблица
Формы и собственные частоты колебаний модели покрышки
|
Порядковый номер |
Форма |
Частота |
|---|---|---|
|
|
25,04 Гц |
|
|
Вторая форма |
35,11 Гц |
|
|
Третья форма |
35,11 Гц |
|
|
Четвертая форма |
68,57 Гц |
|
|
Пятая форма |
|
Эксперимент по определению собственной частоты колебаний методом свободного удара дал результаты, которые хорошо согласовываются с расчетами, выполненными в SolidWorks Simulation.
Данным методом возможно экспериментальное определение низших резонансных частот путем замера частоты свободных колебаний исследуемого объекта после удара. Найденная таким методом частота колебаний будет меньше частоты собственных колебаний в отсутствии трения. Однако влияние трения на частоту свободных колебаний значительно меньше, чем влияние на амплитуду, в связи с чем, даже при достаточно большом коэффициенте затухания можно принять эти частоты равными [6, с.12].
При выполнении этого эксперимента использовалось следующее оборудование: сейсмический вибродатчик измерения вибросторости СГ-10, осциллограф С1-93, низкочастотный звуковой генератор ГЗ-102, молоток.
К протектору покрышки прижимался датчик измерения виброскорости и наносился удар молотком в трех местах: рядом с датчиком, под углом в 90° к оси датчика, а также с противоположной стороны (180°). Показания осциллографа записывались на видеокамеру. Результаты приведены на рис. 5.
Рис. 5. График изменения виброскорости при свободном ударе (1дел. –30 мс)
–30 мс)
Также в результате хаотично направленных постукиваний, был получен график изменения виброскорости наиболее близкий к гармоническому (рис. 6). Видно, что одно колебание происходит за 15 мс. Таким образом, частота собственных колебаний данной покрышки составляет Гц.
Рис. 6. График изменения виброскорости при свободном ударе (1дел. – 30мс)
Используя данные графики виброскорости можно приближенно вычислить коэффициент затухания λ, по времени τ уменьшения амплитуды колебаний в e раз, с использованием формулы:
Эта формула связана с амплитудой колебаний, которая при проведении экспериментов не измерялась. Однако, через 100 мс виброскорость падает практически до нуля, а значит и амплитуда, уменьшается более чем в e раз и с некоторой погрешностью можно определить d и λ. Полученная таким образом λ будет меньше реальной.
Получаем:
с-1
С использованием λ=10 с-1 можно построить расчетный график фазового сдвига, аналогичный рис. 1.
1.
Рис. 7. Фазовый сдвиг ψ при λ=10 с-1 и ω0=66,6 Гц.
На рис. 7 серым цветом выделена область, в которой проводилось экспериментальное определение фазового сдвига. Экспериментальное значение фазового сдвига составило 67°. Как видно из графика это значение попадает в выделенную область. Таким образом, можно сделать вывод, что измеренное значение фазового сдвига верное, а его почти неизменное значение можно объяснить отклонением от линейности свойств материала, погрешностью измерений и высоким значением коэффициента затухания, при котором колебания также становятся нелинейными.
Зная собственную частоту колебаний шины ω0 и ее радиальную жесткость c , которая уже была определена ранее [4], можно вычислить значение присоединенной массы:
кг.
Таким образом значение присоединенной массы составляет почти 200 грамм или около 3% массы всей покрышки. Однако на самом деле значение присоединенной массы также зависит от частоты вынужденных колебаний и амплитуды, поскольку жесткость покрышки нелинейная [4].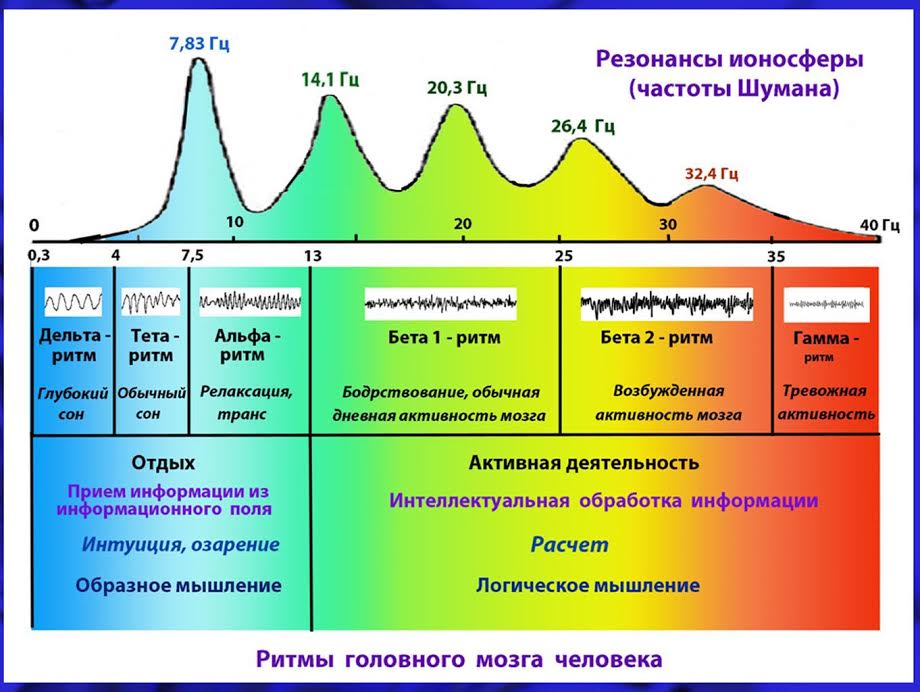
Заключение. В результате определена собственная частота колебаний покрышки, найдено значение ее присоединенной массы, а также найдено приближенное значение коэффициента затухания. Также можно заключить, что метод свободного удара оказался точнее метода фазового сдвига и проще в постановке.
Оптика и волны
В случае вынужденных колебаний система колеблется под действием периодической внешней (вынуждающей) силы. За счет работы этой силы компенсируются потери энергии системы. Частота вынужденных колебаний зависит от частоты изменения внешней силы (для краткости мы будем называть её «вынуждающей частотой»). Практически наиболее интересным является случай, когда вынуждающая сила изменяется по гармоническому закону:
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Это явление называется резонансом.
|
Резонанс — это явление резкого увеличения амплитуды вынужденных колебаний при определенной частоте внешнего воздействия, называемой резонансной частотой системы. |
Видео 1.21 Резонансное взаимодействие маятников
Видео 1.22 Камертоны: резонансное поглощение энергии волны
Видео 1.23 Резонанс доски с мотором
Явление резонанса используется для усиления колебаний, например электрических. Однако при конструировании машин и сооружений необходимо учитывать явление резонанса, чтобы предотвратить чаще всего нежелательные, а иногда и разрушительные последствия резонансного увеличения амплитуды вынужденных колебаний.
Для пружинного маятника уравнение вынужденного колебательного движения имеет вид:
|
|
(1. |
или
|
|
(1.84) |
где
и — вынуждающая частота.
Если рассматривать электрический колебательный контур, то компенсировать потери энергии в контуре можно с помощью подводимой извне периодически изменяющейся по гармоническому закону ЭДС или переменного напряжения
|
|
(1.85) |
Рис. 1.25. Вынужденные колебания в электромагнитном контуре
1.25. Вынужденные колебания в электромагнитном контуре
Уравнение колебаний в контуре (рис. 1.25) можно записать, используя закон Ома для замкнутой цепи
|
|
(1.86) |
или, с учетом, что
|
|
(1.87) |
где
— собственная частота контура,
— коэффициент затухания, a
Таким образом, вынужденные колебания в электрическом контуре описываются тем же самым линейным неоднородным дифференциальным уравнением второго порядка, что и в случае колебаний пружинного маятника. Предположим, что нам известно хотя бы одно решение этого уравнения — некое частное решение . Тогда разность любого другого решения q(t) и этого частного решения будет удовлетворять однородному уравнению (с нулем в правой части), которое мы подробно изучили в предыдущем разделе. Поэтому общее решение уравнения (1.87) может быть записано как
Предположим, что нам известно хотя бы одно решение этого уравнения — некое частное решение . Тогда разность любого другого решения q(t) и этого частного решения будет удовлетворять однородному уравнению (с нулем в правой части), которое мы подробно изучили в предыдущем разделе. Поэтому общее решение уравнения (1.87) может быть записано как
|
|
(1.88) |
где
— частота свободных затухающих колебаний.
С течением времени из-за экспоненциального множителя роль второго слагаемого уменьшается (оно важно на начальной стадии установления колебаний). По прошествии достаточно большого времени, а именно, при
,
им можно пренебречь, сохраняя лишь первое слагаемое. Таким образом, задача исследования установившихся вынужденных колебаний сводится к нахождению хотя бы одного частного решения уравнения (1.87).
Таким образом, задача исследования установившихся вынужденных колебаний сводится к нахождению хотя бы одного частного решения уравнения (1.87).
Частное решение неоднородного уравнения будем искать в виде гармонической функции, частота изменения которой совпадает с частотой вынуждающей силы:
|
|
(1.89) |
Подставим в виде (1.89) в уравнение (1.87):
|
|
(1.90) |
Так как функции синуса и косинуса линейно независимы, коэффициенты при них в левой части (1. 90) должны быть равны нулю:
90) должны быть равны нулю:
|
|
(1.91) |
Решение этой системы имеет вид:
|
|
(1.92) |
Решение (1.89) с коэффициентами (1.92) можно записать в стандартном виде:
|
|
(1. |
где
|
|
(1.94) |
и
|
|
(1.95) |
При знаке минус в фазе косинуса в выражении (1.93) начальная фаза имеет простой физический смысл: это отставание по фазе установившегося вынужденного колебания от гармонической вынуждающей «силы» (1.85).
Видео 1.24 Резонансный язычковый частотомер
Видео 1. 25 Спектр модулированного колебания
25 Спектр модулированного колебания
Рассмотрим отклик системы на изменение частоты внешней силы. Под квадратным корнем в выражении для амплитуды стоит квадратичная функция частоты
Эта функция имеет минимум (а значит, амплитуда имеет максимум).
Для нахождения точки минимума дифференцируем функцию по и приравниваем производную нулю. В итоге получаем следующие выражения для резонансной частоты
|
|
(1.96) |
и амплитуды установившихся вынужденных колебаний при резонансе
|
|
(1. |
Следует отметить, что при значение резонансной частоты практически совпадает с собственной частотой колебательной системы. Поскольку стоит в знаменателе выражения для , резонансная амплитуда колебаний растет с уменьшением затухания. На графике 1.26 видно, что чем меньше затухание, тем выше и правее лежит максимум резонансной кривой.
Рис. 1.26. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы
При увеличении частоты внешнего воздействия амплитуда стремится к нулю:
Физически это понятно: система обладает некой инерционностью и не успевает следовать за быстрыми изменениями внешнего воздействия. В другом предельном случае малой внешней частоты
мы имеем дело со статическим случаем — действием постоянной внешней силы F0 на пружинный маятник, или подсоединением контура к источнику с постоянным напряжением Um. В этом случае предельное значение амплитуды вынужденных колебаний равно
В этом случае предельное значение амплитуды вынужденных колебаний равно
и не зависит от затухания. Последнее вполне естественно, так как затухание обусловлено действием силы сопротивления, которая пропорциональна скорости и проявляется только при движении системы, а не в статическом пределе. В случае механических колебаний
|
|
(1.98) |
что равно удлинению пружины под действием постоянной силы F0.
В случае электромагнитных колебаний в контуре
|
|
(1. |
что равно заряду на конденсаторе при подсоединении его к источнику постоянного напряжения Um.
Найдем отношение резонансной амплитуды к статической при малом затухании, когда :
|
|
(1.100) |
Иными словами, добротность Q характеризует также резонансные свойства колебательной системы: чем больше добротность, тем выше и относительно уже резонансный пик (см. рис. 1.26).
Автоколебательные системы. Параметрический резонанс.
Видео 1.26 Анкерный механизм механических часов
Видео 1.27 Колебания линейки под струёй воды
Видео 1.28 Спираль Роже
Видео 1.29 Параметрический резонанс
Дополнительная информация
http://class-fizika. spb.ru/index.php/slaid/193-kol – Много интересных анимаций, видео, слайд-шоу по колебаниям и волнам.
spb.ru/index.php/slaid/193-kol – Много интересных анимаций, видео, слайд-шоу по колебаниям и волнам.
http://www.fxyz.ru/формулы_по_физике/колебания_и_волны – Основные формулы по колебаниям и волнам (см. Также раздел «подтемы» справа вверху)
http://physics-lectures.ru/category/mexanicheski-kolebaniya-i-volny/ – Лекции по колебаниям и волнам
http://www.alleng.ru/d/phys/phys105.htm – Д.В. Сивухин. Электричество, колебания и волны. Учебник.
http://www.ph5s.ru/book_ph_koleb.html – Ссылки на книги по колебаниям и волнам. Сайт бывшего преподавателя МИФИ А.Н. Варгина.
http://fmclass.ru/math.php?id=485a8e5cc78f8 – Статьи по колебаниям и оптике из журнала «Квант»
http://www.physel.ru/mainmenu-48.html – Полезные материалы по колебаниям и волнам.
http://koi.tspu.ru/waves/index.htm – А.Г. Парфенов, Электронный мультимедиа-учебник по колебаниям и волнам
http://www.alleng.ru/d/phys/phys126.htm – Савельев, Курс общей физики. Т.1 – Механика, колебания и волны, молекулярная физика.
http://www.alleng.ru/d/phys/phys260.htm – А.Я. Исаков , В.В. Исакова. Колебательные и волновые процессы, руководство по самостоятельной работе.
http://lib.mexmat.ru/books/6452 – Г.С. Ландсберг. Элементарный учебник физики. Колебания и волны. Оптика. Атомная и ядерная физика.
http://elkniga.ucoz.ru/ – Г.Я. Мякишев, А.З. Синяков. Учебник по колебаниям и волнам для углубленного изучения в 11-м классе.
http://repetitor.mathematic.of.by/spravka_fizika.htm#M2 – Основные формулы по механике, в том числе – по колебаниям.
http://www.alleng.ru/d/phys/phys194.htm – Л.Н. Коршунова. Колебания и волны. Пособия по решению задач.
http://fizportal.ru/fluctuation-b – Банк задач по колебаниям и волнам с решениями.
http://www.alleng.ru/d/phys/phys127.htm – Савельев, Курс общей физики. Т.2 — Электричество и магнетизм. Волны. Оптика.
http://ligis.ru/effects/science/238/index.htm – Эффект механического резонанса.
http://schools.keldysh.ru/sch2216/students/spr_resh_zad/wob_wave/wob_wave1. htm – Задачи по колебаниям и волнам с решениями.
htm – Задачи по колебаниям и волнам с решениями.
http://sgtnd.narod.ru/papers/TASKS.pdf – А.П. Кузнецов, А.Г. Рожнев, Д.И. Трубецков. Линейные колебания и волны. Сборник задач.
http://www.phys.kemsu.ru/viewpage.php?page_id=178 – Задачи по колебаниям и волнам повышенной сложности для старшеклассников.
http://physbook.ru/index.php/PPT._Маятник_Фуко – Маятник Фуко. История, модели.
Резонансная частота | это… Что такое Резонансная частота?
Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.
Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем. Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.
Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.
Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы
Содержание
|
Механика
Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
- ,
где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).
Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.
В основе работы механических резонаторов лежит преобразование кинетической энергии в потенциальную и обратно. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.
Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.
Электроника
В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.
Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.
Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.
Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.
Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.
Акустика
Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов.
Струна
Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:
где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:
Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:
- ,
где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.
Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.
Примечания
См. также
- Диссипативная структура
- Солитон
- Интерференция
- Журавлёв, Виктор Филиппович (см. в кн. «Прикладные методы в теории колебаний» (1988, совместно с Д. М. Климовым))
Ссылки
Richardson LF (1922), Weather prediction by numerical process, Cambridge.
Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457-472.
J. Fluid Mech., 20, 457-472.
Бломберген Н. (1965), Нелинейная оптика, М.: Мир — 424 с.
Захаров В.Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431-453.
Арнольд В.И. (1979), Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны, ред. А.В. Гапонов-Грехов, М.: Наука, 116-131.
Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275-309.
Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
Филлипс O.М. (1984), Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. М.: Мир, 297-314.
Журавлёв В.Ф., Климов Д.М. (1988), Прикладные методы в теории колебаний, М.:Наука
Сухоруков А.П. (1988), Нелинейные волновые взаимодействия в оптике и радиофизике, М. : Наука — 232 с.
: Наука — 232 с.
Брюно А.Д. (1990), Ограниченная задача трех тел, М.:Наука
Ударный спектр и добротность колебательной системы
Ударный спектр — это график значений максимального отклика на внешнее воздействие системы резонаторов с одной степенью свободы, упорядоченный по собственным частотам резонаторов.
Определение краткое и достаточно точное, но почему-то у людей возникают дополнительные вопросы. Дополнительные вопросы возникают оттого, что людям трудно представить себе образ даже одного резонатора с одной степенью свободы, то что говорить о целой системе.
Если объяснять этот термин на пальцах, то надо подходить к этому вопросу аккуратно и последовательно, чтобы постепенно сложить в голове человека образ описываемого явления. С материальными объектами проще — их достаточно показать, чтобы человеку всё стало ясно. С информационными явлениями гораздо сложнее, но мы эту проблему решим.
Резонатор с одной степень свободы
Представим себе объект, который может совершать колебания в пространстве только в направлении одной оси.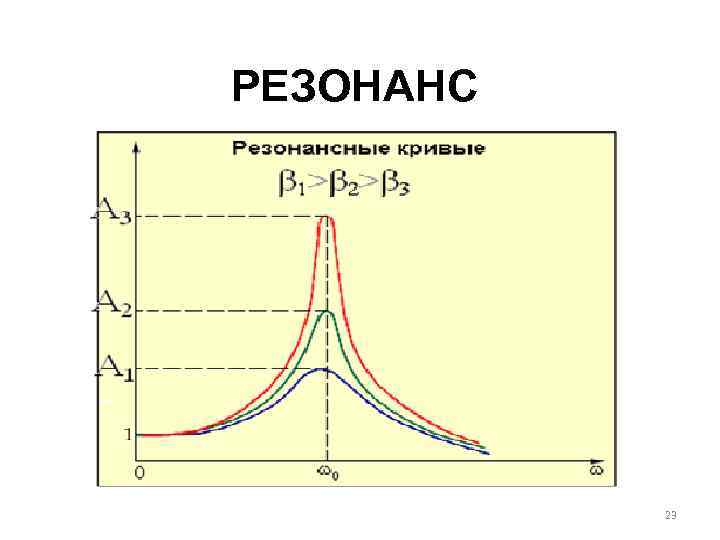 Это и будет резонатор с одной степенью свободы. Пружины и маятники — это всё примеры резонаторов с одной степенью свободы. Хотя природа их колебаний различна в теории они описываются аналогичными уравнениями. У них есть одна собственная частота и одна резонансная частота. Для удобства практического использования эти частоты объединяют в одну, но это две разные частоты. Резонансная частота — это частота действия внешней силы, на которой достигается максимальная амплитуда колебаний. Собственная частота — это частота затухающих колебаний, когда внешняя сила исчезла и система теряет энергию, возвращаясь в положение равновесия (останавливается).
Это и будет резонатор с одной степенью свободы. Пружины и маятники — это всё примеры резонаторов с одной степенью свободы. Хотя природа их колебаний различна в теории они описываются аналогичными уравнениями. У них есть одна собственная частота и одна резонансная частота. Для удобства практического использования эти частоты объединяют в одну, но это две разные частоты. Резонансная частота — это частота действия внешней силы, на которой достигается максимальная амплитуда колебаний. Собственная частота — это частота затухающих колебаний, когда внешняя сила исчезла и система теряет энергию, возвращаясь в положение равновесия (останавливается).
Представим себе знакомый нам всем с детства маятник — качели.
Резонансная частота маятника не зависит от массы груза (то есть не разницы кто сидит на качелях хрупкая маленькая девочка или её большой тяжёлый папа), а зависит только от длины подвеса. Чем длиннее этот подвес, тем меньше резонансная частота. Чем выше качели, тем дольше период одного качания.
Ребёнок, впервые попавший на качели, поначалу прилагает много самых разных усилий с произвольной частотой, но качели почти не двигаются. Достаточно быстро он понимает темп, в котором надо делать усилия, чтобы раскачивать качели и понимает, что делать их надо в момент, когда качели замирают на одном из пиков.
Говоря сухим научным языком, когда частота действия внешней силы совпадает с частотой резонанса система начинает в этот самый резонанс входить, увеличивая амплитуду колебаний.
Сил у ребёнка немного и раскачать качели он сильно не может. В определённый момент все силы его начинают уходит не на увеличение амплитуды колебаний, а на поддержание колебаний на том же уровне. В этот момент вся энергия, которую прикладывает ребёнок, будет тратиться за один период колебаний на преодоление трения подвеса и сопротивление воздуха. Если предположить, что в каждый период колебаний качелей ребёнок прикладывает одинаковое усилие совершая работу A, то достигнув максимальных колебаний за n раз, он затратит количество энергии:
W=n×A,
которая перейдёт в энергию качания качелей (часть этой энергии будет рассеяна, но пока это не существенно).
После этого вся его энергия будет полностью рассеиваться за один такт качения:
A=E×d
После понимания этого момента можно переходит к понятию добротности.
Добротность
Добротность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. В общем виде для любой колебательной системы добротность вычисляется по следующей формуле:
f0 — резонансная частота;
W — запасённая энергия системы;
Pd — рассеиваемая мощность;
Ed — рассеиваемая энергия за один период колебаний;
A — работа, совершаемая внешней силой за один период колебаний;
n — количество колебаний, которое сделал система, прежде чем достигла максимальной амплитуды колебаний.
Из этой формулы можно сделать один очень важный вывод, который нам пригодится:
Чем выше добротность колебательной системы, тем больше колебаний сделает система под действием внешний силы, прежде чем достигнет максимальной амплитуды.
То есть, чем выше качели (чем длиннее маятник — тем выше его добротность) тем больше нужно сделать колебаний, чтобы их раскачать. От величины внешней силы зависит только амплитуда колебаний, которые может совершать система. Если ребёнок не сам качается на качелях, а его качает папа (а у папы силы больше и энергии он даёт больше), качели будут подниматься гораздо выше, но максимальной амплитуды качели достигнут примерно за то же число колебаний, если папа будет качать с одинаковым усилием. В качании на качелях самое главное не переусердствовать иначе ребёнка может укачать или качели сломаются.
Собственная частота
Когда дети становятся старше, им надоедает просто качаться на качелях и они раскачавшись прыгают с них, стараясь подлететь повыше и подальше приземлиться (хорошо что детские площадки посыпают песком). После такого прыжка на качелях не остаётся источника внешней толкающей силы, да и отцу становится «не очень интересно » толкать пустые качели. Постепенно амплитуда качения уменьшается и качели останавливаются. Интервал времени между двумя ближайшими моментами отклонения качелей (маятника, резонатора, сигнала и т.д.) называется периодом собственных колебаний, а обратная ему величина — частотой собственных колебаний.
Постепенно амплитуда качения уменьшается и качели останавливаются. Интервал времени между двумя ближайшими моментами отклонения качелей (маятника, резонатора, сигнала и т.д.) называется периодом собственных колебаний, а обратная ему величина — частотой собственных колебаний.
Одни колебательные системы останавливаются быстро, всего за пару тройку колебаний (большинство качелей во дворе останавливаются не более чем за 7 колебаний), а колебания других могут затухать очень долго (колокола — это тоже колебательные системы). Скорость, с которой колебания затухают, очень важный параметр. Он называется декремент затухания.
Декремент затухания
Декремент затухания или логарифмический декремент колебаний — это безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных (или через некоторое целое количество периодов) амплитуд колеблющейся величины в одну и ту же сторону:
Декремент затухания равен показателю экспоненты в законе затухающих колебаний:
Из декремента затухания можно рассчитать другую величину — коэффициент демпфирования по следующей формуле:
Коэффициент демпфирования (затухания)
Декремент затухания величина расчётная и рассчитывается по графику затухающих колебаний. Для колебательных систем с вязким трением (сила сопротивления пропорциональная скорости движения) физической величиной определяющей характер колебаний является коэффициент демпфирования.
Для колебательных систем с вязким трением (сила сопротивления пропорциональная скорости движения) физической величиной определяющей характер колебаний является коэффициент демпфирования.
, где
c — коэффициент силы сопротивления движению;
k — коэффициент упругости;
m — масса подвижного груза.
При коэффициенте демпфирования меньшем единицы колебательная система будет плавно затухать. Чем меньше будет коэффициент, тем дольше будут длиться колебания. При коэффициенте равном единице или большем никаких колебаний система испытывать не будет, а просто плавно будет стремиться к нулевому положению. Так, например, дверные доводчики настраивают на коэффициент демпфирования 1 и более, чтобы дверь автоматически закрылась через некоторое время без удара о створку. Демпферы для входных дверей в метро наоборот настроены на коэффициент демпфирования меньше 1. После того как человек толкнёт такую дверь она сделает два три колебания и остановится.
Коэффициент демпфирования связан с добротностью следующей формулой:
Из формулы следует, что чем больше добротность колебательной системы, тем меньше декремент затухания. Чем меньше декремент затухания, тем меньше теряется энергии с каждым колебанием и тем больше колебаний совершит система перед остановкой. Этот простой вывод нам пригодится для дальнейшей работы.
Чем меньше декремент затухания, тем меньше теряется энергии с каждым колебанием и тем больше колебаний совершит система перед остановкой. Этот простой вывод нам пригодится для дальнейшей работы.
Если рассматривать качели, маятники и прочие системы с низкой собственной частотой (и большим периодом колебаний соответственно), то считать количество колебаний достаточно легко. Но когда мы рассматриваем колокола, балки и прочие системы с высокой собственной частотой, то «на глаз» подсчитать количество колебаний при затухании становится невозможно.
Система резонаторов
Если собрать несколько резонаторов с разными собственными частотами, но одинаковыми значениями декремента затухания, то получится та самая система резонаторов, о которой шла речь в самом начале статьи. Представьте себе площадку в парке отдыха, на которой установлены качели разных размеров, но похожие по конструкции. От размеров качелей будет зависеть собственная частота, а от конструкции и материалов декремент затухания. Таким образом, у них будут разные собственные частоты и одинаковый декремент затухания.
Таким образом, у них будут разные собственные частоты и одинаковый декремент затухания.
Если представить себе, что все качели одновременно испытывают воздействие внешней возбуждающей силы, от которой они начинают раскачиваться, то максимальная амплитуда колебаний, которую в какой-то момент достигнут качели, будет тем самым максимальным откликом. Подобным внешним воздействием может быть землетрясение. Если упорядочить значения максимальных ответов по возрастанию собственных частот соответствующих резонаторов, то полученный график называется ударным спектром. Если мы имеем дело с землетрясением, то в этом случае ударный спектр называют спектром ответа.
Как мы уже выяснили выше, максимальный отклик некоторых резонаторов может быть достигнут не тогда, когда мгновенное значение силы максимально, а в какой-нибудь другой момент. Этот момент зависит от гармоник, которые присутствуют в сигнале, и от их длительности. Даже если на систему действует гармонический сигнал с одной частотой, то раскачиваться под его воздействием будут все резонаторы.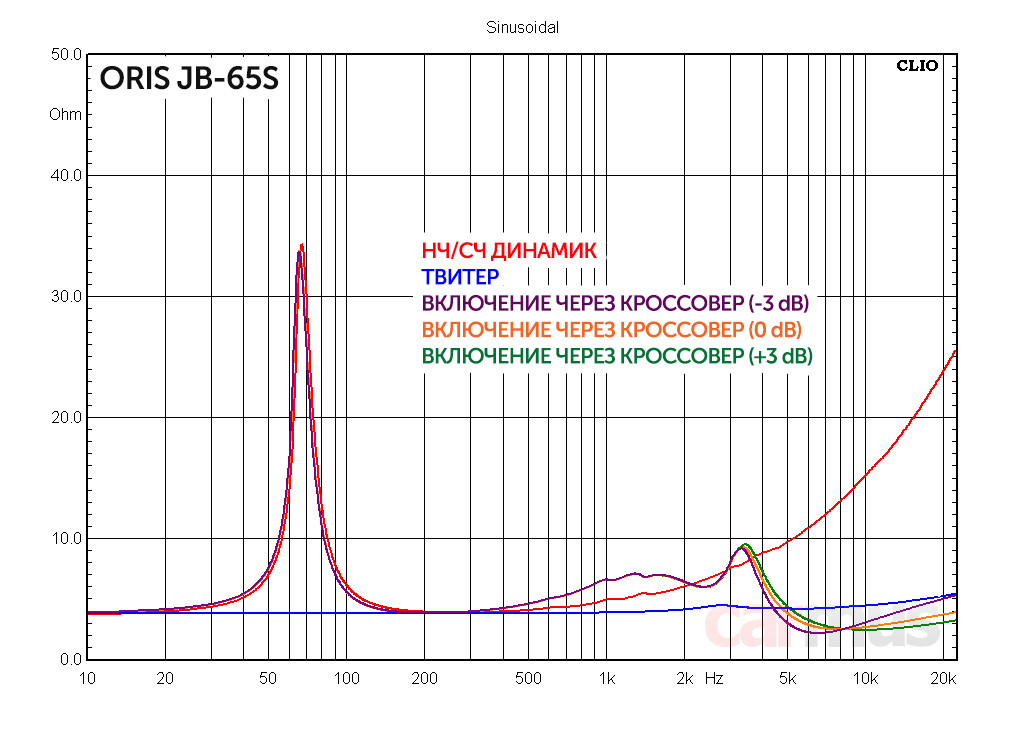 Максимального по амплитуде колебаний отклика достигнет резонатор с собственной частотой наиболее близкой к частоте колебаний, остальные будут колебаться меньше. Наглядно это демонстрирует график резонанса.
Максимального по амплитуде колебаний отклика достигнет резонатор с собственной частотой наиболее близкой к частоте колебаний, остальные будут колебаться меньше. Наглядно это демонстрирует график резонанса.
Если мы имеем дело, не с установившимися колебаниями, а с коротким воздействием, то картина будет иной. Будем на систему резонаторов действовать импульсом, состоящем из нескольких периодов синусоидального сигнала с частотой 1000 Гц от полу-периода до 10 периодов. Скажем заранее, что коэффициент демпфирования всех резонаторов равен 0,05, а добротность соответственно равна 10.
Как мы видим на графиках ударного спектра с ростом длительности воздействия увеличивается максимальный отклик системы резонаторов, причём частота, соответствующая максимальному отклику приближается к частоте сигнала генератора. На этом месте возникает уместный вопрос: «Почему от импульсов с малым числом периодов сильнее откликаются (то есть имеют большее значение) резонаторы с частотами большими частоты действующего импульса?». Для ответа на этот вопрос нужно внимательно рассмотреть график резонанса, приведённый выше.
Для ответа на этот вопрос нужно внимательно рассмотреть график резонанса, приведённый выше.
На графике резонанса изображена зависимость ответной реакции резонатора на входное воздействие постоянной амплитуды при изменяющейся частоте входного сигнала. На графике хорошо видно, что у резонаторов с низкой добротностью резонанс наступает на частоте заметно меньшей чем собственная частота резонатора. По мере роста добротности резонатора пик резонанса становится острее и выше, а частота приближается к собственной частоте резонатора.
В ударном спектре всё наоборот. Частота входного сигнала остаётся неизменной, а варьируются собственные частоты резонаторов. Добротность каждого резонатора ограничена сверху, но длительность входного воздействия позволяет раскачать все резонаторы. Поэтому добротность каждого резонатора будет определяться количеством периодов в сигнале (но не более 10).
Если частота резонатора выше частоты входного сигнала, то соотношение wa/w0a/w0 > 1 и амплитуда отклика быстро падает с уменьшением частоты резонатора. То есть маятники с длинным подвесом от высокочастотных воздействия даже не трогаются с места. Соответственно, большие строения (точнее сказать, строения из крупных блоков) никак не реагируют на работу отбойного молотка на улице, будь их там даже тысячи работающих одновременно.
То есть маятники с длинным подвесом от высокочастотных воздействия даже не трогаются с места. Соответственно, большие строения (точнее сказать, строения из крупных блоков) никак не реагируют на работу отбойного молотка на улице, будь их там даже тысячи работающих одновременно.
Если взять график резонанса соответствующий δ=0.5w0, то он будет примерно соответствовать спектру ударного отклика на полу-период синуса с той лишь разницей, что он будет отражён в другую сторону. Сигналам с большим числом периодов соответствуют графики с большей добротностью. Если совместить несколько графиков ударных спектров в одних осях, то мы увидим график напоминающий график резонанса, приведённый выше, но развёрнутый в обратном направлении.
Подводя итог статьи необходимо сделать вывод, что ударный спектр это прекрасный показатель внутреннего состояния объекта. Так для небольших объектов при построение ударного спектра по выходному сигналу можно выяснить состояние «внутренней системы резонаторов». Усталость материи, внутренние трещины и прочие неприятности вносят изменения в эту «внутреннюю систему резонаторов». Обычно это выражается в том, что происходит изменение собственных и резонансных частот, реже происходит падение добротности колебательных контуров.
Усталость материи, внутренние трещины и прочие неприятности вносят изменения в эту «внутреннюю систему резонаторов». Обычно это выражается в том, что происходит изменение собственных и резонансных частот, реже происходит падение добротности колебательных контуров.
Так, например, церковные колокола со временем «понижают» свои голоса, то есть у них происходит уменьшение собственной частоты (унтертона) и высота их звука падает. Таким образом проявляется эффект «старения» бронзы [1]. Если же колокол треснет (например, в сильный мороз), то он резко потеряет чистоту звука, то есть упадёт его добротность.
Можно представить себе испытуемый объект как систему резонаторов в виде набора струн (можно представить себе рояль), определить и запомнить какие «струны» в нём звучат и как сильно. А после эксплуатации по изменению этого набора откликов можно судить об внутренних изменениях. Так, например, ГОСТы на механические испытания рекомендую измерять и сравнивать АЧХ до и после испытаний. Ещё пример, при изменении основного тона собственных колебаний здания более чем в два раза в меньшую либо в большую сторону (одна из методик контроля), МЧС делает заключение, что здание находится в аварийном состоянии.
Ещё пример, при изменении основного тона собственных колебаний здания более чем в два раза в меньшую либо в большую сторону (одна из методик контроля), МЧС делает заключение, что здание находится в аварийном состоянии.
При землетрясениях наоборот измеряют ударный спектр самого землетрясения. Таким образом учёные оценивают степень разрушения зданий и сооружений [2]. Для каждого типа сооружений вычисляется диапазон наиболее разрушительных частот. Чем выше рассчитанный спектр в определённой полосе, тем больше повреждений получит здание.
При проектировании зданий в сейсмоопасных районах в конструкцию здания закладывают системы демпфирования колебаний. Системы демпфирования рассчитывают на гашение наиболее опасных частот. Такие частоты определяются исходя из анализа сейсмограмм в данной области за всё время наблюдений. И в конце проектных работы модель здания подвергают испытаниям на модельные землетрясения [3].
Ссылки
- https://www.muszone.ru/articles/23.
 html
html - https://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D0%B5%D0%BB%D1%8C_%D1%81%D0%B5%D0%B9%D1%81%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B3%D0%BE_%D0%B2%D0%BE%D0%B7%D0%B4%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D1%8F_%C2%AB%D0%A1%D0%90-482%C2%BB
- https://ru.wikipedia.org/wiki/Сейсмостойкое_строительство
- https://www.iris.edu/hq/inclass/video/building_resonance__boss_model_construction__use
В конце можно позволить отступить от области механики и сейсмики в область социальную. В обществе имеют место аналогичные явления, называемые «общественным резонансом». Если какое-то событие овладевает умами многих людей (говорят «нашло отклик в сердцах людей»), и о нём долго вспоминают и обсуждают (говорят «событие долго будоражит умы»), то налицо общественный резонанс. Такие события могут побудить людей к действиям, например, написать письмо на телевидение, в редакцию газеты или в руководящие органы. Руководство телеканала или администрация отсортируют письма, получат весь спектр ответов, проанализируют ситуацию и примут какие-то действия.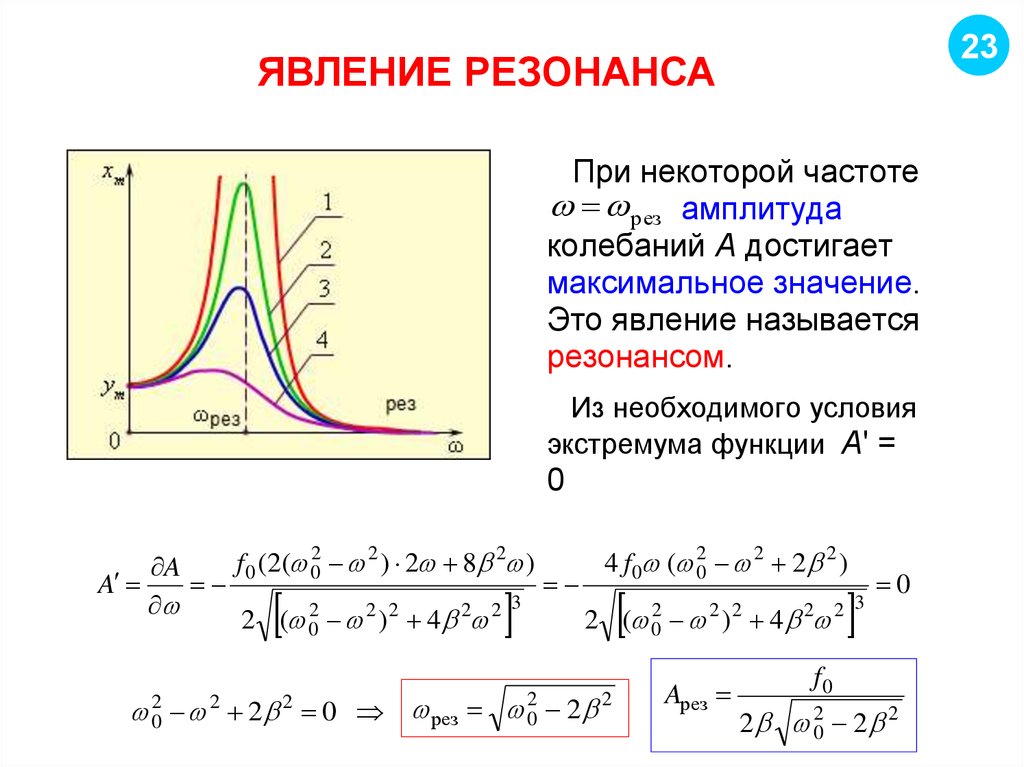
Подобная аналогия из жизни общества может быть не абсолютно точно повторяет свойства резонанса и ударного спектра в механике, но позволяет приблизить к пониманию механического резонанса большое число людей, не имеющих технического образования.
Резонанс: музыка, мосты и лед
Слово «резонанс» происходит от латинского resono и означает «откликаюсь». Суть этого явления заключается в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой к действию этой силы. Впервые резонанс был описан Галилео Галилеем в 1602 году в работах, посвященных исследованию маятников и музыкальных струн.
Резонанс является частой причиной возникновения звука в музыкальных инструментах. Одна из наших лучших моделей резонанса в музыкальном инструменте — это резонансная трубка (полая цилиндрическая трубка), частично заполненная водой и приводящаяся в вибрацию камертоном. Камертон — это объект, который заставил воздух внутри резонансной трубы войти в резонанс. Поскольку зубцы камертона вибрируют на своей собственной частоте, они создают звуковые волны, которые воздействуют на отверстие резонансной трубы. Эти сталкивающиеся звуковые волны, создаваемые камертоном, заставляют воздух внутри резонансной трубки вибрировать с той же частотой. Тем не менее, в отсутствие резонанса звук этих вибраций недостаточно громкий, чтобы его можно было различить. Резонанс возникает только тогда, когда первый объект вибрирует с собственной частотой второго объекта. Так что если частота, с которой вибрирует камертон, не идентична одной из собственных частот столба воздуха внутри резонаторной трубы, резонанса не произойдет, и два объекта не будут звучать вместе с громким звуком. Но расположение уровня воды можно изменить, поднимая и опуская резервуар с водой, тем самым уменьшая или увеличивая длину столба воздуха.
Поскольку зубцы камертона вибрируют на своей собственной частоте, они создают звуковые волны, которые воздействуют на отверстие резонансной трубы. Эти сталкивающиеся звуковые волны, создаваемые камертоном, заставляют воздух внутри резонансной трубки вибрировать с той же частотой. Тем не менее, в отсутствие резонанса звук этих вибраций недостаточно громкий, чтобы его можно было различить. Резонанс возникает только тогда, когда первый объект вибрирует с собственной частотой второго объекта. Так что если частота, с которой вибрирует камертон, не идентична одной из собственных частот столба воздуха внутри резонаторной трубы, резонанса не произойдет, и два объекта не будут звучать вместе с громким звуком. Но расположение уровня воды можно изменить, поднимая и опуская резервуар с водой, тем самым уменьшая или увеличивая длину столба воздуха.
Увеличение длины колебательной системы (в данном случае воздуха в трубе) увеличивает длину волны и уменьшает собственную частоту этой системы. И наоборот, уменьшение длины колебательной системы уменьшает длину волны и увеличивает собственную частоту. Таким образом, поднимая и опуская уровень воды, собственная частота воздуха в трубке может быть согласована с частотой, с которой вибрирует камертон. Когда совпадение достигнуто, камертон заставляет столб воздуха внутри резонансной трубы вибрировать с собственной частотой, и достигается резонанс. Результатом резонанса всегда является большая вибрация, то есть громкий звук.
И наоборот, уменьшение длины колебательной системы уменьшает длину волны и увеличивает собственную частоту. Таким образом, поднимая и опуская уровень воды, собственная частота воздуха в трубке может быть согласована с частотой, с которой вибрирует камертон. Когда совпадение достигнуто, камертон заставляет столб воздуха внутри резонансной трубы вибрировать с собственной частотой, и достигается резонанс. Результатом резонанса всегда является большая вибрация, то есть громкий звук.
Музыкальные инструменты приходят в колебательное движение на своей собственной частоте, когда человек ударяет, ударяет, наигрывает, щипает или каким-либо образом тревожит объект. Каждая собственная частота объекта связана с одним из множества паттернов стоячих волн, по которым этот объект может вибрировать. Собственные частоты музыкального инструмента иногда называют гармониками инструмента. Инструмент можно заставить вибрировать на одной из своих гармоник (с одной из его моделей стоячей волны), если другой взаимосвязанный объект толкает его на одной из этих частот.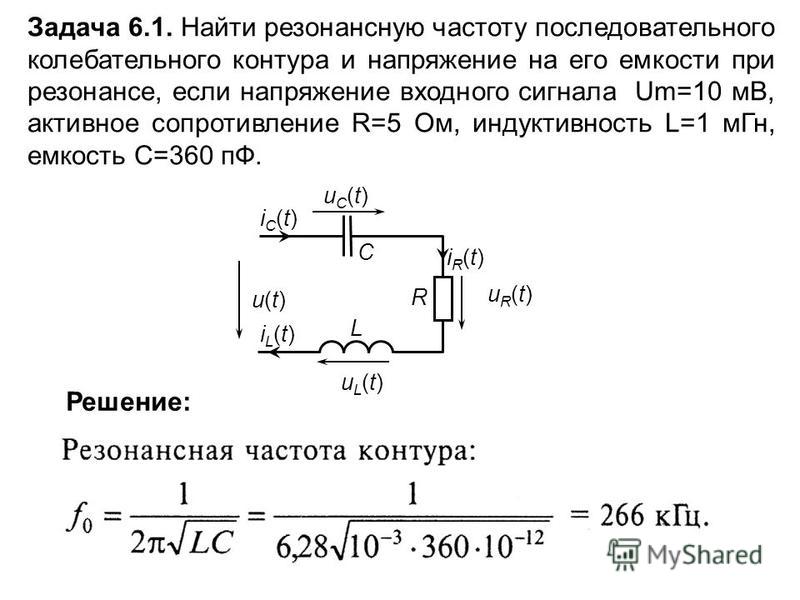 Это и есть резонанс: один объект, вибрирующий с той же собственной частотой, что и второй объект, заставляет этот второй объект колебаться.
Это и есть резонанс: один объект, вибрирующий с той же собственной частотой, что и второй объект, заставляет этот второй объект колебаться.
Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. Этот параметр колебательной системы определяет ширину резонанса и характеризует, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан. Обозначается символом Q (от англиского «quality factor»). Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.
Используется явление резонанса и в электронике. Колебательный контур, состоящий из емкости и индуктивности, используется в элементах настройки и электрических фильтрах. Однако резонанс может быть и вредным, если он вызывает искажение сигнала или паразитные шумы.
Наблюдается резонанс и в космосе, когда два небесных тела, которые имеют периоды обращения, соотносящиеся друг с другом как небольшие целые числа, делают регулярное гравитационное воздействие друг на друга, которое может стабилизировать их орбиты (орбитальный резонанс в небесной механике).
Однако наиболее часто резонанс бывает в классической и строительной механике, а также гидро- и аэромеханике. И, к сожалению, во многих случаях именно тогда, когда он совершенно нежелателен. Известно, что военным подразделениям при прохождении мостов приписывается «сбивать ногу» и идти не строевым, а свободным шагом. Причиной этому ряд случаев, таких как 12 апреля 1831 года, когда разрушился Бротонский подвесной мост через реку Ирвелл в Англии, по которому шел военный отряд. Частота шагов солдат, шагавших в ногу, совпала с частотой собственных колебаний моста, из-за которых амплитуда резко возросла, цепи оборвались и мост рухнул в реку. Именно этот случай, в результате которого два десятка человек были травмированы, способствовал принятию в британской армии правила «идти не в ногу» при прохождении войсками мостов.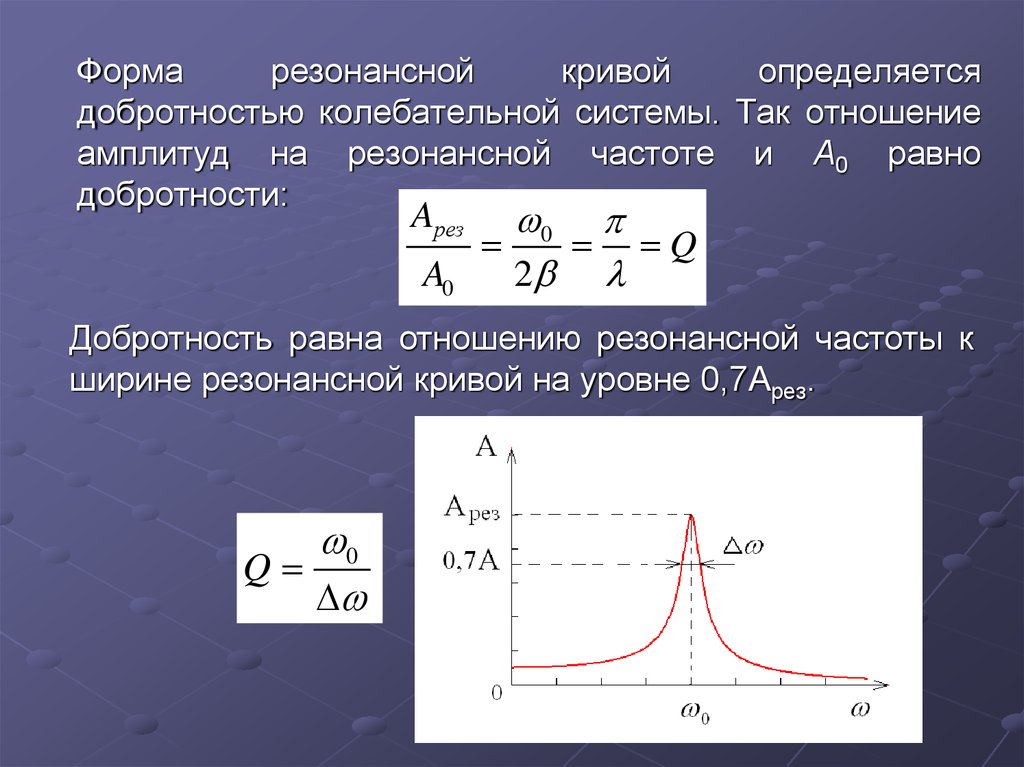 Аналогичный случай произошел в 1850 году неподалеку от французского города Анже, где был разрушен подвесной цепной мост над рекой Мин длиной более ста метров, что привело к многочисленным жертвам. Также существует версия, что в 1905 году в результате прохождения кавалерийского эскадрона по причине резонанса разрушился и Египетский мост через реку Фонтанку в Петербурге. Однако эта версия, скорее всего, безосновательна, поскольку не существует методов дрессировки значительного количества лошадей для их движения «в ногу».
Аналогичный случай произошел в 1850 году неподалеку от французского города Анже, где был разрушен подвесной цепной мост над рекой Мин длиной более ста метров, что привело к многочисленным жертвам. Также существует версия, что в 1905 году в результате прохождения кавалерийского эскадрона по причине резонанса разрушился и Египетский мост через реку Фонтанку в Петербурге. Однако эта версия, скорее всего, безосновательна, поскольку не существует методов дрессировки значительного количества лошадей для их движения «в ногу».
Поезда во время движения по мосту обычно замедляют ход — это делается для исключения совпадения частоты ударов колес по стыкам рельсов с собственной частотой колебаний моста (по этой же причине участок рельсов на мосту часто выполняют сплошной, без стыков).
С резонансом можно столкнуться не только на суше, но и на море и в воздухе. Так, при некоторых частотах вращения гребного вала в резонанс входили даже корабли. А на заре развития авиации некоторые авиационные двигатели вызывали столь сильные резонансные колебания элементов самолета, что он полностью разрушался в воздухе.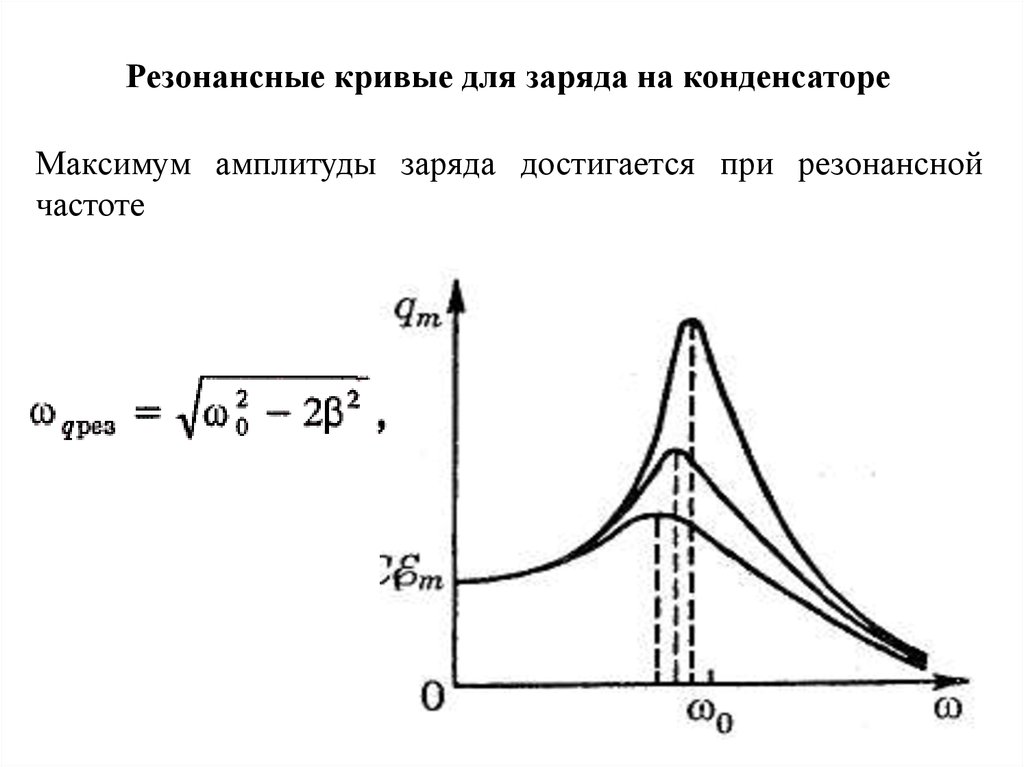
Причиной резонанса элементов летательных аппаратов и их разрушения может стать и флаттер — сочетание самовозбуждающихся незатухающих изгибающих и крутильных автоколебаний элементов конструкции (главным образом крыла самолета или несущего винта вертолета). Одним из путей борьбы с этим явлением является использование так называемых противофлаттерных грузов.
Интересно, что крепления двигателей на пилонах крыльев самолетов — это не прихоть конструкторов и дизайнеров, а насущная необходимость, поскольку двигатели демпфируют колебания крыла в полете воздушного судна, будучи при этом своеобразным противофлаттерным грузом.
Также известны случаи, когда во время выступлений знаменитого русского баса Федора Ивановича Шаляпина часто лопались плафоны в люстрах. И происходило это опять же из-за резонанса: частота собственных колебаний стекла совпадала с частотой акустических волн, воспроизводимых певцом.
Еще более интересным фактом является то, что во время Великой Отечественной войны все тот же резонанс едва не поставил под угрозу существование Дороги жизни, проходившей по льду Ладожского озера, которая связывала блокадный Ленинград с «большой землей».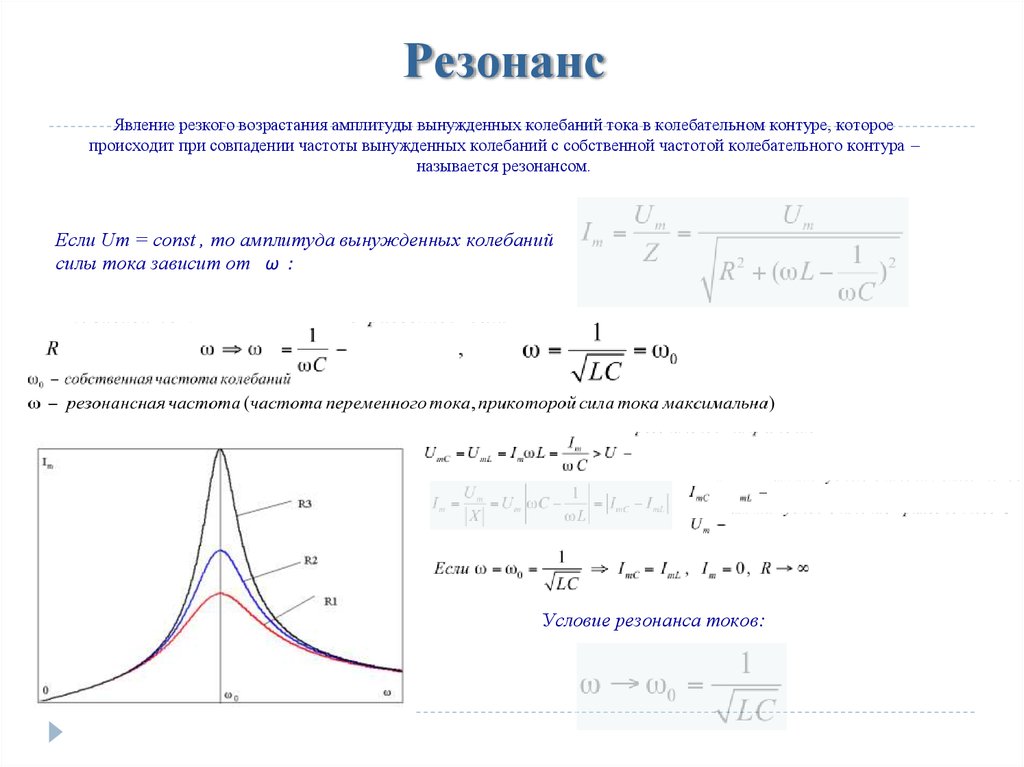 Во время наведения участка дороги защитники Ленинграда неожиданно столкнулись с необычным явлением, когда после нормального прохождения по льду тяжелого грузовика легкая машина, которая шла по тому же пути, нередко проваливалась под лед. Перед учеными была поставлена задача срочно разобраться со сложившейся ситуацией и предоставить рекомендации по преодоления автомобилями ледяного покрова. В южной части Ладожского озера, под артиллерийским и минометным огнем врага гидрограф и гидротехники проводили эксперименты по определению предельных нагрузок на лед. Все выводы ученых поступали в Ледовую службу Морской обсерватории. Изучили деформационную устойчивость льда под статической нагрузкой, получили данные про упругие деформации льда при распространении по льду взрывной волны. При проведении автоколонн по Ладоге наблюдались и неизвестные ранее колебания ледяного покрова: водяной волна, образовавшаяся под проседающим льдом, двигалась с постоянной для определенной толщины льда и глубины водоема скоростью.
Во время наведения участка дороги защитники Ленинграда неожиданно столкнулись с необычным явлением, когда после нормального прохождения по льду тяжелого грузовика легкая машина, которая шла по тому же пути, нередко проваливалась под лед. Перед учеными была поставлена задача срочно разобраться со сложившейся ситуацией и предоставить рекомендации по преодоления автомобилями ледяного покрова. В южной части Ладожского озера, под артиллерийским и минометным огнем врага гидрограф и гидротехники проводили эксперименты по определению предельных нагрузок на лед. Все выводы ученых поступали в Ледовую службу Морской обсерватории. Изучили деформационную устойчивость льда под статической нагрузкой, получили данные про упругие деформации льда при распространении по льду взрывной волны. При проведении автоколонн по Ладоге наблюдались и неизвестные ранее колебания ледяного покрова: водяной волна, образовавшаяся под проседающим льдом, двигалась с постоянной для определенной толщины льда и глубины водоема скоростью. Она могла опережать приложенную нагрузку или отставать от нее, но опасным было совпадения этих скоростей — тогда вода прекращала поддержку ледяного покрова, и поддержка обеспечивалась только упругими свойствами льда. При этом наступал резонанс, что приводило к разрушению льда. Это проявление резонанса было названо изгибно-гравитационной волной.
Она могла опережать приложенную нагрузку или отставать от нее, но опасным было совпадения этих скоростей — тогда вода прекращала поддержку ледяного покрова, и поддержка обеспечивалась только упругими свойствами льда. При этом наступал резонанс, что приводило к разрушению льда. Это проявление резонанса было названо изгибно-гравитационной волной.
По результатам исследований для автомобилей, которые двигались по льду, были установлены определенные скорости и дистанции. Ежедневно по ледяному покрову в обе стороны перевозилось около 6 тыс. тонн грузов, а общее количество доставленных в Ленинград по Дороге жизни грузов за весь период ее существования составила более 1 млн 615 тыс. тонн. Также за это же время из осажденного города было эвакуировано около 1 млн 376 тыс. жителей. С учетом приобретенного опыта позже был разработан резонансный метод разрушения льда, энергоемкость которого в несколько раз меньше энергоемкости традиционного разрушения ледяного покрова с помощью ледоколов и ледокольного навесного оборудования.
|
Что такое резонансная частота?
То, что вы видели в мультфильмах, не обязательно является плодом буйного воображения писателей — некоторые сцены на самом деле уходят корнями в науку. В детстве я думал, что сцена ужасного певца, берущего высокую ноту и разбивающего осколок стекла, была забавной, только чтобы узнать, что это явление возможно в реальной жизни из-за того, что называется резонансной частотой.
Что такое резонансная частота и что она делает? В то время как паршивые навыки пения вряд ли разобьют стекло, воспроизведение звука, равного резонансной частоте стекла, будет. По крайней мере, это то, что я помню со школьного урока физики. Со временем я также обнаружил, что резонансная частота связана не только с разбиванием стекла, но и с важным принципом работы некоторых электронных устройств.
Что такое резонансная частота?
Резонансная частота — это собственная частота, при которой среда вибрирует с максимальной амплитудой
Почему стекло разбивается при воздействии звука? Звук – это акустическая волна, которая заставляет молекулы колебаться. При проецировании от источника вибрация проходит через воздух на физическую структуру стекла. Если акустическая частота звука соответствует собственной частоте стекла, последнее начинает вибрировать с большей амплитудой, потенциально разрушая свою структуру.
Другими словами, стекло может разбиться, когда оно вибрирует на своей резонансной частоте. Резонансную частоту также можно определить как собственную частоту объекта, при котором он имеет тенденцию вибрировать с более высокой амплитудой. Например, вы могли бы почувствовать, как «трясется» мост, если бы общая сила колебаний от транспортных средств заставляла его вибрировать на своей частоте.
Термин «резонансная частота» также часто встречается в электронной технике, хотя он менее драматичен, чем осколки стекла или сильно трясущийся мост.
Резонансная частота в электронных схемах
Резонансная частота в электронных схемах выражается, когда схема демонстрирует максимальную колебательную характеристику на определенной частоте. Это наблюдается для цепи, состоящей из катушки индуктивности и конденсатора.
Чтобы лучше понять, что такое резонансная частота и какую роль она играет в электронике, давайте рассмотрим последовательную RLC-цепь, которая питается от источника переменного тока. Известно, что величина емкостного и индуктивного сопротивления изменяется соответственно частоте. Емкостное реактивное сопротивление определяется уравнением X c = 1/(2ℼfC), а индуктивное сопротивление определяется уравнением X L = 2ℼfL.
Зависимость индуктивного и емкостного сопротивления от частот
На графике уменьшение емкостного сопротивления будет пересекаться с увеличением индуктивного сопротивления на определенной частоте. Частота, на которой оба параметра перекрываются, известна как резонансная частота цепи RLC. Следовательно, резонансную частоту можно получить, выразив равное значение как емкостного, так и индуктивного сопротивления следующим образом:
Частота, на которой оба параметра перекрываются, известна как резонансная частота цепи RLC. Следовательно, резонансную частоту можно получить, выразив равное значение как емкостного, так и индуктивного сопротивления следующим образом:
- Х Д = Х С
- 2ℼfL = 1/(2ℼfC)
- f r = 1/(2ℼ √LC)
В последовательной RLC-цепи импеданс минимален, когда он работает на резонансной частоте. Полное сопротивление цепи выражается следующим уравнением:
Z = R + X L — X C
В резонансе X L равно X C , что означает, что они компенсируют друг друга. Это оставляет импеданс цепи чисто резистивным. В результате ток, протекающий через последовательную цепь RLC, достигает своего пика, когда он работает на своей резонансной частоте.
В параллельной RLC-цепи формула расчета резонансной частоты остается прежней. Однако вы обнаружите, что ток подавлен до минимума, так как полное сопротивление цепи максимально. Это происходит, когда LC цепи выглядит как разомкнутая цепь при параллельном соединении.
Однако вы обнаружите, что ток подавлен до минимума, так как полное сопротивление цепи максимально. Это происходит, когда LC цепи выглядит как разомкнутая цепь при параллельном соединении.
Применение резонансных цепей
Радиочастотные приемники пропускают сигналы, которые колеблются на резонансной частоте цепи
Концепция возбуждения цепи на ее резонансной частоте встречается в различных приложениях. В генераторе в качестве колебательного контура используется параллельный LC, который приводится в движение на своей резонансной частоте. Результатом является непрерывная серия устойчивых, колеблющихся тактовых импульсов, которые управляют такими компонентами, как микроконтроллеры и коммуникационные ИС.
Резонансные контуры также используются в радиочастотных устройствах. Они становятся основой тюнера, усиливая сигналы, соответствующие его резонансной частоте, и подавляя те, которые выходят за пределы его полосы пропускания.
При проектировании резонансных цепей полезно работать с современным программным обеспечением для проектирования печатных плат. Allegro имеет все инструменты компоновки и моделирования, необходимые для обеспечения того, чтобы схема работала соответствующим образом на желаемой резонансной частоте. Вы также можете использовать InspectAR для точной оценки и улучшения печатных плат с помощью дополненной реальности и интуитивно понятного взаимодействия. Проверка, отладка, доработка и сборка печатных плат никогда не были быстрее и проще.
Если вы хотите узнать больше о том, как у Cadence есть решение для вас, обратитесь к нам и нашей команде экспертов. Чтобы посмотреть видео по связанным темам или узнать, что нового в нашем наборе инструментов для проектирования и анализа, подпишитесь на наш канал YouTube.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка — что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостей
Спасибо!
Резонансная частота и собственная частота в цепях генератора | Блог о расширенном проектировании печатных плат
Этот камертон C5 будет вибрировать на своей затухающей собственной частоте
Те, кто знаком с осцилляторами, скорее всего, думают в терминах простого гармонического осциллятора, подобного маятнику или массе на пружине. Эти системы концептуально просты, но их математические модели не учитывают реалистичные свойства этих систем. Любой осциллятор имеет некоторые важные физические параметры, и отклик системы при возбуждении не будет соответствовать отклику, наблюдаемому при свободном возбуждении осциллятора.
Эти системы концептуально просты, но их математические модели не учитывают реалистичные свойства этих систем. Любой осциллятор имеет некоторые важные физические параметры, и отклик системы при возбуждении не будет соответствовать отклику, наблюдаемому при свободном возбуждении осциллятора.
В электронике различные схемы будут функционировать как генераторы, в которых напряжение и ток проявляют периодическую реакцию во времени. Так же, как и механические генераторы, схемы генераторов могут проявлять резонанс при определенных условиях. Для некоторых разработчиков все становится математически запутанным, поскольку реальная характеристика генератора определяется тремя разными частотами. Давайте проясним разницу между резонансной частотой и собственной частотой в схемах чисто линейного генератора.
Частота затухающих колебаний в сравнении с собственной частотой в неуправляемых генераторах
Хотя мы можем количественно определить собственную частоту механических и электрических гармонических генераторов, система никогда не колеблется на собственной частоте. Это связано с тем, что в идеальной модели осциллятора нам нравится игнорировать эффект демпфирования, чтобы мы могли понять некоторые основные аспекты системы. В механическом осцилляторе это означает, что мы ненадолго игнорируем трение или любой другой механизм, рассеивающий кинетическую энергию. В схеме это означает, что мы опускаем элементы схемы, которые рассеивают мощность в виде тепла, т. е. схема содержит только емкостные и индуктивные элементы.
Это связано с тем, что в идеальной модели осциллятора нам нравится игнорировать эффект демпфирования, чтобы мы могли понять некоторые основные аспекты системы. В механическом осцилляторе это означает, что мы ненадолго игнорируем трение или любой другой механизм, рассеивающий кинетическую энергию. В схеме это означает, что мы опускаем элементы схемы, которые рассеивают мощность в виде тепла, т. е. схема содержит только емкостные и индуктивные элементы.
Когда неуправляемый незатухающий осциллятор выходит из равновесия, система будет колебаться на своей собственной частоте. Однако схемы реальных генераторов всегда содержат некоторое демпфирование; в LC-цепи проводники имеют небольшое сопротивление, которое обеспечивает демпфирование в цепи. Это верно и для механических осцилляторов; всегда есть какой-то источник демпфирования, который преобразует кинетическую энергию в тепло, поэтому качающийся маятник в конечном итоге замедляется до полной остановки.
Эффект демпфирования приводит к двум явлениям в неуправляемых осцилляторах, которые могут совершать естественные колебания при отклонении от равновесия:
Колебание со временем затухает.
 Затухание в цепи генератора происходит из-за того, что часть электрической энергии (то есть кинетической энергии текущих зарядов) теряется в виде тепла. Это приводит к тому, что амплитуда колебаний со временем затухает.
Затухание в цепи генератора происходит из-за того, что часть электрической энергии (то есть кинетической энергии текущих зарядов) теряется в виде тепла. Это приводит к тому, что амплитуда колебаний со временем затухает.Частота затухающих колебаний не равна собственной частоте. Демпфирование приводит к тому, что частота затухающих колебаний становится немного меньше собственной частоты. Частота затухающих колебаний определяется следующим уравнением:
Частота колебаний демпфированного невозбужденного генератора вернуться к равновесию; это известно как критическое демпфирование. Поскольку скорость демпфирования продолжает увеличиваться выше собственной частоты, время, необходимое для возврата напряжения и тока к равновесию, становится больше.
Если вы должны выполнить анализ переходных процессов схемы генератора и измерить частоту колебаний, вы не измеряете собственную частоту. Фактически вы измеряете частоту затухающих колебаний, определенную в приведенном выше уравнении. Затем вы можете извлечь коэффициент затухания, нанеся натуральный логарифм данных затухания (показан красными точками на графике ниже) в форме сигнала отклика с течением времени; отрицательный наклон этой линии равен коэффициенту затухания.
Фактически вы измеряете частоту затухающих колебаний, определенную в приведенном выше уравнении. Затем вы можете извлечь коэффициент затухания, нанеся натуральный логарифм данных затухания (показан красными точками на графике ниже) в форме сигнала отклика с течением времени; отрицательный наклон этой линии равен коэффициенту затухания.
Частота колебаний демпфированного невозбужденного генератора
На приведенном выше графике последовательные максимумы отмечены красными точками, а логарифм этих данных электрического тока нанесен на правом графике. Из линии регрессии мы видим, что скорость затухания в этой схеме составляет 0,76 в секунду. Скорость затухающих колебаний определяется между двумя последовательными максимумами на левом графике и имеет значение 3,929 рад/с. Зная коэффициент затухания и частоту затухающих колебаний, можно легко рассчитать собственную частоту, используя приведенное выше уравнение. В этом моделировании собственная частота равна 4 рад в секунду. Из экспоненциальной кривой затухания также видно, что начальный ток составлял 1 А.
В этом моделировании собственная частота равна 4 рад в секунду. Из экспоненциальной кривой затухания также видно, что начальный ток составлял 1 А.
Зависимость резонансной частоты от собственной частоты в управляемых генераторах
Когда схема генератора управляется периодическим сигналом, ток и напряжение будут колебаться с той же частотой повторения, что и управляющий сигнал. Однако формы сигналов не будут идеально совпадать, потому что передаточная функция схемы генератора будет искажать эти сигналы; другими словами, схема генератора также действует как фильтр/усилитель (подробнее об этом ниже). Чтобы увидеть, как могут вести себя различные схемы генератора, полезно рассмотреть механический генератор, который управляется только синусоидальным сигналом.
Резонанс — это явление, которое возникает, когда осциллятор возбуждается периодическим сигналом с определенной частотой, известной как резонансная частота. В ведомом генераторе без демпфирования резонансная частота равна собственной частоте. Это всегда имеет место в незатухающих осцилляторах, но не всегда имеет место в затухающих осцилляторах. Реальные ведомые генераторы имеют демпфирование, а резонансная частота не всегда равна собственной частоте. Для типичного управляемого демпфированного механического генератора резонансная частота определяется следующим уравнением:0003
Это всегда имеет место в незатухающих осцилляторах, но не всегда имеет место в затухающих осцилляторах. Реальные ведомые генераторы имеют демпфирование, а резонансная частота не всегда равна собственной частоте. Для типичного управляемого демпфированного механического генератора резонансная частота определяется следующим уравнением:0003
Зависимость резонансной частоты от собственной частоты демпфированного механического генератора с возбуждением
Обратите внимание, что резонанс может возникнуть только тогда, когда квадратная собственная частота больше, чем коэффициент затухания, умноженный на 2. Если демпфирование слишком велико, то резонанс не может возникнуть.
Как насчет случая малого демпфирования? В пределе, когда постоянная демпфирования равна нулю, резонансная частота равна собственной частоте и в цепи нет рассеяния энергии. В результате, когда незатухающий осциллятор приводится в действие точно на своей собственной частоте, амплитуда результирующего колебания (теоретически) будет расходиться до бесконечности с линейной скоростью. В реальной схеме нелинейные эффекты в конечном итоге возьмут верх при высоком напряжении/токе, что может привести к насыщению отклика или вызвать перегорание схемы.
В реальной схеме нелинейные эффекты в конечном итоге возьмут верх при высоком напряжении/токе, что может привести к насыщению отклика или вызвать перегорание схемы.
Существует определенный диапазон частот, в котором механический осциллятор не будет демонстрировать резонанс при возбуждении, но все равно будет демонстрировать затухающие колебания при отклонении от равновесия. Это затухающее колебание все еще будет происходить с частотой затухающих колебаний, определенной в первом уравнении выше. Возвращаясь к механическому осциллятору, мы имеем:
Случай, когда резонанс устранен, но могут быть затухающие колебания
Обратите внимание, что приведенные выше условия, которые мы обсуждали для механического генератора, также применимы к цепи RL с параллельным конденсатором.
Передаточные функции генератора
Демпфирование в цепи определяет передаточную функцию цепи, которая обычно описывается в терминах ее полосы пропускания. Когда осциллятор управляется синусоидальным сигналом, выходной сигнал также будет синусоидальным. Однако, когда осциллятор управляется несинусоидальным периодическим сигналом (например, пилообразной волной, частотно-модулированным сигналом, потоком тактовых импульсов или другой повторяющейся аналоговой волной), то результирующие формы напряжения и тока в генераторе могут не напоминать сигнал движения. Вы можете извлечь передаточную функцию из развертки частоты, применив синусоидальный источник к вашей схеме генератора. Примеры, которые показывают эти передаточные функции в частотной области для различных скоростей затухания для механического генератора, показаны ниже.
Когда осциллятор управляется синусоидальным сигналом, выходной сигнал также будет синусоидальным. Однако, когда осциллятор управляется несинусоидальным периодическим сигналом (например, пилообразной волной, частотно-модулированным сигналом, потоком тактовых импульсов или другой повторяющейся аналоговой волной), то результирующие формы напряжения и тока в генераторе могут не напоминать сигнал движения. Вы можете извлечь передаточную функцию из развертки частоты, применив синусоидальный источник к вашей схеме генератора. Примеры, которые показывают эти передаточные функции в частотной области для различных скоростей затухания для механического генератора, показаны ниже.
Кривые амплитуды механического осциллятора в зависимости от частоты возбуждения
Обратите внимание, что эти кривые нормированы по отношению к собственной частоте. Опять же, некоторые схемы RLC будут иметь аналогичные кривые, в то время как другие (например, последовательная цепь RLC) будут иметь кривые, которые всегда достигают максимума на собственной частоте, т. Е. Резонансная частота = собственная частота.
Е. Резонансная частота = собственная частота.
Приведенные выше графики для механического осциллятора показывают, как пик на каждой кривой (соответствующий резонансной частоте) смещается к собственной частоте по мере уменьшения скорости затухания. Каждую из этих кривых можно рассматривать как передаточную функцию. Определение того, как каждая из этих кривых влияет на произвольный аналоговый управляющий сигнал во временной области, требует работы с преобразованиями Фурье или преобразованиями Лапласа, что немного выходит за рамки этой статьи.
Независимо от того, какой тип схемы генератора вы проектируете, вы можете легко отличить резонансную частоту от собственной частоты вашей схемы с помощью OrCAD PSpice Simulator от Cadence. Этот мощный пакет включает инструменты анализа, которые берут данные непосредственно из ваших схем и определяют поведение ваших самых сложных конструкций печатных плат.
Если вы хотите узнать больше о решениях, которые Cadence предлагает вам, обратитесь к нам и нашей команде экспертов. Вы также можете посетить наш канал YouTube и посмотреть видеоролики о моделировании и системном анализе, а также узнать, что нового в нашем наборе инструментов для проектирования и анализа.
Вы также можете посетить наш канал YouTube и посмотреть видеоролики о моделировании и системном анализе, а также узнать, что нового в нашем наборе инструментов для проектирования и анализа.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка — что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостей
Спасибо!
Резонанс и собственная частота | Вибрация
Таблица содержимого
Резонанс и собственная частота
Вы когда-нибудь пытались сбалансировать вентилятор, и его вибрация не уменьшилась? Что бы вы ни делали, ты знаешь что такое резонанс?
3 совета по диагностике резонанса и 6 способов его устранения ниже.
Резонанс является причиной 40% повторяющихся случаев дисбаланса, а также, несмотря на то, что его так легко диагностировать, это один из самых игнорируемых дефектов.
Среди самых распространенных неисправностей Резонанс обладает наибольшей разрушительной силой . Он также является причиной 90 % разрушения конструкций из-за усталости материалов и сварных швов, а также сокращения срока службы подшипников, вызванного перегрузкой.
Определение собственной частотыЧтобы понять резонанс, нам сначала нужно понять, что такое собственная частота. Определение звучит примерно так:
Собственная частота — это частота, с которой объект будет продолжать вибрировать после удара. Это не может быть яснее.
Все механические объекты и системы имеют собственную частоту. Они могут даже иметь много собственных частот в зависимости от их геометрии.
СЕЙЧАС! Что происходит, когда вы возбуждаете этот объект до той же частоты, что и его собственная частота? Ну, это резонанс.
Резонанс — это явление, усиливающее вибрацию. Это происходит, когда вибрация передается другому объекту , собственная частота которого такая же или очень близка к частоте источника .
Также проверьте определение Википедии.
Примеры
Посмотрите на пример с маятником.
Когда я толкаю маятник, энергия, которую я применяю, не теряется сразу. Вместо этого он остается в форме движения маятника, который постепенно утрачивается. Если я нажму один раз в каждом цикле, , что новая энергия накапливается к энергии , которая уже была в маятнике в виде движения, точно так же, как когда вы качаете своего малыша на качелях.
Обратите внимание на противоположный случай. Когда я буду возбуждать маятник на другую частоту, я буду бороться с той энергией, которая уже была накоплена, поэтому к имеющейся энергии не будет прибавляться.
Нечто подобное происходит во вращающихся машинах. Когда скорость двигателя близка к его собственной частоте, он резонирует. Таким образом, любая вибрация из-за дисбаланса, какой бы незначительной она ни была, будет усиливаться. Таким образом, небольшие массы вызовут неожиданные изменения вибрации .
Когда скорость двигателя близка к его собственной частоте, он резонирует. Таким образом, любая вибрация из-за дисбаланса, какой бы незначительной она ни была, будет усиливаться. Таким образом, небольшие массы вызовут неожиданные изменения вибрации .
Наконец, как будто всего этого недостаточно, вибрация машины не ведет себя линейно . Количество вибрации вызывает небольшие структурные изменения, которые мгновенно изменяют собственную частоту, а также демпфирование, заставляя его вести себя немного по-разному на разных уровнях вибрации. Все это усложняет балансировку.
Узнайте, как диагностировать резонанс. Резонанс легко диагностировать; однако важно знать, как его обнаружить. Машина во время работы будет постепенно увеличивать свою вибрацию, резонанс приведет к внезапному увеличению вибрации , когда машина достигнет своей конечной скорости. То же самое происходит и при «остывании», когда обороты немного отстают от собственной частоты, вибрация сразу уменьшается.
Existen 3 tipos de pruebas que puedes realizar para Diagnosticar la Resonancia.
Проверка запуска и завершения работы | РезонансEsta prueba se realiza registrando la vibración durante la paro de la máquina. Подтвердите действие vibración disminuye drásticamente en los primeros segundos.
Пруэба-де-Паро
Ударное испытание | Собственная частотаВ «Ударном испытании» запись вибрации производится после удара по машине. Затем в спектре вы увидите резонансные частоты конструкции. Вы можете подтвердить диагноз с вероятностью 95%, если любая из этих частот близка к скорости вращения (убедитесь, что вы точно знаете скорость вращения). Обычно этого исследования достаточно для диагностики резонанса, однако есть еще один тест на случай необходимости подтверждающего теста.
Ударное испытание
Резонансный ударный тест БПФ
Диаграмма Боде в резонансном анализе Диаграмма Боде — это тест на выбег или разгон, который объединяет вибрацию и число оборотов, измеряемых тахометром или датчиком числа оборотов. Этот тест вычисляет БПФ и фазу, связанную с сигналом RPM, для каждого временного интервала. Этот тест подтверждает резонанс, наблюдая изменение фазы 180º между моментами до и после пересечения предполагаемой частоты 9.0003
Этот тест вычисляет БПФ и фазу, связанную с сигналом RPM, для каждого временного интервала. Этот тест подтверждает резонанс, наблюдая изменение фазы 180º между моментами до и после пересечения предполагаемой частоты 9.0003
DigivibeMX
Это ваш выбор, балансируете ли вы с помощью компьютера или смартфона, наши бесплатные приложения для балансировки имеют одинаковое качество.
Узнать больше
Исправление резонансаХорошая новость заключается в том, что явление резонанса легко исправить. Просто отодвиньте собственную частоту от частоты возбуждения.
Действия по коррекции разделены на 2:
Изменение собственной частоты Можно увеличить собственную частоту за счет увеличения жесткости конструкции . Обязательно укрепляйте конструкцию в том же направлении, что и собственная частота. Это наиболее распространенное решение, позволяющее избежать изменения производительности машины.
Вы также можете уменьшить собственную частоту, убрав жесткость конструкции. Это не так распространено, но в равной степени возможно и эффективно, при условии, что производительность машины не снижается.
Вы можете уменьшить собственную частоту, добавив массу . Изменение массы конструкции изменит ее собственную частоту и, следовательно, также отдалит ее от скорости вращения.
Вы также можете увеличить собственную частоту, удалив массу . Это наименее частое действие, но оно одинаково эффективно.
Измените число оборотов, чтобы отдалить их от собственной частоты. Если привод управляет скоростью двигателя, измените число оборотов. Это просто сделать. В случае ременной/шкивной передачи изменение диаметра шкива может быть решением . В любом случае важно убедиться, что производительность машины достаточна для ее функций, и, конечно, потребление тока не превышает рекомендации производителя.
О П О Т АВТОРЕ
Тьерри Эрбесд, мексиканский предприниматель, совершивший революцию в области анализа вибрации и динамической балансировки во всем мире.
Д-р Эрбессд является выпускником Национального политехнического института Мексики, а также страстным программистом. Он является создателем программного обеспечения DigivibeMX, которое конкурирует с лучшими системами для анализа вибрации. В настоящее время он является президентом и директором по инновациям Erbessd Instruments, ведущей компании в области решений для промышленного обслуживания.
ERBESSD INSTRUMENTS является ведущим производителем оборудования для анализа вибрации и динамических балансировочных машин с заводами в Мексике и США и представителями по всему миру. ERBESSD INSTRUMENTS – МАСТЕРА МАШИННОГО ЗДОРОВЬЯ
Наши продукты:
Собственная частота: хорошее, плохое и катастрофическое
Разрушающиеся мосты, бьющееся стекло, крики детей, тяжелый бас — тот, кто считает, что между этими вещами нет ничего общего, ошибается. Все они созданы посредством вибраций и, , в частности, из собственных частот создаются сильные вибрации. Читайте дальше, поскольку мы объясняем науку, стоящую за этим принципом, и что такое резонансные катастрофы, а также изучаем роль резонанса качения, когда речь идет о громкоговорителях.
Все они созданы посредством вибраций и, , в частности, из собственных частот создаются сильные вибрации. Читайте дальше, поскольку мы объясняем науку, стоящую за этим принципом, и что такое резонансные катастрофы, а также изучаем роль резонанса качения, когда речь идет о громкоговорителях.
Все вибрирует, но как?
Вибрация наушников всегда является реакцией на энергетический импульс. Рука может раскачать маятник, ветер может раскачать небоскреб, а катушка с помощью магнита может двигать мембрану громкоговорителя. Насколько сильно что-то вибрирует от приложенной мощности вибрации, а также материала, в том числе конструкции вибрационной системы. С другой стороны, большое значение имеет частота, с которой действуют энергетические импульсы. Ведь если частота подводимой энергии совпадает с собственной частотой тела, то тело вибрирует с особенно большой амплитудой.
Как явление резонансной частоты выглядит на практике, можно понять с помощью маятника: Если пружинный маятник является периодическим, т. е. через равные промежутки времени, снабжаемым энергией, соответствующей собственной частоте маятника, то отклонение маятника равно это самое большое. Если импульсы энергии имеют более низкую или более высокую частоту, чем собственная частота, отклонение маятника будет меньше.
е. через равные промежутки времени, снабжаемым энергией, соответствующей собственной частоте маятника, то отклонение маятника равно это самое большое. Если импульсы энергии имеют более низкую или более высокую частоту, чем собственная частота, отклонение маятника будет меньше.
На качелях вы можете сами проверить, как работает резонансная частота. Когда вы ударяете по качелям в самой высокой точке, подача энергии происходит точно на собственной частоте системы. Вот почему качели имеют такой большой импульс качания. Если вы наносите удар до или после того, как замах достигает высшей точки, сила передается менее эффективно или вообще уходит в никуда.
От хороших вибраций к плохим
Корпус акустической гитары, качели, стакан или бридж могут вибрировать на соответствующей резонансной частоте. Но это не везде желательно и может даже нанести большой ущерб. Это связано с тем, что системы могут вибрировать так сильно, что конструкция не выдерживает нагрузки.
Это связано с тем, что системы могут вибрировать так сильно, что конструкция не выдерживает нагрузки.
Это явление можно наблюдать, когда человек указывает своим голосом на бокал с вином с небольшого расстояния. Если высота голоса точно соответствует собственной частоте стакана, он разбивается через относительно короткое время — происходит так называемая резонансная катастрофа. Если голосовые связки заставляют молекулы воздуха вибрировать с большей или меньшей частотой, стекло остается неповрежденным. Собственную частоту стекла можно услышать, когда вы ударяете по нему каким-либо предметом.
Одна из самых известных резонансных катастроф произошла в США в 1940 году, когда ветер вызвал такую сильную вибрацию моста Такома-Нарроуз, что он рухнул.
Во избежание резонансных катастроф правила дорожного движения запрещают группам людей, например воинским частям, маршировать через мосты в ногу.
С другой стороны, в музыкальных инструментах резонанс является преднамеренным эффектом увеличения громкости звуков. В акустической гитаре корпус действует как механический усилитель звуковых волн, которые запускаются струнами. Корпус гитары сконструирован таким образом, что резонансная частота возникает даже на разных высотах.
Громкоговорители от Teufel
Резонансные эффекты в громкоговорителях нежелательны – за одним исключением
Резонансная частота не приветствуется в громкоговорителях. Громкоговорители сконструированы таким образом, что различные компоненты не вибрируют на своей резонансной частоте. Это означало бы, что звуки в том же частотном диапазоне, что и отдельные компоненты, будут воспроизводиться намного громче, чем другие. Здесь в игру вступает перекрестная сеть: в многоканальных системах она направляет сигналы на динамики в соответствии с их частотой.
Эффекты резонанса также не должны возникать в корпусе громкоговорителя. Это может произойти, когда мембрана на задней стороне излучает звук внутрь громкоговорителя. Этот звук может вызвать вибрацию корпуса и тем самым отрицательно сказаться на звуковом образе. Чтобы предотвратить это, корпус громкоговорителя оснащен демпфером, который поглощает звуковые волны, излучаемые внутрь.
Это может произойти, когда мембрана на задней стороне излучает звук внутрь громкоговорителя. Этот звук может вызвать вибрацию корпуса и тем самым отрицательно сказаться на звуковом образе. Чтобы предотвратить это, корпус громкоговорителя оснащен демпфером, который поглощает звуковые волны, излучаемые внутрь.
Исключением из этого правила являются динамики с фазоинвертором. Эти шкафы имеют трубчатое отверстие, через которое излучаемый внутрь звук на определенных низких частотах может выходить в комнату. Это работает по принципу резонатора Гельмгольца, который мы объясняли в нашем тексте о сабвуферах.
Нам нужен бас: бас Teufel для более глубоких вибраций
Сабвуфер der Kombo 42 BT Power Edition verleiht den Regalautsprechern ordentlich Wumms- ▶ Моно-сабвуфер US 2106/1 SW: этот сабвуфер для новичков предлагает мощные басы без мешающего шума потока, несмотря на его компактный размер. Это достигается с помощью двух фазоинверторных ламп.
- ▶ Ultima 40/20 «2.
 0>5.1 Extension Set Surround»: колонки HiFi Ultima 40/20 — настоящая дьявольская классика для дома. С помощью этого набора вы можете расширить свою стереосистему до объемного звука 5.1. Сабвуфер T 10 обеспечивает достаточный резонанс в басовом диапазоне.
0>5.1 Extension Set Surround»: колонки HiFi Ultima 40/20 — настоящая дьявольская классика для дома. С помощью этого набора вы можете расширить свою стереосистему до объемного звука 5.1. Сабвуфер T 10 обеспечивает достаточный резонанс в басовом диапазоне.
Другие товары от Teufel
Вывод: Резонансная частота полезна
- На резонансной частоте собственная частота колебательной системы совпадает с частотой подводимой энергии.
- В случае резонанса отклонение колебаний становится больше.
- В акустике более высокая амплитуда звуковых волн означает более высокое звуковое давление и, следовательно, большую громкость.
- Резонансные частоты вообще нежелательны для громкоговорителей.
- Динамики с фазоинвертором являются исключением. Они усиливают низкие частоты по принципу резонатора Гельмгольца.
Наконец, классика «Багз Банни» на эту тему:
Изображение заголовка Photo by Jeremy Bishop on Unsplash
Учебник по физике: собственная частота
Как уже упоминалось ранее в этом разделе, звуковая волна создается в результате вибрации объекта. Вибрирующий объект является источником возмущения, которое движется в среде. Вибрирующим объектом, создающим помехи, могут быть голосовые связки человека, вибрирующая струна и дека гитары или скрипки, вибрирующие ножки камертона или вибрирующая диафрагма радиодинамика. Любой объект, который вибрирует, создает звук. Звук может быть музыкальным или шумным; но независимо от ее качества звуковая волна создается вибрирующим объектом.
Вибрирующий объект является источником возмущения, которое движется в среде. Вибрирующим объектом, создающим помехи, могут быть голосовые связки человека, вибрирующая струна и дека гитары или скрипки, вибрирующие ножки камертона или вибрирующая диафрагма радиодинамика. Любой объект, который вибрирует, создает звук. Звук может быть музыкальным или шумным; но независимо от ее качества звуковая волна создается вибрирующим объектом.
Почти все предметы, если их ударить, ударить, щипнуть, наиграть или как-то потревожить, будут вибрировать. Если уронить метровую палку или карандаш на пол, он начнет вибрировать. Если вы дернете гитарную струну, она начнет вибрировать. Если вы подуете на горлышко бутылки из-под поп-музыки, воздух внутри начнет вибрировать. Когда каждый из этих объектов вибрирует, они имеют тенденцию вибрировать на определенной частоте или наборе частот. Частота или частоты, с которыми объект имеет тенденцию вибрировать при ударе, ударе, щипании, ударе по струне или как-либо потревожен, известна как 9. 0249 собственная частота объекта. Если амплитуды колебаний достаточно велики, а собственная частота находится в диапазоне человеческих частот, то вибрирующий объект будет производить слышимые звуковые волны.
0249 собственная частота объекта. Если амплитуды колебаний достаточно велики, а собственная частота находится в диапазоне человеческих частот, то вибрирующий объект будет производить слышимые звуковые волны.
Все объекты имеют собственную частоту или набор частот, на которых они вибрируют. Качество или тембр звука, производимого вибрирующим объектом, зависит от собственных частот звуковых волн, производимых объектами. Некоторые объекты имеют тенденцию вибрировать на одной частоте, и часто говорят, что они производят чистый тон. Флейта имеет тенденцию вибрировать на одной частоте, производя очень чистый тон. Другие объекты вибрируют и производят более сложные волны с набором частот, между которыми существует целочисленное математическое соотношение; говорят, что они производят богатый звук. Туба имеет тенденцию вибрировать на наборе частот, которые математически связаны отношениями целых чисел; он дает насыщенный тон. Другие объекты будут вибрировать на множестве частот, между которыми нет простой математической зависимости. Эти объекты совсем не музыкальные, и звуки, которые они издают, можно назвать шумом. Когда метровая палка или карандаш падают на пол, они вибрируют с рядом частот, создавая сложную звуковую волну, лязгающую и шумную.
Эти объекты совсем не музыкальные, и звуки, которые они издают, можно назвать шумом. Когда метровая палка или карандаш падают на пол, они вибрируют с рядом частот, создавая сложную звуковую волну, лязгающую и шумную.
Фактическая частота, с которой объект будет вибрировать, определяется множеством факторов. Каждый из этих факторов влияет либо на длину волны, либо на скорость объекта. Поскольку частота
, изменение скорости или длины волны приведет к изменению собственной частоты. Роль музыканта состоит в том, чтобы контролировать эти переменные, чтобы получить заданную частоту от инструмента, на котором играют. Рассмотрим гитару в качестве примера. Есть шесть струн, каждая из которых имеет разную линейную плотность (более широкие струны имеют большую плотность на метр), разное натяжение (которое контролируется гитаристом) и разную длину (также контролируемую гитаристом). Скорость, с которой волны проходят через струны, зависит от свойств среды — в данном случае от натяжения (натяжения) струны и линейной плотности струн. Изменения этих свойств повлияют на собственную частоту конкретной струны. Вибрирующая часть конкретной струны может быть укоротил , прижав струну к одному из ладов на грифе гитары. Это изменение длины струны повлияет на длину волны и, в свою очередь, на собственную частоту, с которой вибрирует конкретная струна. Управление скоростью и длиной волны таким образом позволяет гитаристу управлять собственными частотами вибрирующего объекта (струны) и, таким образом, воспроизводить нужные музыкальные звуки. Те же принципы применимы к любому струнному инструменту — будь то арфа, клавесин, скрипка или гитара.
Скорость, с которой волны проходят через струны, зависит от свойств среды — в данном случае от натяжения (натяжения) струны и линейной плотности струн. Изменения этих свойств повлияют на собственную частоту конкретной струны. Вибрирующая часть конкретной струны может быть укоротил , прижав струну к одному из ладов на грифе гитары. Это изменение длины струны повлияет на длину волны и, в свою очередь, на собственную частоту, с которой вибрирует конкретная струна. Управление скоростью и длиной волны таким образом позволяет гитаристу управлять собственными частотами вибрирующего объекта (струны) и, таким образом, воспроизводить нужные музыкальные звуки. Те же принципы применимы к любому струнному инструменту — будь то арфа, клавесин, скрипка или гитара.
В качестве другого примера рассмотрим тромбон с его длинной цилиндрической трубкой, дважды согнутой вокруг себя и заканчивающейся расширяющимся концом. Тромбон является примером духового инструмента. Трубка любого духового инструмента действует как контейнер для вибрирующего столба воздуха. Воздух внутри трубки будет приводиться в вибрацию вибрирующим язычком или вибрацией губ музыканта относительно мундштука. В то время как скорость звуковых волн в воздушном столбе не может быть изменена музыкантом (они могут быть изменены только изменением температуры в помещении), длина воздушного столба изменяется. Для тромбона длина изменяется путем выталкивания трубки наружу от мундштука, чтобы удлинить ее, или втягивания, чтобы укоротить ее. Это приводит к изменению длины столба воздуха и, следовательно, к изменению длины волн, которые он производит. И, конечно же, изменение длины волны приведет к изменению частоты. Таким образом, собственная частота духового инструмента, такого как тромбон, зависит от длины воздушного столба инструмента. Те же принципы можно применить к любому подобному инструменту (туба, флейта, колокольчик, органная труба, кларнет или поп-бутылка), звук которого создается вибрациями воздуха в пределах трубка .
Воздух внутри трубки будет приводиться в вибрацию вибрирующим язычком или вибрацией губ музыканта относительно мундштука. В то время как скорость звуковых волн в воздушном столбе не может быть изменена музыкантом (они могут быть изменены только изменением температуры в помещении), длина воздушного столба изменяется. Для тромбона длина изменяется путем выталкивания трубки наружу от мундштука, чтобы удлинить ее, или втягивания, чтобы укоротить ее. Это приводит к изменению длины столба воздуха и, следовательно, к изменению длины волн, которые он производит. И, конечно же, изменение длины волны приведет к изменению частоты. Таким образом, собственная частота духового инструмента, такого как тромбон, зависит от длины воздушного столба инструмента. Те же принципы можно применить к любому подобному инструменту (туба, флейта, колокольчик, органная труба, кларнет или поп-бутылка), звук которого создается вибрациями воздуха в пределах трубка .
В классе было проведено множество демонстраций (некоторые из которых были забавными, а некоторые банальными), которые иллюстрировали идею собственных частот и их модификации. Бутылка для поп-музыки может быть частично заполнена водой, оставляя внутри объем воздуха, способный вибрировать. Когда человек дует на горлышко бутылки, воздух внутри приходит в колебательное движение; турбулентность над горлышком бутылки создает возмущения внутри бутылки. Эти вибрации приводят к звуковой волне, которую слышно учащимся. Конечно, частоту можно изменить, изменив объем столба воздуха (добавив или удалив воду), что изменит длину волны и, в свою очередь, частоту. Принцип аналогичен соотношению частоты и длины волны воздушных столбов; меньший объем воздуха внутри бутылки означает более короткую длину волны и более высокую частоту.
Бутылка для поп-музыки может быть частично заполнена водой, оставляя внутри объем воздуха, способный вибрировать. Когда человек дует на горлышко бутылки, воздух внутри приходит в колебательное движение; турбулентность над горлышком бутылки создает возмущения внутри бутылки. Эти вибрации приводят к звуковой волне, которую слышно учащимся. Конечно, частоту можно изменить, изменив объем столба воздуха (добавив или удалив воду), что изменит длину волны и, в свою очередь, частоту. Принцип аналогичен соотношению частоты и длины волны воздушных столбов; меньший объем воздуха внутри бутылки означает более короткую длину волны и более высокую частоту.
Оркестр рулонов туалетной бумаги можно создать из рулонов туалетной бумаги (или рулонов оберточной бумаги) разной длины. Валики будут вибрировать с разной частотой при ударе по голове ученика. Правильно подобранный набор роликов приведет к воспроизведению звуков, которые способны исполнить песню «Mary Had a Little Lamb», удостоенную премии «Тони».
Возможно, вы знакомы с популярным трюком с кубком для воды, который часто демонстрируют на уроках физики. Возьмите кубок с водой и вымойте пальцы. Затем аккуратно проведите пальцем по краю стакана с водой. Если вам повезет, вы сможете вызвать вибрацию кубка с помощью трение скольжения . (Не обязательно использовать хрустальный кубок. Часто говорят, что хрустальные кубки работают лучше, но этот трюк так же легко выполняется чистыми пальцами и недорогим кубком.) Подобно скрипичной тетиве, натянутой на струну скрипки, палец прилипает к молекулам стекла, растягивая их в заданной точке до тех пор, пока напряжение не станет таким большим. Затем палец соскальзывает со стекла и впоследствии находит другую микроскопическую поверхность, к которой прилипает ; палец тянет молекулы на этой поверхности, скользит и затем застревает в другом месте. Этого процесса скачкообразного трения, происходящего с высокой частотой, достаточно, чтобы заставить молекулы стекла вибрировать с их собственной частотой. Результата достаточно, чтобы произвести впечатление на ваших гостей за ужином. Попробуйте дома!!
Результата достаточно, чтобы произвести впечатление на ваших гостей за ужином. Попробуйте дома!!
Возможно, вы видели, как маятник качается взад-вперед относительно своего положения равновесия. Хотя маятник не издает звука при колебаниях, он иллюстрирует важный принцип. Маятник, состоящий из более длинной струны, колеблется с более длинным периодом и, следовательно, с более низкой частотой. Опять же, существует обратная зависимость между длиной вибрирующего объекта и собственной частотой, с которой вибрирует объект. Это же отношение распространяется на любой вибрирующий инструмент — будь то гитарная струна, ксилофон, музыкальный инструмент или литавра.
Итак, все объекты имеют собственную частоту или набор частот, на которых они вибрируют при ударе, щипании, ударе или каком-либо нарушении. Фактическая частота зависит от свойств материала, из которого сделан объект (это влияет на скорость волны) и длины материала (это влияет на длину волны). Цель музыкантов состоит в том, чтобы найти инструменты, обладающие способностью вибрировать с наборами частот, музыкально звучащих (т. е. математически связанных простыми соотношениями целых чисел), и изменять длину и (если возможно) свойства для создания желаемых звуков. .
е. математически связанных простыми соотношениями целых чисел), и изменять длину и (если возможно) свойства для создания желаемых звуков. .
Преподаватель физики заставляет кубок с водой петь на своей собственной частоте.
Следующий раздел:
Перейти к следующему уроку:
Резонанс и собственная частота | CBM CONNECT
Доктор Тьерри Эрбесд | Президент и директор по инновациям,
Erbessd Instruments
Сохранить в библиотеке
3 совета по диагностике резонанса и 6 способов его устранения.
Резонанс представляет собой 40% случаев повторяющегося дисбаланса и, несмотря на простоту диагностики, является одной из наиболее часто упускаемых из виду неисправностей.
Среди наиболее распространенных неисправностей резонанс имеет наибольшую разрушительную силу . Он также является причиной 90 % структурных разрушений из-за усталости материалов и сварки, а также сокращения срока службы подшипников из-за перегрузок.
Определение собственной частотыЧтобы понять резонанс, мы должны сначала понять собственную частоту. Определение звучит примерно так:
Собственная частота — это частота, с которой объект будет продолжать вибрировать после удара по нему . Это не может быть яснее (ударить в колокольчик, покачать мою дочь на качелях).
Все объекты и механические системы имеют собственную частоту. Они могут даже иметь много собственных частот в зависимости от их геометрии.
СЕЙЧАС! Что происходит, когда вы возбуждаете этот объект на той же частоте, что и его собственная частота? Ну, это резонанс .
Определение резонансаРезонанс — это явление, усиливающее вибрацию. Это происходит, когда вибрация передается другому объекту, собственная частота которого 90 249 равна или очень близка к частоте источника 90 250 .
См. также Определение Википедии .
Примеры
Посмотрите на пример с маятником.
Когда я толкаю маятник, энергия, которую я применяю, не теряется сразу. Вместо этого он остается в форме маятникового движения, которое постепенно теряется. Если я толкаю его один раз в цикле, эта новая энергия аккумулируется к энергии , которая уже была в маятнике в форме движения, точно так же, как когда вы качаете своего ребенка на качелях.
Обратите внимание на противоположный случай. Когда я настраиваю маятник на другую частоту, я буду бороться с уже накопленной энергией; таким образом, никакая энергия не будет добавлена к существующей.
Нечто подобное происходит во вращающихся механизмах. Когда скорость двигателя близка к его собственной частоте, он резонирует. Таким образом, любая вибрация из-за дисбаланса, какой бы малой она ни была, будет усиливаться. Таким образом, небольшие веса вызовут удивительно большие изменения вибрации .
Наконец, как будто всего этого недостаточно, вибрация машины не ведет себя линейно . Количество вибрации вызывает небольшие структурные изменения, которые мгновенно изменяют собственную частоту, а также демпфирование, заставляя его вести себя немного по-разному на разных уровнях вибрации. Все это усложняет балансировку.
Узнайте, как диагностировать резонанс Резонанс легко диагностировать; однако важно уметь это подозревать. Машина во время разгона будет постепенно увеличивать свою вибрацию; резонанс резко усилит вибрацию , когда машина достигнет своей конечной скорости. То же самое происходит и при движении накатом, когда обороты немного удаляются от собственной частоты, вибрация сразу уменьшается.
Для диагностики резонанса можно выполнить 3 теста.
Тест разгона или выбега | РезонансЭтот тест выполняется путем записи вибрации во время остановки. Убедитесь, что вибрация значительно снижает вибрацию в течение первых нескольких секунд.
Ударное испытание | Собственная частота
При «ударном испытании» запись вибрации производится после удара по машине. Затем в спектре вы увидите резонансные частоты конструкции. Подтвердить диагноз можно с помощью 95% уверенности, в случае любая из этих частот близка к скорости вращения (убедитесь, что вы точно знаете скорость вращения). Обычно этого исследования достаточно для диагностики резонанса; однако есть еще один тест на случай необходимости подтверждающего теста.
Диаграмма Боде в анализе резонанса Диаграмма Боде представляет собой тест на выбег или разгон, объединяющий вибрацию и число оборотов, измеряемых тахометром или датчиком числа оборотов. Этот тест вычисляет БПФ и фазу, связанную с сигналом RPM, для каждого временного интервала. Этот тест подтверждает резонанс, наблюдая изменение фазы 180° между моментами до и после пересечения предполагаемой частоты.
Этот тест вычисляет БПФ и фазу, связанную с сигналом RPM, для каждого временного интервала. Этот тест подтверждает резонанс, наблюдая изменение фазы 180° между моментами до и после пересечения предполагаемой частоты.
Хорошей новостью является то, что явление резонанса легко исправить. Просто отодвиньте собственную частоту от частоты возбуждения.
Действия по исправлению разделены на 2:
Изменение собственной частотыВы можете увеличить собственную частоту, увеличив жесткость конструкции . Обязательно укрепляйте конструкцию в том же направлении, что и собственная частота. Это наиболее распространенное решение, позволяющее избежать изменения производительности машины.
Вы также можете уменьшить собственную частоту, убрав жесткость конструкции. Это не так распространено, но в равной степени возможно и эффективно, при условии, что производительность машины не снижается.


 83)
83) 93)
93) 97)
97) 99)
99)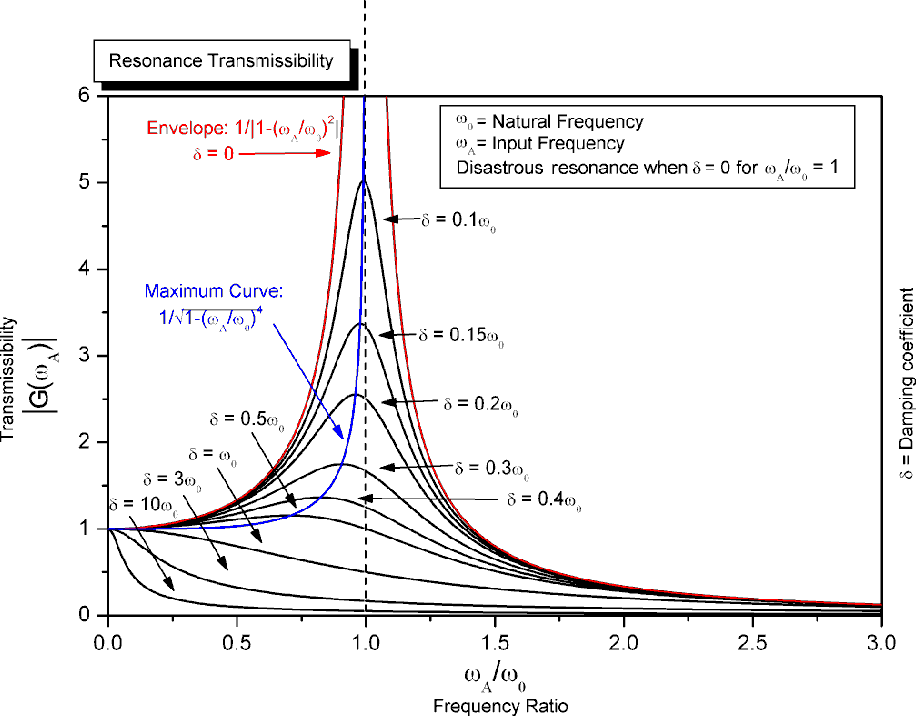 html
html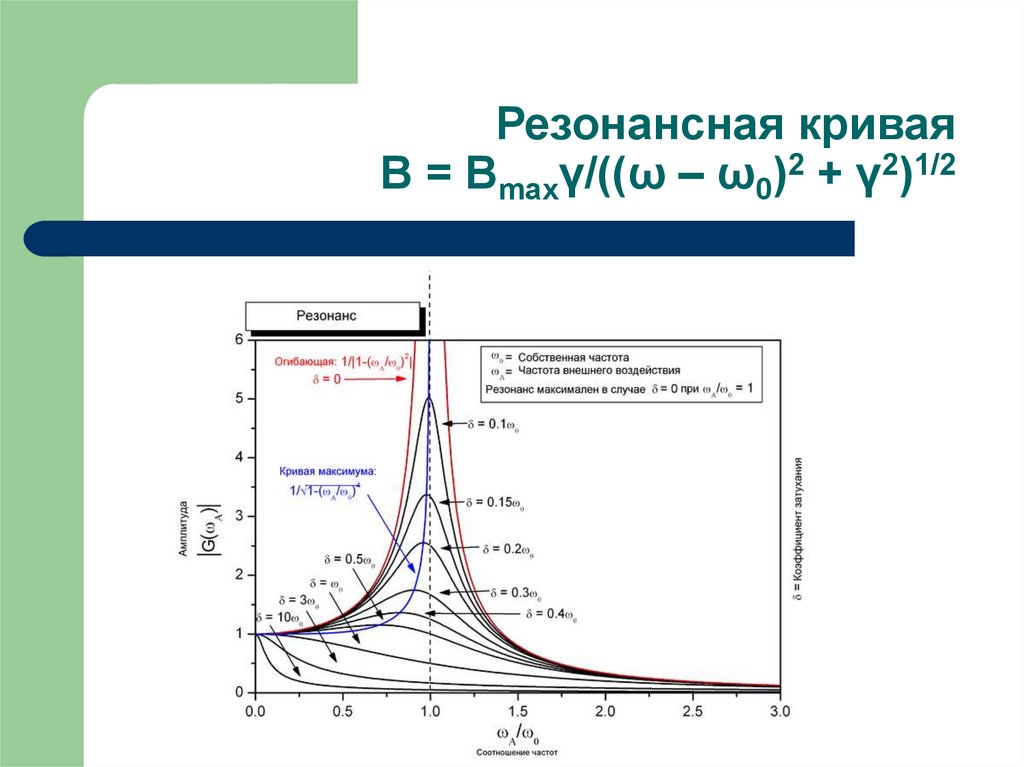 : (3952) 592-836;
: (3952) 592-836; В зависимости от частоты воздействия в тканях происходят квантовые электронные изменения, фотохимические реакции, колебательные, вращательные движения диполей молекул воды, движения ионов и т.п., которые сопровождаются противоспалительным, рассасывающим, болеутоляющим, рефлекторным действием, изменением возбудимости и проводимости нервной системы, микроциркуляции и проницаемости клеточных мембран. Для этого применяются высокие энергии воздействия, которые могут нанести вред не только больному, но и обслуживающему персоналу. В то же время влияние различных физических факторов низкой интенсивности, вступающих в резонансные взаимодействия с собственными колебаниями, колебаниями излучения и другими видами колебаний, обладают высокой биологической активностью. Резонанс — от лат. resono — «звучу в ответ, откликаюсь». Суть явления резонанса: многократное усиление эффекта от воздействия на объект при совпадении частоты внешнего воздействия с собственной частотой объекта. Выявить и усилить с помощью резонанса можно лишь те свойства объекта, которые в нем уже существуют.
В зависимости от частоты воздействия в тканях происходят квантовые электронные изменения, фотохимические реакции, колебательные, вращательные движения диполей молекул воды, движения ионов и т.п., которые сопровождаются противоспалительным, рассасывающим, болеутоляющим, рефлекторным действием, изменением возбудимости и проводимости нервной системы, микроциркуляции и проницаемости клеточных мембран. Для этого применяются высокие энергии воздействия, которые могут нанести вред не только больному, но и обслуживающему персоналу. В то же время влияние различных физических факторов низкой интенсивности, вступающих в резонансные взаимодействия с собственными колебаниями, колебаниями излучения и другими видами колебаний, обладают высокой биологической активностью. Резонанс — от лат. resono — «звучу в ответ, откликаюсь». Суть явления резонанса: многократное усиление эффекта от воздействия на объект при совпадении частоты внешнего воздействия с собственной частотой объекта. Выявить и усилить с помощью резонанса можно лишь те свойства объекта, которые в нем уже существуют. При этом воздействия отнюдь не должны быть интенсивными, энергетически мощными. Коррекция функций организма при воздействии электромагнитных излучений строго определенных параметров, с которыми структуры организма входят в резонанс получило название биорезонансной терапии. Экспериментально были определены биологически эффективные частоты, однако попыток объяснения физических механизмов их существования и с каким видом колебаний они взаимодействуют в живых системах очень мало. В редких случаях исследователи ссылаются на возможный резонанс между колебаниями параметров внешнего ЭМП и собственными колебаниями (34, 35, 36, 38, 40).
При этом воздействия отнюдь не должны быть интенсивными, энергетически мощными. Коррекция функций организма при воздействии электромагнитных излучений строго определенных параметров, с которыми структуры организма входят в резонанс получило название биорезонансной терапии. Экспериментально были определены биологически эффективные частоты, однако попыток объяснения физических механизмов их существования и с каким видом колебаний они взаимодействуют в живых системах очень мало. В редких случаях исследователи ссылаются на возможный резонанс между колебаниями параметров внешнего ЭМП и собственными колебаниями (34, 35, 36, 38, 40). 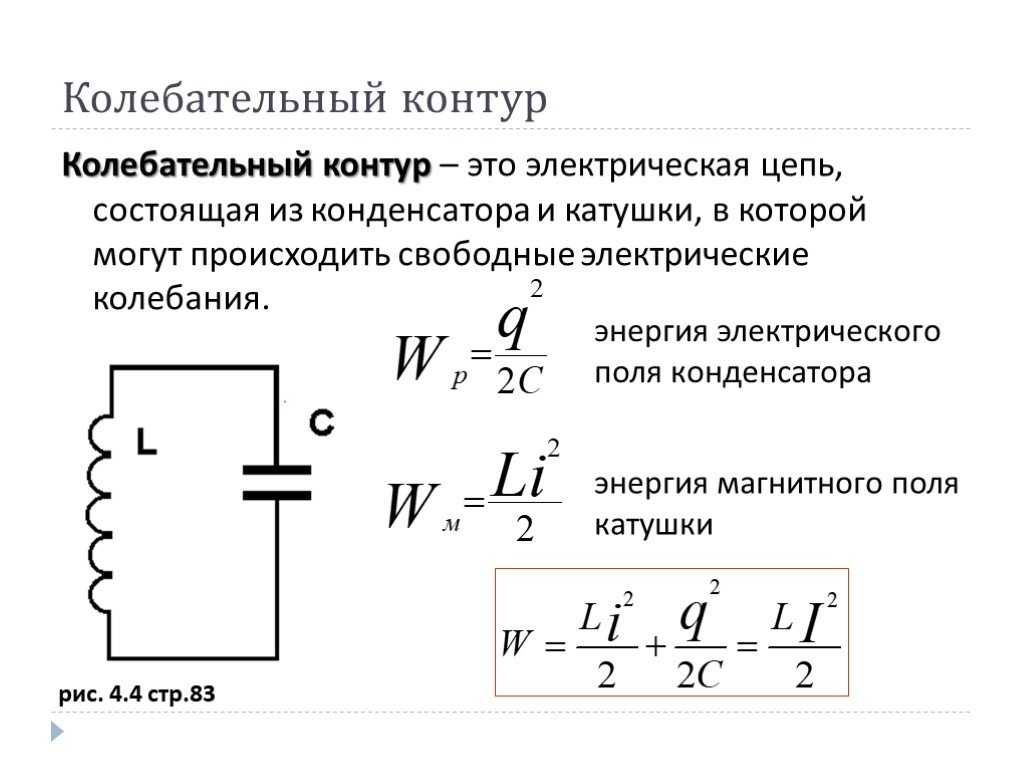 Максимальную частоту колебаний имеют мельчайшие частицы праматери. С ростом массы и сложности объекта частота колебаний снижается. Кроме этого вида колебания существуют и другие виды колебаний — колебания электромагнитного, гравитационного излучения, собственные колебания и т. д.
Максимальную частоту колебаний имеют мельчайшие частицы праматери. С ростом массы и сложности объекта частота колебаний снижается. Кроме этого вида колебания существуют и другие виды колебаний — колебания электромагнитного, гравитационного излучения, собственные колебания и т. д.  В. Шабельников (41) считает, что за целостность природных объектов ответственны силы гравитации, которые организуют все процессы в единый спектр, включая временные колебания в биологических процессах на клеточном, органном и организменных уровнях.
В. Шабельников (41) считает, что за целостность природных объектов ответственны силы гравитации, которые организуют все процессы в единый спектр, включая временные колебания в биологических процессах на клеточном, органном и организменных уровнях. ван де Хюлстом (Н. Ch. van de Hulst) в 1945 году. В 1948 И. С. Шкловский рассчитал ожидаемую интенсивность радиолинии и показал, что она достаточна для того, чтобы 21 см можно было обнаружить методами радиоастрономии (30, 42).
ван де Хюлстом (Н. Ch. van de Hulst) в 1945 году. В 1948 И. С. Шкловский рассчитал ожидаемую интенсивность радиолинии и показал, что она достаточна для того, чтобы 21 см можно было обнаружить методами радиоастрономии (30, 42).  Ряд резонансных частот с частотой электромагнитного
Ряд резонансных частот с частотой электромагнитного

 ..4,0) х 1010 и некоторых структур живой клетки: соматической клетки — 2,39 х 1012; ядра соматической клетки — 9,55 х 1012 (27).
..4,0) х 1010 и некоторых структур живой клетки: соматической клетки — 2,39 х 1012; ядра соматической клетки — 9,55 х 1012 (27). Исследуя физические характеристики диапазонов частот этих ритмов, а именно гармоничность колебательного процесса, было установлено, что частоты 42,32; 21,16; 10,58; 5,29 и 2,65 Гц (середины диапазона ритмов) имеют гармоническую форму сигнала. По мере смещения частоты к границе диапазона сигнал становится все более стохастичным (25). Поэтому при выборе частот внешнего электромагнитного излучения для биорезонансного воздействия на мозг необходимо использовать именно эти частоты, т.к. резонансные отношения в полном объеме возможны только для гармонических сигналов.
Исследуя физические характеристики диапазонов частот этих ритмов, а именно гармоничность колебательного процесса, было установлено, что частоты 42,32; 21,16; 10,58; 5,29 и 2,65 Гц (середины диапазона ритмов) имеют гармоническую форму сигнала. По мере смещения частоты к границе диапазона сигнал становится все более стохастичным (25). Поэтому при выборе частот внешнего электромагнитного излучения для биорезонансного воздействия на мозг необходимо использовать именно эти частоты, т.к. резонансные отношения в полном объеме возможны только для гармонических сигналов. 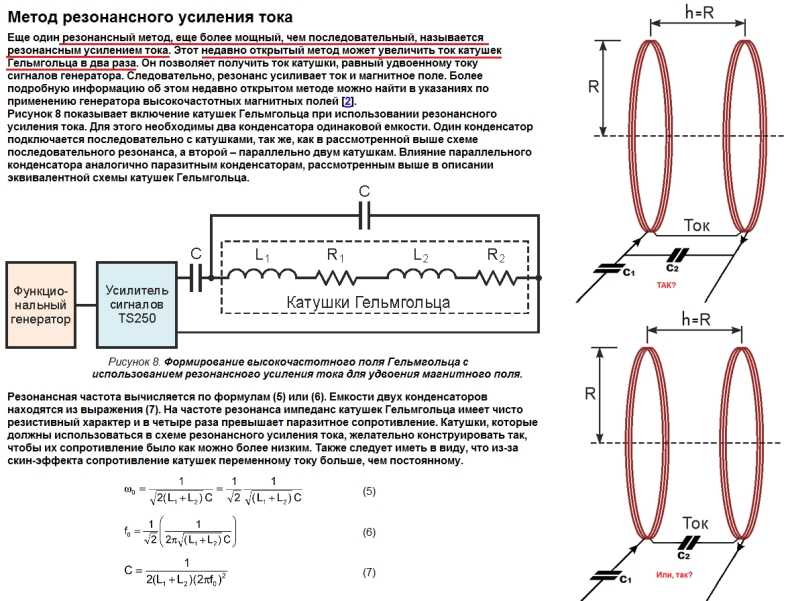
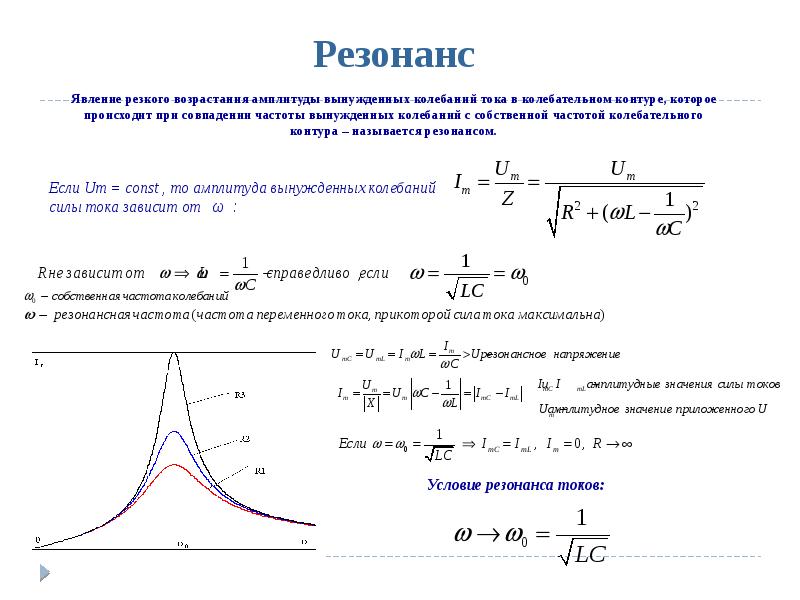 Результат, на первый взгляд, неожиданный, но, принимая во внимание высокое содержание воды в организме (в среднем около 75%), вполне объяснимый. Во всем исследованном диапазоне частот (1…120 ГГц) резонансы наблюдались только в трех поддиапазонах, вблизи: ~ 50 ГГц, 65 ГГц и 100 ГГц (33), два из которых соответствуют нами рассчитанных — 45,44 и 90,88 ГГц, таблица 2.
Результат, на первый взгляд, неожиданный, но, принимая во внимание высокое содержание воды в организме (в среднем около 75%), вполне объяснимый. Во всем исследованном диапазоне частот (1…120 ГГц) резонансы наблюдались только в трех поддиапазонах, вблизи: ~ 50 ГГц, 65 ГГц и 100 ГГц (33), два из которых соответствуют нами рассчитанных — 45,44 и 90,88 ГГц, таблица 2.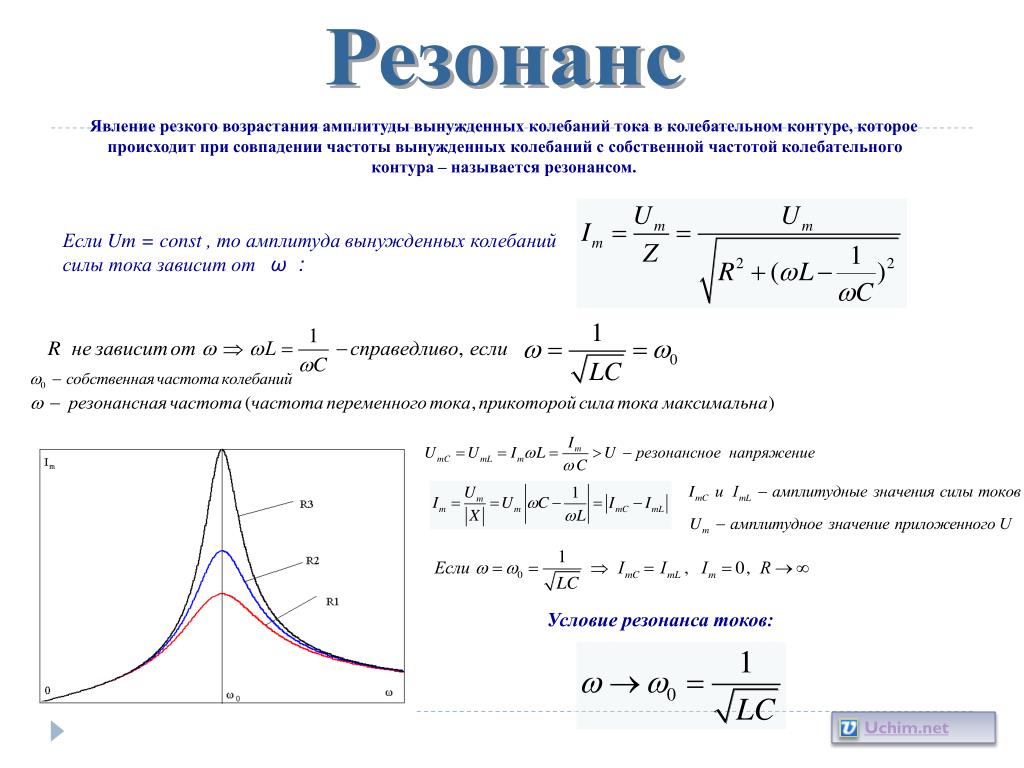 Также любое упругое тело после удара подобно колоколу совершает собственные колебания и когда собственные колебания совпадают с вынужденными,. ведет к резкому увеличению амплитуды (37).
Также любое упругое тело после удара подобно колоколу совершает собственные колебания и когда собственные колебания совпадают с вынужденными,. ведет к резкому увеличению амплитуды (37). 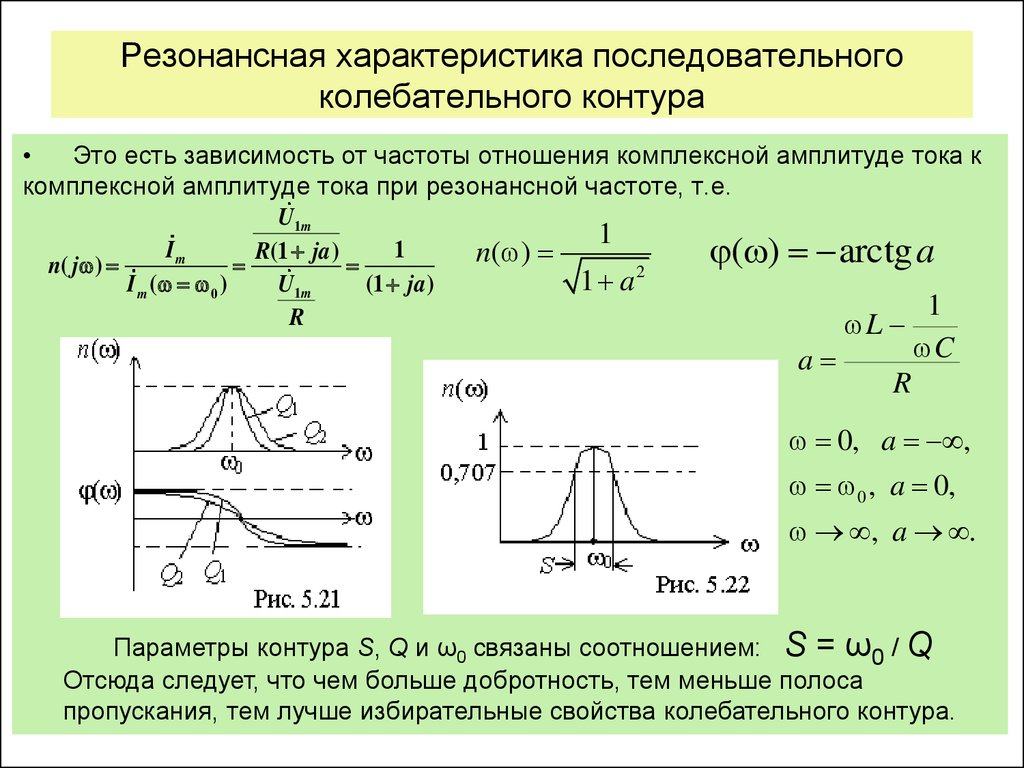
 , K — 0,580 х10 -9 м., Rb — 0,640 х10 -9 м., Сs — 0,796 х10 -9 м. Сравнивая их диаметры с табличными диаметрами было установлено, что они размещаются в диапазоне 0,4332 — 0,8667х10 -9 м. и занимают 3-4-ое места в таблице. Так как калий занимает 19-ое место в таблице Менделеева, следовательно химические элементы с диаметрами меньше диаметра атома калия займут с 1-го по 4-ое место в нашей таблице, а химические элементы, диаметры которых больше диаметра цезия, займут с 4-го по 10-ое места. Таким образом, диаметры всех химических элементов находятся в пределах от 0,1058 до 54,1696х10 в -9 м., занимают с 1-го по 10-ое место в таблице и они кратны диаметру атома водорода.
, K — 0,580 х10 -9 м., Rb — 0,640 х10 -9 м., Сs — 0,796 х10 -9 м. Сравнивая их диаметры с табличными диаметрами было установлено, что они размещаются в диапазоне 0,4332 — 0,8667х10 -9 м. и занимают 3-4-ое места в таблице. Так как калий занимает 19-ое место в таблице Менделеева, следовательно химические элементы с диаметрами меньше диаметра атома калия займут с 1-го по 4-ое место в нашей таблице, а химические элементы, диаметры которых больше диаметра цезия, займут с 4-го по 10-ое места. Таким образом, диаметры всех химических элементов находятся в пределах от 0,1058 до 54,1696х10 в -9 м., занимают с 1-го по 10-ое место в таблице и они кратны диаметру атома водорода.  и от 13,874 до 27,745 х10 -6 м. Средние значения диаметров составили, соответственно, для эритроцита – 10,40 х10 -6 м. и для клетки — 20,81 х10-6 м.
и от 13,874 до 27,745 х10 -6 м. Средние значения диаметров составили, соответственно, для эритроцита – 10,40 х10 -6 м. и для клетки — 20,81 х10-6 м.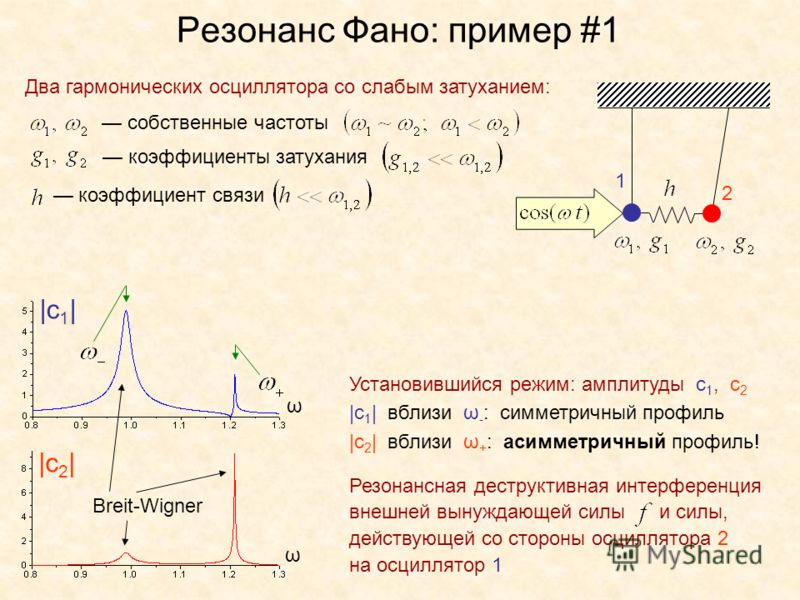 и среднему диаметру условного человека равным 1,36 м.
и среднему диаметру условного человека равным 1,36 м.  , рассчитали собственную частоту атома водорода, которая составила 28,59х10 6 МГц.
, рассчитали собственную частоту атома водорода, которая составила 28,59х10 6 МГц. 

 Например, диаметр химического элемента равен: Na — 0,508 х10 -9 м., K — 0,580 х10 -9 м., Rb — 0,640 х10 -9 м., Сs — 0,796 х10 -9 м., а их расчетные собственные частоты равны: атом натрия — 5,955 х10 6 МГц, атом калия – 5,216 х10 6 МГц, атом рубидия – 4,727 х10 6 МГц, атом цезия – 3,794 х10 6 МГц и занимают диапазон 5,955 – 3,794 х10 6 МГц. Этот диапазон, согласно данным таблицы 4, соответствует диапазону 7,15 – 3,75 х10 6 МГц (3-4 места), который находится в резонансной взаимосвязи с собственной частотой атома водорода.
Например, диаметр химического элемента равен: Na — 0,508 х10 -9 м., K — 0,580 х10 -9 м., Rb — 0,640 х10 -9 м., Сs — 0,796 х10 -9 м., а их расчетные собственные частоты равны: атом натрия — 5,955 х10 6 МГц, атом калия – 5,216 х10 6 МГц, атом рубидия – 4,727 х10 6 МГц, атом цезия – 3,794 х10 6 МГц и занимают диапазон 5,955 – 3,794 х10 6 МГц. Этот диапазон, согласно данным таблицы 4, соответствует диапазону 7,15 – 3,75 х10 6 МГц (3-4 места), который находится в резонансной взаимосвязи с собственной частотой атома водорода. Полученные расчетные и табличные данные разнятся на 9,1%.
Полученные расчетные и табличные данные разнятся на 9,1%.  Несоответствие полученных значений составила 10,9%.
Несоответствие полученных значений составила 10,9%.

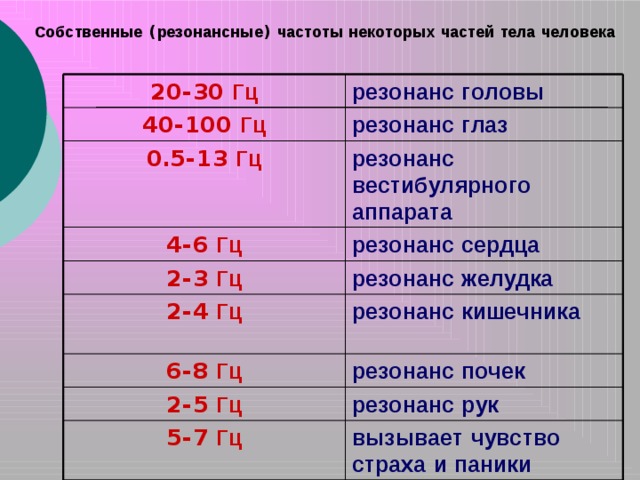 Стоит на несколько минут включить радиопередатчик на определенной частоте, и у больных гнойным воспалением погибают стафилококки и стрептококки, на другой частоте — трихомонады и хламидии, на третьей — вирусы герпеса и грибки. Найдены частоты, губительные для сотен микроорганизмов, для простейших и даже для глистов.
Стоит на несколько минут включить радиопередатчик на определенной частоте, и у больных гнойным воспалением погибают стафилококки и стрептококки, на другой частоте — трихомонады и хламидии, на третьей — вирусы герпеса и грибки. Найдены частоты, губительные для сотен микроорганизмов, для простейших и даже для глистов. Независимо от вида колебаний (электромагнитные, акустические, механические и т. д.) все они находятся в резонансных отношениях с частотой ЭМИ водорода. Нами был определен ряд резонансных частот ЭМИ, где некоторые частоты совпадают с экспериментально зарегистрированными частотами ЭМИ головного мозга, сердца, печени, почки, скелетной мышцы (и других органов), эритроцита, клетки, ядра клетки.
Независимо от вида колебаний (электромагнитные, акустические, механические и т. д.) все они находятся в резонансных отношениях с частотой ЭМИ водорода. Нами был определен ряд резонансных частот ЭМИ, где некоторые частоты совпадают с экспериментально зарегистрированными частотами ЭМИ головного мозга, сердца, печени, почки, скелетной мышцы (и других органов), эритроцита, клетки, ядра клетки.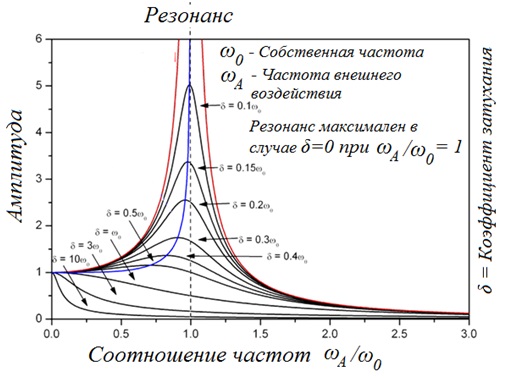 При воздействии ЭМИ с любой частотой резонансной с частотой ЭМИ водорода наблюдается усиление той или ной функции организма. Например, при воздействии на мозг ЭМИ с частотой близкой к 10 Гц, оно будет вступать в резонанс ЭМИ мозга на частоте соответствующей середине диапазона альфа-ритма ЭЭГ в результате чего будет наблюдаться его увеличение. В свою очередь альфа-ритм связан с определенной функцией организма. Оптимизация функции (деятельности) системы, органа, клетки будет всегда наблюдаться, если частота собственного ЭМИ будет совпадать с частотами резонансными с частотой ЭМИ водорода. В тоже время не любое ЭМИ благотворно влияет на организм человека. Например, психотронное оружие, зомбирование, в основе которых лежит применение ЭМИ. Вероятно, в этих случаях, используют частоты ЭМИ соответствующего среднему значению между двумя соседними частотами резонансными с частотой атома водорода. Например, возьмем значения 10,56 и 5,29 Гц (28 и 29 места), среднее — равно 7,975 Гц, таблица 1.
При воздействии ЭМИ с любой частотой резонансной с частотой ЭМИ водорода наблюдается усиление той или ной функции организма. Например, при воздействии на мозг ЭМИ с частотой близкой к 10 Гц, оно будет вступать в резонанс ЭМИ мозга на частоте соответствующей середине диапазона альфа-ритма ЭЭГ в результате чего будет наблюдаться его увеличение. В свою очередь альфа-ритм связан с определенной функцией организма. Оптимизация функции (деятельности) системы, органа, клетки будет всегда наблюдаться, если частота собственного ЭМИ будет совпадать с частотами резонансными с частотой ЭМИ водорода. В тоже время не любое ЭМИ благотворно влияет на организм человека. Например, психотронное оружие, зомбирование, в основе которых лежит применение ЭМИ. Вероятно, в этих случаях, используют частоты ЭМИ соответствующего среднему значению между двумя соседними частотами резонансными с частотой атома водорода. Например, возьмем значения 10,56 и 5,29 Гц (28 и 29 места), среднее — равно 7,975 Гц, таблица 1. Роль этой частоты ЭМИ при воздействия на биологические объекты хорошо известна. Изучая спектр частот диапазона ЭЭГ, нами было установлено, что в середине любого ритма (дельта-, тета-, альфа-, бета- и гамма) ЭЭГ сигнал имеет гармоничную форму и по мере приближения к границам ритмов он становится менее гармоничным и на границе между ритмами становится стохастичным (беспорядочным). Если при воздействии на организм ЭМИ наблюдается усиление или угнетение функции органа, клетки, внутриклеточных структур, то при воздействии на них частотами близкими к собственным колебаниям наблюдается их физическое разрушение. Примером тому являются питерский мост, рухнувший от строевого шага прошедшей по нему роты солдат, исследования американской ученой Хильдой Кларк, которая установила, что радиоволны, настроенные на резонансную частоту бактерий и вирусов, их уничтожают.
Роль этой частоты ЭМИ при воздействия на биологические объекты хорошо известна. Изучая спектр частот диапазона ЭЭГ, нами было установлено, что в середине любого ритма (дельта-, тета-, альфа-, бета- и гамма) ЭЭГ сигнал имеет гармоничную форму и по мере приближения к границам ритмов он становится менее гармоничным и на границе между ритмами становится стохастичным (беспорядочным). Если при воздействии на организм ЭМИ наблюдается усиление или угнетение функции органа, клетки, внутриклеточных структур, то при воздействии на них частотами близкими к собственным колебаниям наблюдается их физическое разрушение. Примером тому являются питерский мост, рухнувший от строевого шага прошедшей по нему роты солдат, исследования американской ученой Хильдой Кларк, которая установила, что радиоволны, настроенные на резонансную частоту бактерий и вирусов, их уничтожают. Бехтерева Н. П. Физиологические методы в клинической практике. // Л., 1966.
Бехтерева Н. П. Физиологические методы в клинической практике. // Л., 1966.
 // Патент №2278699.-2006.
// Патент №2278699.-2006.  //Патент №2334458 -2008.- Бюл. №27.
//Патент №2334458 -2008.- Бюл. №27. 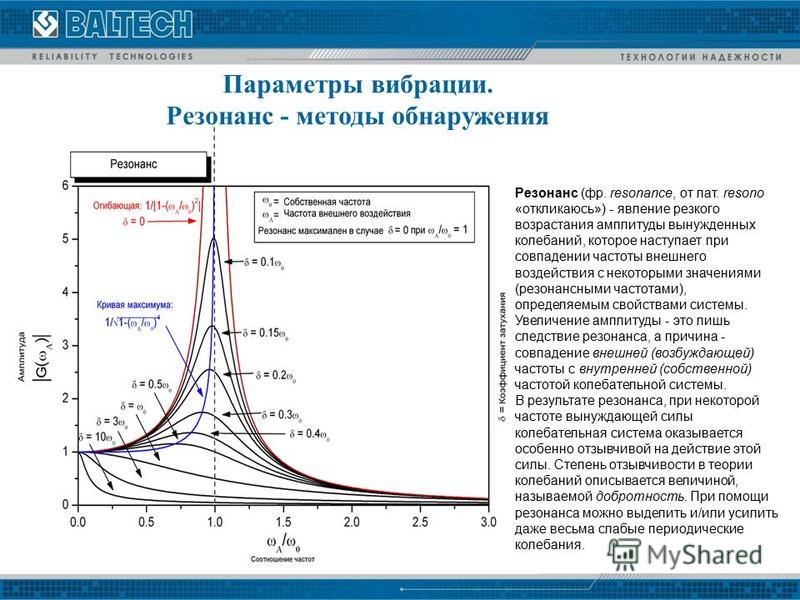 Красовский Ф. Н., Руководство по высшей геодезии, ч. 2, М., 1942.-с.327.
Красовский Ф. Н., Руководство по высшей геодезии, ч. 2, М., 1942.-с.327. Узденский А.Б. // Реализация в клетках резонансных механизмов биологического действия свернизкочастотных магнитных полей. // Материалы 2-й международной конференции «Электромагнитные поля и здоровье человека». М.,1999.- с.43.
Узденский А.Б. // Реализация в клетках резонансных механизмов биологического действия свернизкочастотных магнитных полей. // Материалы 2-й международной конференции «Электромагнитные поля и здоровье человека». М.,1999.- с.43.