Собственная частота и резонанс

ЛЕКЦИЯ № 9

МДК.01.01. Основы эксплуатации, технического обслуживания и ремонта судового энергетического оборудования

(Судовые двигатели внутреннего сгорания)

Тема: Понятие о динамике дизельного двигателя.

Учебные вопросы:

Вступление

1. Терминология по вибрации

2. Внешние неуравновешенные моменты

3. Момент от нормальной силы

4. Аксиальные (осевые) колебания

5. Крутильные колебания

Выводы, ответы на вопросы, задание на самостоятельную подготовку

СОДЕРЖАНИЕ ЛЕКЦИИ

Вступление

Описание характеристик вибрации двухтактных малооборотных дизелей, и конструктивных мер компенсации, которые применяются в связи с их использованием на судах в более полной мере раскрывает этот вопрос и для четырехтактных двигателей.

Терминология по вибрации

Рис.1 Внутренние силы в крейцкопфном двигателе.

Источники возмущения

Источник возмущения – это влияющее возмущение, которое производит и сохраняет колебания возмущения. Этот источник может быть свободным моментом, моментом направляющей силы, произведенный двигателем, влияющим на фундаментную раму двигателя и корпусные конструкции судна в результате аксиальных колебаний системы валопровода или влияния от крутильных колебаний системы валопровода.

Источники возбуждения в дизеле по своей природе являются циклическими, что означает их периодическое изменение в течение рабочего цикла двигателя, см. рис. 1.

Чтобы оценить влияние источника возмущения, выполняется так называемый анализ гармоник, при котором источник возмущения представляется суммой возмущений, действующих с различными частотами, кратными числу вращения частоты двигателя.

Математически, это выражается следующим образом:

F = F₁ · cos (α + φ₁) + F₂ · cos (2α + φ₂) + … F_n · cos (nα + φ_n)

где, α – угол поворота кривошипа

φ_n – угол сдвига фаз

Первый член уравнения F₁ · cos (α + φ₁) называется силой первого порядка, потому что она действует один раз за один оборот коленчатого вала двигателя.

Второй член уравнения F₂ · cos (2α + φ₂) называется силой второго порядка, потому что она действует два раза за один оборот коленчатого вала двигателя.

Собственная частота и резонанс

Собственная частота – это частота характеристики, с которой твердый предмет свободно вибрирует при воздействии возмущения. Любая система из твердых элементов — струны скрипки, балок корпусного набора, валопровода или судна, имеет несколько собственных частот, каждая из которых некоторого вида колебаний как показано ниже.

Резонанс происходит в случаях, когда частота возмущения совпадает с собственной частотой элемента. При этом возникают вибрации очень высокого уровня.

Например:

Запланировано установить на судне двигатель 4L60MC.

Расчеты показывают, что предотвращения вибрации корпус должен иметь собственную частоту 3,83 герц. Это соответствует:

3,83 · 60 циклов/мин = 230 цикломинут

Таким образом, если двигатель 4L60MC эксплуатируется с частотой вращения 117 об/мин на MCR, то очевидно, что нет риска возникновения резонанса с моментом первого порядка, поскольку максимальная частота возбуждения двигателя

117 · 1 цикл/мин = 117 цикломинут

Момент второго порядка имеет частоту возбуждения

117 · 2 цикл/мин = 234 цикломинут

Это означает, что резонанс с моментом 2-го порядка может произойти при:

= 115 об/мин

отношение что равно 95 % нагрузки.

Поэтому в случае установки на судно двигателя 4L60MC, необходимо рассмотреть возможность наступления резонанса с моментом 2-ого порядка.

На рис. 2 показана линия отклонения корпуса для упомянутого вида колебаний.

Рис. 2. Вертикальная вибрация корпуса.

Виды колебаний

Система может иметь несколько собственных частот, каждой из которых соответствует характерный вид колебаний. Например:

Рис. 3. Виды колебаний.

Как видно на рис. 3 верхний вид колебания имеет две точки, которые не двигаются, а нижний вид колебания три точки.

Эти точки называются «узлами», и соответственно количеству узлов колебаний названы “2-х узловая вибрация” и “3-х узловая вибрация”.

Также существуют другие формы колебаний. Например, существуют колебания в продольном направлении, крутящие колебания и их комбинация. Часто фраза “колебательная реакция” понимается как колебание системы в результате возмущения системы.

Демпфирование

Несмотря на то, что во всех системах существует трение, которое поглощает некоторое количество энергии, колебания все-таки достигают определенной величины. Эта величина будет зависеть от величины возмущения и демпфирования (трение) на частоте возмущенияотносительно собственной частоты системы.

Рис. 3. Кривая колебания с и без демпфера.

Определение величины демпфирования должна быть известна, чтобы компенсировать напряжения и колебания, может основываться на теоретических знаниях или опытных методах. На рис. 4 показано форма колебания с и без демпфирования.

Описание и примеры

Описание источников возмущения разделено на четыре секции, потому что характеристики вибрации двухтактных малооборотных дизельных двигателей обычно разделяют на четыре группы.

Для каждой группы дается основное пояснение природы возникновения источника возмущения, и описываются контрмеры противодействия для минимизации или устранения его последствий.

 

Все четыре группы источников возмущения системы показаны на рис. 5:

1 группа

. Внешние неуравновешенные моменты, классифицируемые как моменты 1-го порядка (действующие в горизонтальной и вертикальной плоскостях) и моменты 2-го порядка (действующий в вертикальном направлении только) (рис. 5).

2 группа. Моменты нормальной силы (рис. 5).

3 группа. Аксиальные (осевые) колебания.

4 группа. Крутящие колебания.

Во время рабочего цикла двигателя под воздействием силы газов действующих на кривошипно-шатунный механизм возникают силы инерции.

Силы инерции разделяют на силы инерции вращающихся масс и силы инерции поступательно-движущихся масс.

Силы инерции вращающихся масс постоянны по величине при постоянной частоте вращения двигателя, но переменны по направлению.

Силы инерции поступательно-движущихся масс зависят от фактического положения поршня даже при постоянной частоте вращения двигателя.

То же самое относится к силам газов: они не постоянны в течение всего рабочего цикла.

Для того чтобы составить математическое описание действия сил обычно выполняется гармонический анализ.

Этим силам противодействуют силы реакции в коленчатом валу, которые составляют Уравновешивающую их равнодействующую силу. Но при этом остаются внешние неуравновешенные моменты.

Читайте также:

Рекомендуемые страницы:

Поиск по сайту

Методическое пособие по определению частот собственных колебаний узлов и деталей » Все о транспорте газа

  

   В настоящем методическом пособии приведены сведения о частотах и формах колебаний деталей, а также наиболее распространённые методы экспериментального определения частот собственных колебаний (ЧСК) деталей и конструкций. Пособие не ставит своей целью изложить всё многообразие методов и средств, применяемых при исследовании механических частотных характеристик. При составлении методики предполагалось предварительное знание работниками основных сведений по теории колебаний и правил проведения измерений с помощью стандартных измерительных средств.

 

1.     Основные сведения о частотных характеристиках (ЧСК) деталей.

 

  Каждая деталь имеет бесконечное количество ЧСК, образующих спектр. Каждой частоте собственных колебаний соответствует своя форма колебаний. Форма колебаний определяется картиной знакопеременных смещений или прогибов и положением узловых линий. В узловых линиях перемещения бесконечно малы и считаются нулевыми. По разные стороны узловых линий смещения колеблющихся участков находятся в противофазе. Совокупность форм колебаний детали образуют спектр форм. Способ крепления детали изменяет спектр частот и форм колебаний. Существуют  методы расчёта частот и форм собственных колебаний деталей.

 Расчётная формула для определения частот изгибных колебаний балок имеет следующий вид:

f = α²/2π l² *√EI/m,

где l – длина балки, EI – жёсткость балки на изгиб, m — погонная масса балки,

α — расчётный коэффициент.

Ниже (рис. 1-3) приведены формы изгибных колебаний балки при различных способах крепления. Значения ЧСК одной и той же балки при различных способах крепления и различных формах зависят только от α². Значения α² приведены на рисунках. По ним нетрудно видеть, как изменятся собственные частоты, в зависимости от способа крепления и формы колебаний.

 



 

α² = 3,515             α² = 22,037         α² = 61,68               α² = 120,907         α² = 199,85

Консольная балка.

 Рис.1

 



 

 

α² = 9,869             α² =39,478            α² = 88,826           α² = 157, 91           α² = 246,738

Балка с опертыми концами.

Рис.2

 



 

α² = 22,37            α² = 61,67           α² = 120,912          α² = 199,855            α² = 298,55

Свободная балка.

Рис.3

 

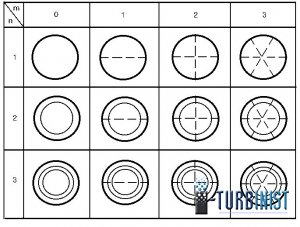
  В таблице 1 представлен спектр рисунков узловых линий эталонной пластинки при изгибных формах колебаний, а в таблице 2 аналогичный спектр осесимметричного диска.

  Значения ЧСК соответствующим формам возрастают в рядах, как по горизонтали, так и по вертикали. В таблицах значения m и n определяют число узловых линий проходящих через оси симметрии.

 Направления прогибов, представленных в таблице 1, перпендикулярны плоскости пластины. Наряду с этим имеются формы колебаний, у которых направления прогибов лежат в плоскости пластин. Однако в этом случае собственные частоты из-за высокой жёсткости настолько велики, что они не имеют практической значимости.


 Таблица 1.

 



 

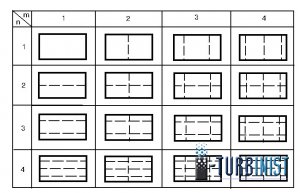
Таблица 2.

 



 

Представленные выше формы колебаний характерны для плоских деталей. Реальные детали, как правило, имеют более сложную геометрию. Поэтому и формы колебаний у реальных деталей более сложны.

   Знание ЧСК позволяет конструкторам избежать условий работы конструкции на длительных эксплутационных режимах при частотах, близких резонансным. Изменение спектра ЧСК конструкции может служить в качестве признака появления и развития дефекта. При исследовании разрабатываемых деталей газотурбинной техники иногда используются методы определения форм колебаний с помощью голографической интерферометрии, которые позволяют выявлять сложные формы колебаний в широком диапазоне частот. В данном пособии этот метод не рассматривается, так как он не применяется в практике производства и ремонта.

   В практике ремонтных предприятий используется контроль ЧСК лопаток газотурбинных двигателей (ГТД) с целью проверки их соответствия техническим условиям. При ремонте турбин чаще всего контролируется первая форма колебаний. При производстве иногда контролируются частоты и формы в более  широком диапазоне

 

 

2.     Методы и средства измерения ЧСК.

 

2.1   Метод измерения ЧСК с использованием вибровозбудителя колебаний переменной частоты.

 

 

  Метод поясняется с помощью блок-схемы, приведенной ниже на рис.4.

С генератора 1 напряжение переменной частоты подаётся на вибровозбудитель 2 (при необходимости использования вибровозбудителя большой мощности используется усилитель мощности 3). Возбуждаемые колебания детали 4 воспринимаются пьезодатчиком (или щупом с датчиком) 5. Сигнал с датчика поступает на вход «У» осциллографа 6. На вход «Х» осциллографа через нормирующий делитель 7 подаётся напряжение с генератора.

  При наличии сигнала с датчика с частотой возбуждения на экране осциллографа будет регистрироваться эллипс. Если частота возбуждения, регистрируемая датчиком, будет отлична от частоты генератора, то на экране будет регистрироваться фигура, отличная от эллипса. Плавным изменением частоты генератора находится резонансная частота по максимальному значению сигнала, поступающего с датчика на вход «У». По шкале частоты генератора фиксируется значение резонансной частоты, соответствующее собственной частоте. С помощью данного метода можно определить резонансные частоты в широком диапазоне частот.

 

 

 

 

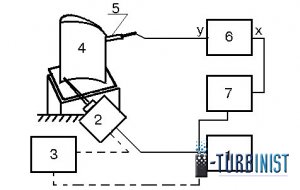
Блок-схема измерения ЧСК с использованием вибровозбудителя колебаний переменной частоты.

1 – генератор переменной частоты, 2 – вибровозбудитель, 3 – усилитель мощности, 4 – деталь, 5 – пьезодатчик, 6 – осциллограф, 7 – делитель.

Рис.4.

 

   Схема рис.4 используется также для определения форм колебаний. Для этого фиксируется положение вибровозбудителя, а щуп перемещается по детали. На узловой линии амплитуда сигнала с датчика, поступающего на вход «У», будет падать до 0, а при её пересечении фаза изменится на 180°. Изменение фазы контролируется по наклону эллипса на экране осциллографа. Сканируя щупом поверхность детали, можно нарисовать картину узловых линий. При консольном защемлении детали и возбуждении на низшей частоте узловая линия находится в заделке и смена фазы при сканировании поверхности детали не происходит.  Следует отметить, что если для данной формы колебаний возбуждение будет осуществляться через узел колебаний, то колебания не будут возбуждаться и эта форма останется незамеченной.

  Аналогичным образом можно определять картину узловых линий, если закрепить пьезодатчик и сканировать вибровозбудителем поверхность детали. Однако если присоединённая масса вибровозбудителя будет соизмерима с массой детали, то картина будет искажена.

 

 

2.2  Метод измерения ЧСК с использованием ударного возбуждения.

 

  Схема реализации этого метода приведена ниже на рис.5.

По данной схеме возбуждение детали 1 осуществляется молотком 2 с мягким наконечником. Колебания регистрируются с помощью акселерометра 3, подключённому на вход виброанализатора 4.

 



 


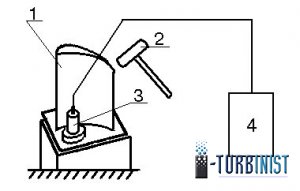
Схема измерения ЧСК с использованием ударного возбуждения.

1 – деталь, 2 – молоток с мягким наконечником, 3 – акселерометр,

4 – виброанализатор типа «Агат», «Кварц».

Рис.5.

 

  Современные анализаторы имеют функцию измерения ЧСК ударным методом. Из отечественных приборов такого класса наибольшее распространение получили виброанализаторы типа «Агат», «Кварц» фирмы «Диамех», в которых реализуется такая функция. Порядок работы с помощью данной функции приведён в техническом описании используемого анализатора. Такой метод эффективен и при определении резонансных свойств опорных конструкций агрегатов. Снятие ЧСК с помощью акселерометра и анализатора при ударном возбуждении лучше производить в режиме измерения ускорения, а не скорости и смещения. В режиме  измерения скорости и смещения осуществляется одно или двукратное интегрирование. Затухающий процесс имеет широкий частотный спектр, который может выйти за область интегрирования. Это может привести к недостоверным результатам.

 

 

3.     Устройства для зажима рабочих лопаток ГТД при  контроле ЧСК в технологической оснастке.

 

    3.1 Требования к устройствам для зажима лопаток.

 

  Точность измерительных средств, как правило, на два порядка выше, чем требуемая точность измерения ЧСК. Поэтому достоверность результатов контроля преимущественно определяется способом и устройствами для закрепления лопаток. Для достоверности было бы правильнее контролировать частоты при реальном защемлении в роторе.  Но контроль  ЧСК рабочих лопаток турбины после установки в диск выполнить нельзя, ввиду наличия качки в замках. Их защемление в замках обеспечивается при работе под действием центробежных сил. Контроль ЧСК рабочих лопаток компрессора хотя и производится в составе ротора, но всё равно приходится проводить контроль частот лопаток до их установки, так как установка лопаток с исходно несоответствующими ТУ частотами может привести к неоправданным затратам.

Поэтому возникает необходимость проводить контроль ЧСК рабочих лопаток турбины и компрессора ГТД с применением технологической оснастки. Для этого необходимо выбрать такую оснастку, чтобы её применение не привело к изменению частотного спектра. При этом должна обеспечиваться стабильность показаний при многократных измерениях. Это возможно, если будут обеспечены достаточная жёсткость зажимных элементов, равномерное защемление замков лопаток, достаточность и стабильность усилия зажима. Масса самого приспособления должна быть, по крайней мере, на порядок больше массы контролируемой лопатки.

  Следует также отметить, что в некоторых случаях имеет значение степень демпфирования колебаний. С этой точки зрения количество сопрягаемых элементов приспособления должно быть минимизировано. При использовании гидравлических приспособлений зазоры между поршнем и цилиндром должны быть максимально допустимыми, для исключения демпфирования при контакте. Размеры замков должны быть такими, чтобы обеспечивался минимальный ход поршня при защемлении лопатки. Минимум объёма масла под поршнем обеспечивает минимум демпфирования колебаний.

  Исходя из этих принципов, разрабатываются технологические устройства для контроля ЧСК лопаток.

 

 

  3.2  Конструкция и принцип работы оснастки, используемой при контроле ЧСК рабочих лопаток ГТД.

 

 

  Зажимные элементы для хвостовиков лопаток, как правило, изготавливаются индивидуально под каждую ступень. Наряду с этим в практике используется универсальное замковое устройство (патент RU 2189023 C2), которое обеспечивает стабильность защемления хвостовиков лопаток всех типов. Зажимные элементы этого замкового устройства самоустанавливаются по плоскости защемляемых поверхностей лопатки за счёт поворота прижимных элементов, выполненных в виде отрезков цилиндров.

  Ниже на рис. 6 приведена схема приспособления, которое используется для контроля ЧСК лопаток ГТД. В нём лопатка 1 устанавливается между зажимными элементами 2, которые помещаются в гидравлическое приспособление 3. Шток с поршнем 3.1 при подаче на него давления масла защемляет зажимными элементами лопатку. При сбросе давления масла пружина 3.2 возвращает поршень в исходное положение. Рабочее давление масла создаётся с помощью пресса 4. Вентиль 4.1 пресса служит для подачи масла в пресс. Вентиль 4.2 перекрывает или открывает магистраль между прессом и гидравлическим



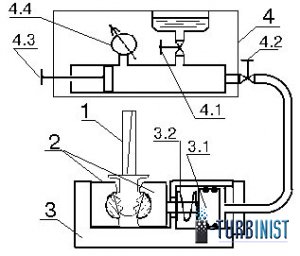
приспособлением. Давление регулируется рукояткой 4.3 поршня пресса. Контроль давления осуществляется с помощью манометра 4.4.

Схема приспособления для зажима рабочих лопаток ГТД при контроле ЧСК.

Рис.6

 

  Для зажима лопатки в приспособлении необходимо:

—         установить лопатку 1 между зажимными элементами 2  гидравлического приспособления 3;

—         закрыть вентиль 4.1 пресса 4;

—         открыть вентиль 4.2 пресса;

—         подать рабочее давление в цилиндр гидравлического приспособления с помощью рукоятки 4.3 поршня пресса;

—         контроль давления осуществлять с помощью манометра 4.4,

—         закрыть вентиль 4.2 пресса.

  Для раскрепления лопатки  и приведения приспособления в исходное состояние необходимо:

—         открыть вентили 4.1 и 4.2 пресса;

—         вынуть лопатку 1 из приспособления;

—         установить поршень 4.3 пресса в крайнее левое положение.

 

 

4.     Меры безопасности при производстве работ.

 

1.1  Работы по определению ЧСК являются составной частью работ по дефектоскопии деталей и узлов ГПА, поэтому при проведении работ следует руководствоваться «Инструкцией по охране труда при проведении работ по дефектоскопии ГПА».

1.2  К работе допускаются лица, изучившие правила эксплуатации приборов используемых при работе.

 

5.     Подготовительные работы.

 

5.1.   Проверить, чтобы детали и узлы, подлежащие контролю, были очищены от грязи, пыли и имели сопроводительную документацию установленного образца.

5.2.   Подготовить рабочее место таким образом, чтобы не было мешающих факторов  и обеспечивался безопасный доступ к рабочей зоне.

5.3.   Подготовить бланки протоколов для проверяемых узлов или деталей.

5.4.   Собрать измерительную схему  согласно техническому описанию.

5.5.   Включить измерительный прибор.

 

6. Производство работ.

 

6.1.   Измерение частот собственных колебаний лопаток ГТД в составе ротора с использованием ударного возбуждения.

6.1.1    Установить на приборе необходимый режим для проведения измерений с помощью ударного возбуждения согласно инструкции по эксплуатации.

6.1.2    Установить на приборе диапазон измерения частот, в котором лежат ЧСК лопаток данной ступени.

6.1.3    Установить акселерометр используемого измерительного прибора на ротор вблизи лопатки, у которой измеряется собственная частота.

6.1.4    Переключить прибор на режим ожидания удара.

6.1.5    Нанести молотком с резиновым наконечником лёгкий удар по лопатке.

6.1.6    Произвести отсчёт измеренной частоты прибором и записать в протокол.

6.1.7    Последовательно произвести измерения ЧСК всех лопаток данной ступени, повторяя  операции п.п. 6.1.3 – 6.1.6.

6.1.8    При необходимости произвести измерения ЧСК лопаток других ступеней повторить операции п.п. 6.1.2 – 6.1.7.

6.2.   Измерение частот собственных колебаний рабочих лопаток ГТД при закреплении в технологическом приспособлении (см. рис.6).

6.2.1      Подготовить приспособление, используя рекомендации п.3.2, к работе.

6.2.2      Установить на приборе необходимый режим для проведения измерений с помощью ударного возбуждения.

6.2.3      Установить на приборе диапазон измерения частот, в котором лежат ЧСК лопаток данного типа.

6.2.4      Установить акселерометр используемого измерительного прибора на приспособление.

6.2.5      Произвести эталонирование усилия зажатия лопатки данного типа, для этого необходимо выполнить следующие операции.

6.2.5.1         Произвести зажим эталонной лопатки для партии лопаток, подлежащей контролю согласно указаниям п.3.2.

6.2.5.2         Переключить прибор на режим ожидания удара.

6.2.5.3         Нанести молотком с резиновым наконечником лёгкий удар по лопатке.

6.2.5.4         Произвести отсчёт измеренной частоты прибором.

6.2.5.5         Сравнить полученные данные с эталонной частотой. При совпадении   измеренной частоты с частотой эталона записать давление масла по манометру.

6.2.5.6         При несовпадении измеренной частоты с эталоном, изменяя давление масла производить измерение частоты. Усилие зажима, контролируемое манометром, при котором измеренная частота совпадёт с эталоном, в дальнейшем устанавливается таким же для контроля данного типа лопаток.

6.2.5.7         Раскрепить лопатку согласно указаниям п. 3.2.

6.2.5.8         Повторить зажим эталонной лопатки.

6.2.5.9         Повторить операции  п.п. 6.2.5.1 – 6.2.5.4.

6.2.5.10     Эталонирование считается законченным, если при перезакреплении эталонной лопатки с одним и тем же усилием зажима собственная частота останется неизменной и будет соответствовать частоте эталона.

6.2.5.11    По окончании эталонирования раскрепить лопатку.

6.2.6      Закрепить в приспособлении лопатку, у которой предстоит измерить собственную частоту с определённым при эталонировании усилием.

6.2.7      Выполнить операции п.п. 6.2.5.2 – 6.2.5.4.

6.2.8      Записать измеренную частоту в протокол.

6.2.9      Раскрепить лопатку.

6.2.10 Для измерения частот следующих лопаток данной партии повторить операции п.п. 6.2.6 – 6.2.9.

 

 

7.     Заключительные работы.

 

7.1    Отключить аппаратуру согласно инструкции по эксплуатации.

7.2    Отсоединить электрические кабели и убрать на место хранения, если  возобновление работ не предполагается.

7.3    Заполнить протокол определения ЧСК исследуемого комплекта лопаток в 2-х экземплярах. Один экземпляр протокола подшить в дело, другой подшивается к паспорту (формуляру) данной партии лопаток.

 

 Источники информации, принятые во внимание при составлении методического пособия по определению частот собственных колебаний узлов и деталей.

 

1. Ананьев И.В., Тимофеев П.Г. Колебания упругих систем в авиационных конструкциях и их демпфирование. Машиностроение  1965г.
2. Иванов В.П. Колебания рабочих колёс турбомашин. М. Машиностроение 1983г.
3. Ковалёв В.К., Россеев Н.И., Монахов А.В. Замковое устройство.

    Патент RU  2189023  C2

 

Автор: Ковалёв В.К. ДОАО «Центрэнергогаз» филиал «Самарский»

 

 

 

 

Прежде чем задать вопрос прочитайте: FAQ


Расчет собственных частот и форм колебаний конструкций в среде T-FLEX Анализ

Александр Сущих, Павел Ануфриков

Мы продолжаем знакомить читателя с новой разработкой АО «Топ Системы» — приложением для осуществления конечно-элементных расчетов T-FLEX Анализ.
В настоящей статье речь пойдет о модуле частотного анализа этой системы.

Необходимость в расчете собственных частот и соответствующих им форм колебаний нередко возникает при анализе динамического поведения конструкции под действием переменных нагрузок. Наиболее распространена ситуация, когда при проектировании требуется убедиться в малой вероятности возникновения в условиях эксплуатации такого механического явления, как резонанс. Как известно, суть резонанса за­ключается в значительном (в десятки раз и более) усилении амплитуд вынужденных колебаний на определенных частотах внешних воздействий — так называемых резонансных частотах (рис. 1). В большинстве случаев возникновение резонанса является крайне нежелательным в плане обеспечения надежности изделия явлением. Многократное увеличение амплитуд колебаний при резонансе и вызываемые этим высокие уровни напряжений — одна из основных причин выхода из строя изделий, эксплуатируемых в усло­виях вибрационных нагрузок. Для защиты от резонансных воздействий можно использовать различные механические устройства, которые принципиально меняют спектральные характеристики конструкции и поглощают энергию колебаний (например, виброизоляторы). Однако есть и другой эффективный способ противодействия резонансам. Известно, что резонансы наблюдаются на частотах, близких к частотам собственных колебаний конструкции. Если при проектировании изделия имеется возможность оценить спектр собственных частот конструкции, то можно со значительной долей вероятности прогнозировать риск возникновения резонансов в известном диапазоне частот внешних воздействий. Во избежание или для значительного уменьшения вероятности появления резонансов необходимо, чтобы б о льшая часть нижних собственных частот конструкции не лежала в диапазоне частот внешних воздействий. В этом случае можно обойтись без применения специальных виброизолирующих систем. Но для оптимизации спектра собственных частот конструкции прежде всего необходимо оценить эти частоты на этапе проектирования изделия. Именно эту функцию и выполняет модуль частотного анализа системы T-FLEX Анализ. Модуль позволяет на этапе проектирования оценить спектр собственных частот конструкции. Далее разработчик может оптимизировать конструктивные параметры изделия таким образом, чтобы вывести б о льшую часть собственных частот из рабочего диапазона вибровоздействий.

Рассмотрим общий порядок выполнения расчета собственных частот в системе конечно-элементного моделирования T-FLEX Анализ.

Шаг 1. Создание объемной твердотельной модели изделия

Аналогично осуществлению статических расчетов (см. «САПР и графика» № 10’2004) для проведения частотного анализа необходимо иметь трехмерную модель изделия. Как мы уже отмечали, модель может быть построена пользователем в среде трехмерного моделирования T-FLEX CAD 3D или импортирована из другой системы объемного моделирования, поддерживающей для обмена данными о твердотельных моделях форматы STEP, IGES или Parasolid. Рассмотрим в качестве примера использование приложения T-FLEX Анализ для проверки надежности работы вала привода с угловой скоростью вращения до 900 об./мин (рис. 2). Для этого осуществим частотный анализ конструкции. Если собственные частоты вала не попадут в рабочий диапазон частот вращения, обеспечиваемый приводом, то можно быть уверенным в отсутствии резонансных явлений в работе механизма. Конструкция, на примере которой мы иллюстрируем работу с модулем частотного анализа, представляет собой сборочную трехмерную модель и состоит из нескольких отдельных твердотельных деталей. Для осуществления конечно-элементного анализа необходимо предварительно осуществить объединение всех деталей в одно тело с помощью команды T-FLEX CAD 3D «Булева операция/Сложение» (рис. 3).

Шаг 2. Создание «Задачи»

После того как трехмерная модель изделия была создана или импортирована в систему T-FLEX CAD 3D, можно приступать непо­средственно к конечно-элементному моделированию. Любой расчет в T-FLEX Анализе начинается с создания «Задачи» с помощью команды «Новая задача» меню «Анализ» T-FLEX CAD (рис. 4). При создании задачи определим ее тип: «Частотный анализ».

Шаг 3. Задание материала

По умолчанию в расчете используются характеристики материала «С операции». В стандартной версии T-FLEX CAD 3D поставляется библиотека конструкционных материалов, которые могут быть назначены операциям твердотельного моделирования, причем пользователь может пополнять стандарт­ную базу материалов другими материалами. Кроме того, в составе системы T-FLEX Анализ есть собственная независимая база материалов, которую также можно использовать для задания физико-механических свойств анализируемого изделия. Выберем для нашей конструкции материал «Сталь» из стандартной библиотеки материалов T-FLEX CAD 3D (рис. 5).

Шаг 4. Генерация конечно-элементной сетки

Как говорилось в нашей предыдущей статье, посвященной системе T-FLEX Анализ, для осуществления конечно-элементного моделирования необходимо построение расчетной сетки из тетраэдральных элементов. Команда построения такой сетки (которая так и называется — «Сетка») инициируется автоматически при создании «Задачи» или может быть вызвана пользователем из меню «Анализ» T-FLEX CAD. При создании сетки пользователь определяет степень дискретизации твердотельной модели, указывая в параметрах ориентировочный размер конечных элементов (тетраэдров), при помощи которых будет описана математическая модель моделируемого изделия. Здесь необходимо отметить следующие моменты. Конечно-элементная сетка может существенным образом влиять на качество получаемых решений в случае сложной пространственной конфигурации изделий. Как правило, более мелкое разбиение обеспечивает лучшие по точности результаты. Однако аппроксимация модели большим количеством малых тетраэдров приводит к системе алгебраических уравнений большого порядка, что может негативно сказаться на скорости выполнения расчета. Вообще, оценить качество конечно-элементной модели можно последовательным решением нескольких задач с различными возрастающими степенями дискретизации. Если результаты решения (собственные частоты) перестают заметно меняться при использовании более густой сетки, то можно со значительной долей уверенности считать, что достигнут определенный оптимальный уровень дискретизации и что дальнейшее увеличение дискретизации сетки нерационально.

Создадим конечно-элементную сетку для нашей конструкции (рис. 6).

Шаг 5. Наложение граничных условий. Задание закреплений

Для успешного решения физической задачи в конечно-элементной постановке помимо создания конечно-элементной сетки необходимо корректно определить так называемые граничные условия. В частотном анализе их роль выполняют закрепления. Этап задания граничных условий — очень ответственный и требующий хорошего понимания расчетчиком сути решаемой задачи. Поэтому, прежде чем приступить к наложению граничных условий, следует хорошо продумать физическую сторону задачи. Для задания закреплений в T-FLEX Анализ предусмотрены две команды: «Полное закрепление» и «Частичное закрепление». Команда «Полное закрепление» применяется к вершинам, граням и ребрам модели и определяет, что данный элемент трехмерного тела полностью неподвижен, то есть сохраняет свое первоначальное расположение и не меняет своего положения под действием приложенных к системе нагрузок. Команда «Частичное закрепление» обладает более широкими возможностями: с ее помощью можно ограничить перемещение тела в определенных координатных направлениях или определить заданное положение элементов модели.

Зададим условия закрепления для нашей конструкции. Используя команду «Частичное закрепление», для опорных шеек вала зададим ограничение (нулевые перемещения) по осям Y и Z глобальной системы координат. Кроме того, с помощью той же команды исключим возможность продольного перемещения вала, наложив соответствующее ограничение на торцовую грань (рис. 7). После задания закреплений мы получим готовую для расчета конечно-элементную модель.

Шаг 6. Выполнение расчета

После создания конечно-элемент­ной сетки и наложения граничных условий можно инициировать команду «Расчет» и запустить процесс формирования систем линейных алгебраических уравнений (СЛАУ) и их решения (рис. 8). В свойствах процессора пользователь может определить такие дополнительные свойства, как точность вычислений или количество нижних собственных частот конструкции, подлежащих определению. Известно, что почти вся энергия механических колебаний аккумулируется на нескольких нижних гармониках изделия, поэтому при частотном анализе в первую очередь представляют интерес первые три-пять наименьших собственных частот.

Шаг 7. Анализ результатов расчета

Результатами частотного анализа являются собственные частоты изделия и соответствующие им собственные формы колебаний. Формы колебаний представляют собой относительные ам­плитуды перемещений конструкции в узлах конечно-элементной сетки. По ним можно определить характер движения, осуществляемого системой на частоте колебаний, соответствующей собственной. Анализ результатов осуществляется в модуле постпроцессора системы T-FLEX Анализ. Постпроцессор полностью интегрирован в среду геометрического моделирования T-FLEX CAD 3D и обладает полным набором удобных инструментов по обработке результатов моделирования (анимацией, динамическим зондированием результатов, гибкой настройкой шкалы и т.п. — см. «САПР и графика № 10’2004).

Проанализируем полученные нами результаты. Первые две формы свободных колебаний нашей конструкции соответствуют изгибным колебаниям вала с частотами, превышающими 135 Гц (рис. 9), что, в свою очередь, соответствует угловой скорости вращения, в девять раз превышающей максимальную рабочую для данного привода. Таким образом, согласно проведенному расчету в рабочем диапазоне частот вращения резонансы данному валу не угрожают.

Для лучшего понимания характера динамических процессов целесообразно использовать специальный инструмент анимации результата, который позволяет увидеть и оценить характер движения в реальном масштабе времени.

Помимо интерактивного изучения результатов в постпроцессоре T-FLEX Анализ есть возможность создать независимый электронный документ в html-формате, с эпюрами результатов и сведениями о конечно-элементной модели (рис. 10). Этот электронный документ может быть передан в стороннюю организацию или сохранен для последующего изучения результатов.

Таким образом, система конечно-элементного моделирования T-FLEX Анализ позволяет пользователям популярной российской системы T-FLEX Parametric CAD (www.topsystems.ru) осуществлять расчет собственных частот и форм колебаний конструкций. Применяя этот инструмент, пользователи T-FLEX CAD 3D и T-FLEX Анализ получают возможность значительно улучшить качество разрабатываемых ими изделий.

«САПР и графика» 11’2004

формула индуктивности катушки и резонансной частоты

Любая колебательная система характеризуется собственной частотой. Если на систему периодически воздействовать извне, и частота воздействия будет совпадать с внутренней периодичностью возмущения силового поля материи, то можно наблюдать резкое увеличение амплитуды колебаний. Данное явление является резонансом. Для ремонта и конструирования радиотехнических устройств необходимо уметь производить расчет резонансных частот колебательных контуров.

Что такое колебательный контур

Колебательный контур это несколько элементов в любой электрической цепи, емкость и индуктивность, которых соединены параллельно или последовательно. Для нормального функционирования колебательного контура в цепи необходим источник энергии.



Параллельный контур колебаний

При параллельном или последовательном соединениях элементов, входящих в состав электрической цепи, та или иная замкнутая проводниковая система получает одноимённое название. Явление резонанса в обоих случаях, возникает аналогичным образом, только в случае параллельного колебательного контура этот показатель относится к силе тока, а в случае с последовательным – возникает предельная частотность мгновенного изменения напряжений.

Как работает контур колебаний

Работа контура колебаний основана на циклическом преобразовании энергии индуктивности в качественный показатель эффективности конденсатора и наоборот. Допустим, что конденсатор полностью заряжен и энергия, запасенная в нем, максимальна. При подключении его к катушке индуктивности, он начинает разряжаться. При этом, через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, направленную на уменьшение протекающего тока. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия прибора становится равной нулю, та же величина для катушки максимальна.

Далее, энергия индуктивности снижается, расходуясь на заряд емкости с противоположной полярностью. После уменьшения показателя коэффициента самоиндукции до нуля, на конденсаторе она опять имеет максимальное значение.



Процессы в системе

Важно! В идеальном случае, данный процесс способен протекать бесконечно. В реальных устройствах колебание затухает со скоростью, пропорциональной потерям в цепи проводников.

Вне зависимости от величины энергии, наличия потерь, частота колебаний постоянна и зависит только от значений параметров коэффициента самоиндукции и емкости. Данная величина называется резонансной. Формула резонанса учитывает значение величины емкости и индуктивности контура колебаний.



Осциллограмма

При воздействии на электрическую цепь с катушкой внешним сигналом с частотой, равной резонансной, амплитуда изменения положения частиц резко возрастает. Резонанс отсутствует при несовпадении частот. Из-за предельных значений электрическую цепь с катушкой индуктивности часто называют резонансной.

Потери в цепи с катушкой индуктивности (потери в диэлектрике конденсатора, сопротивление самого устройства, соединительных проводов) ограничивают величину предельных изменений направления частиц. В следствие этого, введена характеристика электроцепи, именуемая добротностью. Добротность обратно пропорциональна предельной величине потерь.



Зависимость предельной частоты от добротности

Важно! Снижение добротности приводит к тому, что предел изменения направлений наступает не только на основной частоте, но и на некотором приближении к ней, то есть, в некоторой полосе частот, где резонансное значение находится посередине. Чем выше добротность, тем более узкой становится полоса частот.

Формула индуктивности

Расчет резонанса колебательного контура производится на основании значений емкости и индуктивности. Как правило, емкость конденсатора является постоянной величиной, за исключением случаев использования переменных устройств в перестраиваемых электроцепях. Коэффициент самоиндукции катушки зависит от многих факторов:

• Количество и расположение витков обмотки;
• Наличие или отсутствие сердечника;
• Материал сердечника.

Общей формулы для определения индуктивности катушки колебательного контура не существует. Для расчетов используют формулы, соответствующие форме катушки. К сожалению, все формулы определения качественной величины электрической цепи с подсоединённой к ней катушкой индуктивности позволяют производить только приблизительные расчеты.



Приборы индуктивности различных типов

Важно! Для того, чтобы получить катушку с заданными параметрами, приходится принимать дополнительные меры, например, производить подстройку коэффициента самоиндукции путем изменения длины сердечника или корректировки расстояния между витками в однорядных катушках.

Формула резонансной частоты

Формула резонансной частоты колебательного контура не зависит от его типа, а также от метода подключения – последовательного или параллельного. Выглядит она следующим образом:

f0=1/(2∙π∙√L∙C),

где f0 – частота резонанса

Как видно из формулы, для получения заданной частоты резонанса, существует бесконечное количество пар емкостей и индуктивностей. На деле, от выбранного соотношения параметров зависит также и добротность.

Как правильно рассчитать частоту контура колебаний

Для последовательного колебательного контура добротность растет с увеличением значения индуктивности. Таким образом, при расчетах элементов, следует учитывать величину добротности. Также, необходимо иметь в виду, что емкости конденсаторов выбираются из стандартного ряда значений, и на этом основании изготавливается катушка индуктивности.

Явление резонанса позволяет использовать колебательные контуры в качестве частотно зависимых цепей и в элементах фильтров. Радиоприемные устройства наиболее широко используют избирательные свойства колебательных систем. Если вместо емкости использовать кварцевый резонатор, то можно получить электрическую цепь с катушкой индуктивности, обладающей очень высокой добротностью. Такие схемы широко используются в задающих генераторах, где требуется высокая точность для определения периода изменения направления частиц.

Собственная резонансная частота — Большая Энциклопедия Нефти и Газа, статья, страница 1

Собственная резонансная частота

Cтраница 1

Собственная резонансная частота каждого кристаллита определяется моментом, который действует на его намагниченность и складывается из момента, обусловленного приложенным магнитным полем, и момента, обусловленного эффективным полем анизотропии. Если частота поддерживается постоянной, то резонансные значения поля в различных кристаллитах будут, вообще говоря, различными.  [1]

Собственная резонансная частота тела, головы и органов брюшной полости лежит в пределах 6 — 9 гц. Предельная амплитуда вибрации, выносимая человеком, в зависимости от частоты, колеблется от 0 01 до 0 06 мм.  [3]

Собственная резонансная частота полых резонаторов определяется их формой, геометрическими размерами и способом возбуждения колебаний. Например, полый резонатор при частоте колебаний 1 МГц ( К 300 м) должен бы иметь длину и ширину несколько десятков метров. При частотах выше 1000 МГц размеры полых резонаторов характеризуются величинами в несколько сантиметров.  [4]

Собственная резонансная частота объемных резонаторов определяется их формой, геометрическими размерами и способам возбуждения колебаний. Объемный резонатор можно настраивать, изменяя его объем. Подстройка резонаторов в узких пределах осуществляется введением в полость резонатора металлического стержня, который изменяет распределение электрического поля, вследствие чего изменяется частота колебаний.  [5]

Обычно собственная резонансная частота приборов может иметь значения в широком диапазоне, но лежит в основном в пределах 30 — 100 Мгц ( см. гл. В связи с этим значительные погрешности, обусловленные рассматриваемыми причинами, возникают на очень высоких частотах. Для повышения резонансной частоты следует стремиться к обеспечению минимальных значений собственной емкости и индуктивности прибора.  [6]

Собственная резонансная частота язычка вибратора при отрегулированной контактной системе равна примерно 70 гц. При этом при рабочей частоте 50 гц амплитуда колебаний язычка достаточно велика и вместе с тем мало зависит от незначительных изменений резонансной частоты. Вообще же вибратор может работать на различных частотах — от самых низких до нескольких сотен герц. Однако для каждой частоты нужно выбирать соответствующее напряжение возбуждения.  [7]

Собственная резонансная частота отдельных элементов лампы может быть определена также расчетным путем, однако этот метод является значительно более трудоемким чем экспериментальный.  [8]

Собственную резонансную частоту аппаратов приходится учитывать потому, что в некоторых районах аппаратура может подвергнуться колебаниям, вызванным тектонической деятельностью. Кроме того, колебания весьма низкой частоты могут возникнуть в результате разнести частот колебаний машин или механизмов.  [9]

Изменение собственной резонансной частоты при длительной, работе может быть обусловлено старением кварца. Уход частоты вследствие старения у разных типов кварцевых резонаторов лежит в пределах от ( 1 2) 10 — до ( 100 — 150) 10 в за первый год работы.  [11]

Последова

Вынужденные колебания. Резонанс

Вынужденные колебания

В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из состояния равновесия), в случае вынужденных колебаний система поглощает эту энергию от источника внешней периодической силы непрерывно. Эта энергия восполняет потери, расходуемые на преодоление трения, и потому полная энергия колебательной системы no-прежнему остается неизменной.

Вынужденные колебания в отличие от свободных могут происходить с любой частотой. Частота вынужденных колебаний совпадает с частотой внешней силы, действующей на колебательную систему. Таким образом, частота вынужденных колебаний определяется не свойствами самой системы, а частотой внешнего воздействия.

Примерами вынужденных колебаний являются колебания детских качелей, колебания иглы в швейной машине, поршня в цилиндре автомобильного двигателя, рессор автомобиля, движущегося по неровной дороге и т.д.

Резонанс

Резонанс возникает из-за того, что при внешняя сила, действуя в такт со свободными колебаниями, все время имеет одинаковое направление со скоростью колеблющегося тела и совершает положительную работу: энергия колеблющегося тела увеличивается, и амплитуда его колебаний становится большой. Если же внешняя сила действует «не в такт», то эта силы попеременно совершает то отрицательную, то положительную работу и вследствие этого энергия системы меняется незначительно.

На рис.1 показана зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы. Видно, что эта амплитуда достигает максимума при определенном значении частоты, т.е. при , где собственная частота колебательной системы. Кривые 1 и 2 отличаются величиной силы трения. При малом трении (кривая 1) резонансная кривая имеет резкий максимум, при большей силе трения (кривая 2) такого резкого максимума нет.

Рис.1. Резонансные кривые для различных значений силы трения.

С явлением резонанса мы часто встречаемся в повседневной жизни. Если в комнате задрожали стекла при прохождении по улице тяжелого грузовика, это значит, что собственная частота колебаний стекол равна частоте колебаний машины. Если морские волны попадают в резонанс с периодом корабля, то качка становится особенно сильной.

Явление резонанса необходимо учитывать при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены. Однако резонанс также может быть полезен. Явление резонанса используется при настройке радиоприемника на определенную частоту радиовещания, а также во многих других случаях.

Примеры решения задач

Резонансная частота Википедия

Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания Раскачивание человека на качелях — типичный пример резонанса. Нагруженное колебание, маятник, имеет собственную частоту колебаний, свою резонансную частоту и сопротивляется давлению с большей или меньшей скоростью.

Резона́нс (фр. resonance, от лат. resono «откликаюсь») — частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы^[1]. Для линейных колебательных систем значения частот резонанса совпадает с частотами собственных колебаний, а их число соответствует числу степеней свободы^[1].

Под действием резонанса, колебательная система оказывается особенно отзывчивой на действие внешней силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

Явление резонанса впервые было описано Галилео Галилеем в 1602 г. в работах, посвященных исследованию маятников и музыкальных струн.^[2][3]

Механика

Школьный резонансный массовый эксперимент

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если подталкивать качели в определённые моменты времени в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния можно найти по формуле:

f=12πgL{\displaystyle f={1 \over 2\pi }{\sqrt {g \over L}}},

где g — это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна и включает эллиптический интеграл.) Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут приводить как к разрушению, так и к усилению устойчивости механических систем.

В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую и наоборот. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины, массы и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, её частота зависит от скорости v, с которой волна распространяется по струне:

f=v2L{\displaystyle f={v \over 2L}}

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

v=Tρ{\displaystyle v={\sqrt {T \over \rho }}}

Таким образом, частота главного резонанса может зависеть от свойств струны и выражается следующим отношением:

f=Tρ2L=Tm/L2L=T4mL{\displaystyle f={{\sqrt {T \over \rho }} \over 2L}={{\sqrt {T \over m/L}} \over 2L}={\sqrt {T \over 4mL}}},

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f^[4], и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Электроника

В электрических цепях резонансом называется такой режим пассивной цепи, содержащий катушки индуктивности и конденсаторы, при котором ее входное реактивное сопротивление или ее входная реактивная проводимость равны нулю. При резонансе ток на входе цепи, если он отличен от нуля, совпадает по фазе с напряжением.

В электрических цепях резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно (тогда возникает резонанс напряжений), так и параллельно (резонанс токов). При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

ωL=1ωC⇒ω=1LC{\displaystyle \omega L={\frac {1}{\omega C}}\Rightarrow \omega ={\frac {1}{\sqrt {LC}}}},

где ω=2πf{\displaystyle \omega =2\pi f} ; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.

В электронных устройствах также применяются различные электромеханические резонансные системы.

СВЧ

В СВЧ электронике широко используются объёмные резонаторы, чаще всего цилиндрической или тороидальной геометрии с размерами порядка длины волны, в которых возможны добротные колебания электромагнитного поля на отдельных частотах, определяемых граничными условиями. Наивысшей добротностью обладают сверхпроводящие резонаторы, стенки которых изготовлены из сверхпроводника и диэлектрические резонаторы с модами шепчущей галереи.

Оптика

В оптическом диапазоне самым распространенным типом резонатора является резонатор Фабри-Перо, образованный парой зеркал, между которыми в резонансе устанавливается стоячая волна. Применяются также кольцевые резонаторы с бегущей волной и оптические микрорезонаторы с модами шепчущей галереи.

Акустика

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, корпус у барабанов.

Для акустических систем и громкоговорителей резонанс отдельных элементов (корпуса, диффузора) является нежелательным явлением, так как ухудшает равномерность амплитудно-частотной характеристики устройства и верность звуковоспроизведения. Исключением являются акустические системы с фазоинвертором, в которых намеренно создаётся резонанс для улучшения воспроизведения низких частот.

Астрофизика

Орбитальный резонанс в небесной механике — это ситуация, при которой два (или более) небесных тела имеют периоды обращения, которые относятся как небольшие натуральные числа. В результате эти небесные тела оказывают регулярное гравитационное влияние друг на друга, которое может стабилизировать их орбиты.

См. также

Видеоурок: резонанс

Примечания

Литература

• Richardson LF (1922), Weather prediction by numerical process, Cambridge.
• Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457—472.
• Бломберген Н. Нелинейная оптика, М.: Мир, 1965. — 424 с.
• Захаров В. Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431—453.
• Арнольд В. И. Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны / Ред. А. В. Гапонов-Грехов. — М.: Наука, 1979. С. 116—131.
• Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275—309.
• Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
• Филлипс O.М. Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. — М.: Мир, 1984. — С. 297—314.
• Журавлёв В. Ф., Климов Д. М. Прикладные методы в теории колебаний. — М.: Наука, 1988.
• Сухоруков А. П.. Нелинейные волновые взаимодействия в оптике и радиофизике. — Москва: Наука, 1988. — 230 с. — ISBN 5-02-013842-8.
• Брюно А. Д. Ограниченная задача трёх тел. — М.: Наука, 1990.
• Широносов В. Г. Резонанс в физике, химии и биологии. — Ижевск: Издательский дом «Удмуртский университет», 2000. — 92 с.
• Резонанс // Музыкальная энциклопедия. — М.: Советская энциклопедия, 1978. — Т. 4. — С. 585—586. — 976 с.

Ссылки