Скалярное, векторное и смешанное произведения векторов

1. Скалярное произведение векторов.

Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними:

ab = |a||b|cos (5.1)

Скалярное произведение коммутативно и удовлетворяет свойству линейности по каждому из сомножителей.

Из определения скалярного произведения следует часто применяющаяся формула для вычисления длины вектора:

(5.2)

Пусть теперь векторы а и b заданы своими координатами: аи b. Скалярное произведение векторов равно сумме произведений соответствующих координат этих векторов:

ab = (5.

3)

В качестве следствия из этой теоремы получаем формулу для вычисления косинуса угла между векторамиa и b:

(5.4)

2. Векторное произведение векторов.

Упорядоченная тройка некомпланарных векторов (а, b, c), приведенных к общему началу, называется правой, если, находясь внутри трехгранного угла, образованного этими векторами, поворот от а к b, от b к с, от с к а виден против часовой стрелки (рис. 5.1). В противном случае тройка векторов называется левой (рис. 5.2).

правая тройка левая тройка

Рис. 5.1 Рис. 5.2

Векторным произведением векторов а и b называется вектор с, удовлетворяющий условиям:

1. |c| = |a||b| sin , где  – угол между векторами а и b;

2. вектор с перпендикулярен векторам а и b;

3. тройка векторов (а,

   b, c) является правой.

Мы будем обозначать векторное произведение следующим образом: с = а  b.

Свойства векторного произведения.

1. Векторы а и b коллинеарны тогда и только тогда, когда а  b = 0, в частности, а  а = 0.

2. Если векторы а и b привести к общему началу, то длина их векторного произведения |

   а  b| будет равна площади S параллелограмма, построенного на векторах а и b (см. рис. 5.3) (геометрический смысл векторного произведения).

Рис. 5.3

3. Свойство антикоммутативности: а  b = – b  a.

4. Числовой множитель можно выносить за знак векторного произведения:

а  b = (а  b), а  b = (а  b).

5. Свойство дистрибутивности:

(a + b)  c = a  c + b  c, a  (b + c) = a  b + a  c.

Если известны координаты векторов аи b, то векторное произведение вычисляется по формуле:

a

 b = (5.5)

Для координатной записи векторного произведения удобно использовать символы определителя 2-го и 3-го порядков:

a  b =(5. 6)

или

a  b = (5.7)

3. Смешанное произведение векторов.

Смешанным произведением трех векторов a, b и с называется скаляр (а  b)c

.

Геометрический смысл смешанного произведения: смешанное произведение (а  b)c трех некомпланарных векторов равно объему параллелепипеда, построенного на векторах a, b и с, приведенных к общему началу, и взятому со знаком «+», если тройка (a, b, с) правая, и со знаком «–», если тройка (a, b, с) левая.

В связи с этим смешанное произведение принято обозначать abс = (а  b)c =

a(b  c).

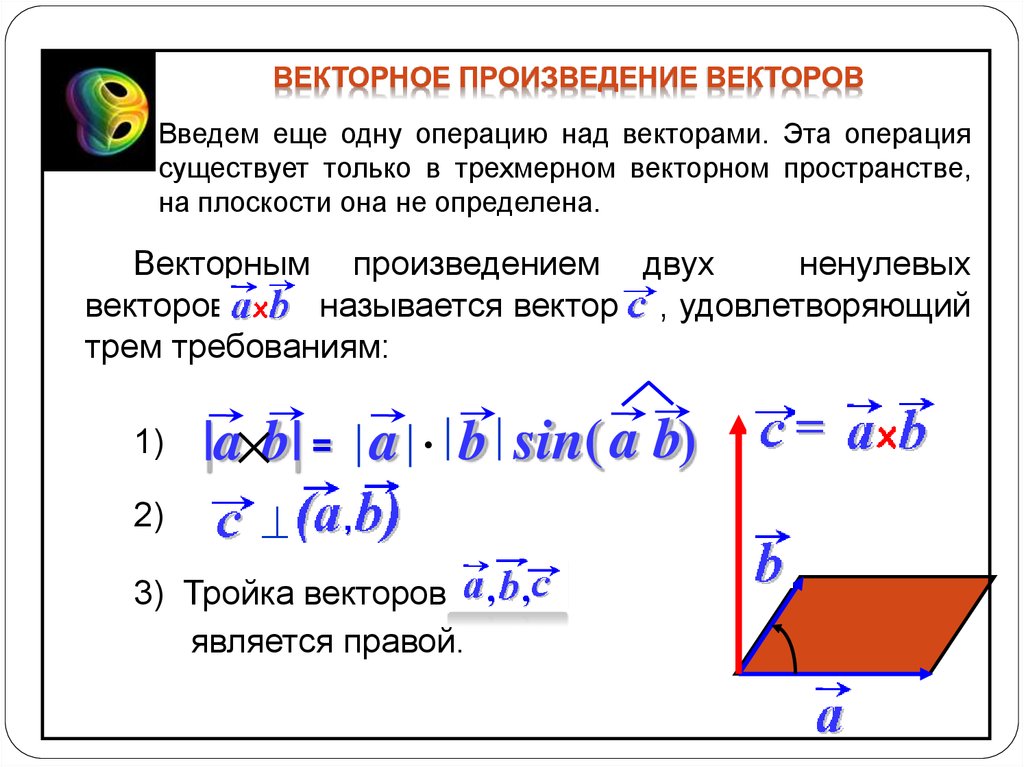
Заметим, что тройка векторов меняет свою ориентацию (т.е. будучи левой становится правой, и наоборот), если в ней переставляются любые два вектора. Поэтому справедливы равенства: abс = – baс = – сbа = –acb.

Если три вектора определены своими координатами: а, bи с, то смешанное произведение вычисляется по формуле:

 abс = (5.8)

Используя смешанное произведение, можно сформулировать простое и удобное условие компланарности трех векторов: три вектора a, b и с компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Следовательно, три вектора a, b и с компланарны тогда и только тогда, когда определитель, составленный из их координат, равен нулю:

 = 0  (5.

9)

Высшая математика Т1

Высшая математика Т1

Высшая математика: Учеб. для вузов: В 3 т. / Я. С. Бугров, С. М. Никольский; Под ред. В. А. Садовничего. — 6-е изд., стереотип. — М.: Дрофа, 2004. — (Высшее образование: Современный учебник). Т.1: Элементы линейной алгебры и аналитической геометрии. — 288 c. Учебник (1-е изд. — 1980 г.) вместе с другими учебниками тех же авторов — «Дифференциальное и интегральное исчисление» (том 2) и «Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного» (том 3) — соответствует требованиям Государственного образовательного стандарта высшего профессионального образования. В книге содержатся основные сведения по теории определителей и матриц, линейных систем уравнений, а также элементы векторной алгебры. Рассматриваются основные вопросы линейной алгебры: линейные операторы, самосопряженные операторы, квадратичные формы, линейное программирование. Включены элементы аналитической геометрии на плоскости и в пространстве. Для студентов инженерно-технических специальностей вузов. Оглавление ПРЕДИСЛОВИЕ § 1. Определители второго порядка 2.1. Определители третьего порядка. 2.2. Определители  n-го порядка. §3. Матрицы 4.1 Система из n линейных уравнений с n неизвестными. 4.2. Формула Крамера 4.3. Однородная система 4.4 Правило решения системы линейных уравнений Системы линейных уравнений: 4.5 Примеры приложения правил Системы линейных уравнений: 4.6 Обоснование правил 4.7. Метод решения системы путем исключения неизвестных 4.8. Нахождение ранга матрицы 5.1. Понятие вектора 5.2. Проекция вектора 5.3. Свойства проекций векторов 5.4 Скалярное произведение векторов 5. 5. Прямоугольная система координат 6.1. n-мерное пространство 6.2 Скалярное произведение в действительном пространстве 6.3 Скалярное произведение в комплексном пространстве 6.4. Неравенства Буняковского 6.5. Неравенство Минковского § 7. Отрезок. Деление отрезка в данном отношении § 8. Прямая линия 9.1. Уравнение плоскости в нормальном виде 9.2. Уравнение плоскости в общем виде 9.3. Уравнение плоскости в отрезках 9.4. Уравнение плоскости, роходящей через точку 9.5. Уравнение плоскости, проходящей через три точки 9.6 Угол между двумя плоскостями 9.7. Расстояние от точки до плоскости 10.1 Уравнение прямой в каноническом виде 10.2 Расположение двух плоскостей 11.1. Двумерная система координат 11.2. Трехмерная система координат 12.1. Два определения векторного произведения 12.2. Геометрический смысл определителя второго порядка 12.3. Свойства векторного произведения § 13. Смешанное (векторно-скалярное) произведение § 14. Линейно независимая система векторов § 15. Линейные операторы § 16. Базисы в Rn § 17. Ортогональные базисы в Rn § 18. Инвариантные свойства скалярного и векторного произведений § 19. Преобразование прямоугольных координат в плоскости § 20. Линейные подпространства в Rn § 21. Теоремы фредгольмова типа § 22. Самосопряженный оператор. Квадратичная форма § 23. Квадратичная форма в двухмерном  пространстве § 24. Кривая второго порядка Эллипс Гипербола Парабола 24.3 Классификация кривых второго порядка § 25. Поверхность второго порядка в трехмерном пространстве Эллипсоид Однополостный гиперболоид Двуполостный гиперболоид Эллиптический и гиперболический параболоиды Конус второго порядка Цилиндры второго порядка Линейчатые поверхности § 26. Общая теория поверхности второго порядка в трехмерном пространстве § 27. Плоскость в Rn. Общие положения 27.2. Плоскость в Rn 27.3. Уравнение плоскости в нормальном виде 27. 4. Уравнение плоскости в векторной форме 27.5. Геометрическая интерпретация уравнений 27.6. Уравнение плоскости, проходящей через n точек 27.7. Условия ортогональности и параллельности плоскостей 27.8. Уравнение плоскости, проходящей через точку 27.9. Прямая в пространстве Rn 27.10. Расположение (n-1) плоскостей 27.11. Расстояние от точки до плоскости 27.12. Различные задачи § 28. Линейное программирование 28.2. Транспортная задача 28.3.Общая задача линейного программирования 28.4. Векторно-матричная форма задачи линейного программирования 28.5. Симплекс-метод 28.7. Выбор разрешающего элемента 28.8. Условия существования базиса

\to } \right)\)

Сначала найдите векторное произведение.

Чтобы сделать это легко, напишите оба вектора горизонтально и найдите определитель 2×2, закрывая рукой столбец, который вы хотите найти.

По сути, у вас есть два вектора 1×3 (строка x столбец), результат также будет 1×3.

Мы покажем это ниже. Обратите внимание, что «i», «j» и «k» просто представляют первое, второе и третье измерения/компоненты, i НЕ является мнимым числом здесь !

\[\begin{array}{*{20}{c}}i&j&k\\2&1&0\\1&1&{ – 1}\end{массив}\]

Нам нужно v x w, поэтому мы пишем сначала v, а затем w.

Чтобы получить первый компонент, положите руку на первый столбец, затем найдите определитель 2×2, который представляет собой просто произведение диагонали минус произведение другой диагонали.

Первый компонент равен (2)(0) – (1)(1) = -1

Теперь положите руку на второй столбец и найдите определитель 2×2, НО вам нужно добавить знак минус к вашему ответу.

Это из-за матрицы кофакторов, которую вы можете записать, но в основном средний определитель должен быть отрицательным. Второй компонент равен -[(2)(0) – (1)(1)] = 1 9\to } \right) = 0\]

Таким образом, тройное произведение равно 0.

Вы можете перепроверить свои результаты с помощью программы MATLAB, которая специализируется на использовании массивов (векторов и матриц), используйте следующий скрипт кода m-файл и не стесняйтесь заменять числа числами для ваших векторов, чтобы найти тройной продукт:

 %bai-gaming. com/math-guides
и = [1;0;1]
v = [2;1;0]
ш = [1;1;-1]
dot(u,(cross(v,w))) 

И вы также получите результат 0 в MATLAB! Хороший!

Нажмите здесь, чтобы увидеть еще одну более сложную задачу , в которой мы находим тройное произведение !

Нажмите здесь, чтобы вернуться на главную страницу Math Guides

Скалярное тройное произведение: примеры и свойства

К настоящему моменту вы, вероятно, столкнулись с большим количеством векторного материала и задались вопросом, как теоретические принципы, такие как умножение точек, соотносятся с реальной жизнью. Вот тут-то и появляется скалярный тройной продукт . Этот продукт обеспечивает простой способ нахождения объемов некоторых сложных форм с помощью комбинации ранее рассмотренных теоретических принципов.

Эта статья покажет, как мы можем взять векторы и применить их к физическому контексту.

Скалярное тройное произведение Значение

Скалярное тройное произведение — это принцип, который мы используем для нахождения объема параллелепипеда — шестигранной фигуры, каждая сторона которой является параллелограммом или тетраэдром.

Скалярное тройное произведение на самом деле включает в себя две ранее замеченные векторные операции — точечное и перекрестное умножение.

Взаимное умножение двух векторов даст векторную величину, но последующее точечное умножение для нахождения скалярного произведения приведет к уменьшению векторов до скалярного значения.

Вот как мы можем вычислить объем фигур, названных выше, из трех векторов — мы получаем одно число в конце процесса.

Вы можете вспомнить определение векторной величины следующим образом.

Векторная величина представлена ​​в терминах \(x,y,z\) и, как таковая, имеет три компонента. Векторы также имеют определенную величину и направление .

Определение скалярной величины следующее.

Скалярная величина — это сингулярное значение, которое имеет только величину. У него нет направления.

Скалярное тройное произведение векторов

Мы знаем, что векторы могут использоваться для описания движения и обычно имеют форму движения в направлениях \(x,\, y,\, z\).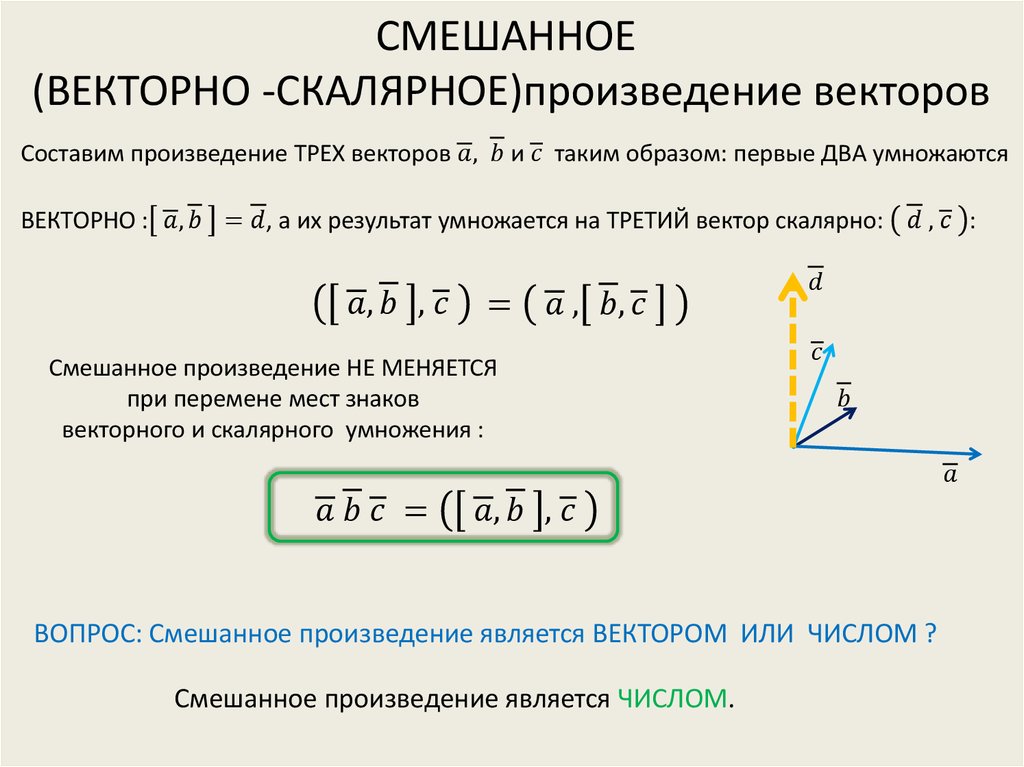 В векторной форме они становятся \(\vec{i},\, \vec{j},\, \vec{k}\) соответственно, и с помощью этих обозначений мы можем выполнять множество операций над векторами.

Чтобы найти скалярное тройное произведение трех векторов, вы должны быть знакомы с принципом скалярного произведения и перекрестного произведения и с тем, как они работают. Если вы этого не сделаете, вы можете проверить наши статьи о скалярных произведениях и векторных произведениях соответственно для освежения знаний.

Скалярное тройное произведение находит скалярное произведение вектора на векторное произведение двух векторов. Это более сложная методология, чем скалярное произведение двух, но она полезна при нахождении объемов определенных форм.

Сначала находим векторное произведение первых двух векторов. Это приведет к одному вектору, который будет использоваться в скалярном произведении с третьим вектором. И это приведет к скалярному значению.

Скалярная формула тройного произведения

Рассмотрим три вектора \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\), где \[\vec{a}=a_1\vec{i }+a_2\vec{j}+a_3\vec{k},\]\[\vec{b}=b_1\vec{i}+b_2\vec{j}+b_3\vec{k},\] и \[\vec{c}=c_1\vec{i}+c_2\vec{j}+c_3\vec{k}. \] Чтобы найти скалярное тройное произведение этих векторов, мы должны найти векторное произведение двух из них и найдите скалярное произведение этого результата с третьим вектором. В математической записи это выглядит как \[\vec{a}\cdot (\vec{b}\times\vec{c}).\]Это абсолютное значение этой формулы дает нам объем параллелепипеда.

Для объема тетраэдра можно применить следующую формулу: \(\frac{1}{6}\left[|\vec{a}\cdot (\vec{b}\times\vec{c}) |\right]\), когда векторы описывают три некомпланарные стороны фигуры.

Из векторного произведения мы знаем, что перекрестное произведение \(\vec{b}\times \vec{c}\) задается как \[\vec{b}\times \vec{c}=(b_2c_3 -b_3c_2)\vec{i}-(b_1c_3-b_3c_1)\vec{j}+(b_1c_2-b_2c_1)\vec{k}.\]Если мы затем рассмотрим скалярное произведение результата векторного произведения и вектора \ (\vec{a}\) получаем формулу скалярного тройного произведения,\[\vec{a}\cdot (\vec{b}\times\vec{c})=a_1(b_2c_3-b_3c_2)+a_2 (b_3c_1-b_1c_3)+a_3(b_1c_2-b_2c_1).\]

Свойства скалярного тройного произведения

Как было сказано ранее, скалярное тройное произведение используется для нахождения объема параллелепипеда, но что это на самом деле означает?

Если мы рассматриваем векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) как три непараллельные стороны параллелепипеда, мы можем провести скалярная формула тройного произведения, чтобы получить результат для объема формы.

Когда мы пытаемся найти объем фигур, порядок применения этих векторов не имеет значения, пока процесс цикличен. Это означает: \[\vec{a}\cdot (\vec{b}\times\vec{c})=\vec{b}\cdot (\vec{c}\times\vec{a})=\ vec{c}\cdot (\vec{a}\times\vec{b}).\]

Давайте рассмотрим пример.

Показать, что \(\vec{a}\cdot (\vec{b}\times\vec{c})=\vec{b}\cdot (\vec{c}\times\vec{a})\ ), используя приведенные ниже векторы,

\[\vec{a}=5\vec{i}+2\vec{j}+6\vec{k},\]\[\vec{b}=-2\ vec{i}+17\vec{j}+1\vec{k},\] и \[\vec{c}=8\vec{i}-5\vec{j}+13\vec{k} .\]

Решение

Используя нашу общую формулу для \(\vec{a}\cdot (\vec{b}\times\vec{c})\),

\[\begin{align} \vec{a}\cdot (\vec{b}\times\vec{c})&=a_1(b_2c_3-b_3c_2)+a_2(b_3c_1-b_1c_3)+a_3(b_1c_2-b_2c_1)\\&=5[( 17\cdot13)-(1\cdot-5)]+2[(1\cdot8)-(-2\cdot13)]\\ & \qquad +6[(-2\cdot-5)-(17\cdot8 )]\\&=5(226)+2(34)+6(-126)\\&=1130+68-756\\&=442.\end{align}\]

Затем мы можем снова использовать общую формулу для \(\vec{b}\cdot (\vec{c}\times\vec{a})\), где мы сдвигаем буквы — там, где были \(a’s\ ) теперь будут \(b’s\), \(b’s\) будут заменены на \(c’s\) и \(c’s\) заменены на \(a’s\). Это будет иметь вид \[\begin{align}\vec{b}\cdot (\vec{c}\times\vec{a})&=b_1(c_2a_3-c_3a_2)+b_2(c_3a_1-c_1a_3)+ b_3(c_1a_2-c_2a_1)\\&=-2[(-5\cdot6)-(13\cdot2)]+17[(13\cdot5)-(8\cdot6)]\\& \qquad+1[( 8\cdot2)-(-5\cdot5)]\\&=-2(-56)+17(17)+1(41)\\&=112+289+41\\&=442.\end{align}\]

Как видите, числа в процессе меняются, но поскольку процесс цикличен, конечный результат один и тот же.

Таким образом, \[\vec{a}\cdot (\vec{b}\times\vec{c})=\vec{b}\cdot (\vec{c}\times\vec{a}). \]

Существует еще одно свойство скалярного тройного произведения, которое еще не обсуждалось. Давайте объединим наши три вектора в матрицу \(3\times 3\),\[\begin{bmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\ \c_1&c_2&c_3\end{bmatrix}\]

Если вы расширите приведенную выше матрицу, вы должны получить скалярное тройное произведение. Посмотрим как!

\[\begin{align} \begin{bmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{bmatrix} &=a_1(b_2c_3-b_3c_2)+a_2(b_3c_1-b_1c_3)+a_3(b_1c_1-b_2) &=\vec{a}\cdot (\vec{b}\times\vec{c}) \end{align}\]

Скалярное тройное произведение совпадает с определителем этой матрицы. Чтобы узнать, почему это так, см. нашу статью о детерминантах матрицы.

Ключевым моментом здесь является то, что миноры и разложение определителя матрицы \(3\times 3\) отражают формулу скалярного тройного произведения, так что это может быть более простым способом запомнить процесс для вас.

Давайте рассмотрим пример нахождения скалярного тройного произведения путем расширения определителя.

Найдите объем параллелепипеда, образованного смежными ребрами, заданными векторами \[\vec{a}=3\vec{i}-1\vec{j}-2\vec{k},\]\[ \vec{b}=\vec{i}+3\vec{j}-2\vec{k},\] и \[\vec{c}=6\vec{i}-2\vec{j} +\vec{k}.\] 93\).

Обратите внимание, что даже если вы получите отрицательный определитель, вам нужно взять модуль скалярного тройного произведения, чтобы получить объем.

Кроме того, есть много других свойств скалярных тройных произведений, которые выходят за рамки дополнительной математики.

1. Скалярное тройное произведение не изменится, если мы поменяем местами операции, не меняя положения векторов. \[\vec{a}\cdot (\vec{b}\times\vec{c})=(\vec{a}\times \vec{b})\cdot\vec{c}.\]
2. Скалярное тройное произведение инвертируется, если поменять местами любые два из трех заданных векторов. \[\vec{a}\cdot (\vec{b}\times\vec{c})=-\vec{a}\cdot (\vec{c}\times\vec{b}).\]
3. Скалярное тройное произведение равно нулю, если любой из трех заданных векторов компланарен, и наоборот.

Пример скалярного тройного произведения

Давайте начнем с примера, где нам нужно найти объем параллелепипеда.

Найдите объем параллелепипеда с тремя непараллельными сторонами, описанными векторами \[\vec{a}=2\vec{i}+1\vec{j}-1\vec{k},\] \[\vec{b}=-5\vec{i}+14\vec{j}-7\vec{k},\] и \[\vec{c}=16\vec{i}-3\ vec{j}+12\vec{k}.\] 93.\end{align}\]

Давайте теперь рассмотрим пример, где нам нужно найти объем тетраэдра.

Найдите объем тетраэдра с тремя некомпланарными сторонами, описанными векторами \[\vec{a}=-4\vec{i}+12\vec{j}+2\vec{k},\ ]\[\vec{b}=3\vec{i}+1\vec{j}-1\vec{k},\] и \[\vec{c}=4\vec{i}+3\ vec{j}+2\vec{k}.