Сложные сигналы
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
«Санкт-Петербургский государственный университет
аэрокосмического приборостроения»
Учебно-методическое пособие
Санкт – Петербург
2010
Составители: доцент, канд. техн. наук
П.В. Маковецкий
профессор, докт. техн. наук А.Г. Охонский
доцент, канд. техн. наук С.С. Поддубный
Учебно-методическое пособие содержит краткие сведения о сложных сигналах, принципах их формирования и обработки.
Предназначено для студентов, изучающих радиотехнические дисциплины. Подготовлено к публикации кафедрой бортовой радиоэлектронной аппаратуры по рекомендации Методической комиссии факультета радиотехники, электроники и связи Санкт-Петербургского государственного университета аэрокосмического приборостроения.
СОДЕРЖАНИЕ
1. Методические указания при подготовке к работе 4
2. Основные сведения из теории сигналов 4
2.1. Простые и сложные сигналы. Виды сложных сигналов 4
2.2. Недостатки простых сигналов 6
2.3. Сложные сигналы как средство преодоления противоречий простых сигналов. 14
2.4. Корреляционная функция сигнала. Коррелятор 17
2.5. Согласованный фильтр 21
2.6. Коэффициент сжатия сложных сигналов 26
2.7. Функция неопределённости и её основные свойства. 27
3. Методические указания при подготовке к зачету 29
3.1. Понятие функции неопределённости 29
3.2. Связь функция неопредёленности с выходным эффектом приёмника 31
3.3. Графическое представление функции неопределённости 33
3.4. Связь функции неопределенности с точностью оценки параметров сигналов, характеристиками обнаружения и разрешения [1] 34
3.5. Функция неопределённости простого сигнала с гауссовой огибающей 38
3.6. Оценка потенциальной разрешающей способности 39
3.7. Сложный сигнал с линейной частотной модуляцией 41
4. Методика вычисления корреляционной функции последовательностей максимального периода на ЦВМ 61
5. Порядок выполнения и интерфейс программы к лабораторной работе 62
6. Содержание и порядок оформления отчета 64
7. Контрольные вопросы 64
8. Дополнительные вопросы для автотестирования. 65
Рекомендуемая литература 68
Цель работы: изучение сложных сигналов, их назначения, принципов формирования и обработки.
1. Методические указания при подготовке к работе
Перед выполнением лабораторной работы студенты должны получить зачёт по коллоквиуму. При подготовке к коллоквиуму необходимо ознакомиться со вторым разделом настоящей методической разработки.
2. Основные сведения из теории сигналов
В этом разделе даются основные сведения из теории сигналов, такие как деление сигналов на простые и сложные, разрешающая способность сигналов по дальности и скорости и их зависимость от вида сигнала, корреляционная функция сигнала, функция и тело неопределенности сигнала.
2.1. Простые и сложные сигналы. Виды сложных сигналов
Модель применяемого в радиолокации радиосигнала U(t) записывается
U(t)=A(t) · cos [2π f0t+(
0 ≤ t ≤ τи
где A(t) и (t) – функции амплитудной и фазовой модуляции, φ0 – начальная фаза, τи – длительность сигнала, f0 – частота заполнения – несущая частота, 2π f0 = ω – круговая частота.
Сигналы принято разделять на простые и сложные.
Простым сигналом называется сигнал, у которого отсутствует внутриимпульсная модуляция (t) = 0. Для простых сигналов произведение эффективной длительности э на эффективную ширину спектра fэ, называемое базой сигнала, равно единице
d=э · f =1. (1)
Простой сигнал U(t) с прямоугольной огибающей A(t) приведён на рис.1, а.
Сложным называется сигнал, у которого имеется внутриимпульсная модуляция – (t) ≠ 0. База сложных сигналов больше единицы (обычно много больше единицы)
d =э · fэ >> 1. (2)
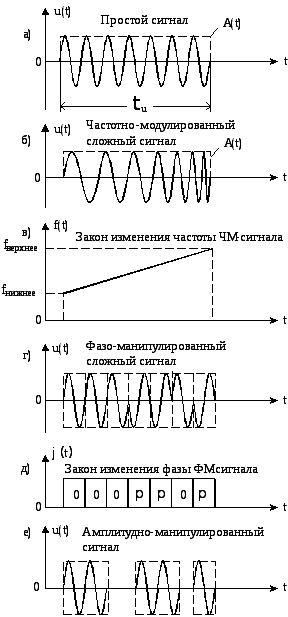
Рис. 1.
Значения э и fэ обычно незначительно отличаются от длительности сигнала u и ширины его спектра f. Поэтому значение
d=э · fэ ≈ u · f.
Увеличение базы у сложных сигналов по сравнению с простыми достигается введением внутриимпульсной модуляции. В зависимости от вида внутриимпульсной модуляции различают следующие виды сложных сигналов:
а) при частотной модуляции – частотно-модулированные (ЧМ) (рис.1, б). На рис. 1, в показан один из возможных законов изменения частоты ЧМ сигнала;
б) при дискретной фазовой модуляции – фазо-манипулированные (ФМ) (рис. 1, г). На рис. 1, д показан закон фазовой манипуляции ФМ сигнала;
в) при амплитудной модуляции – амплитудно-манипулированные (импульсно-кодовая модуляция) (рис. 1, е).
Законы изменения частоты частотно-модулированных сигналов, количество и чередование дискрет фазы у фазо-манипулированных сигналов могут быть различными. Наиболее часто используемыми на практике сложными сигналами являются сигналы с линейной частотной модуляцией (ЛЧМ сигналы) и бинарные, использующие две градации фазы, фазо-манипулированные сигналы.
Кроме перечисленных сложных сигналов возможны и сигналы с комбинациями различных видов модуляции: частотно-фазовой, амплитудно-частотной и амплитудно-фазовой.
2.4. Простые и сложные сигналы.
Простые сигналы. Простой сигнал – это одиночный импульс или последовательность импульсов, вида (2.2).
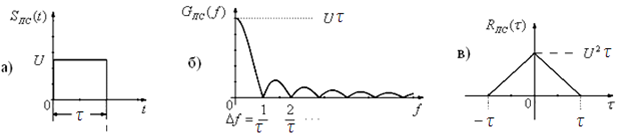
Рис.2.6
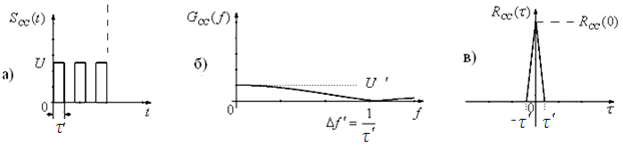
Рис. 2.7
Для одиночного импульса мы будем иметь сплошной спектр (рис. 2.6,б), запись которого имеет вид
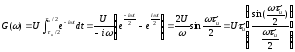
Для последовательности импульсов, или другими словами пачки импульсов — спектр будет иметь дискретный вид.
Размерность
спектра (спектральной плотности) импульса
будет определяться следующим образом 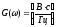
Полоса частот (рис. 2.6,б), где заключено 90% энергии сигнала равна:
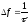 .
.
Корреляционная
функция простого сигнал (рис. 2,6,в) лежит
в пределах от — до . Корреляционная функция – это энергия
сигнала с размерностью 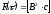 и выражением вида
и выражением вида
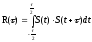
Чем
уже корреляционная функция, тем легче,
например, в радиолокации осуществить
разрешение сигналов и определить
параметры до цели по дальности, углу
прихода, скорости движения объекта и
т.д. Необходимо иметь как можно более
острые КФ особенно при близко расположенных
целях. Для заострения и укорачивания
КФ казалось бы можно брать более короткие
сигналы. Однако, энергия сигнала равна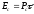 ,
а это значит, что при уменьшении
длительности τ уменьшается энергия сигнала. Следовательно
уменьшается дальность обнаружения и
соотношение сигнал/шум в точке приема,
т.е помехоустойчивость.
,
а это значит, что при уменьшении
длительности τ уменьшается энергия сигнала. Следовательно
уменьшается дальность обнаружения и
соотношение сигнал/шум в точке приема,
т.е помехоустойчивость.
База
простого сигнала равна 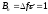 .
.
Сложные сигналы. Задача сложных сигналов, при той же исходной длительности сигнала τ сформировать узкую КФ, не снижая энергии сигнала. Информационный импульс длительностью τ разбивают на ряд импульсов одинаковой или разной длительностью (рис. 2.7,а).
Теперь ширина спектра (рис. 2.7,б) такого сигнала будет определяться самым коротким импульсом , а корреляционная функция (рис. 2.7,в) будет лежать в пределах от — до .
Полоса частот, где заключено 90% сигнала равна (рис. 2.7,б):
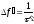 .
()
.
()
Поскольку энергия по отношению к простому сигналу не изменилась то корреляционная функция (рис. 2.7,в), для сохранения своей площади по отношению к простому сигналу будет лежать выше сложного сигнала.
В свою очередь База сложного сигнала будет равна
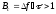 .
()
.
()
В большинстве случаев большой интерес представляют сигналы с Базой сигнала равной
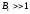 .
()
.
()
Выражение () определяет собой широкополосный шумоподобный сигнал (ШШС). У такого сигнала структура его приближается к белому шуму, а корреляционная функция стремиться к дельта функции, т.е стремиться в бесконечность.
В качестве сложных сигналов могут выступать коды Баркера и сигналы линейной частотной модуляции (ЛЧМ).
Линейные
частотно-модулированные сигналы (ЛЧМ). Исходный
сигнал остается той же длительности,
но внутри него происходит линейное
нарастание частоты с девиацией 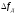 (рис.2.8).
Этот ЛЧМ сигнал уже сложный
(рис.2.8).
Этот ЛЧМ сигнал уже сложный 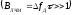 .
Длительность сигнала τ=const,
следовательно, его энергия остается
постоянной. Изменяя
.
Длительность сигнала τ=const,
следовательно, его энергия остается
постоянной. Изменяя 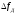 ,
можно варьировать базой и сделать ее
такой большой, что спектр сигнала будет
близок к спектру белого шума, а его КФ
будет стремиться к
,
можно варьировать базой и сделать ее
такой большой, что спектр сигнала будет
близок к спектру белого шума, а его КФ
будет стремиться к 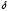 —
функции.
—
функции.
Рис.2.8 |
Рис.2.9 |
Линейный частотно-модулированный сигнал можно представить в виде
| (2.8) |
где 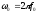 .
.
Ширина
КФ определяется величиной 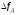 (рис.2.9).
(рис.2.9).
Прием ЛЧМ сигналов осуществляется на согласованный фильтр (СФ), на выходе которого имеется решающее устройство (РУ) (рис.2.10).
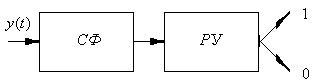
Рис.2.10
Согласованный фильтр представляет собой дисперсионную линию задержки с отводами на общий сумматор. Причем, учитывая разную скорость распространения различных гармонических колебаний, задержки отводов СФ выбраны так, чтобы по окончании импульса ЛЧМ все сигналы (гармоники) сложились бы одновременно в фазе. Это называется балансом фаз.
В результате такого одновременного сложения гармоник происходит сжатие сигнала. Коэффициентом сжатия находиться из выражения
| (2.9) |
где τ – длительность передаваемого сигнала;
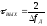 —
длительность сигнала на выходе СФ,
которая обратно пропорциональна девиации
частоты
—
длительность сигнала на выходе СФ,
которая обратно пропорциональна девиации
частоты 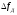 .
.
Чем
больше коэффициент сжатия, тем уже пик
КФ и тем выше разрешающая способность
и помехоустойчивость системы. Кроме
того, при большой базе можно увеличивать
длительность сигнала и тем самым повышать
его энергию, т.к. 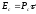 .
Недостатком ЛЧМ сигналов является
достаточно большой уровень
боковых лепестков КФ.
.
Недостатком ЛЧМ сигналов является
достаточно большой уровень
боковых лепестков КФ.
Сигналы Баркера. Баркер предложил коды, которые обладают таким свойством, что боковые лепестки КФ уменьшаются по закону 1/n, где n — значность кода. Правда, исследования показали, что значность кода может быть только такой: n = 2, 3, 4, 5, 7, 11, 13.
Код
Баркера состоит из определенного
количества импульсов равной длительности.
При этом, чем больше элементов n,
тем короче импульс 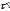 ,
тем шире спектр, а, значит, и уже КФ.
Далее осуществляют фазовое кодирование,
при котором осуществляется скачок фазы
при переходе от 1 к 0 и обратно на 1800 . При любом значении n распределение единиц и нулей может
быть произвольным (рис.2.11). На рис.2.12
приведена КФ для n = 3,7,13.
,
тем шире спектр, а, значит, и уже КФ.
Далее осуществляют фазовое кодирование,
при котором осуществляется скачок фазы
при переходе от 1 к 0 и обратно на 1800 . При любом значении n распределение единиц и нулей может
быть произвольным (рис.2.11). На рис.2.12
приведена КФ для n = 3,7,13.
Основание
КФ прямоугольного импульса длительностью 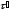 в
2 раза больше, т.к. эта КФ представляет
собой равнобедренный треугольник с
основанием
в
2 раза больше, т.к. эта КФ представляет
собой равнобедренный треугольник с
основанием 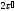 .
База сигналов, построенных по коду
Баркера равна
.
База сигналов, построенных по коду
Баркера равна 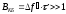 ,
а ширина спектра
,
а ширина спектра 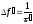 .
.
Рис.2.11
Если принять величину центрального пика КФ R(0)=1, то для выбранного значения n уровень боковых лепестков будет в n раз меньше (рис.2.12).
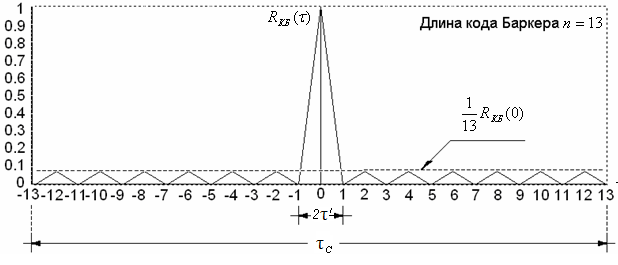
Рис.2.12
Прием сигналов Баркера осуществляется на СФ в виде дисперсионной линии задержки. Здесь так же сигналы складываются в фазе с приходом последней гармонической составляющей. В результате происходит сжатие принимаемого сигнала, энергия его возрастает в n раз в пределах сжатого сигнала, а боковые лепестки в n раз уменьшаются.
Коды Баркера позволяют не только увеличить разрешающую способность, но и увеличить помехоустойчивость и скрытность передачи, т.к. сигнал по своей структуре близок к ШШС.
Выводы:
переход от простых к сложным сигналам
позволяют обострить корреляционную
функцию 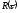 ,
а это значит, что можно существенно
улучшить различение, разрешение и
распознавания цели.
,
а это значит, что можно существенно
улучшить различение, разрешение и
распознавания цели.
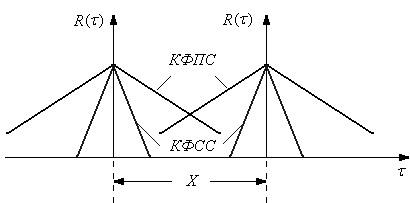
Рис. 2.13
Как
видно из рис. 2.13 зондирующий сигнал надо
брать с острыми корреляционными функциями 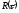 (сложные сигналы), так как легче произвести
различие, разрешение, измерение и т.д.
(сложные сигналы), так как легче произвести
различие, разрешение, измерение и т.д.
Вот почему выгоднее брать сигналы не простые, а сложные.
Сложные сигналы. Теория
.Простой информационный импульс длительностью τu разбивают на ряд импульсов одинаковой или разной длительностью (рис.2.1,а).
а) б) в)
Рис 2.1 Cложный сигнал. Спектр сигнала и его КФ
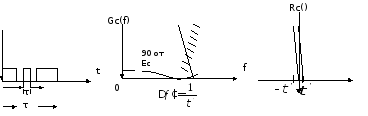
Ширина спектра сигнала G() (рис. 2.1б) будет определяться самым коротким импульсом длительностью τ, а корреляционная функция R() (рис. 2.1,в) будет лежать в пределах от —τ до τ .
Полоса частот, где заключено 90% энергии сигнала равна (рис.2.1,б):
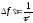 .
(2.1)
.
(2.1)
Поскольку энергия по отношению к простому сигналу не изменилась то корреляционная функция R() (рис.2.1,в), для сохранения своей площади по отношению к простому сигналу будет лежать выше простого сигнала.
База сложного
сигнала 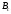 будет равна:
будет равна:
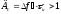 .
(2.2)
.
(2.2)
В большинстве случаев большой интерес представляют сигналы с Базой равной много больше 1.
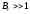 .
(2.3)
.
(2.3)
Выражение (2.3) определяет собой широкополосный шумоподобный сигнал (ШШС). У такого сигнала структура его приближается к белому шуму, а корреляционная функция стремиться к дельта функции, т.е. стремиться в бесконечность.
В качестве сложных сигналов могут выступать и сигналы линейной частотной модуляции (ЛЧМ) и коды Баркера
Выводы:
переход от простых к сложным сигналам
позволяет обострить корреляционную
функцию  ,
а это значит, что можно существенно
улучшить различение, разрешение и
распознавания цели, т.е.
,
а это значит, что можно существенно
улучшить различение, разрешение и
распознавания цели, т.е.
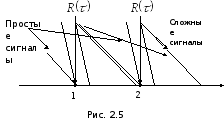
Как видно из рис.
2.5 зондирующий сигнал надо брать с
острыми корреляционными функциями  (сложные сигналы), так как легче произвести
различие, разрешение, измерение и т.д.
(сложные сигналы), так как легче произвести
различие, разрешение, измерение и т.д.
Вот почему выгоднее брать зондирующие сигналы не простые, а сложные
Лабораторная работа № 2 «Сигналы с Линейной частотной модуляцией (лчм)»
Цель работы: Исследование ЛЧМ-сигнала, его спектра и КФ
ТЕОРИЯ
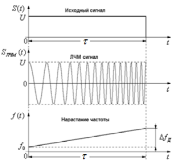
2.1 Лчм-сигнал
ЛЧМ-сигнал
представляет собой радиоимпульс с
длительностью 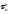 и частотой заполнения радиоимпульса с
длительностью τu которая изменяется по закону
и частотой заполнения радиоимпульса с
длительностью τu которая изменяется по закону 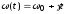 где
где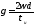 — скорость нарастания частоты при
— скорость нарастания частоты при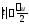 .
Полная фаза (при φ=0) есть:
.
Полная фаза (при φ=0) есть:
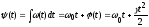 .
(2.4)
.
(2.4)
ЛЧМ-сигнал представляется выражением (Рис. 2.2)
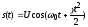 .
(2.5)
.
(2.5)
S(t)
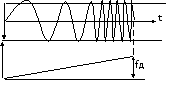
f(t)

t
Рис.2.2 ЛЧМ-сигнал
2.2 Спектр лчм
Спектр ЛЧМ-сигнала определяется выражением:
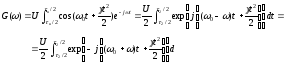 (2.6)
(2.6)
С учетом всех преобразований окончательная формула для спектра ЛЧМ-сигнала будет.
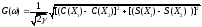 ,
(2.7)
,
(2.7)
где 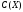 и
и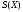 —
интегралы Френеля
—
интегралы Френеля
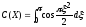 ;
; 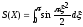 ;
(2.8)
;
(2.8)
а 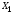 и
и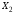 равны:
равны:
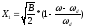 ;
; 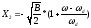 .
(2.9)
.
(2.9)
где B— база ЛЧМ-сигнала:
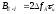 (2.10)
(2.10)
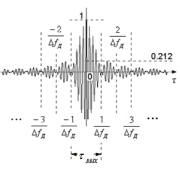
На рис. 2.3 представлены спектры сигналов при разных значениях их базы
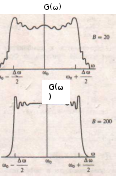
Рис. 2.3 Спектры ЛЧМ-сигналов при различных значениях базы
3. Разрешающая способность и сложные сигналы. Широкополосные сигналы и системы
3.1. Разрешение сигналов
3.2. Заключение
3.1. Разрешение сигналов
Для многих реальных систем весьма характерна ситуация, когда принятый сигнал фактически оказывается суперпозицией множественных реплик исходного «чистого» сигнала, каждая из которых имеет свои значения амплитуды, фазы, запаздывания и частоты. Перекрываясь во времени, эти копии интерферируют между собой, образуя достаточно сложный результирующий сигнал, что часто затрудняет извлечение необходимой информации. Процедура, направленная на разделение интерферирующих сигнальных копий или нейтрализацию их взаимного вредного взаимодействия, получила наименование разрешения сигналов.
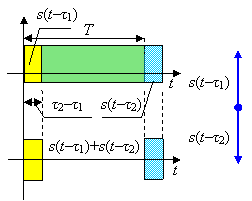
Для более глубокой трактовки смысла проблемы обратимся к весьма показательному сценарию временного разрешения сигналов. В этом случае наблюдаемое колебание помимо шума содержит суперпозицию сдвинутых во времени копий сигнала с соответствующими значениями амплитуд 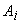 и начальных фаз
и начальных фаз 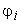 :
:
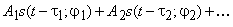 .
.
При взаимных временных сдвигах меньших длительности сигнала T копии суперпозиции перекрываются. Например, в случае только двух копий радиосигнала с 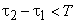 , равными амплитудами и противоположными фазами имеет место ситуация, иллюстрируемая рисунком, на котором также приведена векторная диаграмма. Как видно, сигнальные копии подавляют друг друга, уменьшению общую энергию суперпозиции.
, равными амплитудами и противоположными фазами имеет место ситуация, иллюстрируемая рисунком, на котором также приведена векторная диаграмма. Как видно, сигнальные копии подавляют друг друга, уменьшению общую энергию суперпозиции.
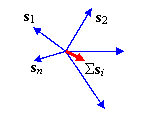
В общем случае векторная диаграмма множества сдвинутых во времени копий с различными амплитудами и фазами, представленная на рисунке, демонстрирует, что результирующая суперпозиция может оказаться существенно ослабленной по сравнению с наиболее сильными сигнальными копиями. Подобный эффект, называемый замиранием (федингом), является чрезвычайно вредным и порождает одну из наиболее серьезных проблем при разработке системы.
Физической причиной подобного феномена служит многолучевое распространение сигнала. Последнее будет обсуждаться в деталях в параграфе 4.5. Здесь же ограничимся лишь несколькими иллюстративными примерами. В цифровой связи, радиовещании, мобильной телефонии и т.п. колебание достигает приемной антенны по различным траекториям: параллельно с распространением по линии прямой видимости может существовать ряд путей, образованных различными отражателями (от земной поверхности, ионосферы, зданий, транспортных средств, элементов рельефа и т.п.). В радиолокации наряду с уже упомянутыми сигналами имеют место многочисленные эхо-сигналы, образованные отражением от различных частей одной и той же цели, либо от множества различных целей. Поскольку все пути распространения имеют различную длину, то значения временного запаздывания и начальной фазы соответствующих сигналов оказываются различными и, как правило, случайными.
Деструктивный эффект замираний мог бы быть полностью нейтрализован, если бы сигнальные копии не перекрывались, т.е. были бы разрешены во времени. Тривиальным путем к надежному временному разрешению является использование короткого сигнала, собственная длительность которого мала по сравнению с минимально возможным взаимным временным сдвигом сигнальных копий. Данный путь, однако, приводит к уже известному противоречию между ограничением на величину пиковой мощности и необходимостью поддержания фиксированной энергии сигнала (т.е. отношения сигнал-шум).
К счастью, как и при оценивании запаздывания (см. параграф 2.6), альтернативным и гораздо более изящным подходом достижения высокой разрешающей способности при удержании пиковой мощности в заданных пределах служит обращение к широкополосной философии. Поскольку очистка сигнала от шума является неотъемлемым этапом любой процедуры приема, то разрешающая способность определяется только длительностью сигнала на выходе согласованного фильтра (интервалом корреляции 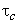 ). Таким образом, необходимо применение сигналов с малым значением
). Таким образом, необходимо применение сигналов с малым значением 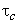 , тогда как достаточная их длительность
, тогда как достаточная их длительность 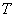 гарантирует вложение в сигнал необходимой энергии (нужное отношение сигнал-шум) при малой пиковой мощности. При использовании широкополосных сигналов с соответствующим законом внутренней угловой модуляции перекрывающиеся сигнальные копии на входе согласованного фильтра будут успешно разделены (разрешены) на его выходе благодаря эффекту временного сжатия, если только интервал корреляции
гарантирует вложение в сигнал необходимой энергии (нужное отношение сигнал-шум) при малой пиковой мощности. При использовании широкополосных сигналов с соответствующим законом внутренней угловой модуляции перекрывающиеся сигнальные копии на входе согласованного фильтра будут успешно разделены (разрешены) на его выходе благодаря эффекту временного сжатия, если только интервал корреляции 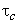 меньше временного сдвига
меньше временного сдвига 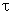 между репликами сигнала (см. рисунок справа). Очевидно, что требование к сигналу в задаче временного разрешения дословно повторяет уже сформулированное в задаче оценки запаздывания: остроконечность АКФ сигнала
между репликами сигнала (см. рисунок справа). Очевидно, что требование к сигналу в задаче временного разрешения дословно повторяет уже сформулированное в задаче оценки запаздывания: остроконечность АКФ сигнала 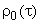 .
.
Понятия, введенные выше в контексте разрешения по времени легко обобщаются на задачи разрешения по другим параметрам. При наблюдении суперпозиции сигнальных реплик, отличающихся только частотным сдвигом, возникает задача разрешения по частоте, разрешающая способность в которой определяется длительностью сигнала, что и при измерении частоты. При этом, естественно, нет какой-либо нужды в применении широкополосной технологии. Если же наложенные друг на друга копии сигналов отличаются как временным, так и частотным сдвигами, то речь идет о частотно-временном разрешении, качество которого зависит от параметров функции неопределенности. Как и при частотно-временных измерениях, решение подобной задачи критически связано с широкополосной технологией: никакой иной путь не позволит добиться остроты функции неопределенности во всех направлениях в плоскости 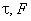 .
.
3.2. Заключение
В трех рассмотренных главах были вкратце исследованы канонические процедуры приема сигналов: обнаружение, различение, оценка параметров и разрешение. В соответствии с классическим подходом повсеместно постулировалась модель канала с аддитивным гауссовским шумом, и конечная цель состояла в выяснении того, в каких случаях в рамках подобной идеализации появляются импульсы к применению технологии расширенного спектра. Полученные выводы сгруппированы в ниже приведенной таблице, включающей параметры сигнала, влияющие на качество выполнения каждой из конкретных процедур, и степень мотивации к применению широкополосных сигналов для энергосберегающего улучшения качества приема.
Как свидетельствуют данные таблицы, было бы преувеличением считать, что классическая теория приема однозначно ориентирует на широкополосную идеологию. Лишь совместное измерение времени и частоты наряду с частотно-временным разрешением стимулируют к ее применению без всяких оговорок. Это может показаться странным и вызывающим вопросы по поводу оснований широкой популярности технологии распределенного спектра в современных беспроводных информационных системах. Как будет видно из дальнейшего, подобные основания весьма значительны и убедительно проявляют себя всякий раз, когда анализ базируется на более реалистичных моделях канала, чем порой излишне «академичная» гауссовская, или связан с привлечением некоторых дополнительных критериев качества.
Роль широкополосных сигналов в классических задачах приема.
|
Задача |
Параметры сигнала, определяющие качество |
Широкополосные сигналы |
|
Обнаружение, амплитудные и фазовые измерения |
Отношение сигнал-шум (только энергия сигнала). |
Не требуются |
|
Двоичная передача данных (M=2) |
Отношение сигнал-шум, коэффициент корреляции |
Не требуются |
|
М-ичная передача данных, M>2 |
Отношение сигнал-шум, коэффициенты корреляции между всеми сигналами |
Не требуются, но могут быть привлекательны в реализационном плане |
|
Измерение запаздывания и временное разрешение |
Отношение сигнал-шум, полоса сигнала |
Не требуются в отсутствие ограничений на мощность, необходимы при ограниченной мощности |
|
Измерение частоты, разрешение по частоте |
Отношение сигнал-шум, длительность сигнала |
Не требуются |
|
Частотно-временные измерения, разрешение по времени и частоте |
Отношение сигнал-шум, полоса и длительность сигнала |
Необходимы |
2.3. Сложные сигналы как средство преодоления противоречий простых сигналов.
Из
предыдущего раздела мы увидели, что для
увеличения дальности действия РЛС
при одноканальном передающем тракте
есть только один путь –
увеличение длительности зондирующих
сигналов u.
Для простых сигналов это вызывает
сужение спектра излучаемого сигнала
(f –
уменьшается), а, следовательно, и ухудшение
разрешающей способности по дальности
–
увеличивается 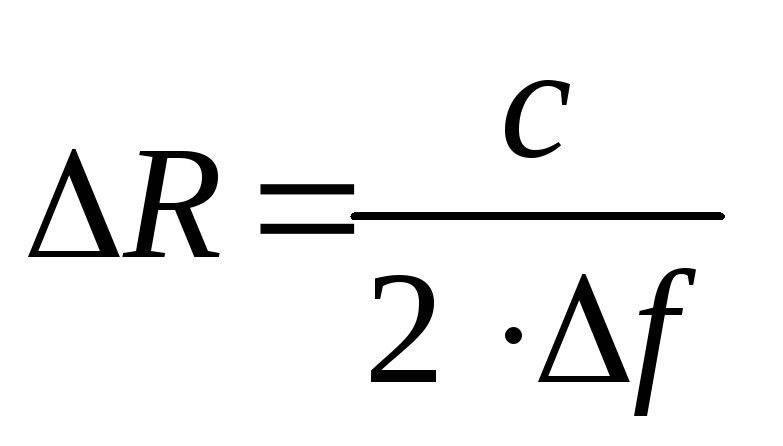 .
.
Сложные сигналы имеют обычно достаточно большую длительность (от десятков до сотен мкс), и в то же время спектр во много раз шире, чем спектр простого сигнала такой же длительности. Несоответствие ширины спектра сложных сигналов их длительности достигается введением внутриимпульсной модуляции – частотной, фазовой или комбинированной. Причина расширения спектра сложного сигнала состоит в том, что функция, модулирующая сигнал, является не прямоугольной, как у простого сигнала (рис. 6, а, б), а более изрезанной, как, например, у ФМ сигнала с дискретной бинарной модуляцией фазы 0, (рис. 7, а, б). Напомним, что ширина спектра радиосигнала определяется только видом его комплексной огибающей (скоростью изменения ее во времени) и не зависит от значения несущей частоты. Чем более изрезана комплексная огибающая сигнала при одной и той же его длительности, тем шире спектр сигнала.
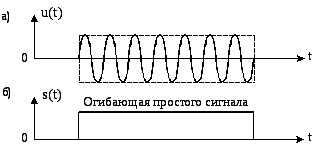
Рис. 6.
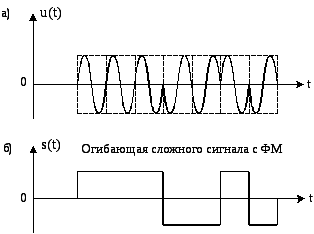
Рис. 7.
Сравнивая эти огибающие рис. 6, б и 7, б, можно сказать, что ширина спектра ФМ сигнала рис.7, а больше, чем у простого сигнала рис.6, а. Таким образом, разрешающая способность по дальности у сложного сигнала больше, чем у простого сигнала той же длительности. В то же время, демодулируя сложный сигнал, т.е. устраняя внутриимпульсную модуляцию при приёме, можно получить из сложного сигнала простой, равный сложному сигналу по длительности. Этот простой сигнал, полученный из сложного, на выходе демодулятора будет иметь большую длительность, а значит − узкий спектр и, следовательно, большую разрешающую способность по скорости.
Таким образом, с одной стороны, сложный сигнал за счёт внутриимпульсной модуляции при большой длительности имеет широкий спектр и обеспечивает высокую разрешающую способность по дальности, а с другой стороны из него с помощью демодуляции можно сделать простой сигнал той же длительности, который обеспечивает высокую разрешающую способность по скорости.
Более кратко указанное положение можно сформулировать так: из сложного сигнала большой длительности можно сформировать простой сигнал малой длительности и простой сигнал большой длительности, такой же, как и длительность принятого сложного сигнала.
Операция получения из сложного сигнала простого сигнала малой длительности называется сжатием по времени и выполняется СФ, а операция получения простого сигнала большой длительности называется сжатием по спектру и выполняется демодулятором. В связи с этим в РЛС должны существовать два канала разрешения – один по дальности (он начинается с СФ), и второй – для разрешения по скорости (начинается с демодулятора). На рис. 8 представлена упрощённая функциональная схема РЛС, использующая возможности сложных сигналов обеспечить одновременное высокое разрешение по дальности и скорости.
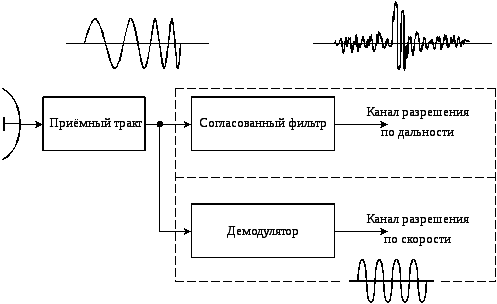
Рис. 8.
Заметим, что выходной сигнал СФ имеет такой же широкий спектр, как и его входной сигнал, поэтому он не может быть использован для разрешения по скорости.
Сложные сигналы при приёме на фоне белых шумов обрабатывают с помощью одного из двух устройств – коррелятора или СФ. Если параметры принимаемого сигнала – время задержки и частота – известны, то эти два устройства дают одинаковые результаты в смысле вероятности правильного обнаружения сигнала на фоне белого шума. Коррелятор или СФ являются неотъемлемой частью любой РЛС, поэтому рассмотрим их назначение и принцип их действия.
2.6. Коэффициент сжатия сложных сигналов
Как было отмечено в п. 2.3, при обработке сложных сигналов для получения одновременно высокой разрешающей способности по дальности и скорости, необходимо осуществлять сжатие сигнала по времени и спектру.
Важнейшим параметром сложных сигналов является коэффициент сжатия по времени и спектру. Коэффициент сжатия по времени показывает улучшение разрешающей способности по дальности у сложного сигнала по сравнению с простым сигналом той же длительности. Коэффициент сжатия по спектру показывает улучшение разрешающей способности сложного сигнала по скорости и по сравнению с простым сигналом с такой же шириной спектра, как и у сложного сигнала.
Рассмотрим последовательно сжатие сложного сигнала по времени и спектру и оценим предельное значение коэффициентов сжатия по этим параметрам.
Сжатие по времени производится согласованным фильтром СФ, вычисляющим АКФ входного сигнала. Выразим энергии сигнала на входе и выходе
Евх = РвхТ; Евых= Рвыхu,
где Т и u – длительности сигналов на входе и выходе СФ.
Из закона сохранения энергии Евых = Евх находим
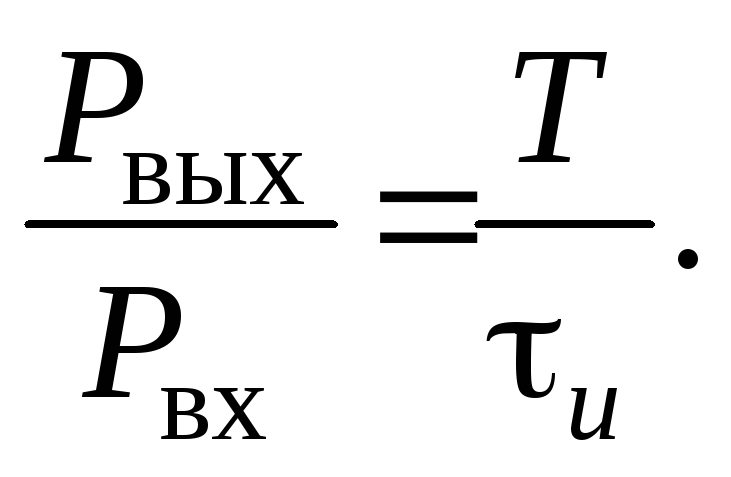 (20)
(20)
Предположим, что сжатие сигнала происходит без изменения полосы сигнала f, и сжатый импульс имеет минимально возможную базу fu = 1. Тогда выражение (20) можно записать в виде
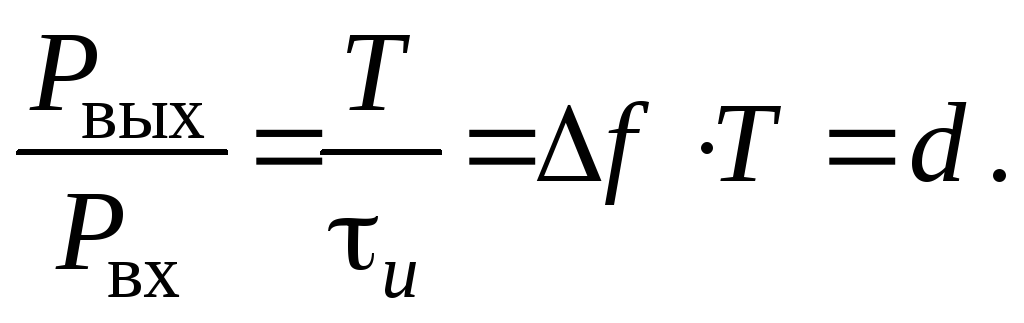 (21)
Из (21) следует,
что при сжатии сигнала по времени выигрыш
в пиковой мощности сжатого импульса
пропорционален базе сигнала.
(21)
Из (21) следует,
что при сжатии сигнала по времени выигрыш
в пиковой мощности сжатого импульса
пропорционален базе сигнала.
Если
длительность сжатого импульса u такова, что обеспечивает необходимое
разрешение по дальности, то применение
этого метода позволяет использовать
сложный излучаемый радиолокационный
импульс большой длительности Т >
u.
В результате использования излучаемого
сложного сигнала большой длительности Т можно
обеспечить его большую энергию E = Pпрд∙Т при малой (допустимой) мощности излучения Pпрд,
меньшей той, при которой происходит
пробой в волноводе передающего тракта.
Таким способом преодолевается
противоречие между дальностью действия
РЛС (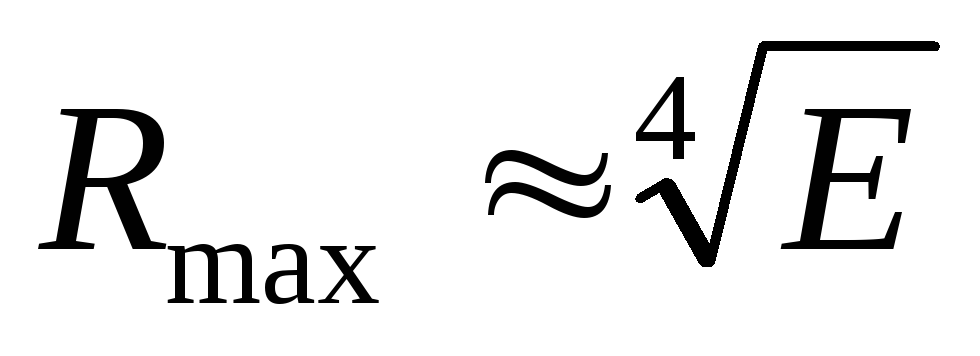 )
и разрешающей способностью по
дальностиR,
характерное для простых сигналов.
)
и разрешающей способностью по
дальностиR,
характерное для простых сигналов.
Сжатие по спектру осуществляется превращением сложного сигнала в простой сигнал той же длительности Т, что и исходный сложный сигнал. Это является демодуляцией сложного сигнала и производится в демодуляторе.
Из равенства энергий сигналов на входе и выходе демодулятора следует, что РвхТ = РвыхТ, или
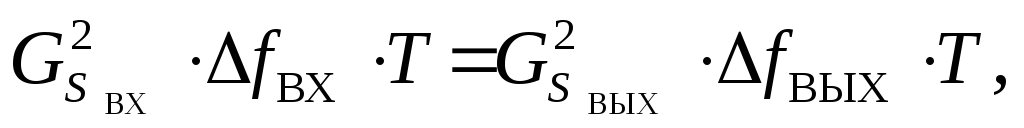 (22)
(22)
где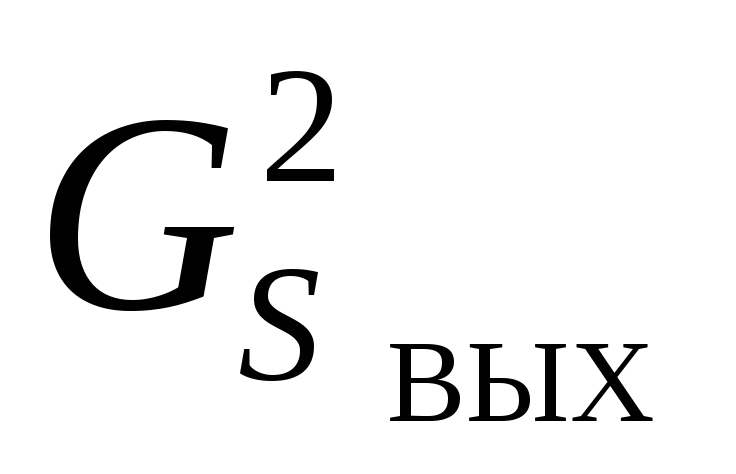 и
и 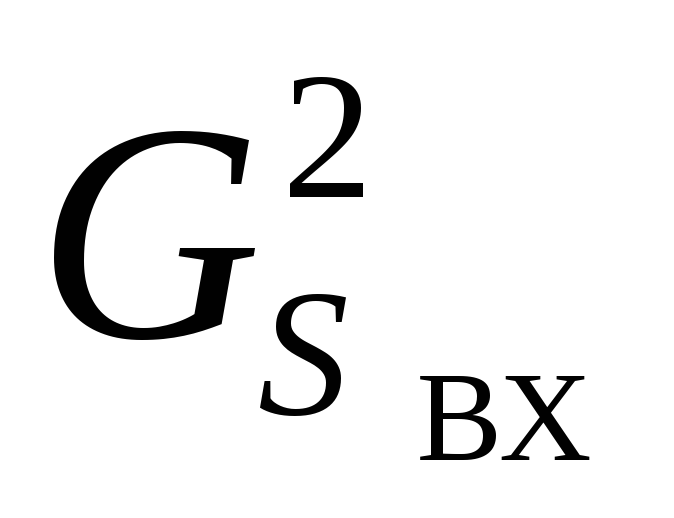 – спектральные
плотности мощности сигнала соответственно
на выходе и входе, ∆fВХT =
d
>>1 – база принятого сложного сигнала.
– спектральные
плотности мощности сигнала соответственно
на выходе и входе, ∆fВХT =
d
>>1 – база принятого сложного сигнала.
Предположим, что на выходе демодулятора получен простой сигнал с базой dВЫХ = fВЫХ· Т = 1. Тогда из выражения (22) получаем
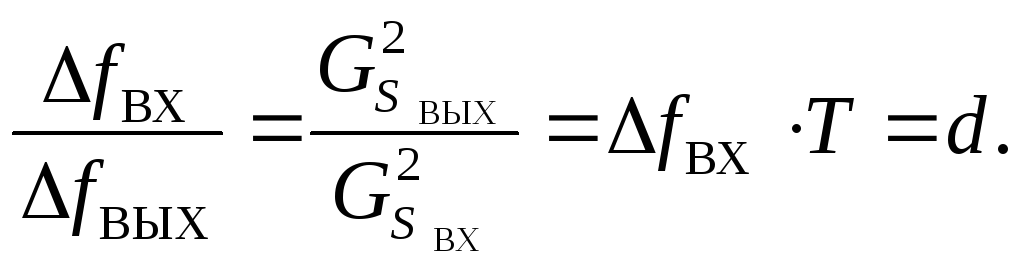 (23)
(23)
Таким образом, предельный коэффициент сжатия и по дальности, и по спектру равен базе сигнала d.
2.7. Функция неопределённости и её основные свойства. Тело неопределённости
Разрешающая способность по дальности и скорости простых и сложных сигналов определяется видом так называемой функции неопределённости (ФН), которая записывается
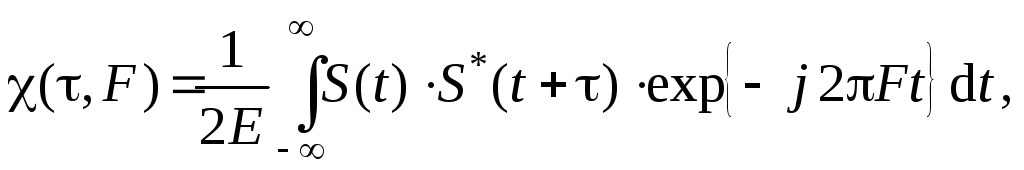 (24)
где
(24)
где 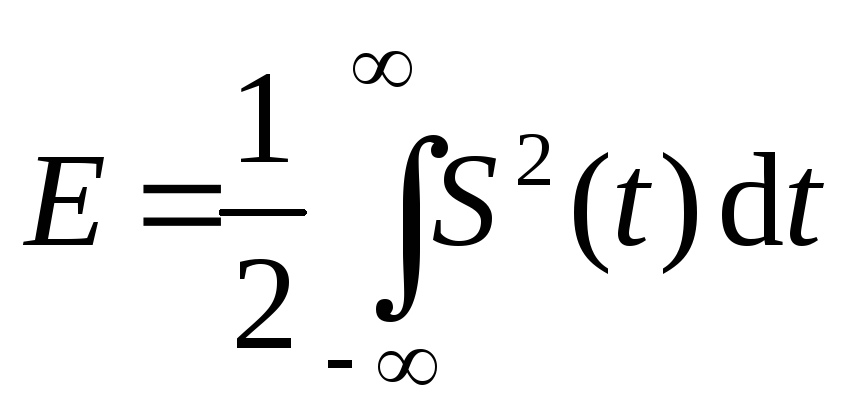 – энергия сигнала,F − рассогласование перемножаемых
сигналов по частоте.
– энергия сигнала,F − рассогласование перемножаемых
сигналов по частоте.
Но чаще под ФН понимается и исследуется модуль ( F)
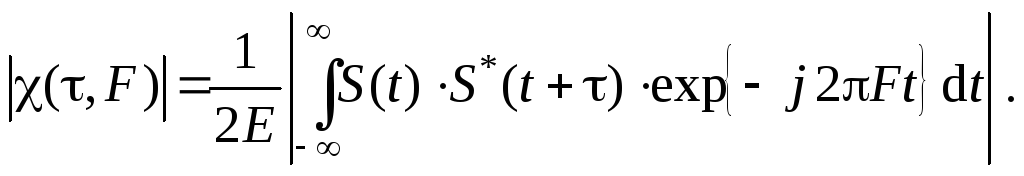 (25)
(25)
Запись ФН в виде (25) удобна при задании сигнала во временной области. Для анализа на частотной оси более удобна запись ФН в форме
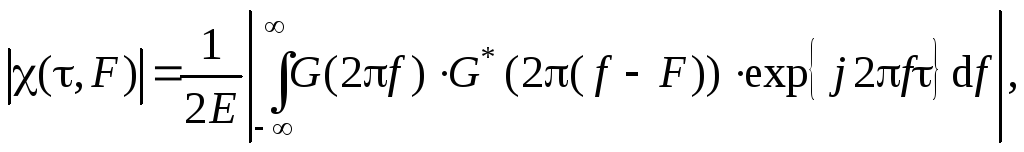 (26)
(26)
где G(2f) – преобразование Фурье от S(t).
ФН связана с выходным эффектом корреляционного приёмника: каждое значение функции |( F)| можно рассматривать как выходной эффект корреляционной обработки, когда на входы коррелятора поступают сигнал без помехи и опорный сигнал, параметры которого (время запаздывания и частота) в общем случае отличаются от ожидаемых параметров сигнала на и F.
ФН также связана с выходным сигналом СФ. Огибающая выходного сигнала СФ представляет собой сечение ФН |( F)|2 по оси F (F – расстройка частоты принимаемого сигнала и частоты настройки фильтра).
Для характеристики остроты пиков ФН удобна функция |( F)|2. Поверхность, образованная |( F)|2 называется поверхностью неопределённости, так как её форма определяет область временных и частотных F расстроек, в пределах которой сигналы неразличимы. Тело, заключённое между этой поверхностью и координатной плоскостью , F, называется телом неопределённости (ТН).
3.7. Сложный сигнал с линейной частотной модуляцией
Условия (27) и (28) накладывают требования только на высоту главного пика ( =1), и объём ФН (VФH = 1). На форму ФН никаких требований не накладывается, её мы можем менять по своему усмотрению (а после этого подбирать сигнал под выбранную форму ФН). Например, мы можем переносить ФН относительно осей координат. При этом, как видно из рис. 17, сечение ФН оказывается малым в направлениях, как оси (см. ), так и Fд (см. Fд). Это даёт возможность получить одновременно хорошую разрешающую способность как по дальности (R ~ между целями 1 и 3), так и по скорости (Vr ~ Fд между целями 1 и 2). В то же время длительность сигнала u, если судить о проекции ФН на ось , оказывается большой. Велика и ширина спектра f, определяемая проекцией ФН на ось частоты f. Для простого сигнала (рис. 17) база сигнала определялась произведением осей эллипса u и Δf
d = Δf = 1.
Здесь же база сигнала
d1 = u f >> 1 = u Δf = d,
и d1 больше d во столько раз, во сколько площадь прямоугольника со сторонами uи f больше площади эллипса, изображающего сечение ФН.
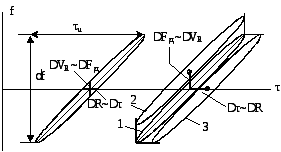
Рис. 17.
ФН, показанной на рис. 17, соответствует входной сигнал в виде длинного импульса с линейной частотной модуляцией (ЛЧМ) внутри импульса в случае, когда частота внутри импульса растёт от начала к концу. Это следует из того, что мгновенная частота спектра f, соответствующая большой оси эллипса, растёт с увеличением временного сдвига .
Сложный ЛЧМ сигнал записывается
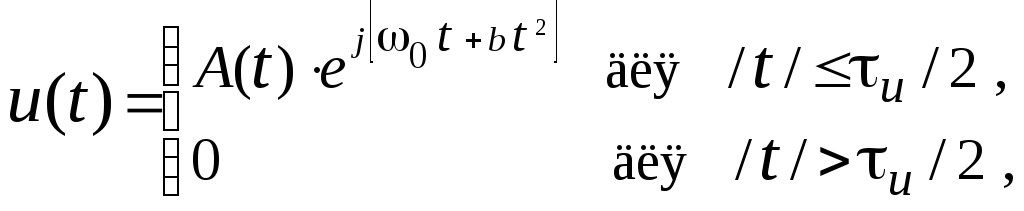
где 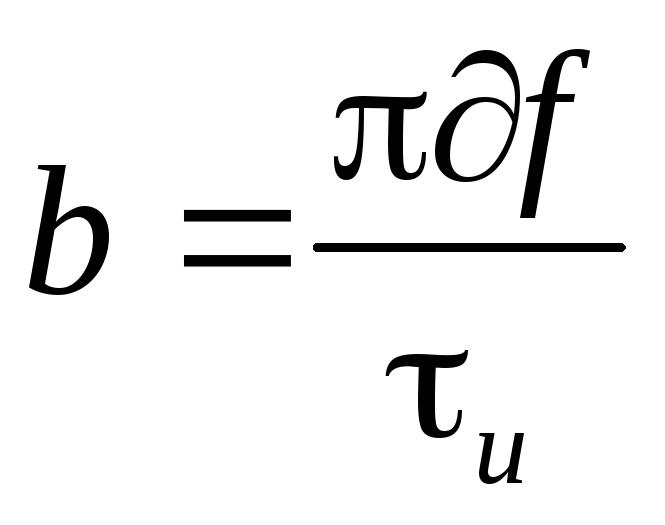 ;f –
девиация частоты. Если девиация частоты
;f –
девиация частоты. Если девиация частоты 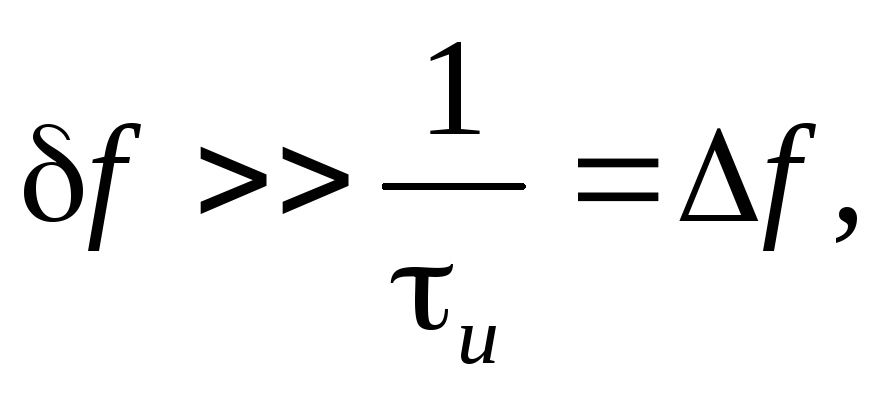 то ширина спектра уже определяется не
Δf,
то есть не длительностью импульса
u,
а девиацией f,
которая может быть очень большой. Рис.17
указывает только на возможность получения
от ЛЧМ сигнала хорошей разрешающей
способности по дальности и скорости,
но ничего не говорит о том, как эту
возможность превратить в действительность.
Для этого необходимо осуществить сжатие
ЛЧМ сигнала по времени и по спектру.
то ширина спектра уже определяется не
Δf,
то есть не длительностью импульса
u,
а девиацией f,
которая может быть очень большой. Рис.17
указывает только на возможность получения
от ЛЧМ сигнала хорошей разрешающей
способности по дальности и скорости,
но ничего не говорит о том, как эту
возможность превратить в действительность.
Для этого необходимо осуществить сжатие
ЛЧМ сигнала по времени и по спектру.
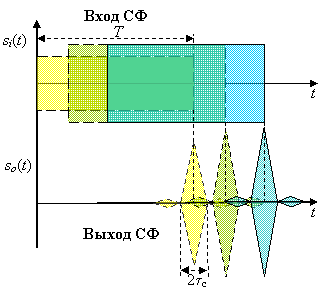
Сжатие по времени – получение из длинного сложного сигнала короткого простого – осуществляется СФ, на выходе которого получается развертка во времени АКФ входного сигнала. Один из возможных вариантов построения СФ для ЛЧМ сигнала на линии задержки с неравномерно расположенными отводами показан на рис. 11. Там же описана его работа.
Второй способ сжатия ЛЧМ импульса реализуется с помощью дисперсионной линии задержки, т.е. такой, в которой скорость распространения колебаний различных частот оказывается различной (например, низкие частоты задерживаются больше высоких – зеркально по отношению к сигналу). Во входном ЛЧМ импульсе ни в один из моментов спектральные составляющие не совпадают по фазе (хотя и связаны определённым законом по фазе), поэтому и их сумма нигде не оказывается большой. Однако за счёт дисперсии все спектральные составляющие задерживаются по-разному, причём так, что на входе дисперсионной линии задержки в некоторый момент оказываются синфазными, образуя короткий сжатый импульс большой амплитуды.
Повышение разрешающей способности по дальности по сравнению с простым сигналом той же длительности показано на рис. 18.
На рис. 18, а приведены два перекрывающихся по времени импульса А и Б. Если эти сигналы простые, то на выходе СФ они дают отклики (рис.18, б), и цели не разрешаются. Если А и Б – сложные ЛЧМ сигналы, то на выходе СФ два сигнала будут наблюдаться раздельно, следовательно, цели, от которых они отражены, разрешаются (рис.18, в). При сжатии ширина спектра не меняется, так как все спектральные составляющие проходят на выход на равных правах. Длительность же выходного сигнала СФ, измеряемая по длительности его центрального пика, уменьшается до 2. Сигнал становится простым, таким, что у него база
d = 2f =1.
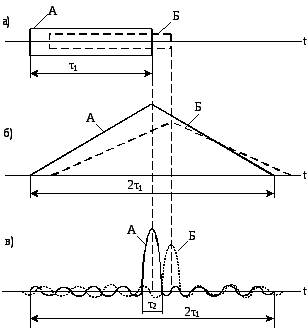
Рис. 18.
До сжатия база сигнала
d1 = 1 f >> 1.


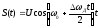 ,
,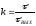 ,
,