Операции над векторами в прямоугольной системе координат, сложение векторов по координатам
Если задана плоскость Oxy с векторами a→=ax, ay и b→=(bx, by), то мы можем разложить их по координатным векторам i→ и j→. Тогда это будет иметь вид a→=ax·i→+ay·j→ и b→=bx·i→+by·j→. Чтобы найти сумму a→ и b→ и произведение a→ на λ, рассмотрим:
a→+b→=ax·i→+ay·j→+bx·i→+by·j→=(ax+bx)·i→+(ay+by)·j→
λ·a→=λ·(ax·i→+ay·j→)=(λ·ax)·i→+(λ·ay)·j→
Это равенство справедливо по свойству операций над векторами.
Определение 1Разложение векторов – это a→+b→ и λ·a→, представленное в частях неравенства по i→ и j→ координатам. Координаты векторов a→+b→ и λ·a→ равны соответственно (ax+bx, ay+by) и (λ·ax, λ·ay).
Таким же образом a→=(ax, ay, az) и b→=(bx, by, bz) записываются как a→+b→=ax·i→+ay·j→+az·k→+bx·i→+by·j→+bz·k→=(ax+bx)·i⇀+(ay+by)·j→+(az+bz)·k→λ·a→=λ·(ax·i→+ay·j→+az·k→)=(λ·ax)·i→+(λ·ay)·j→+(λ·az)·k→
а значит a→+b→=(ax+bx, ay+by, az+bz), λ·a→=(λ·ax, λ·ay, λ·az)
Отсюда делаем вывод, что координаты векторов a→ и b→ равны сумме соответствующих координат векторов a→и b→, координаты произведения вектора a→ на λ приравниваются к соответствующим координатам вектора a→, умноженным на число в заданной системе координат.
При необходимости нахождения координат суммы нескольких векторов, необходимо сложить координаты каждого вектора соответственно. Рассмотрим примеры.
Пример 1Нужно выполнить сложение a→=(2, 3-13) и b→=(-1,-13). Чему равны координаты произведения вектора a→ на 3.
Решение
Из определения имеем, что сумма векторов равна сумме их координат соответственно, тогда a→+b→=(2+(-1),3-13+(-13))=(1, -13).
Числовое значение умножается на каждую координату: 3·a→=(3·2, 3·3-13)=23,3-33.
Ответ: a→+b→=(1, -13), 3·a→=(23, 3-33)
Пример 2Заданы векторы a→=(0, 1, -2), b→=(-1, -1, 3), c→=(4, -3, 2) .
Каковы координаты вектора 2·a→+3·(b→-c→)=2·a→+3·b→+(-3)·c→.
Решение
Применяя свойства векторов, получим: 2·a→+3·(b→-c→)=2·a→+3·b→+(-3)·c→.
Подставляем значения координат и получаем: 2·a→+3·b→+(-3)·c→=2·(0,1,-2)+3·(-1,-1, 3)+(-3)·(4,-3, 2)=
=(2·0, 2·1, 2·(-2))+(3·(-1), 3·(-1), 3·3)+((-3)·4,(-3)·(-3)·2)=
=(0, 2, -4)+(-3, -3, 9) + (-12, 9 -6)=
=(0+(-3)+(-12), 2+(-3)+9, -4+9+(-6))=(-15, 8, -1)
Можно решить другим способом.
Обратим внимание на разложение a→, b→ и c→ :
a→=0·i→+1·j→+(-2)·k→=j→-2·k→
b→=(-1)·i→+(-1)·j→+3 ·k→=-i→-j→+3·k→
c→=4·i→+(-3)·j→+2·k→=4·i→-3·j→+2·k→
Исходя из свойств векторов, видим, что: 2·a→+3·(b→-c→)=2·(j→-2·k→)+3·(-i→-j→+3·k→-(4·i→-3·j→+2·k→))==2·j→-4·k→+3·(-5·i→+2·j→+1·k→)=-15·i→+8·j→-k→
Значит, координаты вектора 2·a→+3·(b→-c→) равны (-15, 8, -1).
Ответ: 2·a→+2·(b→-c→)=(-15, 8, -1)
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Навигация по статьям
Предыдущая статья
Нахождение середины отрезка
Следующая статья
Расстояние между точками
- Векторное произведение
- Векторное пространство
- Векторы на плоскости и в пространстве
- Геометрическая фигура угол
- Все темы по математике
- Курсовые работы
- Рефераты
- Отчет по практике
- Эссе
Узнать подробнее
ПЛАСТИНЧАТЫЙ ТЕПЛООБМЕННИК В Компас А Бумага теплообменник кожухотрубчатый
Вид работы:
Чертёж
Выполнена:
27 июня 2022 г.

Стоимость:
Заказать такую же работу
Математические модели инфодемии
Заказать такую же работу
Нужно рассчитать теплообменник
Вид работы:
Контрольная работа
Выполнена:
28 апреля 2022 г.

Стоимость:
3 600 руб
Заказать такую же работу
Задания прикреплены
Вид работы:
Контрольная работа
Выполнена:
21 января 2022 г.

Стоимость:
1 400 руб
Заказать такую же работу
Особенности исторической застройки Красноярска от появления острога до конца века
Вид работы:
Реферат
Выполнена:
27 декабря 2021 г.

Стоимость:
1 000 руб
Заказать такую же работу
по Строительным материалам
Вид работы:
Решение задач
Выполнена:
30 ноября 2021 г.

Стоимость:
1 100 руб
Заказать такую же работу
Смотреть все работы по чертежам в компас
Векторы. Сложение и вычитание векторов презентация, доклад
Векторы
Вектор — направленный отрезок
нулевой вектор
Длина ненулевого вектора равна длине отрезка
Длина нулевого вектора равна 0
Коллинеарные векторы — ненулевые векторы,
лежащие на одной прямой или на параллельных прямых
Нулевой вектор коллинеарен любому вектору
Коллинеарные векторы,
имеющие одинаковые направления,
называют сонаправленными
Коллинеарные векторы,
имеющие противоположные направления, называют противоположно направленными
Равные векторы
Противоположные векторы
сонаправленные векторы,
длины которых равны
противоположно направленные векторы,
длины которых равны
Равные векторы:
Противоположные векторы:
Равные векторы:
Противоположные векторы:
Сложение и вычитание
векторов
Правило треугольника
Правило треугольника
Правило параллелограмма
Законы сложения векторов
переместительный
сочетательный
Разность векторов
противоположные
векторы
Сумма
нескольких векторов
Правило многоугольника
Умножение
вектора на число
Следствия
Свойства произведения вектора на число
позволяют выполнять преобразования в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, так же, как и в числовых выражениях
Векторы называются компланарными,
если при откладывании их от одной и той же точки они будут лежать в одной плоскости
Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости
Любые 2 вектора являются компланарными
3 вектора являются компланарными,
если среди них есть
пара коллинеарных векторов
Доказательство
Доказательство.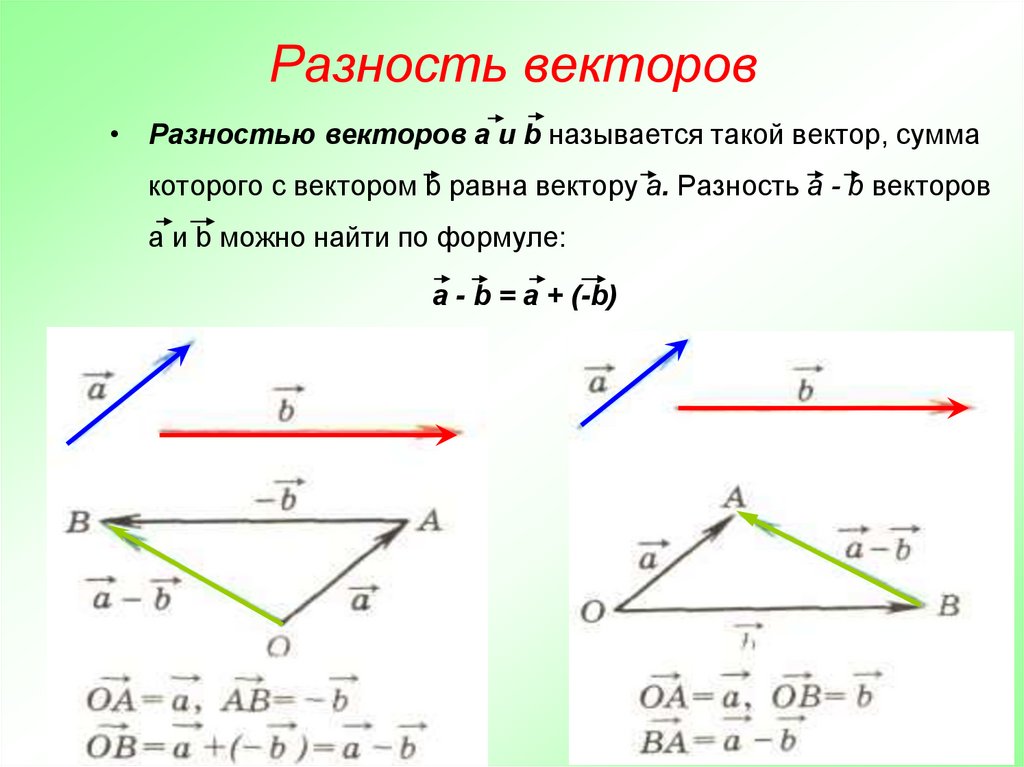
Правило
параллелепипеда
Правило параллелепипеда
Правило параллелепипеда
Разложение вектора по трём
некомпланарным векторам
Теорема
На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом
Прямоугольная
система координат
в пространстве
Рене Декарт
1596 — 1650
Французский философ,
математик, механик, физик и физиолог
Создатель аналитической геометрии и современной
алгебраической символики
ось абсцисс
ось ординат
начало координат
Декартова прямоугольная система координат
на плоскости
ось координат
ось координат
начало координат
ось координат
Декартова прямоугольная система координат
в пространстве
ось абсцисс
ось ординат
ось аппликат
ось координат
ось координат
ось координат
Декартова прямоугольная система координат
в пространстве OXYZ
Декартова прямоугольная система координат
в пространстве OXYZ
положительная полуось
положительная полуось
положительная полуось
отрицательная
полуось
отрицательная
полуось
отрицательная
полуось
Декартова прямоугольная система координат
в пространстве OXYZ
абсцисса
ордината
аппликата
Декартова прямоугольная система координат
в пространстве OXYZ
Координаты вектора
Теорема
Любой вектор можно разложить по трём некомпланарным векторам, причём коэффициенты разложения определяются единственным образом
Пользуясь разложениями векторов по координатным векторам, записать их координаты
Пользуясь координатами векторов, запишем их разложения по координатным векторам
Позволяют определять
координаты любого
вектора,
представленного в виде алгебраической суммы
данных векторов
с известными
координатами
Связь между координатами векторов
и координатами точек
Каждая координата вектора равна разности соответствующих координат его конца и начала
Простейшие задачи
в координатах
1.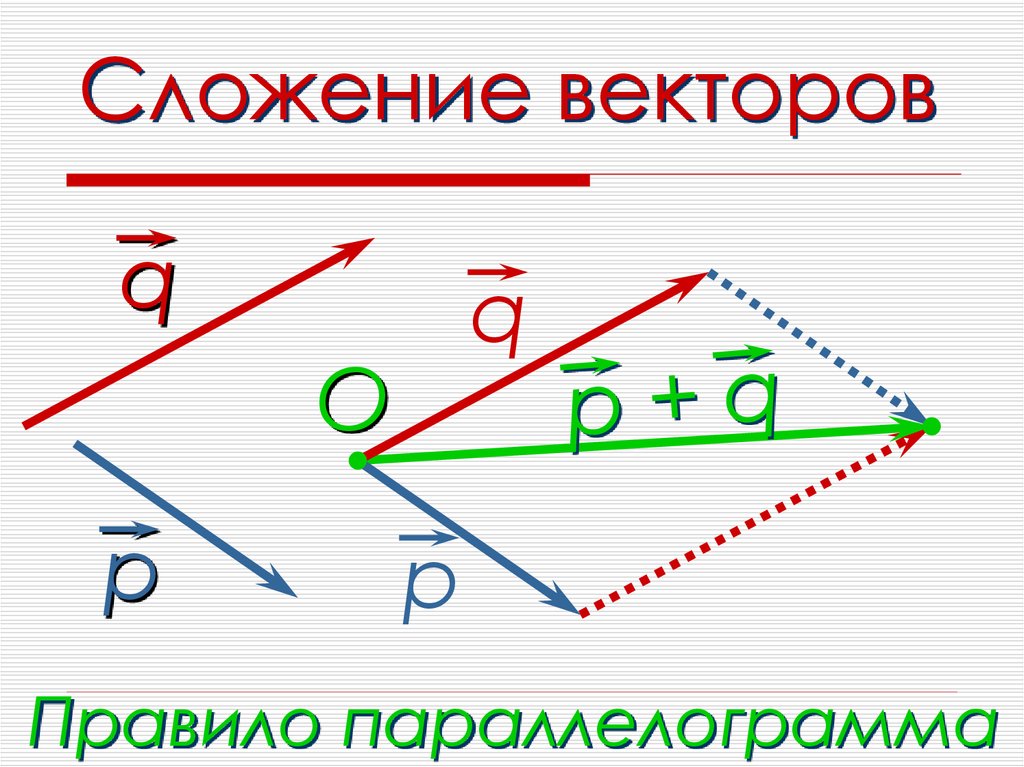 Определение координат середины отрезка
Определение координат середины отрезка
Каждая координата середины отрезка равна полусумме
соответствующих координат его концов
2. Вычисление длины вектора по его координатам
Решение.
3. Определение расстояния между двумя точками
Скалярное
произведение векторов
Скалярное произведение двух векторов −
произведение их длин на косинус угла между ними
Скалярное произведение векторов в координатах
Скалярное произведение векторов в координатах
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
Свойства скалярного произведения векторов
Урок 6.
 Действия над векторами в пространстве
Действия над векторами в пространстве Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяется так же, как и на плоскости. Только координат не две, а три.
Сложение векторов.
Для трёх векторов (АО, ОС, ОО1), которые не лежат в одной плоскости и имеют общее начало О, их сумма изображается диагональю параллелепипеда (ОВ1), построенного на этих векторах, причём начало вектора-суммы совпадает с началом этих векторов.
Координаты
вектора-суммы векторов равны сумме соответствующих координат данных векторов.
Сложение
двух векторов производится покоординатно, то есть, если
то
c = {x3; y3; z3} =
{x1; y1; z1} + {x2; y2; z2} =
{x1 + x2; y1 + y2; z1 + z2}.
Данная формула имеет место для произвольного конечного числа слагаемых.
Правило параллелепипеда сложения векторов.
Пусть даны три вектора
не лежащие в одной плоскости (их называют некомпланарными).
Выполним следующие построения:
1. Отложим от произвольной точки О векторы
2. Построим параллелепипед так, чтобы отрезки
ОА, ОВ, ОС
были его рёбрами.
Из рисунка видно, что
Таким образом, сумма трёх векторов, не параллельных одной плоскости
представляется диагональю параллелепипеда, построенного на данных векторах,
отложенных от одной точки, как на рёбрах.
Получили правило параллелепипеда для сложения векторов в
пространстве.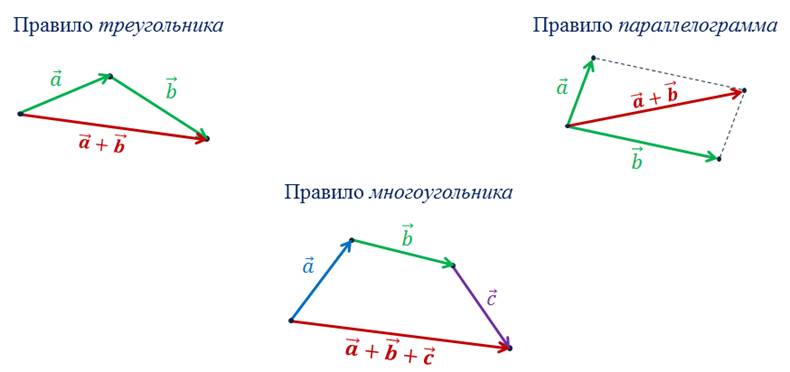
ПРИМЕР:
Возьмём векторы
Сумма векторов равна:
Вычитание векторов.
Вычитание двух векторов производится покоординатно, аналогично сложению, то есть если
то
c = {x3; y3; z3} =
{x1; y1; z1} – {x2; y2; z2} =
{x1 – x2; y1 – y2; z1 – z2}.
Геометрически два вектора складываются по правилу
параллелограмма с учётом того, что разностью векторов является диагональ,
соединяющая концы векторов, причём результирующий вектор направлен из конца
вычитаемого в конец уменьшаемого вектора.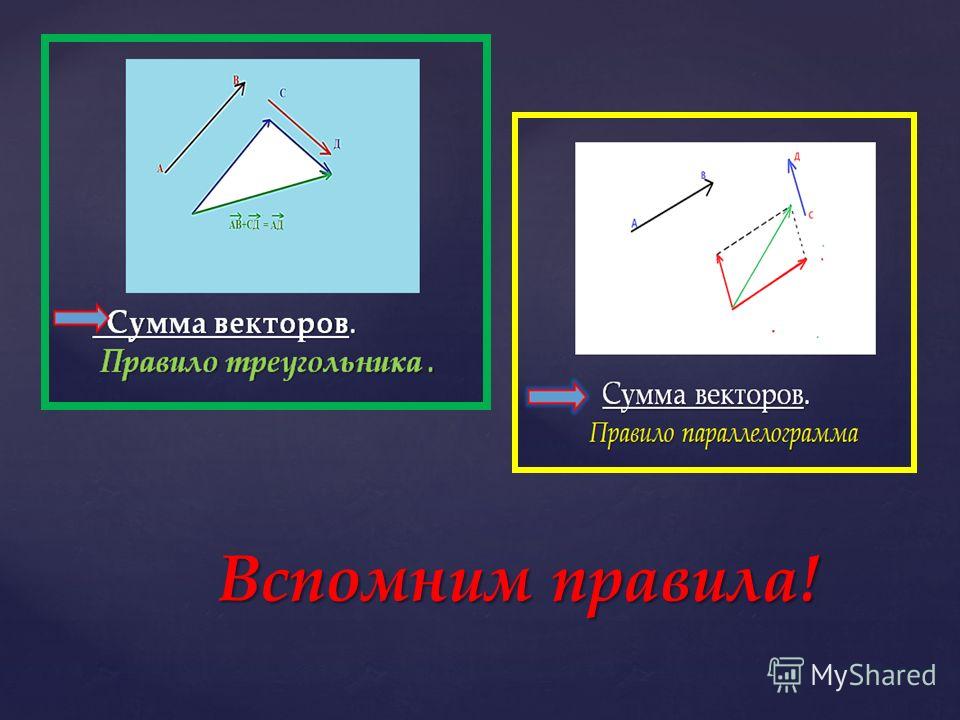
Важным следствием вычитания векторов является тот факт, что если известны координаты начала и конца вектора, то для вычисления координат вектора необходимо из координаты его конца вычесть координаты его начала.
Любой вектор пространства
может быть представлен в виде разности двух векторов, исходящих из начала координат:
Координаты векторов
совпадают с координатами точек А и В, так как начало координат
О(0;
0; 0).
Таким образом, по правилу вычитания векторов следует произвести вычитание координат точки А из координат точки В.
Возьмём векторы
Разность векторов равна:
Произведение векторов.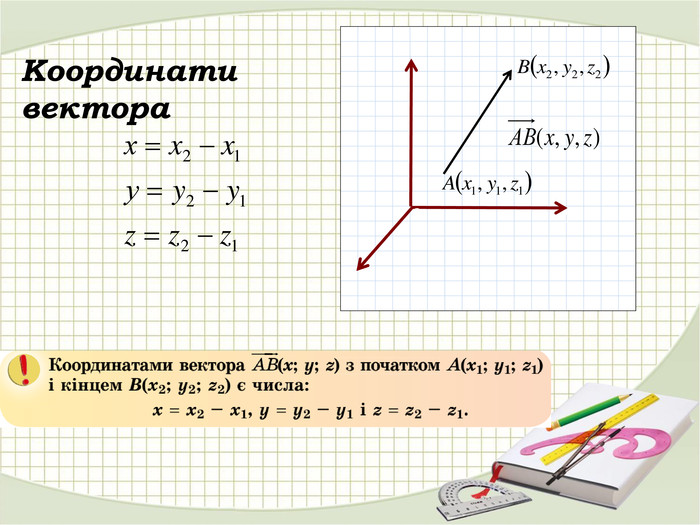
Умножение вектора на
число λ
покоординатно:
При λ ˃ 0 – вектор
сонаправлен
При λ < 0 – вектор
противоположно направлен
При | λ | ˃ 1 – длина вектора
увеличивается в λ раз. При | λ | < 1 – длина вектора
уменьшается в λ раз.
ПРИМЕР:
Даны векторы
Найдите координаты вектора:
РЕШЕНИЕ:
ОТВЕТ:
Скалярное произведение векторов.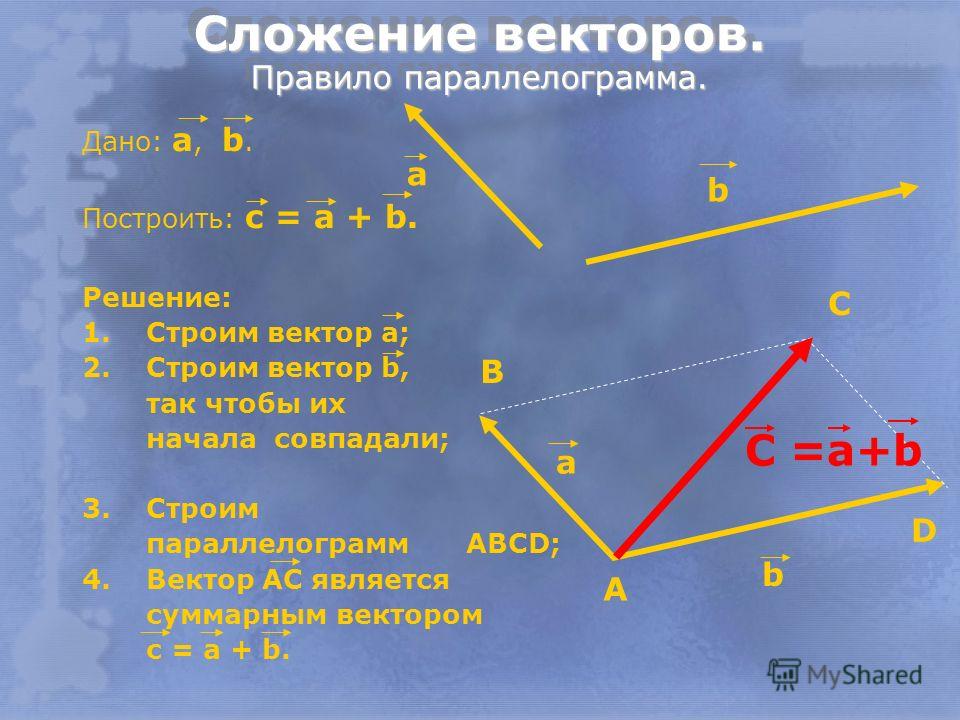
Скалярным произведением
векторов
называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть: скалярное произведение двух векторов
Скалярное произведение двух векторов
заданных своими координатами, равно сумме произведений их одноимённых координат, то есть:
ПРИМЕР:
Найдите угол между векторами
РЕШЕНИЕ:
Воспользуемся формулой:
Тогда Откуда ОТВЕТ:
ПРИМЕР:
Найти скалярное произведение векторовесли даны точки:
РЕШЕНИЕ:
Сначала найдём векторы:
По формулеВычислим скалярное произведениеСкалярное
произведение положительно, значит, угол между пространственными векторами
является острым.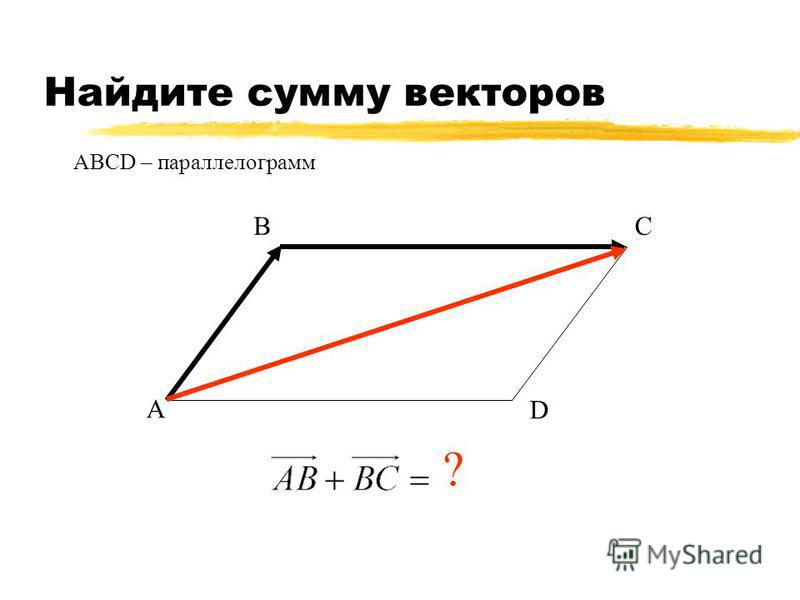
ОТВЕТ: 6
Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол φ = 0, поэтому его косинус равен 1.
Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения.
Если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны.
ПРИМЕР:
При каком значении р векторы
взаимно перпендикулярны ?
РЕШЕНИЕ:
Два ненулевых вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.
3 ∙ р + р ∙ (–2) + (–1) ∙ 5 = 3р – 2р – 5 = р – 5,
тогда
р –
5 = 0.
Откуда р = 5.
ОТВЕТ: р = 5
Попарные скалярные произведения единичных орт равны нулю, то есть:
С помощью скалярного произведения векторов можно вычислить угол между ними. Если заданы два ненулевых вектора своими координатами
то косинус угла φ между ними:
то есть
Отсюда следует условие перпендикулярности ненулевых векторов
х1x2 + y1y2 + z1z2 = 0.
С помощью скалярного произведения векторов находят работу постоянной силы
на прямолинейном участке пути. Предположим, что под действием постоянной силы
материальная точка
перемещается прямолинейно из положения А в положение В. Вектор силы
Вектор силы
образует угол φ с вектором перемещения
Физика утверждает, что работа силы
при перемещении
равна
то есть
Следовательно, работа постоянной силы при прямолинейном перемещении точки её приложения равна скалярному произведению вектора силы на вектор перемещения.
Проекции векторов.
Пусть в пространстве задана прямая (ось l), вектор
задан координатами конца и начала. Обозначим проекции точек А и В на ось l соответственно через А‘ и В‘. Проекцией
вектора
на ось l называется длина вектора
взятая со знаком <<+>>, если вектор
и ось l сонаправлены, и со знаком <<–>>, если
противоположно направлены.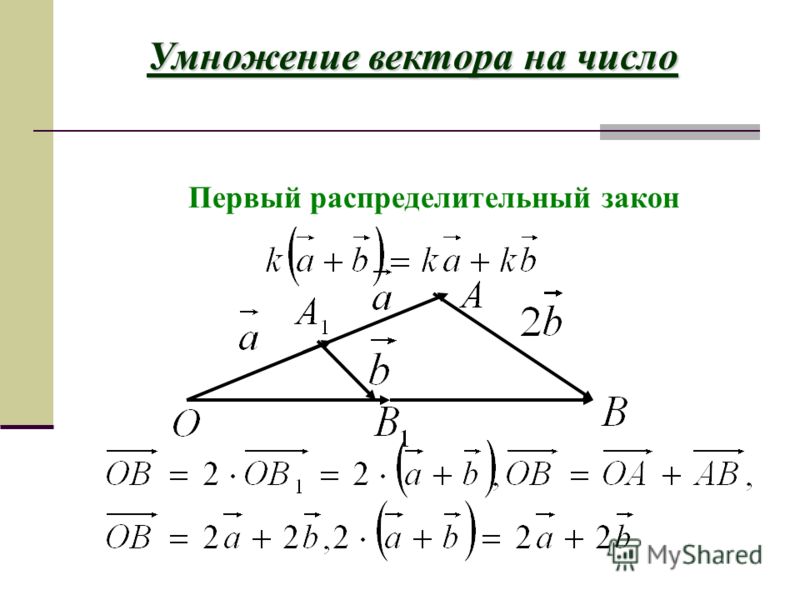
Если в качестве оси l взять
некоторый другой вектор
то получим проекцию вектора
на вектор
Нахождение проекции вектора
на направление, заданное вектором
может осуществляться по формуле:
то есть
Некоторые основные свойства проекций.
1. Проекция вектора
на ось l равна произведению модуля вектора
на косинус угла между векторами и осью, то есть
2. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой.
3. Проекция суммы
нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.
Свойства векторного произведения.
Если векторы заданы своими координатами:
то векторное произведение находится по формуле:
ПРИМЕР:
Найти векторное произведение векторов:
РЕШЕНИЕ:
Составим определитель и вычислим его:
Смешанное произведение векторов.
Смешанным произведением трёх векторов
называется число, равное скалярному произведению векторов
на вектор
Геометрический смысл смешанного произведения.
Если тройка векторов
правая, то их смешанное произведение равно объёму параллелепипеда построенного на этих векторах:
В случае левой тройки
смешанное произведение указанных векторов равно объёму параллелепипеда со знаком минус:
Если
компланарные, то их смешанное произведение равно нулю.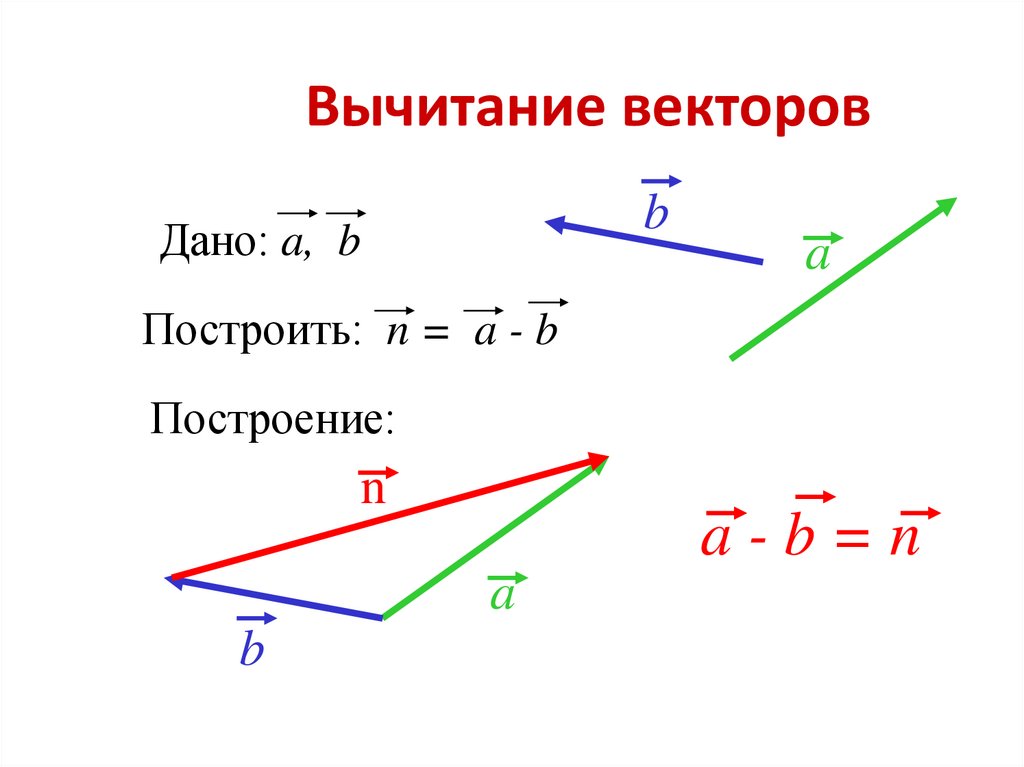 Из выше сказанного можно
сделать вывод, что объём параллелепипеда, построенного на векторах
Из выше сказанного можно
сделать вывод, что объём параллелепипеда, построенного на векторах
равен модулю смешанного произведения этих векторов:
Объём пирамиды, построенный на этой тройке векторов равен:
Свойства смешанного произведения. Три вектора компланарные тогда и только тогда, когда:
Тройка векторов является правой тогда и только тогда, когда
Если же
то векторы
образуют левую тройку векторов.
Если векторы:
заданы своими координатами, то их смешанное произведение вычисляется по формуле:
Задания к уроку 6
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
Как складывать векторы вместе Онлайн-практика
Исследуйте книгу Купить на Amazon
Вас часто просят добавить векторы при решении физических задач.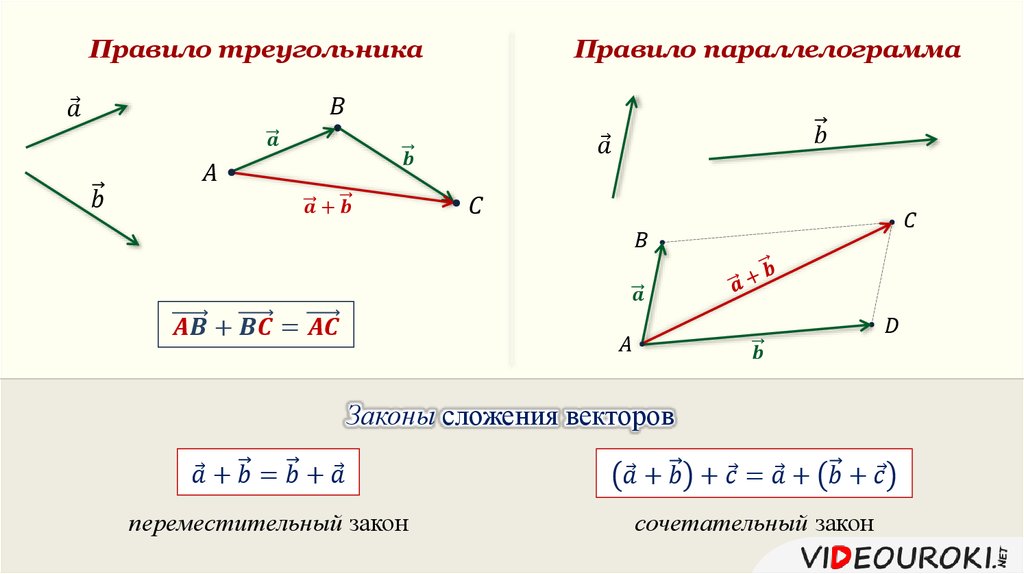 Чтобы сложить два вектора, вы помещаете их голову к хвосту, а затем находите длину и величину результата. Порядок, в котором вы добавляете два вектора, не имеет значения.
Чтобы сложить два вектора, вы помещаете их голову к хвосту, а затем находите длину и величину результата. Порядок, в котором вы добавляете два вектора, не имеет значения.
Например, предположим, что вы направляетесь на большой конгресс по физике, и вам сказали, что вы должны пройти 20 миль на север, а затем 20 миль на восток, чтобы добраться туда. Под каким углом от вашего текущего местоположения находится конференц-центр и как далеко он находится?
Вы можете написать эти два вектора следующим образом (где восток находится вдоль положительной оси x ):
(0, 20)
(20, 0)
В этом случае вам нужно сложить эти два вектора, и вы можете сделать это, просто добавив их x и y компоненты по отдельности:
Посчитайте, и ваш результирующий вектор равен (20, 20). Вы только что завершили сложение векторов. Но вопрос задает вектор в терминах величины/угла, а не в координатах. Итак, какова величина вектора от вас к соглашению о физике? Вы можете увидеть ситуацию на следующем рисунке, где у вас есть x и y и вы хотите найти v .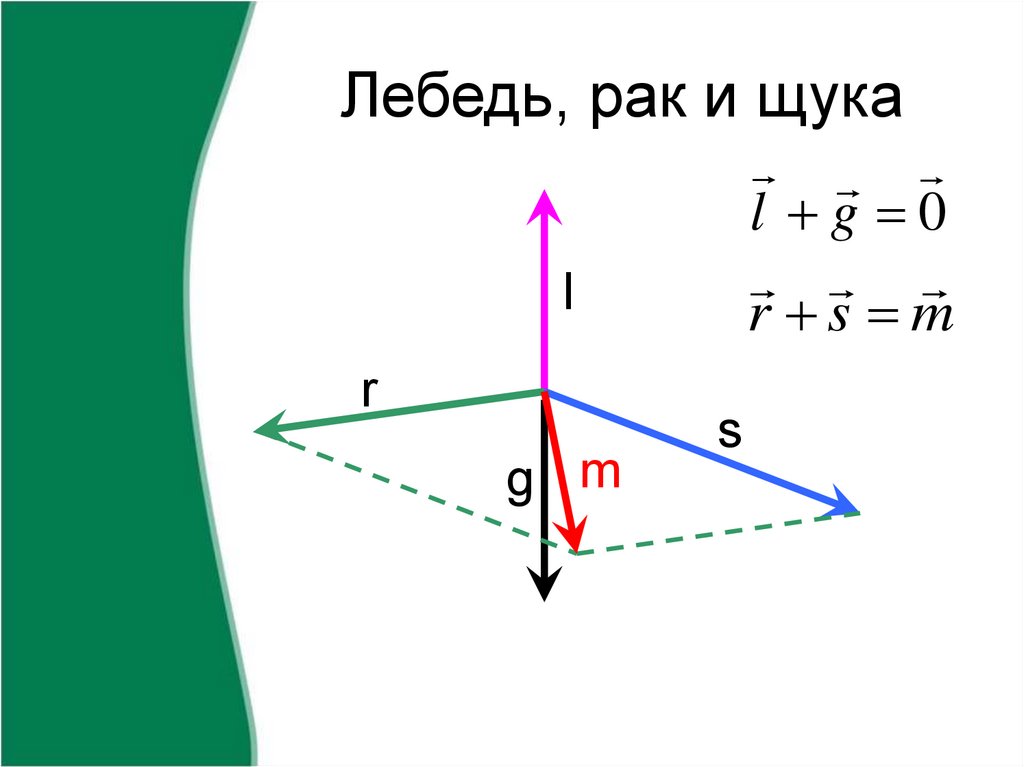
Находка v не так сложно, потому что вы можете использовать теорему Пифагора:
Подставьте цифры, чтобы получить
Значит, до конгресса 48,3 мили. А угол тета? Вы знаете
тета = тангенс –1 ( y / x ) = тангенс –1 (20/20) = 45 градусов
И все — теперь вы знаете, что конвенция находится на расстоянии 28,3 мили под углом 45 градусов.
Пример вопроса
Сложите два вектора на следующем рисунке. Один имеет звездную величину 5,0 и угол 45 градусов, а другой имеет звездную величину 7,0 и угол 35 градусов.
Правильный ответ: звездная величина 12,0, угол 39 градусов.
Разложите два вектора на их компоненты. Для первого вектора примените уравнение v x = v cos тета, чтобы найти координату x . Это 5,0, потому что 45 градусов = 3,5.

Примените уравнение v y = v sin тета, чтобы найти y координата первого вектора. Это 5,0 минус 45 градусов или 3,5. Таким образом, первый вектор равен (3.5, 3.5) в координатной форме.
Для второго вектора примените уравнение v x = v cos тета, чтобы найти координату x . Это 7,0, потому что 35 градусов = 5,7.
Примените уравнение v y = v sin тета, чтобы найти y координата второго вектора. Это 7,0 минус 35 градусов = 4,0. Таким образом, второй вектор равен (5.7, 4.0) в координатной форме.
Чтобы сложить два вектора, сложите их в виде координат: (3.5, 3.5) + (5.7, 4.0) = (9.2, 7.5).
Преобразование (9.2, 7.5) в форму величины/угла. Примените уравнение theta = tan –1 ( y / x ), чтобы найти угол, который равен tan –1 (7,5/9,2) = tan –1 (0,82) = 39.
 градусов.
градусов.Применить уравнение
, чтобы найти величину, которая равна
.Преобразование в две значащие цифры дает 12.
Практические вопросы
Добавьте вектор с величиной 13,0 и углом 27 градусов к вектору с величиной 11,0 и углом 45 градусов.
Добавьте вектор с величиной 16,0 и углом 56 градусов к вектору с величиной 10,0 и углом 25 градусов.
Добавьте два вектора: первый вектор имеет величину 22,0 и угол 19 градусов, а второй вектор имеет величину 19,0 и угол 48 градусов.
Добавьте вектор с величиной 10,0 и углом 257 градусов к вектору с величиной 11,0 и углом 105 градусов.
Ниже приведены ответы на практические вопросы:
Величина 23,7, угол 35 градусов
Для первого вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 13,0 x cos 27 градусов = 11,6.

Используйте уравнение v y = v sin theta , чтобы найти координату y первого вектора: 13,0 x sin 27 градусов, или 5,90. Таким образом, первый вектор равен (11.6, 5.90) в координатной форме.
Для второго вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 11,0 x cos 45 градусов = 7,78.
Используйте уравнение v y = v sin theta , чтобы найти координату y второго вектора: 11,0 x sin 45 градусов = 7,78. Итак, второй вектор равен (7.78, 7.78) в координатной форме.
Сложите два вектора в виде координат: (11.6, 5.90) + (7,78, 7,78) = (19,4, 13,7).
Преобразовать (19.4, 13.7) в форму величины/угла. Используйте уравнение тета = тангенс –1 ( y / x ), чтобы найти угол: тангенс –1 (13,7/19,4) = тангенс –1 (0,71) = 35 градусов.

Применить уравнение
, чтобы найти величину, которая равна
.
Величина 25,1, угол 44 градуса
Для первого вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 16,0 x cos 56 градусов = 8,95.
Используйте уравнение v y = v sin theta , чтобы найти координату y первого вектора: 16,0 x sin 56 градусов, или 13,3. Таким образом, первый вектор равен (8.95, 13.3) в координатной форме.
Для второго вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 10,0 x cos 25 градусов = 9,06.
Используйте уравнение v y = v sin theta , чтобы найти координату y второго вектора: 10,0 x sin 25 градусов = 4,23.
 Таким образом, второй вектор равен (9.06, 4.23) в координатной форме.
Таким образом, второй вектор равен (9.06, 4.23) в координатной форме.Добавьте два вектора в виде координат: (8.95, 13,3) + (9,06, 4,23) = (18,0, 17,5).
Преобразование вектора (18.0, 17.5) в форму величины/угла. Используйте уравнение theta = tan –1 ( y / x ), чтобы найти угол: tan –1 (17,5/18,0) = tan –1 (0,97) = 44 градуса.
Применить уравнение
, чтобы найти величину, которая равна
.
Величина 39,7, угол 32 градуса
Для первого вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 22,0 x cos 19 градусов = 20,8.
Используйте уравнение v y = v sin theta , чтобы найти координату y первого вектора: 22,0 x sin 19 градусов, или 7,16.
 Таким образом, первый вектор равен (20.8, 7.16) в координатной форме.
Таким образом, первый вектор равен (20.8, 7.16) в координатной форме.Для второго вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 19,0 x cos 48 градусов = 12,7.
Используйте уравнение v y = v sin theta , чтобы найти координату y второго вектора: 19,0 x sin 48 градусов = 14,1. Таким образом, второй вектор равен (12.7, 14.1) в координатной форме.
Сложите два вектора в виде координат: (20.8, 7.16) + (12.7, 14.1) = (33.5, 21.3).
Преобразование вектора (33.5, 21.3) в форму величины/угла. Используйте уравнение тета = тангенс –1 ( y / x ), чтобы найти угол: тангенс –1 (21,3/33,5) = тангенс –1 (0,64) = 32 градуса.
Применить уравнение
, чтобы найти величину, которая равна
.
Величина 5,2, угол 170 градусов
1. Для первого вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 10,0 x cos 257 градусов = -2,25.
Используйте уравнение v y = v sin theta , чтобы найти координату y первого вектора: 10,0 x sin 257 градусов, или -9,74. Итак, первый вектор равен (–2,25, –9,74) в координатной форме.
Для второго вектора используйте уравнение v x = v cos theta , чтобы найти координату x : 11,0 x cos 105 градусов = -2,85.
Используйте уравнение v y = v sin theta , чтобы найти координату y второго вектора: 11,0 x sin 105 градусов = 10,6. Таким образом, второй вектор равен (–2,85, 10,6) в координатной форме.

Сложите два вектора в виде координат: (–2,25, –90,74) + (–2,85, 10,6) = (–5,10, 0,86).
Преобразование вектора (–5,10, 0,86) в форму модуля/угла. Используйте уравнение тета = тангенс –1 ( y / x ), чтобы найти угол: тангенс –1 (0,86/–5,10) = тангенс –1 (–0,17) = 170 градусов. Поскольку x отрицательно, а y положительно, этот вектор должен находиться во втором квадранте.
Применить уравнение
, чтобы найти величину, которая равна
Об этой статье
Эта статья из книги:
- Рабочая тетрадь по физике I для чайников с онлайн-практикой,
Об авторе книги:
Эту статью можно найти в категории:
8 Physics ,Объяснение урока: Сложение и вычитание векторов в 2D
В этом объяснении мы узнаем, как складывать и вычитать векторы в 2D.
Мы знаем, что векторы могут быть представлены отрезками определенной длины. (величина) и направление. Мы будем использовать их, чтобы помочь визуализировать сложение векторов и вычитание.
В рамках этого объяснения будут рассматриваться только векторы в двух измерениях; однако описанная методология может быть распространена на переносчиков в трех или более Габаритные размеры.
Напомним, что единичный вектор — это вектор с величиной, равной 1, и что единичные векторы в 𝑥- и 𝑦-направлениях обозначаются ⃑𝑖 и ⃑𝑗 соответственно.
Любой двумерный вектор можно записать в виде 𝑥⃑𝑖+𝑦⃑𝑗. Они могут альтернативно быть представлено в компонентной форме как (𝑥,𝑦) или 𝑥𝑦.
Определение: Сложение векторов
Сложение векторов — это операция сложения двух или более векторов для нахождения их сумма.
Имея два (или более) вектора в компонентной форме, мы можем найти их сумму по формуле
добавление соответствующих компонентов векторов.
Например, если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦).
Сложение векторов — это операция сложения двух или более векторов вместе в векторная сумма. Сумма двух и более векторов называется равнодействующей.
Сейчас мы рассмотрим пару примеров, где нам нужно сложить векторы в два Габаритные размеры.
Пример 1. Нахождение суммы двух векторов
Если ⃑𝑎=(3,2) и ⃑𝑏=(4,−1), найти ⃑𝑎+⃑𝑏.
Ответ
Напомним, что в декартовых координатах сложение векторов можно выполнить с помощью добавление соответствующих компонентов векторов.
Если ⃑𝑎=(𝑥,𝑦) и ⃑𝑏=(𝑥,𝑦), тогда ⃑𝑎+⃑𝑏=(𝑥+𝑥,𝑦+𝑦).
В этом вопросе ⃑𝑎=(3,2) и ⃑𝑏=(4,−1).
Итак, ⃑𝑎+⃑𝑏=(3+4,2+(−1))=(7,1).
Таким образом, ⃑𝑎+⃑𝑏=(7,1).
Пример 2. Нахождение компонентов двух векторов и их суммы по диаграмме
На сетке единичных квадратов показаны векторы
⃑𝑢, ⃑𝑣,
и ⃑𝑢+⃑𝑣.
- Из каких компонентов состоит ⃑𝑢?
- Из каких компонентов состоит ⃑𝑣?
- Какие компоненты ⃑𝑢+⃑𝑣?
Ответ
Любой двумерный вектор можно записать через его 𝑥- и 𝑦-компоненты вида (𝑥,𝑦), где 𝑥 — количество единиц в положительное 𝑥-направление, а 𝑦 — количество единиц в положительном 𝑦-направление.
От начальной точки до конечной точки ⃑𝑢 проходим 2 единицы вправо и 1 единица вверх. Это соответствует 2 единицам в 𝑥-направлении и 1 единице в 𝑦-направление.
Итак, ⃑𝑢=(2,1).
От начальной точки до конечной точки ⃑𝑣, проходим 3 единицы осталось и 4 единицы вниз. Это соответствует −3 единицам в 𝑥-направление и −4 единиц в 𝑦-направлении.
Итак, ⃑𝑣=(−3,−4).
Мы знаем, что сумма двух векторов называется равнодействующей и что в
Декартовы координаты, сложение векторов можно выполнить, добавив
соответствующие компоненты векторов.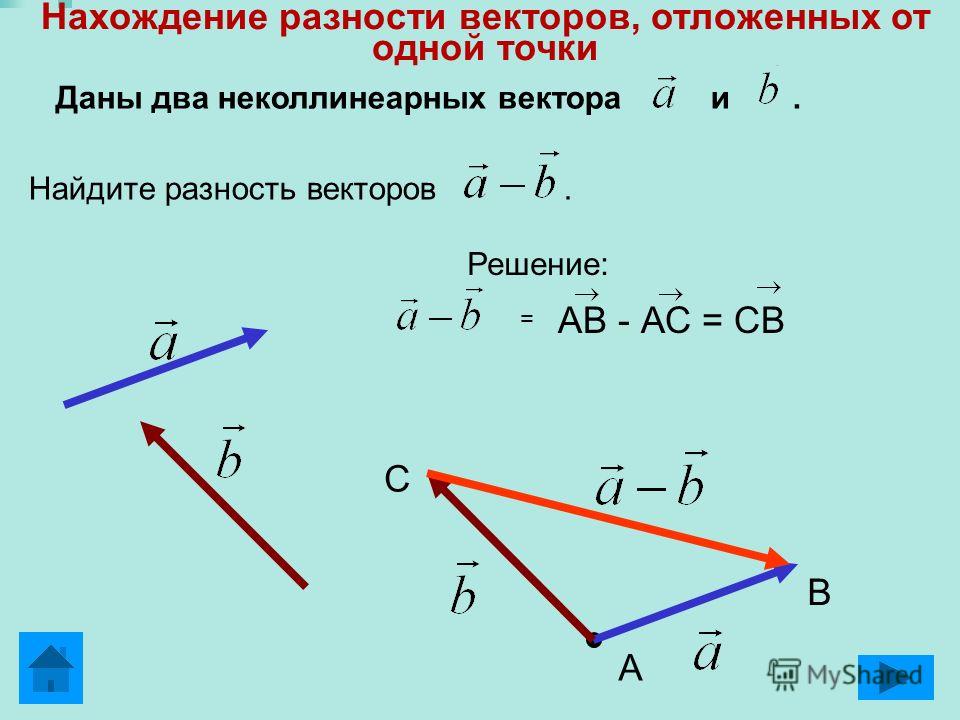
Если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦).
С ⃑𝑢=(2,1)⃑𝑣=(−3,−4) и тогда ⃑𝑢+⃑𝑣=(2+(−3),1+(−4))=(−1,−3).
Мы также можем прочитать эту информацию прямо из векторной диаграммы.
От начальной точки ⃑𝑢 в конечную точку вектора ⃑𝑣, мы перемещаемся на 1 единицу влево и на 3 единицы вниз. Это соответствует -1 единице в 𝑥-направлении и −3 единицы в 𝑦-направление.
Итак, ⃑𝑢+⃑𝑣=(−1,−3).
Таким образом, ⃑𝑢=(2,1), ⃑𝑣=(−3,−4), и ⃑𝑢+⃑𝑣=(−1,−3).
Вычитание векторов — это процесс нахождения разности векторов; это операция, обратная сложению векторов. Это означает, что ⃑𝑢−⃑𝑣=⃑𝑢+−⃑𝑣. При вычитании ⃑𝑣 из ⃑𝑢, находим равнодействующую ⃑𝑢 и −⃑𝑣.
Определение: вычитание векторов
Вычитание векторов — это операция вычитания двух векторов для нахождения их
разница.
Имея два вектора в компонентной форме, мы можем найти их разность по формуле вычитая соответствующие компоненты векторов.
Например, если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢−⃑𝑣=(𝑥−𝑥,𝑦−𝑦).
Стоит отметить, что эффект отрицания ⃑𝑣 является обратным в его направлении. Например, если бы у нас был вектор ⃑𝑣=(5,0), это будет вектор длины 5, параллельный оси 𝑥, указывающей слева направо. Если мы отрицаем ⃑𝑣, мы получаем −⃑𝑣=(−5,0). Величина вектора без изменений; он по-прежнему параллелен оси 𝑥, но его направление изменилось перевернутый; теперь он указывает справа налево.
Теперь мы рассмотрим еще несколько примеров, где мы будем складывать и вычитать векторы в двух измерениях.
Пример 3. Вычитание векторов, выраженных в терминах единичных векторов
При заданных векторах
𝐴𝐵=3⃑𝑖−4⃑𝑗
и 𝐶𝐷=−5⃑𝑖−5⃑𝑗,
рассчитать 𝐴𝐵−𝐶𝐷.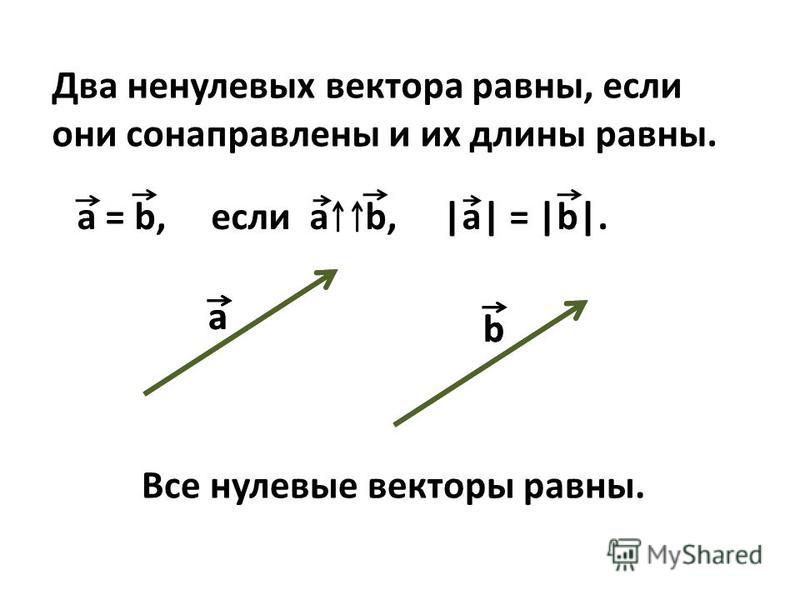
Ответ
Начнем с того, что в декартовых координатах вычитание векторов можно выполнить, вычитая соответствующие компоненты из векторы.
Если ⃑𝑢=𝑎⃑𝑖+𝑏⃑𝑗 и ⃑𝑣=𝑐⃑𝑖+𝑑⃑𝑗, тогда ⃑𝑢−⃑𝑣=(𝑎−𝑐)⃑𝑖+(𝑏−𝑑)⃑𝑗.
Итак, 𝐴𝐵−𝐶𝐷=3⃑𝑖−4⃑𝑗−−5⃑𝑖−5⃑𝑗=(3−(−5))⃑𝑖+(−4−(−5))⃑𝑗=8⃑𝑖+⃑𝑗.
Таким образом, 𝐴𝐵−𝐶𝐷=8⃑𝑖+⃑𝑗.
Пример 4. Сложение и вычитание векторов
Учитывая, что ⃑𝐴=(−2,2), ⃑𝐵=(5,2) и ⃑𝐶=(−3,−2), найти −⃑𝐴+⃑𝐵−⃑𝐶.
Ответ
Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.
Итак, −⃑𝐴+⃑𝐵−⃑𝐶=(−(−2)+5−(−3),−2+2−(−2))=(2+5+3,−2+2+2)=(10, 2).
Таким образом, −⃑𝐴+⃑𝐵−⃑𝐶=(10,2).
Пример 5. Поиск пропущенного вектора по заданному другому вектору и сумме двух векторов
Учитывая, что ⃑𝐴=(−4,5) и
⃑𝐴+⃑𝐵=(2,7),
найти ⃑𝐵.
Ответ
Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.
Если ⃑𝐴=(𝑥,𝑦) и ⃑𝐵=(𝑥,𝑦), тогда ⃑𝐴+⃑𝐵=(𝑥+𝑥,𝑦+𝑦).
Поскольку ⃑𝐴=(−4,5) и ⃑𝐴+⃑𝐵=(2,7), тогда (−4,5)+⃑𝐵=(2,7)((−4,5))⃑𝐵=(2,7)−(−4,5)⃑𝐵=(2−(−4),7−5) ⃑𝐵=(6,2).вычитание из обеих сторон
Итак, ⃑𝐵=(6,2).
Пример 6. Нахождение суммы двух векторов по одному из них и разности между ними
Учитывая, что ⃑𝐴=(7,−1) и ⃑𝐴−⃑𝐵=(3,−2), найти ⃑𝐴+⃑𝐵.
Ответить
Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.
Если ⃑𝐴=(𝑥,𝑦) и ⃑𝐵=(𝑥,𝑦), тогда ⃑𝐴−⃑𝐵=(𝑥−𝑥,𝑦−𝑦).
Так как ⃑𝐴=(7,−1)
и ⃑𝐴−⃑𝐵=(3,−2), то
(7,−1)−⃑𝐵=(3,−2)⃑𝐵(3,−2)⃑𝐵=(7,−1)−(3,−2)⃑𝐵=(7−3,−1−( −2))⃑𝐵=(4,1).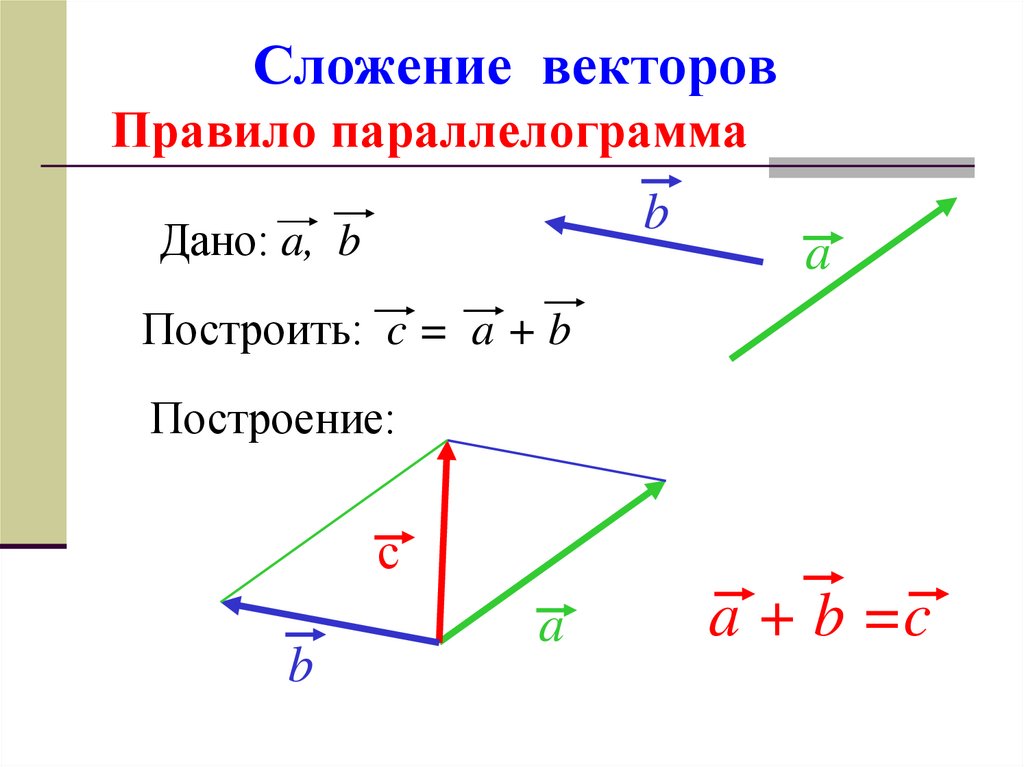 сложением и вычитанием с обеих сторон
сложением и вычитанием с обеих сторон
Теперь мы вычисляем ⃑𝐴+⃑𝐵.
Если ⃑𝐴=(𝑥,𝑦) и ⃑𝐵=(𝑥,𝑦), тогда ⃑𝐴+⃑𝐵=(𝑥+𝑥,𝑦+𝑦).
Так как ⃑𝐴=(7,−1) и ⃑𝐵=(4,1), тогда ⃑𝐴+⃑𝐵=(7,−1)+(4,1)=(7+4,−1+1)=(11,0).
Итак, ⃑𝐴+⃑𝐵=(11,0).
Пример 7. Нахождение вектора по двум другим векторам и выражению между тремя векторами
Учитывая, что ⃑𝐴=(3,−2), ⃑𝐵=(−5,4), и ⃑𝐴−⃑𝐵+⃑𝐶=(6,−1), найти ⃑𝐶.
Ответ
Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.
Если ⃑𝐴=(𝑥,𝑦), ⃑𝐵=(𝑥,𝑦), и ⃑𝐶=(𝑥,𝑦), тогда ⃑𝐴−⃑𝐵+⃑𝐶=(𝑥−𝑥+𝑥,𝑦−𝑦+𝑦).
Так как ⃑𝐴=(3,−2),
⃑𝐵=(−5,4),
и ⃑𝐴−⃑𝐵+⃑𝐶=(6,−1), то
(3,−2)−(−5,4)+⃑𝐶=(6,−1)(8,−6)+⃑𝐶=(6,−1)((8,−6))⃑𝐶=(6, −1)−(8,−6)⃑𝐶=(6−8,−1−(−6))⃑𝐶=(−2,5).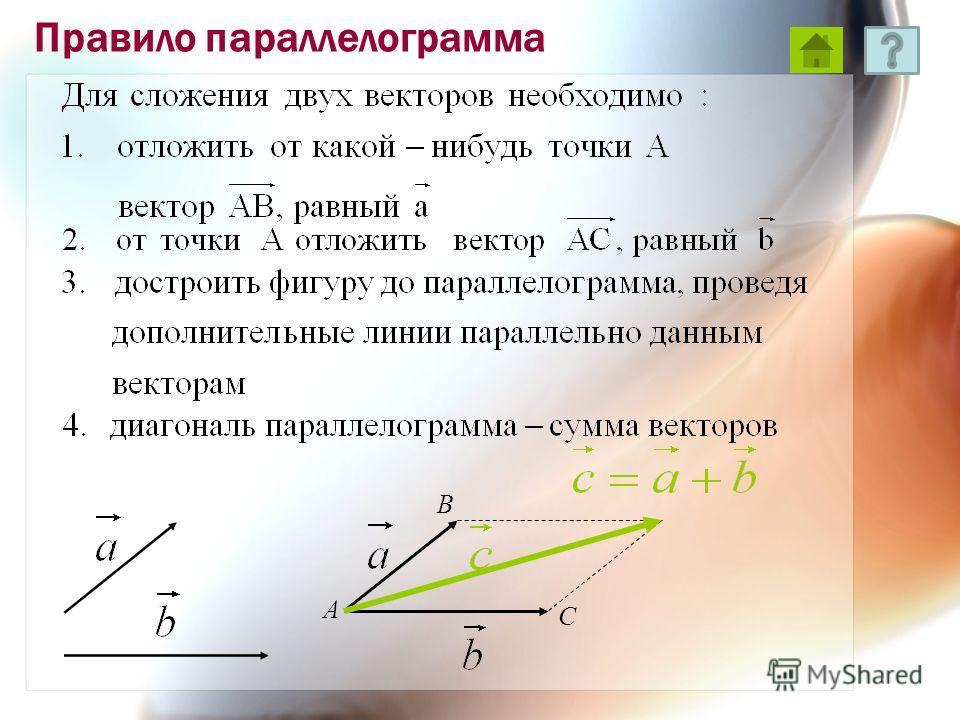 вычитая из обеих сторон
вычитая из обеих сторон
Итак, ⃑𝐶=(−2,5).
Хотя это выходит за рамки этого объяснения, мы можем представить вектор сложение и вычитание графически с помощью метод параллелограмма или метод треугольника .
Мы закончим это объяснение повторением некоторых ключевых моментов.
Ключевые точки
- В декартовых координатах возможно сложение и вычитание векторов. выполняется сложением или вычитанием соответствующих компонент векторов.
- Если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦).
- Если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢−⃑𝑣=(𝑥−𝑥,𝑦−𝑦).
Урок 35. Сложение векторов и полярные координаты
Векторы и полярные координаты
Векторы используются для описания сил. У них есть два компонента: величина (сила силы) и направление (куда направлена сила). Векторы визуально представляются в виде лучей с начальной точкой (начальная точка вектора) и конечной точкой (конец стрелки вектора).
Иногда силы пересекаются. Чистая сила, или результат их взаимодействия, зависит от направления и величины из двух сил. Подумайте о ветре, дующем на ваше лицо когда вы гуляете на свежем воздухе в хороший день. Теперь подумайте о сильном ветре, дующем в лицо во время ливня. В любом случае то, что вы чувствуете на своем лице, является результатом поступательная сила, создаваемая при ходьбе и обратном сила ветра.
До сих пор мы имели дело только с координатами xy. Это нанесен на знакомую декартову или «правильную» координатную плоскость содержащий ось x и ось y. Векторы обычно выражаются с использованием полярных координат, нанесенных на полярную плоскость. Полярная плоскость состоит из лучей, исходящих из источника. Расширяющиеся концентрические окружности также сосредоточены в этой исходной точке. На изображении ниже приведен пример стандартной полярной диаграммы с нанесенными на нее двумя векторами:
Изображение показывает только восемь лучей, каждый из которых разделен на 45°, которые исходят
от происхождения. Теоретически полярные плоскости на самом деле содержат
бесконечные исходящие лучи.
Теоретически полярные плоскости на самом деле содержат
бесконечные исходящие лучи.
Точки на полярной плоскости описываются координатой (r, θ), а не (x, y). Термин «р» означает «радиус», потому что он представляет собой расстояние от начала координат к краю одного из бесконечных концентрических кругов, образующих вверх по полярной плоскости. Другими словами, «r» означает радиус, потому что каждый r — это радиус круга, края которого он достигает. тета (θ) термин обозначает угол размещения относительно к оси 0°. Ноль градусов направлен на восток, а угол меры увеличиваются на 360° по часовой стрелке по окружности. Этот должно выглядеть знакомо, так как это похоже на то, как вы работали с направленными углами в Уроке 30.
На рисунке выше нанесены два вектора: красный вектор о
250° со скоростью 35 узлов (узел — это
морская единица скорости, равная примерно 1 миле в
час.), и синий вектор на 180° со скоростью 20 узлов.
(Хотя это и не отмечено на графике, каждая концентрическая линия
представляет 5 единиц величины. )
)
Добавление векторов
Рассмотрим пример с использованием красного и синего векторов сверху. Допустим, красный вектор представляет торпеду, выпущенную под углом 247°. со скоростью 35 узлов. Синий вектор представляет собой течение воды на 180° с магнитудой 20 узлов. В присутствии водного течения, торпеда фактически не будет выпущена по угол 247° со скоростью 35 узлов. Как изменит ли поток воды траекторию торпеды? К выяснить, мы должны сложить два вектора, найдя сумму два после того, как они «воздействовали» друг на друга.
Наша новая траектория изображена следующим образом:
- Постройте траекторию торпеды.
- Постройте траекторию течения воды.
- Переместите траекторию течения воды так, чтобы ее начальная точка подключается к оконечному концу тока торпеды. Этот Вектор «перемещенного» течения воды выделен темно-синим цветом внизу.
- Добавьте два вектора, нарисовав новый, соединяющий
начальная точка (расположенная в начале координат) вектора торпеды на
конечный конец перемещаемого вектора течения воды.
 Этот
результирующий вектор (показан ниже зеленым цветом) представляет собой сумму двух
оригинальные.
Этот
результирующий вектор (показан ниже зеленым цветом) представляет собой сумму двух
оригинальные. - С помощью транспортира и линейки измерьте угол и величину результирующего вектора зеленого цвета, как показано ниже.
Решение векторов графически помогает визуализировать процесс добавление их, но этот метод также может привести к высокой марже ошибка. Чтобы избежать большой ошибки, мы научимся решать векторы математически с законами косинусов и синусов. Добавление вектора включает в себя треугольники, как вы можете видеть с треугольником, образованным красным, синим и зеленым векторами выше. Следовательно, эти тригонометрические формулы особенно удобны для векторных проблемы сложения.
Пример 1:
Теперь добавим красный и синий векторы сверху. математически. Мы должны найти полярную координату или величину и направление зеленого вектора.
Во-первых, давайте посмотрим, какая информация у нас уже есть о
треугольник, образованный красным, синим и зеленым векторами. Это поможет
мы решаем, следует ли нам использовать закон синусов или закон
Сначала косинусы. Имейте в виду, что углы (или направления ) будут помечены символом угла (∠) и прописной буквой . Все остальные метки, такие как стороны треугольников (или в этом контексте величин ) будут строчными. Обратите внимание на график ниже.
Это поможет
мы решаем, следует ли нам использовать закон синусов или закон
Сначала косинусы. Имейте в виду, что углы (или направления ) будут помечены символом угла (∠) и прописной буквой . Все остальные метки, такие как стороны треугольников (или в этом контексте величин ) будут строчными. Обратите внимание на график ниже.
Приведем всю известную нам информацию об этой проблеме. Мы знаем, что красный вектор имеет величину 35 единиц (подумайте о это длина одной стороны треугольника). Мы также известно, что синий вектор имеет величину 20 единиц.
Угол между исходным красным и синим векторами ∠X равен 67°.
(247° — 180°). Поскольку ∠X и ∠Y являются дополнительными
углов (это означает, что они в сумме составляют 180°), мы знаем, что ∠Y = 180° — 67° = 113°. Мы знаем, что ∠C также равен 113°, потому что C и Y равны соответствующих углов ,
и соответствующие углы всегда равны. Изображение
ниже показано определение соответствующих углов. Углы 1 и 2 являются соответствующими углами, как и ∠3 и ∠4.
Углы 1 и 2 являются соответствующими углами, как и ∠3 и ∠4.
Соответствующие углы образуются, когда линия (например, красная вектор в нашей задаче о торпеде) пересекает две параллельные прямые (т. векторы течения голубой воды, которые на самом деле одинаковы вектор, нанесенный в двух разных местах на полярной плоскости).
Итак, теперь у нас есть три части информации о треугольнике. (?abc), образованных векторами в нашей задаче: мы знаем угол (∠C= 113°) и две стороны (a=35 и b=20). Держите в Имейте в виду, что «длины» «сторон» треугольника образованы на самом деле вектор величин . Мы можем использовать закон косинусов, чтобы найти сторону c, величину результирующего вектора:
(Перед выполнением этих вычислений убедитесь, что ваш калькулятор находится в режиме градусов .)
C 2 = A 2 + B 2 — 2ABCOSC
C 2 = 35 2 + 20 2 — 2 (35) (20) COS113 °
C 2 = 1225.
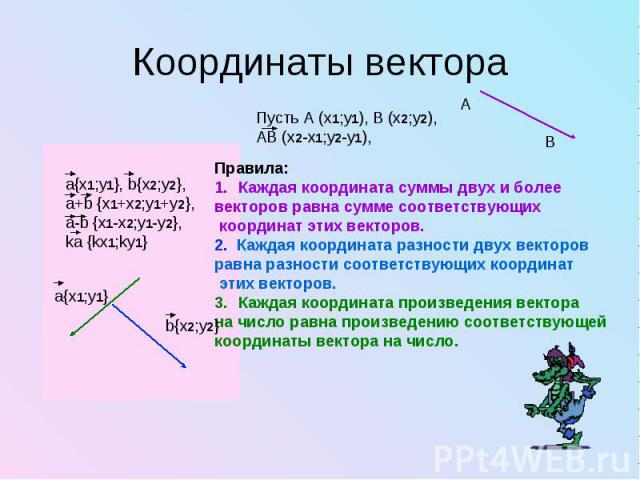 400 — 1400(-0,3907)
400 — 1400(-0,3907)
c 2 = 2171,98
c = 46,60 узлов
Величина результирующего вектора составляет 46,60 узлов. Сейчас Закон синусов можно использовать, чтобы найти ∠B. Как только мы узнаем ∠B, мы сможем выяснить направление результирующей вектор:
грех (113) | = | грех Б | | Подставьте известные нам сведения в формулу закона синусов. | |
(46,60) | (20) | ||||
| | | | | | |
| | | | | | |
(грех 113)(20) | = | | | Перекрестное умножение. | |
| | | | | | |
| | | | | | |
(син 113 • 20) | = | грех Б | | Изолировать sin B с одной стороны. | |
(46,60) | | ||||
| | | | | | |
| | | | | | |
| ∠Б | = | 23,27° | | Найдите ∠B. | |
Имейте в виду, что 23,27° — это , а не направление результирующий (зеленый) вектор — это просто угол между результирующим и исходным (красным) вектором. Ссылаться вернуться к изображению, показывающему все векторы выше. Вы должны вычесть 23,27° из направления оригинала (красный) вектор, чтобы получить направление результирующего (зеленого) вектора. Это означает, что направление равнодействующей:
247° — 23,27° = 223,73°
Таким образом, результирующий вектор составляет 46,60 узлов с пеленгом 223,73°. Иными словами торпеда будет стрелять с магнитудой 46,60 узлов под углом 223,73°, как только вода ток действует на его начальную величину и направление.
Скаляры
Векторы можно умножать на константы, называемые скалярами .
Например, если у нас есть вектор с именем «v», и мы решили
умножьте его на 3, (3v), тогда 3 будет вектором скаляр .
Скаляр может увеличивать или уменьшать величину (r)
вектор. Скаляр, упомянутый выше, 3, является положительным числом.
Положительные скаляры влияют только на величину . В этом
случае скаляр изменит величину v, увеличив ее в три раза.
раз. Положительная скалярная величина , а не повлияет на направление v.
Скаляр, упомянутый выше, 3, является положительным числом.
Положительные скаляры влияют только на величину . В этом
случае скаляр изменит величину v, увеличив ее в три раза.
раз. Положительная скалярная величина , а не повлияет на направление v.
Если, однако, скаляр отрицательный, обе величины и направление вектора изменится. Модуль вектора будет умножен на абсолютное значение скаляра. Тогда направление (θ) изменится на противоположное 180 °, указывающий вектор прямо противоположно направление, с которого он изначально указывал. Давайте попробуем проблема со скалярами.
Пример 2:
Найдите модуль и направление вектора w. Вектор w определяется векторами u и v, приведенными ниже:
u: звездная величина 136, пеленг 160°
v: звездная величина 197, пеленг 300°
w: 2u — v
Изображение выше представляет вектор u красным цветом и v синим цветом. Вектор
w определяется как удвоенный вектор u минус вектор v. Другими словами,
вектор w является функцией векторов u и v со скалярами
применяемый. Вектор u имеет скаляр, равный двум, а вектор v имеет
скаляр отрицательной единицы. Мы будем иметь дело с этими скалярами, чтобы
выяснить величину и направление вектора w.
Другими словами,
вектор w является функцией векторов u и v со скалярами
применяемый. Вектор u имеет скаляр, равный двум, а вектор v имеет
скаляр отрицательной единицы. Мы будем иметь дело с этими скалярами, чтобы
выяснить величину и направление вектора w.
Мы знаем, что w = 2u — v. Сначала найдем 2u. Мы должны умножьте вектор u на скаляр двух. Два — положительная скалярная величина, поэтому величина вектора u удвоится (136 x 2 = 272). Запомнить, положительные скаляры влияют только на величину вектора, , а не его направление. Направление вектора u остается прежним. В настоящее время мы знаем величину и направление 2u: (272, 160°).
Следующей частью решения вектора w является вычитание v из 2u.
Вместо того, чтобы подходить к этому как к задаче на вычитание, полезно
подумайте об этом с точки зрения дополнения. Думайте об этом как добавление минус v .
Это работает, потому что добавление отрицательного числа такое же
вещь, как вычитание этого числа. Если это сбивает с толку, см.
к объяснению ниже:
Если это сбивает с толку, см.
к объяснению ниже:
8 — 2 = 6
8 + (-2) = 6
Следовательно, [8 — 2] = 6 = [8 + (-2)]
Так же:
2u — v = w
2u + (-v) = w
Следовательно, [2u — v] = w = [2u + (-v)]
Таким образом, вычитание вектора похоже на сложение отрицательного значения этого вектор. Нам нужно найти отрицательное v и добавить этот результат к 2u. «Отрицательное v» — это еще один способ сказать «v со скаляром -1.»
Отрицательная скалярная величина заставляет направление вектора v переключиться на его
полная противоположность (разница в 180°). Вектор v становится
300° — 180° = 120° Примечание: мы могли бы добавить или если вычесть здесь 180°, разницы действительно нет. Оба
сложение и вычитание дали бы котерминальных угла.
Однако в этом случае вычитание 180° дает нам угол
мера 120°, которая находится в пределах 0°-360°
диапазон. С углами в этом диапазоне просто легче иметь дело. (Если бы у нас было добавил 180° к 300°, мы бы получили направление
480°, что действительно, но вне этого
диапазон.) Мы установили направление v после того, как
умножается на минус: 120°.
(Если бы у нас было добавил 180° к 300°, мы бы получили направление
480°, что действительно, но вне этого
диапазон.) Мы установили направление v после того, как
умножается на минус: 120°.
Что происходит с величиной (197) вектора v? Величина v умножается на абсолютное значение его скаляра, -1. абсолютное значение отрицательного единицы равно единице. Следовательно, v величина не изменяется скаляром: 1 x 197 = 197. координата -1v (197, 120°). Теперь, когда мы знаем значение -v, мы должны добавить его к 2u, точно так же, как мы добавили векторов в Примере 1 выше. Во-первых, посмотрите на графику представление 2u и -v ниже:
Если мы переставим векторы так, чтобы начальная точка -v
соединяется с конечным концом 2u, мы можем нарисовать результирующий вектор,
w, показанный зеленым цветом ниже. Мы знаем, что ∠x, угол, образованный
между красным (2u) и синим векторами (-v, до этого
перемещен), составляет 160° — 120° = 40°. Отсюда следует, что ∠x’s
дополнительный угол ∠y равен 180° — 40° = 140°. Углы y и W
соответствующие углы, поэтому ∠y = ∠W = 140°.
Углы y и W
соответствующие углы, поэтому ∠y = ∠W = 140°.
Теперь мы знаем три части информации о треугольнике. образованные красным, синим и зеленым векторами: две стороны (величина -v = 197 и величина 2u = 272) и угол (∠W = 140°). Еще раз воспользуемся законом синусов и косинусов, чтобы найти величина и направление результирующего вектора w.
Во-первых, мы будем использовать закон косинусов, чтобы найти вектор w величина. Подставьте величины 2u и -v и ∠W в закон Формула косинусов:
w 2 = (2u )2 + (-v) 2 — 2(2u)(-v)cos(W)
w 2 = 272 2 + 197 2 (272)(197)cos(140)
w 2 = 73984 + 38809 — (-82095,45088)
ш = 441,46
Далее мы воспользуемся законом синусов, чтобы найти направление
вектор ш. Мы знаем, что угол между 2u и -v (или ∠W) равен 170°.
Мы можем использовать величину вектора w, найденную выше, чтобы найти
разница углов между w и 2u, или ∠V.
| грех W | = | | грех В |
| ш | | против | |
| | | | |
| | | | |
| грех 140 | = | | грех В |
| 441.46 | | 197 | |
| | | | |
| | | | |
| грех В | = | | 0,2868 |
| | | | |
| | | | |
| ∠В | = | | 16,67° |
Направление w на 16,67° меньше направления вектора 2u:
(направление w) = (направление 2u) — (∠V)
(направление w) = (160°) — (16,67°)
(направление w) = 143,33°
Мы решили задачу, потому что знаем полярную координату w: (441,46, 143,33°).
Список ниже суммирует то, что мы узнали о скалярах:
- Константа, умноженная на вектор, называется скаляром .
- Положительный скаляр изменяет только вектор величина. Умножьте величину вектора на скаляр и оставить направление без изменений.
- Отрицательная скалярная величина изменяет вектор величину и направление. Величина вектора умножается на абсолютное значение скаляра. Направление вектора изменяется на 180°, эффективно поворачивая вектор в другую сторону.
- Вы можете добавить или вычесть 180° из вектора. Мы рекомендуем вам выбрать операцию, которая дает угол от 0 до 360 градусов.
Векторы и декартовы координаты
До сих пор мы использовали полярные координаты для описания векторов в
по величине и направлению. Но векторы не обязательно должны быть
нанесены в виде полярных координат. Их также можно изобразить с помощью x
и координаты y на обычном Декартова координатная плоскость, также называемая прямоугольной плоскостью. Координаты, состоящие из значений x и y, будут называться декартовыми координатами или прямоугольными координатами .
Ось 0 ° декартовой координатной плоскости — это
неотрицательная ось x (прямо на восток, как в полярной плоскости)
и мы продвигаемся против часовой стрелки на 360° вокруг осей, как
до.
Координаты, состоящие из значений x и y, будут называться декартовыми координатами или прямоугольными координатами .
Ось 0 ° декартовой координатной плоскости — это
неотрицательная ось x (прямо на восток, как в полярной плоскости)
и мы продвигаемся против часовой стрелки на 360° вокруг осей, как
до.
Так как векторы можно описать с помощью полярных координат или xy-координаты, вы столкнетесь с проблемами, связанными с переход из одной системы координат в другую. Полярный координаты преобразуются в xy-координаты следующим образом:
х = rsinθ
у = rsinθ
Как вы помните из полярной системы координат, тета (θ) – это направление вектора, r — его величина. Используйте следующие формулы для преобразования декартовых координат (x, y) в полярные координаты (r, θ):
cosθ = x/r
sinθ = y/r
tanθ =y/x
Вы можете заметить, что формула радиуса дает два ответа:
один положительный и один отрицательный. Координата радиуса r описывает
длина радиуса, которая всегда положительна. Для полярных
координаты, не имеет смысла иметь отрицательное значение r
координировать. Радиус просто описывает величину, или
расстояние от начала координат в полярной плоскости. Тета описывает
направление, на которое указывает величина. Итак, для этого
Конечно, не обращайте внимания на символ ± в приведенной выше формуле и используйте только положительный результат для r.
Координата радиуса r описывает
длина радиуса, которая всегда положительна. Для полярных
координаты, не имеет смысла иметь отрицательное значение r
координировать. Радиус просто описывает величину, или
расстояние от начала координат в полярной плоскости. Тета описывает
направление, на которое указывает величина. Итак, для этого
Конечно, не обращайте внимания на символ ± в приведенной выше формуле и используйте только положительный результат для r.
Приведенный ниже график даст вам хорошее представление о тригонометрии.
за преобразованиями координат. Изучите его, чтобы углубить свои
понимание связи между xy-координатами и полярными координатами
координаты. Это также должно помочь вам понять логику
приведенные выше формулы декартово-полярного преобразования. За
Например, график должен помочь вам понять, почему tanθ =
у/х. Помните свою тригонометрию: тангенс теты (tanθ) равен
равно длине противоположной стороны, деленной на
длина соседней стороны. Другой способ сказать это
у/х.
Другой способ сказать это
у/х.
Теперь научимся переводить полярные координаты в прямоугольные координаты и наоборот. Следующий пример преобразует полярные координаты в xy-координаты. Убедитесь, что ваш калькулятор находится в градусном режиме.
Пример 3:
Найдите xy-координаты для следующего вектора, заданного в полярной форме: (467,26, 124,2°).
Заданы полярные координаты вектора. Признайте, что р = 467,26 и Θ = 124,2° в этой задаче. Мы хотим найти прямоугольная координата вектора. Теперь подставьте значения для r и θ в формулы сверху:
x = rcosq
x = (467,26)cos(124,2)
x = -262,64
y = rsinq
y = 467,26 (sin 124,2)
y = 386,46
Координата xy вектора (-262,64, 386,46).
Короче говоря, вы можете преобразовать полярные координаты в координаты xy следующим образом:
(r, q) —> (rcosθ, rsinθ) —> (x,y)
Теперь давайте поработаем в обратном направлении, изменив найденную нами координату xy
(-262,64, 386,46) обратно в полярную координату. Мы должны ожидать
получить полярные координаты, с которых мы начали в
начало примера 3: (467,26,124,2).
Мы должны ожидать
получить полярные координаты, с которых мы начали в
начало примера 3: (467,26,124,2).
Сначала найдем для r:
г = 467,26
Первая часть преобразования сработала: r = 467,26, т.е. что мы ожидали получить от работы в обратном направлении. Теперь давайте решим для θ с использованием tanθ = y/x:
тангенс θ = y/x
тангенс θ = 386,46/-262,64
θ = тангенс -1 (-1,47)
θ = -55,8
Итак, здесь мы получаем θ = -55,8°. Ожидалось, что мы решить для тета и получить 124,2 °. Что случилось? Обратите внимание, что абсолютное значение -55,8°, 55,8°, равно дополнительный до 124,2°. Иногда, вместо того, чтобы получить настоящую тета значение, преобразование координат xy в полярные координаты может дать вам любое из следующих значений вместо фактического тета (θ):
Как оказалось, результат нашего преобразования, θ = -55,8°,
является отрицательным значением дополнительного угла теты. Другими словами,
дополнительный угол теты равен 55,8°, а его отрицательный угол равен -55,8°.
В следующих параграфах объясняется, как идентифицировать
значение, которое вы получаете, и как его использовать для получения реального тета-значения
ты ищешь.
Другими словами,
дополнительный угол теты равен 55,8°, а его отрицательный угол равен -55,8°.
В следующих параграфах объясняется, как идентифицировать
значение, которое вы получаете, и как его использовать для получения реального тета-значения
ты ищешь.
Идентификация квадранта координат
Прежде чем решать какие-либо проблемы преобразования, вы должны определить квадрант в котором лежат ваши начальные координаты. Когда вы рисуете вектор, определяемый полярной координатой и линией между xy-координата и начало координат, они должны выглядеть так же, как и располагаться в том же квадранте . Единственная разница заключается в том, как они выражаются: (x, y) против (r, θ).
Допустим, вы начинаете с координаты xy (-3,2) и хотите преобразовать его в полярную координату. Вы должны сначала признать, что (-3,2) находится во втором квадранте. Знаки координат подскажет вам, где находится их квадрант. Чтобы уточнить, изучите изображение ниже:
То же самое касается преобразования полярных координат в xy. первый шаг проблемы преобразования состоит в том, чтобы посмотреть на начальный
полярную координату и распознать квадрант, которому она принадлежит.
Для полярных координат координата направления (θ)
определяет квадрант, а не r. Изображение ниже иллюстрирует
размещение в квадрантах полярных координат:
первый шаг проблемы преобразования состоит в том, чтобы посмотреть на начальный
полярную координату и распознать квадрант, которому она принадлежит.
Для полярных координат координата направления (θ)
определяет квадрант, а не r. Изображение ниже иллюстрирует
размещение в квадрантах полярных координат:
Для преобразования полярных координат в координаты xy этот квадрант поможет вам определить, выглядит ли ваша конверсия Правильно. Если полярная координата, с которой вы начали, находилась в третий квадрант, и ваша конверсия привела к xy-координата в другом квадранте, вы будете знать, что сделали Что-то не так. Квадрантное размещение для начального координата всегда должна совпадать с положением квадранта для координата после преобразования.
Для преобразования xy в полярные координаты, идентифицируя начальную
квадрант координаты поможет вам преобразовать в правильную тета.
Найденная полярная координата должна лежать в том же
квадрант в качестве начальной координаты xy. Как указано выше,
решение для тета может быть липким. Вы не всегда найдете
правильное значение тета, но ваш ответ будет связан с
Это. Давайте использовать координаты из последней части
Пример 3, чтобы продемонстрировать, как найти тета.
Как указано выше,
решение для тета может быть липким. Вы не всегда найдете
правильное значение тета, но ваш ответ будет связан с
Это. Давайте использовать координаты из последней части
Пример 3, чтобы продемонстрировать, как найти тета.
Пример 4
Мы хотим преобразовать результаты примера 3 (-262,64, 386,46), обратно в свою форму полярных координат. Мы рассчитываем получить начальная полярная координата из примера задачи (467,26, 124,2°). Как вы помните, преобразование прошло гладко, когда мы решили для r: мы получили 467,26, как и ожидалось. Однако, когда мы решили для θ, мы получили -55,8° вместо 124,2°. Как мы обращаемся Эта проблема?
Первым шагом является определение квадранта, в котором находится наша начальная координата xy. Координата (-262,64, 386,46)
состоит из отрицательного значения x и положительного значения y, поэтому
расположен во втором квадранте. Это означает, что наш
преобразование должно дать полярную координату второго квадранта. Очевидно, что найденное нами значение тета (-55,8°) не является
угол второго квадранта; он находится в четвертом квадранте (вспомним
что отрицательные углы отсчитываются по часовой стрелке от 0°
ось).
Очевидно, что найденное нами значение тета (-55,8°) не является
угол второго квадранта; он находится в четвертом квадранте (вспомним
что отрицательные углы отсчитываются по часовой стрелке от 0°
ось).
При использовании тригонометрии в этих задачах преобразования тета значения, которые вы найдете, могут относиться к оси x. ( угол будет всегда по отношению к оси абсцисс, если вы используете формулу tanθ = y/x для решения θ.) Это означает что тета может быть углом, образованным 1) линией между начало координат и описанная точка xy, и 2) по горизонтали или по оси X. Это не обязательно тета которая принадлежит полярной координате, но связана с Это. Вернитесь к изображению, демонстрирующему тригонометрию. за полярными и прямоугольными координатами (воспроизведено ниже слева). Изображение справа показывает, как это может быть отражено во всех четыре квадранта:
При работе с тригонометрическими функциями, такими как тангенс, синус,
и косинус, тета — это угол внутри прямоугольного треугольника, как показано
выше. Это связано с тем, что значения x и y в исходном
xy-координата (та, которую мы хотим преобразовать в полярную)
соответствуют сторонам прямоугольного треугольника. Угол, который мы
получил, 55,8° (при этом не обращайте внимания на знак минус
точка, это поясняется ниже) соответствует θ 2 на изображении справа вверху.
Это связано с тем, что значения x и y в исходном
xy-координата (та, которую мы хотим преобразовать в полярную)
соответствуют сторонам прямоугольного треугольника. Угол, который мы
получил, 55,8° (при этом не обращайте внимания на знак минус
точка, это поясняется ниже) соответствует θ 2 на изображении справа вверху.
Если вы получаете острое значение тета (менее 90°) и помещает полярная координата в «неправильном» квадранте, вы наверное найти угол между вектором или отрезком прямой и ось х. Оттуда легко решить для фактического тета.
Вернемся к найденной нами тета: θ = -55,8°. Это острый угол, который помещает полярную координату в неправильный квадрант (нам нужен угол второго квадранта). Если вы подозреваете что вы нашли тета между вектором и горизонталью ось, принять его абсолютное значение (мы имеем дело только с положительными здесь углы). Абсолютное значение -55,8° равно 55,8°.
Затем выясните, где находится угол, который вы нашли. Тебе известно
что он должен быть расположен в том же квадранте, что и исходный
Координата найдена. Итак, если вы ожидаете второго
координата квадранта, угол, который вы нашли, будет тем,
между вектором и осью x во втором квадранте. Сейчас мы
нужно вычесть 55,8° из 180°, потому что полярные координаты
измерено от положительной оси x или нуля градусов:
Тебе известно
что он должен быть расположен в том же квадранте, что и исходный
Координата найдена. Итак, если вы ожидаете второго
координата квадранта, угол, который вы нашли, будет тем,
между вектором и осью x во втором квадранте. Сейчас мы
нужно вычесть 55,8° из 180°, потому что полярные координаты
измерено от положительной оси x или нуля градусов:
180° — 55,8° = 124,2° (угол второго квадранта, который мы ожидали получить!)
Изображение ниже должно помочь вам получить визуальное представление об этом:
Короче говоря, при нахождении θ для задачи преобразования xy в полярные координаты:
узнать квадрант, в котором должна находиться ваша координата (это тот же квадрант, что и исходный, до преобразования координата в)
найдите тета с помощью тригонометрии, обычно по формуле tanθ = y/x
, если ваш ответ помещает полярную координату в неправильный квадрант, возьмите ее абсолютное значение
затем определите тэту на основе 1) квадранта, в котором она должна быть в и 2) вероятная возможность того, что угол, который вы нашли, дополнение теты и 3) угол, который вы нашли, вероятно, дано относительно горизонтальной оси.

Следующий пример демонстрирует преобразование xy в полярные координаты.
Пример 5:
Выразите следующую координату xy в полярной форме: (-1, -√3).
Сначала мы определяем квадрант координаты. Координата (-1, -√3) находится в третьем квадранте. Мы знаем, что полярный координаты, которые мы находим, также должны находиться в третьем квадранте.
Затем найдите r, используя формулу для r:
(помните, что мы используем только положительные значения r, поэтому r = 2)
Теперь найдем θ по следующей формуле:
tanθ = y/x
tanθ = (-√3/-1) = √3
tan -1 (√3) = θ
60° = θ
Угловая мера 60° лежит в первой четверти. Наши начальные координаты (-1, √3) находятся в третьем квадранте, а не в первом. Поэтому мы должны использовать наше знание триггера, чтобы указать нам правильный значение тета. Так как наш угол должен вести нас всю дорогу вокруг третьего квадранта мы знаем, что 60° соответствует θ s ниже («s» означает дополнительный):
Тета-значение равно 180° + 60° (или θ s ) = 240°. Это угол третьего квадранта.
Это угол третьего квадранта.
Полярная форма данной xy-координаты: (2, 240°) .
Практическая задача 1:
Найдите модуль и направление заданного вектора:
u: звездная величина 3,62, пеленг 25°
v: звездная величина 14,5, пеленг 105°
ш: у + в
Практическая задача 2:
Найдите прямоугольную координату для следующей точки на полярном графике: (4, 30°)
Практическая задача 3:
Найдите полярную координату для следующей точки на декартовой плоскости: (-√2, -√2)
Прямоугольная система координат распространяться на более высокие измерения.
Если вектор сдвинут так, что его начальная точка находится в начале прямоугольной координатной плоскости, говорят, что он находится в стандартной позиции . Если вектор равен вектору и имеет начальную точку в начале координат, говорят, что он является стандартным вектором для . Другие названия стандартного вектора включают радиус-вектор и вектор положения (рис. 1).
Другие названия стандартного вектора включают радиус-вектор и вектор положения (рис. 1).
Рисунок 1
Векторы, нарисованные на плоскости.
Вектор — это стандартный вектор для всех векторов на плоскости с тем же направлением и величиной, что и . Чтобы найти стандартный вектор для геометрического вектора в координатной плоскости, нужны только координаты точки P должен быть найден, потому что точка 0 находится в начале координат. Если координаты точки A составляют ( x A , Y A ) и координаты точки B ( x B , y ), затем B , Then B, Then B, Then B, Then B, Then B, Then B, Then B, Then B, Then B, Then B, Then B, Then B, Then B, Y ), Then B, B . координаты точки P:
Пример 1: Если конечные точки вектора имеют координаты A (−2, −7) и B (3, 2), то каковы координаты точки P , такой, что это стандартный вектор и = (см. рис. 2)?
рис. 2)?
Рисунок 2
Чертеж для примера 1.
Если координаты точки P равны ( x , y ),
Алгебраический вектор представляет собой упорядоченную пару действительных чисел. Алгебраический вектор, соответствующий стандартному геометрическому вектору, обозначается как ⟨ a, b ⟩ если конечная точка P имеет координаты (a, b) . Числа a и b называются компонентами вектора ⟨ a, b ⟩ (см. рис. 3 ).
Рисунок 3
Компоненты вектора.
Если a, b, c и d — все действительные числа, такие что a = c и b = d , то вектор v = ⟨ a, b ⟩ и вектор u = ⟨ c, d ⟩ считаются равными. То есть алгебраические векторы с равными соответствующими компонентами равны. Если обе компоненты вектора равны нулю, говорят, что вектор является нулевым вектором . Величина вектора v = ⟨a, b⟩ равна .
Если обе компоненты вектора равны нулю, говорят, что вектор является нулевым вектором . Величина вектора v = ⟨a, b⟩ равна .
Пример 2: Какова величина вектора u = ⟨3, −5⟩?
Сложение векторов определяется как сложение соответствующих компонент векторов, т. е. если v = ⟨ a, b ⟩ и u = ⟨c, d ⟩ , то v + 0 4 u = 0 4 u ⟨а + в, б + г⟩ (рис. 4 ).
Рисунок 4
Добавление вектора.
Скалярное умножение определяется как умножение каждого компонента на константу, т. е. если v = ⟨a, b⟩ и q — константа, тогда q v = q⟨a, b⟩ = ⟨qa, qb⟩ .
Пример 3: Если v = ⟨8, −2⟩ и w = ⟨3, 7⟩, то найти 5 v −2 w .
Единичный вектор — это вектор, величина которого равна 1. Единичный вектор v с тем же направлением, что и ненулевой вектор u , можно найти следующим образом:
Пример 4 : Найдите единичный вектор v с тем же направлением, что и вектор u , учитывая, что u = ⟨7, − 1⟩.
Два специальных единичных вектора, i = ⟨1, 0⟩ и j = ⟨0, 1⟩, могут использоваться для выражения любого вектора v = ⟨a, b⟩ .
Пример 5: Запишите u = ⟨5, 3⟩ через i и j единичных вектора (рис. 5 ).
Рисунок 5
Чертеж для примера 5.
Векторы обладают алгебраическими свойствами, аналогичными свойствам действительных чисел (таблица 1).
Пример 6: Найдите 4 u + 5 v , если u = 7 i − 3 j и v = −2 7 i 5 44
Учитывая два вектора, u = ⟨ a, b⟩ = a i + b j and v = ⟨c, d⟩ = c i + d j , скалярное произведение , записанное как u · v , является скалярной величиной u ˙ v = ac + bd . Если u, v и w — векторы, а q — действительное число, то скалярные произведения обладают следующими свойствами:
Последнее свойство, u ˙ v = | и | | против | cos α можно использовать для нахождения угла между двумя ненулевыми векторами u и v . Если два вектора перпендикулярны друг другу и образуют угол 90°, говорят, что они ортогональны . Поскольку cos 90° = 0, скалярное произведение любых двух ортогональных векторов равно 0,
Если два вектора перпендикулярны друг другу и образуют угол 90°, говорят, что они ортогональны . Поскольку cos 90° = 0, скалярное произведение любых двух ортогональных векторов равно 0,
Пример 7: Учитывая, что u = ⟨ 5 , −3⟩ и v = ⟨6, 10⟩, покажите, что u и v ортогональны, показав, что скалярное произведение u и v равно нулю.
Пример 8: Чему равен угол между u = ⟨5, −2⟩ и v = ⟨6, 11⟩?
Говорят, что объект находится в состоянии статического равновесия , если сумма всех векторов сил, действующих на объект, равна нулю.
Пример 9: Канатоходец весом 150 фунтов стоит ближе к одному концу веревки, чем к другому. Веревка меньшей длины отклоняется от горизонтали на 5°. Более длинная веревка отклоняется на 3°. Чему равно натяжение каждой части веревки?
Нарисуйте диаграмму силы со всеми тремя векторами силы в стандартном положении (рис. 6).
6).
Рисунок 6
Чертеж для примера 9.
Сумма векторов силы должна быть равна нулю для каждого компонента.
Для компонента i : − | u |cos 5° + | против | cos 3° = 0
Для компонента j : | и | sin5° + |v| cos 3 ° — 150 =
Решите эти два уравнения для | и | и | против |:
Подстановка значений синусов и косинусов:
Умножьте первое уравнение на 0,0872, а второе на 0,9962:
Сложите два уравнения и решите | против |:
Подставить и решить | и |:
Векторов | безграничная физика |
Компоненты вектора
Векторы представляют собой геометрические представления величины и направления и могут быть выражены в виде стрелок в двух или трех измерениях.
Цели обучения
Сравнение двумерных и трехмерных векторов
Ключевые выводы
Ключевые точки
- Векторы можно разбить на две составляющие: величину и направление.
- Взяв анализируемый вектор за гипотенузу, можно найти горизонтальную и вертикальную составляющие, составив прямоугольный треугольник. Нижний край треугольника — это горизонтальная составляющая, а сторона, противоположная углу, — вертикальная составляющая.
- Угол, который вектор образует с горизонтом, можно использовать для вычисления длины двух компонентов.
Ключевые термины
- координаты : Числа, указывающие положение относительно некоторой оси. Пример: координаты
x\text{x}x
иy\text{y}y
указывают положение относительно осейx\text{x}x
иy\text{y}y
. - ось : Воображаемая линия, вокруг которой вращается или симметрично располагается объект.

- величина : Число, присвоенное вектору, указывающее его длину.
Обзор
Векторы — это геометрические представления величины и направления, которые часто представляются прямыми стрелками, начинающимися в одной точке координатной оси и заканчивающимися в другой точке. Все векторы имеют длину, называемую величиной, которая представляет некоторое интересующее качество, так что вектор можно сравнить с другим вектором. Векторы, будучи стрелками, также имеют направление. Это отличает их от скаляров, которые представляют собой просто числа без направления.
Вектор определяется его величиной и ориентацией относительно набора координат. При анализе векторов часто бывает полезно разбить их на составные части. Для двумерных векторов эти компоненты горизонтальны и вертикальны. Для трехмерных векторов компонент величины одинаков, но компонент направления выражается через
x\text{x}x
,
y\text{y}y
и
z\text {z}z
.
Разложение вектора
Чтобы визуализировать процесс разложения вектора на его компоненты, начните с рисования вектора из начала координат набора координат. Затем нарисуйте прямую линию от начала координат вдоль оси X, пока линия не сравняется с вершиной исходного вектора. Это горизонтальная составляющая вектора. Чтобы найти вертикальную составляющую, проведите прямую линию вверх от конца горизонтального вектора, пока не достигнете вершины исходного вектора. Вы должны обнаружить, что у вас есть прямоугольный треугольник, исходный вектор которого является гипотенузой.
Разложение вектора на горизонтальную и вертикальную составляющие — очень полезный метод для понимания физических задач. Всякий раз, когда вы видите движение под углом, вы должны думать о нем как о движении по горизонтали и вертикали одновременно. Такое упрощение векторов может ускорить вычисления и помочь отслеживать движение объектов.
com/embed/EUrMI0DIh50?feature=oembed» allowfullscreen=»»/>Скаляры и векторы : Г-н Андерсен объясняет разницу между скалярными и векторными величинами. Он также использует демонстрацию, чтобы показать важность векторов и сложения векторов.
Компоненты вектора : Исходный вектор, определенный относительно набора осей. Горизонтальная составляющая простирается от начала вектора до его самой дальней координаты x. Вертикальный компонент простирается от оси x до самой вертикальной точки вектора. Вместе две компоненты и вектор образуют прямоугольный треугольник.
Скаляры против векторов
Скаляры — это физические величины, представленные одним числом, а векторы представлены как числом, так и направлением.
Цели обучения
Различие между величинами, которые представляют скаляры и векторы.
Ключевые термины
- Оси координат : Набор перпендикулярных линий, определяющих координаты относительно начала координат. Пример: оси координат x и y определяют горизонтальное и вертикальное положение.
Физические величины обычно можно разделить на две категории: векторы и скаляры. Эти две категории типизированы тем, какая информация им требуется. Векторы требуют двух частей информации: величины и направления. Напротив, для скаляров требуется только величина. О скалярах можно думать как о числах, тогда как о векторах следует думать скорее как о стрелках, указывающих в определенном направлении.
Вектор A : Пример вектора. Векторы обычно представлены стрелками, длина которых представляет величину, а их направление представлено направлением, на которое указывает стрелка.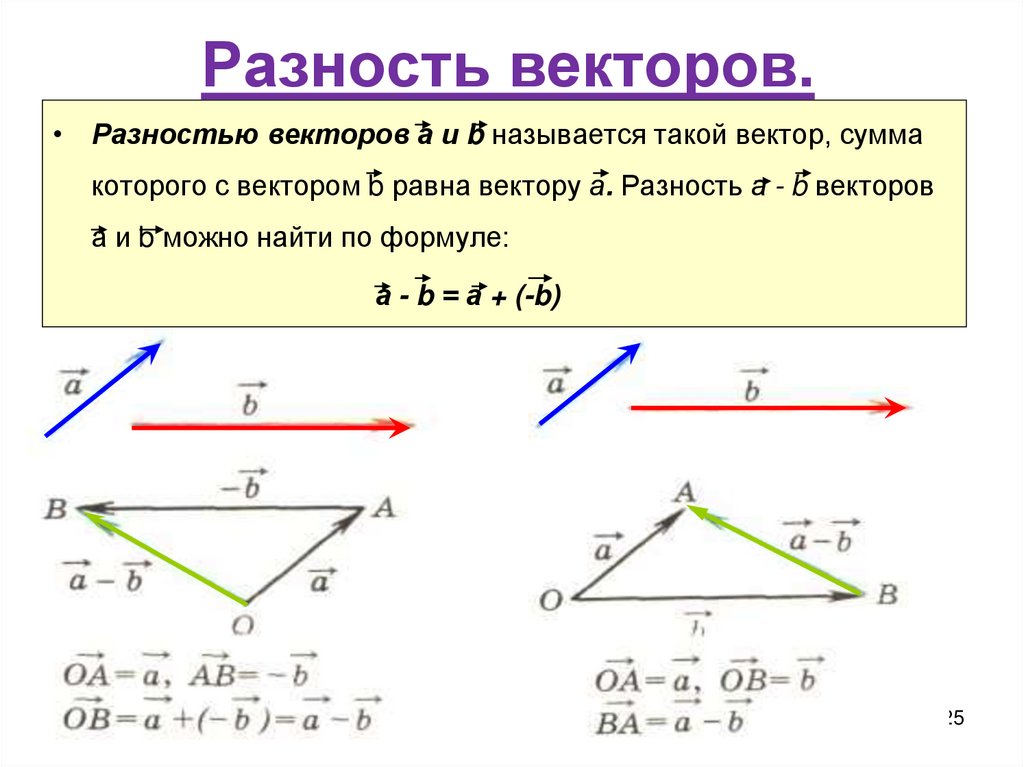
Векторы требуют как величины, так и направления. Величина вектора — это число для сравнения одного вектора с другим. В геометрической интерпретации вектора вектор изображается стрелкой. Стрелка состоит из двух частей, которые ее определяют. Две части — это его длина, которая представляет величину, и его направление относительно некоторого набора координатных осей. Чем больше величина, тем длиннее стрелка. Физические понятия, такие как перемещение, скорость и ускорение, являются примерами величин, которые могут быть представлены векторами. Каждая из этих величин имеет как величину (как далеко или как быстро), так и направление. Чтобы указать направление, должно быть что-то, относительно чего это направление. Обычно эта опорная точка представляет собой набор координатных осей, таких как плоскость x-y.
Скаляры отличаются от векторов тем, что у них нет направления. Скаляры используются в основном для представления физических величин, для которых направление не имеет смысла. Некоторые примеры из них: масса, высота, длина, объем и площадь. Говорить о направлении этих величин бессмысленно, поэтому их нельзя выразить в виде векторов.
Некоторые примеры из них: масса, высота, длина, объем и площадь. Говорить о направлении этих величин бессмысленно, поэтому их нельзя выразить в виде векторов.
Разница между векторами и скалярами, введение и основы : В этом видео представлена разница между скалярами и векторами. Вводятся понятия о величине и направлении и приводятся примеры как векторов, так и скаляров.
Графическое сложение и вычитание векторов
Векторы можно добавлять или вычитать графически, размещая их встык на наборе осей.
Цели обучения
Смоделируйте графический метод сложения и вычитания векторов
Ключевые выводы
Ключевые точки
- Чтобы сложить векторы, положите первый вектор на набор осей хвостом в начале координат. Поместите следующий вектор хвостом в голову предыдущего вектора.
 Когда больше нет векторов, проведите прямую линию от начала координат до начала последнего вектора. Эта линия является суммой векторов.
Когда больше нет векторов, проведите прямую линию от начала координат до начала последнего вектора. Эта линия является суммой векторов. - Чтобы вычесть векторы, действуйте так же, как при сложении двух векторов, но переверните вычитаемый вектор по осям, а затем соедините его хвост к началу, как при сложении.
- Добавление или вычитание любого количества векторов дает результирующий вектор.
Ключевые термины
- начало координат : Центр координатной оси, определяемый как координата 0 по всем осям.
- Оси координат : Набор перпендикулярных линий, определяющих координаты относительно начала координат. Пример: оси координат x и y определяют горизонтальное и вертикальное положение.
Сложение и вычитание векторов
Одним из способов, которым представление физических величин в виде векторов упрощает анализ, является легкость, с которой векторы могут быть добавлены друг к другу.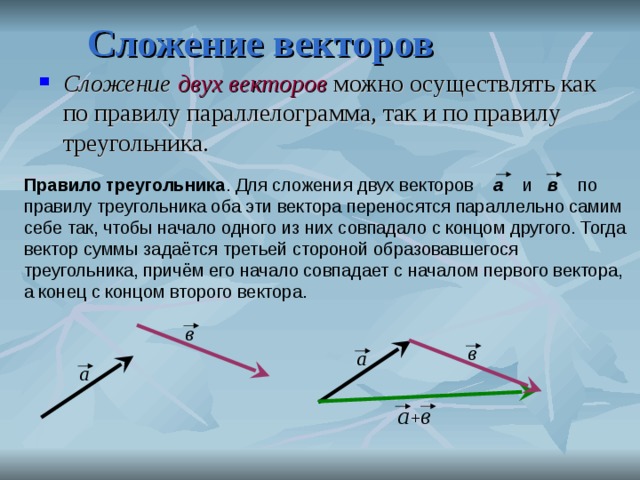 Поскольку векторы являются графическими визуализациями, сложение и вычитание векторов можно выполнять графически.
Поскольку векторы являются графическими визуализациями, сложение и вычитание векторов можно выполнять графически.
Графический метод сложения векторов также известен как метод «голова к хвосту». Для начала нарисуйте набор координатных осей. Затем нарисуйте первый вектор так, чтобы его хвост (база) находился в начале осей координат. Для сложения векторов не имеет значения, какой вектор вы рисуете первым, поскольку сложение является коммутативным, но для вычитания убедитесь, что вектор, который вы рисуете первым, является вектором, который вы вычитаете из . Следующий шаг — взять следующий вектор и нарисовать его так, чтобы его хвост начинался с головы предыдущего вектора (со стороны стрелки). Продолжайте размещать каждый вектор в начале предыдущего, пока все векторы, которые вы хотите добавить, не будут соединены вместе. Наконец, нарисуйте прямую линию от начала до начала последнего вектора в цепочке. Эта новая строка является векторным результатом сложения этих векторов.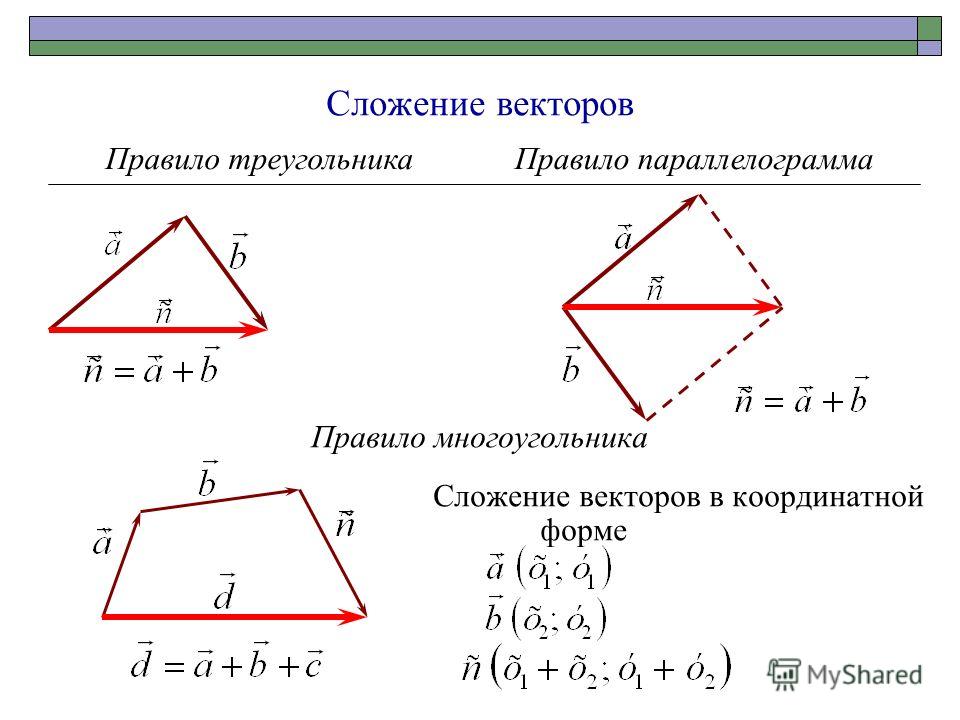
Графическое сложение векторов : Метод сложения векторов «голова к хвосту» требует, чтобы вы разложили первый вектор вдоль набора координатных осей. Затем поместите хвост следующего вектора на голову первого. Нарисуйте новый вектор от начала координат до начала последнего вектора. Этот новый вектор является суммой двух исходных.
Сложение векторов Урок 1 из 2: метод сложения от начала до конца : Это видео знакомит зрителей со сложением и вычитанием векторов. В первом уроке показано графическое сложение, а во втором видео используется более математический подход и показано сложение векторов по компонентам.
Для вычитания векторов метод аналогичен. Убедитесь, что первый вектор, который вы рисуете, является тем, из которого нужно вычесть. Затем, чтобы вычесть вектор, действуйте так же, как если бы складывали напротив 9. 0024 этого вектора. Другими словами, переверните вектор, который нужно вычесть, по осям, а затем соедините его хвост к голове, как при сложении. Чтобы перевернуть вектор, просто поместите его голову туда, где был хвост, а хвост — туда, где была голова.
0024 этого вектора. Другими словами, переверните вектор, который нужно вычесть, по осям, а затем соедините его хвост к голове, как при сложении. Чтобы перевернуть вектор, просто поместите его голову туда, где был хвост, а хвост — туда, где была голова.
Добавление и вычитание векторов с использованием компонентов
Часто бывает проще складывать или вычитать векторы, используя их компоненты.
Цели обучения
Продемонстрируйте, как складывать и вычитать векторы по компонентам
Ключевые выводы
Ключевые точки
- Векторы можно разложить на горизонтальные и вертикальные составляющие.
- После разложения векторов на компоненты можно добавлять компоненты.
- Сложение соответствующих компонентов двух векторов дает вектор, являющийся суммой двух векторов.
Ключевые термины
- Компонент : часть вектора. Например, горизонтальные и вертикальные компоненты.

Использование компонентов для сложения и вычитания векторов
Другой способ добавления векторов — добавление компонентов. Ранее мы видели, что векторы могут быть выражены через их горизонтальные и вертикальные компоненты. Чтобы добавить векторы, просто выразите их оба в терминах их горизонтальных и вертикальных компонентов, а затем сложите компоненты вместе.
Вектор с горизонтальной и вертикальной компонентами : Вектор на этом изображении имеет величину 10,3 единицы и направление 29,1 градуса выше оси x. Его можно разложить на горизонтальную часть и вертикальную часть, как показано на рисунке.
Например, вектор длиной 5 под углом 36,9 градусов к горизонтальной оси будет иметь горизонтальную составляющую 4 единицы и вертикальную составляющую 3 единицы. Если бы мы добавили это к другому вектору той же величины и направления, мы бы получили вектор вдвое длиннее под тем же углом. Это можно увидеть, сложив горизонтальные компоненты двух векторов (
Это можно увидеть, сложив горизонтальные компоненты двух векторов (
4+44+44+4
) и два вертикальных компонента (
3+33+33+3
). Эти добавления дают новый вектор с горизонтальной составляющей 8 (
4+44+44+4
) и вертикальный компонент 6 (
3+33+33+3
). Чтобы найти результирующий вектор, просто поместите конец вертикального компонента в начало (со стороны стрелки) горизонтального компонента, а затем проведите линию от начала координат к началу вертикального компонента. Эта новая линия является результирующим вектором. Он должен быть в два раза длиннее оригинала, так как оба его компонента в два раза больше, чем были ранее.
Чтобы вычесть вектора по компонентам, просто вычтите два горизонтальных компонента друг из друга и сделайте то же самое для вертикальных компонентов. Затем нарисуйте результирующий вектор, как вы это делали в предыдущей части.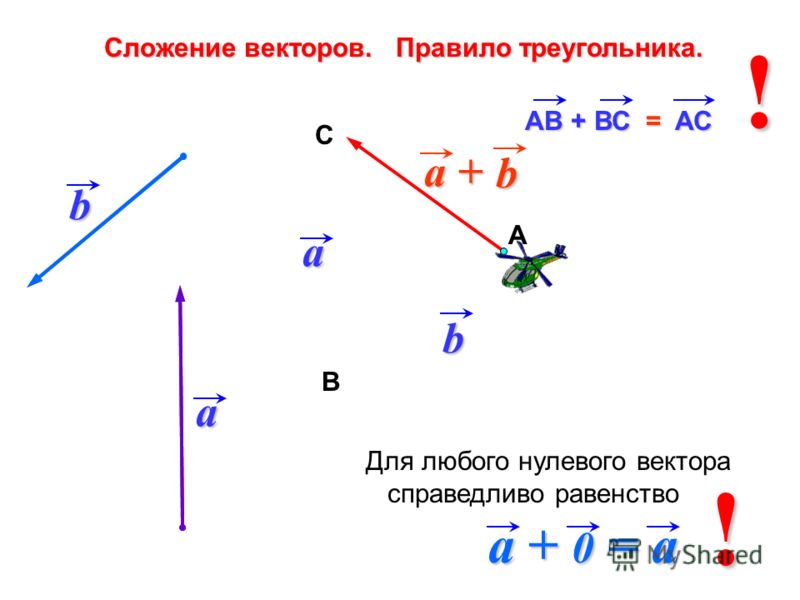
Сложение векторов Урок 2 из 2: Сложение векторов по компонентам : Это видео знакомит зрителей с сложением векторов с использованием математического подхода и демонстрирует сложение векторов по компонентам.
Умножение векторов на скаляр
Умножение вектора на скаляр изменяет величину вектора, но не направление.
Цели обучения
Обобщите взаимодействие между векторами и скалярами
Ключевые выводы
Ключевые моменты
- Вектор — это величина, имеющая как величину, так и направление.
- Скаляр – это величина, имеющая только величину.
- Умножение вектора на скаляр эквивалентно умножению величины вектора на скаляр. Вектор удлиняется или сжимается, но не меняет направление.
Ключевые термины
- вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.

- величина : Число, присвоенное вектору, указывающее его длину.
- скаляр : Величина, имеющая величину, но не направление; сравнить вектор.
Обзор
Хотя векторы и скаляры представляют разные типы физических величин, иногда необходимо, чтобы они взаимодействовали. Хотя добавление скаляра к вектору невозможно из-за их разных измерений в пространстве, можно умножить вектор на скаляр. Однако скаляр нельзя умножить на вектор.
Чтобы умножить вектор на скаляр, просто умножьте аналогичные компоненты, то есть модуль вектора на модуль скаляра. Это приведет к новому вектору с тем же направлением, но произведением двух величин.
Пример
Например, если у вас есть вектор A с определенной величиной и направлением, умножение его на скаляр a с величиной 0,5 даст новый вектор с величиной, равной половине исходной. Точно так же, если вы возьмете число 3, которое является чистым и безразмерным скаляром, и умножите его на вектор, вы получите версию исходного вектора, которая в 3 раза длиннее. В качестве более физического примера возьмем гравитационную силу, действующую на объект. Сила представляет собой вектор, величина которого зависит от скаляра, известного как масса, и направлена вниз. Если масса тела удвоится, то и сила тяжести удвоится.
В качестве более физического примера возьмем гравитационную силу, действующую на объект. Сила представляет собой вектор, величина которого зависит от скаляра, известного как масса, и направлена вниз. Если масса тела удвоится, то и сила тяжести удвоится.
Умножение векторов на скаляры очень полезно в физике. Большинство единиц, используемых в векторных величинах, по сути являются скалярами, умноженными на вектор. Например, единица измерения скорости в метрах в секунду, которая является вектором, состоит из двух скаляров, являющихся величинами: скаляра длины в метрах и скаляра времени в секундах. Чтобы сделать это преобразование из величин в скорость, нужно умножить единичный вектор в определенном направлении на эти скаляры.
Скалярное умножение : (i) Умножение вектора
A\text{A}A
на скаляр
a=0,5\text{a}=0,5a=0,5
6 B 9000 дает вектор \text{B}B, что вдвое короче.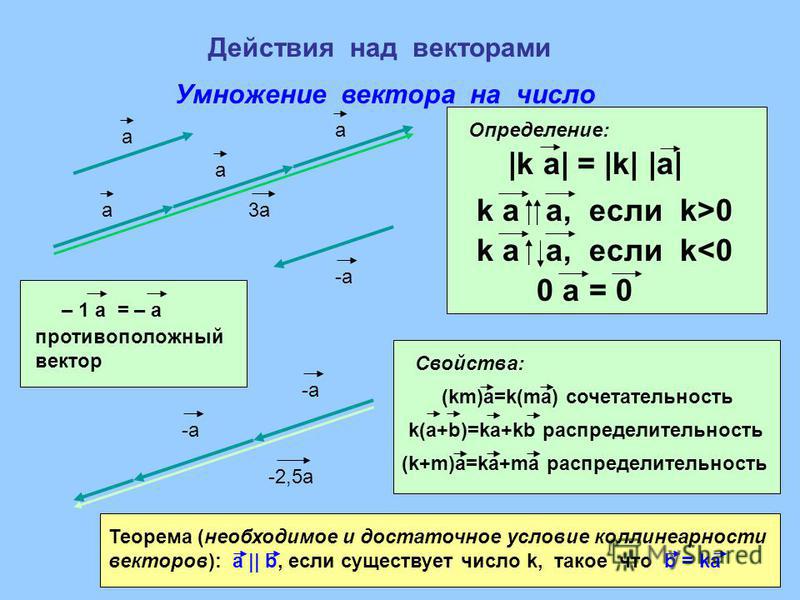 (ii) Умножение вектора
(ii) Умножение вектора
A\text{A}A
на 3 увеличивает его длину в три раза. (iii) Удвоение массы (скалярной) удваивает силу (вектор) силы тяжести.
Единичные векторы и умножение на скаляр
Умножение вектора на скаляр равносильно умножению его величины на число.
Цели обучения
Предсказать влияние умножения вектора на скаляр
Ключевые выводы
Ключевые точки
- Единичный вектор — это вектор величины (длины) 1.
- Скаляр — это физическая величина, которую можно представить одним числом. В отличие от векторов скаляры не имеют направления.
- Умножение вектора на скаляр аналогично умножению величины вектора на число, представленное скаляром.
Ключевые термины
- скаляр : Величина, которая может быть описана одним числом, в отличие от вектора, для которого требуется направление и число.

- Единичный вектор : Вектор величины 1.
Помимо сложения векторов, векторы также можно умножать на константы, известные как скаляры. Скаляры отличаются от векторов тем, что они представлены величиной, но не направлением. Примеры скаляров включают массу, высоту или объем объекта.
Скалярное умножение : (i) Умножение вектора A на 0,5 вдвое уменьшает его длину. (ii) Умножение вектора A на 3 увеличивает его длину в три раза. (iii) Увеличение массы (скалярной) увеличивает силу (вектор).
При умножении вектора на скаляр направление вектора не меняется, а величина умножается на величину скаляра. Это приводит к тому, что новая стрелка вектора указывает в том же направлении, что и старая, но с большей или меньшей длиной. Вы также можете выполнить скалярное умножение, используя компоненты вектора. Получив компоненты вектора, умножьте каждый из компонентов на скаляр, чтобы получить новые компоненты и, следовательно, новый вектор. 9
9
. Треугольник над буквами называется «шляпой». Единичные векторы в декартовых координатах описывают окружность, известную как «единичная окружность», которая имеет радиус один. Это можно увидеть, взяв все возможные векторы длины один под всеми возможными углами в этой системе координат и поместив их в координаты. Если бы вы нарисовали линию, соединяющую все вершины всех векторов вместе, вы бы получили круг радиуса один.
Положение, перемещение, скорость и ускорение в виде векторов
Позиция, смещение, скорость и ускорение могут быть показаны векторами, поскольку они определяются в терминах величины и направления.
Цели обучения
Изучение применения векторов при анализе физических величин
Основные выводы
Ключевые моменты
- Векторы — это стрелки, состоящие из величины и направления. Они используются в физике для представления физических величин, которые также имеют как величину, так и направление.

- Смещение — это физический термин, означающий расстояние объекта от точки отсчета. Поскольку смещение содержит две части информации: расстояние от опорной точки и направление от точки, оно хорошо представлено вектором.
- Скорость определяется как скорость изменения смещения во времени. Чтобы узнать скорость объекта, нужно знать, как быстро меняется смещение и в каком направлении. Поэтому он также хорошо представлен вектором.
- Ускорение, являющееся скоростью изменения скорости, также требует как величины, так и направления относительно некоторых координат.
- При рисовании векторов часто не хватает места, чтобы нарисовать их в масштабе, который они представляют, поэтому важно где-то указать, в каком масштабе они рисуются.
Ключевые термины
- скорость : Скорость изменения смещения по отношению к изменению во времени.
- рабочий объем : Длина и направление прямой линии между двумя объектами.

- ускорение : скорость изменения скорости тела во времени
Использование векторов
Векторы могут использоваться для представления физических величин. Чаще всего в физике векторы используются для представления смещения, скорости и ускорения. Векторы представляют собой комбинацию величины и направления и изображаются в виде стрелок. Длина представляет собой величину, а направление этой величины — это направление, в котором указывает вектор. Поскольку векторы построены таким образом, полезно анализировать физические величины (как с размером, так и с направлением) как векторы.
Приложения
В физике векторы полезны, потому что они могут визуально представлять положение, смещение, скорость и ускорение. При рисовании векторов часто не хватает места, чтобы нарисовать их в том масштабе, который они представляют, поэтому важно где-то указать, в каком масштабе они рисуются. Например, при рисовании вектора, представляющего величину 100, можно нарисовать линию длиной 5 единиц в масштабе
Например, при рисовании вектора, представляющего величину 100, можно нарисовать линию длиной 5 единиц в масштабе
120\displaystyle \frac{1}{20}201
. Когда обратная шкала умножается на нарисованную величину, она должна равняться фактической величине.
Положение и перемещение
Смещение определяется как расстояние в любом направлении от объекта относительно положения другого объекта. Физики используют концепцию вектора положения в качестве графического инструмента для визуализации перемещений. Вектор положения выражает положение объекта от начала системы координат. Вектор положения также можно использовать для отображения положения объекта по отношению к опорной точке, вторичному объекту или исходному положению (при анализе того, насколько далеко объект переместился от своего исходного положения). Вектор положения представляет собой прямую линию, проведенную из произвольного начала координат к объекту. После рисования вектор имеет длину и направление относительно используемой системы координат.
После рисования вектор имеет длину и направление относительно используемой системы координат.
Скорость
Скорость также определяется величиной и направлением. Чтобы сказать, что что-то набирает или теряет скорость, нужно также сказать, насколько и в каком направлении. Например, самолет, летящий со скоростью 200
км/ч на северо-восток, может быть представлен вектором, указывающим в северо-восточном направлении с магнитудой 200.
км/ч\frac{\text{км}}{\text{ч}}чкм
. При рисовании вектора величина важна только как способ сравнения двух векторов с одинаковыми единицами измерения. Итак, если бы другой самолет летел 100
kmh\frac{\text{km}}{\text{h}}hkm
на юго-запад, стрелка-вектор должна быть вдвое короче и указывать в направлении на юго-запад.
Ускорение
Ускорение, являющееся скоростью изменения скорости во времени, состоит из величины и направления и рисуется с той же концепцией, что и вектор скорости.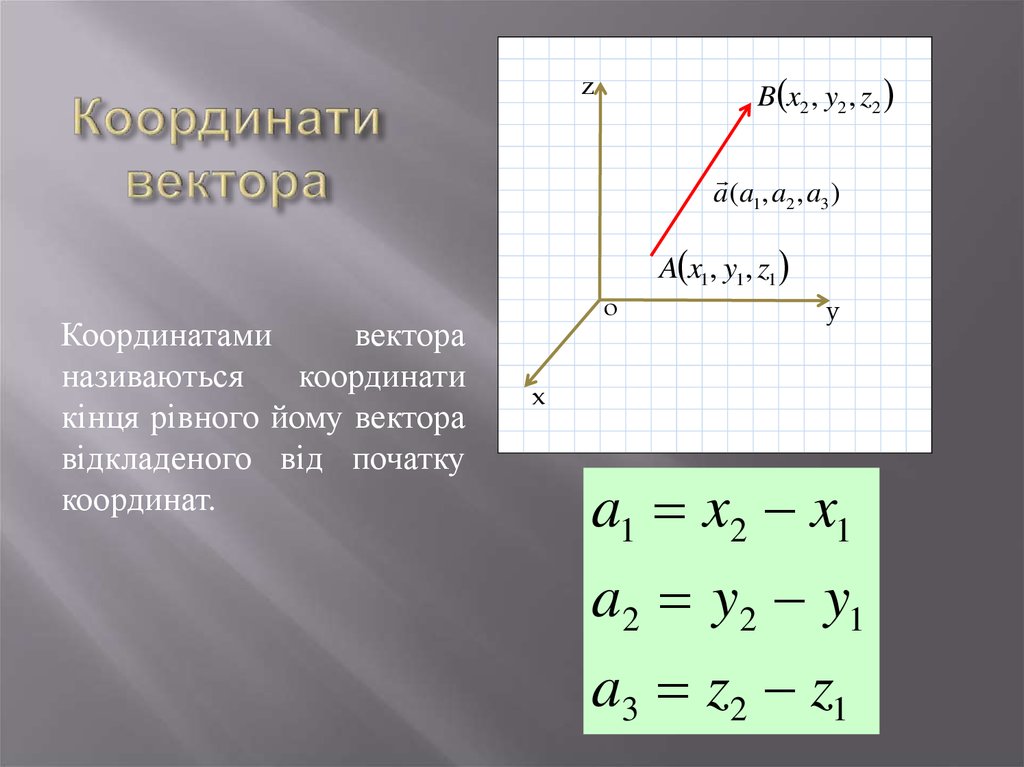 Значение ускорения не было бы полезным в физике, если бы величина и направление этого ускорения были неизвестны, поэтому эти векторы важны. Например, на диаграмме свободного тела падающего объекта было бы полезно использовать вектор ускорения рядом с объектом для обозначения его ускорения по направлению к земле. Если бы гравитация была единственной силой, действующей на объект, этот вектор был бы направлен вниз с величиной 9.2}s2ft
Значение ускорения не было бы полезным в физике, если бы величина и направление этого ускорения были неизвестны, поэтому эти векторы важны. Например, на диаграмме свободного тела падающего объекта было бы полезно использовать вектор ускорения рядом с объектом для обозначения его ускорения по направлению к земле. Если бы гравитация была единственной силой, действующей на объект, этот вектор был бы направлен вниз с величиной 9.2}s2ft
.
Векторная диаграмма : Вот человек, поднимающийся в гору. Направление его движения определяется углом тета относительно вертикальной оси и длиной стрелки, идущей в гору. Он также ускоряется вниз под действием силы тяжести.
Лицензии и атрибуции
Контент под лицензией CC, совместно используемый ранее
- Курирование и доработка. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензионный контент CC, Конкретное указание авторства
- Сунил Кумар Сингх, Компоненты вектора.
 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - Евклидов вектор. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Euclidean_vector. Лицензия : CC BY-SA: Attribution-ShareAlike
- ось. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- координаты. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- величина. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Скаляры и векторы. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Без ограничений.
 Предоставлено : Amazon Web Services. Лицензия : CC BY: Attribution
Предоставлено : Amazon Web Services. Лицензия : CC BY: Attribution - Скаляр (физика). Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Евклидов вектор. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Скаляры и векторы. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Без ограничений. Предоставлено : Amazon Web Services. Лицензия : CC BY: Attribution
- Предоставлено : Wikimedia. Расположен по адресу : https://upload.
 wikimedia.org/wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. Лицензия : CC BY: Attribution
wikimedia.org/wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. Лицензия : CC BY: Attribution - Разница между векторами и скалярами, введение и основы. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, сложение и вычитание векторов: графические методы. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Безграничный. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- происхождение. Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary.org/wiki/origin. Лицензия : CC BY-SA: Attribution-ShareAlike
- Скаляры и векторы.
 Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube - Безграничный. Предоставлено : Amazon Web Services. Лицензия : CC BY: Attribution
- Предоставлено : Wikimedia. Расположен по адресу : https://upload.wikimedia.org/wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. Лицензия : CC BY: Attribution
- Разница между векторами и скалярами, введение и основы. Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, сложение и вычитание векторов: графические методы. 24 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/f6f19897573ef83351c5a79bc6899f489dd579a1/Figure_03_02_03.
 jpg. Лицензия : CC BY: Атрибуция
jpg. Лицензия : CC BY: Атрибуция - Сложение векторов Урок 1 из 2: Метод сложения головы к хвосту. Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, сложение и вычитание векторов: графические методы. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Безгранично. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Скаляры и векторы. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Без ограничений. Предоставлено : Amazon Web Services.
 Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution - Предоставлено : Wikimedia. Расположен по адресу : https://upload.wikimedia.org/wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. Лицензия : CC BY: Attribution
- Разница между векторами и скалярами, введение и основы. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, сложение и вычитание векторов: графические методы. 24 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/f6f19897573ef83351c5a79bc6899f489dd579a1/Figure_03_02_03.jpg. Лицензия : CC BY: Attribution
- Сложение векторов. Урок 1 из 2. Метод сложения «голова к хвосту». Лицензия : Общественное достояние: Нет данных Copyright .
 Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube - Колледж OpenStax, сложение и вычитание векторов: графические методы. 24 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/e393f2ed44776ae52ef846c931b787aaaf154c37/Figure_03_02_06a.jpg. Лицензия : CC BY: Attribution
- Добавление векторов Урок 2 из 2: Добавление векторов по компонентам. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Сунил Кумар Сингх, Scalar (Dot) Product. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- скалярная. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- вектор.
 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike - величина. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Скаляры и векторы. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Безграничный. Предоставлено : Amazon Web Services. Лицензия : CC BY: Attribution
- Предоставлено : Wikimedia. Расположен по адресу : https://upload.wikimedia.org/wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. Лицензия : CC BY: Attribution
- Разница между векторами и скалярами, введение и основы. Лицензия : Общественное достояние: Авторские права неизвестны .
 Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube - Колледж OpenStax, сложение и вычитание векторов: графические методы. 24 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/f6f19897573ef83351c5a79bc6899f489dd579a1/Figure_03_02_03.jpg. Лицензия : CC BY: Атрибуция
- Сложение векторов Урок 1 из 2: Метод сложения головы к хвосту. Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, сложение и вычитание векторов: графические методы. 24 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/e393f2ed44776ae52ef846c931b787aaaf154c37/Figure_03_02_06a.jpg. Лицензия : CC BY: Attribution
- Добавление векторов Урок 2 из 2: Добавление векторов по компонентам.
 Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube - Сунил Кумар Сингх, Scalar (Dot) Product. 12 марта 2014 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/6b401640bd2bf777844b5ba26c0b510bcac61d0b/vm2a.gif. Лицензия : CC BY: Attribution
- Единичный вектор. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Unit_vector. Лицензия : CC BY-SA: Attribution-ShareAlike
- Скаляр (физика). Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Сунил Кумар Сингх, Scalar (Dot) Product. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.
 org/contents/[email protected]. Лицензия : CC BY: Атрибуция
org/contents/[email protected]. Лицензия : CC BY: Атрибуция - скалярная. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- единичный вектор. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Скаляры и векторы. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Без ограничений. Предоставлено : Amazon Web Services. Лицензия : CC BY: Attribution
- Предоставлено : Wikimedia. Расположен по адресу : https://upload.wikimedia.org/wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. Лицензия : CC BY: Attribution
- Разница между векторами и скалярами, введение и основы.
 Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube - Колледж OpenStax, сложение и вычитание векторов: графические методы. 24 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/f6f19897573ef83351c5a79bc6899f489dd579a1/Figure_03_02_03.jpg. Лицензия : CC BY: Атрибуция
- Сложение векторов Урок 1 из 2: Метод сложения головы к хвосту. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, сложение и вычитание векторов: графические методы. 24 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/e393f2ed44776ae52ef846c931b787aaaf154c37/Figure_03_02_06a.jpg. Лицензия : CC BY: Attribution
- Добавление векторов Урок 2 из 2: Как добавлять векторы по компонентам.
 Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube - Сунил Кумар Сингх, Scalar (Dot) Product. 12 марта 2014 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/6b401640bd2bf777844b5ba26c0b510bcac61d0b/vm2a.gif. Лицензия : CC BY: Attribution
- Сунил Кумар Сингх, скалярное (точечное) произведение. 16 января 2015 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Смещение (вектор). Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Displacement_(vector). Лицензия : CC BY-SA: Attribution-ShareAlike
- смещение. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- ускорение.
 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike - скорость. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Скаляры и векторы. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Без ограничений. Предоставлено : Amazon Web Services. Лицензия : CC BY: Атрибуция
- Предоставлено : Wikimedia. Расположен по адресу : https://upload.wikimedia.org/wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. Лицензия : CC BY: Attribution
- Разница между векторами и скалярами, введение и основы. Лицензия : Общественное достояние: Нет данных Copyright .
 Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube - Колледж OpenStax, Сложение и вычитание векторов: графические методы. 24 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/f6f19897573ef83351c5a79bc6899f489dd579a1/Figure_03_02_03.jpg. Лицензия : CC BY: Атрибуция
- Сложение векторов Урок 1 из 2: Метод сложения головы к хвосту. Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Колледж OpenStax, Сложение и вычитание векторов: графические методы. 24 января 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/e393f2ed44776ae52ef846c931b787aaaf154c37/Figure_03_02_06a.jpg. Лицензия : CC BY: Attribution
- Добавление векторов Урок 2 из 2: Добавление векторов по компонентам.
 Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube - Сунил Кумар Сингх, скалярное (точечное) произведение. 12 марта 2014 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/resources/6b401640bd2bf777844b5ba26c0b510bcac61d0b/vm2a.gif. Лицензия : CC BY: Атрибуция
- Сунил Кумар Сингх, скалярное (точечное) произведение. 16 января 2015 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Безгранично. Предоставлено : Amazon Web Services. Лицензия : CC BY: Attribution
Векторы
В физике количественные модели разрабатываются на основе измерений. Их необходимо проверить, сделав дополнительные измерения. Измерения производятся в стандартных приращениях, называемых единицами. Без единиц а
измерение бессмысленно.
Без единиц а
измерение бессмысленно.
Некоторые величины полностью определяются величиной, т. е.
количество и соответствующие единицы измерения.
Действительное число само по себе называется
скаляр, и такие величины называются скалярные величины . Символы, обозначающие эти скалярные величины,
нормальные буквы.
Примеры скалярных величин:
температура (T) T = 10 o C
временной интервал (t) t = 5 с
масса (m) m = 3 кг
Другие величины определяются величиной и направлением. По
направление, мы имеем в виду направление в пространстве.
Такие величины называются векторные величины . Символы, обозначающие
эти векторные величины выделены жирным шрифтом или обычными буквами со стрелками
выше.
Примеры векторных величин:
перемещение ( d ) d = 10 м к северу
скорость ( v ) v = 3 м/с на восток
сила ( F ) F = 9 Н до
Для однозначного указания векторных величин нам нужен опорная точка и опорные линии , т. е. система координат .
е. система координат .
Декартова координата система является наиболее часто используемой системой координат. В два измерения, эта система состоит из пары линий на плоской поверхность или плоскость, пересекающиеся под прямым углом. Линии называется оси и точка в которой они пересекаются, называется началом . Оси обычно проводят горизонтально и вертикально и относят к в качестве осей x и y соответственно.
Точка на плоскости с
координаты (a, b) — это единицы справа от оси y и единицы b вверх.
от оси x, если a и b положительные числа.
Если a и b равны
оба отрицательных числа, точка находится на единицу слева от оси Y
и b единиц вниз от оси x.
На рисунке справа точка
P 1 имеет координаты (3, 4), а точка P 2 имеет
координаты (-1, -3).
В трехмерных декартовых координатах добавляется ось z, так что
есть три оси, перпендикулярные друг другу.
В полярных координатах системе ,
каждой точке плоскости присваиваются координаты (r, φ) относительно
фиксированная линия в плоскости называется осью и точка на этой линии, называемая полюсом . Для точки на плоскости координата r представляет собой расстояние от
указывают на полюс, а координата φ представляет собой угол против часовой стрелки
между осью и линией, соединяющей начало координат с точкой.
Для точки на плоскости координата r представляет собой расстояние от
указывают на полюс, а координата φ представляет собой угол против часовой стрелки
между осью и линией, соединяющей начало координат с точкой.
г.
Координата r всегда положительна, а диапазон φ составляет от 0 до 2π (360 o ).
Уметь преобразовывать декартовы координаты в полярные и наоборот
наоборот, пусть ось полярной системы координат совпадает с
ось x декартовой системы координат и полюс совпадают с
источник.
На рисунке справа точка P 1 имеет
полярные координаты (r 1 , φ 1 ) = (5, 53,1 o ),
и точка Р 2 имеет полярные координаты (r 2 , φ 2 )
= (3,16, 251,6 o ).
Уравнения преобразования:
x = r cosφ, y = r sinφ.
r = (x 2 + y 2 ) ½ , φ = загар -1 (г/х).
Цилиндрические координаты и сферические координаты
два разных расширения полярных координат до трех измерений.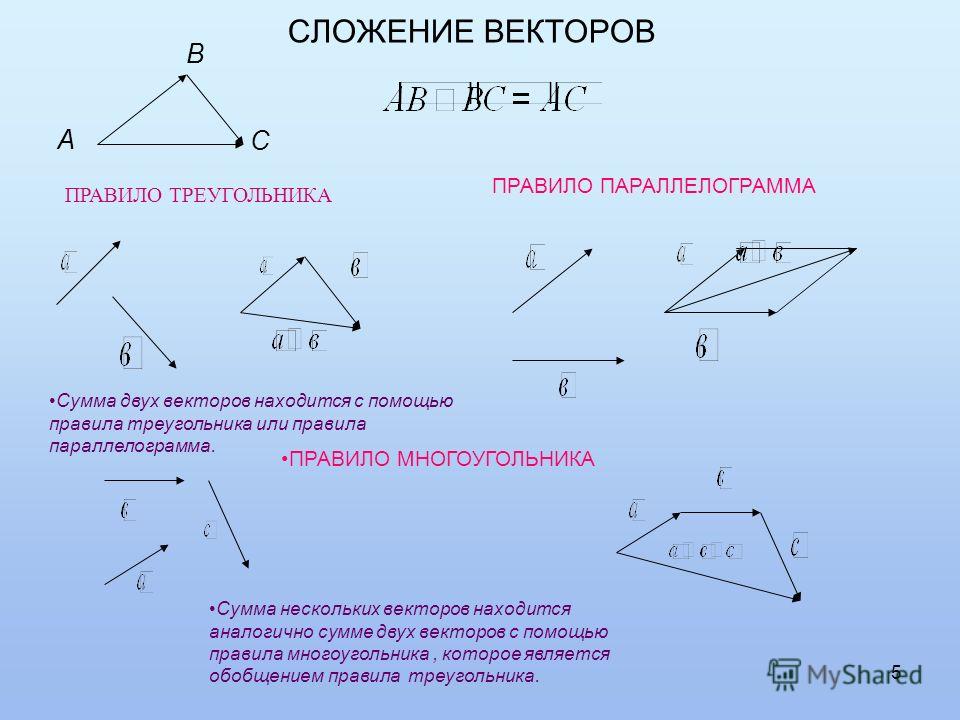
Как только мы выбрали систему координат, физический
векторная величина в двух измерениях может быть представлена парой
числа.
Если мы выберем декартовы координаты, то числа будут проекциями вектора на оси
декартова координата
система.
Вектор и на рисунке справа имеют x-компоненту
a 1 и y-компонента a 2 .
Его длина или величина равна a = (a 1 2 + a 2 2 ) ½ .
Это следует из
Теорема Пифагора.
Полярный угол a , то есть угол a образует с
ось x — это φ.
Проблема:
Вектор A лежит в плоскости xy.
(a) Для каких ориентаций Оба прямоугольных компонента числа будут отрицательными?
(b) Для чего
ориентации будут ли его компоненты иметь противоположные знаки?
Решение:
- Обоснование:
На плоскости (в двух измерениях) мы можем указать направление вектора с помощью установив систему координат и задав угол φ, который вектор образует с положительная ось x. Положительный φ — это угол, измеренный
против часовой стрелки от положительной оси x.
Положительный φ — это угол, измеренный
против часовой стрелки от положительной оси x. - Детали расчета:
(a) X-компонента A равна A x = А cosφ а y-компонента A равна A y = A sinφ. (А — величина вектора.) Если A x и A y отрицательные, мы нужно, чтобы cosφ и sinφ были отрицательными. φ должен лежать между 180 и 270 градусов.
(b) Для того, чтобы A x и A y имели противоположные знаки, φ должен лежать от 90 до 180 градусов или от 270 до 360 градусов.
Примечание. Величина вектора говорит о его длине. это число
(с единицами). Если вектор является вектором скорости, то его величина имеет единицы скорости
(м/с), если это вектор смещения, то его величина имеет единицы расстояния
(м) и др.
Направление в двух измерениях, то есть в плоскости, — это угол, который образует вектор.
с осью x, измеренной против часовой стрелки от направления x.
Вам нужна система координат (система отсчета), прежде чем вы зададите направление.
Добавление векторов
Чтобы добавить физические векторы, они должны быть одинаковые единицы измерения. Чтобы найти сумму двух физических векторные величины с теми же единицами измерения алгебраически , мы складываем x, y и z-компоненты отдельных векторов.
Пример:
Пусть вектор v 1 имеет компоненты (3, 4) и вектор v 2 имеют компоненты (2, -3).
Пусть v = v 1 + v 2 — сумма двух векторов.
Тогда компоненты v равно (3+2, 4+(-3) = (5, 1)).
Величина вектора v равна v = (25 + 1) ½ = 5,1,
.
а угол v , образуемый с осью x, равен φ = tan -1 (1/5)
= 0,197 рад = 11,3 o .
Чтобы вычесть вектор v 2 из вектора v 1 мы вычитаем компоненты вектора v 2 из
компоненты вектора v 1 .
Пример:
Пусть вектор v 1 имеет компоненты (3, 4) и вектор v 2 имеют компоненты (2, -3).
Пусть v = в 1 — в 2 быть разностью двух
векторы.
Тогда компоненты v равны (3-2, 4-(-3) = (1,
7).
Величина вектора v равна v = (1 + 49) ½ = 7,1.
а угол v , образуемый с осью x, равен φ = tan -1 (7/1)
= 1,429 рад = 81,9 o .
Графическое представление векторной величины в виде направленной линии
сегмент. Чтобы найти сумму двух физических векторных величин с
те же единицы графически выстраиваем стрелки, хвост к кончику.
Сумма — это стрелка, проведенная от хвоста первого вектора к кончику
последнего вектора. Чтобы вычесть вектор v 2 из
вектор v 1 инвертируем вектор v 2 и добавляем его в вектор v 1 .
Пусть A — произвольный вектор. Вектор — A имеет одинаковой длины и направлены в противоположную сторону. Вычитание вектора из другого вектора означает добавление вектор — A к другому вектору.
Пример:
Вектор смещения
Пусть d представляет собой вектор смещения из точки А с
координаты (x 1 , y 1 ) = (-4, -1) до точки B с координатами (x 2 , y 2 ) = (3, 4).
Вектор смещения – это разница между векторами положения А и Б , д = Б — А .
Его компоненты
d x = (x 2 — x 1 ) = 3 — (-4) = 7, d y = (у 2 — у 1 ) = 4 — (-1) = 5.
Вектор смещения d имеет величину d = (49 + 25) ½ = 8,6.
Угол d , образуемый с осью x, равен φ = tan -1 (5/7) =
0,62 рад = 35,5· или .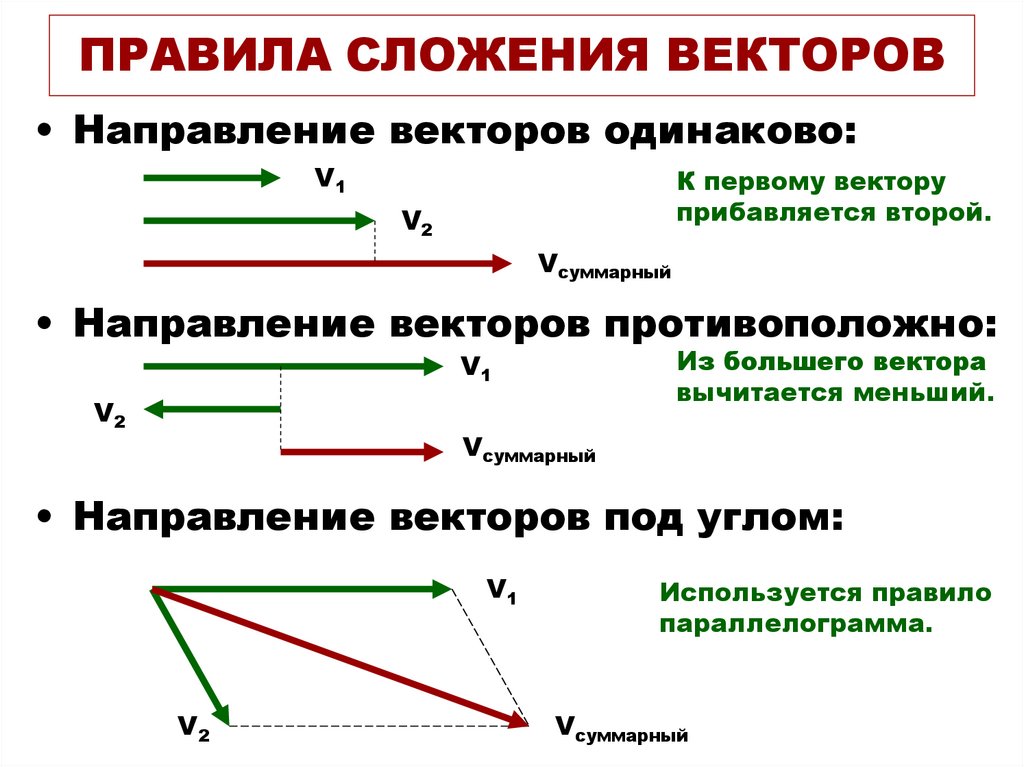


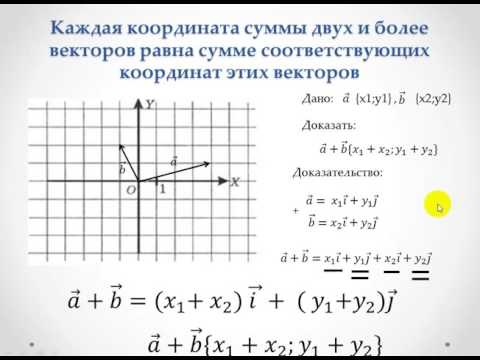
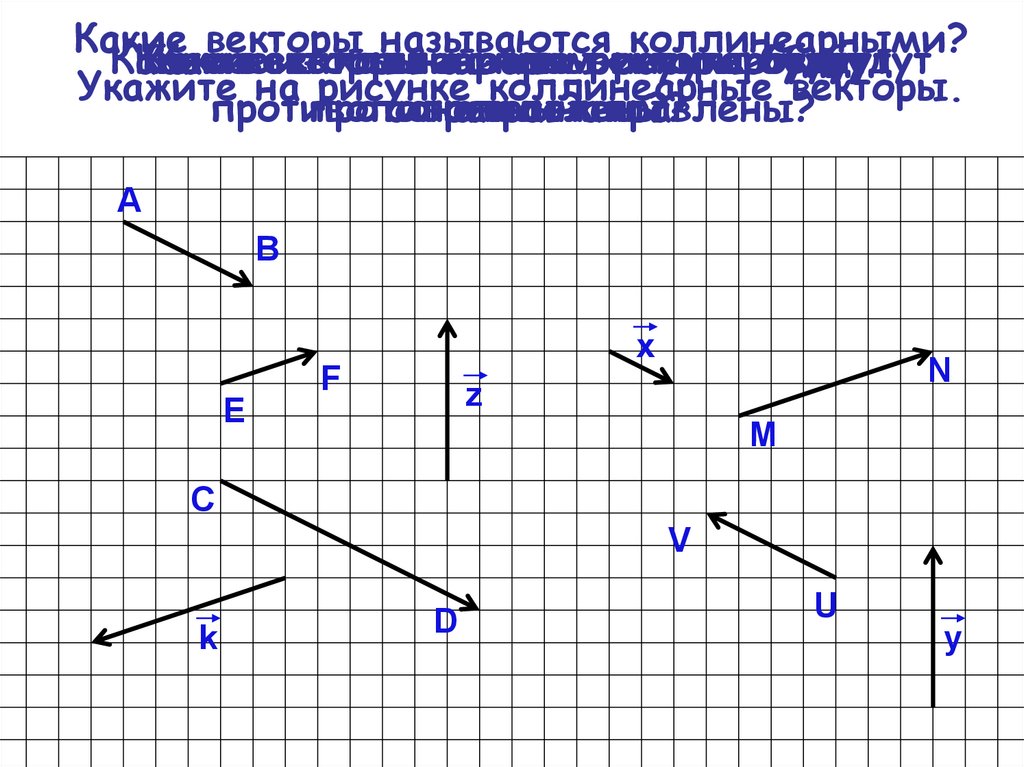


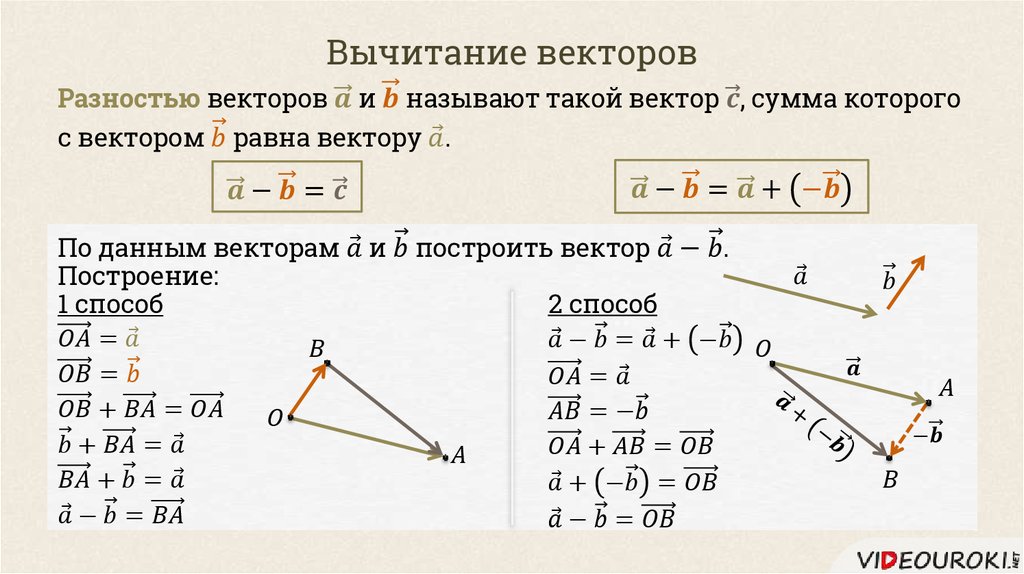

 градусов.
градусов.

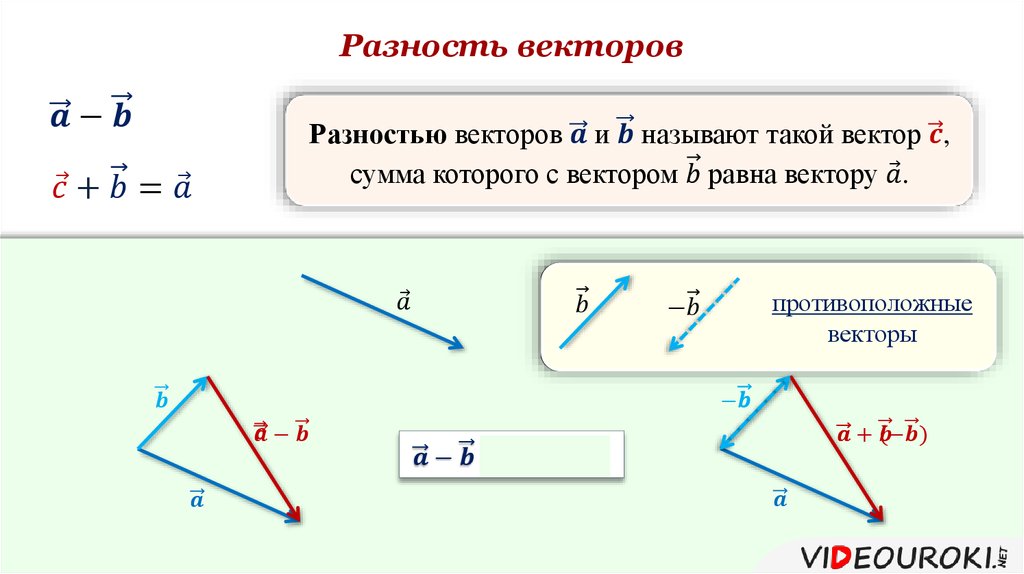 Таким образом, второй вектор равен (9.06, 4.23) в координатной форме.
Таким образом, второй вектор равен (9.06, 4.23) в координатной форме.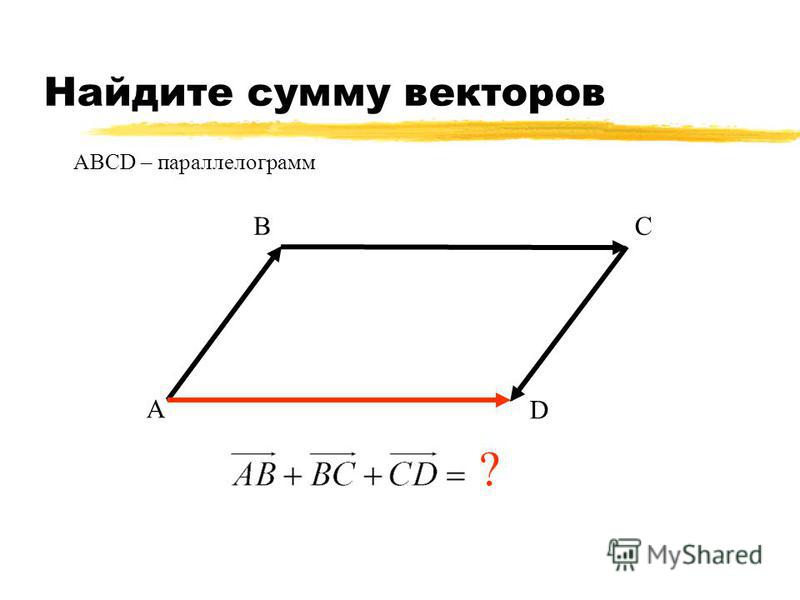 Таким образом, первый вектор равен (20.8, 7.16) в координатной форме.
Таким образом, первый вектор равен (20.8, 7.16) в координатной форме.

 Этот
результирующий вектор (показан ниже зеленым цветом) представляет собой сумму двух
оригинальные.
Этот
результирующий вектор (показан ниже зеленым цветом) представляет собой сумму двух
оригинальные.

 Когда больше нет векторов, проведите прямую линию от начала координат до начала последнего вектора. Эта линия является суммой векторов.
Когда больше нет векторов, проведите прямую линию от начала координат до начала последнего вектора. Эта линия является суммой векторов.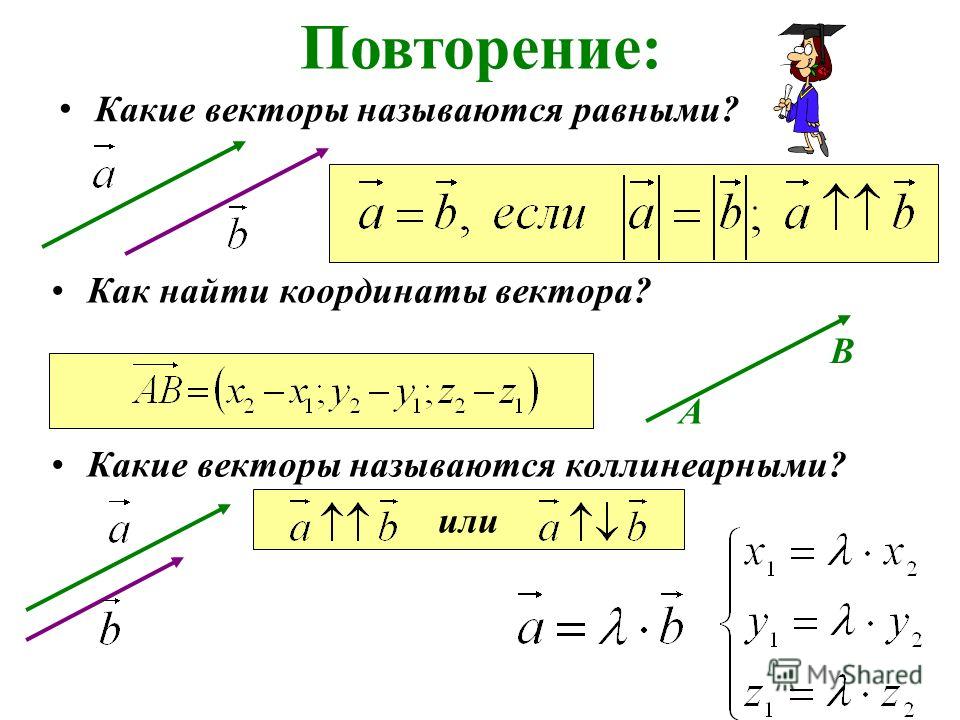


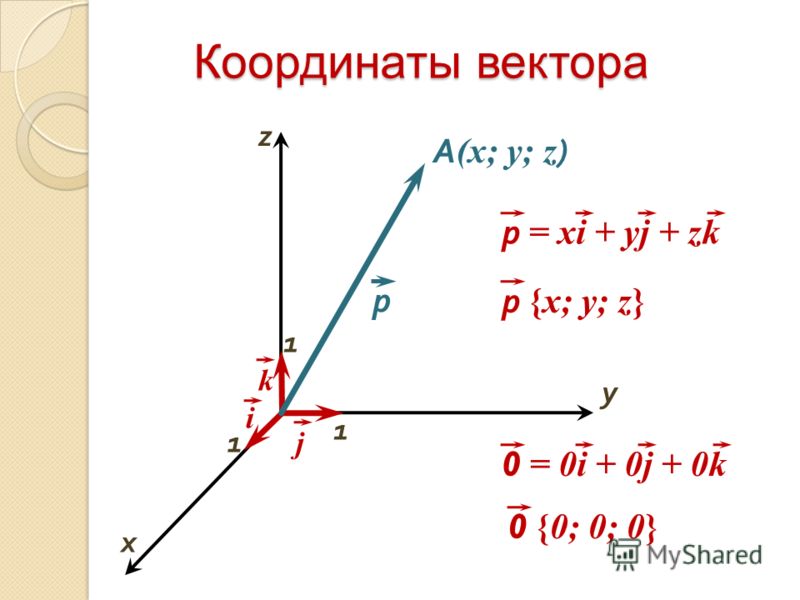

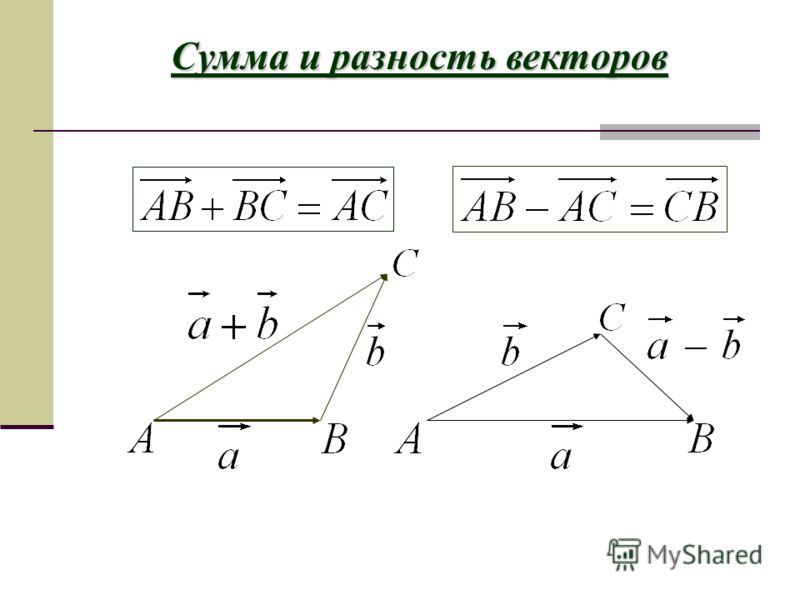 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution 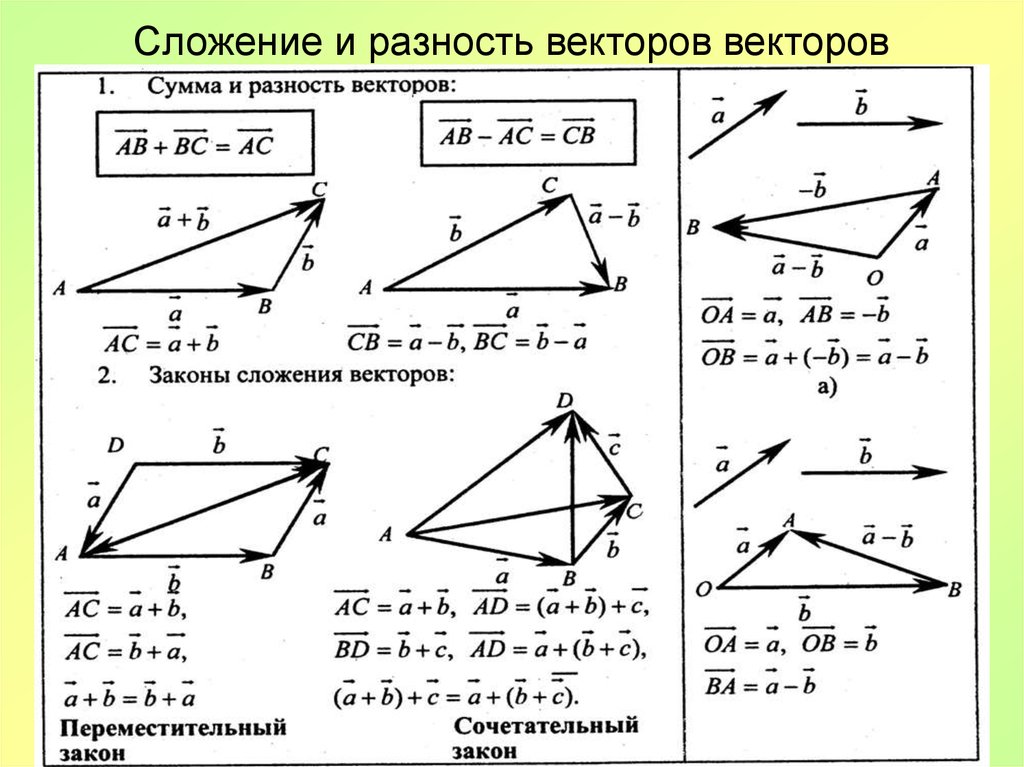 Предоставлено : Amazon Web Services. Лицензия : CC BY: Attribution
Предоставлено : Amazon Web Services. Лицензия : CC BY: Attribution  wikimedia.org/wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. Лицензия : CC BY: Attribution
wikimedia.org/wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. Лицензия : CC BY: Attribution  Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube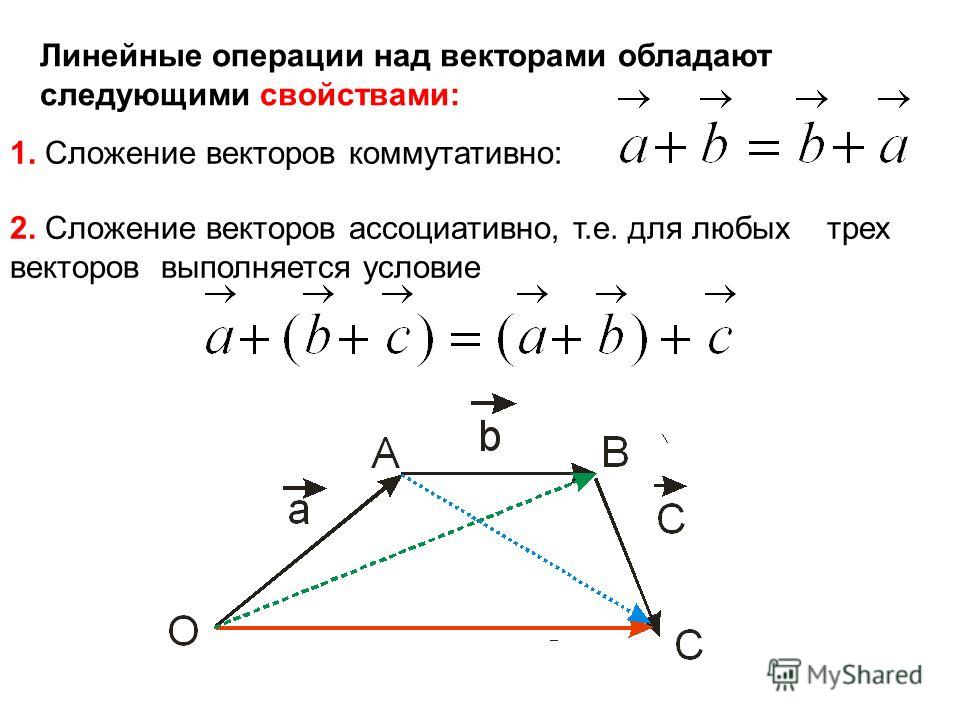 jpg. Лицензия : CC BY: Атрибуция
jpg. Лицензия : CC BY: Атрибуция 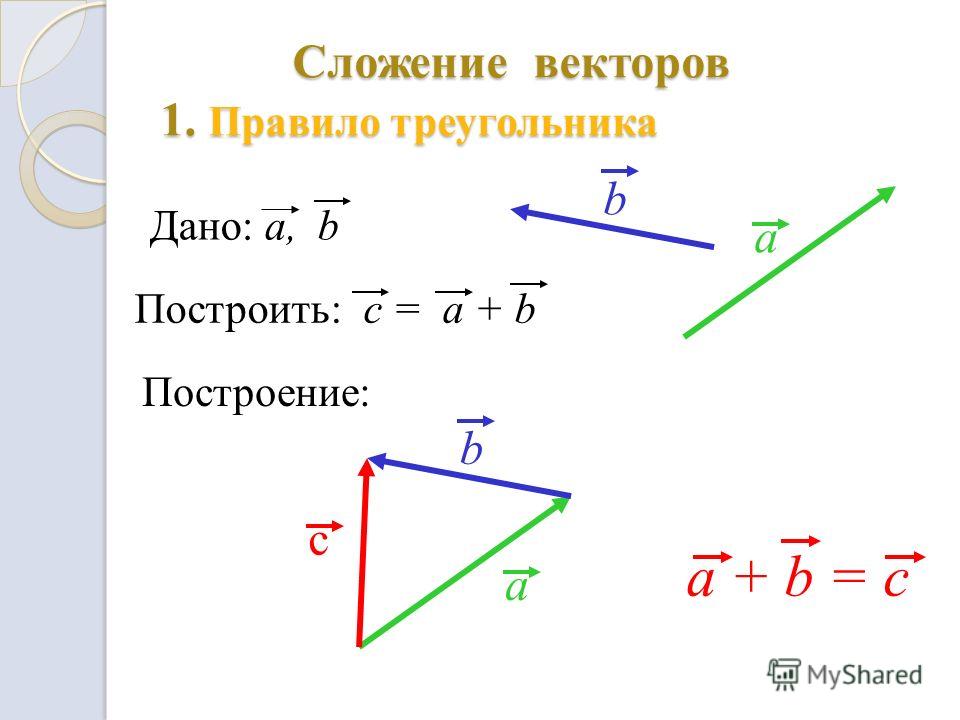 Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution 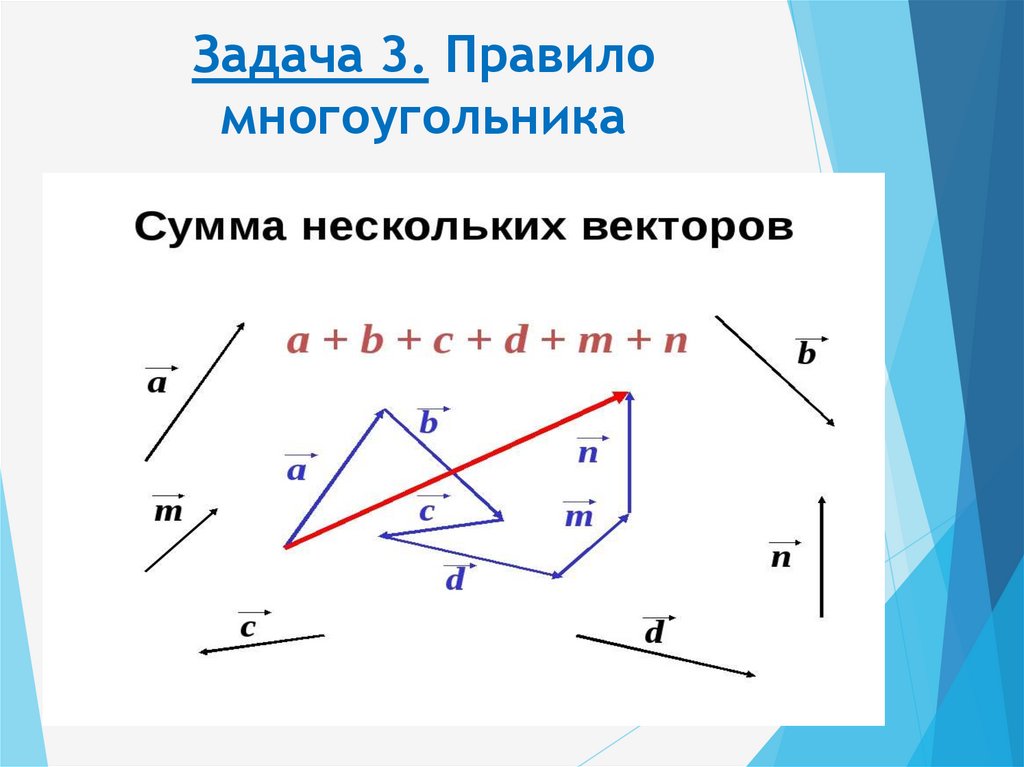 Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike 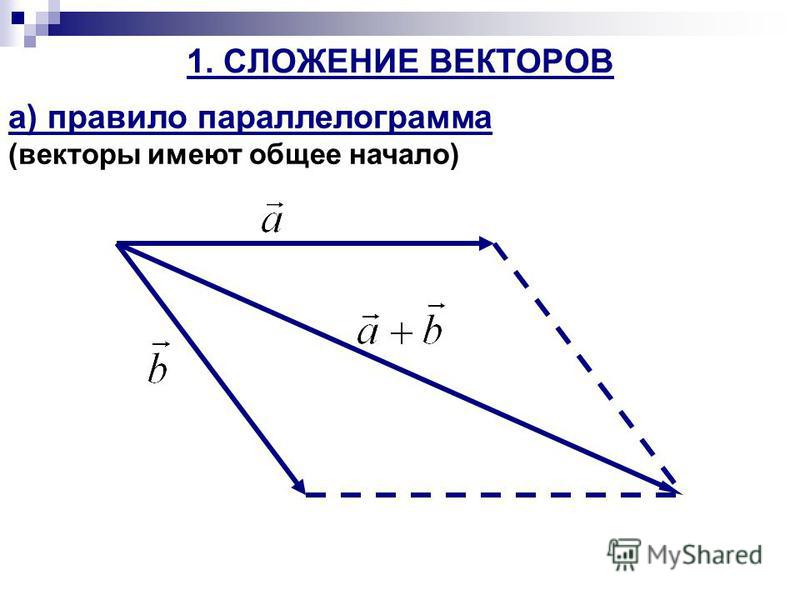 Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Авторские права неизвестны . Условия лицензии : Стандартная лицензия YouTube org/contents/[email protected]. Лицензия : CC BY: Атрибуция
org/contents/[email protected]. Лицензия : CC BY: Атрибуция  Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube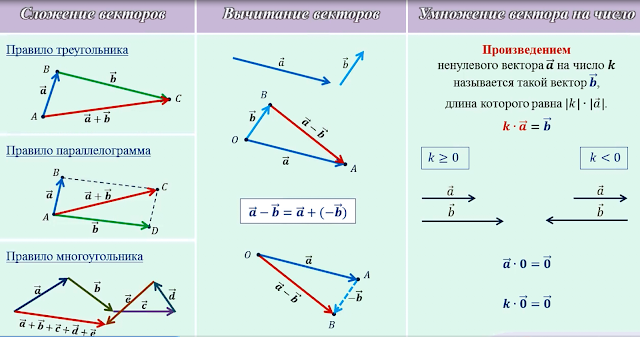 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike  Условия лицензии : Стандартная лицензия YouTube
Условия лицензии : Стандартная лицензия YouTube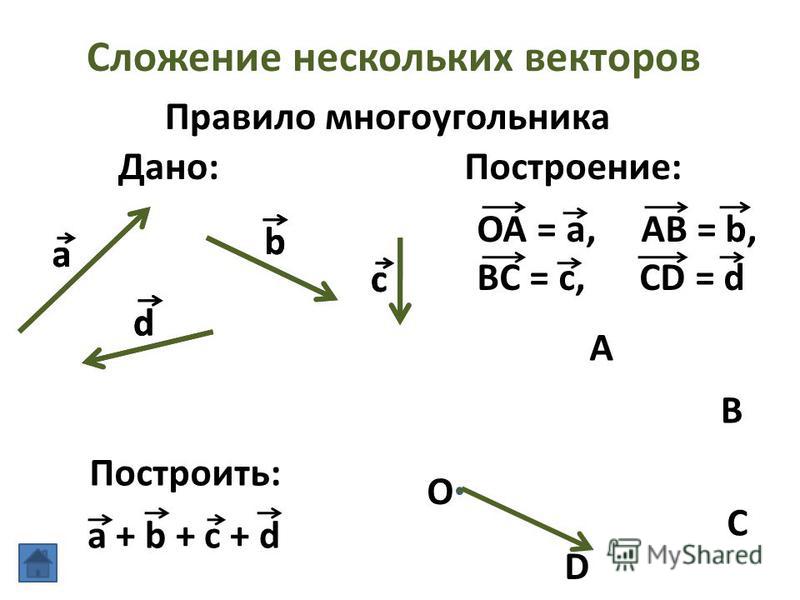 Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube Положительный φ — это угол, измеренный
против часовой стрелки от положительной оси x.
Положительный φ — это угол, измеренный
против часовой стрелки от положительной оси x.