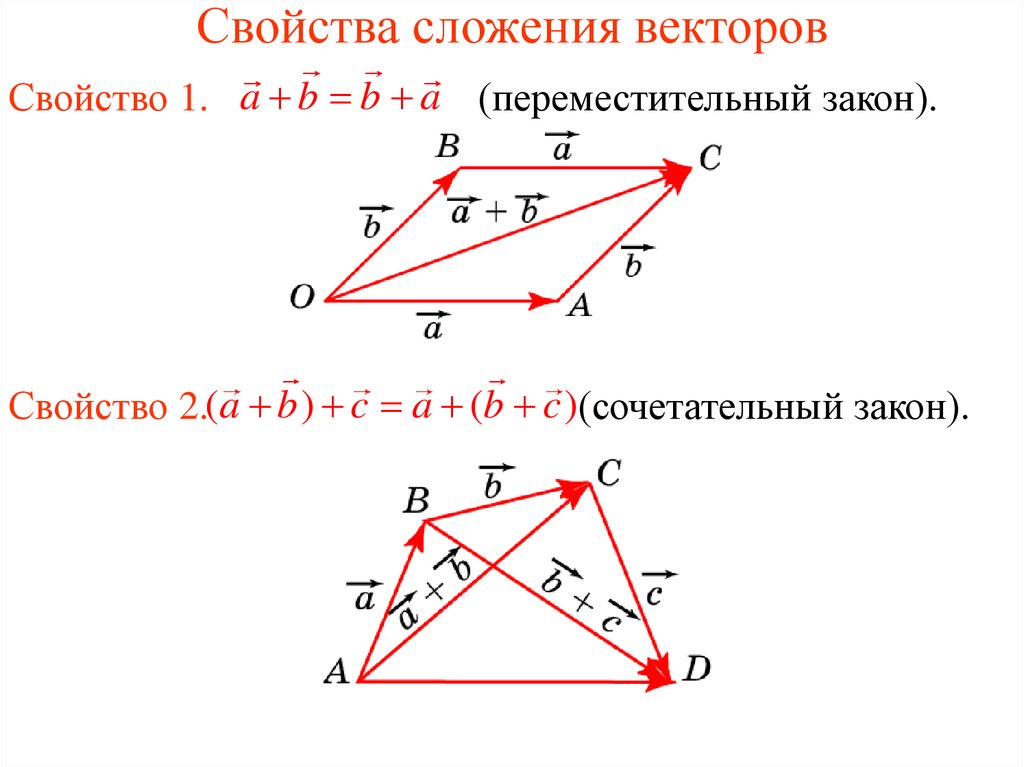
Сложение и вычитание векторов

Определение

Сложение векторов иосуществляется поправилу треугольника.

Суммой двух векторов иназывают такой третий вектор, начало которого совпадает с началом, а конец — с концомпри условии, что конец вектораи начало векторасовпадают (рис. 1).

Для сложения векторов применяется также правило параллелограмма.

Определение

Правило параллелограмма — если два неколлинеарных вектора ипривести к общему началу, то векторсовпадает с диагональю параллелограмма, построенного на векторахи(рис. 2). Причем начало векторасовпадает с началом заданных векторов.

Определение

Вектор называетсяпротивоположным вектором к вектору , если онколлинеарен вектору , равен ему по длине, но направлен в противоположную сторону вектору.

Операция сложения векторов обладает следующими свойствами:

1. — коммутативность

2. — ассоциативность

Определение

Разностью векторов иназывается вектортакой, что выполняется условие:(рис. 3).

Умножение вектора на число

Определение

Произведением вектора на число называется вектор, удовлетворяющий условиям:

3. , если ,, если.

Свойства умножения вектора на число:

Здесь и- произвольные векторы,,- произвольные числа.

Евкли́дово простра́нство (также Эвкли́дово простра́нство

) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность равную 3.

В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов: конечномерное вещественное векторное пространство с введённым на нём положительно определённымскалярным произведением, либо метрическое пространство, соответствующее такому векторному пространству. В этой статье за исходное будет взято первое определение.

-мерное евклидово пространство обозначается также часто используется обозначение(если из контекста ясно, что пространство обладает евклидовой структурой).

Для определения евклидова пространства проще всего взять в качестве основного понятие скалярного произведения. Евклидово векторное пространство определяется как конечномерное векторное пространство над полем вещественных чисел, на векторах которого задана вещественнозначная функция обладающая следующими тремя свойствами:

• Билинейность: для любых векторов и для любых вещественных чисели

• Симметричность: для любых векторов

• Положительная определённость: для любого причём

Аффинное пространство, соответствующее такому векторному пространству, называется евклидовым аффинным пространством, или просто евклидовым пространством^[1].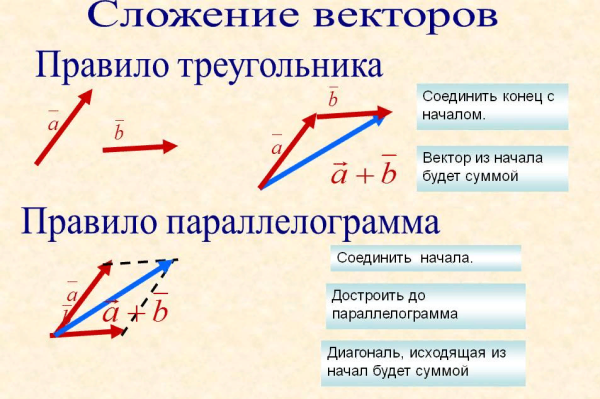

Пример евклидова пространства — координатное пространство состоящее из всевозможныхn-ок вещественных чисел скалярное произведение в котором определяется формулой

22. Базис и координаты вектора

Ба́зис (др.-греч. βασις, основа) — множество таких

векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.

В случае, когда базис бесконечен, понятие «линейная комбинация» требует уточнения. Это ведёт к двум основным разновидностям определения:

• Базис Га́меля, в определении которого рассматриваются только конечные линейные комбинации. Базис Гамеля применяется в основном в абстрактной алгебре (в частности в линейной алгебре).

• Базис Ша́удера, в определении которого рассматриваются и бесконечные линейные комбинации, а именно — разложение в ряды

  . Это определение применяется в основном в функциональном анализе, в частности для гильбертова пространства,

В конечномерных пространствах обе разновидности базиса совпадают.

Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

где — координаты вектора.

23. Скалярное произведение.

операция над двумя векторами, результатом которой является число [когда рассматриваются векторы, числа часто называют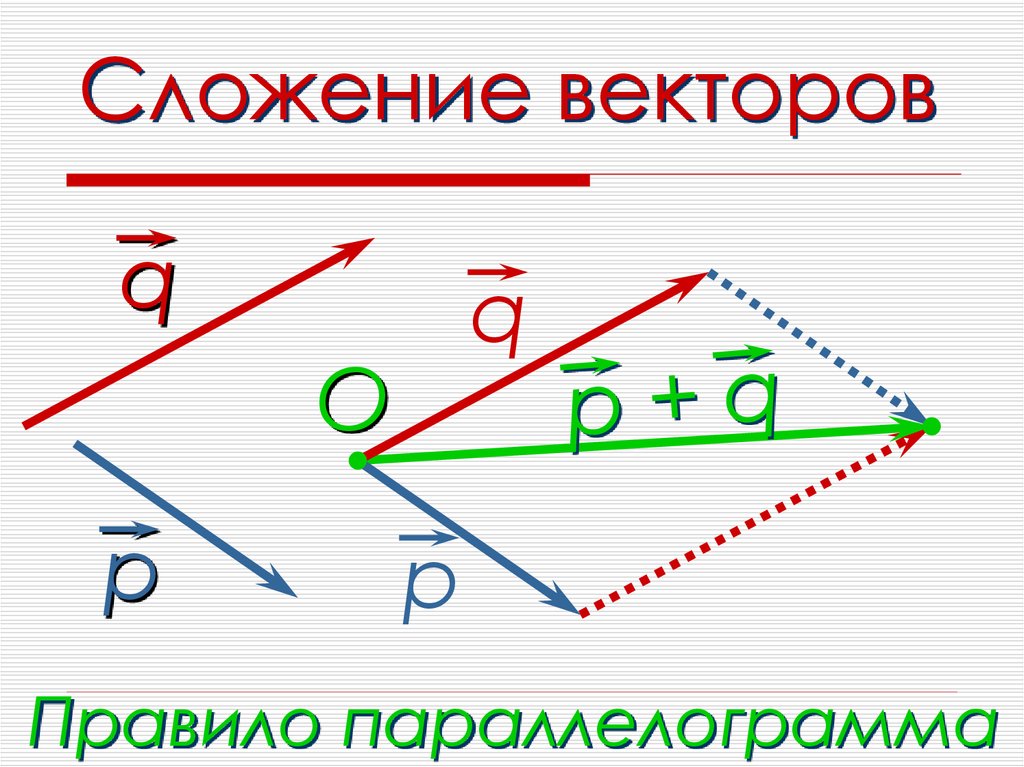

скалярами], не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:

24. Векторное произведение

это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном евклидовом пространстве. Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативным) и, в отличие от скалярного произведения векторов, является вектором. Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения. Векторное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.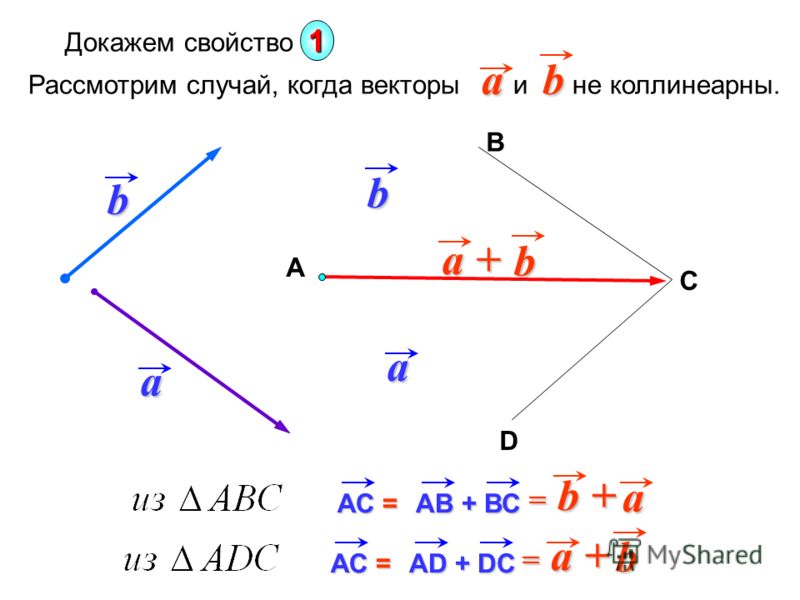

где

25. Смешанное произведение

Сме́шанное произведе́ние векторов —скалярное произведение вектора навекторное произведение векторов и:

.

Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр

).

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами .смешанное произведение трех векторов можно найти через определитель

26. Плоскость в пространстве

Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

Некоторые характеристические свойства плоскости

• Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;

• Две плоскости являются либо параллельными, либо пересекаются по прямой.

• Прямая либо параллельна плоскости, либо пересекает ее в одной точке, либо находится на плоскости.

• Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.

• Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.

Аналогично отрезку и интервалу, плоскость, не включающую крайние точки, можно назвать интервальной плоскостью, или открытой плоскостью.

где и— постоянные, причёмиодновременно не равны нулю; ввекторной форме:

где — радиус-вектор точки, векторперпендикулярен к плоскости (нормальный вектор).Направляющие косинусы вектора :

где ,,— отрезки, отсекаемые плоскостью на осяхи.

в векторной форме:

27. Нормированное уравнение плоскости

нормальное уравнение плоскости вида задает в прямоугольной системе координатOxyz плоскость, удаленную от начала координат на расстояние p в положительном направлении единичного нормального вектора плоскости .

28. Прямая в пространстве

Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.

итак, если уравнения двух непараллельных плоскостей — и, то прямая, являющаяся их линией пересечения, задается системой уравнений

(11.11)

И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.

Уравнения (11.11) называют общими уравнениями прямой в пространстве.

29. Уравнение окружности

Уравнение окружности радиуса с центром вначале координат:

30. Эллипс. Каноническое уравнение. Эксцентриситет, фокальный радиус.

Э́ллипс — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек и(называемыхфокусами) постоянна и больше расстояния между фокусами, то есть

причем

Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.

Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.

Сложение и вычитание двух векторов — онлайн калькулятор

В результате сложения двух векторов a и b получается вектор с, все элементы которого равны попарной сумме соответствующих элементов слагаемых векторов. При вычитании тех же векторов все элементы результирующего вектора с равны попарной разности соответствующих элементов.

Нахождение суммы и разности векторов онлайн позволяет обойтись без самостоятельного проведения расчетов. Нужно просто задать векторы (точками или координатами), выбрать действие (сложение или вычитание) и нажать кнопку «рассчитать». После этого онлайн-калькулятор выдаст результат вместе с подробными промежуточными выкладками

Как сложить и вычесть векторы с помощью онлайн-калькулятора

Чтобы сложить или вычесть векторы при помощи онлайн калькулятора, достаточно лишь задать необходимые векторы. Для этого:

1. Опеделитесь, с какими векторами вы хотите работать. Это могут быть векторы на плоскости или векторы в пространстве.

   В рассматриваемом примере, оставим размерность «2». То есть, мы работаем с векторами на плоскости.

2. Теперь нужно выбрать форму представления векторов: их можно задать координатами либо точками:

   Для наглядности, зададим один вектор точками, а второй – координатами.

3. Теперь в поле «Значение вектора» нужно ввести соответствующие значения. Зададим векторы произвольным образом:
   
4. Осталось нажать «Рассчитать» и получить ответ. Отметим, что складываемые и вычитаемые векторы можно также умножать на число. Для наглядности, умножим первый вектор a на 3 и сложим результат с вектором b:
   
   

Материалы, которые помогут вам лучше разобраться в теме:

• Векторы на плоскости и в пространстве — основные определения
• Операции над векторами и их свойства: сложение и умножение
• Координаты вектора в декартовой системе координат (ДСК)
• Нахождение координат вектора через координаты точек
• Векторное произведение — определения, свойства, формулы, примеры и решения
• Операции над векторами в прямоугольной системе координат

Ответ:

Решение

Ответ:

• list» :key=»`error-${eIdx}`» v-html=»e»/>

Похожие калькуляторы:

• Длина вектора. Модуль вектора
• Векторное произведение векторов
• Умножение вектора на число
• Угол между векторами
• Смешанное произведение векторов
• Скалярное произведение векторов
• Определение вектора по двум точкам
• Разложение вектора по базису
• Проверить являются ли вектора базисом
• Ортогональность векторов
• Компланарность векторов
• Коллинеарность векторов
• Проекция вектора на вектор
• Площадь треугольника, построенного на векторах
• Площадь параллелограмма, построенного на векторах

Как найти сумму и разность векторов без онлайн-калькулятора

Рассмотрим пример с применением формулы для суммы векторов на плоскости. Пусть нужно сложить два вектора: a(3; 5) и b(4; 3). Произведем вычисления:

c→=a→+b→=(ax+bx;ay+by)a→+b→=(3+4;5+3)=(7;8)

Правильность решения можно проверить с помощью онлайн-калькулятора.

Данный сервис будет полезен школьникам и студентам при самостоятельной подготовке к экзаменам и контрольным по векторной алгебре.

Понравился калькулятор? Поделись с друзьями!

Графические методы – физика колледжа

Глава 3 Двумерная кинематика

Резюме

• Понимание правил сложения, вычитания и умножения векторов.
• Применять графические методы сложения и вычитания векторов для определения смещения движущихся объектов.

Рисунок 1. Смещение можно определить графически, используя масштабную карту, например, карту Гавайских островов. Путешествие с Гавайев на Молокаи состоит из нескольких этапов или сегментов пути. Эти сегменты могут быть добавлены графически с помощью линейки, чтобы определить общее двухмерное перемещение пути. (кредит: Геологическая служба США).

Вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.

На рис. 2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассмотренного в главе 3.1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что полужирный символ, такой как [latex]\textbf{D}[/latex] , обозначает вектор. Его величина представлена ​​символом, выделенным курсивом, [латекс]{D},[/латекс], а его направление — [латекс]{\тета}.[/латекс]

ВЕКТОРА В ЭТОМ ТЕКСТЕ

В этом тексте мы будем представлять вектор переменной, выделенной жирным шрифтом.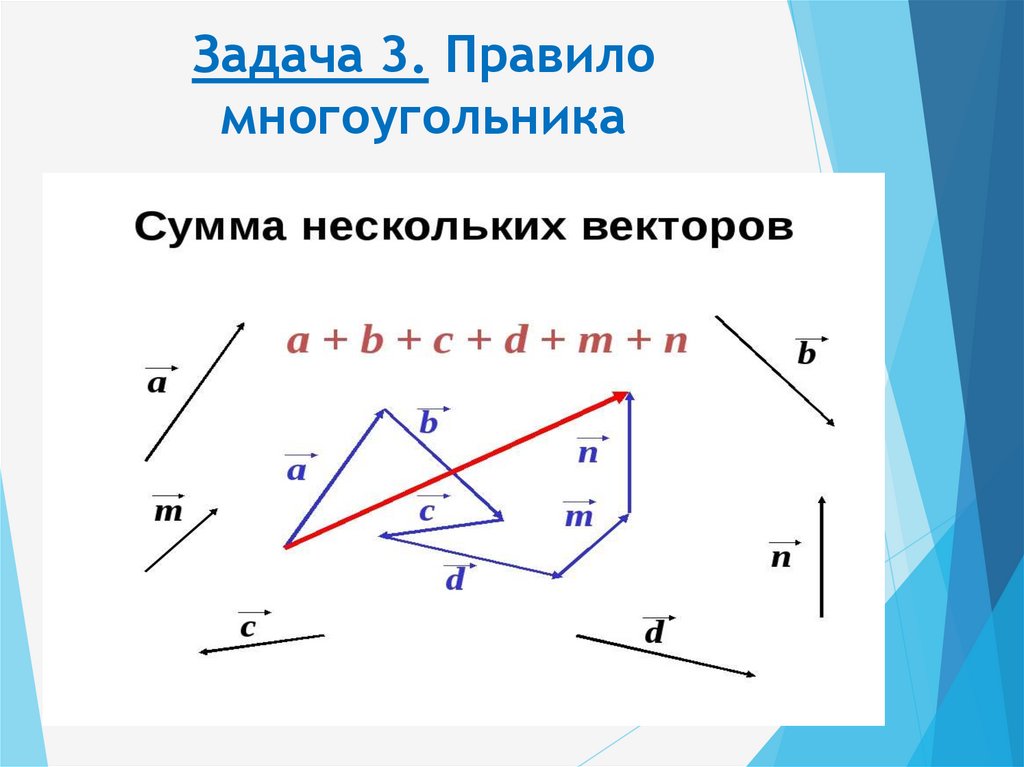 Например, мы представим количественную силу вектором [latex]\textbf{F},[/latex], который имеет как величину, так и направление. Величина вектора будет представлена ​​переменной, выделенной курсивом, например [латекс]{F},[/латекс], а направление переменной будет задано углом [латекс]{\тета}.[/латекс ]

Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Водоизмещение 10,3 блока под углом 29.1 ^o к северу от востока. Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 2, нарисуйте стрелку, представляющую общий вектор смещения D . С помощью транспортира начертите линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере магнитуда D вектора составляет 10,3 единицы, а направление θ равно 29,1 ^o к северу от востока.

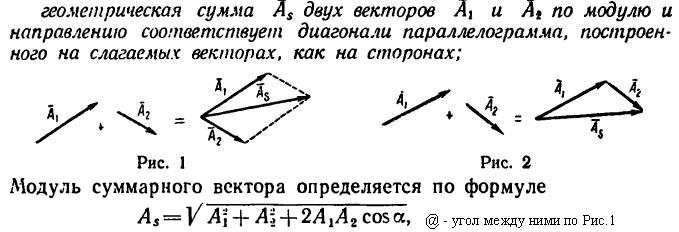
Метод «голова к хвосту» представляет собой графический способ добавления векторов, описанный на рис. 4 ниже и в следующих шагах. Конец вектора является начальной точкой вектора, а конец (или кончик) вектора является конечным заостренным концом стрелки.

Рисунок 4. Метод «голова к хвосту»: метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ , измеренное с помощью транспортира, равно 29,1 ⁰ .

Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .

Рисунок 5.

Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .

Рисунок 6.

Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .

Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результат или сумма других векторов.

Рисунок 7.

Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве расчетов мы будем использовать теорему Пифагора для определения этой длины.)

Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)

Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.

Пример 1. Графическое добавление векторов методом «голова к хвосту»: женщина на прогулке 9{\circ}}[/latex] к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.

Стратегия

Представьте каждый вектор смещения графически стрелкой, обозначив первый [latex]\textbf{A},[/latex], второй [latex]\textbf{B},[/latex] и третий [latex]\textbf{C},[/latex] делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад.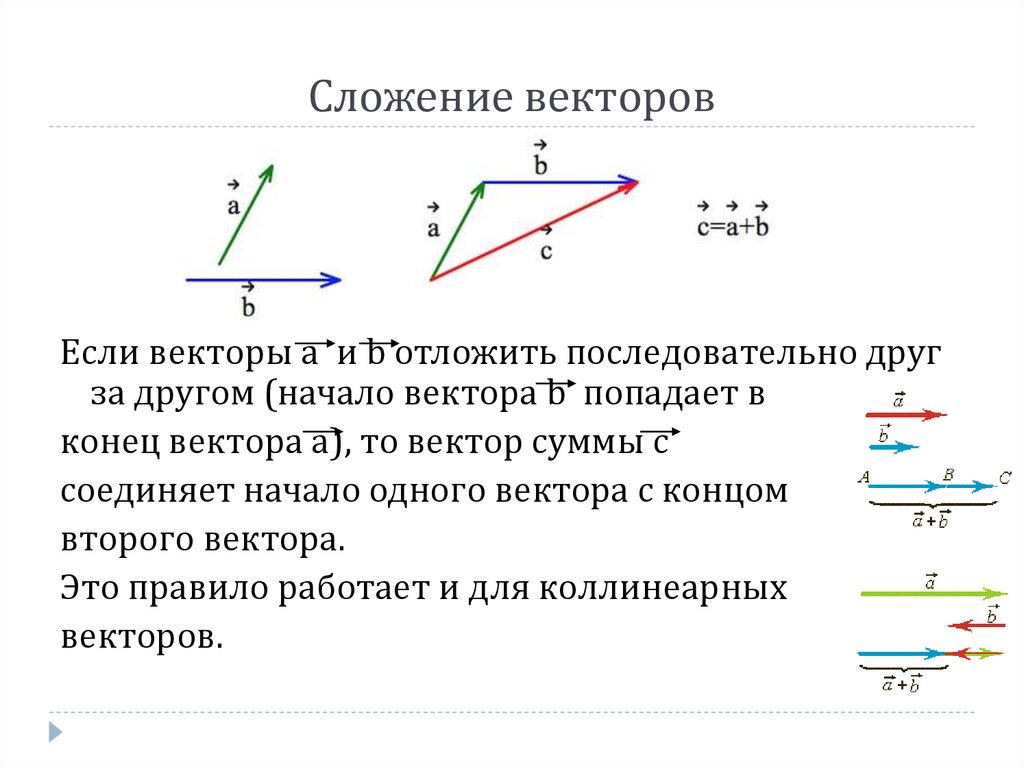 Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого [latex]\textbf{R}.[/latex]

Решение

(1) Нарисуйте три вектора смещения.

Рисунок 8.

(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.

Рисунок 9.

(3) Нарисуйте результирующий вектор [латекс]\textbf{R}.[/latex]

Рисунок 10.

(4) Используйте линейку для измерения величины [латекс]\ textbf{R},[/latex] и транспортир для измерения направления [latex]\textbf{R}.[/latex] Несмотря на то, что направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором. 9{\circ}}[/latex] к югу от востока.

Обсуждение

Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 12, и все равно получим то же решение.

Рисунок 12.

Здесь мы видим, что при сложении одних и тех же векторов в другом порядке результат будет тот же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов равно коммутативный . Векторы можно добавлять в любом порядке.

[latex]{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]

(Это справедливо и для сложения обычных чисел— вы получите тот же результат, если вы добавите, например, [латекс]{2+3}[/латекс] или [латекс]{3+2},[/латекс]).

Вычитание векторов — это прямое расширение сложения векторов.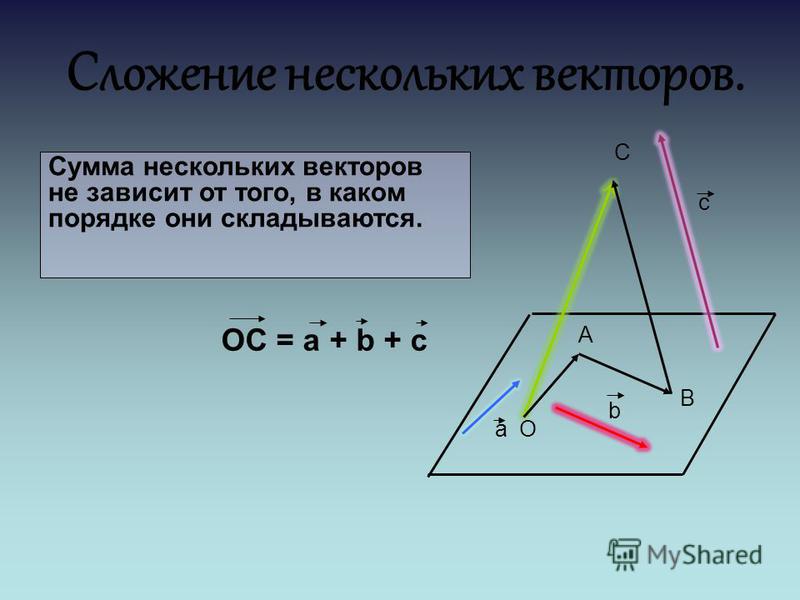 Чтобы определить вычитание (скажем, мы хотим вычесть [латекс]\textbf{B}[/латекс] из [латекс]\текстбф{А},[/латекс], записанного [латекс]{\текстбф{А}-\текстбф{В }}[/latex] , мы должны сначала определить, что мы подразумеваем под вычитанием.0021 отрицательный вектора [latex]\textbf{B}[/latex] определяется как [latex]{-\textbf{B}};[/latex], то есть графически отрицательный любой вектор имеет той же величины, но в противоположном направлении , как показано на рисунке 13. Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]{-\textbf{B}},[/latex ] но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.

Рисунок 13. Отрицательное значение вектора — это просто другой вектор той же величины, но направленный в противоположном направлении. Так B является минусом -B ; он имеет ту же длину, но противоположное направление. {\circ}}[/latex] к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.

Рисунок 14.

Стратегия

Мы можем представить первый этап пути с помощью вектора [latex]\textbf{A},[/latex] и второй этап пути с помощью вектора [latex] \textbf{B}.[/latex] Док находится в месте [latex]{\textbf{A}\:+\:\textbf{B}}.[/latex] Если женщина по ошибке путешествует в напротив 9{\circ}}[/latex] к югу от востока. Мы представляем это как [латекс]{-\textbf{B}},[/латекс], как показано ниже. Вектор [latex]{-\textbf{B}}[/latex] имеет ту же величину, что и [latex]\textbf{B}[/latex], но направлен в противоположном направлении. Таким образом, она окажется в месте [latex]{\textbf{A}+(-\textbf{B})},[/latex] или [latex]{\textbf{A}-\textbf{B}} .[/latex]

Рисунок 15.

Мы выполним сложение векторов, чтобы сравнить местоположение дока, [latex]{\textbf{A}+\textbf{B}},[/latex] с местоположением в которую по ошибке прибывает женщина, [латекс]{\textbf{A}+(-\textbf{B})}. [/latex]

Решение

(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы [latex]\textbf{A}[/latex] и [latex]{-\textbf{B}}.[ /latex]

(2) Разместите векторы «голова к хвосту».

(3) Нарисуйте результирующий вектор [latex]\textbf{R}.[/latex]

(4) Используйте линейку и транспортир для измерения величины и направления [latex]\textbf{R}.[/ латекс]

Рисунок 16.  

}[/latex] к югу от востока. 9{\circ}}[/latex] к северу от востока.

Мы видим, что женщина окажется на значительном расстоянии от причала, если она отправится в противоположном направлении на второй этап поездки.

Обсуждение

Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.

Если бы мы решили пройти в три раза больше расстояния на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли [латекс]{3 \times 27,5\text{ м}},[/latex] или 82,5 м, в направлении [латекс] {66,0 ^ {\ circ}} [/ латекс] к северу от востока. Это пример умножения вектора на положительное число 9.0014 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.

Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору направление, противоположное . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор [latex]\textbf{A}[/latex] умножается на скаляр [latex]{c},[/latex]

• величина вектора становится абсолютной величиной [latex]{cA},[/latex]
• , если [latex]{c}[/latex] положительный, направление вектора не меняется,
• , если [latex]{c}[/latex] имеет отрицательное значение, направление меняется на противоположное.

В нашем случае [латекс]{с=3}[/латекс] и [латекс]{\текстбф{А}=27,5\текст{м}}.[/латекс] Во многих случаях векторы умножаются на скаляры. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.

В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает определение перпендикулярных компонентов одного вектора, например компонентов x – и y , или компонентов север-юг и восток-запад. 9{\circ}}[/latex] к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и на север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, используемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0014 действует на в главе 4 «Динамика: законы движения Ньютона». Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.

PHET EXPLORATIONS: MAZE GAME

Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.

Рисунок 18. Игра «Лабиринт»

• Графический метод сложения векторов [latex]\textbf{A}[/latex] и [latex]\textbf{B}[/latex] включает рисование векторов на графике и их сложение с использованием прямого метод хвоста. Результирующий вектор [latex]\textbf{R}[/latex] определяется таким образом, что [latex]{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex] Величина и направление [latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
• графический метод вычитания вектора [latex]\textbf{B}[/latex] из [latex]\textbf{A}[/latex] включает добавление противоположного вектора [latex]\textbf{B},[/latex ] который определяется как [latex]{-\textbf{B}}.[/latex] В этом случае [latex]{\textbf{A}-\textbf{B}=\textbf{A}+(-\ textbf{B})=\textbf{R}}.[/latex] Затем обычным образом применяется метод сложения головы к хвосту для получения результирующего вектора [latex]\textbf{R}.[/ латекс]
• Сложение векторов коммутативно , такое что [латекс]{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
• Метод «голова к хвосту» сложения векторов включает рисование первого вектора на графике, а затем размещение хвоста каждого последующего вектора в начале предыдущего вектора. Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
• Если вектор [latex]\textbf{A}[/latex] умножить на скалярную величину [latex]{c},[/latex], величина произведения будет равна [latex]{cA}.[/ латекс] Если [латекс]{с}[/латекс] положительный, направление произведения указывает в том же направлении, что и [латекс]\текстбф{А};[/латекс], если [латекс]{с}[/латекс] ] отрицательно, направление произведения указывает в направлении, противоположном направлению [латекс]\текстбф{А}.[/латекс]

 

компонент (двумерного вектора)

часть вектора, указывающая либо в вертикальном, либо в горизонтальном направлении; каждый двумерный вектор может быть выражен как сумма двух компонент вертикального и горизонтального векторов 90 336

коммутативный

относится к взаимозаменяемости порядка в функции; сложение векторов является коммутативным, потому что порядок сложения векторов не влияет на окончательную сумму 90 336

направление (вектора)

ориентация вектора в пространстве

голова (вектора)

конечная точка вектора; расположение кончика стрелки вектора; также называется «наконечник»

метод «голова к хвосту»

метод сложения векторов, при котором конец каждого вектора помещается в начало предыдущего вектора

величина (вектора)

длина или размер вектора; величина является скалярной величиной

результат

сумма двух или более векторов

результирующий вектор

векторная сумма двух или более векторов

скаляр

количество с величиной, но без направления

хвост

начальная точка вектора; напротив наконечника или наконечника стрелки

Операции с векторами — GeeksforGeeks

В физике в основном есть два типа величин – векторы и скаляры. Векторы — это величины, с которыми связаны как направление, так и величина, в то время как скаляры — это величины, с которыми связана единственная величина. Со скалярными величинами можно работать, используя простые алгебраические правила, но это не относится к векторным величинам, с ними нельзя обращаться таким же образом. Таким образом, важно знать, какие и сколько различных операций можно произвести над этими величинами. Рассмотрим подробнее некоторые из этих операций.

Математические операции над векторами

Поскольку векторы содержат направления, с этими величинами следует обращаться таким образом, чтобы учитывать их направления. Основные правила алгебры вообще не применимы к векторам, например, простое сложение величин двух векторов в большинстве случаев даст неверный ответ. В следующем списке перечислены некоторые распространенные операции, которые выполняются над векторами в области физики: 

1. Сложение/вычитание двух векторов.
2. Умножение вектора на скаляр.
3. Продукт двух векторов:
   • DOT Product
   • Крестный продукт

Дополнение векторов

Vectors нельзя добавлять по правилам США. При добавлении двух векторов необходимо учитывать величину и направление векторов. Закон треугольника используется для сложения двух векторов, на диаграмме ниже показаны два вектора «a» и «b» и результат, рассчитанный после их сложения. Сложение векторов следует коммутативному свойству, это означает, что результирующий вектор не зависит от порядка добавления двух векторов.

⇢ (Перестановочное свойство)

Треугольный закон сложения векторов

Рассмотрим векторы, указанные на рисунке выше. Линия PQ представляет вектор «p», а QR представляет вектор «q». Линия QR представляет результирующий вектор. AC направлен от A к C.  

Линия AC представляет собой

Величина результирующего вектора определяется выражением

Представляет собой угол между двумя векторами. Пусть \phi будет углом между результирующим вектором и вектором p.

Умножение векторов на скаляр

Умножение вектора a на постоянный скаляр k дает вектор, направление которого остается тем же, но величина изменяется в k раз. На рисунке показан вектор до и после умножения на константу k. В математических терминах это можно переписать как

, если k > 1, величина вектора увеличивается, а уменьшается, когда k < 1.

Произведение векторов

Векторы можно умножать друг на друга, но нельзя делить. В случае умножения есть в основном два вида умножения — скалярное и векторное. Скалярное умножение (также известное как скалярное произведение) — это вид умножения, в результате которого получается скалярная величина. Умножение векторов (также известное как перекрестное произведение) — это вид умножения, в результате которого получается векторная величина. Векторные произведения используются для определения других производных векторных величин.

Скалярный продукт

Рассмотрим два вектора     и     . Скалярное произведение этих двух векторов определяется уравнением

Здесь θ — угол между двумя векторами.

В случае, если векторы заданы их компонентами. например, a = a ₁ i + a ₂ j + a ₃ k и b = b ₁ i + b ₂ j + b ₃ k. В этом случае скалярный продукт определяется как 

A.B = A ₁ B ₁ I + A ₂ B ₂ J + A ₃ B ₃ K

VECTER Product 9999999999999999999999999999. 9049. } и \vec{B} . Векторное произведение этих двух векторов обозначается  . Направление этого вектора перпендикулярно обоим векторам. Величина этого вектора определяется выражением

Здесь θ — угол между двумя векторами.

Правило правой руки используется для определения направления результирующего вектора векторного произведения. Обратите внимание, что в отличие от сложения и скалярного произведения векторное произведение не является коммутативным по своей природе.

В случае, если векторы заданы их компонентами. например, a = a ₁ i + a ₂ j + a ₃ k и b = b ₁ i + b ₂ j + b ₃ k. В этом случае векторное произведение определяется выражением

 

Примеры задач

Вопрос 1. Вектор определяется выражением v = 2i + j. Найдите модуль вектора, когда он масштабируется на константу 0,4.

Ответ:  

для вектора, v = ai + bj

|в| =

0,4|v| = |0,4 В|

а = 2, б = 1

|0,4v|

⇒ |0,4(2i + j)|

⇒ |0,8i + 0,4j|

|в| =

⇒ |v| =

⇒ |v| = √0,8

Вопрос 2: Два вектора величиной 5 и 10. Эти векторы имеют между собой угол 60°. Найдите величину результирующих векторов.