8 класс. Геометрия. Векторы. Повторение теории. Решение задач с применением векторов. — Векторы. Повторение теории. Решение задач с применением векторов.

Комментарии преподавателя

 По­вто­ре­ние тео­рии. За­да­чи

На­пом­ним, что су­ще­ству­ют такие фи­зи­че­ские ве­ли­чи­ны, для ко­то­рых важна не толь­ко ве­ли­чи­на, но и на­прав­ле­ние. Такие ве­ли­чи­ны на­зы­ва­ют­ся век­тор­ны­ми, или век­то­ра­ми, и обо­зна­ча­ют­ся они на­прав­лен­ным от­рез­ком, то есть таким от­рез­ком, у ко­то­ро­го от­ме­че­ны на­ча­ло и конец. Вве­де­но было по­ня­тие кол­ли­не­ар­ных век­то­ров, то есть таких, ко­то­рые лежат либо на одной пря­мой, либо на па­рал­лель­ных пря­мых.

Мы рас­смат­ри­ва­ем век­тор, ко­то­рый можно от­ло­жить от любой точки, за­дан­ный век­тор от про­из­воль­но вы­бран­ной точки можно от­ло­жить един­ствен­ным об­ра­зом.

Было вве­де­но по­ня­тие рав­ных век­то­ров – это такие со­на­прав­лен­ные век­то­ры, длины ко­то­рых равны. Со­на­прав­лен­ны­ми на­зы­ва­ют­ся кол­ли­не­ар­ные век­то­ры, на­прав­лен­ные в одну сто­ро­ну.

Были вве­де­ны пра­ви­ла тре­уголь­ни­ка и па­рал­ле­ло­грам­ма – пра­ви­ла сло­же­ния век­то­ров.

За­да­ны два век­то­ра – век­то­ры  и . Най­дем сумму этих двух век­то­ров . Для этого от­ло­жим из неко­то­рой точки А век­тор .  – на­прав­лен­ный от­ре­зок, точка А – его на­ча­ло, а точка В – конец. Из точки В от­ло­жим век­тор . Тогда век­тор  на­зы­ва­ют сум­мой за­дан­ных век­то­ров:  – пра­ви­ло тре­уголь­ни­ка (см. Рис. 1).

Рис. 1

За­да­но два век­то­ра – век­то­ры  и . Най­дем сумму этих двух век­то­ров  по пра­ви­лу па­рал­ле­ло­грам­ма.

От­кла­ды­ва­ем из точки А век­тор  и век­тор  (см. Рис. 2). На от­ло­жен­ных век­то­рах можно по­стро­ить па­рал­ле­ло­грамм. Из точки В от­кла­ды­ва­ем век­тор , век­то­ры  и  равны, сто­ро­ны ВС и

Рис. 2

АВ1 па­рал­лель­ны. Ана­ло­гич­но па­рал­лель­ны и сто­ро­ны АВ и В1С, таким об­ра­зом, мы по­лу­чи­ли па­рал­ле­ло­грамм. АС – диа­го­наль па­рал­ле­ло­грам­ма. 

Для сло­же­ния несколь­ких век­то­ров при­ме­ня­ют пра­ви­ло мно­го­уголь­ни­ка (см. Рис. 3). Нужно из про­из­воль­ной точки от­ло­жить пер­вый век­тор, из его конца от­ло­жить вто­рой век­тор, из конца вто­ро­го век­то­ра от­ло­жить тре­тий и так далее, когда все век­то­ры от­ло­же­ны – со­еди­нить на­чаль­ную точку с кон­цом по­след­не­го век­то­ра, в итоге по­лу­чит­ся сумма несколь­ких век­то­ров.

Рис. 3

Кроме того, мы рас­смот­ре­ли по­ня­тие об­рат­но­го век­то­ра – век­то­ра, име­ю­ще­го такую же длину, как за­дан­ный, но ему про­ти­во­на­прав­лен­но­го.

При­мер 1 – за­да­ча 747: вы­пи­ши­те пары кол­ли­не­ар­ных со­на­прав­лен­ных век­то­ров, ко­то­рые опре­де­ля­ют­ся сто­ро­на­ми па­рал­ле­ло­грам­ма; ука­жи­те про­ти­во­по­лож­но на­прав­лен­ные век­то­ры;

Задан па­рал­ле­ло­грамм MNPQ (см. Рис. 4). Вы­пи­шем пары кол­ли­не­ар­ных век­то­ров. В первую оче­редь это век­то­ры  и . Они не толь­ко кол­ли­не­ар­ные, но и рав­ные, т. к. они со­на­прав­ле­ны, и длины их равны по свой­ству па­рал­ле­ло­грам­ма (в па­рал­ле­ло­грам­ме про­ти­во­по­лож­ные сто­ро­ны равны). Сле­ду­ю­щая пара . Ана­ло­гич­но

Рис. 4

вы­пи­шем кол­ли­не­ар­ные век­то­ры вто­рой пары сто­рон: ; .

Про­ти­во­по­лож­но на­прав­лен­ные век­то­ры: , , , .

При­мер 2 – за­да­ча 756: на­чер­ти­те по­пар­но некол­ли­не­ар­ные век­то­ры ,  и . По­строй­те век­то­ры ;; ;.

Для вы­пол­не­ния дан­но­го за­да­ния можем поль­зо­вать­ся пра­ви­лом тре­уголь­ни­ка или па­рал­ле­ло­грам­ма.

Спо­соб 1 – с по­мо­щью пра­ви­ла тре­уголь­ни­ка (см. Рис. 5):

Рис. 5

Спо­соб 2 – с по­мо­щью пра­ви­ла па­рал­ле­ло­грам­ма (см. Рис. 6):

Рис. 6

Ком­мен­та­рий: мы при­ме­ня­ли в пер­вом спо­со­бе пра­ви­ло тре­уголь­ни­ка – от­кла­ды­ва­ли из про­из­воль­но вы­бран­ной точки А пер­вый век­тор, из его конца – век­тор, про­ти­во­по­лож­ный вто­ро­му, со­еди­ня­ли на­ча­ло пер­во­го с кон­цом вто­ро­го, и таким об­ра­зом по­лу­ча­ли ре­зуль­тат вы­чи­та­ния век­то­ров.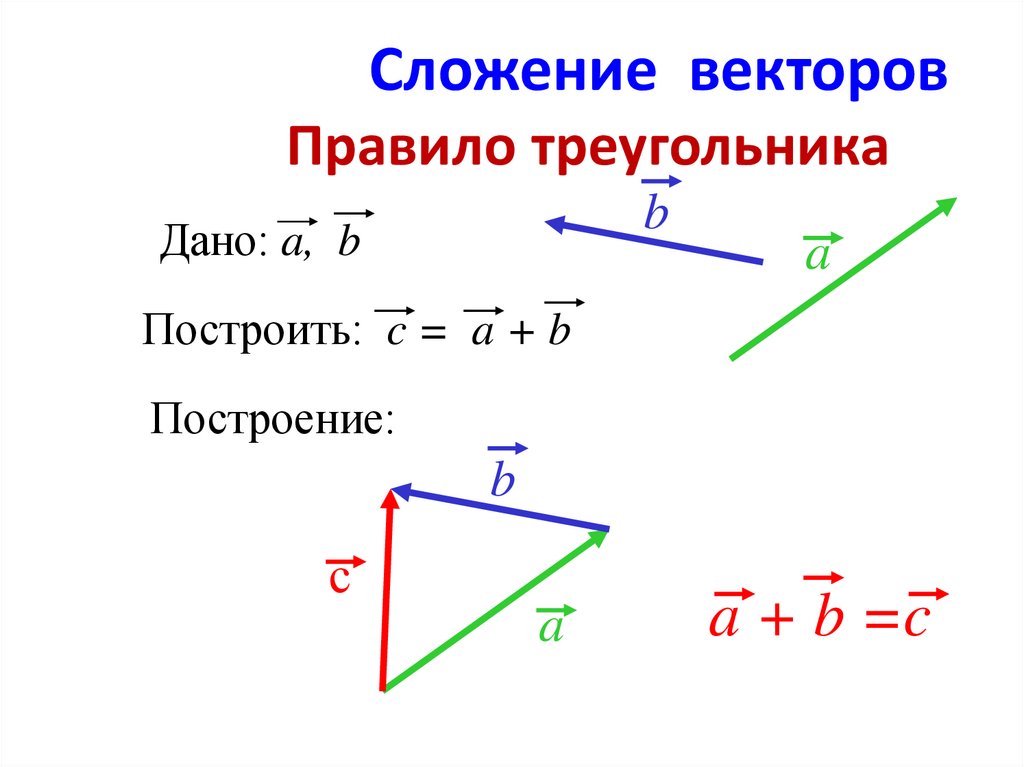 Во вто­ром спо­со­бе мы при­ме­ни­ли пра­ви­ло па­рал­ле­ло­грам­ма – по­стро­и­ли на нуж­ных век­то­рах па­рал­ле­ло­грамм и его диа­го­наль – ис­ко­мую раз­ность, помня тот факт, что одна из диа­го­на­лей – это сумма век­то­ров, а вто­рая – раз­ность.

При­мер 3 – за­да­ча 750: до­ка­жи­те, что если век­то­ры  и  равны, то се­ре­ди­ны от­рез­ков AD и BC сов­па­да­ют. До­ка­жи­те об­рат­ное утвер­жде­ние: если се­ре­ди­ны от­рез­ков AD и BC сов­па­да­ют, то век­то­ры  и  равны (см. Рис. 7).

Из ра­вен­ства век­то­ров  и  сле­ду­ет, что пря­мые АВ и CD па­рал­лель­ны, и что от­рез­ки АВ и CD равны. Вспом­ним при­знак па­рал­ле­ло­грам­ма: если у че­ты­рех­уголь­ни­ка пара про­ти­во­по­лож­ных сто­рон лежит на па­рал­лель­ных пря­мых, и их длины равны, то дан­ный че­ты­рех­уголь­ник – па­рал­ле­ло­грамм.

Рис. 7

Таким об­ра­зом, че­ты­рех­уголь­ник ABCD, по­стро­ен­ный на за­дан­ных век­то­рах, – па­рал­ле­ло­грамм. От­рез­ки AD и BC яв­ля­ют­ся диа­го­на­ля­ми па­рал­ле­ло­грам­ма, одно из свойств ко­то­ро­го: диа­го­на­ли па­рал­ле­ло­грам­ма пе­ре­се­ка­ют­ся и в точке пе­ре­се­че­ния де­лят­ся по­по­лам. Таким об­ра­зом, до­ка­за­но, что се­ре­ди­ны от­рез­ков AD и BC сов­па­да­ют.

До­ка­жем об­рат­ное утвер­жде­ние. Для этого вос­поль­зу­ем­ся дру­гим при­зна­ком па­рал­ле­ло­грам­ма: если в неко­то­ром че­ты­рех­уголь­ни­ке диа­го­на­ли пе­ре­се­ка­ют­ся и точ­кой пе­ре­се­че­ния де­лят­ся по­по­лам, то этот че­ты­рех­уголь­ник – па­рал­ле­ло­грамм. От­сю­да че­ты­рех­уголь­ник ABCD – па­рал­ле­ло­грамм, и его про­ти­во­по­лож­ные сто­ро­ны па­рал­лель­ны и равны, таким об­ра­зом, век­то­ры  и  кол­ли­не­ар­ны, оче­вид­но, что они со­на­прав­ле­ны, и мо­ду­ли их равны, от­сю­да век­то­ры  и  равны, что и тре­бо­ва­лось до­ка­зать.

 

При­мер 4 – за­да­ча 760: до­ка­жи­те, что для любых некол­ли­не­ар­ных век­то­ров  и  спра­вед­ли­во нера­вен­ство  (см. Рис. 8)

От­ло­жим из про­из­воль­ной точки А век­тор , по­лу­чим точку В, из нее от­ло­жим некол­ли­не­ар­ный ему век­тор . По пра­ви­лу па­рал­ле­ло­грам­ма или тре­уголь­ни­ка по­лу­чим сумму век­то­ров  – век­тор . Имеем тре­уголь­ник .

Длина суммы век­то­ров со­от­вет­ству­ет длине сто­ро­ны АС тре­уголь­ни­ка. По нера­вен­ству тре­уголь­ни­ка длина сто­ро­ны АС мень­ше, чем сумма длин двух дру­гих сто­рон АВ и ВС, что и тре­бо­ва­лось до­ка­зать.

Рис. 8

При­ме­не­ние век­то­ров к ре­ше­нию задач

На­пом­ним, что мы уже изу­чи­ли неко­то­рые факты о век­то­рах, и те­перь умеем опре­де­лять рав­ные век­то­ры, кол­ли­не­ар­ные век­то­ры, со­на­прав­лен­ные и про­ти­во­по­лож­но на­прав­лен­ные. Также мы умеем скла­ды­вать век­то­ры по пра­ви­лу тре­уголь­ни­ка и па­рал­ле­ло­грам­ма, скла­ды­вать несколь­ко век­то­ров по пра­ви­лу мно­го­уголь­ни­ка, умеем умно­жать век­тор на число. Ре­ше­ние задач с век­то­ра­ми ис­поль­зу­ет все эти зна­ния. Пе­рей­дем к ре­ше­нию неко­то­рых при­ме­ров.

При­мер 1 – за­да­ча 769: от­ре­зок ВВ1 – ме­ди­а­на тре­уголь­ни­ка . Вы­ра­зи­те через век­то­ры  и  век­то­ры , ,  и .

От­ме­тим, что век­то­ры  и  некол­ли­не­ар­ны, то есть пря­мые АВ и АС не па­рал­лель­ны.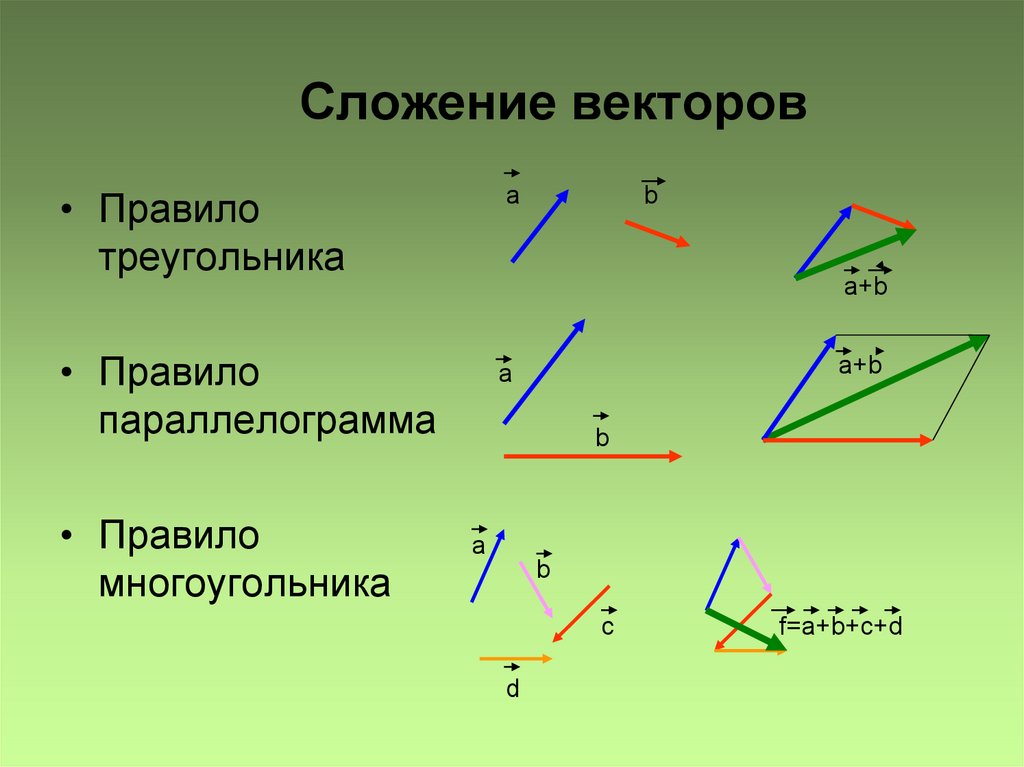

В даль­ней­шем мы узна­ем, что любой век­тор может быть вы­ра­жен через два некол­ли­не­ар­ных век­то­ра.

Вы­ра­зим пер­вый век­тор (см. Рис. 1): , т. к. по усло­вию ВВ1 – ме­ди­а­на тре­уголь­ни­ка, зна­чит, век­то­ры  и  имеют рав­ные мо­ду­ли, кроме того, оче­вид­но, что они кол­ли­не­ар­ны и при этом со­на­прав­ле­ны, зна­чит, дан­ные век­то­ра равны.

Рис. 1

Для вы­ра­же­ния сле­ду­ю­ще­го век­то­ра вос­поль­зу­ем­ся пра­ви­лом па­рал­ле­ло­грам­ма для вы­чи­та­ния. Мы пом­ним, что одна из диа­го­на­лей па­рал­ле­ло­грам­ма, по­стро­ен­но­го на двух век­то­рах, со­от­вет­ству­ет сумме этих век­то­ров, а вто­рая – их раз­но­сти. Диа­го­наль, со­от­вет­ству­ю­щая раз­но­сти век­то­ров, сле­ду­ет от конца к на­ча­лу, таким об­ра­зом, если по­стро­ить на за­дан­ных век­то­рах  и  па­рал­ле­ло­грамм, то его диа­го­наль  будет со­от­вет­ство­вать раз­но­сти .

Век­тор  яв­ля­ет­ся про­ти­во­по­лож­ным к за­дан­но­му век­то­ру , от­сю­да .

Век­тор  ана­ло­гич­но век­то­ру  можно пред­ста­вить в виде раз­но­сти век­то­ров .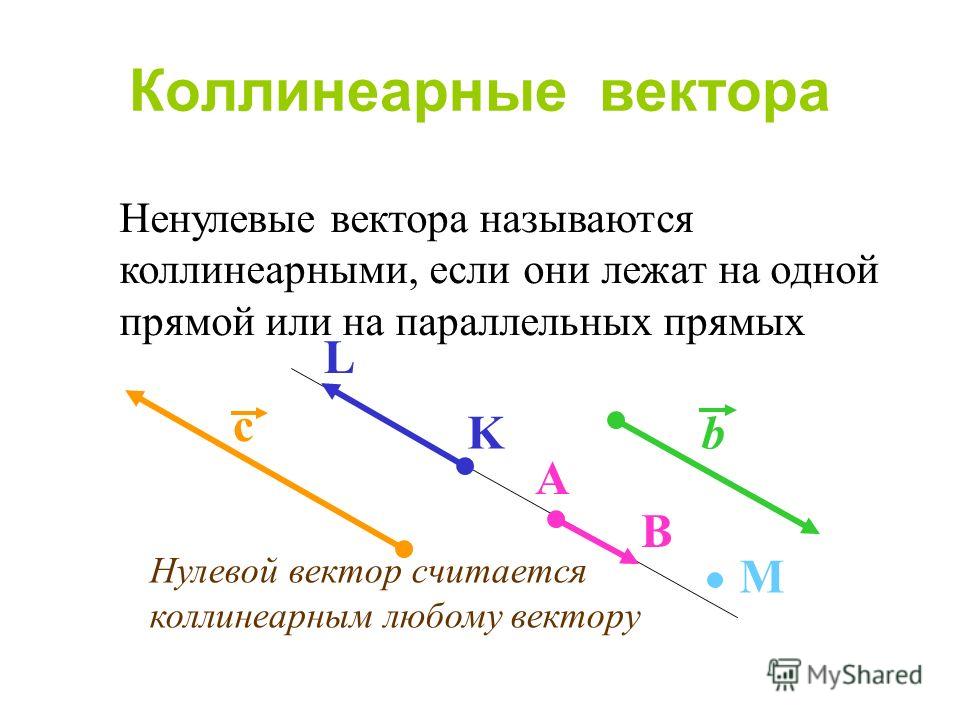 При вы­ра­же­нии сле­ду­ет учесть тот факт, что точка В1 яв­ля­ет­ся се­ре­ди­ной от­рез­ка АС, зна­чит, век­то­ры  и  равны, зна­чит, век­тор  можно пред­ста­вить как удво­ен­ное про­из­ве­де­ние век­то­ра .

Перед ре­ше­ни­ем за­да­чи мы ска­за­ли, что через за­дан­ные два некол­ли­не­ар­ных век­то­ра можно вы­ра­зить любой век­тор. Вы­ра­зим, на­при­мер, ме­ди­а­ну АА1 (см. Рис. 2).

По­лу­чи­ли си­сте­му урав­не­ний, вы­пол­ним их сло­же­ние:

Век­то­ры  в сумме со­став­ля­ют ну­ле­вой век­тор, так как они кол­ли­не­ар­ны и про­ти­во­на­прав­ле­ны, а мо­ду­ли их равны, таким об­ра­зом по­лу­ча­ем:

Рис. 2

По­де­лим обе части урав­не­ния на два, по­лу­чим: 

Из дан­ной за­да­чи можно сде­лать вывод, что если за­да­ны два некол­ли­не­ар­ных век­то­ра, то любой тре­тий век­тор на плос­ко­сти можно од­но­знач­но вы­ра­зить через эти два век­то­ра. Для этого необ­хо­ди­мо при­ме­нить пра­ви­ло сло­же­ния век­то­ров, либо ме­то­дом тре­уголь­ни­ка, либо па­рал­ле­ло­грам­ма, и пра­ви­ло умно­же­ния век­то­ра на число.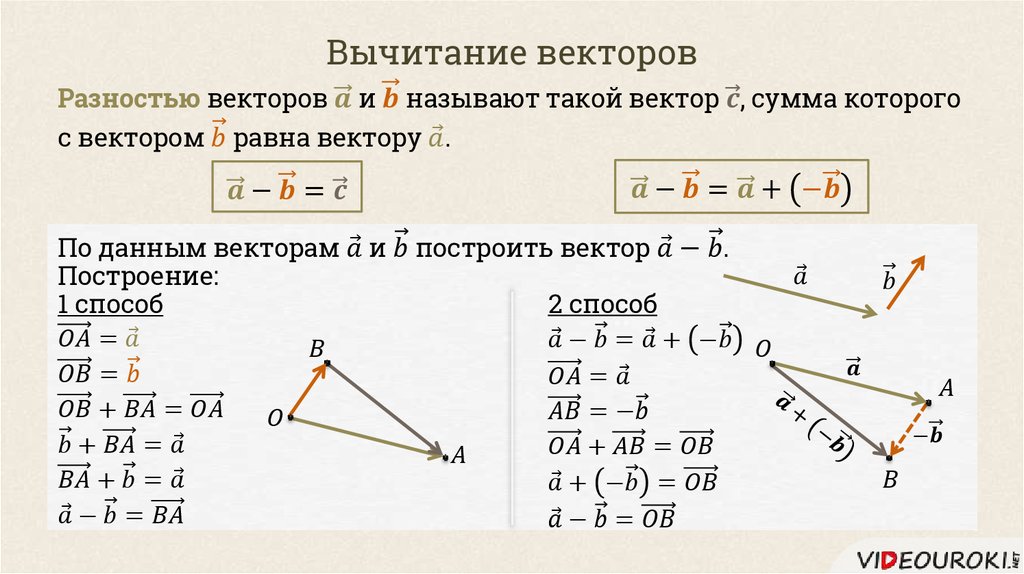

При­мер 2: до­ка­зать с по­мо­щью век­то­ров свой­ство сред­ней линии тре­уголь­ни­ка (см. Рис. 3).

Задан про­из­воль­ный тре­уголь­ник , точки M и N – се­ре­ди­ны сто­рон АВ и АС со­от­вет­ствен­но, MN – сред­няя линия тре­уголь­ни­ка. Свой­ство сред­ней линии: сред­няя линия па­рал­лель­на ос­но­ва­нию тре­уголь­ни­ка и равна его по­ло­вине.

До­ка­за­тель­ство дан­но­го свой­ства ана­ло­гич­но для тре­уголь­ни­ка и тра­пе­ции.

Рис. 3

Вы­ра­зим век­тор  двумя спо­со­ба­ми:

По­лу­чи­ли си­сте­му урав­не­ний:

          Вы­пол­ним сло­же­ние урав­не­ний си­сте­мы:

Сумма век­то­ров  – это ну­ле­вой век­тор, длины этих век­то­ров равны по усло­вию, кроме того, они оче­вид­но кол­ли­не­ар­ны и про­ти­во­на­прав­ле­ны. Ана­ло­гич­но сум­мой век­то­ров  будет ну­ле­вой век­тор. По­лу­ча­ем:

По­де­лим обе части урав­не­ния на два:

Таким об­ра­зом, мы по­лу­чи­ли, что сред­няя линия тре­уголь­ни­ка равна по­ло­вине его ос­но­ва­ния. Кроме того, из ра­вен­ства век­то­ра  по­ло­вине век­то­ра  сле­ду­ет, что эти век­то­ры кол­ли­не­ар­ны и со­на­прав­ле­ны, а зна­чит, пря­мые MN и ВС па­рал­лель­ны.

Таким об­ра­зом, мы до­ка­за­ли свой­ство сред­ней линии тра­пе­ции при по­мо­щи век­то­ров.

При­мер 3: задан про­из­воль­ный тре­уголь­ник  (см. Рис. 4). В нем про­ве­де­ны ме­ди­а­ны АА1, ВВ1, СС1. Точка пе­ре­се­че­ния ме­ди­ан – М. Век­тор  со­от­вет­ству­ет силе ,  – силе ,  – силе . До­ка­зать, что .

На­пом­ним, что ме­ди­а­ны тре­уголь­ни­ка пе­ре­се­ка­ют­ся в одной точке и этой точ­кой де­лят­ся в от­но­ше­нии 2:1, счи­тая от вер­ши­ны.

Ино­гда точку пе­ре­се­че­ния ме­ди­ан на­зы­ва­ют цен­тром тя­же­сти тре­уголь­ни­ка.

Вы­пол­ним сло­же­ние век­то­ров , вос­поль­зу­ем­ся для этого пра­ви­лом па­рал­ле­ло­грам­ма (см. Рис. 5).

Рис. 4

По­лу­ча­ем: 

С дру­гой сто­ро­ны, , так как BMCD – па­рал­ле­ло­грамм, диа­го­на­ли па­рал­ле­ло­грам­ма точ­кой пе­ре­се­че­ния де­лят­ся по­по­лам, А1 – точка пе­ре­се­че­ния диа­го­на­лей па­рал­ле­ло­грам­ма, зна­чит, от­рез­ки МА1 и А1D равны, от­сю­да, по свой­ству точки пе­ре­се­че­ния ме­ди­ан, длины век­то­ров  и  равны, но дан­ные век­то­ры про­ти­во­на­прав­ле­ны, а зна­чит, их сумма

Рис.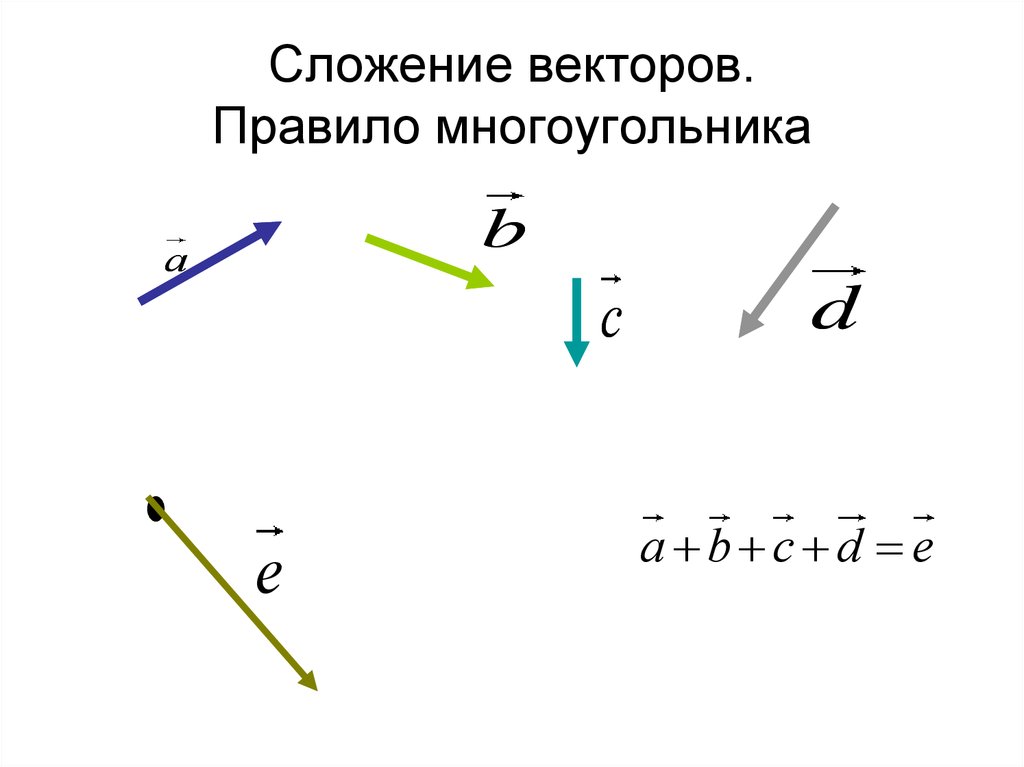 5

равна ну­ле­во­му век­то­ру. Мы пом­ним, что век­тор , а век­тор , таким об­ра­зом, , что и тре­бо­ва­лось до­ка­зать.

При­мер 4 – за­да­ча 773: до­ка­жи­те, что для любых век­то­ров  и  спра­вед­ли­во сле­ду­ю­щее нера­вен­ство: 

Ре­ше­ние: пред­ста­вим раз­ность век­то­ров в виде суммы: . Также об­ра­тим вни­ма­ние на тот факт, что длины про­ти­во­на­прав­лен­ных век­то­ров  и  равны: . Таким об­ра­зом, можно пе­ре­пи­сать ис­ход­ное вы­ра­же­ние:

Для удоб­ства вве­дем новую пе­ре­мен­ную:  и пе­ре­пи­шем вы­ра­же­ние:

. А дан­ное нера­вен­ство – нера­вен­ство тре­уголь­ни­ка – было до­ка­за­но в преды­ду­щем уроке. От­ме­тим, что ра­вен­ство на­блю­да­ет­ся в том слу­чае, когда тре­уголь­ник вы­рож­да­ет­ся в от­ре­зок.

Итак, мы вспом­ни­ли все ос­нов­ные опре­де­ле­ния и свой­ства век­то­ров, вспом­ни­ли ос­нов­ные опе­ра­ции над век­то­ра­ми, рас­смот­ре­ли при­ме­не­ние век­то­ров при ре­ше­нии раз­лич­ных задач, до­ка­за­ли неко­то­рые свой­ства фигур и ре­ши­ли наи­бо­лее рас­про­стра­нен­ные типы задач.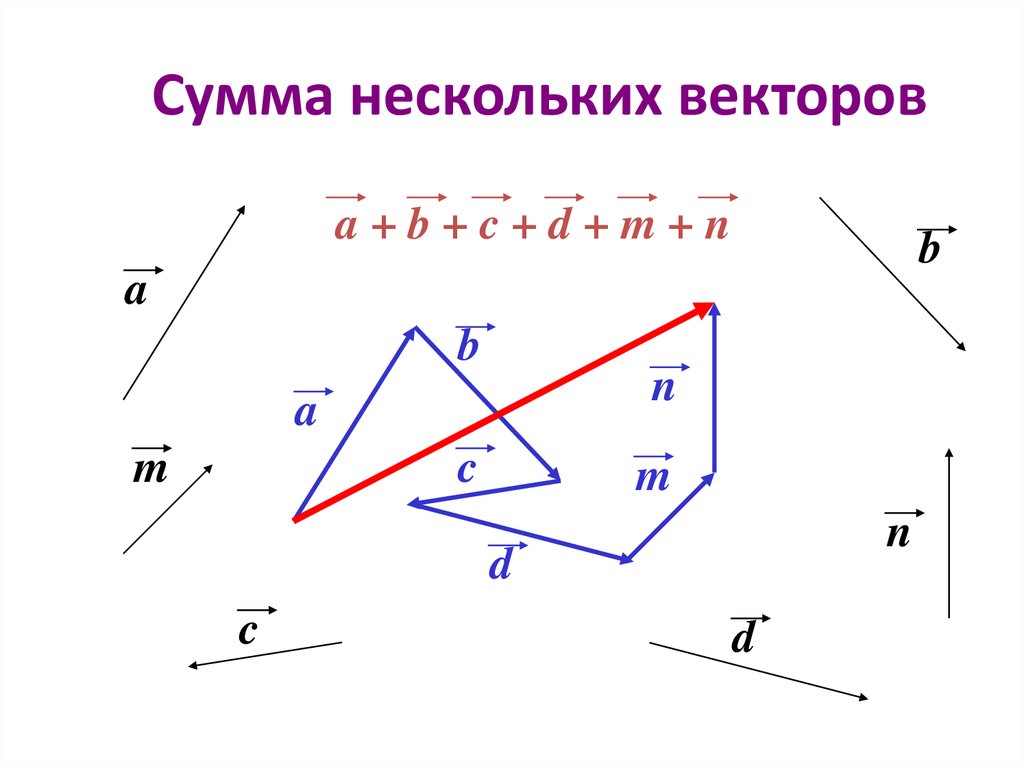

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/vektory/vektory-povtorenie-teorii-zadachi

http://interneturok.ru/ru/school/geometry/8-klass/vektory/primenenie-vektorov-k-resheniyu-zadach

http://metodbook.ru/index.php/matematika/9-testy-po-geometrii-9-klass/8-itogovyj-test-po-teme-vektory-variant-1.html

http://metodbook.ru/index.php/matematika/9-testy-po-geometrii-9-klass/9-itogovyj-test-po-teme-vektory-variant-2.html

http://uslide.ru/images/22/28455/960/img5.jpg

http://www.studfiles.ru/html/2706/538/html_OqWQ3sDQeV.5bGa/htmlconvd-WBhq8w_html_73af1ab4.png

http://uchkollektor39.ru/uploads/images/items/29cc1d8d90989d9f0e3df70c3d95a9ee.jpg

http://rushkolnik.ru/tw_files2/urls_3/891/d-890061/890061_html_m5ff065f.jpg

http://cs1-48v4.vk-cdn.net/p24/3551abddfac0c8.mp3?extra=amJxaBk9gfTT0lPmsOEwb8Rn_T2twbNJh2OUazYT-T9cSSu4_1787ibMzOu6ytv1rZKrpdEq7XnWZN1f-bjAuKyWIFf7mzw

http://matssir.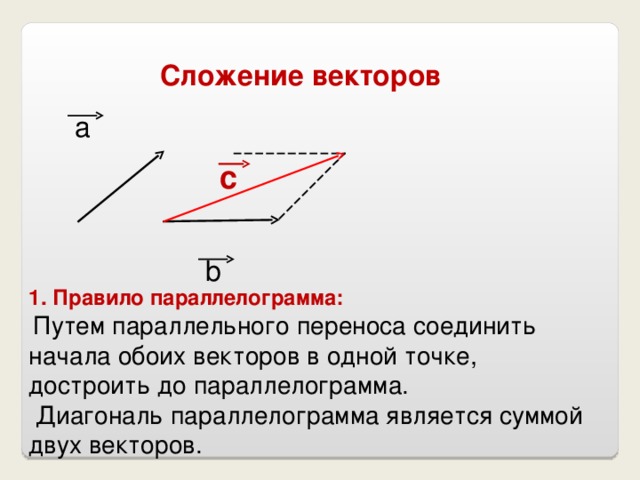 ucoz.ru/_ld/0/33_G8p84-85.pptx

http://nsportal.ru/sites/default/files/2014/05/11/vektory._dokazatelstvo.pptx

http://v.5klass.net/zip/b66d124d0243f848a0bf454b75404034.zip

Справочник по высшей математике

Выгодский М.Я. Справочник по высшей математике. Изд-во «Наука». М. 1977 г. Справочник включает весь материал, входящий в программу основного курса математики высших учебных заведений. Детальная рубрикация и подробный предметный указатель позволяют быстро получать необходимую информацию. Книга окажет неоценимую помощь студентам, инженерам и научным работникам. Оглавление ПРЕДИСЛОВИЕ АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. Понятие о предмете аналитической геометрии § 2. Координаты § 3. Прямоугольная система координат § 4. 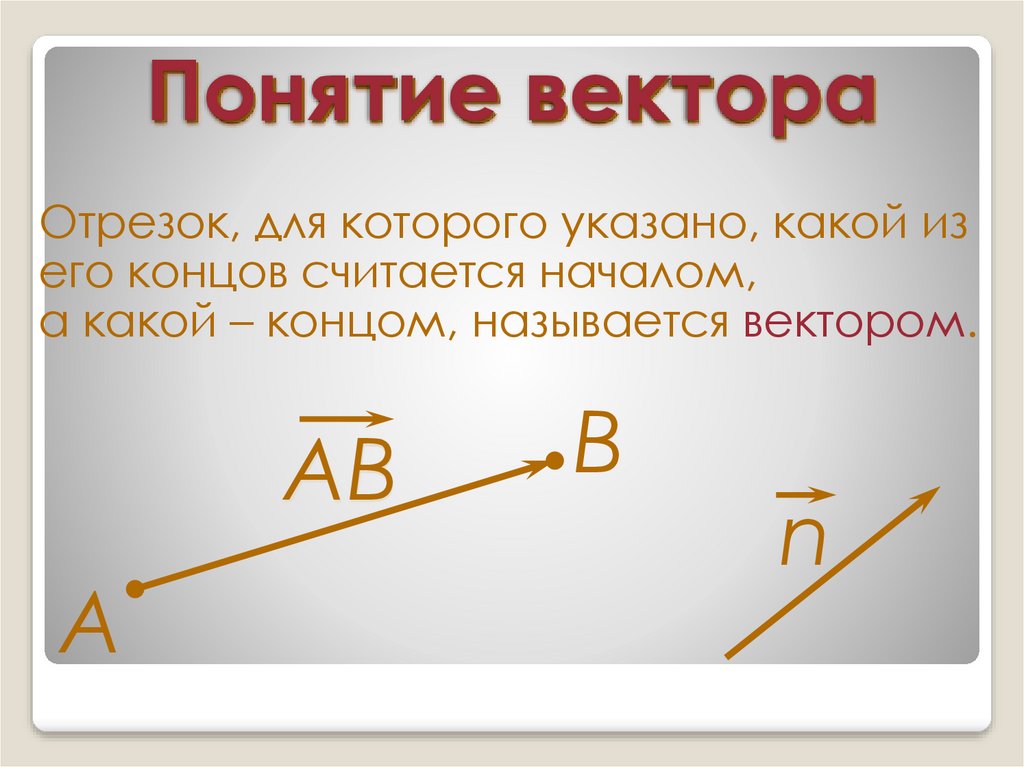Прямоугольные координаты § 5. Координатные углы § 6. Косоугольная система координат § 7. Уравнение линии § 8. Взаимное расположение линии и точки § 9. Взаимное расположение двух линий § 10. Расстояние между двумя точками § 11. Деление отрезка в данном отношении § 11а. Деление отрезка пополам § 12. Определитель второго порядка § 13. Площадь треугольника § 14. Прямая линия; уравнение, разрешенное относительно ординаты (с угловым коэффициентом) § 15. Прямая, параллельная оси § 16. Общее уравнение прямой § 17. Построение прямой по ее уравнению § 18. Условие параллельности прямых § 19. Пересечение прямых § 20. Условие перпендикулярности двух прямых § 21. Угол между двумя прямыми § 22. Условие, при котором три точки лежат на одной прямой § 23. Уравнение прямой, проходящей через две точки § 24. Пучок прямых § 25. Уравнение прямой, проходящей через данную точку параллельно данной прямой § 26. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой § 27. 2+bx+c § 51. Директрисы эллипса и гиперболы § 52. Общее определение эллипса, гиперболы и параболы § 53. Конические сечения § 54. Диаметры конического сечения § 55. Диаметры эллипса § 56. Диаметры гиперболы § 57. Диаметры параболы § 58. Линии второго порядка § 59. Запись общего уравнения второй степени § 60. Упрощение уравнения второй степени; общие замечания § 61. Предварительное преобразование уравнения второй степени § 62. Завершающее преобразование уравнения второй степени § 63. О приемах, облегчающих упрощение уравнения второй степени § 64. Признак распадения линий второго порядка § 65. Нахождение прямых, составляющих распадающуюся линию второго порядка § 66. Инварианты уравнения второй степени § 67. Три типа линий второго порядка § 68. Центральные и нецентральные линии второго порядка § 69. Нахождение центра центральной линии второго порядка § 70. Упрощение уравнения центральной линии второго порядка § 71. Равносторонняя гипербола как график уравнения y=k/x § 72. Равносторонняя гипербола как график уравнения y=(mx+n)/(px+q) § 73. Полярные координаты § 74. Связь между полярными и прямоугольными координатами § 75. Архимедова спираль § 76. Полярное уравнение прямой § 77. Полярное уравнение конического сечения АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ § 78. Понятие о векторах и скалярах § 79. Вектор в геометрии § 80. Векторная алгебра § 81. Коллинеарные векторы § 82. Нуль-вектор § 83. Равенство векторов § 84. Приведение векторов к общему началу § 85. Противоположные векторы § 86. Сложение векторов § 87. Сумма нескольких векторов § 88. Вычитание векторов § 89. Умножение и деление вектора на число § 90. Взаимная связь коллинеарных векторов (деление вектора на вектор) § 91. Проекция точки на ось § 92. Проекция вектора на ось § 93. Основные теоремы о проекциях вектора § 94. Прямоугольная система координат в пространстве § 95. Координаты точки § 96. Координаты вектора § 97. Выражения вектора через компоненты и через координаты § 98. Действия над векторами, заданными своими координатами § 99. Выражение вектора через радиусы-векторы его начала и конца § 100. Длина вектора. Расстояние между двумя точками § 101. Угол между осью координат и вектором § 102. Признак коллинеарности (параллельности) векторов § 103. Деление отрезка в данном отношении § 104. Скалярное произведение двух векторов § 104а. Физический смысл скалярного произведения § 105. Свойства скалярного произведения § 106. Скалярные произведения основных векторов § 107. Выражение скалярного произведения через координаты сомножителей § 108. Условие перпендикулярности векторов § 109. Угол между векторами § 110. Правая и левая системы трех векторов § 111. Векторное произведение двух векторов § 112. Свойства векторного произведения § 113. Векторные произведения основных векторов § 114. Выражение векторного произведения через координаты сомножителей § 115. Компланарные векторы § 116. Смешанное произведение § 117. Свойства смешанного произведения § 118. Определитель третьего порядка § 119. Выражение смешанного произведения через координаты сомножителей § 120. Признак компланарности в координатной форме § 121. Объем параллелепипеда § 122. Двойное векторное произведение § 123. Уравнение плоскости § 124. Особые случаи положения плоскости относительно системы координат § 125. Условие параллельности плоскостей § 126. Условие перпендикулярности плоскостей § 127. Угол между двумя плоскостями § 128. Плоскость, проходящая через данную точку параллельно данной плоскости § 129. Плоскость, проходящая через три точки § 130. Отрезки на осях § 131. Уравнение плоскости в отрезках § 132. Плоскость, проходящая через две точки перпендикулярно данной плоскости § 133. Плоскость, проходящая через данную точку перпендикулярно двум плоскостям § 134. 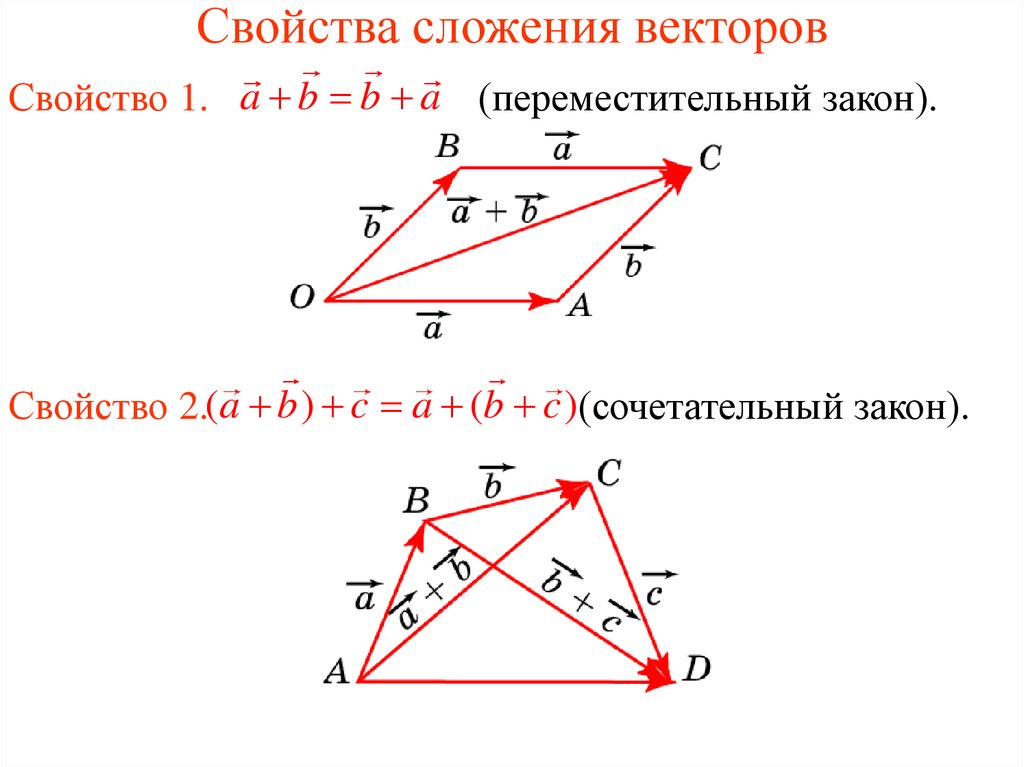Точка пересечения трех плоскостей § 135. Взаимное расположение плоскости и пары точек § 136. Расстояние от точки до плоскости § 137. Полярные параметры плоскости § 138. Нормальное уравнение плоскости § 139. Приведение уравнения плоскости к нормальному виду § 140. Уравнения прямой в пространстве § 141. Условие, при котором два уравнения первой степени представляют прямую § 142. Пересечение прямой с плоскостью § 143. Направляющий вектор § 144. Углы между прямой и осями координат § 145. Угол между двумя прямыми § 146. Угол между прямой и плоскостью § 147. Условия параллельности и перпендикулярности прямой и плоскости § 148. Пучок плоскостей § 149. Проекции прямой на координатные плоскости § 150. Симметричные уравнения прямой § 151. Приведение уравнений прямой к симметричному виду § 152. Параметрические уравнения прямой § 153. Пересечение плоскости с прямой, заданной параметрически § 154. Уравнения прямой, проходящей через две данные точки § 155. Уравнение плоскости, проходящей через данную точку перпендикулярно данной прямой § 156. Уравнения прямой, проходящей через данную точку перпендикулярно данной плоскости § 157. Уравнение плоскости, проходящей через данную точку и данную прямую § 158. Уравнение плоскости, проходящей через данную точку и параллельной двум данным прямым § 159. Уравнение плоскости, проходящей через данную прямую и параллельной другой данной прямой § 160. Уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости § 161. Уравнения перпендикуляра, опущенного из данной точки на данную прямую § 162. Длина перпендикуляра, опущенного из данной точки на данную прямую § 163. Условие, при котором две прямые пересекаются или лежат в одной плоскости § 164. Уравнения общего перпендикуляра к двум данным прямым § 165. Кратчайшее расстояние между двумя прямыми § 165а. Правые и левые пары прямых § 166. Преобразование координат § 167. Уравнение поверхности § 168. Цилиндрические поверхности, у которых образующие параллельны одной из осей координат § 169. Уравнения линии § 170. Проекция линии на координатную плоскость § 171. Алгебраические поверхности и их порядок § 172. Сфера § 173. Эллипсоид § 174. Однополостный гиперболоид § 175. Двуполостный гиперболоид § 176. Конус второго порядка § 177. Эллиптический параболоид § 178. Гиперболический параболоид § 179. Перечень поверхностей второго порядка § 180. Прямолинейные образующие поверхностей второго порядка § 181. Поверхности вращения § 182. Определители второго и третьего порядков § 183. Определители высших порядков § 184. Свойства определителей § 185. Практический прием вычисления определителей § 186. Применение определителей к исследованию и решению системы уравнений § 187. Два уравнения с двумя неизвестными § 188. Два уравнения с двумя неизвестными § 189. Однородная система двух уравнений с тремя неизвестными § 190. Два уравнения с двумя неизвестными § 190а. Система n уравнений с n неизвестными ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 192. Рациональные числа § 193. Действительные (вещественные) числа § 194. Числовая ось § 195. Переменные и постоянные величины § 196. Функция § 197. Способы задания функции § 198. Область определения функции § 199. Промежуток § 200. Классификация функций § 201. Основные элементарные функции § 202. Обозначение функции § 203. Предел последовательности § 204. Предел функции § 205. Определение предела функции § 206. Предел постоянной величины § 207. Бесконечно малая величина § 208. Бесконечно большая величина § 209. Связь между бесконечно большими и бесконечно малыми величинами § 210. Ограниченные величины § 211. Расширение понятия предепа § 212. Основные свойства бесконечно малых величин § 213. Основные теоремы о пределах § 214. Число е § 215. Предел sinx/x при x стремящемся к 0 § 216. Эквивалентные бесконечно малые величины § 217. Сравнение бесконечно малых величин § 217а. Приращение переменной величины § 218. Непрерывность функции в точке § 219. Свойства функций, непрерывных в точке § 219а. Односторонний предел; скачок функции § 220. Непрерывность функции на замкнутом промежутке § 221. Свойства функций, непрерывных на замкнутом промежутке ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ § 223. Скорость § 224. Определение производной функции § 225. Касательная § 226. Производные некоторых простейших функций § 227. Свойства производной § 228. Дифференциал § 229. Механический смысл дифференциала § 230. Геометрический смысл дифференциала § 231. Дифференцируемые функции § 232. Дифференциалы некоторых простейших функций § 233. Свойства дифференциала § 234. Инвариантность выражения f'(x)dx § 235. Выражение производной через дифференциалы § 236. Функция от функции (сложная функция) § 237. Дифференциал сложной функции § 238. Производная сложной функции § 239. Дифференцирование произведения § 240. Дифференцирование частного (дроби) § 241. Обратная функция § 242. Натуральные логарифмы § 243. Дифференцирование логарифмической функции § 244. Логарифмическое дифференцирование § 245. Дифференцирование показательной функции § 246. Дифференцирование тригонометрических функций § 247. Дифференцирование обратных тригонометрических функций § 247а. Некоторые поучительные примеры § 248. Дифференциал в приближенных вычислениях § 249. Применение дифференциала к оценке погрешности формул § 250. Дифференцирование неявных функций § 251. Параметрическое задание линии § 252. Параметрическое задание функции § 253. Циклоида § 254. Уравнение касательной к плоской линии § 254а. Касательные к кривым второго порядка § 255. Уравнение нормали § 256. Производные высших порядков § 257. Механический смысл второй производной § 258. Дифференциалы высших порядков § 259. Выражение высших производных через дифференциалы § 260. Высшие производные функций, заданных параметрически § 261. Высшие производные неявных функций § 262. Правило Лейбница § 263. Теорема Ролля § 264. Теорема Лагранжа о среднем значении § 265. Формула конечных приращений § 266. Обобщенная теорема о среднем значении (Коши) § 267. Раскрытие неопределенности вида 0/0 § 268. Раскрытие неопределенности вида бесконесность на бесконечность § 269. Неопределенные выражения других видов § 270. Исторические сведения о формуле Тейлора § 271. Формула Тейлора § 272. Применение формулы Тейлора к вычислению значений функции § 273. Возрастание и убывание функции § 274. Признаки возрастания и убывания функции в точке § 274а. Признаки возрастания и убывания функции в промежутке § 275. Максимум и минимум § 276. Необходимое условие максимума и минимума § 277. Первое достаточное условие максимума и минимума § 278. Правило нахождения максимумов и минимумов § 279. Второе достаточное условие максимума и минимума § 280. Нахождение наибольшего и наименьшего значений функции § 281. Выпуклость плоских кривых; точка перегиба § 282. Сторона вогнутости § 283. Правило для нахождения точек перегиба § 284. Асимптоты § 285. Нахождение асимптот, параллельных координатным осям § 286. Нахождение асимптот, не параллельных оси ординат § 287. Приемы построения графиков § 288. Решение уравнений. Общие замечания § 289. Решение уравнений. Способ хорд § 290. Решение уравнений. Способ касательных § 291. Комбинированный метод хорд и касательных ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ § 293. Первообразная функция § 294. Неопределенный интеграл § 295. Геометрический смысл интегрирования § 296. Вычисление постоянной интегрирования по начальным данным § 297. Свойства неопределенного интеграла § 298. Таблица интегралов § 299. Непосредственное интегрирование § 300. Способ подстановки (интегрирование через вспомогательную переменную) § 301. Интегрирование по частям § 302. Интегрирование некоторых тригонометрических выражений § 303. Тригонометрические подстановки § 304. Рациональные функции § 304а. Исключение целой части § 305. О приемах интегрирования рациональных дробей § 306. Интегрирование простейших рациональных дробей § 307. Интегрирование рациональных функций (общий метод) § 308. О разложении многочлена на множители § 309. Об интегрируемости в элементарных функциях § 310. Некоторые интегралы, зависящие от радикалов § 311. Интеграл от биномиального дифференциала § 312. Интегралы вида … § 313. Интегралы вида S R(sinx, cosx)dx § 314. Определенный интеграл § 315. Свойства определенного интеграла § 316. Геометрический смысл определенного интеграла § 317. Механический смысл определенного интеграла § 318. Оценка определенного интеграла § 318а. Неравенство Буняковского § 319. Теорема о среднем интегрального исчисления § 320. Определенный интеграл как функция верхнего предела § 321. Дифференциал интеграла § 322. Интеграл дифференциала. Формула Ньютона — Лейбница § 323. Вычисление определенного интеграла с помощью неопределенного § 324. Определенное интегрирование по частям § 325. Способ подстановки в определенном интеграле § 326. О несобственных интегралах § 327. Интегралы с бесконечными пределами § 328. Интеграл функции, имеющей разрыв § 329. О приближенном вычислении интеграла § 330. Формулы прямоугольников § 331. Формула трапеций § 332. Формула Симпсона (параболических трапеций) § 333. Площади фигур, отнесенных к прямоугольным координатам § 334. Схема применения определенного интеграла § 335. Площади фигур, отнесенных к полярным координатам § 336. Объем тела по поперечным сечениям § 337. Объем тела вращения § 338. Длина дуги плоской линии § 339. Дифференциал дуги § 340. Длина дуги и ее дифференциал в полярных координатах § 341. Площадь поверхности вращения ОСНОВНЫЕ СВЕДЕНИЯ О ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ ЛИНИЯХ § 342. Кривизна § 343. Центр, радиус и круг кривизны плоской линии § 344. Формулы для кривизны, радиуса и центра кривизны плоской линии § 345. Эволюта плоской линии § 346. Свойства эволюты плоской линии § 347. Развертка (эвольвента) плоской линии § 348. Параметрическое задание пространственной линии § 349. Винтовая линия § 350. Длина дуги пространственной линии § 351. Касательная к пространственной линии § 352. Нормальная плоскость § 353. Вектор-функция скалярного аргумента § 354. Предел вектор-функции § 355. Производная вектор-функции § 356. Дифференциал вектор-функции § 357. Свойства производной и дифференциала вектор-функции § 358. Соприкасающаяся плоскость § 359. Главная нормаль. Сопутствующий трехгранник § 360. Взаимное расположение линии и плоскости § 361. Основные векторы сопутствующего трехгранника § 362. Центр, ось и радиус кривизны пространственной линии § 363. Формулы для кривизны, радиуса и центра кривизны пространственной линии § 364. О знаке кривизны § 365. Кручение РЯДЫ § 367. Определение ряда § 368. Сходящиеся и расходящиеся ряды § 369. Необходимое условие сходимости ряда § 370. Остаток ряда § 371. Простейшие действия над рядами § 372. Положительные ряды § 373. Сравнение положительных рядов § 374. Признак Даламбера для положительного ряда § 375. Интегральный признак сходимости § 376. Знакопеременный ряд. Признак Лейбница § 377. Абсолютная и условная сходимость § 378. Признак Даламбера для произвольного ряда § 379. Перестановка членов ряда § 380. Группировка членов ряда § 381. Умножение рядов § 382. Деление рядов § 383. Функциональный ряд § 384. Область сходимости функционального ряда § 385. О равномерной и неравномерной сходимости § 386. Определение равномерной и неравномерной сходимости § 387. Геометрический смысл равномерной и неравномерной сходимости § 388. Признак равномерной сходимости; правильные ряды § 389. Непрерывность суммы ряда § 390. Интегрирование рядов § 391. Дифференцирование рядов § 392. Степенной ряд § 393. Промежуток и радиус сходимости степенного ряда § 394. Нахождение радиуса сходимости § 395. Область сходимости ряда, расположенного по степеням х – х0 § 396. Теорема Абеля § 397. Действия со степенными рядами § 398. Дифференцирование и интегрирование степенного ряда § 399. Ряд Тейлора § 400. Разложение функции в степенной ряд § 401. Разложение элементарных функций в степенные ряды § 402. Применение рядов к вычислению интегралов § 403. Гиперболические функции § 404. Обратные гиперболические функции § 405. Происхождение наименований гиперболических функций § 406. О комплексных числах § 407. Комплексная функция действительного аргумента § 408. Производная комплексной функции § 409. Возведение положительного числа в комплексную степень § 410. Формула Эйлера § 411. Тригонометрический ряд § 412. Исторические сведения о тригонометрических рядах § 413. Ортогональность системы функций cos nx, sin nx § 414. Формулы Эйлера-Фурье § 415. Ряд Фурье § 416. Ряд Фурье для непрерывной функции § 417. Ряд Фурье для четной и нечетной функции § 418. Ряд Фурье для разрывной функции ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ АРГУМЕНТОВ § 420. Функция трех и большего числа аргументов § 421. Способы задания функций нескольких аргументов § 422. Предел функции нескольких аргументов § 424. Непрерывность функции нескольких аргументов § 425. Частные производные § 426. Геометрический смысл частных производных для случая двух аргументов § 427. Полное и частное приращения § 428. Частный дифференциал § 429. О выражении частной производной через дифференциал § 430. Полный дифференциал § 431. Геометрический смысл полного дифференциала (случай двух аргументов) § 432. Инвариантность выражения … полного дифференциала § 433. Техника дифференцирования § 434. Дифференцируемые функции § 435. Касательная плоскость и нормаль к поверхности § 436. Уравнение касательной плоскости § 437. Уравнения нормали § 438. Дифференцирование сложной функции § 439. Замена прямоугольных координат полярными § 440. Формулы для производных сложной функции § 441. Полная производная § 442. Дифференцирование неявной функции нескольких переменных § 443. Частные производные высших порядков § 444. Полные дифференциалы высших порядков § 445. Техника повторного дифференцирования § 446. Условное обозначение дифференциалов § 447. Формула Тейлора для функции нескольких аргументов § 448. Экстремум (максимум и минимум) функции нескольких аргументов § 449. Правило нахождения экстремума § 450. Достаточные условия экстремума (случай двух аргументов) § 451. Двойной интеграл § 452. Геометрический смысл двойного интеграла § 453. Свойства двойного интеграла § 454. Оценка двойного интеграла § 455. Вычисление двойного интеграла (простейший случай) § 456. Вычисление двойного интеграла (общий случай) § 457. Функция точки § 458. Выражение двойного интеграла через полярные координаты § 459. Площадь куска поверхности § 460. Тройной интеграл § 461. Вычисление тройного интеграла (простейший случай) § 462. Вычисление тройного интеграла (общий случай) § 463. Цилиндрические координаты § 464. Выражение тройного интеграла через цилиндрические координаты § 465. Сферические координаты § 466. Выражение тройного интеграла через сферические координаты § 467. Схема применения двойного и тройного интегралов § 468. Момент инерции § 471. Криволинейный интеграл § 472. Механический смысл криволинейного интеграла § 473. Вычисление криволинейного интеграла § 474. Формула Грина § 475. Условие, при котором криволинейный интеграл не зависит от пути § 476. Другая форма условия предыдущего параграфа ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 478. Уравнение первого порядка § 479. Геометрический смысл уравнения первого порядка § 480. Изоклины § 481. Частное и общее решения уравнения первого порядка § 482. Уравнения с разделенными переменными § 483. Разделение переменных. Особое решение § 484. Уравнение в полных дифференциалах § 484а. Интегрирующий множитель § 485. Однородное уравнение § 486. Линейное уравнение первого порядка § 487. Уравнение Клеро § 488. Огибающая § 489. Об интегрируемости дифференциальных уравнений § 490. Приближенное интегрирование уравнений первого порядка по методу Эйлера § 491. Интегрирование дифференциальных уравнений с помощью рядов § 492. О составлении дифференциальных уравнений § 493. Уравнение второго порядка § 494. Уравнение n-го порядка § 495. Случаи понижения порядка § 496. Линейное уравнение второго порядка § 497. Линейное уравнение второго порядка с постоянными коэффициентами § 498. Линейное уравнение второго порядка с постоянными коэффициентами без правой части § 498а. Связь между случаями 1 и 3 § 498 § 499. Линейное уравнение второго порядка с постоянными коэффициентами с правой частью § 500. Линейные уравнения любого порядка § 501. Метод вариации постоянных § 502. Системы дифференциальных уравнений. Линейные системы НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ § 503. Строфоида § 504. Циссоида Диокла § 505. Декартов лист § 506. Верзьера Аньези § 507. Конхоида Никомеда § 508. Улитка Паскаля; кардиоида § 509. Линия Кассини § 510. Лемниската Бернулли § 511. Архимедова спираль § 512. Эвольвента (развертка) круга § 513. Логарифмическая спираль § 514. Циклоиды § 515. Эпициклоиды и гипоциклоиды § 516. Трактриса § 517. Цепная линия

Коллинеарные векторы и примеры

они коллинеарные векторы.  Это один из трех существующих типов векторов. Речь идет о векторах, которые находятся в одном направлении или линии действия. Это означает следующее: два или более вектора будут линейными, если расположить их на прямой, параллельной друг другу.

Вектор определяется как количество, применяемое к объекту, и характеризуется направлением, вкусом и масштабом. Векторы могут быть найдены на плоскостях или в пространстве и могут быть различных типов: коллинеарные векторы, параллельные векторы и параллельные векторы.

Индекс

• 1 вектор холина
• 2 Характеристики
  • 2.1 Пример 1
  • 2.2 Пример 2
  • 2.3 Пример 1
• 3 многоуровневая векторная система
  • 3.1 Коллинеарные векторы с противоположными направлениями
  • 3.2 Коллинеарные векторы с одинаковым значением
  • 3.3 Векторные коллекторы с одинаковой величиной и противоположными направлениями
• 4 Разница между коллинеарными и параллельными векторами
• 5 Каталожные номера

Коллинеарный вектор

Вектор является линейным, если линия действия одного вектора точно совпадает с линией действия всех других векторов, независимо от размера и вкуса каждого вектора.

Векторы используются в качестве представлений в различных областях, таких как математика, физика, алгебра, а также в геометрии, где векторы коллинеарны только тогда, когда направления совпадают, независимо от того, что они означают.

Функция

— Два или более вектора являются линейными, если отношения между координатами одинаковы.

Пример 1

У нас есть вектор m = m_x; m_y и n = n_x; н_у. Это коллинеарно, если:

Пример 2

– Два или более вектора являются линейными, если произведение или векторное произведение равно нулю (0). Это связано с тем, что в системе координат каждый вектор характеризуется своими координатами, и если они пропорциональны друг другу, векторы будут линейными. Это выражается следующим образом:

Пример 1

Имеем векторы a = (10, 5) и b = (6, 3). Для определения того, коллинеарны ли они, применяется определяющая теория, устанавливающая равенство перекрестных произведений.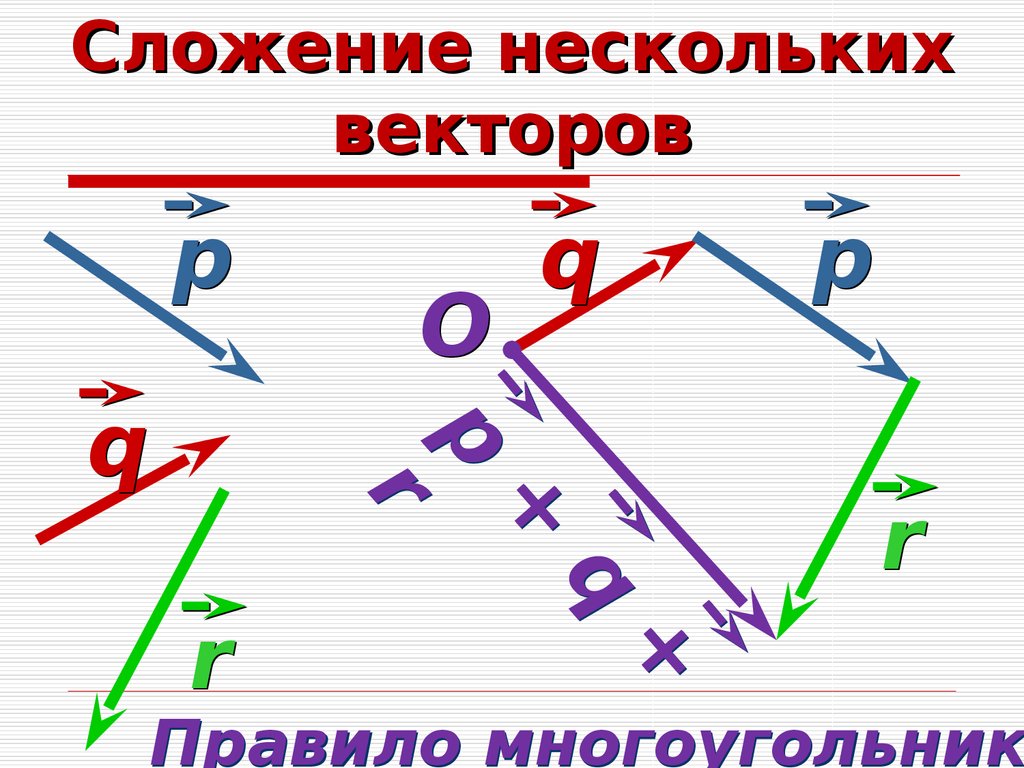 Таким образом, вы должны:

Коллинеарная система векторов

Коллинеарные векторы представлены графически с использованием направления и вкуса этого — учитывая, что они должны проходить через точку приложения и модуль, которые имеют определенный масштаб или длина.

Колинеарная векторная система образуется, когда два или более вектора воздействуют на объект или объекты, представляют собой силу и действуют в одном направлении.

Например, если к объектам приложены две коллинеарные силы, результат этого будет зависеть только от направления их действия. Возможны три случая, а именно:

Коллинеарный вектор с противоположными направлениями

Результаты двух коллинеарных векторов равны этому числу:

R = Σ F = F ₁  + F _2.

Пример

Если на поезд действуют две силы F ₁ = 40 Н и F ₂ = 20 Н в противоположном направлении (как показано на рисунке), результат составляет:

R = Σ F = (- 40 Н) + 20 Н.

R = – 20 Н.

Коллинеарные векторы с одинаковым значением

Величина равнодействующей силы будет равна сумме коллинеарных векторов:0102 + F _2.

Пример

Если на поезд действуют две силы F ₁ = 35 Н и F ₂ = 55 Н в одном и том же направлении (как показано на рисунке), результат составляет:

R = Σ F = 35 Н + 55 Н.

R = 90 Н.

Положительные результаты указывают на то, что коллинеарный вектор работает влево.

Спинальный вектор с той же величиной и противоположными направлениями

Результат двух коллинеарных векторов будет таким же, как сумма коллинеарных векторов:

R = Σ F = F ₁  + F _2.

Поскольку сила имеет одинаковую величину, но в противоположном направлении, то есть одна будет положительной, а другая отрицательной, при сложении двух сил результат будет нулевой.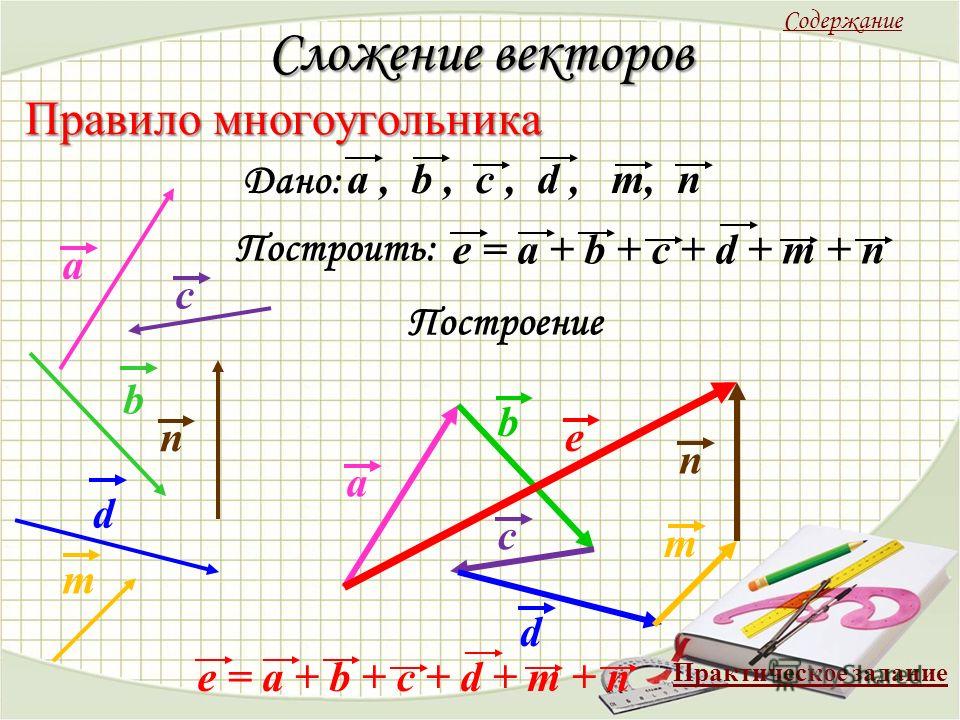

Пример

Если на поезд действуют две силы F ₁  = -7 Н и F ₂  = 7 Н, которые имеют одинаковую величину, но в противоположном направлении (как показано на рисунке), то результат:

R = Σ F = (-7 Н) + 7 Н.

R = 0.

Поскольку равнодействующая равна 0, это означает, что векторы уравновешены друг с другом и, следовательно, тело находится в равновесии или покоится (оно не будет двигаться).

Разница между коллинеарными и параллельными векторами

Коллинеарные векторы характеризуются тем, что они имеют одинаковое направление на одной линии или потому, что они параллельны этой линии; то есть они являются прямыми параллельными линейными векторами.

С другой стороны, параллельные векторы определяются, потому что они находятся на разных линиях действия, пересекающихся в одной точке.

Другими словами, они имеют одно и то же происхождение или прибытие – независимо от их модуля, направления или направления – образуя между собой угол.

Параллельные векторные системы решаются математическими или графическими методами, такими как метод параллелограмма силы и метод силы многоугольника. Благодаря этому будет определено результирующее значение вектора, указывающее направление, в котором будет двигаться тело.

Основное различие между коллинеарными векторами и параллельными векторами заключается в линии действия, в которой они действуют: коллинеарные действуют в одной и той же линии, будучи параллельными в разных.

То есть коллинеарные векторы действуют в одной плоскости, «X» или «Y»; и одновременные действия на обеих плоскостях, начиная с одной и той же точки.

Коллинеарные векторы не находятся в одной точке, как и одинаковые времена, потому что они параллельны друг другу.

На левом изображении вы видите блок. Связан веревкой и узлом, разделяющим ее на две части; при вытягивании в разные стороны и с разной силой блоки будут двигаться в одном направлении.

Представлены два вектора, совпадающие в точке (блоке), независимо от модуля, понимания или направления.

И наоборот, на правом рисунке показан шкив, который поднимает коробку. Веревка представляет линию действия; при рисовании на него действуют две силы (вектора): одна сила натяжения (при подъеме на блок) и другая, сила, оказывающая воздействие веса балки. Оба имеют одно и то же направление, но в противоположном направлении; не согласен в одном.

Номер по каталогу

Абдулла Сэм

Я преподаватель, исследователь и писатель. Я пишу об учебных предметах, чтобы улучшить обучение студентов колледжей и университетов. Я пишу высококачественные учебные заметки, в основном, о технологиях, играх, образовании, а также о решениях / советах и ​​​​хитростях. Я человек, который помогает студентам приобретать знания, компетентность или добродетель.

Определение коллинеарных векторов.

Последняя обновленная дата: 09 -й февраля 2023

•

Общее представление: 246,3K

•

Просмотры сегодня: 3,37K

Ответ

Проверено

246,3K+ просмотры

Hint:

8. вспоминая определение коллинеарных векторов, что они располагаются на одной линии или параллельных линиях. Воспользуемся тем, что компоненты одного из коллинеарных векторов кратны другому вектору. Мы используем тот факт, что векторное произведение коллинеарного вектора равно нулю, чтобы доказать все условия о коллинеарных векторах.

Полный пошаговый ответ:
Коллинеарные векторы: — Векторы, параллельные одной или лежащие на одной прямой, называются коллинеарными векторами.
Условие коллинеарности: — Два вектора коллинеарны, если выполнено любое из этих условий.
Условие-1:- Два вектора a, b коллинеарны, если существует такое число, что приведенное ниже уравнение становится верным. $\bar{a}=n.\bar{b}$
Условие-2: Два вектора коллинеарны, если отношение их координат равно.
Это неверно, если один из компонентов равен нулю.
Условие-3: Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
Это действительно только в том случае, когда 2 вектора являются трехмерными (пространственными) векторами.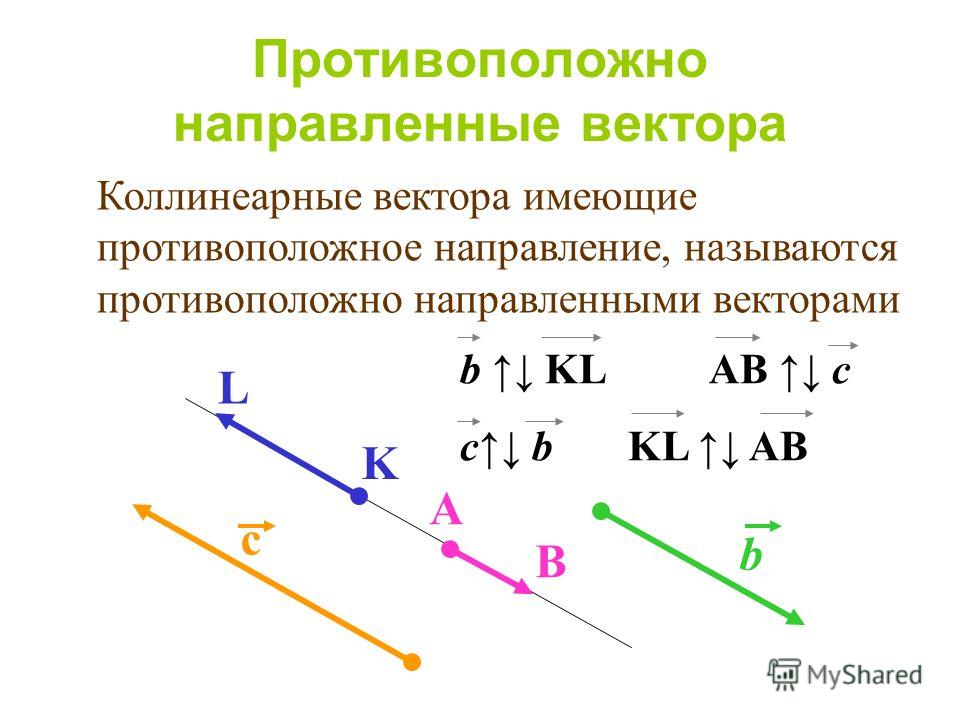
Перекрестное произведение:- Перекрестным произведением вектора а на вектор b называется вектор с, длина которого численно равна площади параллелограмма, построенного на векторах а, b, направление перпендикулярно плоскости векторов а, б. Если векторы a, b записать как $xi+yj+zk;\text{ pi+qj+rk}$, мы получим векторное произведение a, b, представленное $a\times b$, как:
$a\times b=\left|\begin{matrix}
  &i &j &k \\
  &x &y &z \\
  &p &q &r \\
\end{matrix} \right|$

Применить это определение к условию -3 получаем:
Перекрестное произведение a, b равно 0. Из условия 1 получаем:
$a=nb$. Если $b=xi+yj+zk,$ мы получаем значение a as,
$a=nxi+nyj+nzk$.
Перемножение $a\times b$ записывается как:
$a\times b=\left| \begin{matrix}
  &i &j &k \\
  &nx &ny &nz \\
  &x &y &z \\
\end{matrix} \right|$
Расширяя это, мы получаем следующее:

\[\begin{align}
 & a\times b=\left( nzy-nzy \ right)i-\left( nxz-nxz \right)j+\left( nxy-nxy \right)k \\
 & a\times b=oi-oj+ok\text{ = нулевой вектор}\text{.