Сумма нескольких векторов

Урок 6. Геометрия 9 класс ФГОС

В этом уроке излагается правило сложения нескольких векторов — правило многоугольника. Так же на конкретных примерах рассматриваются его частные случаи.

Конспект урока «Сумма нескольких векторов»

Вам уже известны правила сложения двух векторов.

Cегодня мы будем учиться складывать несколько векторов.

Построим вектор суммы векторов , , . От некоторой точки А отложим вектор
. Далее от точки B отложим вектор . А от точки C отложим вектор
.

Будем последовательно складывать наши векторы, пользуясь правилом треугольника.

 

Сумма векторов , равна вектору .

Теперь к вектору  добавим вектор . В результате мы получаем вектор .

Тогда можем сказать, что сумма .

Так, последовательно складывая первый вектор со вторым, затем их сумму с третьим и так далее, можно найти суммы четырёх, пяти и большего числа векторов.

Такое правило построения суммы векторов называют правилом многоугольника.

Сформулируем его в общем виде.

Если А₁, А₂, …, A_n — произвольные точки плоскости, то сумма векторов

.

Это равенство справедливо для любых точек А₁, А₂, …, A_n. И, в частности, для случая, когда некоторые из них совпадают.

Например, если начало первого вектора совпадает с концом последнего, то сумма данных векторов равна нулевому вектору.

Задача. Построить вектор суммы попарно неколлинеарных векторов , , ,  и .

Построение

 

 

 

 

 

.

Задача. В соответствии с правилом многоугольника составить равенство,выражающее сумму нескольких векторов.

 Посмотрим на первый рисунок. Мы видим, что последовательно складывают векторы . Но, так как начало вектора  совпадает с концом вектора , то сумма данных векторов равна нулевому вектору .

Перейдём к следующему случаю.

Видим, что сумма состоит из векторов . А вот вектор , как раз таки, и равен ей.

На рисунке в последовательно, друг за другом, отложены векторы  Ну, а вектор  равен их сумме.

На последнем рисунке последовательно, друг за другом, отложены векторы . При этом Начало вектора К совпадает с концом вектора С. Поэтому сумма данных векторов равна нулевому вектору  .

Задача.  равнобокая трапеция. и  — её основания, боковая сторона равна . Построить вектор  и найти его длину.

Построение

Решение.

Ответ:

А теперь подведём итоги нашего урока.

Сегодня мы познакомились с правилом многоугольника, которое позволяет строить вектор суммы нескольких векторов.

Его суть заключается в том, что векторы-слагаемые последовательно откладывают друг от друга, суммой является вектор, начало которого совпадает с началом первого вектора-слагаемого, а конец совпадает с концом последнего вектора-слагаемого.

Если эти точки совпадают, то сумма данных векторов равна нулевому вектору.

Предыдущий урок 5 Законы сложения векторов. Правило параллелограмма

Следующий урок 7 Вычитание векторов

Получите полный комплект видеоуроков, тестов и презентаций Геометрия 9 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Урок по геометрии «Сложение нескольких векторов» | План-конспект урока по геометрии (9 класс):

Технологическая карта урока 
Ф.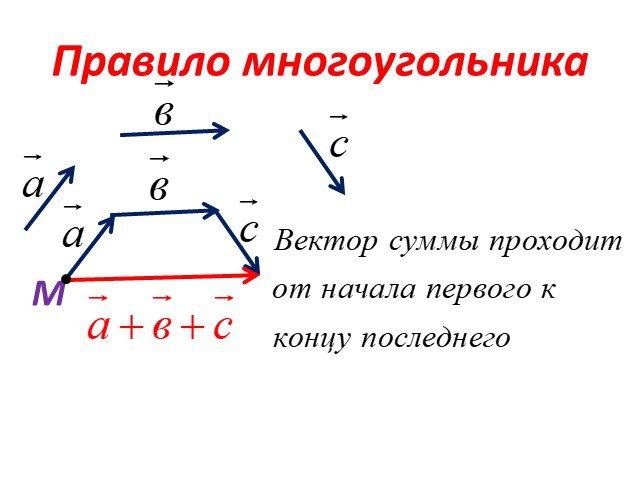 И.О. Ширкаева Людмила Александровна

Предмет: математика(геометрия)
Класс: 9
Тип урока: усвоение новых знаний

Тема	Сложение нескольких векторов.
Цель	Изучение правила сложения нескольких векторов
Задачи	Образовательные: формировать умение строить сумму нескольких векторов, используя правило многоугольника; Развивающие: умение обрабатывать информацию, формировать коммуникативную компетенцию учащихся, выбирать способы решения задач в зависимости от конкретных условий; Воспитательные: умение слушать и вступать в диалог, воспитывать ответственность и аккуратность.
УУД	Личностные УУД:  умение выделять нравственный аспект поведения, ориентация в межличностных отношениях.  Регулятивные УУД: прогнозирование своей деятельности для решения поставленных задач, целеполагание и выдвижение гипотез. Коммуникативные УУД: умение слушать и вступать в диалог, умение выражать свои мысли, поддержание здорового духа соперничества. Познавательные УУД: овладение геометрическим языком; развитие пространственных представлений; развитие умений применять изученные понятия, результаты, методы для решения задач практического характера.
Планируемые результаты	Предметные: Знать понятие вектора, правило сложения нескольких векторов; Уметь применить правило сложения нескольких векторов при решении практических задач. Личностные:  умение слушать и вступать в диалог. Метапредметные: применять полученные знания при решении практических задач.
Основные понятия	Вектор, сумма нескольких векторов.
Ресурсы:  основные  дополнительные	Геометрия.7-9 классы: учебник для общеобразовательных учреждений/Л.С.Атанасян, В.Ф.Бутузов, С.Д.Кадомцев.-7-е изд.-М.: Просвещение, 2017.-383с.:ил. Интерактивная панель с выходом в интернет, микрофон.
Формы урока	дистанционная
Технология	проблемного обучения
Время	30 минут

№

Этап урока

Название используемых ЭОР

Деятельность учителя (с указанием действий с ЭОР, например, демонстрация)

Деятельность ученика

Время (в мин. )

Формируемые УУД

Познаватель- ные

Регулятивные

Коммуникатив- ные

Личност- ные

1

2

3

5

6

7

8

9

10

1

Организационный момент

Сферум

Выход на платформу сферум; приветствие учащихся в беседе класса; проверка учителем готовности класса            к уроку; осуществляется групповой видеозвонок

Заходят на платформу сферум; приветствуют учителя в беседе класса; Подключаются к видеозвонку

2

осознанное и произвольное построение речевого высказывания

Прогнозирование своей деятельности

Умение слушать и вступать в диалог

умение выделять нравственный аспект поведения.

2

Вводная беседа. Актуализация знаний

Сферум

Вступительное слово учителя. Повторение необходимых понятий, демонстрация экрана Учитель продолжает  беседу с проблемной задачей  по будущей теме урока. Задает учащимся наводящие вопросы

Участвуют в работе по повторению, в беседе с учителем, отвечают на поставленные вопросы, приводят примеры. Работают с экраном.

2

Поиск и выделение необходимой информации

Выделение и осознание того, что уже пройдено. Постановка цели учебной задачи, синтез

Умение с достаточной полнотой и точностью выражать свои  мысли, слушать и вступать в диалог.

Смысло- образование

3

Изучение нового материала

Сферум

Вместе с учениками определяет цель урока.  Демонстрация экрана.

Учащиеся вместе с учителем определяют цель; выполняют задание в тетради

4

Поиск и выделение необходимой информации. Структурирование знаний. Анализ объектов.

Целеполагание, выдвижение гипотез

Умение слушать и вступать в диалог

4

Первичное осмысление и закрепление знаний.

Сферум

Комментирует,   направляет работу учащихся (правилу сложения нескольких векторов просит выполнить задание)

Один ученик на экране, а остальные в тетради выполняют задание по теме

6

Выделение и формулирование познавательной цели, рефлексия способов и условий действия. Анализ объектов и синтез

Планирование своей деятельности для решения поставленной задачи и контроль полученного результата

Умение слушать и вступать в диалог, Коллективное обсуждение проблем (при необходимости)

Ориента- ция в межличностных отношени-ях.

5

Закрепление изученного на  уроке, решение задач

Сферум

Выступает в роли тьютора для слабых учащихся

Учащиеся выполняют задания в тетради. После выполнения задания демонстрируют на камеру свою работу.

13

Выделение и формулирование познавательной цели, рефлексия способов и условий действия. Анализ и синтез объектов

Планирование своей деятельности для решения поставленной задачи,  контроль полученного результата, коррекция полученного результата, саморегуляция

Умение слушать и вступать в диалог.

Смыслообразование

6

Подведение итогов урока, оценивание знаний

Сферум

Учитель просит прислать фото записей тетради слабых учащихся. Активные награждаются оценками, с последующим выставлением в электронный журнал

В беседу, в сферум присылают фото

2

Оценка промежуточных результатов и саморегуляция для повышения мотивации учебной деятельности

управление поведением партнёра- контроль, коррекция, оценка

нравственно-этическая ориентация

8.

Домашнее задание

Сферум

Задает задание на дом

Учащиеся записывают домашнее задание

1

Ход урока

Деятельность учителя	Деятельность ученика
1.  Организационный момент Учитель заходит на платформу сферум и в беседе класса приветствует учеников. Осуществив групповой звонок, проверяет готовность класса к уроку. — Сегодня мы будем работать онлайн. В течение урока, мы с вами будем выполнять различные задания. В конце урока я назову учащихся, кто мне пришлёт фото заданий личным сообщением.	Учащиеся заходят на платформу сферум и в беседе класса приветствуют учителя. Отмечают своё присутствие знаком плюс. Подключаются к звонку.
2. Вводная беседа. Актуализация знаний. Учитель включает демонстрацию экрана и на экране прописывает задание на повторение. а) Упростить:  а) ;                            б) ;                          в) . б) Найти неизвестную:           1)  ;           2)  ;           3)   Учитель:  выполним задание (рисует на экране векторы и предлагает учащимся их сложить) Учитель:  — Каким образом это можно сделать? — Правильно! — Данный способ имеет название — правило многоугольника.	У учащихся есть возможность пользоваться экраном. По желанию, выполняют задание, прописывая решение на экране. Вспоминают правила сложения векторов. Проговаривают в ходе выполнения задания. Чертят в тетради и предлагают свои варианты решения.
3. Изучение нового материала Учитель:  давайте попробуем сформулировать, чего мы хотели добиться при решении данного задания? (корректируя ответы учащихся, вместе формулируют цель урока. «Изучение правила сложения нескольких векторов») Учитель:  — запишите в тетрадь тему урока «Сложение нескольких векторов»	Учащиеся формулируют цель урока совместно с учителем. Записывают в тетрадь тему в тетрадь
4. Первичное осмысление и закрепление знаний Учитель:  — теперь я попрошу каждого из вас самостоятельно выполнить сложение нескольких векторов. № 755 (начертите попарно неколлинеарные векторы и, пользуясь правилом многоугольника, постройте вектор  )	Учащиеся выполняют номер самостоятельно в тетради, затем показывают в камеру свою работу.
5. Закрепление изученного на уроке, решение задач Учитель:  — пользуясь правилом многоугольника и законами сложения векторов попробуйте упростить выражение: а)  ; — укажите такой вектор , что: б)  .	Двое учащихся, по желанию, отвечают, демонстрируя ответ на экране.  Остальные в тетрадях.
6. Подведение итогов урока, оценивание знаний Учитель: — наш урок подходит к концу. Вернёмся к цели, поставленной вначале урока. В беседе поставьте «+», если цель достигнута и «-», если нет. Учитель называет фамилии тех, кто присылает фото-отчёт по уроку, а самых активных награждает отметками.	Учащиеся самостоятельно учатся оценивать, продуктивно прошёл урок или нет
7. Домашнее задание Учитель проговаривает задание на дом, дублируя в беседе. Учитель: — всем спасибо! До свидания!	Учащиеся записывают домашнее задание и прощаются с учителем.
Видеозвонок закончен!

Добавление и вычитание векторов — Club Z! Репетиторство

В математике вектор — это объект, который имеет как величину, так и направление. Векторы можно складывать и вычитать друг из друга. Процесс сложения и вычитания векторов называется соответственно сложением и вычитанием векторов. В этой статье мы рассмотрим определения и примеры сложения и вычитания векторов. Мы также рассмотрим различные типы векторного сложения и вычитания, такие как покомпонентное сложение и скалярное умножение.

Что такое вектор?

Вектор — это математический объект, который имеет как величину, так и направление. Векторы часто используются в физике и технике для представления таких вещей, как сила, скорость и ускорение.

Векторы можно складывать и вычитать друг из друга. Когда два вектора складываются вместе, результат называется суммой векторов. Сумма двух векторов — это вектор, который имеет ту же величину, что и исходные векторы, но его направление определяется углом между исходными векторами.

Когда два вектора вычитаются друг из друга, результат называется разностью векторов. Разность двух векторов — это вектор, который имеет ту же величину, что и исходные векторы, но его направление противоположно углу между исходными векторами.

В чем разница между скаляром и вектором?

Скаляры — это отдельные числа, такие как 1, 2, 3, 4 и т. д. Векторы — это математические величины, которые имеют как величину, так и направление. Другими словами, векторы можно рассматривать как стрелки.

Величина вектора равна длине стрелки. Направление вектора — это направление, на которое указывает стрелка. Векторы можно складывать и вычитать так же, как отдельные числа (скаляры).

При сложении или вычитании векторов необходимо учитывать как величину, так и направление векторов.

Как добавлять векторы?

Существует несколько способов добавления векторов. Самый распространенный способ — просто сложить компоненты вместе. Итак, если у вас есть вектор A с компонентами (2,1) и другой вектор B с компонентами (-3,4), то вы можете найти результирующий вектор C, складывая компоненты каждого вектора: 92)
Где R — результирующий вектор, а A и B — складывающиеся отдельные векторы.

Как вычитать векторы?

В векторной математике вычитание — это процесс нахождения разницы между двумя векторами. Результат вычитания одного вектора из другого называется разностным вектором.

Чтобы вычесть один вектор из другого, нам сначала нужно найти компоненты каждого вектора. Компонент вектора — это величина этого вектора в заданном направлении. Например, если у нас есть вектор с величиной 5 в положительном направлении x, то его компонент в положительном направлении x будет равен 5.

Зная компоненты каждого вектора, мы можем вычесть их, чтобы найти разностный вектор. Например, если у нас есть вектор с величиной 4 в положительном направлении x и другой вектор с величиной 2 в отрицательном направлении x, то их разность будет вектором с величиной 6 в положительном направлении x. -направление.

Как складывать и вычитать векторы?

Существует несколько различных способов сложения и вычитания векторов. Наиболее распространенным способом является использование метода компонентов, который включает в себя разбиение векторов на их компоненты x и y. Чтобы сложить два вектора с помощью метода компонентов, просто сложите вместе соответствующие компоненты x и соответствующие компоненты y. Например, если вы сложите векторы (3,4) и (-2,5), вы получите (3+-2=1, 4+5=9).), поэтому сумма этих двух векторов равна (1,9).

Чтобы вычесть один вектор из другого с помощью метода компонентов, вы должны вычесть компонент x одного вектора из компонента x другого вектора, и аналогично для компонентов y. Итак, если вы вычитаете вектор (-2,5) из (3,4), вы получите (3-(-2)=5, 4-5=-1), и разница между этими двумя векторами равна (5,-1).

Существует также графический метод сложения и вычитания векторов, который может помочь визуализировать происходящее. Чтобы сложить два вектора с помощью этого метода, просто поместите их лицом к хвосту, чтобы они образовали параллелограмм. Диагональ этого параллелограмма и есть результирующий вектор.

Графическое сложение и вычитание векторов в одном измерении

Чтобы сложить или вычесть два вектора, мы объединяем их, соединяя начало второго вектора с хвостом первого вектора (или наоборот). Результирующий вектор идет от свободного хвоста к свободной голове. Величина равнодействующей представляет собой сумму (или разность) величин отдельных векторов, а направление определяется углом между ними.

Мы можем изобразить это графически, используя стрелки, чтобы указать направление каждого вектора, и прямую линию, чтобы показать их соединение.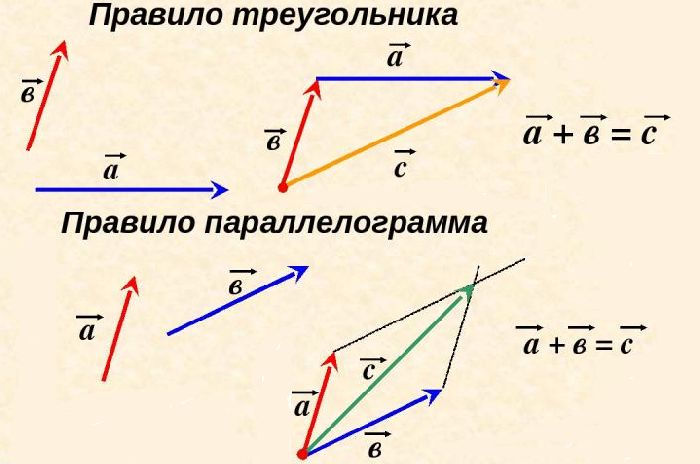 Величина затем представлена ​​длиной каждого вектора:

В этом примере у нас есть два вектора, A и B, которые мы хотим сложить. Начнем с рисования буквы А на бумаге, убедившись, что ее стрелка указывает правильное направление. Затем мы рисуем B так, чтобы его наконечник указывал в том же направлении, что и хвост A. Чтобы найти результирующий вектор, мы просто проводим линию от хвоста А к голове Б. Длина этой линии равна сумме длин A и B, а ее направление определяется углом между A и B.

Математическое сложение и вычитание векторов в одном измерении

Когда мы складываем или вычитаем векторы, мы на самом деле просто складываем или вычитаем компоненты, составляющие эти векторы. В одном измерении это довольно просто. Допустим, у нас есть два вектора, A и B. Вектор A имеет величину 5 и указывает в положительном направлении, а вектор B имеет величину 3 и указывает в отрицательном направлении. Чтобы найти результирующий вектор (C), мы должны просто сложить величины отдельных векторов и использовать знак результирующего вектора, чтобы указать его направление. В этом случае C будет иметь величину 2 и указывать в положительном направлении.

Если бы мы вычли вектор B из вектора A, результирующий вектор имел бы величину 8 и был бы направлен в положительном направлении.

Графическое сложение и вычитание векторов в двух измерениях

Графическое сложение и вычитание векторов в двух измерениях — это процесс сложения или вычитания векторов путем их графического отображения на координатной плоскости. Для этого каждый вектор изображается стрелкой, проведенной от начала координат к его конечной точке. Хвосты векторов помещаются в одну и ту же точку, а голова добавляемого вектора помещается в конец вектора, к которому он добавляется. Результирующий вектор затем рисуется из хвоста первого вектора в голову последнего вектора. Этот результирующий вектор представляет собой сумму или разность исходных векторов, в зависимости от того, были ли они добавлены или вычтены. 92). Это известно как величина векторов.

B. Пример 2

В этом примере мы будем складывать и вычитать векторы, которые не находятся под прямым углом друг к другу.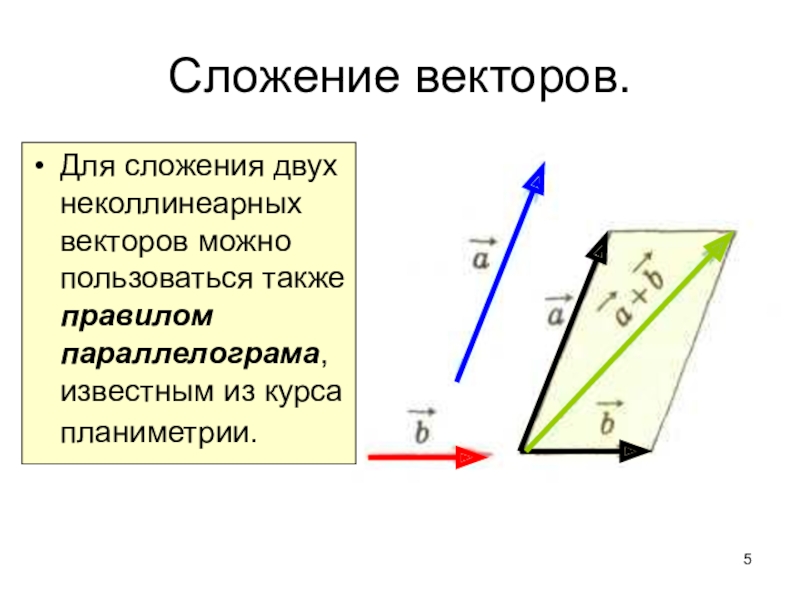 Это может быть немного сложнее визуализировать, но может быть полезно думать о векторах как о стрелках. Начало первого вектора (стрелка) будет начинаться с хвоста второго вектора (стрелка). Затем мы нарисуем новый вектор от начала первого вектора до начала второго вектора. Этот новый вектор и есть наш ответ.

Давайте рассмотрим пример. Скажем, у нас есть два вектора, вектор A и вектор B. Вектор A имеет длину 5 единиц и указывает строго на север. Вектор B имеет длину 4 единицы и направлен строго на восток. Чтобы сложить эти векторы вместе, мы должны начать с хвоста вектора B и провести стрелку к голове вектора A. Нашим ответом будет новый вектор длиной 9 единиц, указывающий строго на северо-восток.

Если бы мы хотели вычесть вектор B из вектора A, мы бы сделали то же самое — начали с хвоста вектора B и нарисовали стрелку к началу вектора A — но нашим ответом был бы новый вектор, равный 1 единице. длинный и направленный строго на северо-запад.

Когда вы используете сложение и вычитание векторов?

Сложение и вычитание векторов — это две математические операции, которые используются для нахождения результирующего вектора двух или более векторов. Результирующий вектор — это вектор, полученный в результате сложения или вычитания двух или более векторов.

Заключение

В заключение отметим, что векторы являются очень важной частью математики и физики. Их можно использовать для представления чего угодно, от силы и скорости до электрических и магнитных полей. Векторы можно складывать и вычитать друг из друга, в результате чего получается новый вектор. Эта операция известна как сумма векторов. Векторные суммы очень важны во многих областях науки, таких как расчет сил, действующих на объект, или определение результирующего электрического поля в определенной точке.

Сложение и вычитание векторов | Физика I

Обзор

Источник: Николас Тиммонс, Асанта Курей, доктор философии, факультет физики и астрономии, Школа физических наук, Калифорнийский университет, Ирвин, Калифорния

Этот эксперимент демонстрирует, как векторы складываются и вычитаются в нескольких направлениях. Целью будет аналитический расчет сложения или вычитания нескольких векторов, а затем экспериментальное подтверждение расчетов.

Вектор — это объект, имеющий как величину, так и направление. Величина вектора просто обозначается как длина, а направление обычно определяется углом, который он образует с осью x-. Поскольку силы являются векторами, их можно использовать как физическое представление векторов. Создав систему сил и найдя, какая дополнительная сила создаст равновесие между силами, можно экспериментально проверить систему векторов.

Принципы

В На рисунке 1 показан вектор , а также оси x- и y- и угол θ, который составляет с осью x-.

Рисунок 1 .

Чтобы сложить или вычесть два вектора, полезно описать вектор в терминах его компонентов x- и y-. Компонент x- представляет собой величину вектора, который указывает на x-9009.6 направление, которое математически представляется как:

. (Уравнение 1)

Компонент y- представлен как:

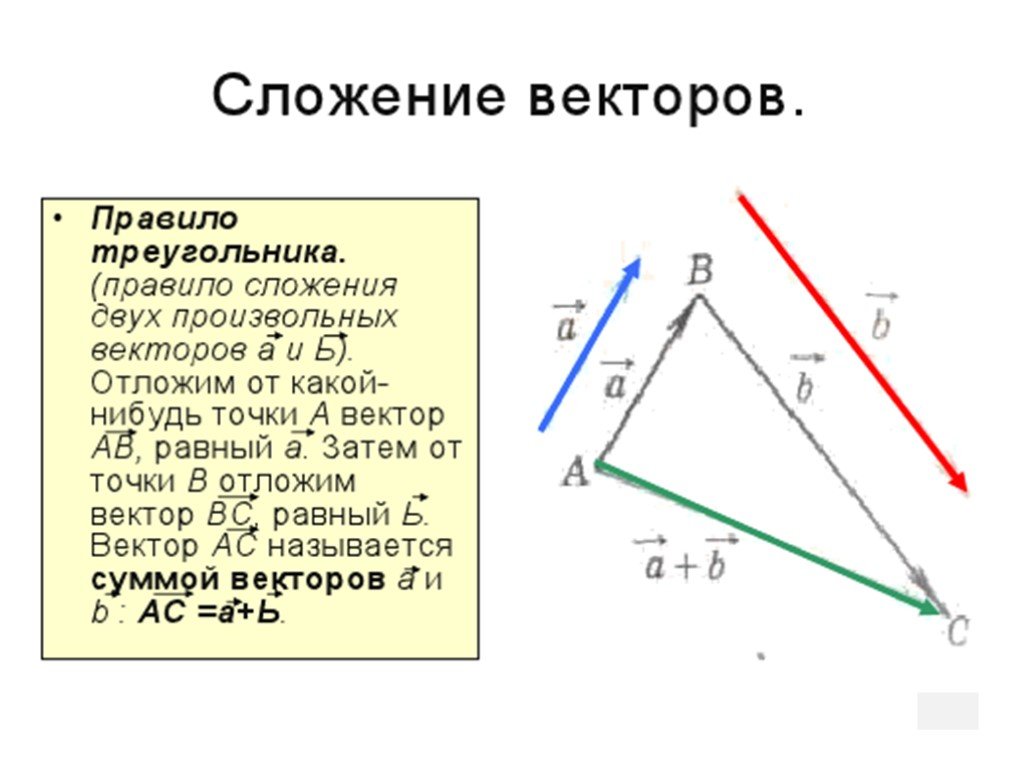. (Уравнение 2)

Величина определяется как:

. (Уравнение 3)

Чтобы сложить или вычесть два вектора, просто разбейте векторы на их компоненты x- и y-, а затем добавьте или вычтите соответствующие компоненты соответственно.

Например, если вектор и вектор , то сложение двух векторов .

Чтобы определить угол θ, который вектор образует с осью x-, используйте следующее уравнение:

. (Уравнение 4)

Поскольку векторы имеют как величину, так и направление, умножение двух векторов не так просто, как умножение двух чисел. Существует два способа умножения векторов: скалярное произведение и перекрестное произведение. Скалярное произведение может быть записано как  или   Здесь θ – это угол между двумя векторами. Результат имеет только величину, а не направление. Применением скалярного произведения в физике является работа (W), где работа определяется как произведение силы на расстояние.

Перекрестное произведение двух векторов может быть записано как. определяется как вектор с величиной 1, который перпендикулярен двум векторам и . Результатом перекрестного произведения является вектор. Одним из примеров перекрестного произведения в физике является крутящий момент, который является результатом произведения силы на радиус, равный 9.0003

Векторы полезны в физике, потому что такие силы, как гравитация или трение, могут быть представлены в виде векторов. В этой лабораторной работе сила тяжести используется для демонстрации векторной природы сил и того, как эти силы складываются в нескольких направлениях. Сила тяжести на поверхности Земли записывается как:

, (Уравнение 5)

где — масса объекта, а  — ускорение свободного падения у поверхности Земли (9,8 м/с ² ) .

Требуется подписка. Пожалуйста, порекомендуйте JoVE вашему библиотекарю.

Процедура

1. Баланс сил.

1. На силовом столе установите два шкива одинаковой массы, направленные в противоположные стороны (разность углов 180°).
2. Сила каждого будет равна . Проверьте, равны ли две силы и противоположны ли они, исследуя кольцо в центре таблицы сил, которое не должно двигаться.
3. Обратите внимание, что если сложить компоненты векторов, связанных с этими силами, результирующий вектор будет иметь нулевую величину. Так можно определить, что все силы находятся в равновесии.

2. Аналитические расчеты.

1. Эта лаборатория будет состоять из трех сил в равновесии. Две силы будут известны, а третья будет найдена сначала аналитически, с помощью теории векторов, а затем экспериментально. Для этой лабораторной работы держите температуру на уровне 0° в течение всего времени.
2. Обратите внимание, что если и  известны и , при добавлении к системе, приводит две силы в равновесие, то имеет одинаковую величину, но в направлении, противоположном сумме (  +  ).
3. Рассчитайте величину и . Используйте тот факт, что и что 1 Ньютон (Н) является единицей силы, равной .
4. Используя теорию векторов, рассчитайте, какой была бы величина , если бы это была сумма (  +  ).
5. Используя теорию векторов, вычислите, каким был бы угол, если бы он был суммой (  + ).

3. Эксперимент.

1. Следуя значениям в первой строке таблицы 1 для  и , настройте две силы в таблице сил. Не забудьте сохранить значение 0 °.
2. Установите третью силу, добавляя веса и изменяя угол, пока не будет достигнуто равновесие. Запишите эти значения в Таблица 2 .
3. Повторите шаг 3.2 для каждого из четырех случаев.
4. Определите процентное отличие от аналитического результата, рассчитав значение . Заполните Таблицу 2 этими расчетными значениями.

Векторы — это величины, имеющие как величину, так и направление, в отличие от скаляров, которые имеют только величину и знак.

Сила, ускорение и скорость являются примерами векторов. В то время как масса, энергия и время являются примерами скаляров.

Вектор обычно обозначается стрелкой. Длина стрелки соответствует ее величине, а угол указывает направление.

В этом видео показана система сил, которую можно анализировать с помощью векторного сложения и вычитания, а также показано, как такие операции дают результаты, важные для понимания некоторых физических явлений.

Для описания вектора требуется система координат. В этой выбранной системе отсчета этот пример мяча, подброшенного в воздух, имеет начальный вектор скорости. Как объяснялось ранее, длина стрелки представляет собой величину скорости. А направление вектора — это его угол от земли.

Любой вектор можно разложить на компонентов , которые сами являются векторами вдоль осей x и y. Если начальная скорость мяча составляет 20 метров в секунду под углом 60 градусов, горизонтальная составляющая равна скорости, умноженной на косинус 60 градусов, и имеет величину 10 метров в секунду. Вертикальная составляющая равна скорости, умноженной на синус 60 градусов, и имеет величину около 17,3 метра в секунду.

Сложение векторов горизонтальной и вертикальной составляющих восстанавливает исходный вектор скорости. Чтобы добавить векторы, представьте, что голова одного из них помещена в хвост другого. В этом примере векторы оказались под прямым углом. Сумма получается при путешествии прямо из хвоста первого в голову второго.

Эти компоненты находятся под прямым углом, поэтому величина суммы определяется теоремой Пифагора. Угол — это арктангенс вертикальной составляющей, деленной на горизонтальную составляющую.

При добавлении двух неперпендикулярных векторов разложите каждый из них на x- и y-компоненты, а затем добавьте соответствующие компоненты. Наконец, рассчитайте векторную сумму горизонтальной и вертикальной составляющих, как описано выше. Вычитание одного вектора из другого эквивалентно отрицанию второго вектора и добавлению его к первому. Как и прежде, разложите каждый вектор на x- и y-компоненты. Затем вычтите меньшую x-компоненту из большей и сделайте то же самое для y-компонент. Затем, как и раньше, вычислите векторную сумму полученных x- и y-компонент.

Чтобы продемонстрировать сложение и вычитание векторов в лаборатории физики, обычно используется таблица силы.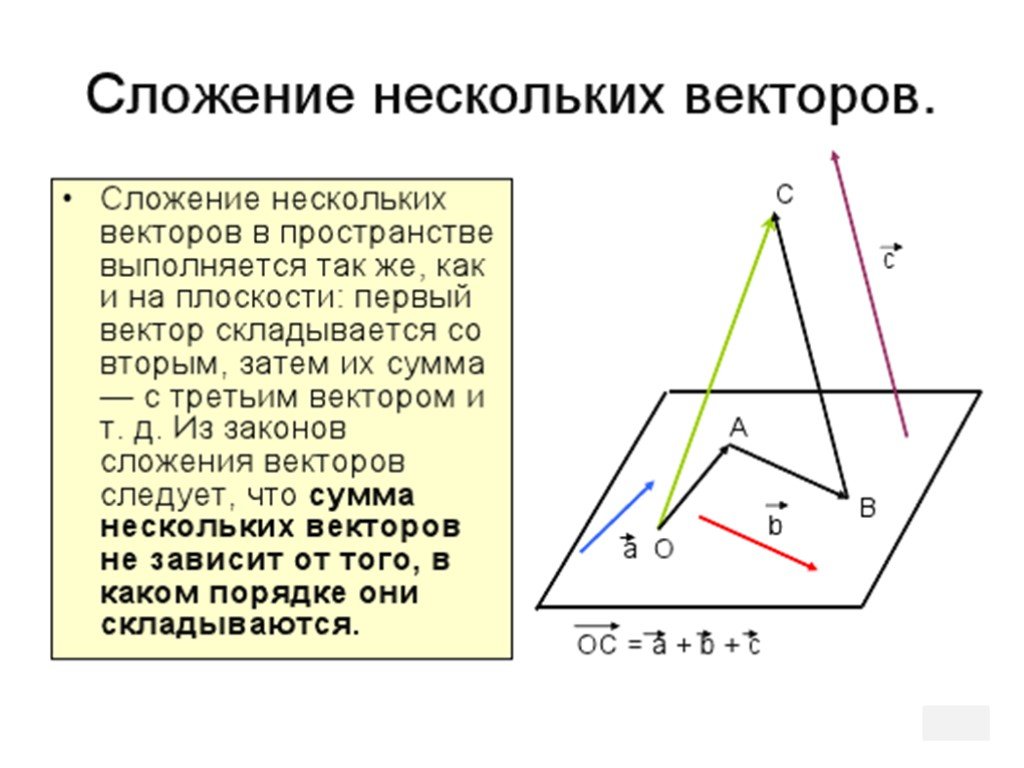 Это диск с размеченными по периметру углами, кольцо в центре, прикрепленное к шнурам с грузами на другом конце, подвешенными на шкивах. Массы производят силы, которые являются изучаемыми векторами. Сила вдоль каждого шнура равна силе гравитации, или мг с единицами Ньютонов.

Теперь, в этой схеме, если есть только две равные массы, расположенные под углом 180 градусов друг к другу, то они производят силы с векторной суммой, равной нулю. Это состояние называется равновесие , что приводит к нулевому ускорению и, следовательно, кольцо не будет двигаться.

Но если две силы, тянущие кольцо, не компенсируют друг друга, например, из-за изменения угла, то ненулевая результирующая сила заставит кольцо двигаться. В таких случаях, если мы знаем величины и направления этих сил, мы можем использовать сложение и вычитание векторов для вычисления третьей силы, необходимой для восстановления равновесия.

В следующем разделе мы покажем, как проводить такие эксперименты с таблицами сил, которые проверяют теоретические принципы сложения и вычитания векторов

Если две силы равны и противоположны, кольцо в центре стола не должно двигаться. В этом случае каждый вектор силы точно противоположен другому по величине и направлению. Сумма векторов имеет нулевую величину, что является условием нулевой суммарной силы или равновесия .

Чтобы проверить принципы сложения и вычитания векторов, установите массы и углы для сил A и B , как указано в первой строке этой таблицы. Держите угол на A при нуле градусов. Теперь создайте третью силу, добавляя массы и изменяя угол до тех пор, пока кольцо не перестанет двигаться.

После достижения равновесия вычислите силу C , умножив его массу на ускорение свободного падения. Также запишите величину и угол силы C .

Повторите этот тест для трех разных случаев и каждый раз записывайте величину и угол силы C .

Для четырех экспериментальных установок в этой таблице показаны расчетные величины сил A и B и углы B по отношению к A. Используя в качестве примера первую установку, мы можем рассчитать силу C, необходимую для установления равновесия. на столе.

Здесь сила А имеет величину 0,98 ньютона при 0°. Сила B имеет ту же величину 0,98 ньютона, но угол 20°. Чтобы определить вектор для C, разложите силы A и B на их компоненты x- и y-. Обратите внимание, что сила A направлена ​​только вдоль оси x и не имеет составляющей y. Затем добавьте компоненты, чтобы получить векторы x и y, которые представляют собой сумму векторов A и B.

Для достижения равновесия x- и y-компоненты C должны быть противоположны этим векторам. Чтобы получить вектор C , переместите хвост его y-компоненты в начало x-компоненты. Затем сложите два вектора, используя теорему Пифагора, чтобы найти величину вектора C. А угол для C равен арктангенсу вертикальной составляющей, деленной на горизонтальную составляющую. Таким образом, расчетная величина C оказывается равной 1,93 ньютона при угле 10° по отношению к оси x.

Теперь в ходе эксперимента вычисляем C путем наблюдения, проб и ошибок, регулируя веса и углы, чтобы предотвратить движение кольца на силовом столе.

Эта таблица показывает, что экспериментальные и расчетные результаты по величине и углу близко совпадают для всех четырех установок. Это соглашение подтверждает представление сил в виде векторов. Разница может быть связана с ограничениями точности весов, точности измерения угла и неучтенных сил, вызванных трением о силовой стол и о шкивы.

Сложение и вычитание векторов используются как в простых, так и в сложных приложениях. Давайте посмотрим на некоторые из них.

При путешествии по такому городу, как Нью-Йорк, расстояние обычно измеряется кварталами, а направлениями являются север, юг, восток и запад.

Человек, проходящий четыре квартала на восток и три квартала на север, претерпевает изменение положения, которое является векторной величиной. Следовательно, применяя уравнения сложения векторов, можно вычислить величину и направление вектора между начальной и конечной точками прогулки.

От ходьбы к полету: пилот постоянно выполняет мысленное сложение и вычитание векторов, чтобы маневрировать самолетом. Используя закрылки и элероны, пилот может регулировать подъемную силу против силы тяжести. Если подъемная сила больше силы тяжести, самолет поднимается. Если подъемная сила меньше силы тяжести, он опускается.

Точно так же пилот использует двигатели для регулировки тяги по отношению к сопротивлению. Если тяга больше сопротивления, самолет разгоняется. Если тяга меньше сопротивления, он замедляется.

Когда сумма этих четырех сил равна нулю, самолет находится в равновесии и движется с постоянной скоростью и высотой.

Вы только что посмотрели введение JoVE в векторы. Теперь вы должны знать, как складывать и вычитать векторы, и понимать, как определенные физические величины ведут себя как векторы. Спасибо за просмотр!

Требуется подписка. Пожалуйста, порекомендуйте JoVE вашему библиотекарю.

Результаты

Результаты лаборатории показаны в Таблица 1 и Таблица 2 .

within-page=»1″> Таблица 1. Настройка.

Настройка #	А		Б
	Масса	Угол	Масса	Угол
1	100	0	100	20
2	100	0	150	40
3	200	0	150	60
4	200	0	250	80

Таблица 2. Результаты анализа.

Настройка #	Величина (N)	Величина (N)	Угол (°)	Величина (N)	Угол (°)
1	0,98	0,98	20	1,93	10
2	0,98	1,47	40	2,31	24
3	1,96	1,47	60	2,98	25
4	1,96	2,45	80	3,39	45

within-page=»1″> Таблица 3. Экспериментальные результаты.

Настройка #	Экспериментальная магнитуда (N)	Аналитическая величина (N)	Разница (%)	Экспериментальный угол (°)	Аналитический угол (°)	Разница (%)
1	2.1	1,93	9	11	10	10
2	2,2	2,31	5	26	24	8
3	2,8	2,98	6	28	25	12
4	3,5	3,39	3	43	45	5

Результаты эксперимента согласуются с аналитическими расчетами. Сумма двух векторов и угол между ними могут быть рассчитаны с помощью уравнений 1-5 . Уравнения действительны для расчета физических векторов, таких как сила.

Требуется подписка. Пожалуйста, порекомендуйте JoVE вашему библиотекарю.

приложений и резюме

Аутфилдер в бейсболе должен понимать векторы, чтобы поймать мяч на ходу. Если бы аутфилдер знал только скорость мяча, он мог бы убежать влево, а не вправо, и промахнуться. Если бы он только знал направление удара, он мог бы атаковать, только чтобы увидеть, как мяч пролетел над его головой. Если он понимает векторы, то, как только мяч будет отбит, он сможет учитывать как величину, так и направление, чтобы оценить, где мяч окажется, когда он поймает мяч.

Когда самолет находится в небе, его скорость и направление можно записать в виде вектора. При сильном ветре вектор ветра добавляется к вектору самолета, чтобы получить результирующий вектор системы. Например, если самолет летит против ветра, величина результирующего вектора будет меньше исходной величины.