Коллинеарность векторов: условия, правила и примеры

Поможем понять и полюбить математику

Начать учиться

С 7‑го класса вы знакомы с такими физическими величинами, как сила, скорость, ускорение, перемещение, импульс. А что отличает их от другой группы величин, таких как длина, время, масса, объем, температура и плотность? Первая группа величин — векторные, то есть они характеризуются не только числовым значением, но и направлением. Нам важно знать не только скорость, но и ее направление; не только силу, с которой толкают груз, но и в каком направлении его толкают.

Ученики 9-го класса, помимо понятия вектора, должны знать, что такое коллинеарные векторы, а также условия коллинеарности векторов.

Вектор — это направленный отрезок. Вектор обозначается двумя заглавными латинскими буквами со стрелочкой над ними или одной маленькой со стрелочкой над ней .

Нулевой вектор — вектор, начало которого совпадает с концом. То есть в геометрической интерпретации это просто точка.

Теперь, когда мы вспомнили базовые понятия, можно переходить к определению коллинеарных векторов.

Что значит «коллинеарные векторы»

Коллинеарные векторы — это ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Причем считается, что нулевой вектор коллинеарен каждому другому вектору. То есть, попросту говоря, коллинеарность — это параллельность векторов. Если векторы и коллинеарны, то это записывают так: .

Коллинеарные векторы можно разделить по направлению на две группы: сонаправленные и противоположно направленные.

Векторы и лежат на параллельных прямых, а также имеют одно направление, поэтому и — сонаправленные векторы: .

Векторы и лежат на параллельных прямых, но имеют разное направление, поэтому и — противоположно направленные векторы: .

Задача № 1

Найдите сонаправленные и противоположно направленные векторы.

Благодаря клетчатому фону мы можем определить, что все векторы на рисунке коллинеарны, то есть лежат на параллельных прямых. Осталось посмотреть на направление векторов и сделать выводы:

• ,

• ,

• ,

• .

Но не забываем о нулевом векторе — он будет сонаправлен с каждым вектором.

Но согласитесь, что визуальная оценка параллельности не самая точная вещь на планете, а математика славится своей точностью и четкостью. Поэтому возникает вопрос: как проверить коллинеарность векторов алгебраическими способами? Для этого существуют признаки коллинеарности векторов. Рассмотрим их.

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Признаки коллинеарности векторов

1. Первый критерий коллинеарности векторов: векторы и коллинеарны, если .

2. Второй критерий коллинеарности векторов: два вектора коллинеарны, если отношения их координат равны.

   Но здесь важно понимать, что это условие параллельности векторов работает только для всех ненулевых координат. Значит, если хотя бы один компонент вектора равен нулю, то правило неприменимо.

3. Третий критерий коллинеарности векторов, который могут применять одиннадцатиклассники, взрослые и все, кто увлечен математикой: два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Применим условия коллинеарности векторов при решении задач.

Задача № 2

Докажите, что векторы и коллинеарны.

У нас с вами есть два способа определить или доказать коллинеарность векторов, однако в координатах каждого вектора есть нули — значит, подходит только первый критерий, который еще называется свойством коллинеарных векторов: если , то .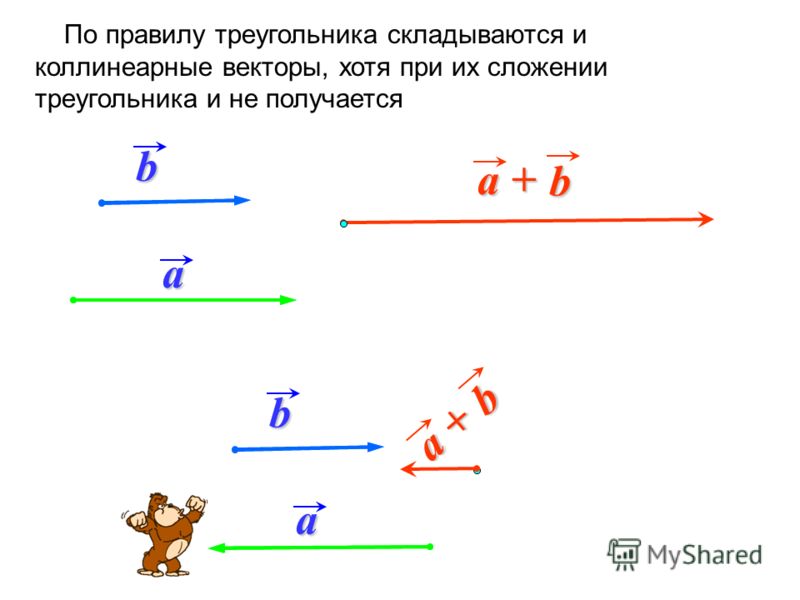

Для начала определим . А теперь проверим, выполняется ли условие :

, значит, . Что и требовалось доказать.

Задача № 3

Какие из векторов , и коллинеарны?

А здесь очень удобно использовать второй критерий коллинеарности векторов, который звучит так: отношения соответствующих координат коллинеарных векторов равны.

1. Проверим коллинеарность векторов и : должно выполняться условие , т. е. — верно, значит, .

2. Проверим коллинеарность векторов и : должно выполняться условие , т. е. — неверно, значит, и неколлинеарны.

3. Проверим коллинеарность векторов и : должно выполняться условие , т. е. — неверно, значит, и неколлинеарны.

Задача № 4

Определите, при каком значении k векторы и коллинеарны.

Так как по условию векторы должны быть коллинеарны, а в их координатах не содержится нуля, то можно использовать второй критерий коллинеарности, а именно — должно выполняться условие , то есть .

По свойству пропорции выразим k:

;

k = 27.

Значит, при k = 27 векторы и коллинеарны.

Если же вам нужно проверить коллинеарность векторов в пространстве, а не на плоскости, то все эти условия продолжают работать, но помните, что к проверке присоединяется третья координата векторов. Рассмотрим пару примеров.

Задача № 5

Докажите, что векторы и коллинеарны.

Поступим аналогично решению в задаче 2 — применим первый критерий, который еще называется свойством коллинеарных векторов, т. е. если , то .

Для начала определим . А теперь проверим, выполняется ли условие :

, значит, . Что и требовалось доказать.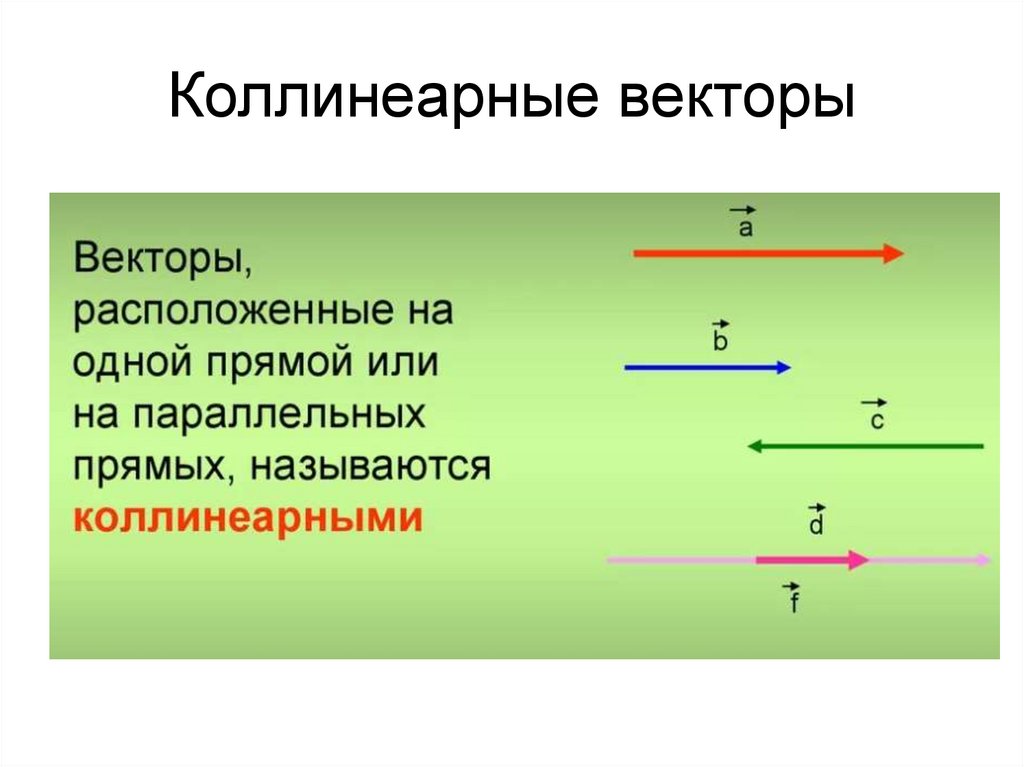

Задача № 6

Определите, при каких значениях k и f векторы и коллинеарны.

Аналогично задаче 4: так как по условию векторы должны быть коллинеарны и в их координатах не содержится нуля, то можно использовать второй критерий коллинеарности. А именно — должно выполняться условие , то есть .

Рассмотрим первую и вторую дроби, по свойству пропорции выразим k:

;

k = 27.

Рассмотрим первую и третью дроби, по свойству пропорции выразим f:

;

f = 2.

Значит, при k = 27 и f = 2 векторы и коллинеарны.

Векторы — удивительная тема, с помощью которой можно решить многие физические задачи, легко и просто доказать самые сложные геометрические теоремы. Сегодня вы узнали, какие векторы называются коллинеарными, но это лишь один аспект большой главы о векторах. Чтобы узнать остальные действия с векторами, познакомиться с интересными задачами и способами решений, приходите на онлайн-курсы математики для детей в Skysmart.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Кристина Тоскина

К предыдущей статье

Как подготовиться к ОГЭ по математике в 2023 году

К следующей статье

Уравнение касательной к графику функции

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Вычитание векторов – примеры по правилу треугольника

4.6

Средняя оценка: 4.6

Всего получено оценок: 184.

4.6

Средняя оценка: 4.6

Всего получено оценок: 184.

Вычитание векторов часто вызывает проблемы у учеников. Это связано с тем, что вычитание в геометрии нужно выполнять очень осторожно, чтобы не получалось отрицательных чисел.

А вектор может быть отрицательным, положительным, нулевым – это вызывает много ошибок, которых можно избежать просто один раз разобравшись в вопросе.

Вектор

Вектор – одно из самых интересных явлений в математике. Это первая величина во всем школьном курсе, которая имеет две характеристики: направление и размер. Вектором называют направленный отрезок, то есть отрезок, у которого стрелкой указали направление движения.

Представьте, вы прошли километр от дома до парка. Если поставить точку в начальном положении и стрелку в конечном, то результат движениям будет являться вектором. Ведь он имеет направление: от дом до парка. При этом у результата движения есть и размер, в нашем случае это один километр.

Ученики часто пугаются отрицательных векторов, но в этом нет ничего страшного. Вектор это направление некого движения, а любое движение относительно, то есть зависит от системы отсчета.

В любую систему отчета входит точка отчета, система координат и прибор для измерения времени.

Если вектор поместить в любую систему координат, даже если это будет простой координатный луч, то вектор может быть направлен в одну сторону с системой координат, но может и в разные. Если вектор и система координат направлены в разные стороны, то вектор будет отрицательным.

Рис. 1. Вектор в системе координат.

При этом противоположным направлением считается любое в половине плоскости, в другую сторону которой направлен вектор.

Особые случаи векторов

Первый вопрос, который возникает у множества учеников, это возможность существования нуля в системе векторов. Ноль у векторов есть, только это не число, а точка. Любую точку можно считать нулевым вектором. Нулевой вектор появляется в результате сложения коллинеарных разнонаправленных векторов.

Рис. 2. Нулевой вектор.

Коллинеарными называют вектора, которые лежат на одной прямой. Эти векторы могут быть сонаправлены или противоположно направлены. При этом векторы, которые лежат на одной прямой так же считаются коллинеарными, так как любая прямая параллельна самой себе. Это не трудно понять, но запомнить название лучше наизусть, так как в тематике векторов, это определение встречается довольно часто.

Результат сложения или вычитания коллинеарных векторов будет коллинеарным для каждого из начальных построений. Поэтому найти результат такой операции можно арифметически, да и построить треугольник или параллелограмм из коллинеарных векторов не получится.

Вычитание векторов

Результатом вычитания векторов может быть:

• Вектор. Если вычитание производилось в системе координат, то результат может быть положительным или отрицательным
• Нулевой вектор или точка
• Никаких других результатов быть не может

Рис. 3. Вычитание векторов.

Для того, чтобы вычесть один вектор из другого, любой из векторов заменяется на противоположный и выполняется сложение по правилу треугольника или параллелограмма. Таким образом, меняется знак вектора.

В математической записи это выглядит так:

АВ-МР=АВ+РМ – в математической записи первая буква означает начало вектора, вторая – конец.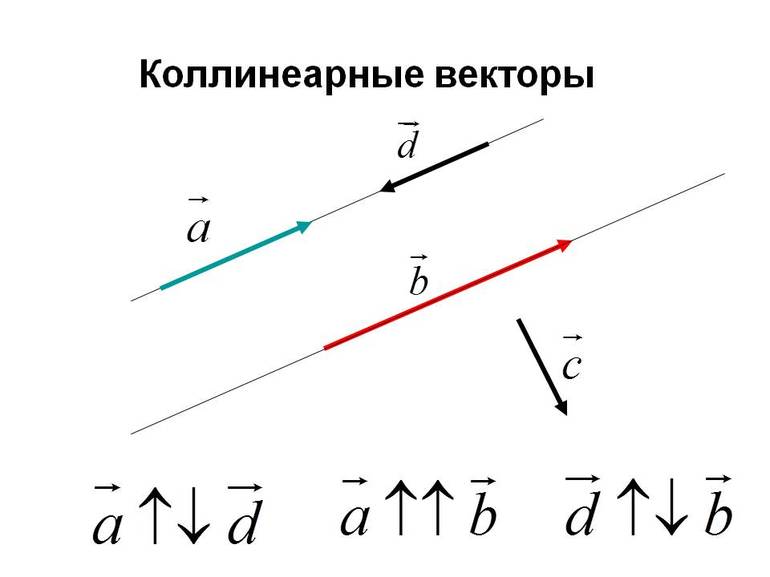 Так можно без чертежа обозначить направление.

Что мы узнали?

Мы поговорили о векторах и их частных случаях. Обсудили, как правильно вычитать вектора и что может получиться в результате такого вычитания. Привели пример правильной записи вычитания 2 векторов.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Руслан Галандских

  10/10

• Нина Трофимова

  5/10

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 184.

---

А какая ваша оценка?

Коллинеарные векторы — определения, условия, примеры

Коллинеарные векторы считаются одним из важных понятий в векторной алгебре. Когда два или более заданных вектора лежат вдоль одной и той же заданной прямой, то их можно рассматривать как коллинеарные векторы. Мы можем рассматривать два параллельных вектора как коллинеарные векторы, поскольку эти два вектора указывают точно в одном и том же направлении или в противоположном направлении.

В этой статье давайте узнаем о коллинеарных векторах, их определении, условиях коллинеарности векторов на решенных примерах.

1.	Что такое коллинеарные векторы?
2.	Условия коллинеарных векторов
3.	Часто задаваемые вопросы о коллинеарных векторах

Что такое коллинеарные векторы?

Любые два заданных вектора можно рассматривать как коллинеарные векторы, если эти векторы параллельны одной и той же заданной прямой. Таким образом, мы можем рассматривать любые два вектора как коллинеарные векторы тогда и только тогда, когда эти два вектора либо лежат на одной прямой, либо эти векторы параллельны друг другу. Чтобы любые два вектора были параллельны друг другу, условие состоит в том, что один из векторов должен быть скалярно кратным другому вектору.

На приведенной выше диаграмме векторы, параллельные одной и той же прямой, коллинеарны друг другу, а пересекающиеся векторы неколлинеарны.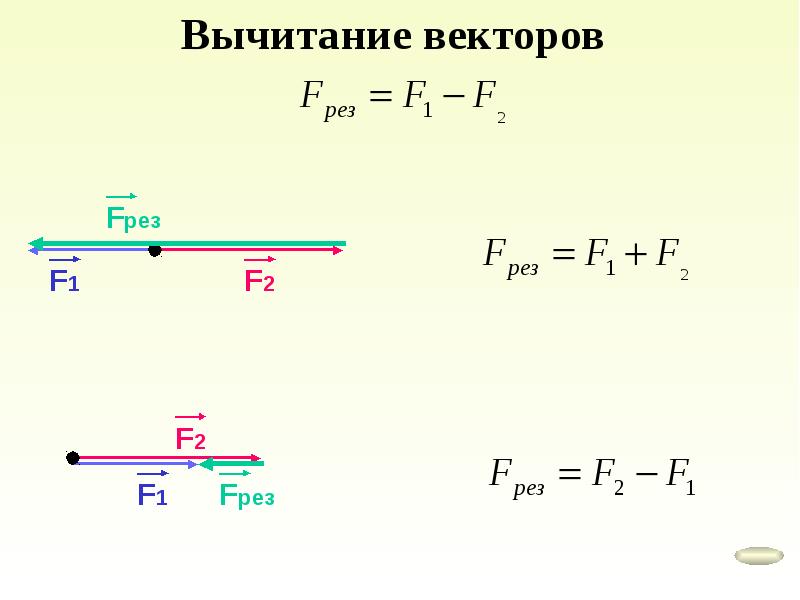

Условия коллинеарных векторов

Для того чтобы любые два вектора были коллинеарными, они должны удовлетворять определенным условиям. Вот важные условия коллинеарности векторов:

• Условие 1: Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными векторами, если существует скаляр ‘n’ такое, что \(\overrightarrow{p}\) = n · \(\overrightarrow{q}\)
• Условие 2. Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными тогда и только тогда, когда отношения их соответствующих координат равны. Это условие не выполняется, если одна из компонент данного вектора равна нулю.
• Условие 3. Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными векторами, если их векторное произведение равно нулевому вектору. Это условие применимо только к трехмерным или пространственным задачам.

Доказательство условия 3:

Рассмотрим два коллинеарных вектора \(\overrightarrow{a}\) = {\(a_{x}\),\(a_{y}\),\(a_{z}\ )} и \(\overrightarrow{b}\) = {n\(a_{x}\),n\(a_{y}\),n\(a_{z}\)}.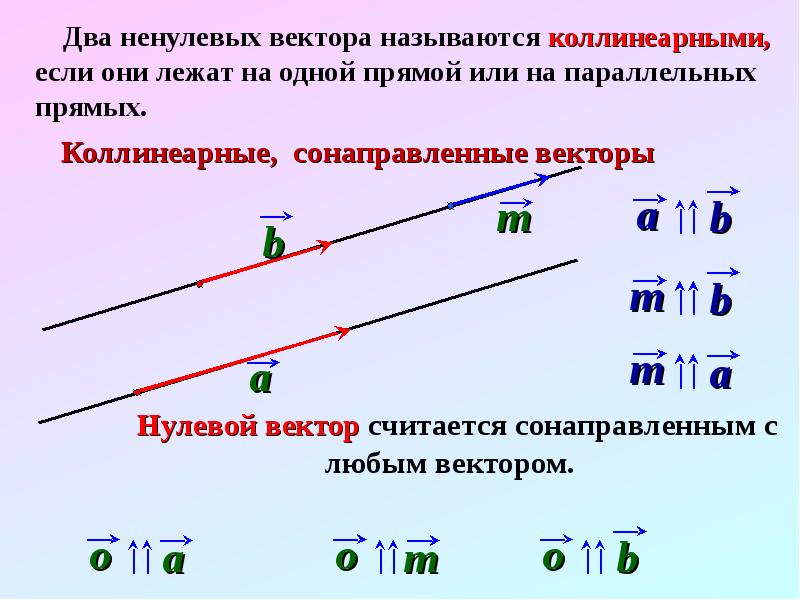 Мы можем найти перекрестное произведение между ними как:

\(\overrightarrow{a}\) × \(\overrightarrow{b}\) = \(\left|\begin{array}{ccc}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
а_{х} и а_{у} и а_{г} \\
b_{x} & b_{y} & b_{z}
\end{массив}\right|\)

= i (\(a_{y}\)\(b_{z}\) — \(a_{z}\)\(b_{y}\)) — j (\(a_{x}\)\(b_{z}\) — \(a_{z}\)\(b_{x}\)) + k (\(a_{x}\)\(b_ {y}\) — \(a_{y}\)\(b_{x}\))

= i (\(a_{y}\)n\(a_{z}\) — \(a_{ z}\)n\(a_{y}\)) — j (\(a_{x}\)n\(a_{z}\) — \(a_{z}\)n\(a_{x} \)) + k (\(a_{x}\)n\(a_{y}\) — \(a_{y}\)n\(a_{x}\))

= 0i + 0j + 0k = \(\overrightarrow{0}\) [Поскольку разные компоненты одного и того же вектора перпендикулярны друг другу и, следовательно, их произведение равно 0.]

Похожие статьи о коллинеарных векторах

Ознакомьтесь со следующими страницами, посвященными коллинеарным векторам

• Добавление калькулятора векторов
• Калькулятор угла между двумя векторами
• Обработка векторов, указанных в форме i-j
• Неравенство треугольников в векторах
• Вычитание двух векторов

Важные примечания о коллинеарных векторах

Вот несколько моментов, которые следует помнить при изучении коллинеарных векторов

• Любые два заданных вектора можно рассматривать как коллинеарные векторы, если эти векторы параллельны одной и той же заданной прямой.
• Таким образом, мы можем считать любые два вектора коллинеарными тогда и только тогда, когда эти два вектора либо лежат на одной прямой, либо эти векторы параллельны друг другу.

 

Примеры коллинеарных векторов

1. Пример 1: Определите, являются ли заданные векторы коллинеарными векторами. \(\overrightarrow{P}\) = (3,4,5), \(\overrightarrow{Q}\) = (6,8,10).

   Решение: Два вектора считаются коллинеарными, если отношения их соответствующих координат равны.

   P ₁ /Q ₁ = 3/6 = 1/2

   P ₂ /Q ₂ ​​​​​= 4/8 = 1/2

   900 02 П ₃ /Q ₃  = 5/10 = 1/2

   Поскольку P ₁ /Q ₁ = P ₂ /Q ₂ = P ₃ / Q ₃ , векторы \( \overrightarrow{P}\) и \(\overrightarrow{Q}\) можно рассматривать как коллинеарные векторы.

2. Пример 2: Определите, являются ли заданные векторы коллинеарными векторами. \(\overrightarrow{P}\) = i + j + k, \(\overrightarrow{Q}\) = — i — j — k

   Решение: Два вектора считаются коллинеарными, если один вектор скаляр, кратный другому вектору.

   Вектор Q = — i — j — k = — (i + j + k) = — (Вектор P)

   ⇒ Вектор Q является скалярным множителем вектора P.

   Кроме того, поскольку P ₁ /Q ₁ = P ₂ /Q ₂ = P ₃ /Q ₃ = -1, векторы \(\overrightarrow{P}\) и \(\overrightarrow{Q}\) могут быть рассматриваются как коллинеарные векторы.

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы по коллинеарным векторам

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о коллинеарных векторах

Что такое коллинеарные векторы?

Любые два заданных вектора можно рассматривать как коллинеарные векторы, если эти векторы параллельны одной и той же заданной прямой. Таким образом, мы можем считать любые два вектора коллинеарными тогда и только тогда, когда эти два вектора либо лежат на одной прямой, либо эти векторы параллельны друг другу. Чтобы любые два вектора были параллельны друг другу, условие состоит в том, что один из векторов должен быть скалярно кратным другому вектору.

Как узнать, является ли вектор коллинеарным?

Для того чтобы любые два вектора были коллинеарными, они должны удовлетворять определенным условиям. Вот важные условия коллинеарности векторов:

• Условие 1: Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными векторами, если существует число ‘n’ такое, что \(\overrightarrow{p}\) = n · \(\overrightarrow{q}\)
• Условие 2. Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными тогда и только тогда, когда отношения их соответствующих координат равны. Это условие не выполняется, если одна из компонент данного вектора равна нулю.
• Условие 3. Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными векторами, если их векторное произведение равно нулевому вектору. Это условие применимо только к трехмерным или пространственным задачам.

Параллельные и коллинеарные векторы — одно и то же?

Да, параллельные и коллинеарные векторы — это одно и то же. Два вектора называются коллинеарными, если они имеют одинаковое направление, параллельны или антипараллельны. Два вектора параллельны, если они имеют одинаковое или противоположное направление.

Как доказать, что вектора трех положений лежат на одной прямой?

Рассмотрим три отрезка PQ, QR и PR. Если PQ + QR = PR, то мы можем считать эти три точки коллинеарными. Три заданных сегмента линии могут быть переведены в соответствующие векторы PQ, QR и PR. Величины этих трех векторов равны длине трех отрезков, упомянутых здесь.

Приведите пример коллинеарных векторов

Рассмотрим два вектора \(\overrightarrow{P}\) = (3,4,5), \(\overrightarrow{Q}\) = (6,8,10). Два вектора считаются коллинеарными, если отношения их координат равны.

P ₁ /Q ₁ = 3/6 = 1/2

P ₂ /Q ₂ ​​​​​= 4/8 = 1/2

900 02 П ₃ /Q ₃  = 5/10 = 1/2

Поскольку P ₁ /Q ₁ = P ₂ /Q ₂ = P ₃ / Q ₃ , векторы \( \overrightarrow{P}\) и \(\overrightarrow{Q}\) можно рассматривать как коллинеарные векторы.

Что такое неколлинеарные векторы?

Векторы считаются неколлинеарными, если они расположены в одной плоскости, но не действуют вдоль одной и той же линии действия.

Как найти коллинеарные векторы в трех измерениях?

Два вектора \(\overrightarrow{P}\) и \(\overrightarrow{Q}\) считаются коллинеарными векторами, если их векторное произведение равно нулевому вектору. Это условие применимо только к трехмерным или пространственным задачам.

Почему мы не можем применить правило параллелограмма сложения векторов для двух параллельных векторов?

спросил 2 года, 7 месяцев назад

Изменено 2 года, 7 месяцев назад

Просмотрено 570 раз

$\begingroup$

В моем учебнике сказано, что мы не можем применить правило параллелограмма сложения векторов для двух параллельных векторов.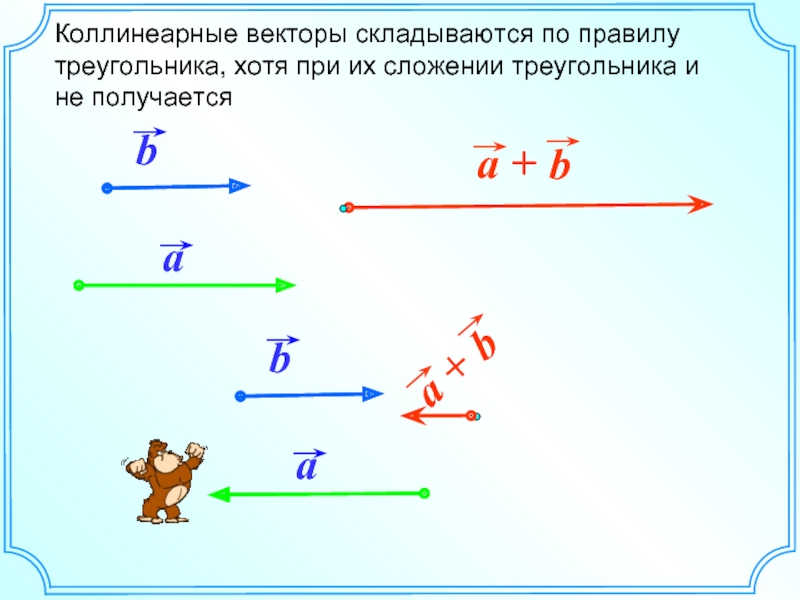 Почему мы не можем применить правило?

• векторов

$\endgroup$

1

$\begingroup$

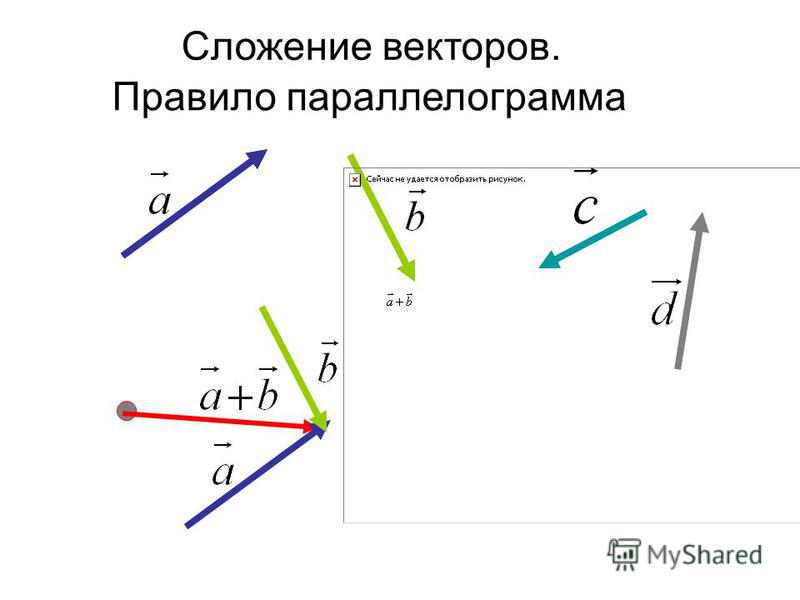
Сложение векторов параллелограмма гласит, что если два вектора имеют одну и ту же точку в качестве хвоста или начала координат, то они рассматриваются как две смежных сторон параллелограмма и строятся параллелограммы. И тогда диагональ этого параллелограмма (через хвост этих векторов) даст вам направление результирующего вектора, а для величины вы знаете правила.

Если вам даны два параллельных вектора, совершенно очевидно, что вы не можете рассматривать их как смежных сторон параллелограмма и, следовательно, они перекрываются, и у вас остается только один вектор, величина которого равна алгебраически добавили величину двух векторов и указывали в одном направлении.

Вы не можете построить параллелограмм (я не говорю о вырожденном параллелограмме), взяв две параллельные стороны за смежных сторон, так как в этом случае они больше не будут параллельны друг другу.

Надеюсь поможет ☺️.

$\endgroup$

5

$\begingroup$

Потому что нельзя построить правильный параллелограмм из двух коллинеарных отрезков.

$\endgroup$

2

$\begingroup$

Если вы называете параллелограмм с углами 0 параллелограммом , вы все равно можете его использовать, но большинство людей просто добавляют два параллельных вектора, как в одну линию.

$\endgroup$

0

$\begingroup$

Если вы называете вырожденный параллелограмм, все четыре вершины которого лежат на одной прямой, а четыре внутренних угла равны 0, 180, 0 и 180 градусов, все еще «параллелограммом», то вы можете используйте правило параллелограмма для параллельных (и антипараллельных) векторов. Точно так же, если вы позволяете стороне параллелограмма иметь нулевую длину, то вы можете использовать правило параллелограмма, если один или оба вектора являются нулевыми векторами.