Скорость света — Википедия
 | |
| метров в секунду | 299 792 458 |
|---|---|
| Планковских единиц | 1 |
| километров в секунду | 300 000 |
| километров в час | 1,08 млрд |
| астрономических единиц в сутки | 173 |
| расстояние | время |
| один метр | 3,3 нс |
| один километр | 3,3 мкс |
| от геостационарной орбиты до Земли | 119 мс |
| длина экватора Земли | 134 мс |
| от Луны до Земли | 1,255 с |
| от Солнца до Земли (1 а. е.) | 8,3 мин. |
| от Вояджера-1 до Земли | |
| один световой год | 1 год |
| один парсек | 3,26 лет |
| от Проксимы Центавра до Земли | 4,24 лет |
| от Альфы Центавра до Земли | 4,37 лет |
| от ближайшей галактики (Карликовой галактики в Большом Псе) до Земли | 25 000 лет |
| через Млечный Путь | 100 000 лет |
| от галактики Андромеды до Земли | 2,5 млн лет |
| от самой удалённой известной галактики до Земли | 13,4 млрд лет[2] |
Ско́рость све́та (в вакууме) — абсолютная величина скорости распространения электромагнитных волн в вакууме
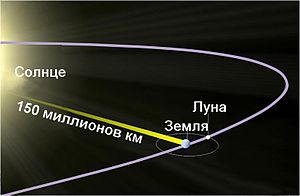
 Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 с
Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 сНа данный момент считают, что скорость света в вакууме — фундаментальная физическая постоянная, по определению, точно равная 299 792 458 м/с, или 1 079 252 848,8 км/ч. Точность значения связана с тем, что с 1983 года метр в Международной системе единиц (СИ) определён как расстояние, которое проходит свет в вакууме за промежуток времени, равный 1 / 299 792 458 секунды[11].
В планковской системе единиц скорость света в вакууме равна 1 c{\displaystyle c}. Можно сказать, что свет проходит 1 планковскую длину за планковское время, но в планковской системе единиц скорость света c{\displaystyle c} является основной единицей, а единицы времени и расстояния — производными (в отличие от СИ, где основными являюся метр и секунда).
В природе со скоростью света распространяются (в вакууме):
Массивные частицы могут иметь скорость, приближающуюся почти вплотную к скорости света[Прим. 4], но всё же не достигающую её точно. Например, околосветовую скорость, лишь на 3 м/сек меньше скорости света, имеют массивные частицы (протоны), полученные на ускорителе (Большой адронный коллайдер) или входящие в состав космических лучей.[источник не указан 831 день
В современной физике считается хорошо обоснованным утверждение, что причинное воздействие не может переноситься со скоростью, большей скорости света в вакууме (в том числе посредством переноса такого воздействия каким-либо физическим телом). Существует, однако, проблема «запутанных состояний» частиц, которые, судя по всему, «узнают» о состоянии друг друга мгновенно. Однако и в этом случае сверхсветовой передачи информации не происходит, поскольку для передачи информации таким способом необходимо привлечь дополнительный классический канал передачи со скоростью света[Прим. 5].
Хотя в принципе движение каких-то объектов со скоростью, большей скорости света в вакууме, вполне возможно, однако это могут быть, с современной точки зрения, только такие объекты, которые не могут быть использованы для переноса информации с их движением (например, солнечный зайчик в принципе может двигаться по стене со скоростью большей скорости света, но никак не может быть использован для передачи информации с такой скоростью от одной точки стены к другой) .
.
Скорость света в прозрачной среде — скорость, с которой свет распространяется в среде, отличной от вакуума. В среде, обладающей дисперсией, различают фазовую и групповую скорость.
Фазовая скорость связывает частоту и длину волны монохроматического света в среде (λ=cν{\displaystyle \lambda ={\frac {c}{\nu }}}). Эта скорость обычно (но не обязательно) меньше c{\displaystyle c}. Отношение скорости света в вакууме к фазовой скорости света в среде называется показателем преломления среды. Если угловая частота ω{\displaystyle \omega }волны в среде зависит от волнового числа k{\displaystyle k} нелинейным образом, то групповая скорость равняется первой производной ∂ω∂k{\displaystyle {\frac {\partial \omega }{\partial k}}}, в отличие от фазовой скорости ωk{\displaystyle {\frac {\omega }{k}}}.[14]
Групповая скорость света определяется как скорость распространения биений между двумя волнами с близкой частотой и в равновесной среде всегда меньше c{\displaystyle c}. Однако в неравновесных средах, например, сильно поглощающих, она может превышать c{\displaystyle c}. При этом, однако, передний фронт импульса всё равно движется со скоростью, не превышающей скорости света в вакууме. В результате сверхсветовая передача информации остаётся невозможной.
Арман Ипполит Луи Физо на опыте доказал, что движение среды относительно светового луча также способно влиять на скорость распространения света в этой среде.
Скорость, с которой световые волны распространяются в вакууме, не зависит ни от движения источника волн, ни от системы отсчёта наблюдателя[Прим. 6]. Эйнштейн постулировал такую инвариантность скорости света в 1905 году[15].Он пришёл к этому выводу на основании теории электромагнетизма Максвелла и доказательства отсутствия светоносного эфира[16].
Инвариантность скорости света неизменно подтверждается множеством экспериментов[17]. Существует возможность проверить экспериментально лишь то, что скорость света в «двустороннем» эксперименте (например, от источника к зеркалу и обратно) не зависит от системы отсчёта, поскольку невозможно измерить скорость света в одну сторону (например, от источника к удалённому приёмнику) без дополнительных договоренностей относительно того, как синхронизировать часы источника и приёмника. Однако, если применить для этого синхронизацию Эйнштейна, односторонняя скорость света становится равной двусторонней по определению
Специальная теория относительности исследует последствия инвариантности c{\displaystyle c} в предположении, что законы физики одинаковы во всех инерциальных системах отсчёта[20][21]. Одним из последствий является то, что c{\displaystyle c} — это та скорость, с которой должны двигаться в вакууме все безмассовые частицы и волны (в частности, и свет).
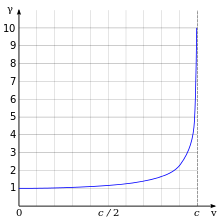
Специальная теория относительности имеет много экспериментально проверенных последствий, которые противоречат интуиции[22]. Такие последствия включают: эквивалентность массы и энергии (E0=mc2){\displaystyle (E_{0}=mc^{2})}, сокращение длины (сокращение объектов во время движения)[Прим. 7] и замедление времени (движущиеся часы идут медленнее). Коэффициент γ{\displaystyle \gamma }, показывающий, во сколько раз сокращается длина и замедляется время, известен как фактор Лоренца (Лоренц-фактор)
- γ=11−v2c2,{\displaystyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},}
где v{\displaystyle v} — скорость объекта. Для скоростей гораздо меньших, чем c{\displaystyle c} (например, для скоростей, с которыми мы имеем дело каждый день) разница между γ{\displaystyle \gamma } и 1 настолько мала, что ею можно пренебречь. В этом случае специальная теория относительности хорошо аппроксимируется относительностью Галилея. Но на релятивистских скоростях разница увеличивается и стремится к бесконечности при приближении v{\displaystyle v} к c{\displaystyle c}.
Объединение результатов специальной теории относительности требует выполнения двух условий: (1) пространство и время являются единой структурой, известной как пространство-время (где c{\displaystyle c} связывает единицы измерения пространства и времени), и (2) физические законы удовлетворяют требованиям особой симметрии, которая называется инвариантность Лоренца (Лоренц-инвариантность), формула которой содержит параметр c{\displaystyle c}[25]. Инвариантность Лоренца встречается повсеместно в современных физических теориях, таких как квантовая электродинамика, квантовая хромодинамика, стандартная модель физики элементарных частиц и общая теория относительности. Таким образом, параметр c{\displaystyle c} встречается повсюду в современной физике и появляется во многих смыслах, которые не имеют отношения собственно к свету. Например, общая теория относительности предполагает, что гравитация и гравитационные волны распространяются со скоростью c{\displaystyle c}[26][27]. В неинерциальных системах отсчёта (в гравитационно искривлённом пространстве или в системах отсчёта, движущихся с ускорением), локальная скорость света также является постоянной и равна c{\displaystyle c}, однако скорость света вдоль траектории конечной длины может отличаться от c{\displaystyle c} в зависимости от того, как определено пространство и время[28].
Считается, что фундаментальные константы, такие как c{\displaystyle c}, имеют одинаковое значение во всём пространстве-времени, то есть они не зависят от места и не меняются со временем. Однако некоторые теории предполагают, что скорость света может изменяться со временем[29][30]. Пока нет убедительных доказательств таких изменений, но они остаются предметом исследований[31][32].
Кроме того, считается, что скорость света изотропна, то есть не зависит от направления его распространения. Наблюдения за излучением ядерных энергетических переходов как функции от ориентации ядер в магнитном поле (эксперимент Гугса — Древера), а также вращающихся оптических резонаторов (эксперимент Майкельсона — Морли и его новые вариации), наложили жёсткие ограничения на возможность двусторонней анизотропии[33][34].
В ряде естественных систем единиц скорость света является единицей измерения скорости[35]. В планковской системе единиц, также относящейся к естественным системам, она служит в качестве единицы скорости и является одной из основных единиц системы.
Верхний предел скорости[править | править код]
Согласно специальной теории относительности, энергия объекта с массой покоя m{\displaystyle m} и скоростью v{\displaystyle v} равна γmc2{\displaystyle \gamma mc^{2}}, где γ{\displaystyle \gamma } — определённый выше фактор Лоренца. Когда v{\displaystyle v} равна нулю, γ{\displaystyle \gamma } равен единице, что приводит к известной формуле эквивалентности массы и энергии E=mc2{\displaystyle E=mc^{2}}. Поскольку фактор γ{\displaystyle \gamma } приближается к бесконечности с приближением v{\displaystyle v} к c{\displaystyle c}, ускорение массивного объекта до скорости света потребует бесконечной энергии. Скорость света — это верхний предел скорости для объектов с ненулевой массой покоя. Это экспериментально установлено во многих тестах релятивистской энергии и импульса[36].
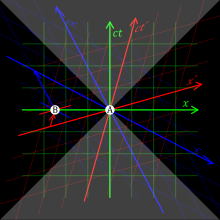 Событие A предшествует событию B в красной системе отсчёта (СО), одновременно с B в зелёной СО и происходит после B в синей СО
Событие A предшествует событию B в красной системе отсчёта (СО), одновременно с B в зелёной СО и происходит после B в синей СОВообще информация или энергия не могут передаваться в пространстве быстрее, чем со скоростью света. Один из аргументов в пользу этого следует из контринтуитивного заключения специальной теории относительности, известного как относительность одновременности. Если пространственное расстояние между двумя событиями А и В больше, чем промежуток времени между ними, умноженный на c{\displaystyle c}, то существуют такие системы отсчёта, в которых А предшествует B, и другие, в которых B предшествует А, а также такие, в которых события А и B одновременны. В результате, если объект двигался бы быстрее скорости света относительно некоторой инерциальной системы отсчёта, то в другой системе отсчёта он бы путешествовал назад во времени, и принцип причинности был бы нарушен[Прим. 8][38]. В такой системе отсчёта «следствие» можно было бы наблюдать раньше его «первопричины». Такое нарушение причинности никогда не наблюдалось[19]. Оно также может приводить к парадоксам, таким как тахионный антителефон[39].
Античные учёные, за редким исключением, считали скорость света бесконечной[40]. В Новое время этот вопрос стал предметом дискуссий. Галилей и Гук допускали, что она конечна, хотя и очень велика, в то время как Кеплер, Декарт и Ферма по-прежнему отстаивали бесконечность скорости света.
Первую оценку скорости света произвёл Олаф Рёмер (1676). Он заметил, что, когда Земля на своей орбите находится дальше от Юпитера, затмения Юпитером спутника Юпитера Ио запаздывают по сравнению с расчётами на 22 минуты. Отсюда он получил значение для скорости света около 220 000 км/с — неточное значение, но близкое к истинному. В 1676 году он сделал сообщение в Парижской Академии, но не опубликовал свои результаты в виде формальной научной работы, в результате чего научное сообщество приняло идею о конечной скорости света только в 1727 году[41].
Спустя полвека, в 1728 году, открытие аберрации позволило Дж. Брэдли подтвердить конечность скорости света и уточнить её оценку: полученное Брэдли значение составило 308 000 км/с[42][43].
Впервые измерения скорости света, основанные на определении времени прохождения светом точно измеренного расстояния в земных условиях, выполнил в 1849 году А. И. Л. Физо. В своих экспериментах Физо использовал разработанный им «метод прерываний», при этом расстояние, преодолеваемое светом, составляло 8,63 км. Полученное в результате выполненных измерений значение оказалось равным 313 300 км/с. В дальнейшем метод прерываний значительно усовершенствовали и его использовали для измерений М. А. Корню (1876 г.), А. Ж. Перротен (1902 г.) и Э. Бергштранд[sv]. Измерения, выполненные Э. Бергштрандом в 1950 году, дали для скорости света значение 299 793,1 км/с, при этом точность измерений была доведена до 0,25 км/с[42].
Другой лабораторный метод («метод вращающегося зеркала»), идея которого была высказана в 1838 году Ф. Араго, в 1862 году осуществил Леон Фуко. Измеряя малые промежутки времени с помощью вращающегося с большой скоростью (512 об/с) зеркала, он получил для скорости света значение 298 000 км/с с погрешностью 500 км/с. Длина базы в экспериментах Фуко была сравнительно небольшой — двадцать метров[43][42][44][45][46]. В последующем за счёт совершенствования техники эксперимента, увеличения используемой базы и более точного определения её длины точность измерений с помощью метода вращающегося зеркала была существенно повышена. Так, С. Ньюком в 1891 году получил значение 299 810 км/с с погрешностью 50 км/с, а А. А. Майкельсону в 1926 году удалось понизить погрешность до 4 км/с и получить для скорости величину 299 796 км/с. В своих экспериментах Майкельсон использовал базу, равную 35 373,21 м[42].
Дальнейший прогресс был связан с появлением мазеров и лазеров, которые отличаются очень высокой стабильностью частоты излучения, что позволило определять скорость света одновременным измерением длины волны и частоты их излучения. В начале 1970-х годов погрешность измерений скорости света приблизилась к 1 м/с[47]. После проверки и согласования результатов, полученных в различных лабораториях, XV Генеральная конференция по мерам и весам в 1975 году рекомендовала использовать в качестве значения скорости света в вакууме величину, равную 299 792 458 м/с, с относительной погрешностью (неопределённостью) 4⋅10-9[48], что соответствует абсолютной погрешности 1,2 м/с[49].
Существенно, что дальнейшее повышение точности измерений стало невозможным в силу обстоятельств принципиального характера: ограничивающим фактором стала величина неопределённости реализации определения метра, действовавшего в то время. Проще говоря, основной вклад в погрешность измерений скорости света вносила погрешность «изготовления» эталона метра, относительное значение которой составляло 4⋅10-9[49]. Исходя из этого, а также учитывая другие соображения, XVII Генеральная конференция по мерам и весам в 1983 году приняла новое определение метра, положив в его основу рекомендованное ранее значение скорости света и определив метр как расстояние, которое проходит свет в вакууме за промежуток времени, равный 1 / 299 792 458 секунды[50].
Из специальной теории относительности следует, что превышение скорости света физическими частицами (массивными или безмассовыми) нарушило бы принцип причинности — в некоторых инерциальных системах отсчёта оказалась бы возможной передача сигналов из будущего в прошлое. Однако теория не исключает для гипотетических частиц, не взаимодействующих с обычными частицами[51], движение в пространстве-времени со сверхсветовой скоростью.
Гипотетические частицы, движущиеся со сверхсветовой скоростью, называются тахионами. Математически движение тахионов описывается преобразованиями Лоренца как движение частиц с мнимой массой. Чем выше скорость этих частиц, тем меньше энергии они несут, и наоборот, чем ближе их скорость к скорости света, тем больше их энергия — так же, как и энергия обычных частиц, энергия тахионов стремится к бесконечности при приближении к скорости света. Это самое очевидное следствие преобразования Лоренца, не позволяющее массивной частице (как с вещественной, так и с мнимой массой) достичь скорости света — сообщить частице бесконечное количество энергии просто невозможно.
Следует понимать, что, во-первых, тахионы — это класс частиц, а не один вид частиц, и во-вторых, тахионы не нарушают принцип причинности, если они никак не взаимодействуют с обычными частицами[51].
Обычные частицы, движущиеся медленнее света, называются тардионами. Тардионы не могут достичь скорости света, а только лишь сколь угодно близко подойти к ней, так как при этом их энергия становится неограниченно большой. Все тардионы обладают массой, в отличие от безмассовых частиц, называемых люксонами. Люксоны в вакууме всегда движутся со скоростью света, к ним относятся фотоны, глюоны и гипотетические гравитоны.
C 2006 года показано, что в так называемом эффекте квантовой телепортации кажущееся взаимовлияние частиц распространяется быстрее скорости света. Например, в 2008 г. исследовательская группа доктора Николаса Гизена (Nicolas Gisin) из университета Женевы, исследуя разнесённые на 18 км в пространстве запутанные фотонные состояния, показала, что это кажущееся «взаимодействие между частицами осуществляется со скоростью, примерно в сто тысяч раз большей скорости света». Ранее также обсуждался так называемый «парадокс Хартмана[en]» — кажущаяся сверхсветовая скорость при туннельном эффекте[52]. Анализ этих и подобных результатов показывает, что они не могут быть использованы для сверхсветовой передачи какого-либо несущего информацию сообщения или для перемещения вещества[53].
В результате обработки данных эксперимента OPERA[54], набранных с 2008 по 2011 год в лаборатории Гран-Сассо совместно с ЦЕРН, было зафиксировано статистически значимое указание на превышение скорости света мюонными нейтрино[55]. Сообщение об этом сопровождалось публикацией в архиве препринтов[56]. Полученные результаты специалисты подвергли сомнению, поскольку они не согласуются не только с теорией относительности, но и с другими экспериментами с нейтрино[57]. В марте 2012 года в том же тоннеле были проведены независимые измерения, и сверхсветовых скоростей нейтрино они не обнаружили[58]. В мае 2012 года OPERA провела ряд контрольных экспериментов и пришла к окончательному выводу, что причиной ошибочного предположения о сверхсветовой скорости стал технический дефект (плохо вставленный разъём оптического кабеля)[59].
- ↑ От поверхности Солнца — от 8 мин. 8,3 сек. в перигелии до 8 мин. 25 сек. в афелии.
- ↑ Скорость распространения светового импульса в среде отличается от скорости его распространения в вакууме (меньше, чем в вакууме), и может быть различной для разных сред. Когда говорят просто о скорости света, обычно подразумевается именно скорость света в вакууме; если же говорят о скорости света в среде, это, как правило, оговаривается явно.
- ↑ В настоящее время наиболее точные методы измерения скорости света основаны на независимом определении значений длины волны λ{\displaystyle \lambda } и частоты ν{\displaystyle \nu } света или другого электромагнитного излучения и последующего расчёта в соответствии с равенством c=λν{\displaystyle c=\lambda \nu }.[10]
- ↑ См. например «Частица Oh-My-God».
- ↑ Аналогом может быть посылка наудачу двух заклеенных конвертов с белой и чёрной бумагой в разные места. Открытие одного конверта гарантирует, что во втором будет лежать второй лист — если первый чёрный, то второй белый, и наоборот. Эта «информация» может распространяться быстрее скорости света — ведь вскрыть второй конверт можно в любое время, и там всегда будет этот второй лист. При этом принципиальная разница с квантовым случаем состоит только в том, что в квантовом случае до «открытия конверта»-измерения состояние листа внутри принципиально неопределённо, как у кота Шрёдингера, и там может оказаться любой лист.
- ↑ Однако, частота света зависит от движения источника света относительно наблюдателя, благодаря эффекту Доплера
- ↑ Помимо того, что измеряемые движущиеся объекты оказываются короче вдоль линии относительного движения, они также выглядят повёрнутыми. Этот эффект, известный как вращение Террелла, связан с разницей во времени между пришедшими к наблюдателю сигналами от разных частей объекта.[23][24]
- ↑ Считается, что эффект Шарнхорста позволяет сигналам распространяться немногим выше c{\displaystyle c}, но особые условия, при которых эффект может возникать, мешают применить этот эффект для нарушения принципа причинности[37]
- ↑ Where Are the Voyagers — NASA Voyager (неопр.). Voyager — The Interstellar Mission. Jet Propulsion Laboratory, California Istitute of Technology. Дата обращения 12 июля 2011. Архивировано 3 февраля 2012 года.
- ↑ Amos, Jonathan. Hubble sets new cosmic distance record, BBC News (3 марта 2016). Дата обращения 3 марта 2016.
- ↑ Is The Speed of Light Everywhere the Same?
- ↑ Начала теоретической физики, 2007, с. 169.
- ↑ Неванлинна, 1966, с. 122.
- ↑ 1 2 Чудинов Э. М. Теория относительности и философия. — М.: Политиздат, 1974. — С. 222—227.
- ↑ Эволюция физики, 1948, с. 167.
- ↑ Начала теоретической физики, 2007, с. 170.
- ↑ Неванлинна, 1966, с. 184.
- ↑ Сажин М. В. Скорость света // Физика космоса. Маленькая энциклопедия / Гл. ред. Р. А. Сюняев. — 2-е изд. — М.: Советская энциклопедия, 1986. — С. 622. — 783 с.
- ↑ ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин. (неопр.) (недоступная ссылка). Дата обращения 14 августа 2012. Архивировано 10 ноября 2012 года.
- ↑ Abbott B. P. et al. (LIGO Scientific Collaboration, Virgo Collaboration, Fermi Gamma-ray Burst Monitor, and INTEGRAL). Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A // The Astrophysical Journal. — 2017. — Vol. 848. — P. L13. — doi:10.3847/2041-8213/aa920c. [исправить]
- ↑ Болотовский Б. М., Гинзбург В. Л. Эффект Вавилова — Черенкова и эффект Допплера при движении источников со скоростью больше скорости света в вакууме (рус.) // Успехи физических наук. — Российская академия наук, 1972. — Т. 106, № 4. — С. 577—592.
- ↑ Миллер М. А., Суворов E. В. Групповая скорость // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1. — С. 544—545. — 704 с.
- ↑ Stachel, J. J. Einstein from «B» to «Z» – Volume 9 of Einstein studies (нем.). — Springer, 2002. — S. 226. — ISBN 0-8176-4143-2.
- ↑ Einstein, A. Zur Elektrodynamik bewegter Körper (нем.) // Annalen der Physik. — 1905. — Т. 17. — С. 890—921. — doi:10.1002/andp.19053221004. English translation: Perrett, W On the Electrodynamics of Moving Bodies (неопр.). Fourmilab. Дата обращения 27 ноября 2009. Архивировано 1 февраля 2013 года.
- ↑ Александров Е. Б. Теория относительности: прямой эксперимент с кривым пучком // Химия и жизнь. — 2012. — № 3.
- ↑ Hsu, J-P; Zhang, Y. Z. Lorentz and Poincaré Invariance (неопр.). — World Scientific, 2001. — Т. 8. — С. 543ff. — (Advanced Series on Theoretical Physical Science). — ISBN 981-02-4721-4.
- ↑ 1 2 Zhang, Y. Z. Special Relativity and Its Experimental Foundations (англ.). — World Scientific, 1997. — Vol. 4. — P. 172—173. — (Advanced Series on Theoretical Physical Science). — ISBN 981-02-2749-3. Архивная копия от 19 мая 2012 на Wayback Machine
- ↑ d’Inverno, R. Introducing Einstein’s Relativity (англ.). — Oxford University Press, 1992. — P. 19—20. — ISBN 0-19-859686-3.
- ↑ Sriranjan, B. Postulates of the special theory of relativity and their consequences // The Special Theory to Relativity (неопр.). — PHI Learning, 2004. — С. 20 ff. — ISBN 81-203-1963-X.
- ↑ Roberts, T What is the experimental basis of Special Relativity? (неопр.). Usenet Physics FAQ. University of California, Riverside (2007). Дата обращения 27 ноября 2009. Архивировано 1 февраля 2013 года.
- ↑ Terrell, J. Invisibility of the Lorentz Contraction (англ.) // Physical Review : journal. — 1959. — Vol. 116, no. 4. — P. 1041—1045. — doi:10.1103/PhysRev.116.1041. — Bibcode: 1959PhRv..116.1041T.
- ↑ Penrose, R. The Apparent Shape of a Relativistically Moving Sphere (англ.) // Proceedings of the Cambridge Philosophical Society (англ.)русск. : journal. — 1959. — Vol. 55, no. 01. — P. 137—139. — doi:10.1017/S0305004100033776. — Bibcode: 1959PCPS…55..137P.
- ↑ Hartle, J. B. Gravity: An Introduction to Einstein’s General Relativity (англ.). — Addison-Wesley, 2003. — P. 52—9. — ISBN 981-02-2749-3.
- ↑ Hartle, J. B. Gravity: An Introduction to Einstein’s General Relativity (англ.). — Addison-Wesley, 2003. — P. 332. — ISBN 981-02-2749-3.
- ↑ The interpretation of observations on binary systems used to determine the speed of gravity is considered doubtful by some authors, leaving the experimental situation uncertain; seeSchäfer, G; Brügmann, M. H. Propagation of light in the gravitational filed of binary systems to quadratic order in Newton’s gravitational constant: Part 3: ‘On the speed-of-gravity controversy’ // Lasers, clocks and drag-free control: Exploration of relativistic gravity in space (англ.) / Dittus, H; Lämmerzahl, C; Turyshev, S. G.. — Springer, 2008. — ISBN 3-540-34376-8.
- ↑ Gibbs, P Is The Speed of Light Constant? (неопр.). Usenet Physics FAQ. University of California, Riverside (1997). Дата обращения 26 ноября 2009. Архивировано 17 ноября 2009 года.
- ↑ Ellis, GFR; Uzan, J-P. ‘c’ is the speed of light, isn’t it? (англ.) // American Journal of Physics (англ.)русск. : journal. — 2005. — Vol. 73, no. 3. — P. 240—247. — doi:10.1119/1.1819929. — Bibcode: 2005AmJPh..73..240E. — arXiv:gr-qc/0305099.
- ↑ An overview can be found in the dissertation of Mota, DF (2006), Variations of the fine structure constant in space and time, arΧiv:astro-ph/0401631 [astro-ph]
- ↑ Uzan, J-P. The fundamental constants and their variation: observational status and theoretical motivations (англ.) // Reviews of Modern Physics : journal. — 2003. — Vol. 75, no. 2. — P. 403. — doi:10.1103/RevModPhys.75.403. — Bibcode: 2003RvMP…75..403U. — arXiv:hep-ph/0205340.
- ↑ Amelino-Camelia, G (2008), Quantum Gravity Phenomenology, arΧiv:0806.0339 [gr-qc]
- ↑ Herrmann, S; Senger, A; Möhle, K; Nagel, M; Kovalchuk, EV; Peters, A. Rotating optical cavity experiment testing Lorentz invariance at the 10−17 level (англ.) // Physical Review D : journal. — 2009. — Vol. 80, no. 100. —
Фазовая скорость — Википедия
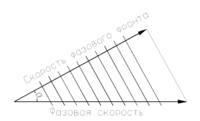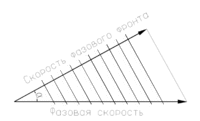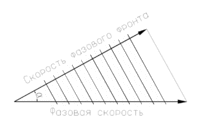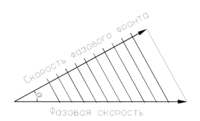 Фазовая скорость вдоль направления, отклонённого от волнового вектора на угол α. Рассматривается монохроматическая плоская волна.
Фазовая скорость вдоль направления, отклонённого от волнового вектора на угол α. Рассматривается монохроматическая плоская волна.Фа́зовая ско́рость — скорость перемещения точки, обладающей постоянной фазой колебательного движения в пространстве, вдоль заданного направления. Обычно рассматривают направление, совпадающее с направлением волнового вектора, и фазовой называют скорость, измеренную именно в этом направлении, если противное не указано явно (то есть если явно не указано направление, отличное от направления волнового вектора). Фазовая скорость по направлению волнового вектора совпадает со скоростью движения фазового фронта (поверхности постоянной фазы). Её можно рассматривать при желании как векторную величину.
Наиболее употребительное обозначение: vϕ {\displaystyle v_{\phi }\ }.
Строго говоря, понятие фазы применимо только при описании гармонических или монохроматических (то есть синусоидальных sin(ϕ){\displaystyle \sin(\phi )} или являющихся мнимыми экспонентами eiϕ{\displaystyle e^{i\phi }}) волн, а также — приближенно — для волн близкой формы (например, почти монохроматических волновых пакетов) или легко сводящихся к синусоидальным (например, сферических волн вида cos(ϕ)/r{\displaystyle \cos(\phi )/r}), или, что менее корректно, при описании периодических волн другой формы. Тем не менее, волну (практически) любой формы с помощью преобразования Фурье можно представить как сумму монохроматических волн, и тогда к каждой из этих волн понятие фазы и фазовой скорости применимо вполне строго (впрочем, тогда у каждой монохроматической волны в разложении будет, вообще говоря, своя фазовая скорость, не совпадающая с другими; только в частных случаях они могут все точно совпадать или быть близки).
Для описания волн, отличных от гармонических, (особенно для описания волновых пакетов), используют, кроме понятия фазовой скорости, понятие скорости групповой (описывающей движение не отдельного гребня в волновом пакете, а его огибающей, например, максимума огибающей).
Основная формула, определяющая фазовую скорость (монохроматической) волны в одномерном пространстве или фазовую скорость вдоль волнового вектора для волны в пространстве большей размерности:
- vϕ=ω/k{\displaystyle v_{\phi }=\omega /k}
которая является прямым следствием того факта, что фаза плоской волны в однородной среде есть
- ϕ=ωt−kx{\displaystyle \phi =\omega t-kx} для одномерного случая
или ϕ=ωt−k→⋅x→{\displaystyle \phi =\omega t-{\vec {k}}\cdot {\vec {x}}} для размерности, большей единицы.
Конкретное соотношение между ω{\displaystyle \omega } и k{\displaystyle k} — так называемый закон дисперсии для каждого конкретного типа волн получают обычно из дифференциального уравнения, описывающего данный тип волн, подставляя в него монохроматическую (чаще всего плоскую) волну[1].
В случае, когда фазовая скорость не зависит для данного типа волн от частоты или волнового числа (и направления волнового вектора), тогда и групповая скорость совпадает с нею.
Фазовая скорость электромагнитной волны[править | править код]
В вакууме для электромагнитной волны любой частоты (по крайней мере, в тех диапазонах частот и интенсивностей, которые исследованы) фазовая скорость, измеренная в направлении волнового вектора, всегда равна одной и той же величине — скорости света в вакууме, универсальной константе.
В средах закон дисперсии электромагнитных волн достаточно сложен (см. Дисперсия света), и фазовая скорость может заметно меняться, вплоть до отрицательных[2] значений.
Для волнового уравнения[править | править код]
Любая волна, описываемая волновым уравнением
- ∂2f∂t2=C2∂2f∂x2{\displaystyle {\frac {\partial ^{2}f}{\partial t^{2}}}=C^{2}{\frac {\partial ^{2}f}{\partial x^{2}}}}
имеет фазовую скорость С (причем C здесь — какой-то постоянный коэффициент; этот коэффициент равен скорости света в волновом уравнении для электромагнитных волн).
Такой результат получается прямой подстановкой в это уравнение монохроматической волны вида cos(kx−ωt){\displaystyle \cos(kx-\omega t)} и затем вычислением ω/k{\displaystyle \omega /k}.
Этот результат верен не только для волнового уравнения на одномерном пространстве (мы его использовали выше лишь для краткости; всё остается совершенно аналогичным при любом количестве производных по координатам в правой части).
Для уравнения Клейна—Гордона[править | править код]
Для уравнения Клейна—Гордона
- ∂2f∂t2=C2∂2f∂x2+C4m2f,{\displaystyle {\frac {\partial ^{2}f}{\partial t^{2}}}=C^{2}{\frac {\partial ^{2}f}{\partial x^{2}}}+C^{4}m^{2}f,}
отличающееся только последним членом, дает при аналогичной подстановке
- ω2=C2k2+C4m2,{\displaystyle \omega ^{2}=C^{2}k^{2}+C^{4}m^{2},}
откуда:
- ω=C2k2+C4m2{\displaystyle \omega ={\sqrt {C^{2}k^{2}+C^{4}m^{2}}}}
и
- vφ=ω/k=C1+C2m2/k2{\displaystyle v_{\varphi }=\omega /k=C{\sqrt {1+C^{2}m^{2}/k^{2}}}}.
Это выражение при ненулевых вещественных m всегда больше, чем C и может быть сколь угодно большим при k → 0.
В некотором смысле фазовая скорость не является вектором. Говоря так, имеют в виду тот факт, что фазовые скорости по разным направлениям (например по направлениям координатных осей), определяемые как это описано выше, не являются ни координатами, ни проекциями[3] никакого вектора[4], в том числе очевидно не являются проекциями или координатами вектора, совпадающего по направлению с волновым вектором, и с абсолютной величиной, равной фазовой скорости в этом направлении.
Но это, конечно, не мешает при желании ввести чисто формально вектор фазовой скорости, по определению совпадающий по направлению с волновым вектором, и с абсолютной величиной, равной фазовой скорости в этом направлении. Вопрос о том, корректно ли называть такой вектор вектором фазовой скорости, является чисто терминологическим (конвенциональным), фактом является лишь то, что его проекции на оси координат или компоненты по этим осям не будут соответствовать фазовой скорости вдоль этих направлений в соответствии с определением фазовой скорости по направлению, данным в начале статьи (и вообще с каким-то разумным определением, кроме чисто формального, описанного в данном абзаце).
Конкретно же, для случая плоской гармонической волны фазовую скорость вдоль волнового вектора можно выразить следующим образом:
- vϕ≡vϕ,0=ω/k{\displaystyle v_{\phi }\equiv v_{\phi ,0}=\omega /k},
где k{\displaystyle k} — волновое число, ω{\displaystyle \omega } — угловая частота. При этом, фазовая скорость вдоль направления, отклонённого от волнового вектора на угол α{\displaystyle \alpha }, будет равна:
- vϕ,α=vkcosα{\displaystyle v_{\phi ,\alpha }={\frac {v_{k}}{\cos \alpha }}}
Непонимание этого факта часто служит причиной недоразумений и ошибок. Например, из приведенного выше ясно, что фазовая скорость может быть больше скорости света (это вытекает прямо из только что приведенной формулы, учитывая что cosα{\displaystyle \cos \alpha } может принимать сколь угодно малые значения при стремлении угла к прямому, и, соответственно, фазовая скорость по направлению, близкому к ортогональному, оказывается сколь угодно велика, стремясь к бесконечности)[5].
Может ли фазовая скорость превосходить скорость света[править | править код]
Фазовая скорость может превосходить скорость света в вакууме, и нередко её превосходит. Это никак не противоречит известному принципу максимальности скорости света, необходимость которого возникает, чтобы одновременно соблюдались принцип причинности (чтобы не возникало причинных парадоксов) и принцип относительности (лоренц-инвариантность).
Дело в том, что эти принципы накладывают ограничение только на скорость распространения таких физических объектов, посредством которых можно передать информацию. А фазовая скорость[6] не относится к скоростям таковых объектов. Чисто монохроматическая (синусоидальная) волна бесконечна в пространстве и во времени, не может никак измениться, чтобы передать информацию (если мы промодулируем волну, она перестанет быть монохроматической, а скорость распространения модуляции — не совпадает с фазовой скоростью, обычно совпадая со скоростью групповой для почти монохроматических волн).
Фазовая скорость по направлению, не совпадающему с волновым вектором[править | править код]
Поскольку фазовая скорость, измеренная вдоль произвольного направления, не совпадающего с волновым вектором и направлением распространения волны, не является скоростью движения «физического объекта», то есть, объекта, состояние которого в последующие моменты времени причинно обусловлено состоянием в предыдущие, а по сути характеризует просто состояние осциллирующего поля в искусственно выбранных точках, часто (а именно если выбрать достаточно большой угол с волновым вектором), фазовая скорость по данному направлению любой, даже сколь угодно медленной (как показано в параграфе выше), волны может превышать скорость света, стремясь к бесконечности при стремлении угла к прямому.
В частности, фазовая скорость света (или вообще любой бегущей электромагнитной волны) в вакууме, измеренная по любому направлению, не совпадающему с её волновым вектором, всегда больше скорости света.
Но дело не ограничивается фазовой скоростью по произвольному направлению. Скорость света может быть превзойдена даже и фазовой скоростью, измеренной вдоль волнового вектора.
Фазовая скорость для квантовой частицы[править | править код]
Фазовая скорость квантовой волны, соответствующей любой массивной частицы (то есть частицы, имеющей массу больше нуля), всегда больше скорости света. Это легко видеть из формул vϕ=ω/k{\displaystyle \ v_{\phi }=\omega /k}, E=ℏω{\displaystyle E=\hbar \omega } и p=ℏk{\displaystyle p=\hbar k}, из чего vϕ=E/p{\displaystyle \ v_{\phi }=E/p}, в то время как E для массивных частиц всегда больше p за счет массы (энергии покоя).
Однако эта фазовая скорость в принципе не может наблюдаться (так как в квантовой физике фаза ненаблюдаема вообще). Доступна же наблюдению лишь групповая скорость, которая и является квантовым аналогом обычной скорости классической частицы.
Фазовая скорость для уравнения Клейна—Гордона[править | править код]
Но дифференциальные уравнения, описывающие квантовые частицы, могут быть реализованы в принципе и на других физических системах (например, на достаточно простых механических моделях). В этом случае фазовая скорость — вполне доступна наблюдению.
Тем не менее и здесь фазовая скорость может быть сделана сколь угодно большой (достаточно подобрать достаточно малое k), и в принципе — её нетрудно сделать большей, чем скорость света.
Этот на вид парадоксальный результат связан с тем, что «распространение» такой волны является иллюзией[7] в том смысле, что между разными частями волны нет причинной связи (состояние волны, продвинувшейся вправо не определяется тем, какой она была слева).
- ↑ cos(kx−ωt){\displaystyle \cos(kx-\omega t)} или exp(i(kx−ωt)){\displaystyle \exp(i(kx-\omega t))} или аналогичный многомерный вариант.
- ↑ Материалы с отрицательным показателем преломления — Виктор Веселаго
- ↑ В случае использования, например, косоугольных координат понятия координаты вектора и проекции на ось не совпадают.
- ↑ Конечно, в определенной фиксированной системе координат любая тройка (будем говорить для определенности о трехмерном случае) чисел определяет вектор; однако если мы имеем дело с настоящим вектором, то при смене системы координат, например, при повороте осей, мы должны получить согласованные по определенным правилам результаты для любой системы координат, а уже такое оказывается для рассматриваемой нами тройки чисел неверным.
- ↑ Это не противоречит теории относительности. См. следующий параграф.
- ↑ Как, например, и скорость зайчика на экране — см. статью Сверхсветовое движение.
- ↑ Распространение как факт, конечно, имеет место; под иллюзией здесь понимается то, что мы склонны интуитивно вкладывать в этот факт больше, чем в нём реально есть, а именно мы интуитивно склонны считать, что, для волны, движущейся слева направо, предыдущие состояния волны слева являются причиной последующих состояний справа, что не так. На самом деле более верным было бы сказать, что разные части этой волны колеблются независимо друг от друга, и наложение таких колебаний и дает бегущую волну (действительно, чем-то похоже на оптический обман).
Скорость света — это… Что такое Скорость света?
Солнечному свету требуется около 8 минут 19 секунд, чтобы достигнуть Земли | |
| Точные значения | |
|---|---|
| Метров в секунду | 299 792 458 |
| Планковских единиц | 1 |
| Приблизительные значения | |
| километров в секунду | 300 000 |
| километров в час | 1,08 млрд |
| миль в секунду | 186 000 |
| миль в час | 671 млн |
| астрономических единиц в день | 173 |
| Приблизительное время путешествия светового сигнала | |
| Расстояние | Время |
| один фут | 1,0 нс |
| один метр | 3,3 нс |
| один километр | 3,3 мкс |
| одна статутная миля | 5,4 мкс |
| от геостационарной орбиты до Земли | 119 мс |
| длина экватора Земли | 134 мс |
| от Луны до Земли | 1,255 с |
| от Солнца до Земли (1 а. е.) | 8,3 мин. |
| от Вояджера-1 до Земли | 16,6 часов (на март 2012)[1]. |
| Один световой год | 1 год |
| один парсек | 3,26 лет |
| от Проксимы Центавра до Земли | 4,24 лет |
| от Альфы Центавра до Земли | 4,37 лет |
| от ближайшей галактики (Карликовой галактики в Большом Псе) до Земли | 25 000 лет |
| через Млечный Путь | 100 000 лет |
| от Галактики Андромеды до Земли | 2,5 млн лет |
| от самой удалённой известной галактики до Земли | 13 млрд лет |
Ско́рость све́та в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме[2]. В физике традиционно обозначается латинской буквой «c» (произносится как [це]). Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбора инерциальной системы отсчёта (ИСО). Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства пространства-времени в целом. По современным представлениям, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий.
В вакууме (пустоте)
 Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 с.
Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 с.Наиболее точное измерение скорости света 299 792 458 ± 1,2 м/с на основе эталонного метра было проведено в 1975 году. На данный момент считают, что скорость света в вакууме — фундаментальная физическая постоянная, по определению, точно равная 299 792 458 м/с, или 1 079 252 848,8 км/ч. Точность значения связана с тем, что с 1983 года метр в Международной системе единиц (СИ) определён, как расстояние, которое проходит свет в вакууме за промежуток времени, равный 1 / 299 792 458 секунды[3]. Для решения школьных задач и разного рода оценок, не требующих большой точности, обычно используют значение 300 000 000 м/с (3×108 м/с).
В природе со скоростью света распространяются (в вакууме):
Массивные частицы могут иметь скорость, приближающуюся почти вплотную к скорости света, но всё же не достигающую её точно. Например, околосветовую скорость имеют массивные частицы, полученные на ускорителе или входящие в состав космических лучей.
В современной физике считается хорошо обоснованным утверждение, что причинное воздействие не может переноситься со скоростью, большей скорости света в вакууме (в том числе посредством переноса такого воздействия каким-либо физическим телом).
Хотя в принципе движение каких-то объектов со скоростью, большей скорости света в вакууме, вполне возможно, однако это могут быть, с современной точки зрения, только такие объекты, которые не могут быть использованы для переноса информации с их движением (например — солнечный зайчик в принципе может двигаться по стене со скоростью большей скорости света, но никак не может быть использован для передачи информации с такой скоростью от одной точки стены к другой)[4]. (Подробнее см. Сверхсветовое движение, также соответствующий раздел данной статьи ниже).
В прозрачной среде
Скорость света в прозрачной среде — скорость, с которой свет распространяется в среде, отличной от вакуума. В среде, обладающей дисперсией, различают фазовую и групповую скорость.
Фазовая скорость связывает частоту и длину волны монохроматического света в среде (λ = c/ν). Эта скорость обычно (но не обязательно) меньше c. Отношение фазовой скорости света в вакууме к скорости света в среде называется показателем преломления среды. Групповая скорость света в равновесной среде всегда меньше c. Однако в неравновесных средах она может превышать c. При этом, однако, передний фронт импульса все равно движется со скоростью, не превышающей скорости света в вакууме. В результате сверхсветовая передача информации остаётся невозможной.
Арман Ипполит Луи Физо на опыте доказал, что движение среды относительно светового луча также способно влиять на скорость распространения света в этой среде.
История измерений скорости света
Античные учёные, за редким исключением, считали скорость света бесконечной[5]. В Новое время этот вопрос стал предметом дискуссий. Галилей и Гук допускали, что она конечна, хотя и очень велика, в то время как Кеплер, Декарт и Ферма по-прежнему отстаивали бесконечность скорости света.
Первую оценку скорости света дал Олаф Рёмер (1676). Он заметил, что когда Земля и Юпитер находятся по разные стороны от Солнца, затмения спутника Юпитера Ио запаздывают по сравнению с расчётами на 22 минуты. Отсюда он получил значение для скорости света около 220 000 км/с — неточное, но близкое к истинному. Спустя полвека открытие аберрации позволило подтвердить конечность скорости света и уточнить её оценку.
Сверхсветовое движение
Из специальной теории относительности следует, что превышение скорости света физическими частицами (массивными или безмассовыми) невозможно, так как это нарушило бы фундаментальный принцип причинности — в некоторых инерциальных системах отсчёта оказалась бы возможной передача сигналов из будущего в прошлое. Однако теория не исключает для гипотетических частиц, не взаимодействующих с обычными частицами, движение в пространстве-времени со сверхсветовой скоростью.
Гипотетические частицы, движущиеся со сверхсветовой скоростью, называются тахионами. Математически движение тахионов описывается преобразованиями Лоренца как движение частиц с мнимой массой. Чем выше скорость этих частиц, тем меньше энергии они несут, и наоборот, чем ближе их скорость к скорости света, тем больше их энергия — так же, как и энергия обычных частиц, энергия тахионов стремится к бесконечности при приближении к скорости света. Это самое очевидное следствие преобразования Лоренца, не позволяющее массивной частице (как с вещественной, так и с мнимой массой) достичь скорости света — сообщить частице бесконечное количество энергии просто невозможно.
Следует понимать, что, во-первых, тахионы — это класс частиц, а не один вид частиц, и во-вторых, никакое физическое взаимодействие не может распространяться быстрее скорости света. Из этого следует, что тахионы не нарушают принцип причинности — с обычными частицами они никак не взаимодействуют, а разность их скоростей также не достигает скорости света.
Обычные частицы, движущиеся медленнее света, называются тардионами. Тардионы не могут достичь скорости света, а только лишь сколь угодно близко подойти к ней, так как при этом их энергия становится неограниченно большой. Все тардионы обладают массой, в отличие от безмассовых частиц, называемых люксонами. Люксоны в вакууме всегда движутся со скоростью света, к ним относятся фотоны, глюоны и гипотетические гравитоны.
В планковской системе единиц скорость света в вакууме равна 1, то есть свет проходит 1 единицу планковской длины за единицу планковского времени.
C 2006 года появляются сообщения о том, что в так называемом эффекте квантовой телепортации взаимодействие распространяется быстрее скорости света. Например, в 2008 г. исследовательская группа доктора Николаса Гизена (Nicolas Gisin) из университета Женевы, исследуя разнесённые на 18 км в пространстве запутанные фотонные состояния, якобы показала, что «взаимодействие между частицами осуществляется со скоростью, примерно в сто тысяч раз большей скорости света». Ранее также обсуждался так называемый парадокс Хартмана — сверхсветовая скорость при туннельном эффекте. Анализ этих и подобных результатов показывает, что они не могут быть использованы для сверхсветовой передачи какого-либо несущего информацию сообщения или для перемещения вещества[6].
В результате обработки данных эксперимента OPERA[7], набранных с 2008 по 2011 год в лаборатории Гран-Сассо совместно с ЦЕРН, было зафиксировано статистически значимое указание на превышение скорости света мюонными нейтрино[8]. Сообщение об этом сопровождалось публикацией в архиве препринтов[9]. Полученные результаты специалисты подвергли сомнению, поскольку они не согласуются не только с теорией относительности, но и с другими экспериментами с нейтрино[10]. В марте 2012 года в том же тоннеле были проведены независимые измерения, и сверхсветовых скоростей нейтрино они не обнаружили[11][12]. В мае 2012 года OPERA провела ряд контрольных экспериментов и пришла к окончательному выводу, что причиной ошибочного предположения о сверхсветовой скорости стал технический дефект (плохо вставленный разъём оптического кабеля)[13].
В культуре
В фантастическом рассказе «Светопреставление» Александр Беляев описывает ситуацию, когда скорость света снижается до нескольких метров в секунду.
См. также
Примечания
- ↑ Where Are the Voyagers — NASA Voyager. Voyager — The Interstellar Mission. Jet Propulsion Laboratory, California Istitute of Technology. Архивировано из первоисточника 3 февраля 2012. Проверено 12 июля 2011.
- ↑ Скорость распространения светового импульса в среде отличается от скорости его распространения в вакууме (меньше, чем в вакууме), и может быть различной для разных сред. Когда говорят просто о скорости света, обычно подразумевается именно скорость света в вакууме; если же говорят о скорости света в среде, это, как правило, оговаривается явно.
- ↑ ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин.
- ↑ Болотовский Б. М., Гинзбург В. Л. Эффект Вавилова — Черенкова и эффект Допплера при движении источников со скоростью больше скорости света в вакууме // УФН. — 1972. — Т. 106. — № 4. — С. 577-592.
- ↑ Гиндикин С. Г. Рассказы о физиках и математиках. — издание третье, расширенное. — М.: МЦНМО, 2001. — С. 105-108. — ISBN 5-900916-83-9
- ↑ И. Иванов. Проведены новые эксперименты по проверке механизма квантовой запутанности. Элементы.ру.
- ↑ Oscillation Project with Emulsion-tRacking Apparatus
- ↑ OPERA experiment reports anomaly in flight time of neutrinos from CERN to Gran Sasso
- ↑ OPERA Collaboration (Adam T. et al.) (2011), «Measurement of the neutrino velocity with the OPERA detector in the CNGS beam», arΧiv:1109.4897 .
- ↑ И.Иванов. Эксперимент OPERA сообщает о наблюдении сверхсветовой скорости нейтрино. Элементы.ру, 23 сентября 2011 года.
- ↑ Measurement of the neutrino velocity with the ICARUS detector at the CNGS beam.
- ↑ Эйнштейн оказался прав.
- ↑ Эксперимент OPERA окончательно «закрыл» сверхсветовые нейтрино.
Литература
Ссылки
Электромагнитная волна — это… Что такое Электромагнитная волна?
Электромагни́тное излуче́ние (электромагнитные волны) — распространяющееся в пространстве возмущение электрических и магнитных полей.
Характеристики электромагнитного излучения
Основными характеристиками электромагнитного излучения принято считать частоту, длину волны и поляризацию. Длина волны зависит от скорости распространения излучения. Групповая скорость распространения электромагнитного излучения в вакууме равна скорости света, в других средах эта скорость меньше. Фазовая скорость электромагнитного излучения в вакууме также равна скорости света, в различных средах она может быть как меньше, так и больше скорости света (принцип максимальности скорости света не нарушается, так как скорость переноса энергии и информации в любом случае не превышает световой скорости).
Описанием свойств и параметров электромагнитного излучения занимается электродинамика.
Существуют различные теории, позволяющие смоделировать и исследовать свойства и проявления электромагнитного излучения. Наиболее фундаментальной из них является квантовая электродинамика, из которой путём тех или иных упрощений можно в принципе получить все перечисленные ниже теории, имеющие широкое применение в своих областях. Для описания относительно низкочастотного электромагнитного излучения в макроскопической области используют, как правило, классическую электродинамику, основанную на уравнениях Максвелла, причём существуют упрощения в прикладных применениях. Для оптического излучения (вплоть до рентгеновского диапазона) применяют оптику (в частности, волновую оптику, когда размеры некоторых частей оптической системы близки к длинам волн; квантовую оптику, когда существенны процессы поглощения, излучения и рассеяния фотонов; геометрическую оптику — предельный случай волновой оптики, когда длиной волны излучения можно пренебречь). Гамма-излучение чаще всего является предметом ядерной физики, с других позиций изучается воздействие электромагнитного излучения в радиологии.
Некоторые особенности электромагнитных волн c точки зрения теории колебаний и понятий электродинамики:
- наличие трёх взаимно перпендикулярных (в вакууме) векторов: волнового вектора, вектора напряжённости электрического поля E и вектора напряжённости магнитного поля H.
- Электромагнитные волны — это поперечные волны, в которых вектора напряжённостей электрического и магнитного полей колеблются перпендикулярно направлению распространения волны, но они существенно отличаются от волн на воде и от звука тем, что их можно передать от источника к приёмнику в том числе и через вакуум.
Диапазоны электромагнитного излучения
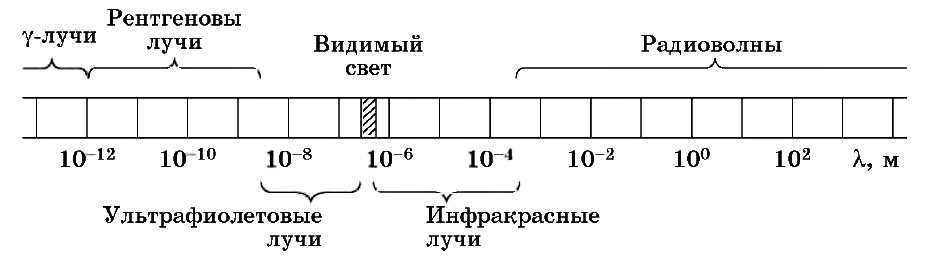
Электромагнитное излучение принято делить по частотным диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.
Радиоволны. Ультракороткие радиоволны принято разделять на метровые, дециметровые, сантиметровые, миллиметровые и субмиллиметровые (микрометровые). Волны с длиной λ < 1 м (ν > 300 МГц) принято также называть микроволнами или волнами сверхвысоких частот (СВЧ). Деление радиоволн на диапазоны см. в статьях Радиоизлучение и Диапазоны частот.
Ионизирующее электромагнитное излучение. К этой группе традиционно относят рентгеновское и гамма-излучение, хотя, строго говоря, ионизировать атомы может и ультрафиолетовое излучение, и даже видимый свет. Границы областей рентгеновского и гамма-излучения могут быть определены лишь весьма условно. Для общей ориентировки можно принять, что энергия рентгеновских квантов лежит в пределах 20 эВ — 0,1 МэВ, а энергия гамма-квантов — больше 0,1 МэВ. В узком смысле гамма-излучение испускается ядром, а рентгеновское — атомной электронной оболочкой при выбивании электрона с низколежащих орбит, хотя эта классификация неприменима к жёсткому излучению, генерируемому без участия атомов и ядер (например, синхротронному или тормозному излучению).
Радиоволны
Из-за больших значений λ распространение радиоволн можно рассматривать без учёта атомистического строения среды. Исключение составляют только самые короткие радиоволны, примыкающие к инфракрасному участку спектра. В радиодиапазоне слабо сказываются и квантовые свойства излучения, хотя их всё же приходится учитывать, в частности, при описании квантовых генераторов и усилителей сантиметрового и миллиметрового диапазонов, а также молекулярных стандартов частоты и времени, при охлаждении аппаратуры до температур в несколько кельвинов.
Радиоволны возникают при протекании по проводникам переменного тока соответствующей частоты. И наоборот, проходящая в пространстве электромагнитная волна возбуждает в проводнике соответствующий ей переменный ток. Это свойство используется в радиотехнике при конструировании антенн.
Естественным источником волн этого диапазона являются грозы. Считается, что они же являются источником стоячих электромагнитных волн Шумана.
Микроволновое излучение
Инфракрасное излучение (Тепловое)
Видимое излучение (Оптическое)
Видимое, инфракрасное и ультрафиолетовое излучение составляет так называемую оптическую область спектра в широком смысле этого слова. Выделение такой области обусловлено не только близостью соответствующих участков спектра, но и сходством приборов, применяющихся для её исследования и разработанных исторически главным образом при изучении видимого света (линзы и зеркала для фокусирования излучения, призмы, дифракционные решётки, интерференционные приборы для исследования спектрального состава излучения и пр.).
Частоты волн оптической области спектра уже сравнимы с собственными частотами атомов и молекул, а их длины — с молекулярными размерами и межмолекулярными расстояниями. Благодаря этому в этой области становятся существенными явления, обусловленные атомистическим строением вещества. По этой же причине, наряду с волновыми, проявляются и квантовые свойства света.
Самым известным источником оптического излучения является Солнце. Его поверхность (фотосфера) нагрета до температуры 6000 градусов и светит ярко-белым светом (максимум непрерывного спектра солнечного излучения расположен в «зелёной» области 550 нм, где находится и максимум чувствительности глаза). Именно потому, что мы родились возле такой звезды, этот участок спектра электромагнитного излучения непосредственно воспринимается нашими органами чувств.
Излучение оптического диапазона возникает, в частности, при нагревании тел (инфракрасное излучение называют также тепловым) из-за теплового движения атомов и молекул. Чем сильнее нагрето тело, тем выше частота, на которой находится максимум спектра его излучения (см. Закон смещения Вина). При определённом нагревании тело начинает светиться в видимом диапазоне (каление), сначала красным цветом, потом жёлтым и так далее. И наоборот, излучение оптического спектра оказывает на тела тепловое воздействие (см. Болометрия).
Оптическое излучение может создаваться и регистрироваться в химических и биологических реакциях. Одна из известнейших химических реакций, являющихся приёмником оптического излучения, используется в фотографии. Источником энергии для большинства живых существ на Земле является фотосинтез — биологическая реакция, протекающая в растениях под действием оптического излучения Солнца.
Ультрафиолетовое излучение
Жёсткое излучение
В области рентгеновского и гамма-излучения на первый план выступают квантовые свойства излучения. Рентгеновское излучение возникает при торможении быстрых заряженных частиц (электронов, протонов и пр.), а также в результате процессов, происходящих внутри электронных оболочек атомов. Гамма-излучение появляется в результате процессов, происходящих внутри атомных ядер, а также в результате превращения элементарных частиц. Оно появляется и при торможении быстрых заряженных частиц.
Особенности электромагнитного излучения разных диапазонов
Распространение электромагнитных волн, временны́е зависимости электрического и магнитного полей, определяющий тип волн (плоские, сферические и др.), вид поляризации и прочие особенности зависят от источника излучения и свойств среды.
Электромагнитные излучения различных частот взаимодействуют с веществом также по-разному. Процессы излучения и поглощения радиоволн обычно можно описать с помощью соотношений классической электродинамики; а вот для волн оптического диапазона и, тем более, жестких лучей необходимо учитывать уже их квантовую природу.
История исследований
В 1800 году английский учёный У. Гершель открыл инфракрасное излучение.
Существование электромагнитного излучения теоретически предсказал английский физик Фарадей в 1832 году.
В 1865 году английский физик Дж. Максвелл рассчитал теоретически скорость электромагнитных волн в вакууме.
В 1888 году немецкий физик Герц подтвердил теорию Максвелла опытным путём. Интересно, что Герц не верил в существование этих волн и проводил свой опыт с целью опровергнуть выводы Максвелла.
Электромагнитная безопасность
Излучения электромагнитного диапазона при определённых уровнях могут оказывать отрицательное воздействие на организм человека, животных и других живых существ, а также неблагоприятно влиять на работу электрических приборов. Различные виды неионизирующих излучений (электромагнитных полей, ЭМП) оказывают разное физиологическое воздействие. На практике выделяют диапазоны магнитного поля (постоянного и квазипостоянного, импульсного), ВЧ- и СВЧ-излучений, лазерного излучения, электрического и магнитного поля промышленной частоты от высоковольтного оборудования, СВЧ-излучения и др..
Влияние на живые существа
Существуют национальные и международные гигиенические нормативы уровней ЭМП, в зависимости от диапазона, для селитебной зоны и на рабочих местах.
Оптический диапазон
Существуют гигиенические нормы освещённости; также разработаны нормативы безопасности при работе с лазерным излучением.
Радиоволны
Допустимые уровни электромагнитного излучения (плотность потока электромагнитной энергии) отражаются в нормативах, которые устанавливают государственные компетентные органы, в зависимости от диапазона ЭМП. Эти нормы могут быть существенно различны в разных странах.
Нахождение в зоне с повышенными уровнями ЭМП в течение определённого времени приводит к ряду неблагоприятных последствий: наблюдается усталость, тошнота, головная боль. При значительных превышениях нормативов возможны повреждение сердца, мозга, центральной нервной системы. Излучение может влиять на психику человека, появляется раздражительность, человеку трудно себя контролировать. Возможно развитие трудно поддающихся лечению заболеваний, вплоть до раковых. В частности, корреляционный анализ показал прямую средней силы корреляцию заболеваемости злокачественными заболеваниями головного мозга с максимальной нагрузкой от ЭМИ даже от использования такого маломощного источника, как мобильные радиотелефоны.[1] Эти данные не должны быть причиной для радиофобии, однако очевидна необходимость в существенном углублении сведений о действии ЭМИ на живые организмы.
В России действует СанПиН 2.2.4.1191—03 Электромагнитные поля в производственных условиях, на рабочих местах. Санитарно-эпидемиологические правила и нормативы, а также гигиенические нормативы ГДР (ПДУ) 5803-91 (ДНАОП 0.03-3.22-91) Предельно допустимые уровни (ПДУ) воздействия электромагнитных полей (ЭМП) диапазона частот 10—60 кГц Промышленное электроснабжение 50 Гц [2][3]
- Допустимые уровни излучения базовых станций мобильной связи (900 и 1800 МГц, суммарный уровень от всех источников) в санитарно-селитебной зоне в некоторых странах заметно различаются:
- Украина: 2,5 мкВт/кв.см. (самая жёсткая санитарная норма в Европе)
- Россия, Венгрия: 10 мкВт/кв.см.
- США, Скандинавские страны: 100 мкВт/кв.см.
Параллельное развитие гигиенической науки в СССР и западных странах привело к формированию разных подходов к оценке действия ЭМИ. Для части стран постсоветского пространства сохраняется преимущественно нормирование в единицах плотности потока энергии (ППЭ), а для США и стран ЕС типичным является оценка удельной мощности поглощения (мобильных радиотелефонов (МРТ) не позволяют прогнозировать все неблагоприятные последствия, многие аспекты проблемы не освещены в современной литературе и требуют дополнительных исследований. В связи с этим, согласно рекомендациям ВОЗ, целесообразно придерживаться предупредительной политики, т. е. максимально уменьшить время использования сотовой связи.»
Проникающая неионизирующая радиация
Допустимые нормативы регулируются нормами радиационной безопасности — НРБ-99.
Влияние на радиотехнические устройства
Существует административные и контролирующие органы — инспекция по радиосвязи (на Украине, например, Укрчастотнадзор), которая регулирует распределение частотных диапазонов для различных пользователей, соблюдение выделенных диапазонов, отслеживает незаконное пользование радиоэфиром.
См. также
Ссылки
Литература
- Физика. Большой энциклопедический словарь/Гл. ред. А. М. Прохоров. — 4-е изд. — М.: Большая Российская энциклопедия, 1999. — С. 874—876. ISBN 5-85270-306-0 (БРЭ)
- Кудряшов Ю. Б., Перов Ю. Ф. Рубин А. Б. Радиационная биофизика: радиочастотные и микроволновые электромагнитные излучения. Учебник для ВУЗов. — М.: ФИЗМАТЛИТ, 2008. — 184 с — ISBN 978-5-9221-0848-5
Примечания
- ↑ В. Н. Дунаев «Электромагнитные излучения и риск популяционному здоровью при использовании средств сотовой связи» //Гигиена и санитария, № 6, 2007, с. 56—57
- ↑ ПДУ магнитных полей частот 50 Гц. Харьков, 1986, СН-3206-85.2
- ↑ Методические указания но гигиенической оценке основных параметров полей частотой 50Гц. Харьков, 1986. СН 3207-85
Wikimedia Foundation. 2010.
Скорость звука и света в вакууме, воде, воздухе — журнал «Рутвет»
Оглавление:
- Чему равна скорость света
- Что быстрее — скорость света или скорость звука?
- Какова скорость звука в воздухе
- Скорость звука в вакууме
- Скорость звука в воде
- Скорость распространения звука
На таких элементарных и фундаментальных постоянных как звуковая и световая скорость держится наша вселенная, это аксиомы в мире физики. Понятное дело, что все мы задумывались над вопросом – от чего же зависят эти скорости? Когда мы наблюдаем молнию, то сначала видим свет, а потом до нас докатывается раскат. Почему так происходит и от чего зависит время, которое проходит от вспышки к грому? На самом деле все очень просто и легко объясняется, нужно просто вспомнить некоторые основные положения из школьного курса физики, они все расставят по своим местам, ну почти все… Но обо всем по порядку…
Чему равна скорость света
Свет распространяется — 299 792 458 м/с, в более привычном нам километровом эквиваленте это 1 079 252 848,8 км/ч, но для простоты оперирования эту сложную цифру принято округлять и считать, что она составляет 300 тысяч км/с. Скорость света — максимальная величина распространения чего-либо в нашей вселенной. Но самое интересное во всем этом то, что она абсолютно не зависит от скорости движения источника, излучающего ее.  Как же обстоят дела в нашем мире? Разница темпа брошенного тела и объекта, с которого его бросили может увеличиваться или уменьшаться, в зависимости от того, в какое ускорение был совершен бросок. Давайте рассмотрим пример: вы едете на автомобиле, скорость которого составляет 100 км в час и бросаете камень по ходу движения (примем скорость запущенного камня в 10 км/ч), для стороннего наблюдателя, который стоит на обочине, камень будет лететь уже со скоростью – 110 км/ч. В данном случае скорость броска и автомобиля суммируются. Но это не касается скорости света. В какую бы сторону не летел источник, свет будет распространяться с одинаковой быстротой, он не ускорится и не замедлится. В этом и состоит парадокс. По крайней мере так думали раньше, но как же обстоят дела сейчас? Об этом немного позже…
Как же обстоят дела в нашем мире? Разница темпа брошенного тела и объекта, с которого его бросили может увеличиваться или уменьшаться, в зависимости от того, в какое ускорение был совершен бросок. Давайте рассмотрим пример: вы едете на автомобиле, скорость которого составляет 100 км в час и бросаете камень по ходу движения (примем скорость запущенного камня в 10 км/ч), для стороннего наблюдателя, который стоит на обочине, камень будет лететь уже со скоростью – 110 км/ч. В данном случае скорость броска и автомобиля суммируются. Но это не касается скорости света. В какую бы сторону не летел источник, свет будет распространяться с одинаковой быстротой, он не ускорится и не замедлится. В этом и состоит парадокс. По крайней мере так думали раньше, но как же обстоят дела сейчас? Об этом немного позже…
Что быстрее — скорость света или скорость звука?
Ученым известно, что скорость света примерно в миллион раз больше звуковой. Но темп звука может меняться. Среднее его значение составляет 1450 м/с. Быстрота продвижения звука зависит от типа среды, вода это или воздух, от температуры и даже давления. Выходит, что точного значения этой величины не существует, есть лишь примерная величина в привычной для нас среде — воздухе. Касательно скорости света до сих пор ведутся целые серии экспериментов передовых ученых со всей планеты.
Какова скорость звука в воздухе
Определить скорость звука в воздухе в первый раз удалось в 1636 году ученому из Франции М. Мерсенну. Температура окружающей среды была 20 °С и при таком показателе звук летел со значением 343 м/с, в километрах — 1235 км/ч. Темп движения звука напрямую зависит от температуры окружающей среды в которой он распространяется: если температура газа растет, звук тоже начинает двигаться быстрее, соответственно, наоборот, чем ниже температура воздуха, тем медленнее распространяется звук.
 Например, при нулевой температуре звук передается уже на скорости 331 м/с. Также скорость звука зависит и от типа газа. Чем больше диаметр молекул из которых состоит газ, тем медленнее двигается звук. Например, при нулевой температуре, в водороде быстрота звука составит 1284 м/с, гелии — 965 м/с. Заметная разница.
Например, при нулевой температуре звук передается уже на скорости 331 м/с. Также скорость звука зависит и от типа газа. Чем больше диаметр молекул из которых состоит газ, тем медленнее двигается звук. Например, при нулевой температуре, в водороде быстрота звука составит 1284 м/с, гелии — 965 м/с. Заметная разница.
Скорость звука в вакууме
Звук по своей сути — это колебание молекул по ходу распространения. Понятно, что для того чтобы звук мог как-то передаваться, нужна среда из молекул, которые будут колебаться. В вакууме же нет никакой материи, поэтому звук там проходить не может. Но по результатам последних исследований, стало ясно, что звук может преодолеть прослойку из вакуума, толщиной мене микрона. Данное явление назвали — «вакуумное туннелирование фононов», информацию по нему появилась одновременно в двух статьях, которые появились в печатном издании «Physical Review Letters». Следует помнить, что колебание молекул кристаллической решетки переносят не один звук, но и тепловую энергию, следовательно, через вакуум можно передавать и тепло.
Скорость звука в воде
Обычно, скорость звука в жидкостях, в том числе воде, больше чем в газообразной среде. Первый замер такой стремительности в воде произвели в 1826 г. ученые Ж- Колладон и Я. Штурм. Эксперимент проходил в Швейцарии, а именно на одном из озер. Последовательность действий, по которой проходило измерение, была таковой:
- На лодке, которая стояла на якоре, поджигали пакет с порохом и в то же время били в подводный колокол;
- На расстоянии в 14 километров стояла вторая, наблюдательная лодка, помимо вспышки пороха, которую было видно из далека, на лодке улавливали и звук колокола посредством подводного рупора;
- Именно по разнице времени между вспышкой и приходом звуковой волны удалось вычислить скорость звука. Тогда вода имела температуру в 8 °С и скорость звука составила 1440 м/с.
Также стоит уделить внимание следующим статьям:
 Между двумя разными средами звуковая волна ведет себя интересно. Одна ее часть заходит в другую среду, вторая попросту отражается. Если звук попадает из воздуха в жидкость, то 99,9 % его отражается, но давление в той доле звука что все-таки проходит в воду в два раза вырастает. Именно этим и пользуются рыбы. Если возле воды кричать и шуметь, хвостатые обитатели глубин быстро уйдут куда подальше.
Между двумя разными средами звуковая волна ведет себя интересно. Одна ее часть заходит в другую среду, вторая попросту отражается. Если звук попадает из воздуха в жидкость, то 99,9 % его отражается, но давление в той доле звука что все-таки проходит в воду в два раза вырастает. Именно этим и пользуются рыбы. Если возле воды кричать и шуметь, хвостатые обитатели глубин быстро уйдут куда подальше.
Скорость распространения звука
Даже свет, равно как звук и электромагнитные колебания может менять свою скорость в разных физических средах. Новейшие исследования в этой области, доказали теоретическую возможность запустить тело быстрее света. Дело в том, что в некоторых газах быстрота фотонов (частички из которых состоит свет) заметно замедляются. Понятное дело, что увидеть такое явление невооруженным глазом не выйдет, но в точной науке, такой как физика, это имеет огромное значение. Так вот, ученные доказали, что, если пропустить свет через газ, его скорость снизится на столько, что быстро запущенное тело сможет двигаться быстрее фотонов.
Обсуждайте вопросы распространения звука в разных средах комментариях. Смотрите видео, где подробнейшим образом объясняющее аспекты скорости звука «на пальцах»
ФИЗИКА: Задачи на Электромагнитные волны — Ответы и решения
Задачи на Электромагнитные волны с решениями
Формулы, используемые на уроках «Задачи на Электромагнитные волны».
Название величины | Обозначение | Единица измерения | Формула |
Длина волны | λ | м | λ = сT ;λ = с / v |
Скорость волны в вакууме | с | м/с | с = 3•108 |
Период колебаний | T | с | T = λ / с ;T = 1 / v |
Частота колебаний | v | Гц | v = c / λ ;v = 1 / T |
Число колебаний | N | N = t / T ;N = vt |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Радиостанция работает на волне длиной 25 м. Какова частота излучаемых колебаний?

Задача № 2. Определите расстояние от Земли до Луны в момент локации, если посланный сигнал вернулся через 2,56 с.

Задача № 3. В каком диапазоне длин волн может работать приёмник, если ёмкость конденсатора в его колебательном контуре плавно изменяется от C1 = 50 пФ до С2 = 500 пФ, а индуктивность катушки постоянна и равна L = 20 мкГн?

Задача № 4.
ОГЭ
На каком расстоянии s от антенны радиолокатора А находится объект С, если отражённый от него радиосигнал возвратился обратно через промежуток времени τ = 200 мкс?

Задача № 5.
ЕГЭ
Каким может быть максимальное число импульсов, испускаемых радиолокатором за время t = 1с, при разведывании цели, находящейся на расстоянии s = 30 км от него?

Таблица для решения Задачи на Электромагнитные волны.
Это конспект по теме «ЗАДАЧИ на Электромагнитные волны». Выберите дальнейшие действия:
Ответы Mail.ru: скорость света в вакууме
Скорость света в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме \Large c=3*10^8=299 792 458 \left[ мс^{-1}\right] Согласно специальной теории относительности, скорость света в вакууме не зависит ни от скорости движения источника света, ни от скорости движения наблюдателя. В природе со скоростью света распространяются: — Видимый свет — Другие виды электромагнитного излучения (радиоволны, рентгеновские лучи) — Гравитационные волны Частицы, движущиеся медленнее скорости света, называются тардионами. Тардионы не могут достичь скорости света, а только лишь сколь угодно близко подойти к ней, так как при этом их энергия становится неограниченно большой. Все тардионы обладают массой покоя, в отличие от безмассовых фотонов и гравитонов, которые всегда движутся со скоростью света. В формуле мы использовали : c — Скорость света в вакууме <a href=»/» rel=»nofollow» title=»39567364:##:skorost-sveta-v-vakuume/» target=»_blank» >[ссылка заблокирована по решению администрации проекта]</a>
вики вам в помощь.
Согласно классическому закону сложения скоростей, который является следствием из преобразований Галилея, скорости света в вакууме в подвижной и неподвижной инерциальных системах отсчета должны быть разными c ⃗ =c ⃗ ′ +υ ⃗ отсюда c=c±υ, где c — скорость света в вакууме в неподвижной и c’ — в подвижной системе отсчета; υ — скорость движения подвижной системы отсчета относительно неподвижной. Из уравнений Максвелла следовало, что скорость света (скорость распространения электромагнитных волн) в вакууме одинакова по всем направлениям и равна c = 3⋅108 м/с.

