Скользящий вектор — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Скользящий вектор — может перемещаться вдоль прямой, отрезком которой он является. Прямую эту называют основанием или линией действия вектора. [1]
Скользящие векторы, сходящиеся в одной точке. [2]
Скользящие векторы представляют собой векторные величины, остающиеся неизменными вдоль линии действия вектора и изменяющиеся при переходе к другой точке пространства, не лежащей на линии действия. [3]
Скользящие векторы в заданном пространстве определяют такие векторные физические величины, которые не меняются вдоль линии действия вектора. Вдоль линии действия они имеют одно и то же значение и направление и представляются одним и тем же вектором. При переходе к другой точке, не расположенной на линии действия, эти физические величины имеют уже другое значение. Скользящими векторами представляются силы, действующие на абсолютно твердое тело, вектор мгновенной угловой скорости вращения твердого тела и другие физические величины.
Скользящий вектор определяется пятью независимыми величинами. [5]
Скользящий вектор может перемещаться вдоль прямой, отрезком которой он является. Прямую эту называют основанием или линией действия вектора. [6]
Скользящий вектор — и, приложенный в С, и вектор — F, приложенный в В, в сумме дают скользящий вектор — R, приложенный в точке О. Векторы R и — R, приложенные в О, уничтожаются; от всей системы остается пара скользящих векторов и и — и, соответственно приложенных в точках С и D, с назначенным плечом CD, эквивалентная данной. В силу (1.6) момент результирующей пары равен и параллелен моменту исходной пары; направление моментов этих пар одно и то же. [7]
| К определе — [ IMAGE ] — 2. Скользящий нию вектора. вектор.| Свободный вектор. [8] |
Скользящий вектор нельзя переносить с одной прямой на другую.
Сила, действующая на твердое тело, является примером скользящего вектора.
[9]
Скользящие векторы — это такие векторы, которые считаются равными, если они не только имеют одинаковые длины и одинаково направлены, но и расположены на одной и той же прямой. [10]
Аналитически скользящий вектор определяется пятью числами, например тремя проекциями ах, ау, аг вектора а и координатами xv y точки пересечения прямой, вдоль которой направлен этот вектор, с плоскостью Оху. [11]
Всякий скользящий вектор е, приложенный в точке А, можно, не изменяя его действия, перенести в любую точку В, н прибавив при этом пару с моментом, равным моменту приложенного в точке А вектора to относительно точки В. [12]
Введем скользящий вектор ш ( см. раздел 1.2), основание которого совпадает с осью вращения. Ориентируем его так, чтобы из его конца вращение было видно происходящим против хода часовой стрелки.
Рассматривая скользящие векторы, следует помнить, что они являются обобщенной формой частных физических величин, например мгновенных угловых скоростей. [14]
Система скользящих векторов, образующих пучок, всегда эквивалентна одному вектору. Система скользящих векторов, не образующих пучок, лишь в частных случаях эквивалентна одному-вектору. [15]
Страницы: 1 2 3 4
Свободные, скользящие и фиксированные векторы
Вектор — понятие, определяемое в разных разделах математики различно.
Содержание
|
1
Сложение векторовОпределения
Алгебраический подход
В
где —
это базис, а — координаты
вектора в
заданном базисе.
Геометрический подход
Понятие вектор в геометрии отлично от определяемого в алгебре. Различают понятие свободного и связанного (приложенного, закреплённого) вектора.
При этом два направленных отрезка считаются эквивалентными, если они:
коллинеарны
равны по длине
одинаково направлены (сонаправлены)
Существует естественный изоморфизм свободных векторов и параллельных переносов пространства (каждый перенос взаимно однозначно соответствует какому-то свободному вектору). На этом также строят геометрическое определение свободного вектора, просто отождествляя его с соответственным переносом.
Большую роль играют векторы в изучении бесконечно малых трансформаций пространства.
Иногда
вместо того, чтобы рассматривать в
качестве векторов множество всех равных направленных отрезков, берут
только некоторую модификацию этого
множества (фактормножество).
Так, говорят о «свободных» (когда
отождествляются все равные по длине и
направлению направленные отрезки,
считаясь полностью равными или одним
и тем же вектором), «скользящих»
(отождествляются между собой все
направленные отрезки, равные в смысле
свободных векторов, начала и концы
которых расположены на одной прямой) и
«фиксированных» векторах (по сути дела,
просто о направленных отрезках, когда
разное начало означает уже неравенство
векторов).
Определение. Говорят, что свободные векторы и равны, если найдутся точки E и F такие, что четырёхугольники ABFE и CDFE — параллелограммы.
Замечание. «Ухищрение» (введение дополнительных точек) в определении равенства касается, прежде всего, случая, когда точки A,B,C,D располагаются на одной прямой. В противном случае определение выглядит проще:
Определение. Говорят, что свободные векторы и , не лежащие на одной прямой, равны, если четырёхугольник
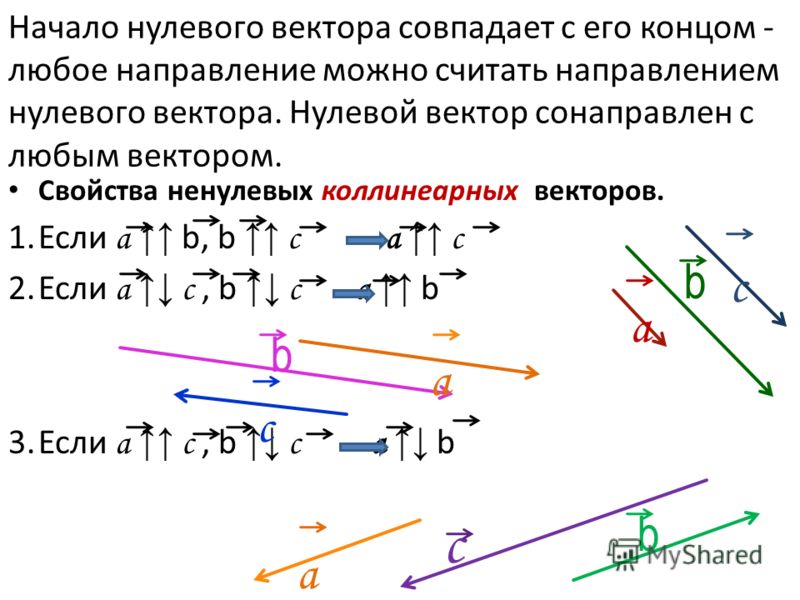
Определение. Говорят, что скользящие векторы и равны, если
точки A,B,C,D располагаются на одной прямой,
векторы и равны между собой как свободные векторы.
Неформально говоря, скользящему вектору разрешено двигаться вдоль его прямой без изменения величины и направления.
Замечание. Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила. Перенос такого начала вектора вдоль прямой, на которой он лежит, не меняет момента силы ни относительно никакой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (скорее даже почти всегда вызовет): поэтому нельзя рассматривать силу как свободный вектор.
Определение.
Говорят, что фиксированные векторы
и
равны,
если попарно совпадают точки A и C, B и D.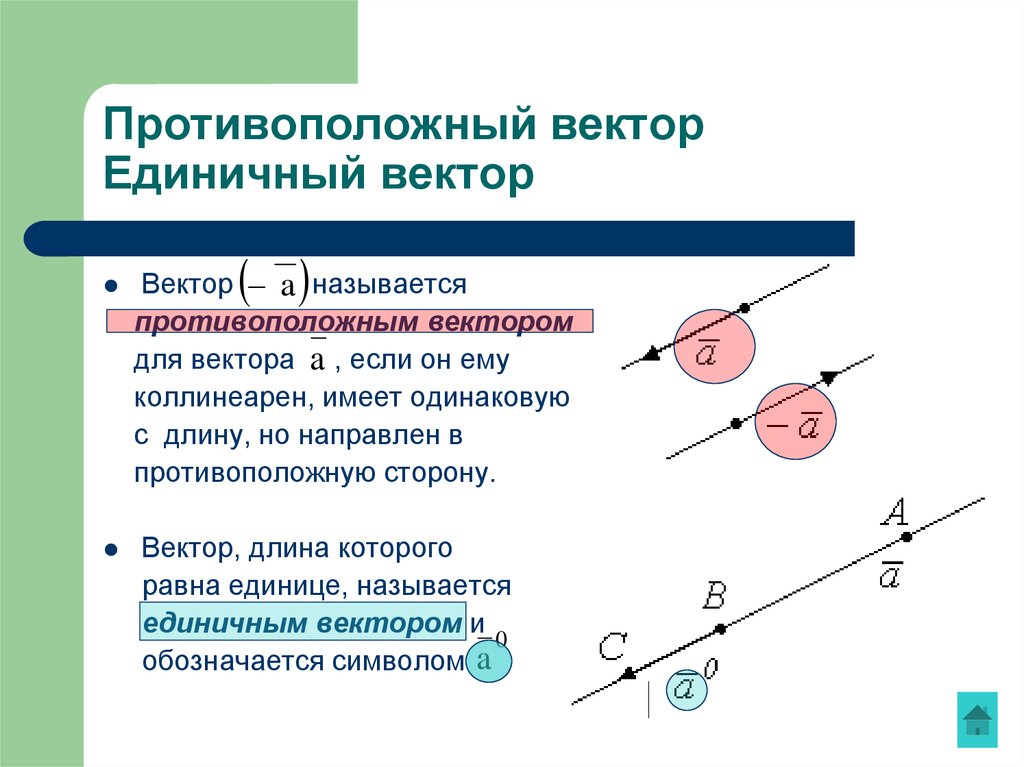
Вектором в простейшем случае называется
направленный отрезок, а в других случаях
различные векторы — это разные
Вектор — упорядоченная
пара чисел (последовательность, кортеж)
однородных элементов. Это наиболее
общее определение в том смысле, что
может быть не задано обычных векторных
операций вообще, их может быть меньше,
или они могут не удовлетворять обычным аксиомам линейного
пространства.
Именно в таком виде вектор понимается
в программировании,
где, как правило, обозначается
именем-идентификатором с квадратными скобками (например, object[]).
Перечень свойств моделирует принятое
в теории
систем определение класса и состояния объекта. Так типы элементов вектора
определяют класс объекта, а значения
элементов — его состояние. Впрочем,
вероятно, это употребление термина уже
выходит за рамки обычно принятого в
алгебре, да и в математике вообще.
Многие математические объекты (например матрицы, тензоры, функции и т. д.), в том числе обладающие структурой более общей, чем счётный или конечный упорядоченный список, удовлетворяют аксиомам векторного пространства, то есть являются с точки зрения алгебры векторами.
Скользящий вектор
Скользящий вектор объясняет действие вектора на твердое тело. Вектор называется скользящим вектором, когда он заменяется любым другим вектором, имеющим то же направление и ту же величину. Передаваемость сил: «Если силу, действующую в точке на твердое тело, перенести в любую другую точку, лежащую на линии действия силы, то внешнее действие силы на тело останется неизменным».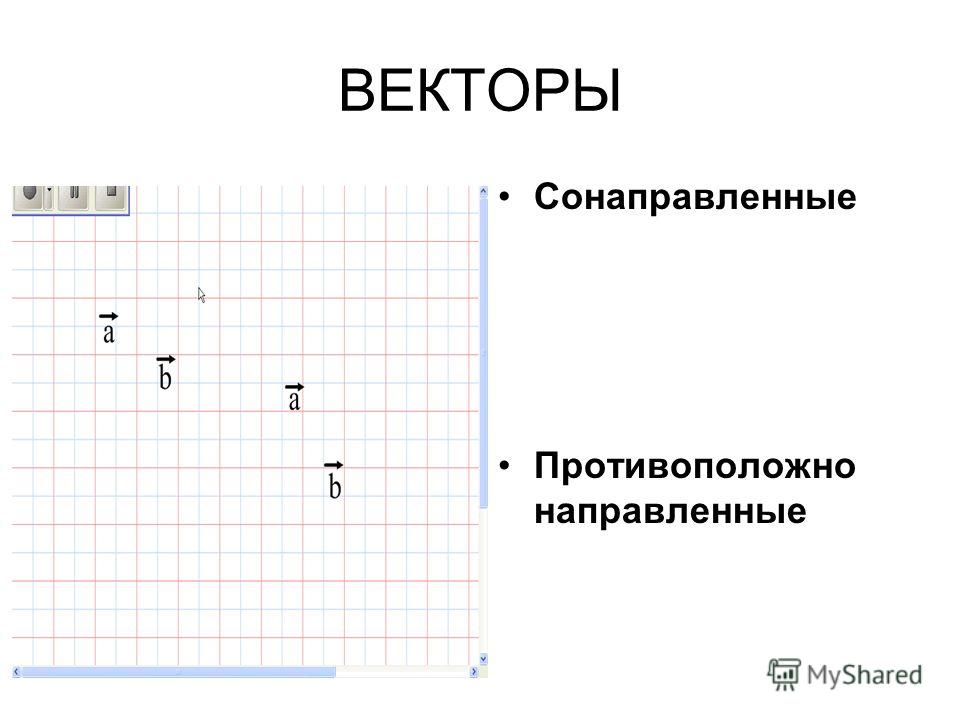
Это означает, что движение и равновесие твердого тела должны получить соответствующее возмущение. Только в этом случае вектор называется скользящим вектором.
По данному рисунку легко понять, на каком твердом теле A действие вектора F’ заменяет ту же величину F. Согласно этому принципу, а также согласно определению скользящего действия, F смещается из точки O1 к О2.
Полная линия действия на твердом теле является единственной линией действия. Таким образом, любой может легко получить решение скользящего вектора, правильно поняв факт или теорию. Также важно понимать, что линия действий проходит в разных точках.
Ссылки предыдущей основной темы: —
- Введение в статику
- Идеализация механики
- Законы механики
- Закон параллелограмма
- Виды сил
- Копланарно-коллинеарно
- Копланарно-параллельный
- Компланарные параллельные силы
- Копланарные непараллельные и непараллельные
Ссылки на следующие темы машиностроения: —
- Фиксированный вектор
- Закон треугольника сил
- Теорема Ламиса
Trustpilot
Наш рейтинг Отлично
4.
1 из 5 на основании 39 отзывов рассказать о нашей службе помощи с домашними заданиями.
общий рейтинг
в LiveChat
подробнее
пользователей
рекомендовать сервис
подробнее
Как это работает
1. Рассчитать стоимость.
1. Получить оценку стоимости.
Отправить.
Пришлите нам домашнее задание. Укажите крайний срок и загрузите соответствующие файлы.
2. Безопасная оплата.
2. Безопасная оплата.
Оплата.
Мы принимаем все основные кредитные карты. Также принимаются частичные платежи.
3. Получить решения.
3. Получить решения.
Доставлено
Получайте безошибочные пошаговые решения по электронной почте.
Часто задаваемые вопросы
Зачем использовать Myhomeworkhelp?
Мы предоставляем вам помощь в выполнении домашних заданий от лучших опытных экспертов. Ваше удовлетворение является приоритетом для нас.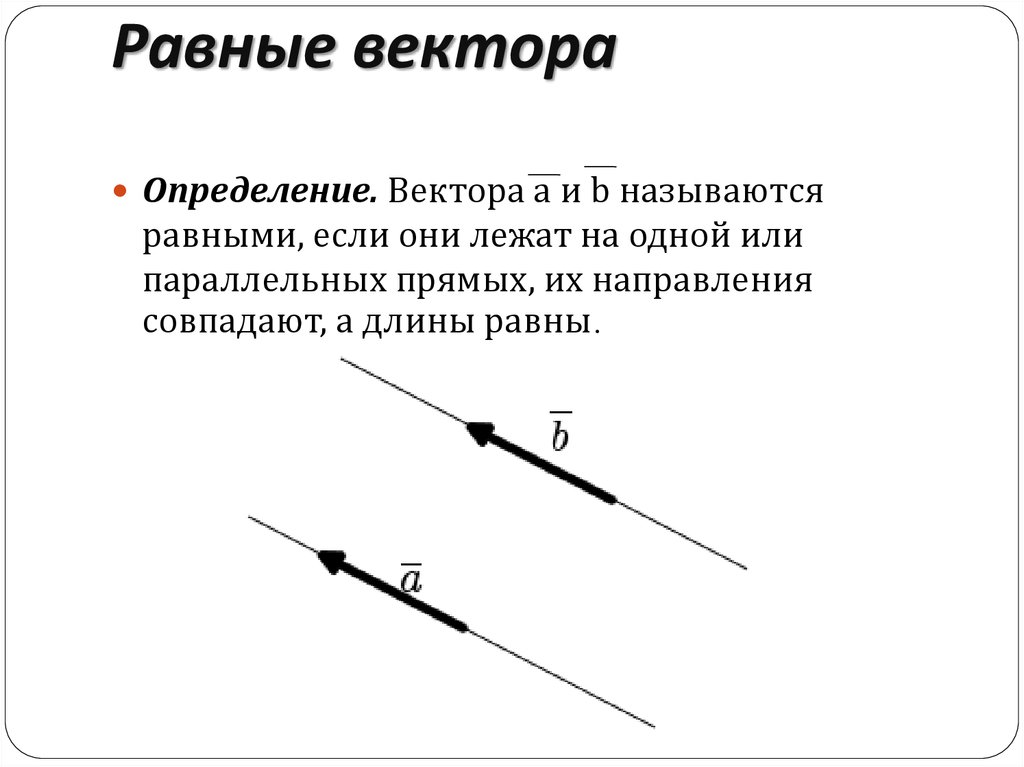
Получите лучшие оценки или верните деньги . Вот это без риска! Кроме того, все о вас хранится конфиденциально .
Как быстро вы поможете мне с домашним заданием?
Мы гордимся тем, что круглосуточно и без выходных оказываем помощь в выполнении домашних заданий. Это означает, что студент может обратиться к нам в любое время, чтобы получить помощь даже в короткие сроки. Всего несколько часов! И да, мы предоставляем дополнительный отчет без плагиата.
Сколько это будет стоить?
У нас нет ежемесячной платы или минимальных платежей. Каждое домашнее задание имеет уникальную цену. Он основан на оценке наставником времени, которое потребуется им для выполнения вашего задания. Никаких обязательств, и вы можете обсудить ценовое предложение с репетитором.
Мы принимаем частичную оплату (в соответствии с нашей политикой), чтобы начать работу над вашей помощью по заданию. Вы можете оплатить оставшуюся сумму, когда ваша задача будет выполнена.
Нет давления авансового платежа. Никаких скрытых затрат.
Кто ваши наставники?
Все наши специалисты являются высококвалифицированными специалистами, имеющими как минимум степень магистра в соответствующих областях знаний. Мы очень избирательны и выбираем только самых квалифицированных преподавателей по каждому учебному предмету. Все соискатели репетиторов должны предоставить академические справки для каждой степени, которую они имеют, и тщательно проверяются и проверяются нашими сотрудниками.
У меня проблемы с конфиденциальностью. Могу я доверять тебе?
Myhomeworkhelp выполнил более 250 000 домашних заданий за последние 12 лет. Но не верьте нам на слово! Смотрите наши здесь и на Trustpilot. Кроме того, все о вас сохраняется конфиденциально . Информация о вашей кредитной карте нигде не хранится, и использование PayPal зависит от их безопасных платежных сетей. Ваша личность, оплата и помощь с выполнением домашних заданий в надежных руках.
Посмотрите наше видео
Наши обзоры
Общайтесь с нами с помощью LiveChat- →
Статья о скольжении+вектор от The Free Dictionary
Скольжение+вектор | Статья о скольжении+векторе от The Free DictionaryРаздвижные+вектор | Статья о скольжении+векторе от The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.
Возможно, Вы имели в виду:
Пожалуйста, попробуйте слова отдельно:
скользящий вектор
Некоторые статьи, соответствующие вашему запросу:
Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.