Законы Кирхгофа — презентация онлайн

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

1. Законы Кирхгофа

Урок 1

2. Цель обучения

• 10.4.2.6 — применять законы Кирхгофа к
разветвленным электрическим цепям

3. Цели урока

—
изучить первый закон Кирхгофа;
—
изучить второй закон Кирхгофа;
— изучить универсальный метод расчета
сложных цепей.

4. Повторение изученного материала

• 1.
Что называется электрическим током?
• 2.
Что такое сила тока?
• 3.
Какова единица измерения силы тока?
• 4.
Что такое напряжение?
• 5.
Какова единица измерения напряжения?
• 6.
Что такое электрическое сопротивление?
• 7. От
чего
сопротивление?
зависит
электрическое
• 8.
Сформулируйте закон Ома для участка цепи
• 9.
Какая цепь называется полной?
• 10. Что такое ЭДС источника?
• 11. Сформулируем закон Ома для полной цепи.
• 12. Как
определить
сопротивлению
при
соединении?
эквивалентное
последовательном

7. Сложная цепь

• Узел – место соединения 3-х и более
проводников.
• Ветвь – участок цепи, на котором сила тока
постоянна.
• Контур – любой замкнутый путь по
ветвям.

8. Сложная цепь

1) Сколько узлов в цепи?
2) Обозначьте узлы буквами латинского
назовите их
3) Сколько ветвей в цепи?
4) Перечислите независимые контуры.
алфавита
и

9. Формулировка I закона Кирхгофа

• Алгебраическая сумма токов в каждом
узле любой цепи равна нулю. При этом
направленный к узлу ток принято считать
положительным, а направленный от узла
— отрицательным.
n
I
i 1
i
0

10. Формулировка II закона Кирхгофа

• Алгебраическая сумма падений
напряжений на всех ветвях,
принадлежащих любому замкнутому
контуру цепи, равна алгебраической
сумме ЭДС ветвей этого контура.
n
n
U E
i 1
i
i 1
i

11. Сложная цепь

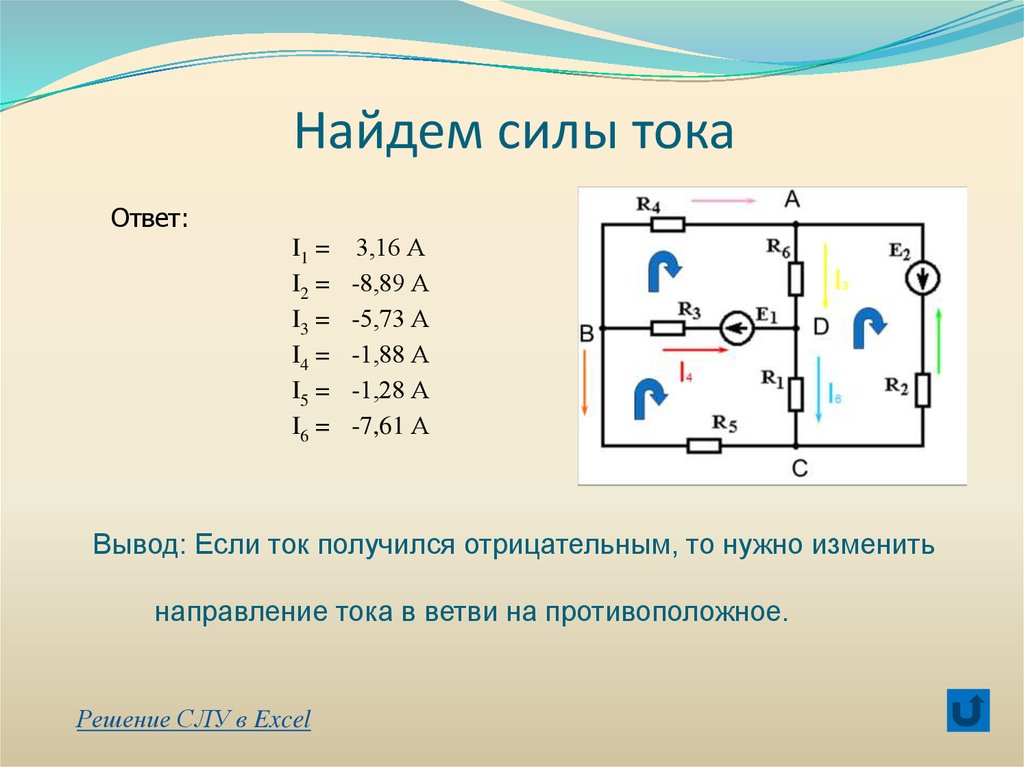
12. Решение задачи

13. Определить токи во всех ветвях данной электрической цепи

14. Найдем общее количество уравнений

• Для определения токов во всех ветвях
данной электрической цепи,
необходимо составить систему
уравнений по законам Кирхгофа.
• Общее число уравнений в системе должно
соответствовать числу неизвестных
токов, т. е. числу ветвей.

15. Посчитаем количество ветвей в нашей электрической цепи

R1
Итого
5 ветвей, т.е.
5 уравнений
R2
I2
I4
Е1
R4
Е2
R5
I5
I1
R3
I3
Е3

16.

Найдем количество уравнений по I закону Кирхгофа• По первому закону Кирхгофа составляется
число уравнений, на единицу меньшее
числа узлов цепи, т.к. уравнение для
последнего узла есть следствие всех
предыдущих уравнений и не дает
ничего нового для расчета.

17. Посчитаем количество узлов электрической цепи

2
R1
Итого
3 узла, т.е.
2 уравнения
R2
I2
I4
Е1
R4
Е2
R5
I5
I1
R3
1
I3
Е3
3

18. Зададим направление токов во всех ветвях цепи

2
R1
R2
I2
I4
Е1
R4
Е2
R5
I5
I1
R3
1
I3
Е3
3

19. Составим уравнения по I закону Кирхгофа

• Токи, подходящие к узлу, будем считать
положительными и брать со знаком (+),
а токи, отходящие от узла – (–).
2
R1
R2
I2
I4
Е1
R4
Е2
R5
I5
I1
R3
1
I3
Е3
Для узла № 1: –I1 – I3 – I4 = 0
Для узла № 2: I1 – I2 + I4 + I5 = 0
3

21.

Найдем количество уравнений по II закону Кирхгофа• По второму закону Кирхгофа
составляются все недостающие
уравнения для любых произвольно
выбранных контуров цепи.
• Посчитаем количество недостающих
уравнений: 5 – 2 = 3.

22. Зададим направление обхода выбранных контуров

2
R1
R2
I2
I
Е1
III
I4
R4
Е2
R5
II
I5
I1
R3
1
I3
Е3
3

23. Составим уравнения по II закону Кирхгофа

• При составлении уравнений ЭДС и
токи, совпадающие с выбранным
направлением обхода контура будем
брать со знаком (+), а несовпадающие –
со знаком (–).
2
R1
R2
I2
I
Е1
III
I4
R4
Е2
R5
II
I5
Е3
I1
R3
1
I3
3
Для I контура: I1R1 – I4R4 = Е1
Для II контура: I4R4 – I5R5 – I3R3 = Е3
Для III контура: I2R2 + I5R5 = –Е2

25. Получилась система уравнений

–I1 – I3 – I4 = 0
I1 – I2 + I4 + I5 = 0
I1R1 – I4R4 = E1
I4R4 – I5R5 – I3R3 = E3
I2R2 + I4R4 = –E2
Решив ее, получаем пять значений
токов.

English     Русский Правила

Закон кирхгофа для электрической цепи для чайников

Законы Кирхгофа

Закон Ома устанавливает зависимость между силой тока, напряжением и сопротивлением для простейшей электрической цепи, представляющей собой один замкнутый контур. В практике встречаются более сложные (разветвленные) электрические цепи, в которых имеются несколько замкнутых контуров и несколько узлов, к которым сходятся токи, проходящие по отдельным ветвям. Значе­ния токов и напряжений для таких цепей можно находить при помощи законов Кирхгофа.

Законы Кирхгофа для магнитной цепи

Магнитная цепь (МЦ), как электрическая (ЭЦ), может быть рассчитана по данным правилам. По аналогии цепей можно выделить следующую связь:

• магнитный поток – электрический ток;
• МДС (магнитодвижущая сила) – ЭДС.

Общее сопротивление

Первое правило для МЦ – магнитные потоки в узлах в алгебраической сумме дают ноль (ΣΦк= 0). Оно основано на физическом принципе непрерывности Φ.

Второе правило говорит о том, что падения магнитного напряжения (напряжённости) Uм в сомкнутом контуре в алгебраической сумме равны сумме МДС этого контура:

ΣUм = ΣI*ω, где:

• I – ток, проходящий по проводнику;
• ω – количество витков в обмотке.

Второй закон Кирхгофа – это по-другому записанная форма закона полного тока.

Внимание! Для магнитных цепей алгоритм составления уравнений тот же самый, как и для ЭЦ. Правила знаков действуют аналогично.

Первый закон

Первый закон Кирхгофа устанавливает зависимость между то­ками для узлов электрической цепи, к которым подходит несколько ветвей. Согласно этому закону алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:

?I = 0 (16)

При этом токи, направленные к узлу, берут с одним знаком (например, положительным), а токи, направленные от узла,— с противоположным знаком (отрицательным). Например, для узла А

I1 + I2 + I3 – I4 – I5 = 0 (17)

Это интересно! Все о полупроводниковых диодах.

Преобразуя это уравнение, получим, что сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла:

I1 + I2 + I3 = I4 + I5 (17′)

В данном случае имеет место полная аналогия с распределением потоков воды в соединенных друг с другом трубопроводах.

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.

Первый закон Кирхгофа.

Второй закон Кирхгофа устанавливает зависимость между э. д. с. и напряжением в замкнутой электрической цепи. Согласно этому закону во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур:

?E = ?IR (18)

При составлении формул, характеризующих второй закон Кирхгофа, значения э. д. с. E и падений напряжений IR считают положительными, если направления э. д. с. и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления э. д. с. и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие э. д. с. и падения напряжения считают отрицательными.

Рассмотрим в качестве примера электрическую цепь, в которой имеются два источника с электродвижущими силами E1 и E2, внутренними сопротивлениями Ro1, Ro2 и два приемника с сопротивлениями R1 и R2. Применяя второй закон Кирхгофа для «этой цепи и выбирая направление ее обхода по часовой стрелке,

Будет интересно➡ Чему равна электроемкость конденсатора?

получим:

E1 – E2 = IR01 + IR02 + IR1 + IR.

При этом э.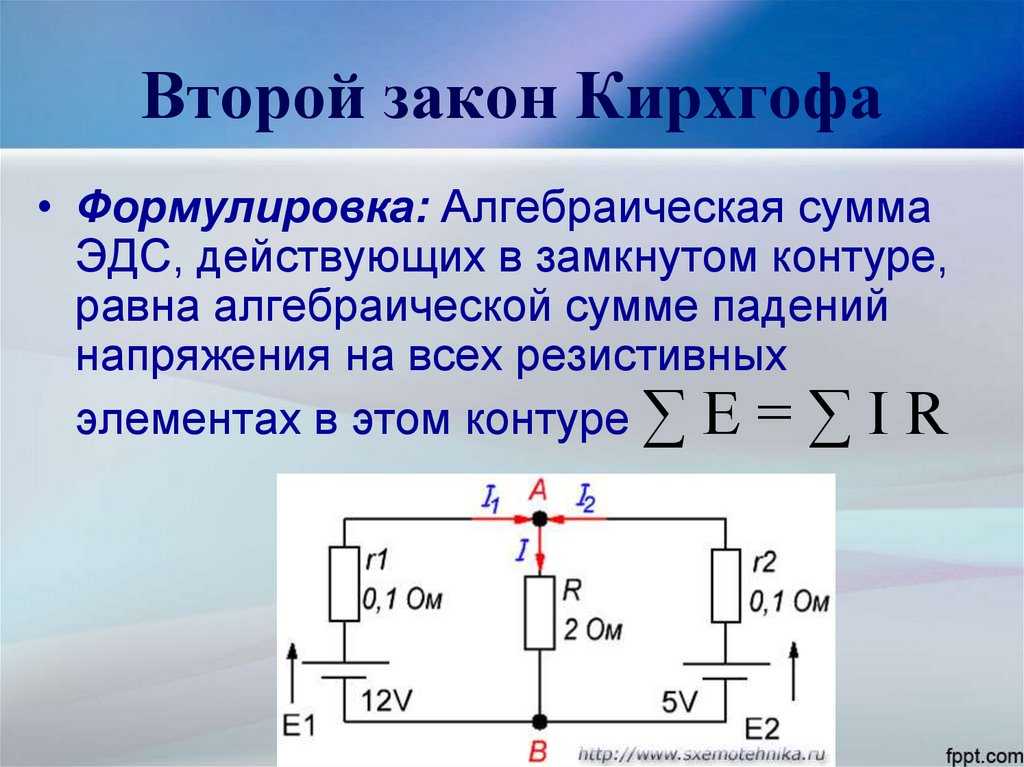 д. с. E1 и ток I совпадают с выбранным направлением обхода контура и считаются положительными, а э. д. с. Е2, противоположная этому направлению, считается отрицательной. Если в электрической цепи э. д. с. источников электрической энергии при обходе соответствующего контура направлены навстречу друг другу (см. рис. 24, а), то такое включение называют встречным. В этом случае на основании второго закона Кирхгофа ток I = (E1-E2)/(R1+R2+R01+R02).

Встречное направление э. д. с. имеет место, например, на э. п. с.при включении электродвигателей постоянного тока (их можно рассматривать как некоторые источники э. д. с.) в две параллельные группы, а также при параллельном включении аккумуляторов в батарее.

Если же э. д. с. источников электрической энергии имеют по контуру одинаковое направление (рис. 24, б), то такое включение называют согласным и ток I = (E1-E2)/(R1+R2+R01+R02). В некоторых случаях такое включение недопустимо, так как ток в цепи резко возрастает.

Если в электрической цепи имеются ответвления (рис. 24, в), то по отдельным ее участкам проходят различные токи I1 и I2. Согласно второму закону Кирхгофа E1-E2=I1R01+I1R1-I2R2-I2R02-I2R3+I1R4.

При составлении этого уравнения э. д. с. Е1 и ток I1 считаются положительными, так как совпадают с принятым направлением обхода контура, э. д. с. Е2 и ток I2 — отрицательными.

Второй закон Кирхгофа — практическое применение

На практике второй закон Кирхгофа применяется успешно для расчета электрических цепей. Благодаря его разъяснению можно рассчитать необходимые параметры в сложных электрических цепях. Когда присутствует необходимость рассчитать значение тока и/или направление всегда выручит второй закон Кирхгофа. Невзирая на то, что правила Кирхгофа были сформулированы в далеком 1845 году, они показали себя как рабочие и не вызывают вопросы ни у кого. Теория электрических цепей была бы неполной без наличия этих законов, которые так хорошо подходят для решения различных уравнений в этой области.

Если материал был полезен, вы можете
отправить донат или поделиться данным материалом в социальных сетях:

Второй закон

Для расчетов сложных электрических цепей с несколькими источниками энергии используют второй закон Кирхгофа, который может быть сформулирован так: во всяком замкнутом электрическом контуре алгебраическая сумма всех э. д. с. равна алгебраической сумме падений напряжения в сопротивлениях, включенных последовательно в эту цепь, т. е.

E1 + E2 + E3 + . . . = I1r1 + I2r2 + I3r3 + . . .

Будет интересно➡ Как устроен трехфазный выпрямитель

При этом положительными следует считать э. д. с. и токи, направление которых совпадает с направлением обхода контура. Если в электрическую цепь включены два источника энергии, э. д. с. которых совпадает по направлению (рис. 20, а), то э. д. с. всей цепи равна сумме э. д. с. этих источников, т. е. E = E1 + E2. Если же в цепи э. д. с. источников имеют противоположные направления, то результирующая э. д. с. равна разности э. д. с. этих источников, т. е.

E = E1 – E2.

Второй закон Кирхгофа.

При последовательном включении в электрическую цепь нескольких источников энергии с различным направлением э. д. с. общая э. д. с. равна алгебраической сумме э. д. с. всех источников. При суммировании э. д. с. одного направления берут со знаком плюс, а э. д. с. противоположного направления — со знаком минус. При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.

Замкнутая цепь обозначена буквами а, б, в и г. Ввиду наличия ответвлений в точках а, б, в, г токи I1, I2, I3 и I4, отличаясь по силе, могут иметь различные направления. Для такой цепи в соответствии со вторым законом Кирхгофа можно написать:

E1 – E2 – E3 = I1(r01 + r1) – I2(r02 + r2) – I3(r03 + r3) + I4r4,

где r01, r02, r03 — внутренние сопротивления источников энергии, r1, r2, r3, r4 — сопротивления приемников энергии. В частном случае при отсутствии ответвлений и последовательном соединении проводников общее сопротивление равно сумме всех сопротивлений. Если внешняя цепь источника энергии с внутренним сопротивлением r состоит, например, из трех последовательно соединенных проводников с сопротивлениями, соответственно равными r1, r2, r3, то на основании второго закона Кирхгофа можно написать следующее равенство:

E = I r + I r1 + I r2 + I r3.

При нескольких источниках тока в левой части этого равенства была бы алгебраическая сумма э. д. с. этих источников.

Второй закон Кирхгофа и его определение

В едином замкнутом контуре алгебраическая сумма ЭДС будет равняться на значение, которое суммирует изменения напряжения на всеобщее количество резистивных элементов данного контура.

Второе правило Кирхгофа актуально в сетях с постоянным и/или переменным током. В формулировке закона используется именно понятие алгебраическая сумма, так как она может быть указана со знаком плюс или минус. Точное определение возможно в таком случае только посредством простого, но эффективного алгоритма. Для начала надо подобрать какое-то направление для обхода контура, по/против часовой стрелке, на собственное усмотрение. Само направление тока подбирается только через элементы цепи. После следует определить знаки «+» и «-» для напряжениях и ЭДС. Напряжения нужно записывать с отрицательным знаком, когда ток не соответствует обходу контура в плане направления и с плюсом в случае совпадения. То же самое правило нужно использовать и в том случае, когда необходимо отметить ЭДС.

Закон кирхгофа расчет цепи

МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА

Метод эквивалентного генератора рационально применять в том случае, когда требуется определить ток (или найти его аналитическое выражение) лишь в одной ветви цепи, без нахождения токов в остальных ветвях.

В основе метода лежит замена части цепи, подключенной к зажимам заданной ветви, эквивалентным источником и определение параметров этого источника. В зависимости от выбора вида эквивалентного источника различают метод эквивалентного генератора напряжения (источник ЭДС) или эквивалентного генератора тока (источник тока).

Расчёт методом эквивалентного генератора напряжения заключается в определении ЭДС и внутреннего сопротивления эквивалентного источника и состоит в следующем.

Что такое правило напряжений Кирхгофа (второй закон Кирхгофа)?

Принцип, известный как правило напряжений Кирхгофа (открытое в 1847 году немецким физиком Густавом Р. Кирхгофом), можно сформулировать следующим образом:

«Алгебраическая сумма всех напряжений в замкнутом контуре равна нулю»

Под алгебраической я подразумеваю, помимо учета величин, учет и знаков (полярностей). Под контуром я подразумеваю любой путь, прослеживаемый от одной точки в цепи до других точек в этой цепи, и, наконец, обратно в исходную точку.

Закон кирхгофа расчет цепи онлайн

То есть сколько току вытекло в качестве тока I3 в точке А, столько его и вернулось к нам в точке B в виде тока I4. Высшая справедливость всё-таки восторжествовала. А помогло нам при этом здравое рассуждение, о том, что в любой точке цепи, где электрическая сеть разветвляется, общее количество тока, вытекающего из узла, то есть этой точки, равно количеству тока, втекающего в этот узел. Поэтому смело рисуем схему, зная, что нам помог уже первый, а не второй закон Кирхгофа:

Почему-то оказалось, что токи I3 и I4 оказались точно равными -I1, и значит… наши лампочки загорелись полным накалом.

Ох уж эти выдумки инопланетянские! С нашей стороны осталось только в схеме поставить стрелочки токов (и ЭДС у источника ЭДС Eин) в противоположное направление.

Закон кирхгофа расчеты параметров цепей постоянного тока

для всех ветвей (кроме ветвей с источниками тока) произвольно задать направления протекания токов;

для всех узлов, кроме одного, выбранного произвольно, составить уравнения по первому закону Кирхгофа;

произвольно выбрать на схеме электрической цепи замкнутые контуры таким образом, чтобы они отличались друг от друга по крайней мере одной ветвью и чтобы все ветви, кроме ветвей с источниками тока, входили по крайней мере в один контур;

произвольно выбрать для каждого контура направление обхода и составить уравнения по второму закону Кирхгофа, включая в правую часть уравнения ЭДС действующие в контуре, а в левую падения напряжения на резисторах.

21.3 Правила Кирхгофа – Колледж физики, главы 1-17

21 Цепи и приборы постоянного тока

Резюме

• Проанализируйте сложную схему, используя правила Кирхгофа, используя соглашения для определения правильных знаков различных термов.

Многие сложные схемы, такие как схема на рис. 1, не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в главе 21.1 Резисторы в последовательном и параллельном соединении и главе 21.2 Электродвижущая сила: напряжение на клеммах. Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Правила известны как Правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).

Рисунок 1. Эту схему нельзя свести к комбинации последовательного и параллельного соединений. Для его анализа можно использовать правила Кирхгофа, специальные приложения законов сохранения заряда и энергии. (Примечание: буква Е на рисунке обозначает электродвижущую силу, ЭДС.)

Правила Кирхгофа

• Первое правило Кирхгофа — правило пересечения. Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
• Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любой замкнутой цепи (петли) должна быть равна нулю.

Теперь будут даны объяснения двух правил, за которыми следуют советы по решению проблем для применения правил Кирхгофа и рабочий пример, который их использует.

Первое правило Кирхгофа (правило соединения ) представляет собой применение закона сохранения заряда к соединению; это показано на рис. 2. Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу. Первое правило Кирхгофа требует, чтобы [латекс]\boldsymbol{I_1 = I_2 + I_3}[/латекс] (см. рисунок). Подобные уравнения могут и будут использоваться для анализа схем и решения схемных задач.

Установление соединений: законы сохранения

Правила Кирхгофа для анализа цепей представляют собой применение

законов сохранения к цепям. Первое правило — применение закона сохранения заряда, а второе правило — применение закона сохранения энергии. Законы сохранения, даже используемые в конкретных приложениях, таких как анализ цепей, настолько просты, что составляют основу этого приложения.

Рисунок 2. Правило соединения. На диаграмме показан пример первого правила Кирхгофа, где сумма токов, поступающих в соединение, равна сумме токов, выходящих из соединения. В этом случае ток, входящий в переход, разделяется и выходит в виде двух токов, так что I ₁ = I ₂ + I ₃ . Здесь I ₁ должно быть 11 А, так как I ₂ равно 7 А, а I ₃ 4 равно 9 А.

Второе правило Кирхгофа ( петлевое правило ) является применением закона сохранения энергии. Правило цикла сформулировано с точки зрения потенциала, [латекс]\boldsymbol{V}[/латекс], а не потенциальной энергии, но они связаны, поскольку [латекс]\boldsymbol{\textbf{PE}_{\textbf{ elec}} = qV}[/latex]. Напомним, что ЭДС — это разность потенциалов источника при отсутствии тока. В замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. На рис. 3 показаны изменения потенциала в простой последовательной цепи.

Второе правило Кирхгофа требует [латекс]\жирныйсимвол{\текстбф{ЭДС} — Ir — IR_1 — IR_2 = 0}[/латекс]. В перестановке это [латекс]\boldsymbol{\textbf{ЭДС} = Ir + IR_1 + IR_2}[/latex], что означает, что ЭДС равна сумме [латекс]\boldsymbol{IR}[/латекс] (напряжение ) попадает в петлю.

Рисунок 3. Правило цикла. Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) На этой стандартной схеме простой последовательной цепи ЭДС подает напряжение 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, для всего 18 В.

(b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и снижается за счет сопротивления. (Обратите внимание, что буква E означает emf.)

Применяя правила Кирхгофа, мы получаем уравнения, позволяющие находить неизвестные в цепях. Неизвестными могут быть токи, ЭДС или сопротивления. Каждый раз, когда применяется правило, создается уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема. При применении правил Кирхгофа вы должны принять два решения. Эти решения определяют знаки различных величин в уравнениях, которые вы получаете, применяя правила.

1. Применяя первое правило Кирхгофа, правило соединения, вы должны пометить ток в каждой ветви и решить, в каком направлении он течет. Например, на рис. 1, рис. 2 и рис. 3 токи помечены [латекс]\boldsymbol{I_1}[/латекс], [латекс]\boldsymbol{I_2}[/латекс], [латекс]\boldsymbol{I_3 }[/latex] и [latex]\boldsymbol{I}[/latex], а стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным.
2. Применяя второе правило Кирхгофа, правило петли, вы должны определить замкнутую петлю и решить, в каком направлении ее обойти, по часовой или против часовой стрелки. Например, на рис. 3 петля была пройдена в том же направлении, что и ток (по часовой стрелке). Опять же, нет никакого риска; Обход цепи в противоположном направлении меняет знак каждого члена в уравнении, что похоже на умножение обеих частей уравнения на -1.

Рисунок 4 и следующие пункты помогут вам правильно расставить знаки «плюс» или «минус» при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b. Во многих схемах будет необходимо построить более одного контура. При обходе каждой петли необходимо следить за знаком изменения потенциала. (См. пример 1.)

Рисунок 4. Каждый из этих резисторов и источников напряжения проходит от a до b. Возможные изменения показаны под каждым элементом и пояснены в тексте. (Обратите внимание, что буква E означает ЭДС.)

• Когда резистор перемещается в том же направлении, что и ток, изменение потенциала составляет [латекс]\жирный символ{-IR}[/латекс]. (См. рис. 4.)
• Когда резистор перемещается в направлении, противоположном току, изменение потенциала составляет [латекс]\boldsymbol{+IR}[/латекс]. (См. рис. 4.)
• Когда ЭДС перемещается от – к + (в том же направлении, что и положительный заряд), изменение потенциала составляет +ЭДС. (См. рис. 4.)
• Когда ЭДС перемещается от + к – (противоположно направлению движения положительного заряда), изменение потенциала равно −ЭДС. (См. рис. 4.)

Пример 1. Расчет тока: использование правил Кирхгофа

Найдите токи, протекающие в цепи на рисунке 5.

Рисунок 5. Эта цепь аналогична схеме на рисунке 1, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.

Стратегия

Эта схема настолько сложна, что токи нельзя найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. На рисунке токи обозначены как [латекс]\boldsymbol{I_1}[/latex], [латекс]\boldsymbol{I_2}[/latex] и [латекс]\boldsymbol{I_3}[/latex]. сделал о своих направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.

Решение

Начнем с применения первого правила Кирхгофа или правила соединения в точке а. Это дает

[латекс]\boldsymbol{I_1 = I_2 + I_3} ,[/latex]

, так как [латекс]\boldsymbol{I_1}[/latex] впадает в соединение, а [латекс]\boldsymbol{I_2} [/latex] и [latex]\boldsymbol{I_3}[/latex] вытекают наружу. Применение правила соединения в точке e дает точно такое же уравнение, так что никакой новой информации не получается.

Это одно уравнение с тремя неизвестными — нужны три независимых уравнения, поэтому необходимо применить правило цикла.

Теперь рассмотрим цикл abcdea. Переходя от a к b, мы пересекаем [латекс]\boldsymbol{R_2}[/латекс] в том же (предполагаемом) направлении, что и текущий [латекс]\boldsymbol{I_2}[/латекс], поэтому изменение потенциала равно [латекс]\boldsymbol{-I_2R_2}[/латекс]. Затем, переходя от b к c, мы переходим от – к +, так что изменение потенциала составляет [латекс]\boldsymbol{+ \textbf{emf}_1}[/латекс]. Перемещение внутреннего сопротивления [латекс]\boldsymbol{r_1}[/латекс] от c к d дает [латекс]\boldsymbol{-I_2r_1}[/латекс]. Завершение цикла путем перехода от d к a снова пересекает резистор в том же направлении, что и его ток, что дает изменение потенциала [latex]\boldsymbol{-I_1R_1}[/latex].

Правило цикла гласит, что сумма изменений потенциала равна нулю. Таким образом,

[латекс]\boldsymbol{-I_2R_2 + \textbf{emf}_1 — I_2r_1 — I_1R_1 = -I_2(R_2 + r_1) + \textbf{emf}_1 — I_1R_1 = 0}. [/latex]

Подстановка значений сопротивления и ЭДС из принципиальной схемы и отмена единиц измерения ампер дает

[latex]\boldsymbol{-3I_2 + 18 -6I_1 = 0}.[/latex]

Теперь применим правило цикла к aefgha ( мы могли бы выбрать и abcdefgha) аналогично дает

[латекс]\boldsymbol{+I_1R_1 + I_3R_3 + I_3r_2 — \textbf{emf}_2 = +I_1R_1 + I_3(R_3+r_2) — \textbf{emf}_2 = 0} .[/latex]

Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы проходятся в противоположном направлении. С введенными значениями это становится

[латекс]\boldsymbol{+6I_1 + 2I_3 — 45 = 0}.[/латекс]

Этих трех уравнений достаточно, чтобы решить для трех неизвестных токов. Сначала решим второе уравнение для [латекс]\boldsymbol{I_2}[/латекс]:

[латекс]\boldsymbol{I_2 = 6 — 2I_1}.[/latex]

Теперь решите третье уравнение для [латекс]\boldsymbol{I_3}[/латекс]:

[латекс]\boldsymbol{I_3 = 22.5 — 3I_1}.[/latex]

Подстановка этих двух новых уравнений в первое позволяет нам найти значение для [latex]\boldsymbol{I_1}[/latex]:

[latex]\boldsymbol{I_1 = I_2 + I_3 = (6 — 2I_1) + (22,5 — 3I_1) = 28,5 — 5I_1}. [/latex]

Объединение терминов дает

[latex]\boldsymbol{6I_1 = 28,5}[/latex] и

[латекс]\boldsymbol{I_1 = 4,75 \;\textbf{A}}.[/latex]

Подстановка этого значения вместо [латекс]\boldsymbol{I_1}[/латекс] обратно в четвертое уравнение дает

[латекс]\boldsymbol{I_2 = 6 — 2I_1 = 6 — 9,50}[/латекс]

[латекс]\boldsymbol{I_2 = -3,50 \;\textbf{A}}.[/latex]

Знак минус означает, что [латекс]\boldsymbol{I_2}[/латекс] течет в направлении, противоположном предполагаемому на рисунке 5.

Наконец, подстановка значения для [латекс]\жирныйсимвол{I_1}[/латекс] в пятое уравнение дает

[латекс]\boldsymbol{I_3 = 22,5 — 3I_1 = 22,5 — 14,25}[/latex]

[латекс]\boldsymbol{I_3 = 8,25 \;\textbf{A}}.[/latex]

Обсуждение

Просто для проверки отметим, что действительно [латекс]\boldsymbol{I_1 = I_2 + I_3}[/latex]. Результаты также можно проверить, введя все значения в уравнение для цикла abcdefgha.

Стратегии решения задач по правилам Кирхгофа

1. Убедитесь, что имеется четкая принципиальная схема, на которой вы можете отметить все известные и неизвестные сопротивления, ЭДС и токи. Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
2. Примените правило соединения к любому соединению в цепи. Каждый раз, когда применяется правило соединения, вы должны получать уравнение с током, которого не было в предыдущем приложении — если нет, то уравнение избыточно.
3. Примените правило цикла к такому количеству циклов, которое необходимо для поиска неизвестных в задаче. (Независимых уравнений должно быть столько же, сколько и неизвестных.) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 4.9.0010
4. Решите уравнения для неизвестных. Это может включать в себя множество алгебраических шагов, требующих тщательной проверки и перепроверки.
5. Проверьте, разумны ли и последовательны ли ответы. Числа должны быть правильного порядка, ни чрезмерно большими, ни исчезающе малыми. Признаки должны быть разумными — например, отсутствие сопротивления не должно быть отрицательным. Убедитесь, что полученные значения удовлетворяют различным уравнениям, полученным в результате применения правил. Например, токи должны удовлетворять правилу соединения.

Теоретически материал в этом разделе верен. Мы должны быть в состоянии проверить это, произведя измерения тока и напряжения. На самом деле, некоторые из устройств, используемых для проведения таких измерений, представляют собой прямое применение принципов, рассмотренных до сих пор, и рассматриваются в следующих модулях. Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину.

• Правила Кирхгофа можно использовать для анализа любой схемы, простой или сложной.
• Первое правило Кирхгофа — правило соединения: сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
• Второе правило Кирхгофа — правило петли: алгебраическая сумма изменений потенциала вокруг любого замкнутого контура (петли) должна быть равна нулю.
• Два правила основаны соответственно на законах сохранения заряда и энергии.
• При расчете потенциала и тока по правилам Кирхгофа необходимо соблюдать ряд правил для определения правильных знаков различных членов.
• Простые ряды и параллельные правила являются частными случаями правил Кирхгофа.

Правила Кирхгофа

набор из двух правил, основанных на сохранении заряда и энергии, регулирующих ток и изменения потенциала в электрической цепи

соединительная линейка

первое правило Кирхгофа, применяющее закон сохранения заряда к соединению; ток — это поток заряда; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу; правило может быть сформулировано [латекс]\boldsymbol{I_1 = I_2 + I_3}[/latex]

правило цикла

Второе правило Кирхгофа, которое гласит, что в замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. Таким образом, ЭДС равна сумме [latex]\boldsymbol{IR}[/latex] (напряжения) падений в контуре и может быть сформулирована следующим образом: [latex]\boldsymbol{\textbf{ЭДС} = Ir + IR_1 + IR_2 }[/латекс]

законы сохранения

требуют сохранения энергии и заряда в системе

 

законов Кирхгофа и их применение в проектировании печатных плат | Блог Advanced PCB Design

 

Законы созданы для того, чтобы их нарушать? Ну, это так, когда речь идет о воспитании детей. В детстве слова мамы – закон, и я уже не помню, сколько раз я их нарушал. Теперь я нахожусь на принимающей стороне, поскольку у меня есть сын, и я собираюсь отказаться от требований послушания.

Но законы существуют не просто так. Это помогает поддерживать порядок и обеспечивать мирное разрешение конфликтов. При проектировании печатной платы необходимо помнить о нескольких фундаментальных законах, поскольку они напрямую влияют на ваш подход к самому проектированию. Одним из таких законов является закон Кирхгофа, с которым должен быть знаком каждый выпускник электроники.

Что такое закон Кирхгофа?

Давайте совершим путешествие по закоулкам памяти и заново откроем для себя суть закона Кирхгофа. Вы хорошо помните, как ваш лектор утверждает, что закон Кирхгофа касается значений напряжения и силы тока в замкнутой цепи.

Чтобы быть точным, закон Кирхгофа состоит из двух частей: закона тока Кирхгофа и закона напряжения Кирхгофа.

Текущий закон Кирхгофа определяет, что сумма всех текущих входов и выходов из одного узла должна равняться нулю. Другими словами, закон указывает, как применяется сохранение зарядов в замкнутой цепи.

Между тем закон Кирхгофа о напряжении утверждает, что сумма напряжений в замкнутой цепи всегда будет равна нулю.

Оба закона Кирхгофа легли в основу проектирования схем и определили передовой опыт, обеспечивающий надежность и функциональность печатных плат.

Закон Кирхгофа и токовая петля 4–20 мА.

В большинстве коммерческих и бытовых электронных устройств вы привыкли к цифровым сигналам. Но при проектировании для промышленных приложений вы обнаружите, что сигнализация токовой петли, например 4–20 мА, является предпочтительным методом.

Преобразователи обычно используют токовую петлю 4–20 мА. Такие параметры, как воздушный поток, давление и скорость, передаются током, а не напряжением. Значения от 4 мА до 20 мА соответствуют фактическим показаниям. Эти датчики обычно размещаются далеко от принимающего контроллера, и входные значения имеют решающее значение для работы контроллера.

 

Промышленные датчики 4–20 мА основаны на законе тока Кирхгофа. Закон Кирхгофа о напряжении подразумевает, что падение напряжения следует ожидать по длине кабеля. Кроме того, электрические помехи могут быть связаны и влиять на достоверность показаний.

Токовая петля 4–20 мА использует закон Кирхгофа о токах, который гласит, что общий ток, входящий и выходящий из узла, должен быть равен. Это означает, что ток, генерируемый датчиком, не будет теряться при перемещении по кабелю. Теоретически значение, которое улавливает приемник, равно тому, что генерирует датчик.

Закон Кирхгофа и плотность тока.

Легко размышлять и руководствоваться законом Кирхгофа, когда это простое приложение, такое как токовая петля 4–20 мА. Но есть аспекты проектирования печатных плат, где закон Кирхгофа верен, но его часто упускают из виду.

И мы говорим о плотности тока.

Общеизвестно, что дорожки на печатных платах могут выдерживать ток только до нагревания. Чрезмерное тепло изнашивает медные дорожки или, в некоторых случаях, приводит к поломке дорожек. Токопроводящая способность дорожки печатной платы определяется шириной и толщиной меди.

У большинства проектировщиков печатных плат нет проблем с прямым подключением дорожек печатной платы к сильноточному компоненту. Но проблемы обычно возникают на дорожках, где объединено более одной сильноточной трассы.

 

Существует ограничение на то, какой ток может потреблять дорожка печатной платы.

 

Текущий закон Кирхгофа гласит, что общая сумма текущих входов и входов в узел должна равняться нулю. Этот закон означает, что дорожка печатной платы, по которой протекает комбинированный ток, должна иметь достаточно большую ширину, чтобы предотвратить накопление тепла.

Например, обратный путь, ведущий к GND, должен иметь правильные физические размеры, чтобы выдерживать пиковый ток. Неспособность обнаружить эти горячие точки плотности тока приведет к потенциальным проблемам при их развертывании.

Чтобы предотвратить это, вам нужно помнить о законе Кирхгофа и использовать расширенные функции программного обеспечения для проектирования печатных плат, которое вы используете для обнаружения дорожек с высокой плотностью тока. Вам понадобится что-то вроде PSpice Simulator OrCAD для точного моделирования текущих параметров.