Системы счисления
Тема «Системы счисления. Кодирование чисел.» рассматривается после того, как введены ключевые понятия: язык (естественный и формальный), алфавит, символ, код, кодирование, декодирование, двоичный код. Необходимость изучения этой темы в курсе информатики связана с тем фактом, что числа в памяти компьютера представлены в двоичной системе счисления, а для внешнего представления содержимого памяти, адресов памяти используют шестнадцатеричную или восьмеричную системы.
Существуют разные способы записи чисел (римские и арабские цифры, запись времени), римские цифры используются для обозначения столетий в учебниках истории, с помощью 10 арабских цифр можно обозначить любое количество предметов, т.е. записать любое число и т.п.
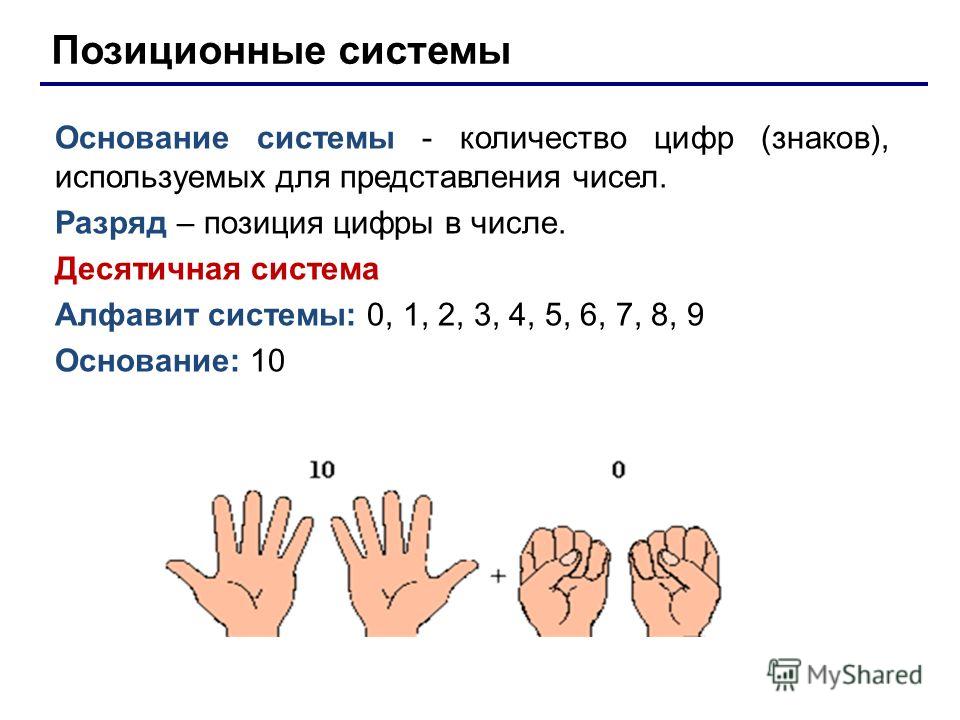
Значение, которое несет каждая цифра числа в привычном способе записи чисел, зависит не только от того, какая это цифра, но и от позиции, которую она занимает в числе.
Десятичная система счисления является позиционной.
1) Разложите по разрядам 5004, 10506, 3800
2) Найди общее и отличия в группах:
А) 800, 80, 8 Б) 800, 080, 008 В) 8/1, 8/10, 8/100
Рассмотрим обобщенную формулу записи числа:
Запись произвольного числа N в некоторой позиционной системе счисления основывается на представлении этого числа в виде многочлена:
где С – основание системы счисления.
Система
счисления — это определенный способ представления чисел и соответствующие ему
правила действия над числами.
Следует показать ученикам алфавиты различных позиционных систем счисления. Далее нужно научить учеников записывать натуральный ряд чисел в различных позиционных системах.
Одно важное замечание: ни в коем случае нельзя называть недесятичные числа так же, как десятичные. Например, нельзя называть восьмеричное число 238 как двадцать три. Надо говорить: «Два – три».
Примеры развернутых записей чисел в различных системах счисления:
1) 235,43210 = 2*102 + 3*101+ 5*100+ 4*10-1+3*10-2 +2*10-3
2) 235,4326 = 2*62 + 3*61+ 5*60+ 4*6-1+3*6-2
3) 235,4328 = 2*82 + 3*81+ 5*80+ 4*8-1+3*8-2 +2*8-3
Развернутая
форма служит для перевода чисел из любой системы счисления в десятичную.
Примеры перевода чисел из пятеричной и восьмеричной систем счисления в десятичную систему счисления:
1) 423,3125 = 4*52 + 2*51+ 3*50+ 3*5-1+1*5-2 +2*5-3
2) 423,3128 = 4*82 + 2*81+ 3*80+ 3*8-1+1*8-2 +2*8-3 = 275,00407410
Задания:
1. Запишите в развернутом виде числа:
1435110; 143518; 143516; 1435116; 143513
2. Запишите в десятичной системе числа:
8819 423,28 1203 100,34
 Суть его состоит в том, что развернутая запись числа преобразуется в
эквивалентную форму с вложенными скобками.
Суть его состоит в том, что развернутая запись числа преобразуется в
эквивалентную форму с вложенными скобками.Если число в b-ричной системе счисления равно
то для перевода в десятичную систему вычисляем такую сумму:
или, в более наглядном виде:
либо, наконец, в виде схемы Горнера:
17538 = (1×83 + 7×82 + 5×81 + 3)10 =((1×8 + 7) ×8 + 5) × 8 + 3.
Схема Горнера сводит вычисление таких выражений к минимальному числу операций.
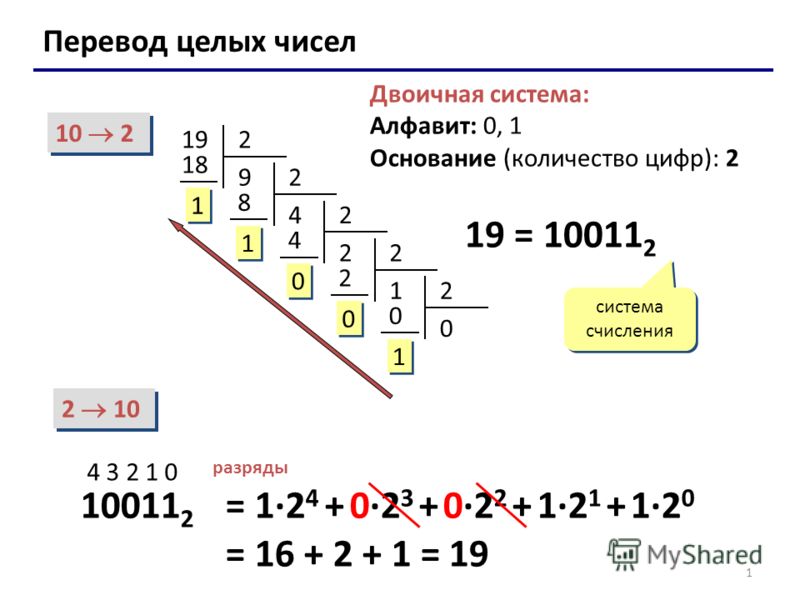
Перевод десятичных чисел в другие системы счисления — задача более сложная.
Алгоритм: чтобы перевести целую часть числа из
десятичной системы в систему счисления основанием С, нужно разделить ее на С, а остаток даст
младший разряд числа.
Задания:
1) Перевести из 10 системы счисления в двоичную, восьмеричную и шестнадцатеричную:
a. 155
b. 3205
c. 119
e. 170
f. 111
g. 273
h. 4096
2) Какое число предшествует числу 102 в двоичной системе счисления?
3) Какое из чисел в двоичном представлении содержит равное количество нулей и единиц (двоичное представление числа начинается с цифры «1»)?
4) Сколько единиц в двоичной записи числа 195?
5)
Переведите
число 0,0112 в десятичную систему счисления.
6) Переведите число 0, 75 в двоичную систему счисления.
7) Переведите число 0,3214 в двоичную систему счисления.
Ссылки на литературу и Интернет-ресурсы по теме:
1. http://ivan101.narod.ru/gos/timoi/
2. http://www.ict.edu.ru/ft/006124/mpi-pr.pdf
3. http://ru.wikibooks.org/wiki/%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F
4. http://comp-science.hut.ru/Progr/Syst_Sch.html
5. http://school-collection.edu.ru/catalog/rubr/a30a9550-6a62-11da-8cd6-0800200c9a66/63374/
http://demashov.edurm.ru/uroki%20i%20cor/9klass/urok28/28.htm
Домашние задания по информатике для 10 класса
Домашние задания по информатике для 10 классаУчебник Информатика и ИКТ.
 Профильный уровень: учебник для 10 класса
Профильный уровень: учебник для 10 класса Н.Д. Угринович
М., Бином, Лаборатория знаний, 2011
Домашнее задание №1
Параграф 2.1 (все подпункты)
Составить сравнительную характеристику понятия «ИНФОРМАТИКА» в различных областях деятельности человека. Оформить в тетради в виде таблицы
Домашнее задание №2
Параграф 2.1 (подготовиться к письменному опросу)
Параграф 2.2 (формула Хартли)
- Сколько существует различных последовательностей из символов «а» и «б», длиной ровно в 10 символов?
- В зрительном зале две прямоугольные области зрительских кресел: одна 10 на 12, а другая 17 на 8. Какое минимальное количество бит потребуется для кодирования каждого места в автоматизированной системе?
- Азбука Морзе позволяет кодировать символы для радиосвязи. задавая комбинацию точек и тире. Сколько различных символов можно закодировать, используя код Морзе длиной не менее трех и не более пяти сигналов?
- Метеостанция ведет наблюдение за атмосферным давлением.
 Результатом одного измерения является целое число, принимающее значение от 720 до 780 мм ртутного столба, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определить информационный объем результатов наблюдений.
Результатом одного измерения является целое число, принимающее значение от 720 до 780 мм ртутного столба, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определить информационный объем результатов наблюдений.
Домашнее задание №3
Решите следующие задачи:
- Производится одноканальная (моно) звукозапись с частотой дискретизации 48 кГц и глубиной кодирования 16 бит.
Запись длится 2 минуты, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных
ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?
1) 11
2) 12
3) 13
4) 20 - Производится двухканальная (стерео) звукозапись с частотой дискретизации 48 кГц и глубиной кодирования 24
бита. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какое из
приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?
1) 0,3
2) 4
3) 16
4) 132 - Два текста содержат одинаковое количество символов.
 Первый текст составлен в алфавите мощностью 16
символов, а второй текст – в алфавите из 256 символов. Во сколько раз количество информации во втором тексте
больше, чем в первом?
Первый текст составлен в алфавите мощностью 16
символов, а второй текст – в алфавите из 256 символов. Во сколько раз количество информации во втором тексте
больше, чем в первом?1) 12
2) 2
3) 24
4) 4 - Объем сообщения – 7,5 Кбайт. Известно, что данное сообщение содержит 7680 символов. Какова мощность
алфавита?
1) 77
2) 256
3) 156
4) 512 - Объем сообщения равен 11 Кбайт. Сообщение содержит 11264 символа. Какова мощность алфавита?
1) 64
2) 128
3) 256
4) 512
Домашнее задание №4
Переведите следующие целые числа из 10 системы счисления в:
- двоичную 345, 1608, 21
- восьмеричную 6621, 1204, 35
- пятиричную 45, 180, 16
- шестнадцатиричную 10000, 253, 16
Сложить числа в различных системах счисления:
- В двоичной: 111011+10111, 101101+11001
- В пятиричной: 142+424, 234+412
- В восьмеричной: 456+725, 446+554
- В шестнадцатиричной: F5A+DCD, AA7+443
Домашнее задание №5
1.
 Сложить в разных системах счисления следующие числа:
Сложить в разных системах счисления следующие числа:- В двоичной системе счисления: 111011101+11011111; 11011101+1111011
- В восьмеричной системе счисления: 322+605; 435+664; 563+346
- В шестнадцатиричной системе счисления: ABC7+F4D; 8954+D67A
345, 1022, 3006
3. Сложить числа, представленные соответственно: первое — в двоичной, второе — в восьмеричной, третье — в десятичной, четвертое — в шестнадцатиричной системах счисления (результат представить во всех четырех системах счисления):
- 110011+153+100+A9C
- 101010+67+91+DD1
Домашнее задание №6
- Готовимся к контрольной работе
- Представить десятичное число 275 в двоичной, восьмеричной и шестнадцатиричной системах счисления
- Определить количество значащих нулей в двоичной записи числа 1234
- Сложить восьмеричное число 45 с шестнадцатиричным числом АС, результат представить в двоичной, десятичной и шестнадцатиричной системах счисления
- Считая, что каждый символ заодирован в Unicode, определить информационный объем фразы: «Учись учиться — потом пригодится»
- Запишите в двоичной системе счисления число, которое удовлетворяет неравенству:
a Для 5 букв русского алфавита заданы их двоичные коды, представленные в таблице:
Из четырех полученных сообщений в этой кодировке только одно прошло без ошибки и может быть корректно декодировано.В К А Р Д 000 11 01 001 10  Найдите его:
Найдите его:1 2 3 4 110100000100110011 111010000010010011 110100001001100111 110110000100110010 - Для передачи секретного сообщения используется код, состоящий из заглавных латинских букв и арабских цифр (всего 36). При этом все символы кодирруются одним и тем же минимально возможным количеством бит. Определите информационный объем сообщения длиной в 150 символов:
1 2 3 4 900 бит 160 байт 800 бит 120 байт - Сколько секунд потребуется модему, передающему сообщения со скоростью 28800 бит/с, чтобы передать 100 страниц текста в 30 строк по 60 символов каждая, при условии, что каждый символ кодируется одним байтом?
Домашнее задание №6
На отдельном листе привести по три примера на каждую форму мышления с пояснениями.
Прочитать параграф «Логика»
Домашнее задание №7
Составить таблицы истинности для следующих логических выражений:
◦ ((C V B)->B) & (A & B) -> B
◦ ((C V B)->B) & (A V B)
Домашнее задание №8
Параграф 3.
 2.3, 3.2.4
2.3, 3.2.4- Упростить следующее логическое выражение
Проверить правильность упрощения с помощью таблиц истинности, построенных на исходную и на упрощенную функцию
(В таблице истинности записывайте само действие, а не порядковый номер)
Домашнее задание №9
Выполнить следующие задания:
Домашнее задание №10
Параграф 3.2.1 и 3.2.2
- Написать логические выражения, имеющие значения ИСТИНА, если точки находятся в выделенных областях:
- Используя логические операции, запишите высказывания, которые являются истинными при выполнении следующих условий:
- только одно из чисел X, Y, Z является отрицательным
- ни одно из чисел X, Y, Z не равно 104
- треугольник со сторонами A, B, C является равнобедренным, но не является равносторонним
- Сформулируйте высказывание на обычном языке для следующих логических выражений:
- (x>0 и x5)
- не ((x
Домашнее задание №11
Выполнить следующие задания:
Выполнить следующее задание:
- Пусть F1 — высказывание вида: «Если все стороны четырехугольника равны и один из его углов прямой, то этот четырехугольник является квадратом»
- F2 — «Если все стороны четырехугольника равны, а он не является квадратом, то один из его углов не является прямым»
- Для записи логических выражений используйте следующие обозначения
А – стороны четырехугольника равны
В – угол прямой
С – четырехугольник является квадратом - Постройте таблицы истинности для сложных высказываний F1 и F2 и сравните полученный результат
- Сделайте вывод на основании полученных результатов
Решить следующие логические задачи:
- Девять школьников, остававшихся в классе на перемене, были вызваны к директору.
 Один из них разбил окно в кабинете. На вопрос директора, кто это сделал, были получены следующие ответы:
Один из них разбил окно в кабинете. На вопрос директора, кто это сделал, были получены следующие ответы:- Володя: «Это сделал Саша».
- Аня: «Володя лжет!»
- Егор: «Маша разбила».
- Саша: «Аня говорит неправду!»
- Рома: «Разбила либо Маша, либо Нина…»
- Маша: «Это я разбила!»
- Нина: «Маша не разбивала!»
- Коля: «Ни Маша, ни Нина этого не делали».
- Олег: «Нина не разбивала!»
- Володя: «Это сделал Саша».
- Семья, состоящая из 5 человек (отца, матери и дочерей – Ани, Веры, Светы), купила телевизор. Все хотят смотреть его в первый вечер.
— Нам нужно распределить обязанности, чтобы не остаться без ужина, — сказал папа.
— Верно,- сказала мама. – Но только когда ты будешь смотреть телевизор, я сяду его смотреть вместе с тобой.
— Хорошо, — сказал папа и улыбнулся. Кому повезло – так это Вере и Свете. По крайней мере одна из них сегодня вечером будет смотреть телевизор.
— А с тобой, Анечка, нам придется смотреть телевизор только по очереди,- сказала мама
— Я согласна, — ответила Аня. Только ты разреши нам с Верой вместе работать на кухне или вместе быть у телевизора
— Пожалуй, Свету одну нельзя оставлять,- сказал папа. – Если она захочет смотреть передачу, то придется и мне с Верой посидеть с ней
Все предложения были приняты. Кто смотрел передачу в первый вечер?- Аня, Вера и Света
- Аня и Вера
- Папа и мама
- Мама и Аня
- Папа, Вера и Света
- Аня, Вера и Света
Домашнее задание №12
Выполнить следующие задания из вложенного файла:
Домашнее задание 12
На главную
Числа до 5 цифр — определение, разрядное значение, расширенная форма, примеры
Пятизначные числа — это целые числа в числовой строке, которые начинаются с 10 000 и достигают 99 999. Эти числа содержат в общей сложности 5 цифр в своей числовой форме.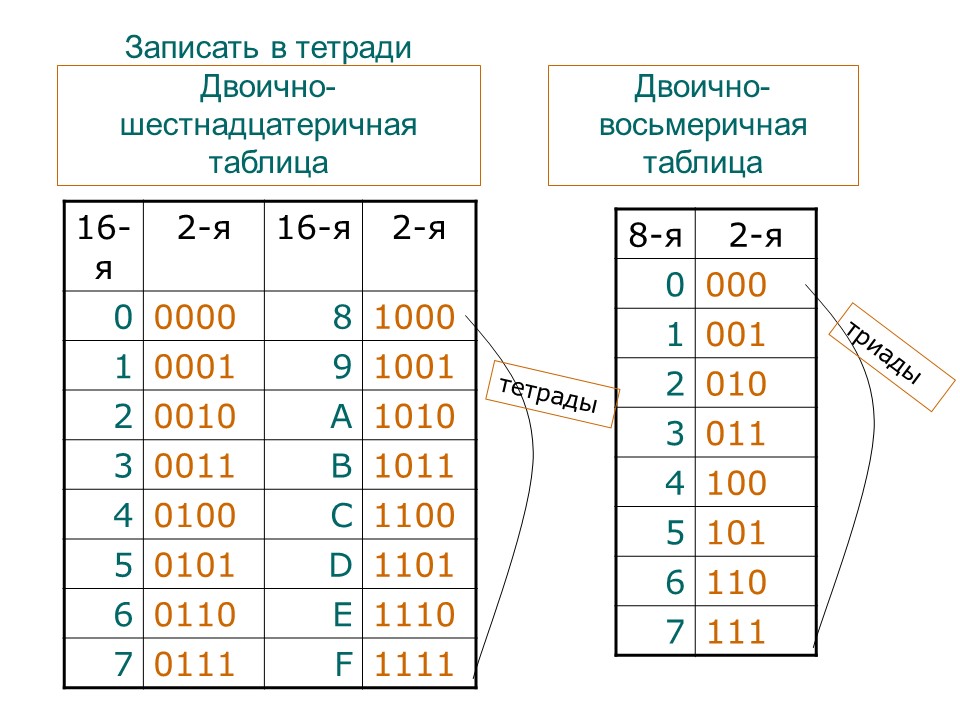 Давайте узнаем больше о номерах до 5 цифр на этой странице.
Давайте узнаем больше о номерах до 5 цифр на этой странице.
| 1. | Что такое числа до 5 цифр? |
| 2. | Размещение значений цифр в числах до 5 цифр |
| 3. | Как разложить пятизначные числа? |
| 4. | Запятые в пятизначных числах |
| 5. | Сколько можно составить пятизначных чисел? |
| 6. | Часто задаваемые вопросы о номерах до 5 цифр |
Что такое числа до 5 цифр?
Пятизначные числа начинаются с десяти тысяч и доходят до девяноста девяти тысяч девятисот девяноста девяти. Эти числа содержат целые числа вместо единиц, десятков, сотен, тысяч и десятков тысяч. На эти места можно поставить любое положительное целое число, имея в виду, что 0 нельзя поставить на разряд десятков тысяч. Это связано с тем, что если здесь поставить 0, оно станет 4-значным числом, например, 04356 станет 4356. На следующем рисунке показано, как случайное 5-значное число 86953 помещается на счеты. Разрядное значение пяти цифр, составляющих 5-значное число, будет получено путем последовательного умножения соответствующей цифры на 1, 10, 100, 1000 и 10 000, начиная с самой правой цифры и двигаясь влево.
На следующем рисунке показано, как случайное 5-значное число 86953 помещается на счеты. Разрядное значение пяти цифр, составляющих 5-значное число, будет получено путем последовательного умножения соответствующей цифры на 1, 10, 100, 1000 и 10 000, начиная с самой правой цифры и двигаясь влево.
Наименьшее пятизначное число
Наименьшее пятизначное число равно 10 000, поскольку пятизначные числа начинаются с 10 000, а число до 10 000 равно 9999, то есть четырехзначному числу.
Наибольшее пятизначное число
Наибольшее 5-значное число — 99 999, потому что число после 99 999 равно 1 00 000, которое становится 6-значным числом.
Размещение значений цифр в числах до 5 цифр
Как показано выше, в 5-значном числе каждое прогрессивное разрядное значение равно предыдущему разрядному значению, умноженному на 10. Например, возьмем число: 37 159. Это число можно представить словами, как « тридцать семь тысяч сто пятьдесят девять ».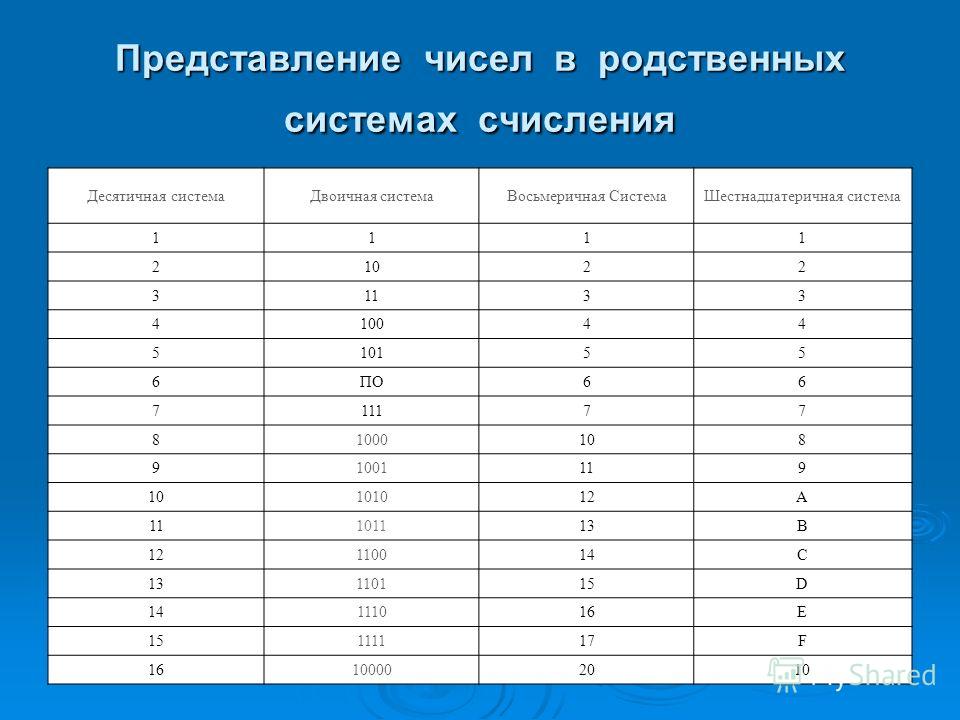 На следующем рисунке показаны разряды этого 5-значного числа.
На следующем рисунке показаны разряды этого 5-значного числа.
Как разложить пятизначные числа?
Когда мы видим 5-значное число, пять цифр будут соответствовать 5 разрядным значениям — Единицы, Десятки, Сотни, Тысячи и Десятки Тысяч. Давайте посмотрим, как можно разложить 5-значное число на его разрядные значения. Продолжим с тем же числом 20340. 2 в разряде десятков тысяч = 2 × 10000 = 20000. Здесь 0 в разряде тысяч = 0 × 1000 = 0, а 3 в разряде сотен = 3 × 100 = 300, 4 стоит в разряде десятков = 4 × 10 = 40, а 0 стоит в разряде единиц = 0 × 1 = 0. Следовательно, пятизначное число можно выразить следующим образом: 20000 + 0 + 300 + 40 + 0 = 20340 .
Итак, как изменились бы 5 разрядов, если бы мы поменяли местами некоторые цифры? Давайте заменим число 20 340 на другое пятизначное число, имеющее те же числа с переставленными цифрами, например, 32 004. Изменение разрядного значения тех же 5 цифр дает следующие результаты:
- Разрядное значение 2 становится 2 × 1000 = 2000 (ранее разрядное значение 2 было 20000)
- Разрядное значение 3 становится 3 × 10000 = 30000 (ранее разрядное значение 3 равнялось 300)
- Разрядное значение 4 становится 4 × 1 = 4 (ранее разрядное значение было 40)
- Ноль — это единственная цифра от 0 до 9, разрядность которой остается неизменной (нулем) независимо от ее положения.

В обоих приведенных выше числах все нулевые цифры имеют нулевой разряд.
Запятые в пятизначных числах
Мы видели использование запятых в четырехзначных числах, причем запятая стоит прямо перед цифрой на разряде сотен, то есть слева от разряда сотен. В 5-значном числе также должна использоваться только одна запятая, и она должна быть помещена слева от разряда сотен. Например, пятизначные числа 32958 и 20340 могут быть лучше выражены как 32 958 и 20 340, что помогает правильно читать числа.
Сколько можно составить пятизначных чисел?
Как мы уже говорили ранее, 02340 — это не пятизначное число, а четырехзначное число 2340. В пятизначном числе не может быть 0 в качестве первой цифры слева, то есть десятитысячного разряда. В целом, каждое из 5 мест 5-значного числа можно заполнить десятью способами, потому что оно может состоять из 0, 1, 2, 3, 4, 5, 6, 7, 8 или 9.. Таким образом, каждое из пяти мест можно заполнить десятью способами.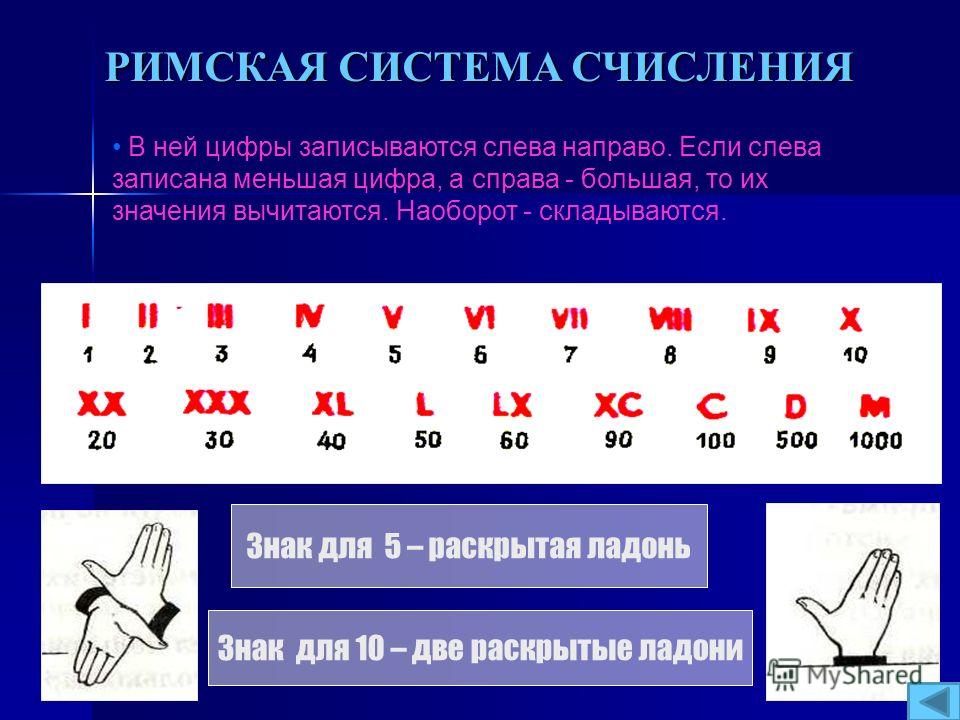 Следовательно, общее количество возможных комбинаций равно 10 × 10 × 10 × 10 × 10 = 1 00 000.
Следовательно, общее количество возможных комбинаций равно 10 × 10 × 10 × 10 × 10 = 1 00 000.
Из этих 1 00 000 способов составить пятизначное число нам нужно исключить все возможности, в которых ноль стоит на первой позиции слева (или на десятитысячном разряде). Когда на первом месте стоит ноль, следующая позиция (тысячи) может быть заполнена десятью способами, как и места сотен, десятков и единиц. Итак, количество пятизначных чисел, у которых первой цифрой является ноль, равно 10 × 10 × 10 × 10 = 10 000. Если мы вычтем эти 10 000 способов из общего числа 1 00 000 способов, у нас останется 9.0,000. Следовательно, возможно 90 000 уникальных пятизначных чисел.
Важные примечания о числах до 5 цифр
Ниже приведен список некоторых важных примечаний, касающихся чисел до 5 цифр. Они полезны, когда мы решаем вопросы, связанные с этой темой.
- Как следует из названия, пятизначное число обязательно должно состоять из пяти цифр.
- Наименьшее пятизначное число равно 10 000, а самое большое пятизначное число равно 99 999.

- Всего существует 90 000 пятизначных чисел.
- Цифра в разряде десятков тысяч в пятизначном числе никогда не может быть 0.
☛ Статьи по теме
- Номера до 2 цифр
- Номера до 3 цифр
- Номера до 4 цифр
- Номера до 6 цифр
- Числа до 7 цифр
- Числа до 8 цифр
- Номера до 9 цифр
- Номера до 10 цифр
- Системы счисления
Часто задаваемые вопросы о номерах до 5 цифр
Что такое пятизначные числа?
5-значный номер — это номер, состоящий из 5 цифр, в котором первая цифра должна быть 1 или больше 1, а остальные цифры могут быть любым числом от 0 до 9. Он начинается с десяти тысяч (10 000) и достигает девяноста девяти тысяч девятисот девяноста девяти (99 999).
Сколько существует пятизначных чисел?
Есть 90,000 пятизначных чисел, включая наименьшее пятизначное число, равное 10,000, и самое большое пятизначное число, равное 99,999.
Как прочитать пятизначное число?
Читаем пятизначное число слева направо, начиная с разряда десятков тысяч до разряда единиц. Например, число 21 356 читается слева направо, начиная с 2, затем 1, 3, 5 и затем 6. В названиях чисел оно читается как двадцать одна тысяча триста пятьдесят шесть.
Как писать пятизначные числа словами?
Мы пишем название пятизначного числа так, как мы его читаем. Начиная слева направо, от разряда десятков тысяч до разряда единиц. Например, число 31 279 записывается как тридцать одна тысяча двести семьдесят девять.
Какое самое маленькое пятизначное число?
Наименьшее пятизначное число — 10 000. В именах чисел читается как десять тысяч.
Какое самое большое пятизначное число?
Самое большое пятизначное число 99999 и записывается как девяносто девять тысяч девятьсот девяносто девять прописью.
Какова сумма наибольшего и наименьшего пятизначных чисел?
Наибольшее пятизначное число — 99 999, а наименьшее пятизначное число — 10 000.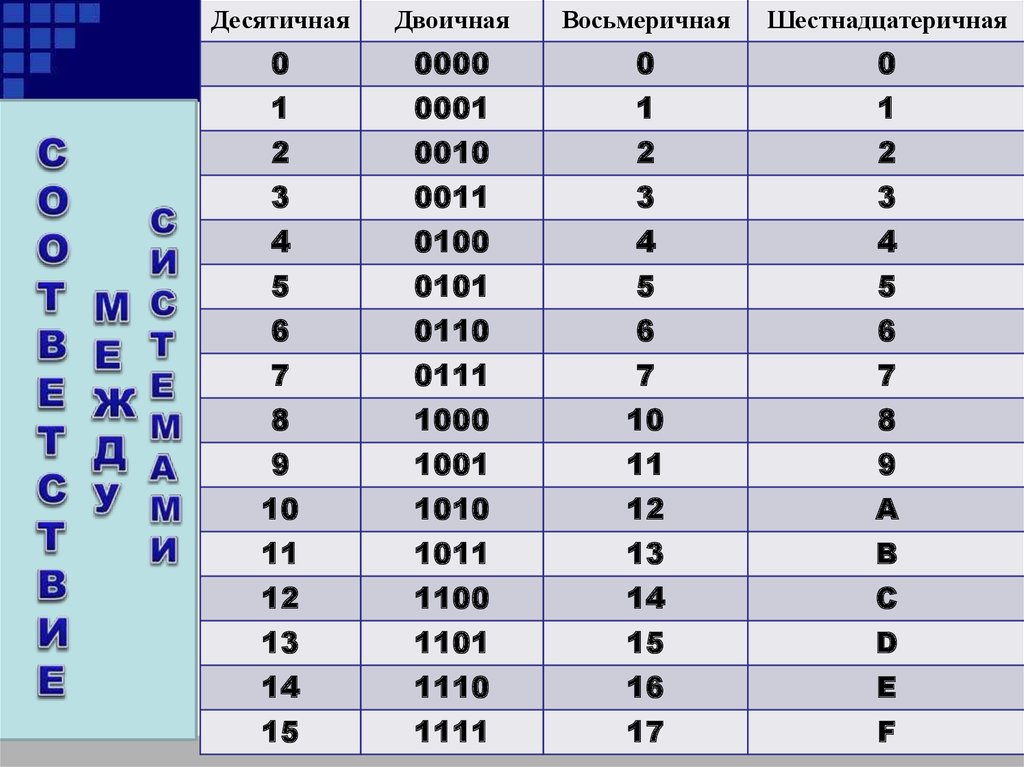


 Результатом одного измерения является целое число, принимающее значение от 720 до 780 мм ртутного столба, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определить информационный объем результатов наблюдений.
Результатом одного измерения является целое число, принимающее значение от 720 до 780 мм ртутного столба, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определить информационный объем результатов наблюдений. Первый текст составлен в алфавите мощностью 16
символов, а второй текст – в алфавите из 256 символов. Во сколько раз количество информации во втором тексте
больше, чем в первом?
Первый текст составлен в алфавите мощностью 16
символов, а второй текст – в алфавите из 256 символов. Во сколько раз количество информации во втором тексте
больше, чем в первом? Найдите его:
Найдите его: Один из них разбил окно в кабинете. На вопрос директора, кто это сделал, были получены следующие ответы:
Один из них разбил окно в кабинете. На вопрос директора, кто это сделал, были получены следующие ответы: