В шестнадцатеричной системе счисления присутствуют символы. Шестнадцатеричная и двоичная системы счисления

Шестнадцатеричная система счисления имеет алфавит, состоящий из 16 цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, b, c, d, e, f.

При записи числа в шестнадцатеричной системе для записи цифр обозначающих числа 10, 11, 12. 13, 14. 15 используются соответственно буквы А, В, С, D, E, F.

Перевод чисел из шестнадцатеричной системы в десятичную

Перевести любое шестнадцатеричное число в десятичное можно по уже известной формуле

Примеры.

АЕ07 16 =10∙16 3 +14∙16 2 +0∙16 1 +7∙16 0 =44551 10 .

100 16 =1∙16 2 +0∙16 1 +0∙16 0 =256 10 .

58 16 =5∙16 1 +8∙16 0 =.88 10 .

2А 16 =2∙16 1 +10∙16 0 =42 10 .

Перевод числа из десятичной системы в шестнадцатеричную осуществляется также, как в двоичную.

Перевод чисел из шестнадцатеричной системы в двоичную и обратно

Перевести любое шестнадцатеричное число в двоичное можно следующим образом. Каждая цифра шестнадцатеричной записи числа записывается четырехзначным двоичным числом —

тетрадой . После этого нули, стоящие слева, можно отбросить.

2) 2A= 0010 1010 2 = 101010 2 .

3) 58 16 = 0101 1000 2 = 1011000 2 .

И наоборот, перевести любое двоичное число в шестнадцатеричное можно аналогичным образом. Каждые четыре двоичные цифры, считая справа налево, записываются одной шестнадцатеричной цифрой. Эти цифры располагаются также справа налево.

Примеры.

2. 101010 2 = 10 1010 2 = 2A.

3. 1011000 2 = 101 1000 2 = 58 16 .

Восьмеричная система счисления

Восьмеричная система счисления имеет алфавит, состоящий из 8 цифр:

0, 1, 2, 3, 4, 5, 6, 7.

Перевод числа из десятичной системы в восьмеричную и обратно осуществляется по аналогии с переводом в двоичную / из двоичной.

Перевод чисел из восьмеричной системы в двоичную и обратно

Каждая цифра восьмеричной записи числа записывается трехзначным двоичным числом — триадой .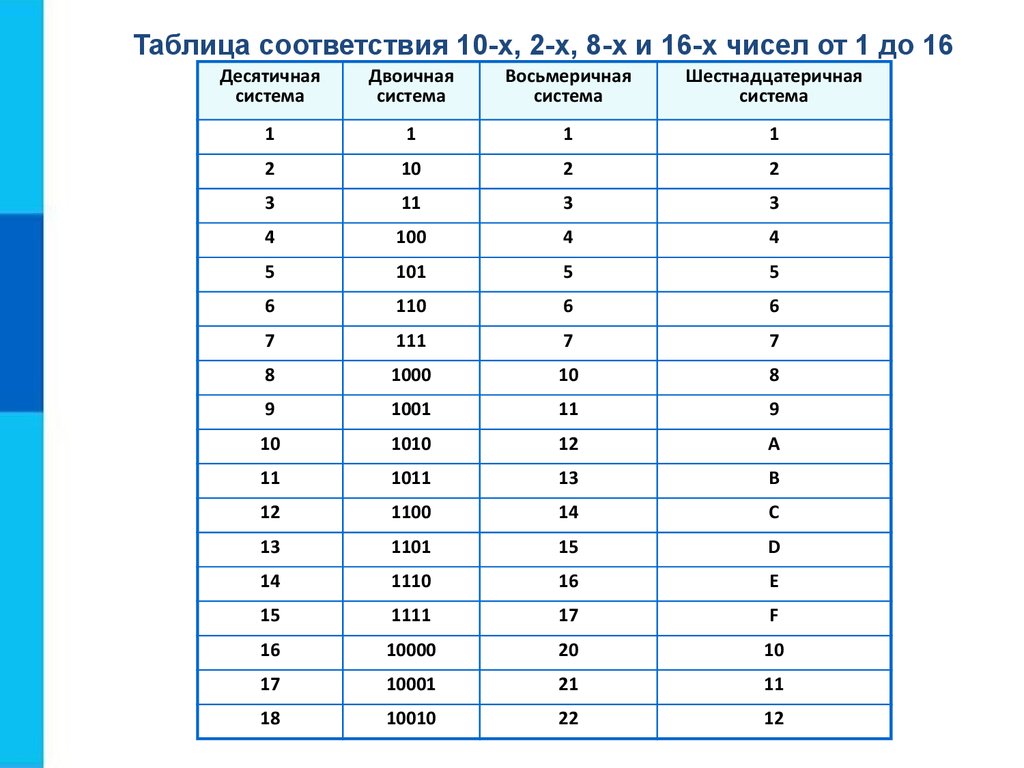

Примеры.

2563 8 = 010 101 110 011 2 =10101110011 2 .

1001101 2 = 001 001 101 2 = 115 8 .

Методические материалы для лабораторного занятия №1

Тема лабораторного занятия: Системы счисления. Измерение информации.

Количество часов: 2.

Примеры с решениями

Перевод из p -ичной системы в 10-ичную.

Пусть надо перевести число в некоторой системе счисления в десятичную. Для этого надо представить его в виде

11100110 2 = 1∙2 7 + 1∙2 6 + 1∙2 5 + 0∙2 4 + 0∙2 3 + 1∙2 2 + 1∙2 1 + 0∙2 0 = 128 + 64 + 32 + 4 + 2 = 230 10 .

2401 5 = 2∙5 3 + 4∙5 2 + 0∙5 1 + 1∙5 0 = 250 + 100 + 0 + 1 = 351.

Перевод из 10-ичной системы в p -ичную.

2.1 98 10 → Х 2 .

Делим число на 2. Затем делим неполное частное на 2. Продолжаем до тех пор, пока неполное частное не станет меньше 2, т.е. равным 1.

98: 2 = 49. Остаток — 0 .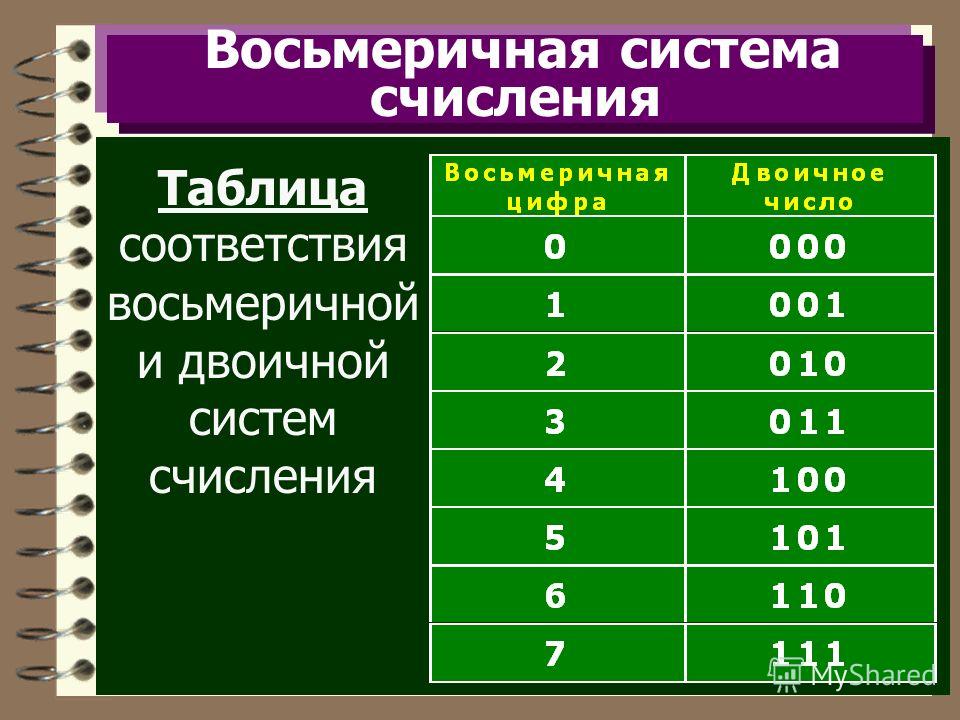

49: 2 = 24. Остаток — 1 .

24: 2 = 12. Остаток — 0 .

12: 2 = 6. Остаток — 0 .

6: 2 = 3. Остаток — 0 .

3: 2 = 1 . Остаток — 1 .

Так как последнее неполное частное равно 1, процесс окончен. Записываем все остатки снизу вверх, начиная с последнего неполного частного, и получаем число 1100010. Итак 98 10 = 1100010 2 .

2.2 2391 10 → Х 16 .

Делим число на 16. Затем делим неполное частное на 16. Продолжаем до тех пор, пока неполное частное не станет меньше 16.

2391: 16 = 149. Остаток — 7 .

149: 16 = 9 . Остаток — 5 .

Так как последнее неполное частное (9) меньше 16, процесс окончен. Записываем, начиная с последнего неполного частного, все остатки снизу вверх и получаем число 957. Итак 2391 10 = 957 16 .

2.3 12165 10 → Х 2 .

Если переводить делением в двоичную систему, то получится довольный громоздкий процесс. Можно сначала перевести число в восьмеричную систему, а затем заменять восьмеричные цифры справа налево триадами.

12165 10 = 27605 8 = 010 111 110 000 101 = 10111110000101.

Определение основания системы счисления p .

Один мальчик так написал о себе: «Пальцев у меня 24, на каждой руке по 5, а на ногах 12». Как такое может быть?

Решение. Надо определить основание системы счисления p . Так как мы знаем, что пальцев на ногах всего 10 10 , то 12 p =1∙p +2 = 10 10 . Отсюда получаем уравнение p + 2 = 10  p = 8. Значит, мальчик имел в виду числа в восьмеричной системе. Действительно, всего пальцев 24 8 = 2∙8+4 = 20 10 , а на ногах — 12 8 = 1∙8+2 = 10 10 .

Шестнадцатеричная система счисления , на сегодняшний день является наиболее популярным средством компактной записи двоичных чисел. Очень широко используется при разработке и проектировании цифровой техники.

Как следует из названия, основанием данной системы является число шестнадцать 16 или в шестнадцатеричной системе

10 16 . Чтобы не было путаницы, при записи чисел в системах счисления отличных от десятичных, справа внизу от основной записи числа будем указывать основание системы счисления. Раз основанием системы является число шестнадцать, значит, для изображения чисел нам потребуется шестнадцать цифр. Первые десять цифр берутся из, привычной нам, десятичной системы (0,1,..,8,9) и еще добавляются шесть букв латинского алфавита (a,b,c,d,e,f) . Например в шестнадцатеричном числе 3f7c2 буквы «f» и «c» являются шестнадцатеричными цифрами.

Счет в шестнадцатеричной системе происходит аналогично счету в десятичной. Давайте попробуем считать и записывать числа конструируя их из имеющихся шестнадцати цифр:

Ноль — 0 ;
Один — 1 ;
Два — 2 ;
…
и так далее…
…
Восемь — 8 ;
Девять — 9 ;
Десять — a ;
Одиннадцать — b ;
Двенадцать — c ;
Тринадцать — d ;
Четырнадцать — e ;
Пятнадцать — f ;

А что делать дальше? Все цифры кончились.

Как же изобразить число Шестнадцать? Поступим аналогично тому как мы поступали в десятичной системе. Там мы вводили понятие десятка, здесь же введем понятие «шестнадцать» и скажем, что шестнадцать — это одина «шестнадцать» и ноль единиц. А это уже можно и записать — «10 16 «.

Итак, Шестнадцать — 10 16 (одна «шестнадцать», ноль единиц)
Семнадцать — 11 16 (одна «шестнадцать», одна единица)
…
и так далее…
…
Двадцать пять — 19 16 (одна «шестнадцать», девять единиц)
Двадцать шесть — 1a 16 (одна «шестнадцать», десять единиц)
Двадцать семь — 1b 16 (одна «шестнадцать», одинадцать единиц)

…
и так далее…
…
Тридцать — 1e 16 (одна «шестнадцать», четырнадцать единиц)
Тридцать один — 1f 16 (одна «шестнадцать», пятнадцать единиц)
Тридцать два — 20 16 (две «шестнадцать», ноль единиц)
Тридцать три — 21 16 (две «шестнадцать», одна единица)
. ..
и так далее…
…
Двести пятьдесят пять — ff 16 (пятнадцать по «шестнадцать», пятнадцать единиц)

Двести пятьдесят шесть — 100 16 (одна «Двести пятьдесят шесть», ноль по «шестнадцать», ноль единиц)
Двести пятьдесят семь

— 101 16 (одна «Двести пятьдесят шесть», ноль по «шестнадцать», одна единица)
Двести пятьдесят восемь — 102 16 (одна «Двести пятьдесят шесть», ноль по «шестнадцать», две единицы)
…
и так далее…
…

Всегда, когда у нас исчерпался набор цифр для отображения следующего числа, мы вводим более крупные единицы счета (т.е. считаем по «шестнадцать», по «Двести пятьдесят шесть» и т.д.) и записываем число с удлинением на один разряд.

Рассмотрим число 3e2c 16 записанное в шестнадцатиричной системе счисления. Про него можно сказать, что оно содержит: три по четыре тысячи девяносто шесть, «e» (четырнадцать) по двести пятьдесят шесть, два по шестнадцать и «c» (двенадцать) единиц.

И получить его значение через входящие в него цифры можно следующим образом.

3e2c 16 = 3 *4096+14 *256+2 *16+12 *1, здесь и далее знак * (звездочка) означает умножение.

Но ряд чисел 4096, 256, 16, 1 есть не что иное, как целые степени числа шестнадцать (основания системы счисления) и поэтому можно записать:

3e2c 16 = 3 *16 3 +14 *16 2 +2 *16 1 +12 *16 0

Подобным образом для шестнадцатиричной дроби (дробного числа) например: 0.5a2 16 про него можно сказать, что оно содержит: пять шестнадцатых, «a» (десять) двести пятьдесят шестых и две четыретысячи девяносто шестых долей. И его значение можно вычислить следующим образом:

0.5a2 16 = 5 *(1/16) + 10 *(1/256) + 2 *(1/4096)

И здесь ряд чисел 1/16; 1/256 и 1/4096 есть не что иное, как целые степени числа шестнадцать и мы также можем записать:

0.5a2 16 = 5 *16 -1 + 10 *16 -2 + 2 *16 -3

Для смешанного числа 7b2. 1f9 аналогичным образом можем записать:

7b2.1f9 = 7 *16 2 +11 *16 1 +2 *16 0 +1 *16 -1 +15 *16 -2 +9 *16 -3

Пронумеруем разряды целой части некоторого шестнадцатиричного числа, справа налево, как 0,1,2…n (нумерация начинается с нуля!). А разряды дробной части, слева направо, как -1,-2,-3…-m, то значение некоторого шестнадцатиричного числа может быть вычислено по формуле:

N = d n 16 n +d n-1 16 n-1 +…+d 1 16 1 +d 0 16 0 +d -1 16 -1 +d -2 16 -2 +…+d -(m-1) 16 -(m-1) +d -m 16 -m

Где: n — количество разрядов в целой части числа минус единица;
m — количество разрядов в дробной части числа
d i — цифра стоящая в i -м разряде

Эта формула называется формулой поразрядного разложения шестнадцатиричного числа, т.е. числа записанного в шестнадцатиричной системе счисления. Если мы в этой формуле заменим число шестнадцать на некоторое произвольное число q , то получим формулу разложения для числа записанного в q-й системе счисления, т. е. с основанием q :

N = d n q n +d n-1 q n-1 +…+d 1 q 1 +d 0 q 0 +d -1 q -1 +d -2 q -2 +…+d -(m-1) q -(m-1) +d -m q -m

По этой формуле всегда можно вычислить значение числа записанного в любой позиционной системе счисления с основанием q .

С другими системами счисления можно познакомиться на нашем сайте по следующим ссылкам.

Всем, кто общается с компьютером или другой цифровой техникой, приходилось встречать загадочные записи типа 10FEF, которые кажутся непосвященным каким-то шифром. Что скрывается за этими символами? Оказывается, это просто цифры. Те, которые использует шестнадцатиричная

Системы счисления

Каждый школьник знает или хотя бы где-то слышал, что все цифры, которые мы обычно используем, образуют Это название она носит просто потому, что различных символов в ней всего десять (от 0 до 9). Любое число в нашей привычной системе может быть записано с их помощью. Однако, оказывается, использовать ее удобно бывает далеко не всегда. Например, при обмене информацией между цифровыми устройствами проще всего применять систему счисления, в которой есть только две цифры: «0» — нет сигнала — или «1» — есть сигнал (напряжение или что-то еще). Она называется двоичной. Однако, чтобы описать процессы внутри таких устройств с ее помощью, придется выполнять слишком длинные и трудные для понимания записи. Поэтому была придумана шестнадцатиричная система счисления.

Понятие шестнадцатеричной системы

Почему же для цифровых устройств используется именно система, которая содержит шестнадцать разных символов? Как известно, информация в компьютерах передается в виде байтов, которые обычно содержат 8 бит. А единица данных — машинное слово — включает в себя 2 байта, то есть 16 бит. Таким образом, с помощью шестнадцати разных символов можно описать ту информацию, которая является мельчайшей частицей при обмене. Шестнадцатиричная система счисления включает наши привычные цифры (естественно, от 0 до 9), а также первые буковки (A, B, C, D, E, F). Именно с помощью этих символов принято записывать любую единицу информации. С ними можно производить любые арифметические действия. То есть сложение, вычитание, умножение, деление. Результатом также будет шестнадцатеричное число.

Где применяется

Шестнадцатиричная система используется для записи кодов ошибок. Они могут возникать при работе различных программных продуктов. Например, так кодируются ошибки операционной системы. Каждое число при этом стандартное. Можно выяснить, какая именно ошибка произошла в процессе работы, расшифровав его с помощью инструкции. Также применяются такие символы при написании программ на языках низкого уровня, например ассемблере. Шестнадцатиричная система счисления любима программистами еще и потому, что ее составляющие очень легко могут быть переведены в двоичные, которые являются «родными» для всей цифровой техники. С помощью таких символов описывают также цветовые схемы. Кроме того, абсолютно все файлы в компьютере (и текстовые, и графические, и даже музыкальные или видео) представляются после трансляции в виде последовательности Просматривать исходный удобнее всего как раз в виде шестнадцатеричных символов.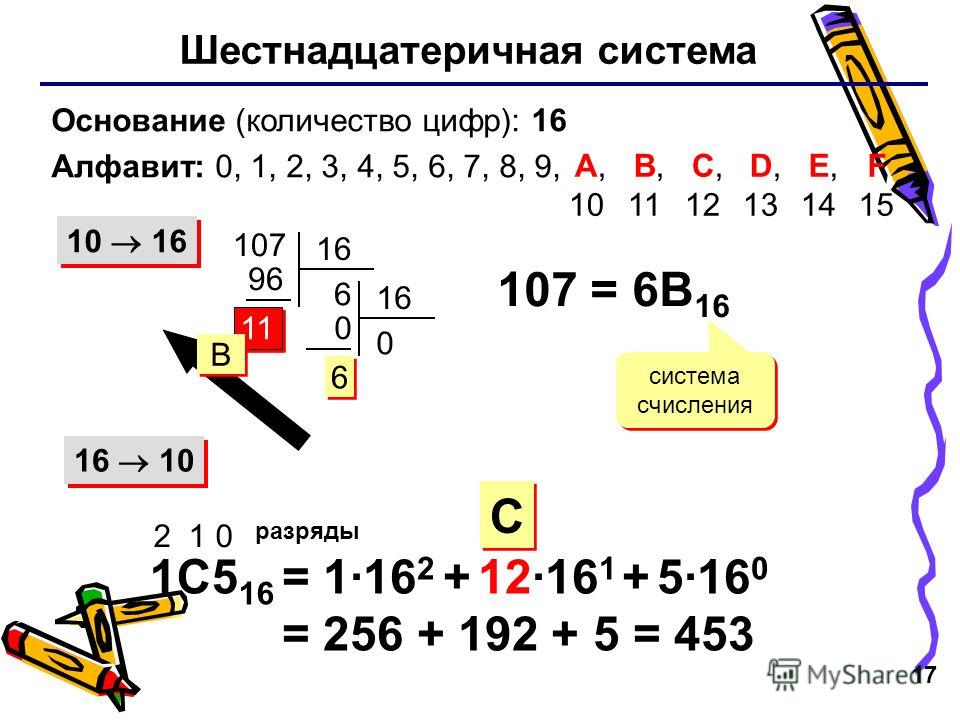

Конечно, любое число можно записать в различных системах счисления. Это и десятичная, и двоичная, и шестнадцатеричная. Чтобы перевести слово из одной из них в другую, следует воспользоваться таким сервисом, как переводчик систем счисления, или сделать это самостоятельно с помощью определенного алгоритма.

Возникла в древнем Вавилоне. В Индии система работает в виде позиционной десятичной нумерации с использованием нуля, у индусов данную систему чисел позаимствовала арабская нация, у них, в свою очередь, взяли европейцы. В Европе эту систему стали называть арабской.

Позиционная система счисления — значение всех цифр зависит от позиции (разряда) данной цифры в числе.

Примеры , стандартная десятичная система счисления — это позиционная система. Допустим, дано число 453 . Цифра 4 обозначает сотни и соответствует числу 400, 5 — кол-во десятков и соответствует значению 50 , а 3 — единицы и значению 3 . Легко заметить, что с увеличением разряда увеличивается значение. Таким образом, заданное число запишем в виде суммы 400+50+3=453.

Шестнадцатеричная система счисления.

Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления. Основанием шестнадцатеричной системы счисления является число 16.

Записывая числа в восьмеричной системе счисления мы получаем довольно компактные выражения, однако в шестнадцатеричной системе мы получаем выражения более компактными.

Первыми десятью цифрами из шестнадцати шестнадцатеричных цифрах является стандартный интервал 0 — 9 , последующие шесть цифр выражают при помощи первых букв латинского алфавита: A , B , C , D , E , F . Перевод из шестнадцатеричной системы в двоичную систему и в обратную сторону делают аналогично процессу для восьмеричной системы.

Применение шестнадцатеричной системы счисления.

Шестнадцатеричную систему счисления довольно хорошо используют в современных компьютерах, например с ее помощью указывают цвет: #FFFFFF — белый цвет.

Перевод чисел из одной системы счисления в другую.

Перевод чисел из шестнадцатеричной системы в десятичную.

Что бы перевести шестнадцатеричное число в десятичное , нужно заданное число привести к виду суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например , переведем шестнадцатеричное число 5A3 в десятичное. Здесь 3 цифры. Исходя их выше сказанного правила, приведем его к виду суммы степеней с основанием 16:

5A3 16 = 3·16 0 +10·16 1 +5·16 2 = 3·1+10·16+5·256 = 3+160+1280 = 1443 10

Перевод чисел из двоичной системы в шестнадцатеричную и наоборот.

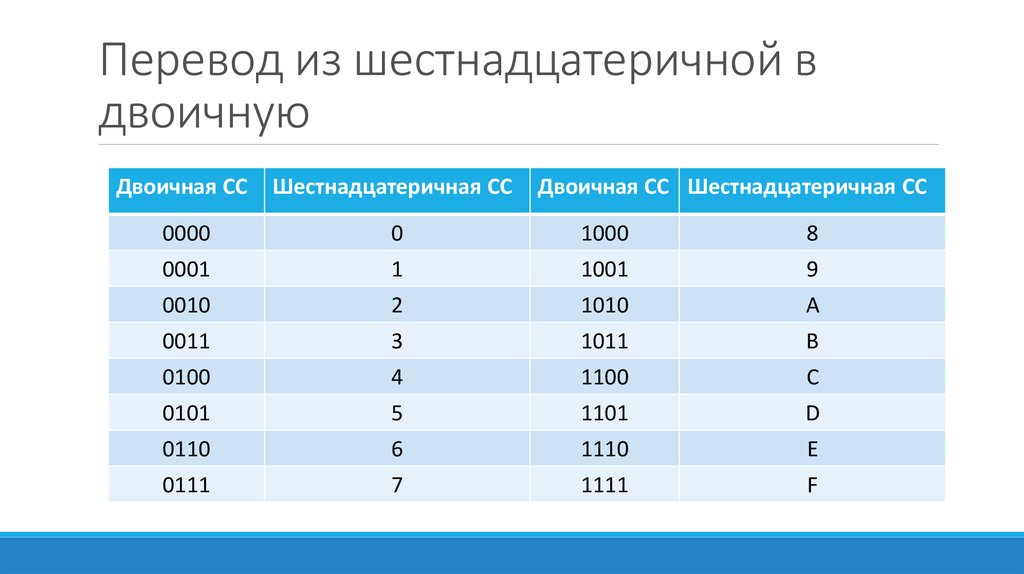
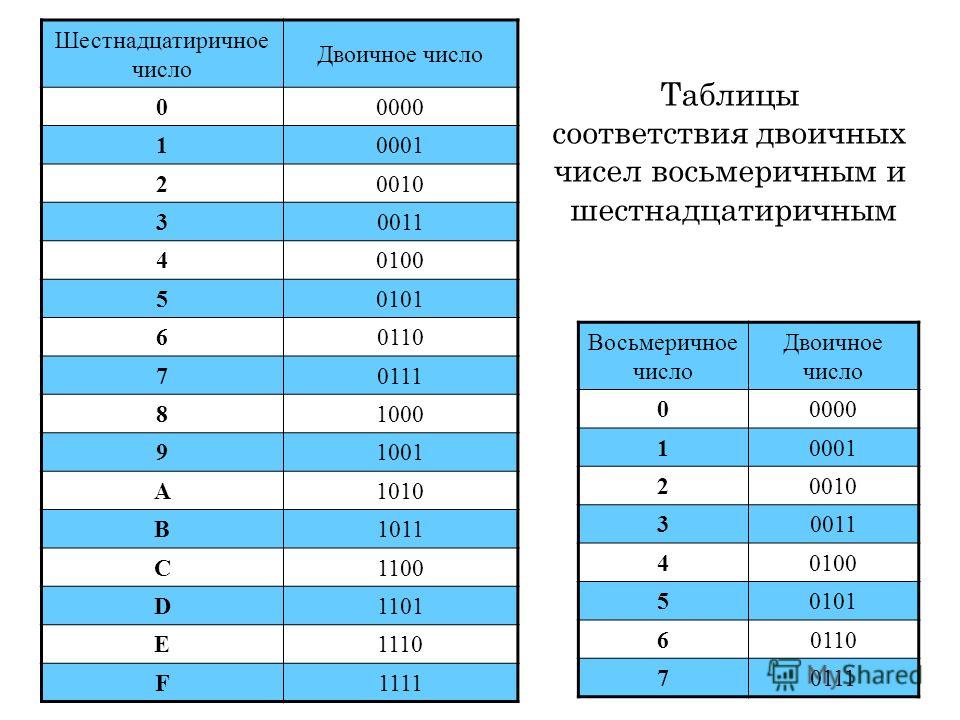
Для перевода многозначного двоичного числа в шестнадцатеричную систему необходимо разделить его на тетрады справа налево и поменять все тетрады соответствующей шестнадцатеричной цифрой.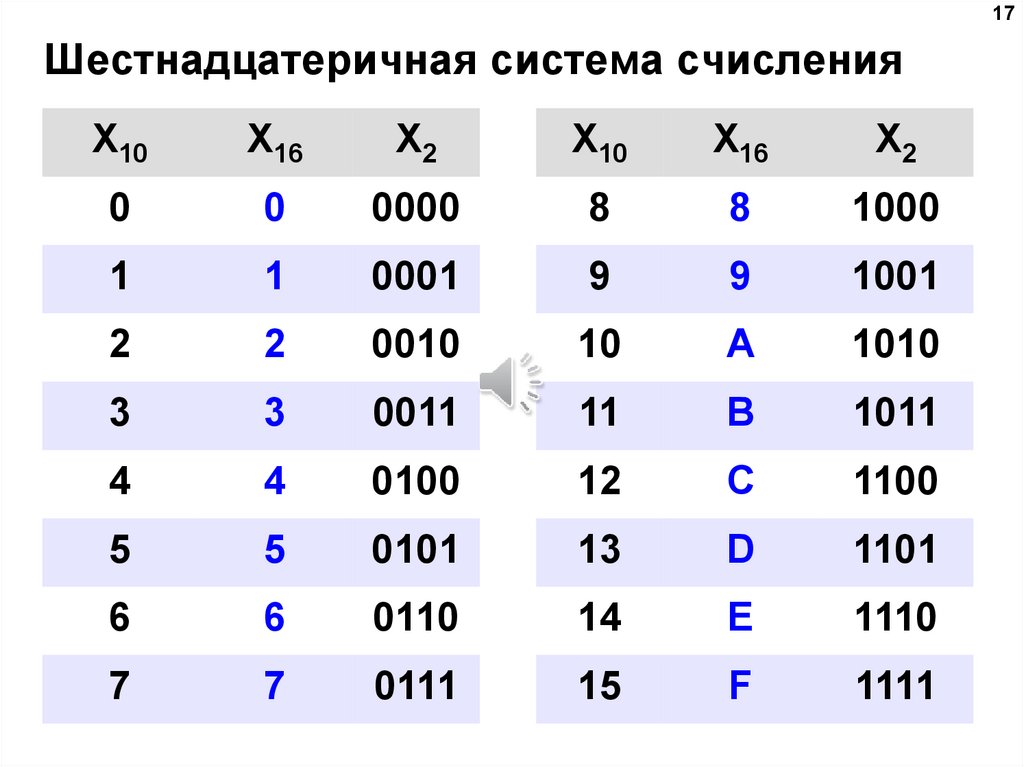 Для перевода числа из шестнадцатеричной системы в двоичную необходимо поменять каждую все цифры на соответствующие тетрады из таблицы перевода, которую вы найдете ниже.

Например :

010110100011 2 = 0101 1010 0011 = 5A3 16

Таблица перевода чисел.

Алгоритм перевода чисел из одной системы счисления в другую.

1. Из десятичной системы счисления:

• делим число на основание переводимой системы счисления;
• находим остаток от деления целой части числа;
• записываем все остатки от деления в обратном порядке;

2. Из двоичной системы счисления:

• для перевода в десятичную систему счисления находим сумму произведений основания 2 на соответствующую степень разряда;
• для перевода числа в восьмеричную разбиваем число на триады.

Например, 1000110 = 1 000 110 = 1068

• для перевода числа из двоичной системы счисления в шестнадцатеричную разбиваем число на группы по 4 разряда.

Например, 1000110 = 100 0110 = 4616.

Таблицы для перевода:

Двоичная СС	Шестнадцатеричная СС
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111

Двоичная СС

Многие пользователи компьютеров понимают, что компьютер работает в двоичной системе счисления. Традиционно состояния двоичной системы представляются цифрами 0 и 1, хотя, если говорить более точнее, каждое состояние обозначает наличие или отсутствие сигнала, т. е. правильнее будет назвать состояния «выключено» и «включено», либо «нет» и «да». Состоянию «выключено» или «нет» соответствует цифра 0, а состоянию «включено» или «да» цифра 1. Простым пользователям обычно нет необходимости полностью понимать устройство компьютера, однако двоичная система счисления дает о себе знать в виде различных ограничений основанных на степени двойки. Более компактный вариант двоичной системы называют шестнадцатеричной. Число шестнадцать является четвертой степенью числа два. Из этого следует, что можно достаточно просто переводить длинных двоичные последовательностей из нулей и единиц в короткие шестнадцатеричные. Для этого достаточно разбить двоичную последовательность на группы по четыре разряда (цифры) начиная с младшего разряда (справа) и заменить каждую группу на соответствующее шестнадцатеричное значение.

Шестнадцатеричную систему принято использовать для удобства восприятия двоичных данных, так как переводы из шестнадцатеричной системы в двоичную и обратно осуществляются простой заменой строк. Компьютер работает исключительно с двоичными последовательностями, а шестнадцатеричная запись этой последовательности в четыре раза компактнее, так как у этой системы основание 16 (2 16), а двоичной 2. Двоичная последовательность может быть достаточно громоздкой. Например, запись числа 513 требует десять двоичных разрядов (1000000001), а в шестнадцатеричной только три (201). Тем не менее, для представления любых шестнадцатеричных чисел требуется шестнадцать разных символов, а не десять, которые используются в привычной нам десятичной системе счисления. Первые десять символов это символы в интервале от 0 по 9, остальные это буквы латинского алфавита в интервале от A по F. Буквы обычно (но не всегда) пишут в верхнем регистре (заглавные) в шестнадцатеричной записи числа. Первые десять символов (от 0 по 9) записываются аналогично цифрам в десятичной системе счисления и соответствуют им.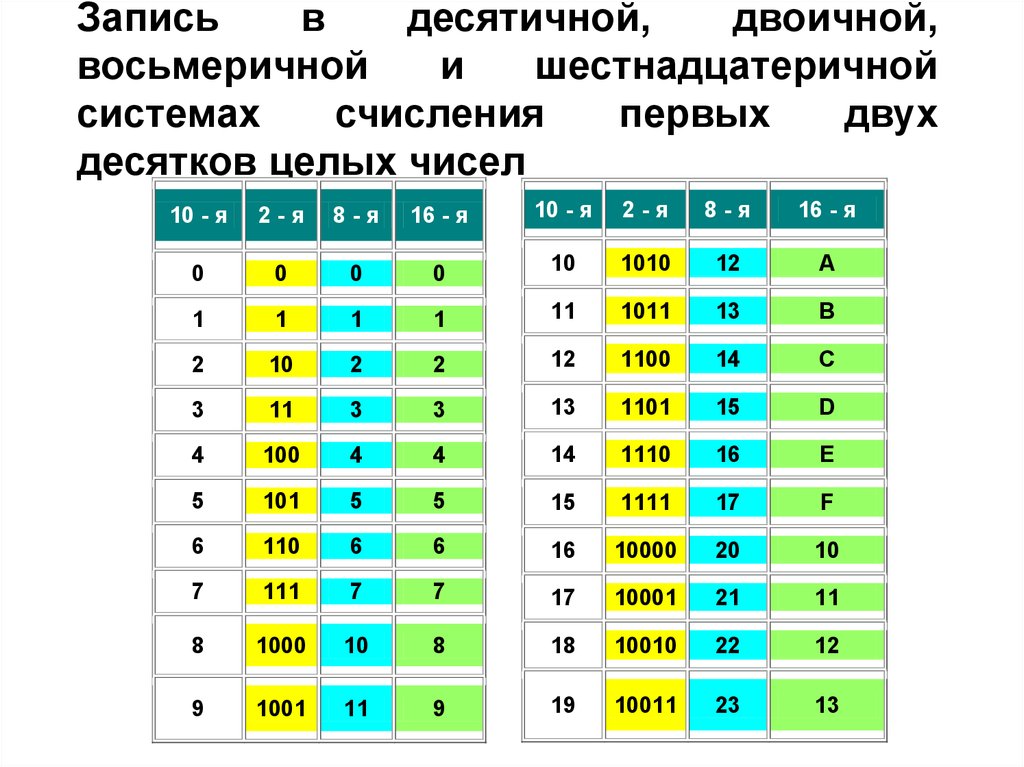 Буквы в интервале от A по F соответствуют значениям в интервале от 10 до 15.

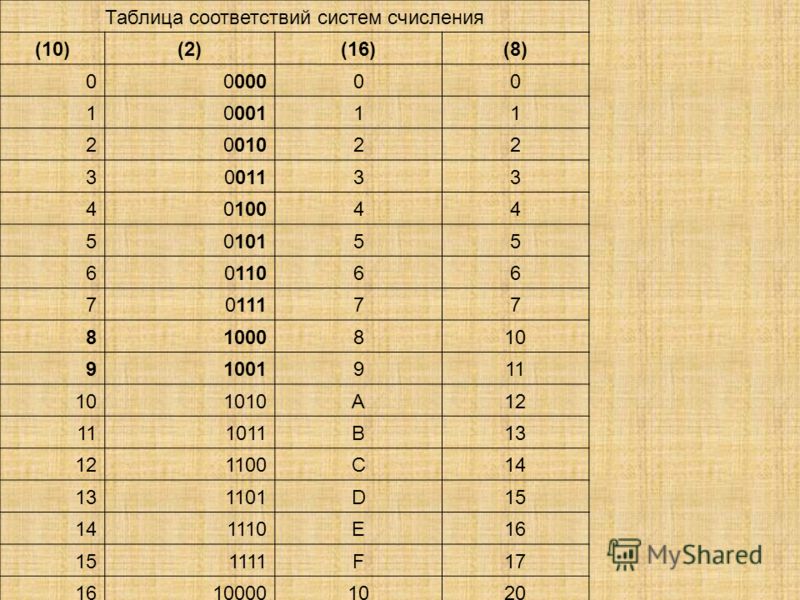
Рассмотрим соответствие чисел от 0 по 15 шестнадцатеричной и двоичной системам счисления.

Десятичная запись	Шестнадцатеричная запись	Двоичная запись
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Записи 10, 11 и т.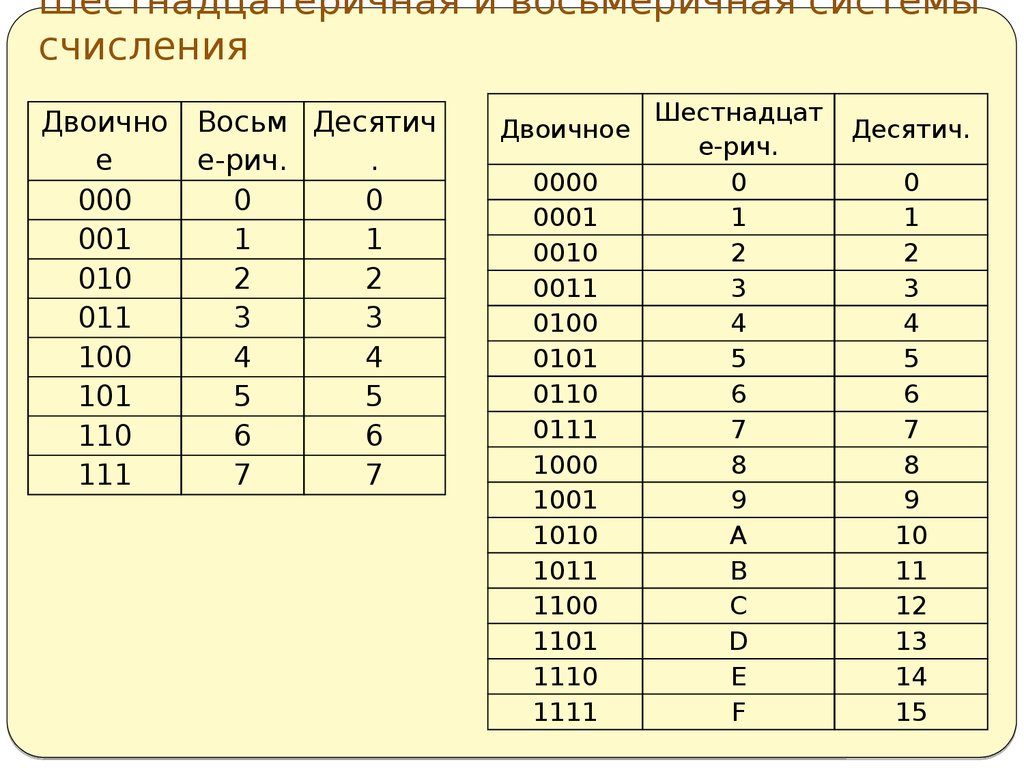 д. в десятичной, двоичной и шестнадцатеричной системах не соответствуют друг другу. Рассмотрим небольшой пример. Пусть у нас имеется шестнадцатеричное число число 1A5E. для перевода в двоичную запись достаточно просто заменить шестнадцатеричные разряды на соответствующие двоичные группы. Получится 0001 1010 0101 1110. Если убрать незначащие нули перед числом и записать его без разделителей получим 1101001011110. Для обратного перевода разделим число на группы по четыре разряда начиная с младшего (с правой стороны), а также для удобства добавим незначащие нули в старшей группе до 4 разрядов. Получим 0001 1010 0101 1110. Заменим группы на соответствующие шестнадцатеричные значения, получим 1A5E.

Для перевода шестнадцатеричного числа в десятичное представление можно воспользоваться схемой по которой мы записываем десятичные числа. В десятичном числе каждый разряд обозначает соответствующую степень числа десять начиная с нулевой с возрастанием справа налево. Например, десятичное число 123 обозначает 1*10 2 + 2*10 1 + 3*10 0 . Аналогичным методом переведем число 1A5E в десятичную систему счисления. В шестнадцатеричной системе счисления, также как и в десятичной каждый разряд обозначает соответствующую степень числа шестнадцать начиная с нулевой с возрастанием справа налево. Символы 1 и 5 в шестнадцатеричной системе счисления соответствуют значениям 1 и 5 в десятичной, а символы A и E — 10 и 14. Тогда 1A5E можно представить в десятичной системе счисления как 1*16 3 + 10*16 2 + 5*16 1 + 14*16 0 = 6750. Однако для оценки шестнадцатеричных чисел вовсе не обязательно переводить их в десятичные. Правила сравнения, сложения и умножения в этой системе такие же как и в десятичной, главное не забывать, что каждый разряд может содержать значения от 0 до 15. Для более быстрого перевода числе между система счисления можно воспользоваться стандартным калькулятором в Windows, для этого достаточно в расширенном режиме калькулятора выбрать систему счисления, ввести в ней число и выбрать нужную систему счисления, в которой следует отобразить результат.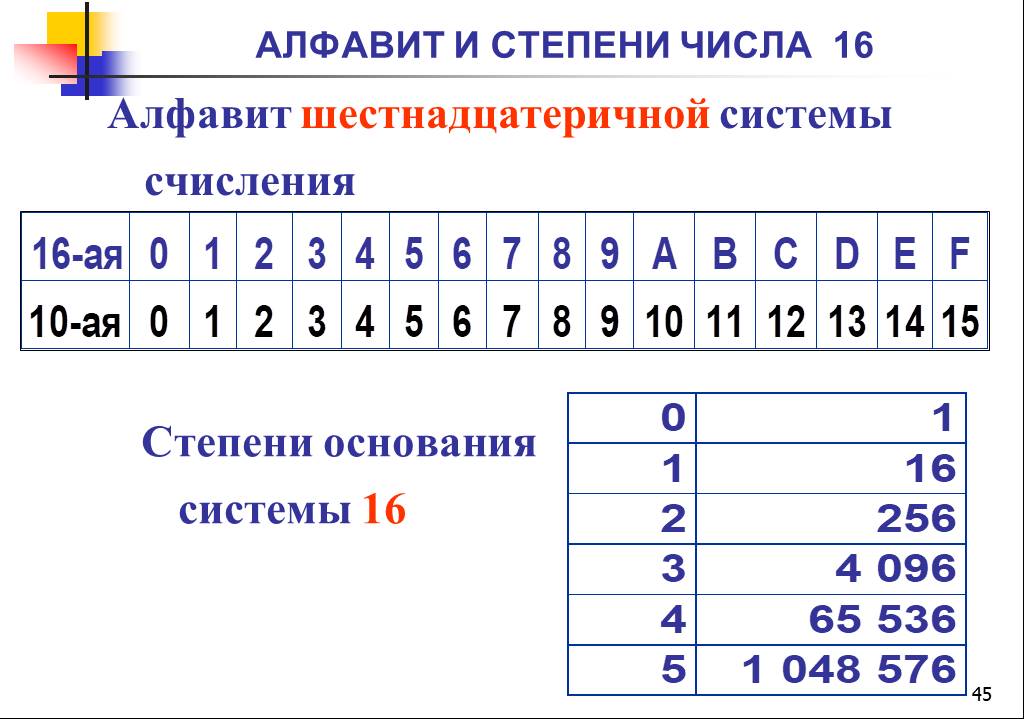

Так как шестнадцатеричные числа, состоящие только из чисел, легко спутать с десятичными, их обычно помечают так, чтобы было ясно, что используется именно шестнадцатеричная запись. Шестнадцатеричные записи обычно помечают либо добавлением в конец строчной буквы „h”, либо приставки „0x” перед записью числа. Таким образом шестнадцатеричное число 1A5E может быть записано как 1A5Eh или 0x1A5E, где „h” на конце или „0x” в начале обозначают, что используется шестнадцатеричная запись.

Шестнадцатеричные числа | это… Что такое Шестнадцатеричные числа?

ТолкованиеПеревод

Шестнадцатеричные числа

Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.

Содержание 1 Применение 2 Способы записи 2.1 В математике 2.2 В языках программирования 3 Перевод чисел из одной системы счисления в другую 3.1 Перевод чисел из шестнадцатеричной системы в десятичную 3.2 Перевод чисел из двоичной системы в шестнадцатеричную 3.3 Таблица перевода чисел 4 См. также 5 Ссылки

Применение

Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.

В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).

Способы записи

В математике

В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 1443₁₀ или как 5A3₁₆.

В языках программирования

В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:

• В Ада и
• В Си и языках схожего синтаксиса, например, в
• В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (255₁₀)
• Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
• Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т. д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
• Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
• В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.

Перевод чисел из одной системы счисления в другую

Перевод чисел из шестнадцатеричной системы в десятичную

Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:

5A3₁₆=5·16²+10·16¹+3·16⁰
=5·256+10·16+3·1=1280+160+3=1443₁₀

Перевод чисел из двоичной системы в шестнадцатеричную

Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.

Например:

10110100011₂=0101 1010 0011=5A3₁₆

Таблица перевода чисел

	0hex	=	0dec	=	0oct		0	0	0	0
	1hex	=	1dec	=	1oct		0	0	0	1
	2hex	=	2dec	=	2oct		0	0	1	0
	3hex	=	3dec	=	3oct		0	0	1	1
	4hex	=	4dec	=	4oct		0	1	0	0
	5hex	=	5dec	=	5oct		0	1	0	1
	6hex	=	6dec	=	6oct		0	1	1	0
	7hex	=	7dec	=	7oct		0	1	1	1
	8hex	=	8dec	=	10oct		1	0	0	0
	9hex	=	9dec	=	11oct		1	0	0	1
	Ahex	=	10dec	=	12oct		1	0	1	0
	Bhex	=	11dec	=	13oct		1	0	1	1
	Chex	=	12dec	=	14oct		1	1	0	0
	Dhex	=	13dec	=	15oct		1	1	0	1
	Ehex	=	14dec	=	16oct		1	1	1	0
	Fhex	=	15dec	=	17oct		1	1	1	1

См.

также

• Система счисления
• Двоичные приставки
• Шестнадцатеричный редактор

Ссылки

• Шестнадцатеричные числа и операции с ними
• Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
• Онлайн калькулятор для перевода чисел из одной системы счисления в другую

Wikimedia Foundation. 2010.

Игры ⚽ Нужно решить контрольную?

• Шестнадцатиричная система счисления
• Шестнадцать

Полезное

Сколько символов в шестнадцатеричной системе счисления?

8

12

16

20

Ответ:

16

Объяснение:

Изображение еще не загружено! Скоро будет обновлено

11

12

13

14

Ответ:

12

Объяснение:

Д = 14

Д = 13

Д = 12

Д = 11

Ответ:

D = 13

Объяснение:

1248

2481

4286

8421

Ответ:

8421

Объяснение:

1248

2481

4812

8421

Ответ:

8421

Объяснение:

For More Digital Electronics MCQ — Электрик (набор-1) с ответами

Щелкните здесь

Как читать шестнадцатеричные цветовые коды — шестнадцатеричный цвет

Перейти к содержимому

Независимо от того, являетесь ли вы цифровым художником и работаете с Adobe Creative Suite, в 3D-приложении или в UX-дизайне, вы, вероятно, использовали шестнадцатеричные цвета. Но даже если вы используете шестнадцатеричный код каждый день, есть большая вероятность, что вы не совсем понимаете, что происходит с этими комбинациями букв и цифр. Вот тут-то и пригодится это удобное руководство по чтению шестнадцатеричных цветовых кодов.

Что такое шестнадцатеричный код?

Шестнадцатеричные цветовые коды — это один из типов цветового кода HTML, который часто называют шестнадцатеричным цветом или шестнадцатеричным кодом. Причиной использования шестнадцатеричных чисел является удобное представление значений в двоичном коде.

Что означают цифры и буквы в шестнадцатеричном коде?

Шестнадцатеричные коды цветов начинаются со знака решетки или хэштега (#) и сопровождаются шестью буквами и/или цифрами. Первые две буквы/цифры относятся к красному цвету, следующие две — к зеленому, а последние две — к синему. Значения цвета определяются значениями от 00 до FF (вместо от 0 до 255 в RGB).

Числа используются, когда значение равно 1-9. Буквы используются, когда значение больше 9. Например:

• A=10

• В=11

• С=12

• Г=13

• Е=14

• F=15

Чтобы получить шестнадцатеричный цвет, выполните следующие три шага:

1. Умножьте первое число на 16.

2. Умножить второе число на 1.

3. Сложите две суммы вместе.

Понимание Hex в RGB для контекста

Перед тем, как перейти к чтению шестнадцатеричных цветовых кодов, лучше всего начать с изучения того, как понимать цвета RGB. Числа RGB основаны на настройках монитора красного, зеленого и синего света. Изменяя числа RGB, вы сообщаете своему монитору, сколько именно этого цвета света вы хотите сиять.

Что такое цветовые коды RGB?

В цветовой системе RGB цвета представлены следующим образом:

RGB(255, 0, 0)

RGB определяет значения красного (первое число), зеленого (второе число) или синего (третье число). Число 0 означает отсутствие представления цвета, а 255 означает максимально возможную концентрацию цвета.

Итак, в приведенном выше примере вы получаете максимально яркий красный цвет без присутствия зеленого или синего. Если бы вам нужен был только зеленый, вы бы использовали RGB(0, 255, 0), а для синего — RGB(0, 0, 255). Для других цветов вы будете использовать комбинацию цветовых значений, чтобы добиться желаемого результата.

Разница между шестнадцатеричными цветовыми кодами и кодами RGB

Поняв, что означают числа в шестнадцатеричных цветовых кодах, вы сможете лучше предсказать, какой цвет вы можете увидеть. Между использованием шестнадцатеричного или RGB-цвета нет большой разницы, за исключением того, что в CSS можно также добавить альфа-значение, так что у вас действительно будет цвет RGBA.

Это может быть очень полезно, если вы хотите контролировать непрозрачность цвета. Добавление альфа-значения к вашему RGB, безусловно, является одним из самых простых способов изменить непрозрачность.

Как читать шестнадцатеричные коды цветов

Как только вы действительно поймете RGB, вы можете двигаться дальше и научиться читать шестнадцатеричные коды. Это действительно очень просто, если вы знаете формулу. Как упоминалось выше, значения 1-9 указаны в числовом виде. Однако для значений 10 и выше цифры заменяются буквами. Итак, А=10, В=11, С=12 и так далее.

Теперь, чтобы вычислить шестнадцатеричное число, есть три быстрых шага (как указано выше):

1. Умножьте первое число (или преобразованное число из буквы) на 16.

2. Умножить второе число (или преобразованное число из буквы) на 1.

3. Сложите эти две суммы, чтобы получить одно значение.

Пример расчета шестнадцатеричного цветового кода

Например, шестнадцатеричное число для числа 83 на самом деле 131. Мы приходим к такому выводу:

1. Умножая 8 в 83 на 16 (8×16=128).

2. Умножение 3 из 83 на 1 (3×1=3).

3. Сложение двух итогов (128+3=131).

Другой способ представить это так:

(8×16) + (3×1) = 131

Работа с буквами — это та же концепция. Например, FF = 255, потому что вы умножаете число, представляющее F (15), на 16, а затем умножаете число, представляющее второе F (15), на 1. Затем сложите две суммы вместе, чтобы получить 255. Признайте, что число 255 такое же, как число RGB 255, которое является ярко-красным.

Если вы не хотите выполнять расчеты в уме, используйте инструмент преобразования RGB в HEX.

Оценка шестнадцатеричных кодов в реальном мире

Как только вы поймете числа, вы сможете предсказать, как будет выглядеть цвет, основываясь на значениях интенсивности красного, зеленого и/или синего. Итак, если вы знаете, что максимальный красный цвет без зеленого или синего равен #FF0000, то вы можете мысленно немного изменить значения, чтобы получить оценку для другого цвета.

Другой пример шестнадцатеричного кода цвета — #7DD0D7, что дает вам зеленовато-синий цвет.

Общие преобразования Hex в RGB

Может быть полезно запомнить некоторые из наиболее распространенных шестнадцатеричных цветовых кодов не только тогда, когда вы хотите использовать именно эти цвета, но и для того, чтобы лучше предсказывать, какими будут другие цвета, когда вы видите шестнадцатеричный цветовой код.

• Красный = #FF0000 = RGB(255, 0, 0)

• Зеленый = #008000 = RGB(1, 128, 0)

• Синий = #0000FF = RGB(0, 0, 255)

 

• Белый = #FFFFFF = RGB(255,255,255)

• Цвет слоновой кости = #FFFFF0 = RGB(255, 255, 240)

• Черный = #000000 = RGB(0, 0, 0)

• Серый = #808080 = RGB(128, 128, 128)

• Серебро = #C0C0C0 = RGB(192, 192, 192)

 

• Желтый = #FFFF00 = RGB(255, 255, 0)

• Фиолетовый = #800080 = RGB(128, 0, 128)

• Оранжевый = FFA500 = RGB(255, 165, 0)

• Бордовый = #800000 = RGB(128, 0, 0)

• Фуксия = #FF00FF = RGB(255, 0, 255)

 

• Салатовый = #00FF00 = RGB(0, 255, 0)

• Цвет морской волны = #00FFFF = RGB(0, 255, 255)

• Бирюзовый = #008080 = RGB(0, 128, 128)

• Оливковый = #808000 = RGB(128, 128, 0)

• Темно-синий = #000080 = RGB(0, 0, 128)

Найдите другие шестнадцатеричные коды цветов или выберите цвет HTML и получите его совпадающее имя и коды.

Помимо шестнадцатеричных цветовых кодов: выбор цветовой схемы

Самый быстрый способ выбрать цветовую схему для вашего проекта — использовать инструмент цветовой палитры, который позволяет вам искать группы по:

Этот же инструмент позволяет вам создать собственную схему, случайным образом выбирая и фиксируя цвета, которые вы как и что хорошо смотрятся вместе.

Выбрав цветовую схему, вы можете:

• Создать коллаж

• Исследование и создание градиента

• Проверка контрастности

• Настройка оттенка, насыщенности, яркости и температуры

Каждому цвету присваивается шестнадцатеричный цветовой код, который вы можете использовать. В конце концов, у вас будет собственная цветовая схема, которая идеально олицетворяет ваш проект.

Но прежде чем выбрать палитру, запомните следующие советы по цветовому дизайну:

• Учитывайте контекст.

• См. цветовой круг.

• Выберите монохроматическую, триадную или разделенную комплементарную цветовую схему.

• Не ограничивайтесь пресетами.

Часто задаваемые вопросы о шестнадцатеричных кодах цветов

Мы знаем, что у вас есть еще вопросы о шестнадцатеричных цветах, поэтому мы создали этот краткий раздел часто задаваемых вопросов.

Что означает «гекс»?

Hex — это сокращение от Hexa, что в переводе с греческого означает шесть.

Когда мне следует конвертировать шестнадцатеричный формат в RGB (или наоборот)?

Хотя обе системы работают, согласованность имеет первостепенное значение. При разработке для определенного бренда проверьте их руководство по бренду, чтобы узнать, какой системе следовать, и соответствующим образом преобразовать цвета.

Как получить шестнадцатеричный код цвета для цвета изображения?

Существует множество бесплатных онлайн-инструментов для выбора цвета, которые позволяют очень легко получить шестнадцатеричный код цвета для определенного изображения.

Как правило, все, что вам нужно сделать, это либо вставить URL-адрес изображения, либо загрузить свое изображение в инструмент выбора цвета и выбрать цветовой пиксель. Вы получите шестнадцатеричный код цвета и значения RGB.

Как изменить шестнадцатеричный цвет в Adobe Illustrator?

Чтобы изменить шестнадцатеричный цвет в Adobe Illustrator, выполните следующие действия:

1. В новом документе Illustrator нажмите F6.

2. Дважды щелкните поле обводки или заливки в окне «Цвет».

3. Дважды щелкните внутри поля рядом с #.

4. Введите в поле новый шестнадцатеричный код цвета.

5. Нажмите OK.

Шестнадцатеричные инструменты цвета в этом руководстве

В этом руководстве мы предоставили вам множество полезных инструментов, поэтому они снова собраны в одном месте:

• Инструмент для преобразования шестнадцатеричного формата в RGB

• Цветовые коды HTML

• Другая таблица цветовых кодов HTML

• Инструмент цветовой палитры

• Советы по цветовому оформлению

• Палитра цветов

• Шестнадцатеричный инструмент цвета CSS

Обертывание шестнадцатеричных цветовых кодов

В заключение несколько напоминаний:

• Типы цветов Hex и RGB предназначены для использования на экране при разработке веб-сайтов.

• В CSS можно добавить альфа-значение для управления непрозрачностью цвета.

• Для бренда ключевое значение имеет постоянство цвета.

• Всегда стремитесь узнать больше о своей работе, просматривая ресурсы и посещая курсы, предлагаемые Pluralsight!

С помощью плана Pluralsight вы можете:

С помощью 14-дневного пилотного проекта вы можете:

• Доступ к тысячам видеороликов для развития важнейших навыков
• Предоставьте до 10 пользователей доступ к тысячам видеокурсов
• Практика и применение навыков с интерактивными курсами и проектами
• Просмотр данных о навыках, использовании и тенденциях для ваших команд
• Подготовьтесь к сертификации с помощью лучших в отрасли практических экзаменов
• Измерение уровня владения навыками и ролями
• Согласуйте обучение с вашими целями с помощью путей и каналов

Готовы повысить уровень

всей своей команды?

10

Подписки

Нужно больше подписок? Свяжитесь с отделом продаж.