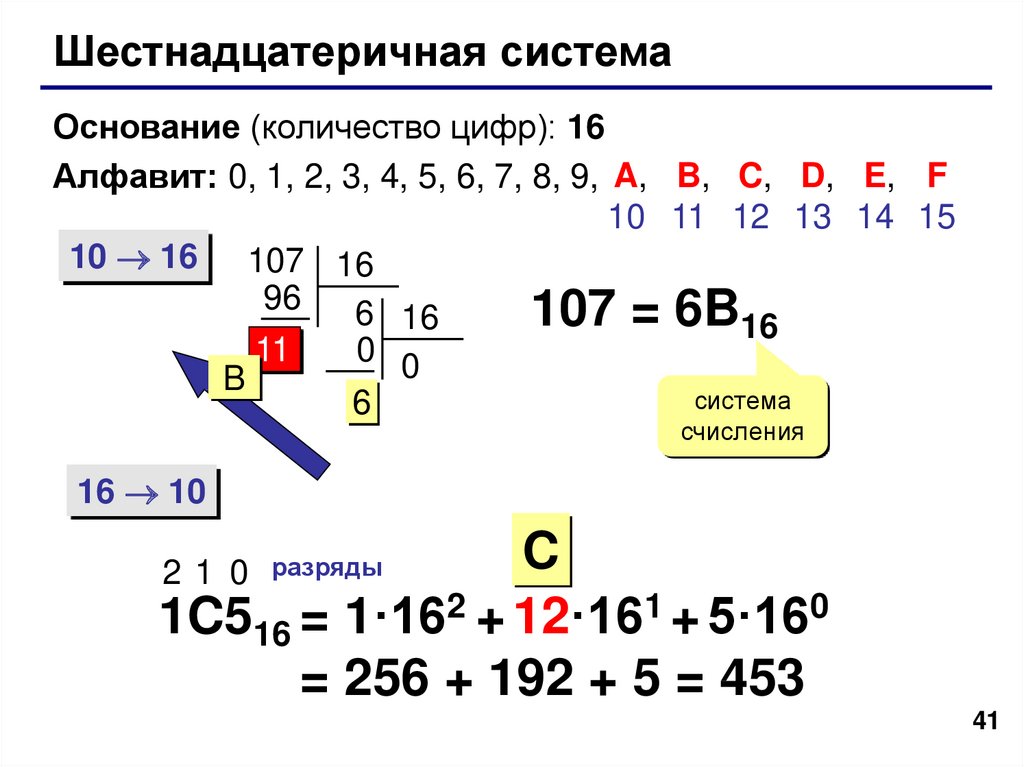
Шестнадцатеричная система счисления
Главная / Ассемблер / Для чайников / Системы счисления /
Как мы увидели выше, с двоичным числом удобно работать при поразрядных операциях, однако запись двоичного числа получается довольно громоздкой. Чтобы немного упростить жизнь программистам, была придумана шестнадцатеричная система счисления, которая использует 16 цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Соответственно, основание шестнадцатеричной системы равно 16.
Шестнадцатеричное число является компактным и лёгким для чтения. Его легко преобразовать в двоичное и наоборот. Каждый разряд шестнадцатеричного числа – это тетрада. Каждую тетраду легко преобразовать в двоичное число и наоборот (см. таблицу 2.3).
Таблица 2.
| Десятичное | Двоичное | Шестнадцатеричное |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 1111 | F |
В конец шестнадцатеричного числа принято ставить букву h.
Таким образом мы
можем отличить шестнадцатеричное число от чисел в других системах исчисления. Например
11 – десятичное число 11 11b – двоичное число, которое эквивалентно десятичному числу 3 11h – шестнадцатеричное число, которое эквивалентно десятичному числу 17
В исходных кодах программ на ассемблере, если шестнадцатеричное число начинается с буквы, то перед ним нужно поставить ноль, иначе ассемблер подумает, что это не число, а имя переменной. Например, число FF в исходном коде на ассемблере должно быть записано как 0FFh.
Шестнадцатеричная система счисления
Шестнадцатеричная система цифр, часто сокращаемая до «калаб», представляет собой систему цифр, состоящую из 16 символов (основание 16). Стандартная система цифр называется десятичной (основа 10) и использует десять символов: 0,1,2,3,4,5,6,7,8,9. В шестнадцатеричной системе используются десятичные числа и шесть дополнительных символов.
Нет цифровых символов, представляющих значения больше девяти, поэтому используются буквы, взятые из английского алфавита, а именно: A, B, C, D, E и F. Шестнадцатеричная A = десятичная 10, а шестнадцатеричная F = десятичная 15.
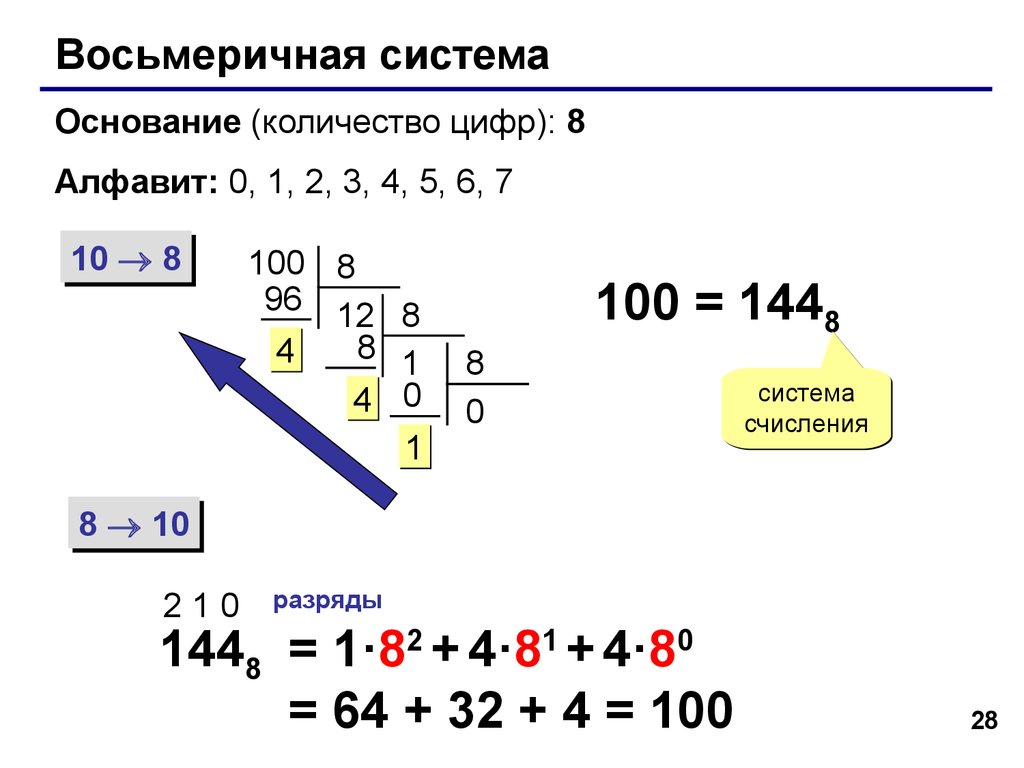
Люди в основном используют десятичную систему. Вероятно, это потому, что у человека на руках десять пальцев. Компьютеры, однако, имеют только вкл и выкл, называемый двоичной цифрой (или бит, для краткости). Двоичное число — это просто строка из нулей и единиц: 11011011, например. Для удобства инженеры, работающие с компьютерами, склонны группировать биты. В более ранние времена, например, в 1960-е, они группировали по 3 бита за раз (так же, как большие десятичные числа группируются по 3, как и число 123 456 789). Три бита, каждый из которых включен или выключен, могут представлять собой восемь чисел от 0 до 7: 000 = 0; 001 = 1; 010 = 2; 011 = 3; 100 = 4; 101 = 5; 110 = 6 и 111 = 7. Это называется восьмеричным числом.
По мере того, как компьютеры становились больше, было удобнее группировать биты на четыре, а не на три.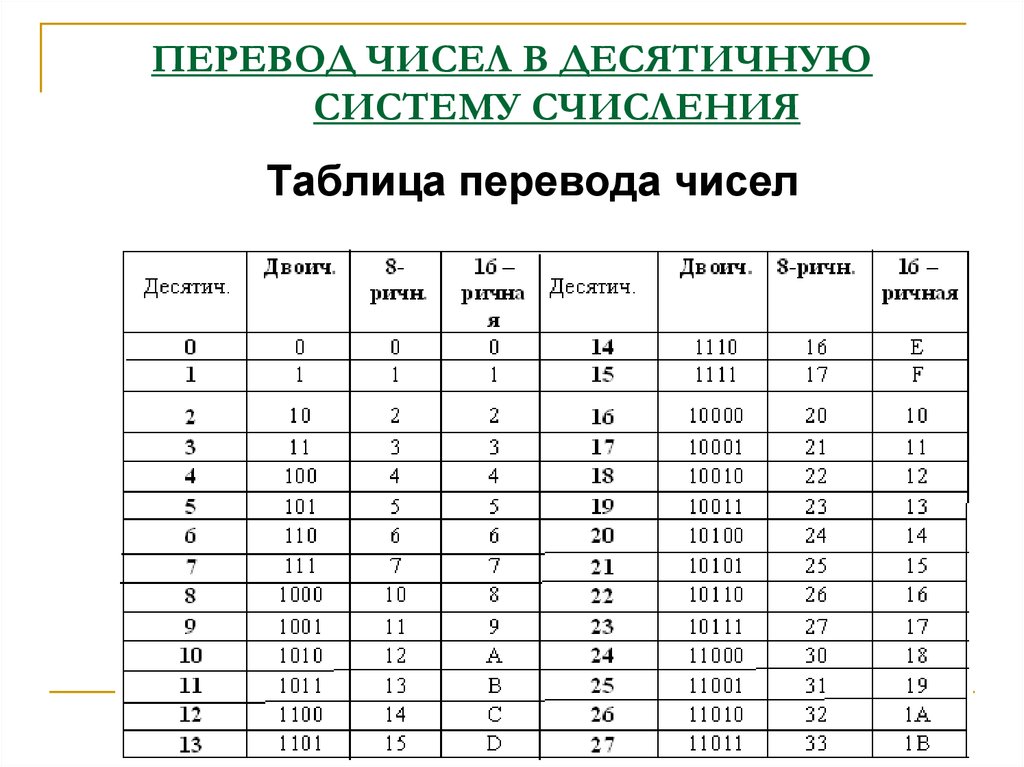
Это удваивает числа, которые символ будет представлять; он может иметь 16 значений вместо восьми. Гекс = 6 и десятичный = 10, поэтому он называется шестнадцатеричным. На компьютерном жаргоне четыре бита делают зазубрины (иногда пишутся зазубрины). Клёв — это одна шестнадцатеричная цифра, записанная символом 0-9 или A-F. Два куска делают байт (8 бит). В большинстве компьютерных операций используется байт или кратное ему число (16 бит, 24, 32, 64 и т.д.). Шестнадцатеричная система упрощает запись этих больших двоичных чисел.
Чтобы избежать путаницы с десятичными, восьмеричными или другими системами нумерации, шестнадцатеричные числа иногда пишутся с буквой «h» после или «0x» перед числом. Например, 63h и 0x63 означают 63 шестнадцатеричных числа.
шестнадцатеричные значения
Шестнадцатеричная система похожа на восьмеричную систему цифр (основа 8), потому что каждая из них легко сравнивается с двоичной системой цифр. Шестнадцатеричная система использует четырехразрядную двоичную кодировку.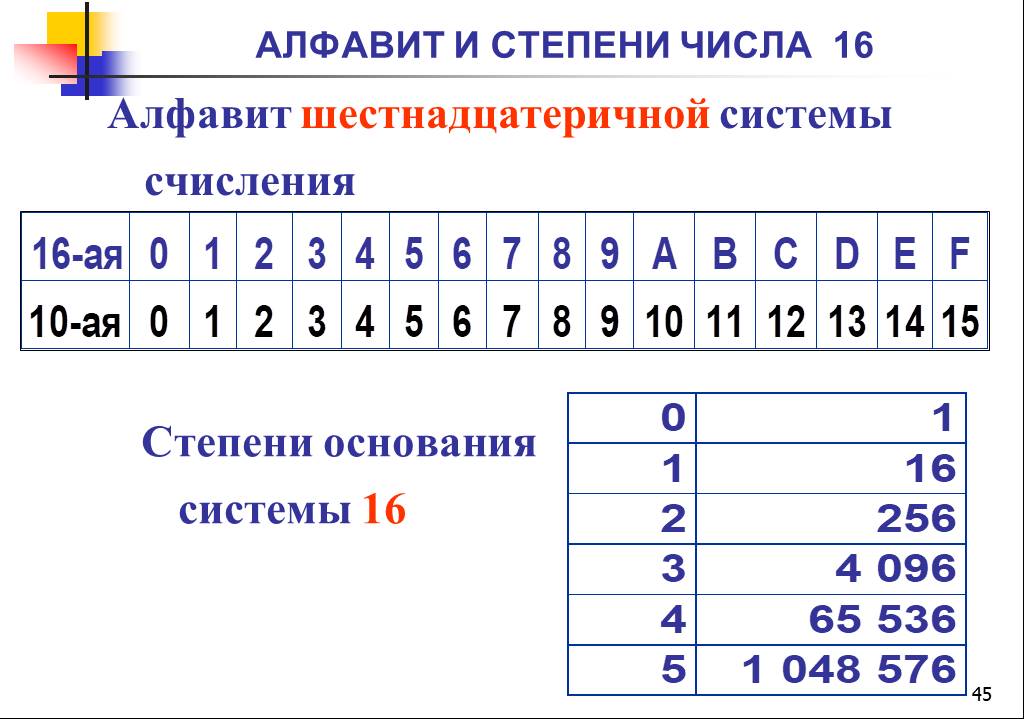
Это означает, что каждая цифра в шестнадцатеричной системе счисления совпадает с четырьмя цифрами в двоичной. Окталь использует трехразрядную двоичную систему.
В десятичной системе первая цифра — это место человека, следующая цифра слева — это место десяти, следующая — это место сотни и т.д. В шестнадцатеричной системе каждая цифра может быть 16, а не 10. Это означает, что цифры стоят на месте одного, шестнадцать — на месте, а следующая цифра — на месте 256. То есть 1h = 1 десятичная, 10h = 16 десятичная, и 100h = 256 десятичная.
Примеры значений шестнадцатеричных чисел, преобразованных в двоичные, восьмеричные и десятичные.
|
Преобразование
Двоичный до шестнадцатиричного
Изменение числа с двоичного на гекс использует метод группировки.
Двоичное число разбивается на группы по четыре цифры, начиная с правой. Затем эти группы преобразуются в шестнадцатеричные цифры, как показано на графике выше для шестнадцатеричных чисел от 0 до F. Для перехода от шестнадцатеричной к шестнадцатеричной производится обратное преобразование. Каждая шестнадцатеричная цифра меняется на двоичную, и группировка обычно удаляется.
Двоичный | Группировки | Гекс | |||
01100101 | 0110 | 0101 | 65 | ||
010010110110 | 0100 | 1011 | 0110 | 4B6 | |
1101011101011010 | 1101 | 0111 | 0101 | 1010 | D75A |
Когда количество битов в двоичном числе не кратно 4, для этого оно дополняется нулями.
Примеры:
- двоичный 110 = 0110, то есть 6 Гекс.
- двоичный 010010 = 00010010, что означает 12 Гекс.
от шестнадцатиричного до десятичного
Для преобразования числа из шестнадцатеричного в десятичный существует два общих способа.
Первый метод чаще всего используется при преобразовании вручную:
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0-9 это то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14, и F = 15.
- Сохраняйте сумму цифр, конвертированных на каждом шаге ниже.
- Начните с наименее значимой шестнадцатеричной цифры. Это цифра с правого конца. Это будет первый пункт в сумме.
- Возьмите вторую последнюю значащую цифру. Это рядом с цифрой на правом конце. Умножьте десятичное значение цифры на 16. Добавьте это к сумме.
- Сделайте то же самое для третьей крайней значащей цифры, но умножьте ее на 162 (т.е. 16 в квадрате или 256). Прибавьте к сумме.
- Продолжайте для каждой цифры, умножая каждое место на другую мощность 16. (4096, 65536 и т.д.)
| Местоположение | |||||
6 | 5 | 4 | 3 | 2 | 1 | |
Значение | 1048576 (165) | 65536 (164) | 4096 (163) | 256 (162) | 16(161) | 1 (160) |
Следующий метод чаще всего используется при преобразовании числа в программном обеспечении. Ему не нужно знать, сколько цифр имеет число до его начала, и оно никогда не умножается более чем на 16, но на бумаге оно выглядит дольше.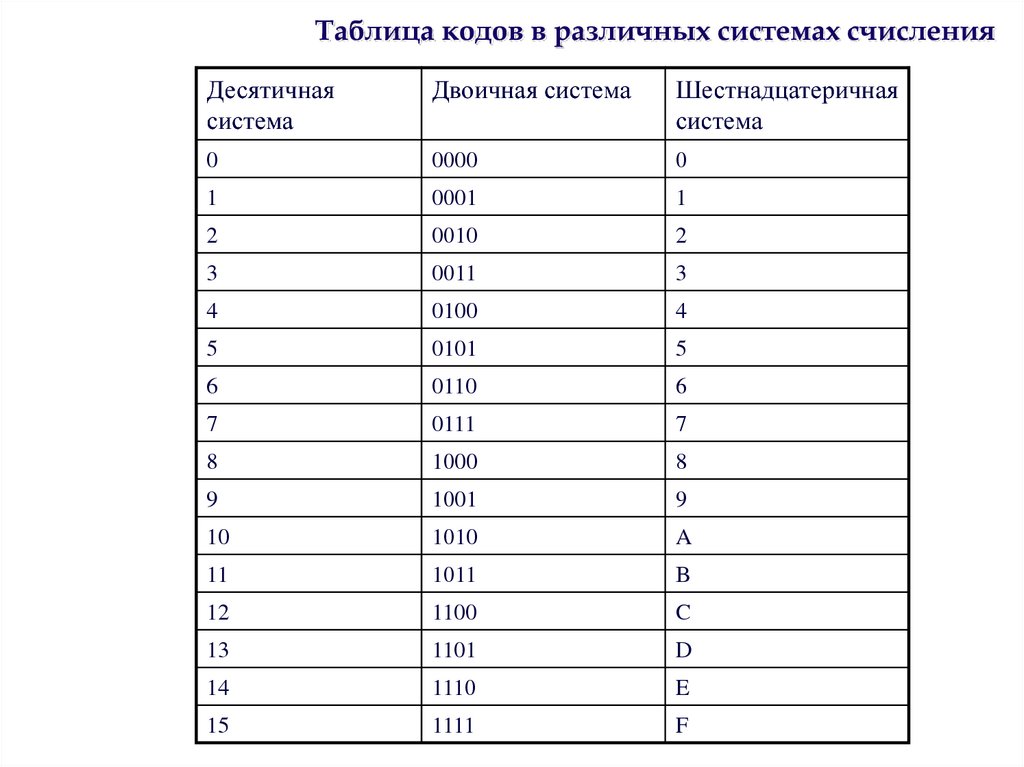
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0-9 это то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14, и F = 15.
- Сохраняйте сумму цифр, конвертированных на каждом шаге ниже.
- Начните с наиболее значимой цифры (цифра слева). Это первый пункт в сумме.
- Если существует другая цифра, умножьте сумму на 16 и прибавите десятичное значение следующей цифры.
- Повторяйте вышеописанный шаг до тех пор, пока больше нет цифр.
Пример: 5Fh и 3425h до десятичной дроби, метод 1
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример: 5Fh и 3425h до десятичной дроби, метод 2
|
|
|
| |||||||||||||||||||||||||||||||||||||||||
Связанные страницы
- двоичная система цифр
- система октябрьских цифр
- Система десятичных цифр
Вопросы и ответы
В: Что такое шестнадцатеричная система счисления?О: Шестнадцатеричная система счисления — это система счисления по основанию 16, состоящая из 16 символов.
В: Какие десять символов используются в десятичной системе (основание 10)?
О: В десятичной системе счисления (основание 10) используются следующие десять символов: 0,1,2,3,4,5,6,7,8 и 9.
В: Какие шесть дополнительных символов используются в шестнадцатеричной системе?
О: В шестнадцатеричной системе используются буквы из английского алфавита — A, B, C, D, E и F.
В: Сколько битов содержит один байт в современных компьютерах?
О: В современных компьютерах каждый байт обычно содержит восемь битов.
В: Что инженеры и компьютерщики называют четырехбитовыми значениями?
О: Инженеры и компьютерщики называют четырехбитные значения ниблами (иногда пишется nybble).
В: Как избежать путаницы с другими системами нумерации при записи шестнадцатеричных чисел?
О: Чтобы избежать путаницы с другими системами нумерации при написании шестнадцатеричных чисел, Вы можете добавить «h» после или «0x» перед числом. Например, 63h или 0x63 означает 63 в шестнадцатеричной системе счисления.
Автор
Alegsaonline.com — Шестнадцатеричная система счисленияШестнадцатеричные числа (с основанием 16) — катализатор2
Последнее обновление:
использовать в нашей повседневной жизни и числа по основанию 2. В этой статье рассматриваются шестнадцатеричные числа (с основанием 16). Понимание системы base-16 имеет решающее значение для понимания адресов IPv6.
Сводка по основанию 10 и 2
В качестве краткого обзора, десятичная система использует десять цифр: от 0 до 9. Конечно, вы можете считать больше 9. Для этого вы просто используете более одной цифры. Итак, чтобы пройти дальше 9, вы меняете значение на 0 и добавляете 1 слева. Это дает вам число 10.
Система с основанием 2 имеет только два значения: 0 и 1. Чтобы представить число больше 1, вы снова используете более одной цифры.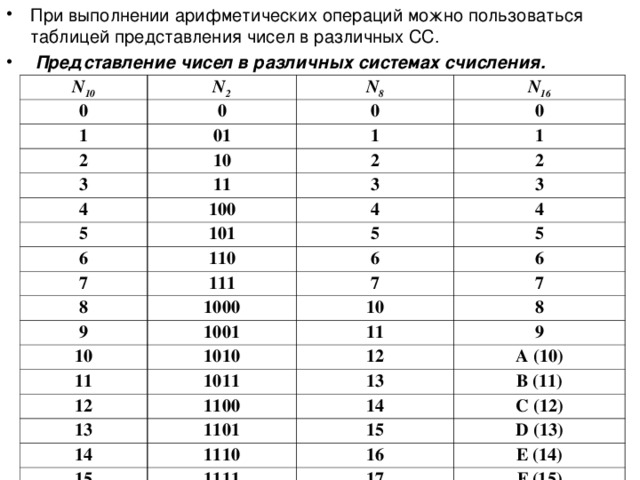
Чтобы получить число 2, вы меняете число на 0 и ставите перед ним 1. Итак, в системе счисления 2 число 2 записывается как 10.
База-16
База-16 использует 16 значений: числа от 0 до 9и буквы от A до F. До числа 9 десятичная и шестнадцатеричная системы идентичны: число 9 с основанием 10 также является 9 в основании 16. У нас нет единого числа для десяти, поэтому в базе 16 используются буквы от A до F. Буква A равна 10, B равна 11 и т. д. увеличены. Можете ли вы догадаться, что такое десятичное число 16 по основанию 2 и 16?
База-10 | База-2 | База-16 ---------+--------+-------- 0 | 0 | 0 1 | 1 | 1 2 | 10 | 2 3 | 11 | 3 4 | 100 | 4 5 | 101 | 5 6 | 110 | 6 7 | 111 | 7 8 | 1000 | 8 9| 1001 | 9 10 | 1010 | А 11 | 1011 | Б 12 | 1100 | С 13 | 1101 | Д 14 | 1110 | Е 15 | 1111 | Ф
Для обоих вам нужно изменить число на 0 и добавить 1 слева. Представление десятичного числа 15 по основанию 2 равно 1111, поэтому 16 становится 10000.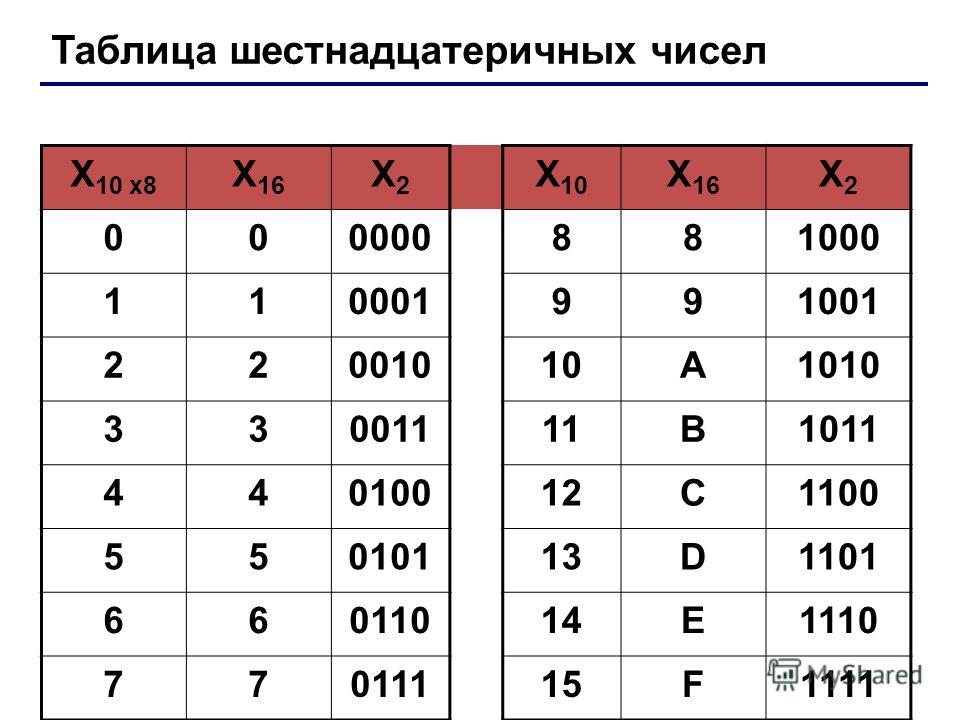
Точно так же буква F является наибольшим значением в основании 16. Таким образом, следующим значением становится 10.
Преобразование шестнадцатиричного числа в десятичное
Приведенная выше таблица удобна, но она не поможет вам преобразовать большие числа с основанием 16 в основание 10. Конечно, есть формула для преобразования основания 16 в основание 10. Для каждого шестнадцатеричного символа вам необходимо вычислить десятичное значение, а затем сложить итог. Чтобы вычислить отдельные десятичные значения, вы работаете справа налево. Самое правое шестнадцатеричное значение умножается на 16
Это немного абстрактно, поэтому давайте рассмотрим несколько примеров. Начнем с внесения изменений в приведенную выше таблицу. Все значения base-16 имеют только один символ. Итак, формула представляет собой просто число с основанием 16, умноженное на 16 0 . Поскольку 16 * 0 равно 0, значения не меняются:
Base-10 | База-16 в базу-10 ---------+------------------------ 0 | 0 х 16 0 = 0 1 | 1 х 16 0 = 1 2 | 2 х 16 0 = 2 3 | 3 х 16 0 = 3 4 | 4 х 160 = 4
Стоит отметить, что «нулевая степень» всегда возвращает 1, а не 0, как можно было бы ожидать (почему я рассказываю в своей статье о числах с основанием 2).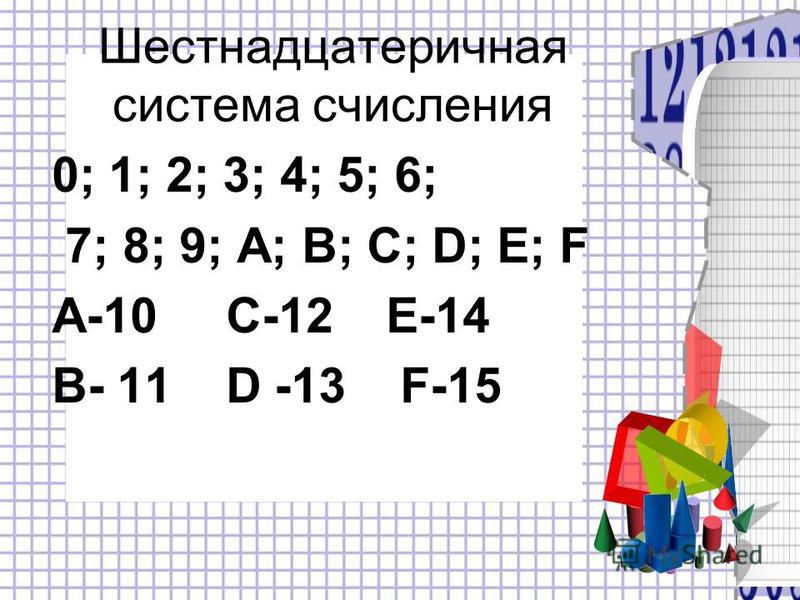
Таким образом, мы просто умножаем самое правое значение на 1.
Далее, давайте посмотрим на число 10 с основанием 16. Теперь у нас есть два значения: 1 и 0. Чтобы преобразовать шестнадцатеричное число, мы начнем с правого- наибольшее значение и умножьте его на 16 0 . Это дает нам ноль, так как 0 * 1 ничему не равно. Далее мы берем 1 и умножаем на 16 1 . Это возвращает 16, поэтому шестнадцатеричное число 10 преобразуется в десятичное число 16 (16 + 0 = 16).
Расчет можно записать следующим образом:
(1x16 1 ) + (0x16 0 ) = 16
Или вам может показаться более читаемым:
1 x 16 1 16
0 х 16 0 0
----
База-10 16
Если это имеет смысл, то мы можем попробовать что-то более сложное: преобразование ACDC в десятичном виде. Для этого вы выполняете ту же магию. Вы начинаете с самого правого значения ( D , что является десятичным числом 12) и продвигаетесь влево:
10 x 16 3 = 10 x 4096 = 40960
12 х 16 2 = 12 х 256 = 3072
13 х 16 1 = 13 х 16 = 208
12 х 16 0 = 12 х 1 = 12
-----
База-10 44252
Преобразование числа с основанием 10 в число 16
Преобразование числа с основанием 10 в шестнадцатеричное работает так же, как преобразование числа с основанием 10 в двоичное число.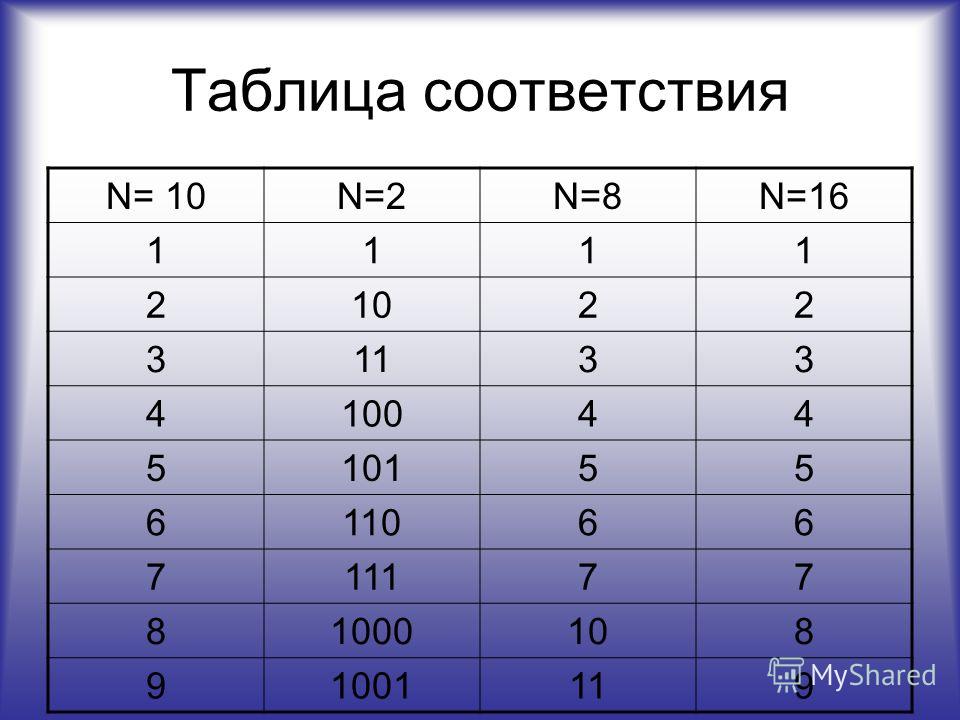
Вы делите число на показатель степени (16) и продолжаете делить результат до тех пор, пока частное не станет равным 0. На каждом шаге вы умножаете остаток на 16, чтобы получить шестнадцатеричное значение.
Как всегда, проще всего объяснить это на нескольких примерах. Давайте переработаем десятичное число 44252 и проверим, переводится ли оно в ACDC :
Частное | 16 * Остаток | Шестнадцатеричный
------------------------------+----+ -----
44252/16 = 2765,75 (2765) | 16 * 0,75 = 12 | С
2765/16 = 172,8125 (172) | 16 * 0,8125 = 13 | Д
172 / 16 = 10,75 (10) | 16 * 0,75 = 12 | С
10/16 = 0,625 (0) | 16 * 0,625 = 10 | А
Последним шагом является объединение шестнадцатеричных значений, начиная с последнего значения. Итак, это дает нам ACDC .
Еще один пример: тот же рецепт работает для десятичного числа 16 :
Частное | 16 * Остаток | Шестнадцатеричный
------------------------------+----+ -----
16/16 = 1,0 (1) | 16 * 0 = 0 | 0
1/16 = 0,0625 (0) | 16 * 0,0625 = 1 | 1
Преобразование базы 2 в базу 16
Конечно, вы также можете конвертировать из двоичного в шестнадцатеричный и наоборот.
Чтобы преобразовать базу 2 в базу 10, вы разбиваете двоичное значение на блоки из четырех цифр (известные как полубайтов ), а затем ищете шестнадцатеричное значение для каждого блока. Чтобы найти шестнадцатеричные значения, вы можете обратиться к слегка измененной таблице base-2, 10 и 16:
Base-10 | База-2 | База-16 ---------+--------+-------- 0 | 0000 | 0 1 | 0001 | 1 2 | 0010 | 2 3 | 0011 | 3 4 | 0100 | 4 5 | 0101 | 5 6 | 0110 | 6 7 | 0111 | 7 8 | 1000 | 8 9| 1001 | 9 10 | 1010 | А 11 | 1011 | Б 12 | 1100 | С 13 | 1101 | Д 14 | 1110 | Е 15 | 1111 | Ф
Единственная разница с таблицей, которую я показал ранее, заключается в том, что все числа с основанием 2 теперь состоят из четырех цифр (т. е. они используют ведущие нули, если применимо). Это упрощает поиск шестнадцатеричных значений.
Например, десятичное число 16 равно 10000 в двоичном формате. Число состоит из пяти цифр, поэтому вы добавляете три начальных нуля, чтобы получить две группы из четырех цифр:
0001 0000
Затем вы можете использовать приведенную выше таблицу, чтобы найти шестнадцатеричные значения для двух блоков:
0001 = 1 0000 = 0
Итак, мы получили 1 и 0, что дает нам шестнадцатеричное значение 10 .
Попробуем еще раз, используя большее число:
1010 1100 1101 1100 ПЕРЕМЕННЫЙ ТОК
Правильно, мы вернулись с ACDC !
Преобразование шестнадцатеричной системы счисления в двоичную
Преобразование шестнадцатеричного числа в двоичное — это обратный процесс. Вы берете каждую шестнадцатеричную цифру и ищете двоичное значение. Превратим ACDC и 10 еще раз:
Base-16 | ПЕРЕМЕННЫЙ ТОК База-2 | 1010 1100 1101 1100 База-16 | 1 0 База-2 | 0001 0000
ДЕСЯТИЧНАЯ функция — служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для Mac 2011 Дополнительно…Меньше
В этой статье описывается синтаксис формулы и использование ДЕСЯТИЧНЫЙ функция в Microsoft Excel.
Описание
Преобразует текстовое представление числа в заданной системе счисления в десятичное число.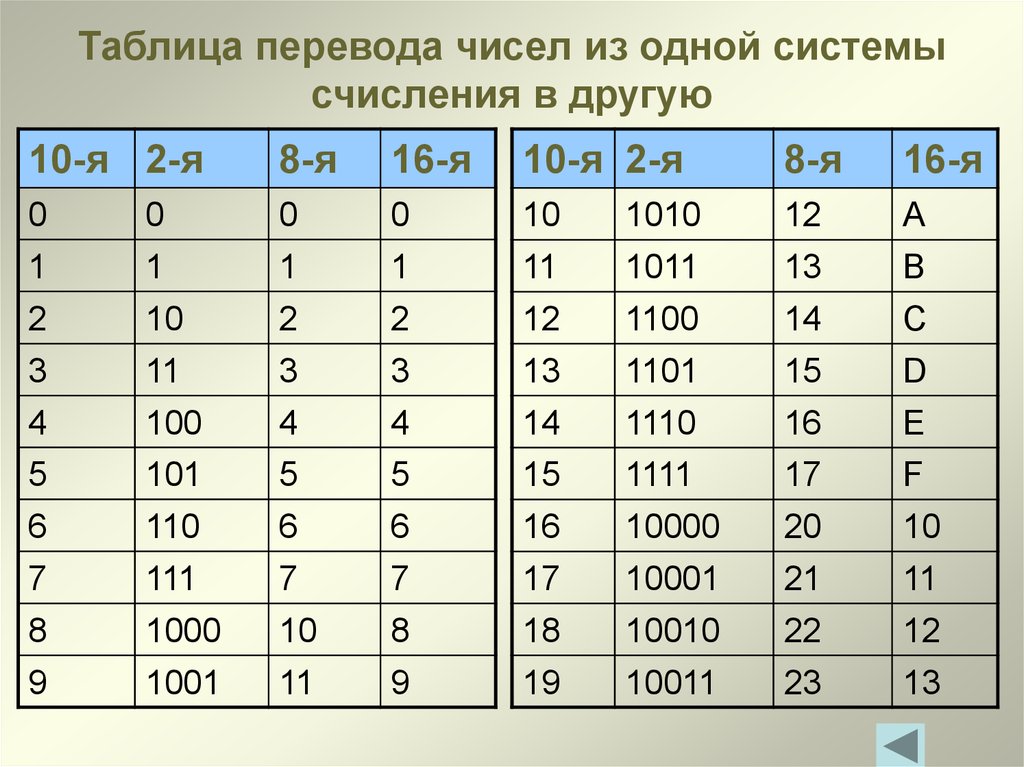
Синтаксис
ДЕСЯТИЧНОЕ (текст, основание)
Синтаксис функции DECIMAL имеет следующие аргументы.
Замечания
953 может привести к потере точности. Основание должно быть больше или равно 2 (двоичное или по основанию 2) и меньше или равно 36 (по основанию 36).
В системе счисления больше 10 используйте числовые значения 0–9 и буквы A–Z по мере необходимости. Например, основание 16 (шестнадцатеричное) использует 0-9 и A-F, а основание 36 использует 0-9 и A-Z.
Если какой-либо из аргументов выходит за пределы ограничений, функция DECIMAL может вернуть ошибку #NUM! или #ЗНАЧ! значение ошибки.
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
Формула | Описание | Результат | Как это работает |
‘= ДЕСЯТИЧНОЕ («FF», 16) | Преобразует шестнадцатеричное (с основанием 16) значение FF в его эквивалентное десятичное (с основанием 10) значение (255). | = ДЕСЯТИЧНОЕ («FF», 16) | «F» находится в позиции 15 в системе счисления с основанием 16. Поскольку все системы счисления начинаются с 0, 16-й символ в шестнадцатеричном формате будет на 15-й позиции. В приведенной ниже формуле показано, как оно преобразуется в десятичную форму: . |
Функция HEX2DEC в ячейке C3 проверяет этот результат. | =HEX2DEC(«ff») 90)) | ||
‘= ДЕСЯТИЧНОЕ (111,2) | Преобразует двоичное (с основанием 2) значение 111 в его эквивалентное десятичное (с основанием 10) значение (7). | = ДЕСЯТИЧНОЕ (111,2) | «1» находится в позиции 1 в системе счисления с основанием 2. |
Функция BIN2DEC в ячейке C6 проверяет этот результат. | =БИН2ДЕК(111) | 90)) | |
‘= ДЕСЯТИЧНОЕ («зап», 36) | Преобразует значение «zap» по основанию 36 в его эквивалентное десятичное значение (45745). | = ДЕСЯТИЧНОЕ («зап», 36) | «z» находится в позиции 35, «a» — в позиции 10, а «p» — в позиции 25.  |
В приведенной ниже формуле показано, как оно преобразуется в десятичную форму: