Векторы и скаляры
Величины, с которыми приходится встречаться в физике, механике и других прикладных дисциплинах, бывают двоякого рода: скалярные и векторные.
Скалярными величинами, или скалярами, называются величины, которые определяются только числовым значением.
Например: время, масса, плотность, длина отрезка, площадь, объем и т. д
Векторными величинами, или векторами, называются величины, которые определяются не только численным значением, но направлением и точкой приложения.
Например: сила, скорость, ускорение и т. д.
Векторные величины геометрически изображаются в виде отрезков, снабженных стрелками. Стрелка указывает направление, а длина отрезка изображает численные значения вектора и называется длиною, или модулем, или абсолютной величиной вектора.
Рис.1
Векторы обычно обозначаются либо буквой и черточкой над ней а, либо двумя буквами и черточкой над ними АВ, причем в этом случае первая буква указывает начало вектора, а вторая — его конец (рис.1).
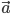 обозначается символом
обозначается символом  , либо символом
, либо символом  .
.Два вектора называются равными, если они имеют одинаковые длины, лежат на параллельных прямых, либо на одной прямой, и направлены в одну сторону. Из определения равенства векторов следует, что при параллельном переносе вектора получается вектор, равный исходному. Поэтому начало вектора можно помещать в любой точке пространства. Выбрав некоторое начало — точку О, — удобно считать все векторы исходящими из этой точки. В таком случае мы будем говорить, что
Если начало вектора совпадает с его концом, то вектор называется нулевым. Направление нулевого вектора неопределенно. Все нулевые векторы считаются равными друг другу.
Векторы, параллельные одной прямой, называются коллинеарными.
Векторы, параллельные одной плоскости, называются
Введение в скаляры и векторы
Физика > Введение в скаляры и векторы
Скаляр и вектор – описание понятий и определений в физике: координаты, длина, произведение векторов, скалярное произведение векторов, отличие скаляра и вектора.
Вектор – любая величина, обладающая размером и направлением, а скаляр может похвастаться лишь величиной.
Задача обучения
- Отличать скаляры от векторов.
Основные пункты
- Вектор – любое количество с величиной и направлением.
- Скаляр – любое количество с величиной, но лишенное направления.
- Смещение и скорость – векторы, а расстояние и скорость – скаляры.
Термины
- Вектор – количество, обладающее величиной и направлением (между двумя точками).
- Скаляр – количество с величиной, но без направления.
Пример
Скорость человека способна оставаться стабильной при повороте за угол или смене направления. Учитывая этот факт, с чем же мы столкнулись: вектор или скаляр? Скорость – скалярная величина, так как не меняется из-за направления.
В чем отличие между расстоянием и смещением? Первая характеризуется только величиной, в то время как смещение – величиной и направлением. Смещение – пример векторной величины, а расстояние – скалярной.
Вектор отображает геометрический объект, обладающий величиной и направлением. В соответствии с векторной алгеброй, его можно добавить к другим векторам. Направление задается знаками + или -. Вектор отображается отрезком линии с конкретным направлением или стрелой, объединяющей точки А и В — направление вектора.

Вектор часто изображают в виде линейного отрезка с определенным направлением или же как стрелу, соединяющую А и В
Некоторые физические величины, вроде дистанции, не обладают направлением. Здесь и появляется скаляр, который остается стабильным при смене системы координат. Может выражаться числом и обладает величиной, но лишен направления. Например, 45°C, 150 калорий, дистанция в 3 метра – все это скаляры. Если располагаем температурой в -23°C, то отрицательный знак указывает не на направление, а на точку в шкале. Скаляры никогда не отображаются стрелками.
К скалярным величинам относятся длина, площадь, время, температура и т. д.
К векторным величинам относятся: Сила, ускорение, импульс, скорость, индукция, напряжённость…
Скалярные и векторные величины. Линейные операции над векторами
Величины которые определяются только числовым значением называются скалярными. Те которые определяются числовым значением и направлением называются векторными.
Вектором
называется направленный отрезок и
обозначается  .
.
Вектор, начло и конец которого совпадают, называется нулевым. Направление такого вектора считается произвольным.
Два
не нулевых вектора  называются коллинеарными если прямые
АВ и СМ параллельны или совпадают
называются коллинеарными если прямые
АВ и СМ параллельны или совпадают 
Противоположным
для вектора  называется
вектор той же длинны, но с противоположным
направлением.
называется
вектор той же длинны, но с противоположным
направлением.
Длинной
(модулем) не нулевого вектора  называется расстояние между его началом
и концом и обозначается
называется расстояние между его началом
и концом и обозначается  .
.
Вектор называется свободным если положение их начала не имеет значения.
Свободные векторов называются равными если они коллинеарные, одинаково направлены и имеют одинаковую длину.
Скользящие вектора это вектора которые считаются равными если они имеют равную длину, одинаково направлены и лежат на одной прямой.
Связанные вектора это вектора которые считаются равными если они имеют одинаковую длину, одинаково направлены и имеют одинаковые начала.
Линейные операции над векторами:
Сложение (вычитание) векторов – результатом суммы ( разности) двух векторов является вектор.
Правило
треугольника сложения векторов: суммой
двух векторов 
 идущий из начала
идущий из начала  в конец
в конец  .
. Правило
параллелограмма: суммой двух векторов  является вектор
является вектор  определяемый диагональю параллелограмма
АВСМ.
определяемый диагональю параллелограмма
АВСМ.
Разностью
векторов 
 для которого исполняется равенство
для которого исполняется равенство  .
.Свойства сложения векторов:
Смешанное произведение векторов. Условие компланарности трех векторов

Условие
компланарности: три вектора  компланарны тогда и только тогда когда
компланарны тогда и только тогда когда 
 вычисляется по формуле:
вычисляется по формуле: 
Проекция вектора на ось и ее свойства
Пусть
задана ось координат Ох и вектор  .
Проведем прямые перпендикулярные к
оси Ох через точки А и В. Точки пересечения
.
Проведем прямые перпендикулярные к
оси Ох через точки А и В. Точки пересечения  .
.
Проекцией
вектора 
длинна вектора
 если направления вектора
если направления вектора  и ос Ох совпадают
и ос Ох совпадаютминус длинна
 в противоположном случае —
в противоположном случае — .
.
Свойства проекции вектора на ось:
Проекции равных векторов на одну и ту же ось равны между собой.
При умножении вектора на число его проекция умножается на это же число.
Проекция суммы вектора на ось равна сумме проекций на эту ось складываемых векторов.
Проекция вектора
 на ось Ох равна произведению длинны
вектора
на ось Ох равна произведению длинны
вектора  на косинус угла наклона вектора
на косинус угла наклона вектора  к
оси Ох.
к
оси Ох.

Векторное произведение векторов и его свойства
Векторным
произведением вектора  называется вектор
называется вектор  такой что:
такой что:
Если
вектора  коллинеарны, то их векторное произведение
называется нулевой вектор.
коллинеарны, то их векторное произведение
называется нулевой вектор.
Свойства векторного произведения:
Векторное
произведение в координатной форме 

Скаляры и векторы
Физика > Скаляры и векторы
Скаляр и вектор – чем отличаются понятия в физике и какая связь: определения и термины, величина и направление, скаляры без направления, величины и график.
Скаляры – физические величины, отображенные числом, а векторы используют числа и направления.
Задача обучения
- Научиться различать вектор и скаляр.
Основные пункты
- Скаляр – физическая величина, представленная числом.
- Вектор – физическая величина, характеризующаяся величиной и направлением.
- Среди скаляров можно вспомнить высоту, площадь, объем и массу.
- Векторы – смещение, ускорение и скорость.
Термин
Координатная ось – набор перпендикулярных линий, определяющих координаты относительно начала координат. Например, х и у указывают на горизонтальное и вертикальное положения.
Чаще всего, физические величины можно поделить на две категории: вектор и скаляр. Они отличаются необходимой для характеристики информацией. Векторы нуждаются в величине и направлении, а скаляры обходятся лишь первым критерием. Скаляры можно воспринимать как числа, а векторы – стрелки, указывающие на определенное направление.

Пример вектора. Обычно они отображаются стрелками с длиной, показывающей величину, а направление указано стрелой
Вектор нуждается в величине и направлении. Величина отображается числом, чтобы можно было сравнить два вектора. Стрелка состоит из двух частей: длина, определяющая величину, и направление на оси координат. Чем больше величина, тем длиннее стрелка. Вектор может отображать скорость, смещение и ускорение. Чтобы указать направление, нужно располагать опорной точкой, которой часто выступают координатные оси.
Скаляры лишены направления. Их используют для отображения величин, которые не нуждаются в направлении (высота, масса, объем).
Единичный вектор и умножение на скаляр
Физика > Векторы единиц и умножение на скаляр
Единичный вектор и процесс умножения вектора на число в физике: вектор и скаляр, термины и определения, координаты единичного вектора, отображение на графике.
Умножение вектора скаляром соответствует умножению его величины на число.
Задача обучения
- Предсказать влияние умножения вектора на скаляр.
Основные пункты
- Единичный вектор выступает вектором величины (длины) 1.
- Скаляр может представляться одним числом, и лишен направления.
- Умножение вектора на скаляр проходит так же, как умножение величины вектора на число, отображенное скаляром.
Термины
- Скаляр – количество, лишенное направления. Его можно описать одним числом.
- Единичный вектор – вектор величины 1.
Векторы можно не только добавлять, но и умножать на скаляры. Последние отличаются от векторов тем, что обладают величиной, но лишены направления (масса, объем, высота).
В процессе умножения вектора на скаляр, направление вектора остается стабильным, а величина умножается на аналогичную характеристику скаляра. Это создает новую более удлиненную векторную стрелу. Для скалярного умножения можно также использовать компоненты вектора. Просто умножьте каждый на скаляр и получите новые компоненты.

(I) – Умножение вектора А на 0.5 уменьшает его длину.
(Ii) – Умножение вектора А на 3 утраивает длину.
(Iii) – Увеличение массы (скаляр) увеличивает и силу (вектор).
Чтобы все стало намного проще, следует разобраться в единичном векторе. Это вектор, соответствующий по величине или длине 1. В декартовых координатах обычно отображается как x^ и y^. Треугольник над буквами прозвали «шляпой». Координаты единичного вектора описывают круг, чей радиус достигает единицы. Чтобы это увидеть, просто возьмите все векторы длины 1 и поместите на координаты. Если объединить векторы линией, то получится круг.
1.2. Лекция 2. Скалярное, векторное и смешанное
произведения
Скалярное произведение. Векторное произведение. Смешанное произведение. Двойное векторное произведение. Решение векторных уравнений. Законы физики и векторный язык.
Скалярное произведение
Определение. Пусть a, b – ненулевые вектора, приведенные к
общему началу. В качестве угла между
ними можно принять как угол  ,
так и угол
,
так и угол ,
косинусы которых одинаковы. Значит
формула
,
косинусы которых одинаковы. Значит
формула
 ,
(2.1)
,
(2.1)
где  и
и – длины векторов
– длины векторов иb,
однозначно определяет некоторое число
иb,
однозначно определяет некоторое число  ,
называемое скалярным произведением
двух векторов
,
называемое скалярным произведением
двух векторов иb.
Если
иb.
Если  или
или  ,
то, по определению,
,
то, по определению,  .
.
Скалярное
произведение возникло в физике. Работа,
которую совершает сила  при перемещении
тела из точки
при перемещении
тела из точки  в точкуB (рис.2), равна
в точкуB (рис.2), равна

 (2.2)
(2.2)


Рис. 2. Работа силы
В этом выражении мы узнаем скалярное
произведение 
Геометрические свойства скалярного произведения
Непосредственно из определения скалярного произведения легко получить следующие свойства:
1)  ,
(2.3)
,
(2.3)
2) 
 ,
(2.4)
,
(2.4)
3)  .
(2.5)
.
(2.5)
Таким образом, с одной стороны, скалярное произведение определено через длины векторов и угол между ними, с другой − длины векторов и угол между ними выражаются через скалярное произведение. Эта взаимная определимость является исходной идеей для введения понятия расстояния и угла в абстрактных линейных пространствах.
Векторы  и
и называютсяортогональными,
если их скалярное произведение равно
нулю:
называютсяортогональными,
если их скалярное произведение равно
нулю:
 . (2.6)
. (2.6)
При  и
и это равносильно тому, что угол между
векторами
это равносильно тому, что угол между
векторами и
и равен
равен .
.
Проекцией вектора  на прямую
на прямую называется вектор
называется вектор ,
началом которого служит проекция начала
вектора
,
началом которого служит проекция начала
вектора ,
а концом — проекция конца вектора
,
а концом — проекция конца вектора на прямую
на прямую (рис.3). Проекцию вектора
(рис.3). Проекцию вектора на неориентированную прямую, определяемую
вектором
на неориентированную прямую, определяемую
вектором ,
будем обозначать
,
будем обозначать .
.
Лемма 2.1.  .
.
Доказательство легко усмотреть из рис. 4.


Рис. 3. Проекция вектора Рис. 4. Проекция суммы векторов
на прямую на прямую
Лемма 2.2.  .
.
Доказательство. Действительно,  .
.
Лемма 2.3. .
.
Доказательство. Упражняйтесь.
Алгебраические свойства скалярного произведения
Так называют следующие свойства:
1) (a,b)=(b,a) – коммутативность;
2)  − однородность;
− однородность;
3) (a+b,c)=(a,c)+(b,c) − дистрибутивность;
4)  − положительная определенность.
− положительная определенность.
Свойства 1, 2, 4 легко вывести из определения. Докажем свойство 3. По лемме 2.2
 .
(2.7)
.
(2.7)
Отсюда и из леммы 2.1
 .
(2.8)
.
(2.8)
С другой стороны, по лемме 2.2
 .
(2.9)
.
(2.9)
Пусть  – орт вектора
– орт вектора т.е. вектор, имеющий единичную длину и
сонаправленный векторус (Легко проверить, что
т.е. вектор, имеющий единичную длину и
сонаправленный векторус (Легко проверить, что  .)
Тогда для некоторых чисел
.)
Тогда для некоторых чисел имеем
имеем
 ,
,  ,
,  .
(2.10)
.
(2.10)
Подставляя это в (2.8), (2.9), получим
 ,
(2.11)
,
(2.11)
 ,
(2.12)
,
(2.12)
что и требовалось доказать.
Если векторы  и
и  ортогональны, то
ортогональны, то
 .
(2.13)
.
(2.13)
В качестве приложения
скалярного произведения докажем
известную из школьного курса теорему
косинусов. В треугольнике  обозначим
обозначим ,
, и
и .
Тогда
.
Тогда и
и
 , (2.14)
, (2.14)
что и требовалось.
При  треугольник
треугольник прямоугольный и теорема косинусов дает
теорему Пифагора.
прямоугольный и теорема косинусов дает
теорему Пифагора.


 если направления вектора
если направления вектора  и ос Ох совпадают
и ос Ох совпадают в противоположном случае —
в противоположном случае — .
.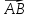 на ось Ох равна произведению длинны
вектора
на ось Ох равна произведению длинны
вектора  на косинус угла наклона вектора
на косинус угла наклона вектора  к
оси Ох.
к
оси Ох.