Лекция № 7 Скалярное произведение двух векторов.

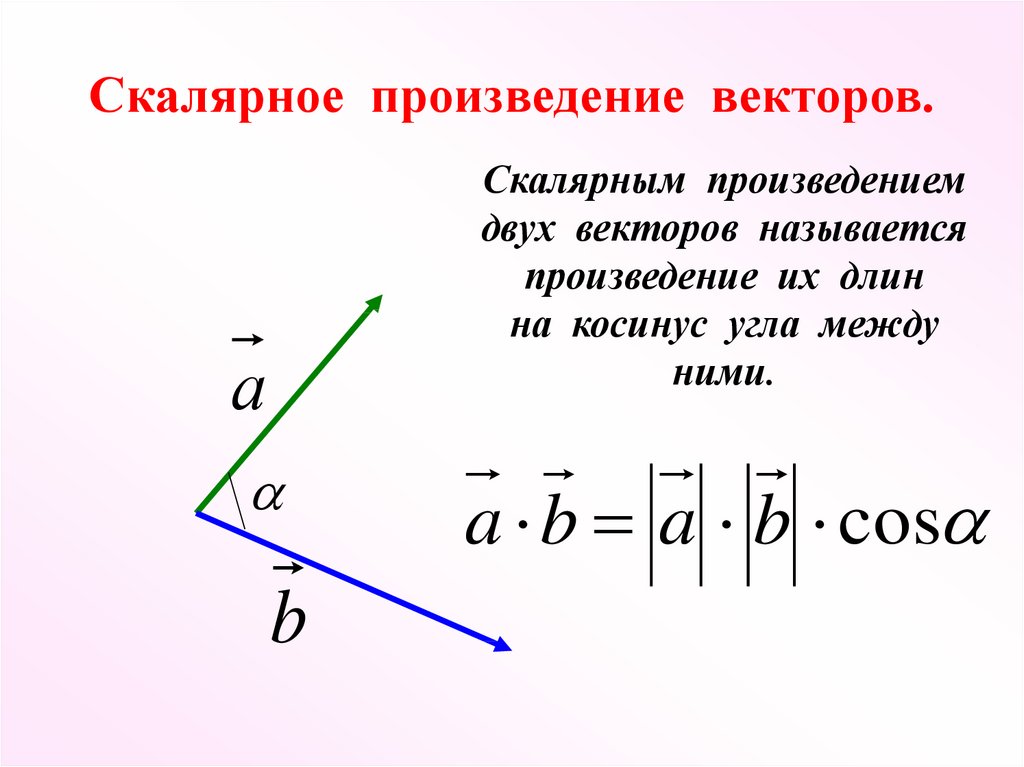
Определение: Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Обозначение скалярного произведения: .

Скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию на него другого.

В результате скалярного умножения двух векторов получается число, скаляр, а не новый вектор.

Рис. 1

Знак скалярного произведения зависит от угла между векторами.

Замечание. В частности, , если или .

, если  — острый угол;

, если  — тупой угол;

, если

Свойства скалярного произведения

1. — переместительный закон

2. — сочетательный закон

3. — распределительный закон

5. или

Если векторы коллинеарны, то или , а .

Скалярный квадрат вектора равен квадрату его модуля.

Определение: Скалярное произведение двух векторов, заданных своими координатами, равно сумме произведений одноименных координат этих векторов.

Пусть заданы два вектора , , тогда

Замечание.

Если , угол  — острый,

, угол  — тупой.

Приложения скалярного произведения

Угол между векторами: .

Угол между векторами в координатной форме:

Определение: Векторы перпендикулярны тогда и только тогда, когда скалярное произведение этих векторов равно нулю: или

Нахождение проекции вектора на направление, заданное вектором .

или

Проекция произвольного вектора на какую – нибудь ось u определяется формулой , — единичный вектор, направленный по оси u.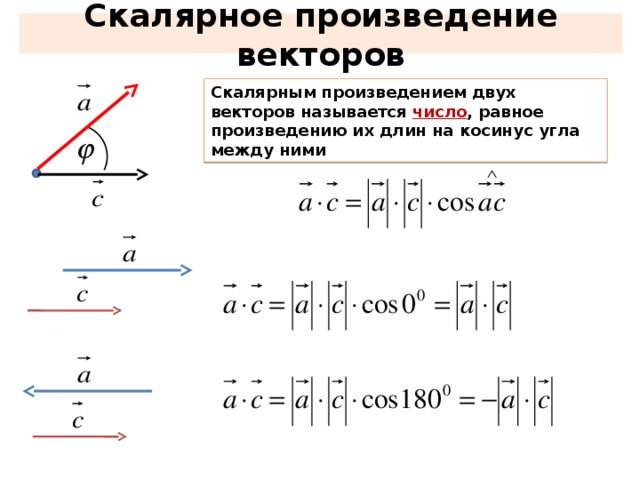

Замечание.

Если даны углы , , , которые ось u составляет с координатными осями, то и для вычисления проекции вектора на ось u служит формула:

Рис. 2

Если вектор изображает перемещение материальной точки под действием постоянной силы (Рис. 3), то работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.

Рис. 3

Работа силы: .

Задачи

Задача 1. Найти скалярное произведение векторов и , если .

Решение: Имеем (используем свойства скалярного произведения – формулы (5), (6), (7)). По формулам (2) и (9), получаем , ,

Задача 2. Даны точки .

Вычислить .

Решение: Найдем координаты векторов .

.

— противоположен вектору , следовательно, . Аналогично .

; .

По формуле (10) найдем

.

Задача 3. Вычислить угол, образованный векторами и .

Решение: Используя формулу (11′), получаем

Задача 4. Даны векторы и . Найти и .

Решение: Используя формулу (13), получаем

Задача 5. Дан вектор . Найти его проекцию на ось u, составляющую с координатными осями равные острые углы.

Решение: Т. к. ось u составляет с координатными осями равные острые углы, т. е. , то .

Но , и т. к. в этой сумме все слагаемые между собой равны, то ; ; , тогда (знак плюс перед корнем взят потому, что по условию углы , ,  — острые, значит косинусы их положительны). Т. к. по условию , , , то по формуле получаем .

Что такое скалярное произведение двух векторов?

Что такое скалярное произведение двух векторов?

Определение. Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними. … Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Что называется векторным произведением двух векторов?

Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть . ..

Чему равно скалярное произведение векторов?

Скалярным произведением двух векторов a → и b → будет скалярная величина (число), равная произведению модулей этих векторов, умноженная на косинус угла между ними: a → ⋅ b → = a → ⋅ b → ⋅ cos α .

Чему равно скалярное произведение коллинеарных векторов?

Скалярное произведение коллинеарных векторов равно произведению их длин (взятых со знаком «минус», если векторы противоположно направлены).

Какие операции можно выполнять с векторами?

Операции над векторами и их свойства: умножение, сложение векторов по правилу многоугольника

Как обозначаются Сонаправленные вектора?

Вектор обозначается либо двумя большими буквами — своим началом и концом: ¯AB либо одной малой буквой: ¯a. Если начало и конец вектора совпадают, то такой вектор называется нулевым. … Два коллинеарных вектора ¯a и ¯b называются сонаправленными, если их направления совпадают: ¯a↑↑¯b (рис. 3, а).

Что называется углом между двумя векторами?

Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором. … Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.

В чем смысл скалярного произведения?

Скаля́рное произведе́ние (иногда называемое внутренним произведением) — операция над двумя векторами, результатом которой является скаляр, то есть число, не зависящее от выбора системы координат. Используется в определении длины векторов и угла между ними. используется одно из следующих обозначений.

Как найти косинус скалярного произведения?

Чтобы найти косинус угла между векторами нужно, скалярное произведение этих векторов разделить на произведение их длин.

Как найти косинус угла а?

Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.

Как найти косинус в любом треугольнике?

Формула теоремы косинусов Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Теорема косинусов является обобщением теоремы Пифагора.

Как найти косинус угла между сторонами треугольника?

Теорема косинусов Т. е. косинус угла равен сумме квадратов двух сторон минус квадрат стороны, противолежащий углу, и все это деленное на удвоенное произведение первых двух сторон.

Как найти косинус угла зная все стороны?

Формулировка теоремы косинусов Теорема косинусов гласит: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

Как определить угол треугольника по сторонам?

Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.

Когда работает теорема косинусов?

Теорема косинусов используется для вычисления: неизвестной стороны треугольника, если даны две стороны и угол между ними; вычисления косинуса неизвестного угла треугольника, если даны все стороны треугольника.

Как звучит теорема косинусов?

Формулировка и доказательство теоремы косинусов Она звучит так: Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. Чтобы записать формулой данную теорему, принимаем стандартные значения.

Как доказать теорему косинусов?

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а.

Когда использовать теорему синусов а когда косинусов?

Как применять: если в вашей задаче необходимо найти сторону треугольника, а известны два угла и любая сторона, то легче использовать теорему синусов если в вашей задаче необходимо найти угол треугольника, а известны три стороны, то легче использовать теорему косинусов

Объяснение урока: Скалярное произведение двух векторов

В этом объяснении мы научимся вычислять скалярное произведение двух векторов, используя как компоненты векторов, так и величины двух векторов и угол между ними.

Скалярное произведение — это операция, которую можно применить к двум векторам для получения скаляра.

Напомним, что в то время как вектор имеет и величину, и направление, скаляр имеет только величину.

Скалярное произведение используется во многих областях физики. Один расчет, для которого это может быть полезно, — это расчет работы, совершаемой силой над объектом, когда этот объект перемещается на определенное смещение.

Представьте, что человек толкает коробку по полу, как показано на диаграмме ниже.

Сила, приложенная к ящику, равна F, и он перемещается со смещением d. Сила действует в том же направлении, что и перемещение. В этом сценарии работа силы 𝑊 просто равна величине силы 𝐹, умноженной на величину смещения 𝑑: 𝑊=𝐹𝑑.

Но что, если сила , а не действовала в том же направлении, что и смещение (возможно, потому, что человек, толкающий коробку, также немного давит на нее), как показано на диаграмме ниже?

В этом сценарии мы не можем использовать 𝑊=𝐹𝑑 для вычисления работы силы. Вместо этого мы должны вычислить скалярное произведение F и d.

Скалярное произведение обозначается точкой в ​​центре между двумя векторами: Фд⋅.

Из-за этого скалярное произведение также называют скалярное произведение . Его также иногда называют внутренним продуктом .

Существует два способа определения скалярного произведения двух векторов. Первый подход — геометрический.

Определение: скалярное произведение двух векторов

Рассмотрим два вектора, A и B. Угол между двумя векторами равен 𝜃. Это показано на диаграмме ниже.

Скалярное произведение A и B равно величине A, умноженной на величину B, умноженной на косинус угла между ними, 𝜃, что мы можем записать как ABAB⋅=||||(𝜃).cos

Написание двух прямых линий по обе стороны от символа вектора, например, ||A, означает получение величины вектора. Мы можем записать это определение проще, если просто скажем, что 𝐴 — это величина A, а 𝐵 — величина B: AB⋅=𝐴𝐵(𝜃).cos

Мы можем думать об этом как о мере того, насколько велики два вектора, и насколько они указывают в одном и том же направлении . Если 𝐴 или 𝐵 больше, скалярное произведение будет больше, и мы можем увидеть, как скалярное произведение зависит от 𝜃, угла между векторами, посмотрев на график cos(𝜃), который показан ниже.

Когда 𝜃 равно 0∘, cos(𝜃) равно 1, что является максимальным значением, которое производит функция косинуса. Итак, когда два вектора указывают в одном направлении, как показано на диаграмме ниже, их скалярное произведение имеет максимальное значение.

Когда 𝜃 равно 90∘, cos(𝜃) равно 0. Итак, когда два вектора расположены под прямым углом друг к другу, как показано ниже, их скалярное произведение равно нулю.

Когда 𝜃 равно 180∘, cos(𝜃) равно −1, что является наименьшим значением, которое выдает функция косинуса. Итак, когда два вектора указывают в противоположном направлении, как показано ниже, скалярное произведение имеет значение, равное того же размера , что и когда 𝜃 равно 0∘, но с отрицательным знаком .

Итак, чем меньше угол между векторами, чем больше значение скалярного произведения, и чем больше угол между векторами, тем

меньше значение скалярного произведения.

Обратите также внимание, что поскольку 𝐴𝐵=𝐵𝐴, 𝐴𝐵(𝜃)=𝐵𝐴(𝜃)coscos, это означает, что ABBA⋅=⋅. Другими словами, не имеет значения, каким образом мы делаем скалярное произведение; AB⋅ и BA⋅ дают одно и то же значение.

Давайте рассмотрим пример вопроса.

Пример 1: вычисление скалярного произведения двух векторов по их величинам и углу между ними

Рассмотрим два вектора: r с величиной 12 и s с величиной 26. Угол между ними, 𝜃, равен 68∘ . Чему равно скалярное произведение r и s? Дайте ответ до ближайшего целого числа.

Ответ

Поскольку нам известны величины двух векторов, а также угол между ними, мы можем использовать формулу rsrs⋅=||||(𝜃)cos найти скалярное произведение.

Подставляя значения, получаем rsrs⋅=12×26×(68)⋅=116,87725…,cos∘ что до ближайшего целого равно 117.

Этот геометрический подход полезен, если нам известны величины двух векторов и угол между ними, но вместо этого мы можем знать горизонтальную и вертикальную составляющие двух векторов.

В этом случае мы можем использовать второй способ определения скалярного произведения, который является алгебраическим подходом.

Определение: скалярное произведение двух векторов

Допустим, что AijBij=𝐴+𝐴,=𝐵+𝐵, где 𝐴 и 𝐴 — горизонтальная и вертикальная компоненты A, а 𝐵 и 𝐵 — горизонтальная и вертикальная компоненты B. Тогда скалярное произведение A и B определяется выражением AB⋅=𝐴𝐵+𝐴𝐵.

Другими словами, мы перемножаем 𝑥-компоненты векторов вместе и 𝑦-компоненты векторов вместе, а затем суммируем два числа.

Еще раз обратите внимание, что не имеет значения, каким образом мы делаем скалярное произведение. Поскольку 𝐴𝐵=𝐵𝐴 и 𝐴𝐵=𝐵𝐴, 𝐴𝐵+𝐴𝐵=𝐵𝐴+𝐵𝐴.

Итак, ABBA⋅=⋅.

Давайте рассмотрим несколько примеров вопросов, в которых мы должны использовать этот подход.

Пример 2. Вычисление скалярного произведения двух векторов, заданных в компонентной форме

Рассмотрим два вектора pij=2+3 ​​и qij=6+4. Вычислите pq⋅.

Ответ

Поскольку нам даны два вектора в компонентной форме, мы можем использовать pq⋅=𝑝𝑞+𝑝𝑞 найти скалярное произведение. Подставим значения: pqpq⋅=2×6+3×4⋅=24.

Скалярное произведение p и q равно 24,9.0003

Пример 3. Вычисление скалярного произведения двух векторов, заданных в компонентной форме

Постоянная сила Fij=(1+4)N действует на объект, заставляя его двигаться. Через некоторое время смещение объекта от его начального положения равно dij=(5+2)м. Вычислите Fd⋅.

Ответ

Поскольку нам даны два вектора в компонентной форме, мы можем использовать Fd⋅=𝐹𝑑+𝐹𝑑 найти скалярное произведение. Подставим значения: FdFdFd⋅=1×5+4×2⋅=5⋅+8⋅⋅=13⋅.NmNmNmNmNm

Скалярное произведение F и d равно 13 Н⋅м. На самом деле это равно работе, совершаемой силой над объектом, а единицы ньютон-метров эквивалентны джоулям, поэтому ответ также равен 13 Дж.

Пример 4. Вычисление скалярного произведения двух векторов, изображенных на Сетка

На диаграмме показаны два вектора, A и B. Каждый из квадратов сетки на диаграмме имеет длину стороны, равную 1. Вычислите AB⋅.

Ответ

Поскольку два вектора нанесены на сетку, мы можем определить их компоненты. Вектор A имеет горизонтальную длину 3 квадрата сетки и вертикальную длину 3 квадрата сетки, поэтому мы можем записать его как Aij=3+3. Вектор B имеет горизонтальную длину 6 квадратов сетки и вертикальную длину 1 квадрат сетки, поэтому мы можем записать его как Bij=6+1.

Теперь мы можем использовать AB⋅=𝐴𝐵+𝐴𝐵 найти скалярное произведение. Подставим значения: АБАВ⋅=3×6+3×1⋅=21.

Скалярное произведение A и B равно 21.

Пример 5. Вычисление скалярного произведения двух векторов, изображенных на сетке

На диаграмме показаны два вектора, A и B. Каждый из квадратов сетки на диаграмме имеет длина стороны 1. Вычислите AB⋅.

Ответ

Есть два способа получить ответ на этот вопрос. Первый заключается в вычислении скалярного произведения компонентов векторов.

Так как два вектора были нарисованы на сетке, мы можем выяснить, каковы их компоненты. Вектор A имеет горизонтальную длину 5 квадратов сетки и вертикальную длину 0 квадратов сетки, поэтому мы можем записать его как Aij=5+0. Вектор B имеет горизонтальную длину 0 квадратов сетки и вертикальную длину 4 квадрата сетки, поэтому мы можем записать его как Bij=0+4.

Теперь мы можем использовать AB⋅=𝐴𝐵+𝐴𝐵 найти скалярное произведение. Подставим значения: АБАВ⋅=5×0+0×4⋅=0.

Скалярное произведение A и B равно 0,

Но более быстрый способ найти ответ — вспомнить, что для двух перпендикулярных векторов их скалярное произведение всегда равно нулю. Из диаграммы видно, что эти два вектора перпендикулярны — вектор A указывает вдоль оси 𝑥, а вектор B указывает вдоль оси 𝑦, поэтому их скалярное произведение равно нулю.

На первый взгляд кажется, что эти два разных метода вычисления скалярного произведения не дадут одного и того же результата, но на самом деле это так. Давайте применим оба метода к одному и тому же примеру, чтобы показать, что они дают одинаковый результат.

На приведенной ниже диаграмме показаны два вектора.

В компонентной форме мы можем записать A как 15+8ij и B как 5+12ij. Теперь мы можем использовать алгебраический метод для вычисления скалярного произведения: ABABAB⋅=𝐴𝐵+𝐴𝐵⋅=15×5+8×12⋅=171.

Мы можем использовать теорему Пифагора, чтобы вычислить длины двух векторов. При этом мы находим, что длина A равна ровно 17, а длина B равна ровно 13. Угол между векторами равен 39,30764…∘. Давайте пока округлим до 39,3∘. Теперь мы можем использовать геометрический метод для вычисления скалярного произведения: АБАБАБ⋅=𝐴𝐵(𝜃)⋅=17×13×(39.3)⋅=171.01868….coscos∘

Обратите внимание, что это не в точности 171 — это потому, что мы решили округлить значение, которое у нас было для 𝜃. Это упрощает использование числа на калькуляторе, но снижает точность результата. Если мы используем точное значение угла в наших расчетах, ответ действительно будет равен 171. В качестве альтернативы мы можем просто округлить полученный ответ, используя 𝜃=39,3∘, что округлит до 171.

Ключевые точки

• Скалярное произведение — это операция, которую можно применить к двум векторам для получения скаляра.
• Скалярное произведение также называется скалярным произведением или внутренним произведением .
• Если мы знаем длину каждого вектора и угол между ними, мы можем использовать ABAB⋅=||||(𝜃)cos найти скалярное произведение.
• Если мы знаем компоненты каждого вектора, мы можем использовать AB⋅=𝐴𝐵+𝐴𝐵 найти скалярное произведение.

Раздел 7.3. Скалярное произведение двух векторов

Цели обучения

Изучив этот раздел, вы должны уметь:

1. Вычислять скалярное произведение двух векторов независимо от того, представлены ли эти векторы в виде единичного вектора и/или в форме величины/угла.
2. Используйте знание скалярного произведения, чтобы найти угол между двумя векторами.
3. Вычислить проекцию одного вектора вдоль направления другого вектора.
4. Решите задачи на скалярное произведение двух векторов.

Блок 3, Векторы — Введение, объяснил, как найти компоненты вектора и как сложить и вычесть два вектора. Вы часто использовали эти навыки для изучения многомерной кинематики и применения законов движения Ньютона. Но, возможно, вас мучил какой-то вопрос. Если можно сложить два вектора, можно ли также умножить два вектора? Ответ, который, вероятно, вас не удивит: да . Однако вас может удивить то, что существует более одного способа умножения двух векторов! В этом разделе вы узнаете о методе умножения двух векторов, в результате которого получается скалярная величина. Это называется скалярное произведение двух векторов. Многие также называют его скалярным произведением из-за обозначения, используемого для обозначения произведения (а именно, точка $\cdot$).

Мы начнем с геометрического подхода к скалярному произведению. Это приведет к использованию скалярного произведения для вычисления работы, совершаемой над частицей постоянной силой. Рассмотрим два произвольных вектора, $\vec{A}$ и $\vec{B}$, как показано на рис. 7.8. $\vec{A}$ и $\vec{B}$ представляют любую векторную величину, например, силу, перемещение, скорость, ускорение. Кроме того, $\vec{A}$ и $\vec{B}$ могут представлять разные типы векторов, например, $\vec{A}$ может представлять силу, а $\vec{B}$ может представлять смещение. На рис. 7.8 векторы изображены с общим хвостом, а $\theta_{AB}$ — это угол между векторами, где $\theta_{AB}$ всегда выбирается как меньший из двух углов между векторы. На рис. 7.8 показаны две скалярные компоненты $\vec{A}$, где одна скалярная компонента направлена ​​вдоль второго вектора, $\vec{B}$, а вторая скалярная компонента $\vec{A}$ равна перпендикулярно направлению $\vec{B}$. Скалярная компонента $\vec{A}$ вдоль направления $\vec{B}$ называется проекция $\vec{A}$ вдоль направления $\vec{B}$.

Рисунок 7.8: Нарисованы два вектора с общим хвостом. Один вектор проецируется на направление другого вектора.

Чтобы вычислить скалярное произведение $\vec{A}\cdot\vec{B}$, выполните следующие шаги:

• Найдите проекцию одного вектора, скажем, $\vec{A}$, вдоль направление другого вектора. На основе рис. 7.9, эта проекция равна $|\vec{A}|\cos\theta_{AB}$.
• Умножьте эту проекцию на величину другого вектора, $|\vec{B}|$:\begin{equation} \vec{A}\cdot\vec{B} \equiv{(|\vec{A}|\cos\theta_{AB})|\vec{B}| = |\vec{A}||\vec{B}|\cos\theta_{AB}} \tag{7.6} \end{уравнение}

Обратите внимание

Уравнение 7.6 говорит, что по определению скалярное произведение двух векторов является произведением величин векторов на косинус угла между двумя векторами (когда эти векторы нарисованы с общим хвостом). Результат выполнения операции, определенной в уравнении. 7,6 — скалярная величина, т.е. , без количества в правой части уравнения. 7.6 имеет связанное с ним направление.

Где мы сейчас?

Поскольку концепция скалярного произведения очень важна в физике, Практика 7.3 , рабочая задача и дополнительные материалы Подробнее дают вам возможность «познакомиться» со скалярным произведением. После этого мы применим этот новый инструмент скалярного произведения к понятию работы.

Практика 7.3 (Скалярное произведение двух векторов)

Открытая практика 7.3

На вставке к рисунку 7.3 в Практике 7.3 показано значение произведения $A_{x}B_{x}$ и произведения $A_{ у}В_{у}$. Также отображается сумма этих произведений: $A_{x}B_{x} + A_{y}B_{y}$. Обратите внимание, что $A_{x}B_{x} + A_{y}B_{y}$ численно равно $\vec{A}\cdot\vec{B}$ независимо от того, где вы расположите $\vec{A}$. Проверьте это сами, переместив $\vec{A}$. Далее докажем, что $\vec{A}\cdot\vec{B} = A_{x}B_{x} + A_{y}B_{y}$.

Начните с выражения обоих векторов в виде единичного вектора:

$$\vec{A} = A_{x}\hat{i} + A_{y}\hat{j}\mbox{ и }\vec{ B} = B_{x}\hat{i} + B_{y}\hat{j}$$

Вычислить скалярное произведение двух векторов:

$$\vec{A}\cdot\vec{B } = (A_{x}\шляпа{i} + A_{y}\шляпа{j})\cdot(B_{x}\шляпа{i} + B_{y}\шляпа{j})$$

Используйте распределительное свойство скалярного произведения:

$$\Downarrow$$

$$\vec{A}\cdot\vec{B} = A_{x}B_{x}(\hat{i}\cdot \ шляпа {i}) + A_ {x} B_ {y} (\ шляпа {i} \ cdot \ шляпа {j}) + A_ {y} B_ {x} (\ шляпа {j} \ cdot \ шляпа {я }) + A_{y}B_{y}(\hat{j}\cdot\hat{j})$$

Вот где полезен вопрос 3 в Практике 2. Из этого вопроса видно, что скалярное произведение единичного вектора на самого себя равно единице, а скалярное произведение двух различных единичных векторов равно нулю, потому что два разных единичных вектора перпендикулярны друг другу. В результате вы знаете, что $\hat{i}\cdot\hat{i} = 1$, $\hat{j}\cdot\hat{j} = 1$, $\hat{i}\cdot\ hat{j} = 0$ и $\hat{j}\cdot\hat{i} = 0$, а приведенное выше скалярное произведение упрощается до:

$$\vec{A}\cdot\vec{B} = A_{x}B_{x} + A_{y}B_{y}$$

, что является желаемым выражением.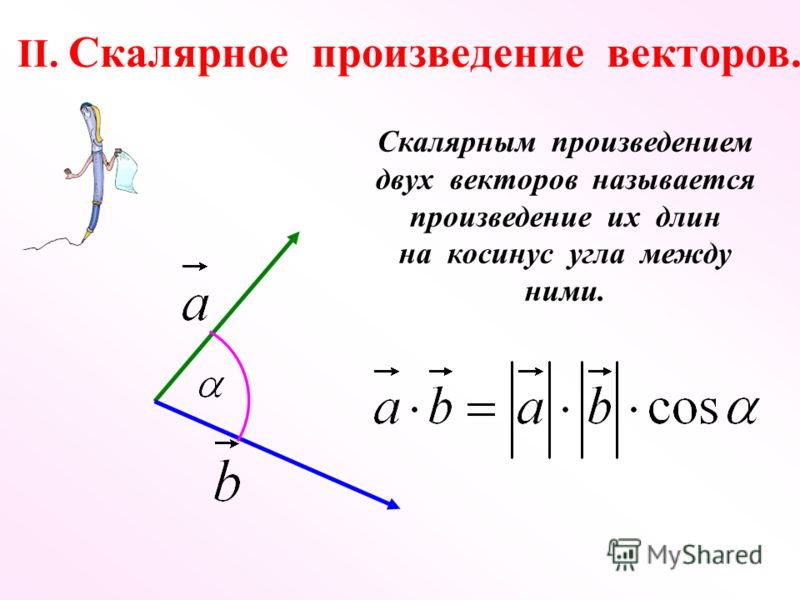 Этот результат, кстати, легко распространяется на трехмерные векторы:\begin{equation} \vec{A}\cdot\vec{B} = A_{x}B_{x} + A_{y}B_{y} + A_{z}B_{z} \tag{7.7} \end{equation}

Принять к сведению

Уравнение 7.7$\vec{A}\cdot\vec{B} = A_{x}B_{x} + A_{y}B_{y} + A_{z}B_ {z}$ — это выражение для скалярного произведения двух векторов, которое эквивалентно определению скалярного произведения, данному в уравнении. 7.6$\vec{A}\cdot\vec{B} \equiv{(|\vec{A}|\cos\theta_{AB})|\vec{B}| = |\vec{A}||\vec{B}|\cos\theta_{AB}}$. Уравнение 7.7 наиболее полезно, если вам даны два вектора в виде единичного вектора.

Итак, теперь у вас есть два различных, но эквивалентных метода вычисления скалярного произведения двух векторов, уравнение. 7.6$\vec{A}\cdot\vec{B} \equiv{(|\vec{A}|\cos\theta_{AB})|\vec{B}| = |\vec{A}||\vec{B}|\cos\theta_{AB}}$ и уравнение. 7.7$\vec{A}\cdot\vec{B} = A_{x}B_{x} + A_{y}B_{y} + A_{z}B_{z}$. В следующей обработанной задаче используются преимущества обоих методов.

---

Рабочая задача 7.2 (удар футбольного мяча)
Связанные цели обучения: 7.2.1, 7.2.2, 7.2.4

Футболист бежит, чтобы ударить по футбольному мячу. Позиция игрока описывается в системе координат $xy$ (где $x$ по горизонтали и $y$ по вертикали). При $t=0$ вектор положения футбольного мяча равен $\vec{r}=(1~\mbox{m})\hat{i}+(0,5~\mbox{m})\hat{j }$. В этот момент футбольный мяч имеет скорость $\vec{v}=(1\frac{\mbox{m}}{\mbox{s}})\hat{i}+(-1\frac{\mbox{ m}}{\mbox{s}})\hat{j}$. Ногой игрок прикладывает к мячу силу $\vec{F}=(1~\mbox{N})\hat{i}+(2~\mbox{N})\hat{j}$ — см. рис. 7.10. Чему равен угол $\theta_{F_{v}}$ между скоростью футбольного мяча и силой, действующей на него при $t=0$?

Видео 7.4: Видео решение: рабочая проблема 7. 2

Рисунок 7.10: Футболист только что ударил ногой по футбольному мячу. (Источник: Corbis #42-18818618.)

Рисунок 7.11: Рабочая задача – При $t=0$ футболист бьет по движущемуся футбольному мячу.

Решение

Эскиз

См. рис. 7.11. Показаны положение $\vec{r}$ и векторы скорости $\vec{v}$ футбольного мяча в этот момент. Кроме того, показана сила $\vec{F}$, действующая на мяч со стороны ноги игрока.

Таблица

Известные количества	Желаемое количество
Положение футбольного мяча в точке $t=0$: $\vec{r}=(1~\mbox{m})\hat{i}+(0,5~\mbox{m})\hat{j} $	Угол между силой и скоростью при $t=0$, $\theta_{F_{v}}$
Скорость футбольного мяча при $t=0$: $\vec{v}=(1\frac{\mbox{m}}{\mbox{s}})\hat{i}+(-1\ frac{\mbox{m}}{\mbox{s}})\шляпа{j} $
Сила, действующая на футбольный мяч со стороны игрока в точке $t=0$: $\vec{F}=(1~\mbox{N})\hat{i}+(2~\mbox{N})\hat {к} $

Объясните физику

Эта задача предназначена для практики со скалярным произведением. Между прочим, скалярное произведение скорости частицы на силу — это мощность, связанная с силой, как будет обсуждаться в гл. 7.10. Второй закон Ньютона не нужен, потому что нас не интересует последующее движение футбольного мяча после удара по нему ногой. Вектор положения футбольного мяча хоть и указан, но тоже не нужен.

Math

Используйте уравнение 7.6$\vec{A}\cdot\vec{B} \equiv{(|\vec{A}|\cos\theta_{AB})|\vec{B}| = |\vec{A}||\vec{B}|\cos\theta_{AB}}$, чтобы записать выражение для скалярного произведения скорости мяча и силы, действующей на футбольный мяч в рассматриваемый момент: \begin{уравнение} \vec{F}\cdot\vec{v}=|\vec{F}||\vec{v}|\cos\theta_{F_{v}} \tag{7.8} \end{equation}

где $\theta_{F_{v}}$ – это угол между $\vec{F}$ и $\vec{v}$, когда векторы рисуются с общим хвостом. Угол $\theta_{F_{v}}$ показан на рис. 7.11. Угол $\theta_{F_{v}}$ и есть искомая величина. Поскольку сила и скорость задаются в виде единичного вектора, величину каждой из них вычислить несложно. 2}$. Далее используйте уравнение 7.7$\vec{A}\cdot\vec{B} = A_{x}B_{x} + A_{y}B_{y} + A_{z}B_{z}$, чтобы выразить скалярное произведение силы и скорость с точки зрения компонентов:\begin{equation} \vec{F}\cdot\vec{v}=F_{x}v_{x}+F_{y}v_{y} \tag{7.9} \end{equation}

Наконец, приравняем два выражения для скалярного произведения, уравнение 7.8$\vec{F}\cdot\vec{v}=|\vec{F}||\vec{v}|\cos\theta_{F_{v}}$ и уравнение. 7.9$\vec{F}\cdot\vec{v}=F_{x}v_{x}+F_{y}v_{y}$ и найти $\theta_{F_{v}}$. Вот алгебра:

$$|\vec{F}||\vec{v}|\cos\theta_{F_{v}}=F_{x}v_{x}+F_{y}v_{y }$$

$$\Downarrow (\mbox{решить для }\cos\theta_{F_{v}})$$

$$\cos\theta_{F_{v}}=\frac{F_{x }v_{x}+F_{x}v_{y}}{|\vec{F}||\vec{v}|}$$ 9{\circ}$. Алгебра, используемая для решения этой задачи, демонстрирует очень мощный метод нахождения угла между двумя векторами — метод, который особенно полезен в случае движения в трех измерениях — см. Подробнее 7.2 .

---

Следующее исследование содержит необязательные упражнения со скалярным произведением.