Как легко рассчитать скалярный продукт в Excel

---

В этом руководстве объясняется, как рассчитать скалярный продукт в Excel.

Что такое скалярный продукт?

Для данного вектора a = [a 1 , a 2 , a 3 ] и вектора b = [b 1 , b 2 , b 3 ] скалярное произведение вектора a и вектора b, обозначаемое как a · b , определяется как:

а · b = а 1 * b 1 + а 2 * b 2 + а 3 * b 3

Например, если a = [2, 5, 6] и b = [4, 3, 2], то скалярное произведение a и b будет равно:

а · б = 2*4 + 5*3 + 6*2

а · б = 8 + 15 + 12

а · б = 35

По сути, скалярное произведение — это сумма произведений соответствующих элементов двух векторов.

Как найти точечный продукт в Excel

Чтобы найти скалярное произведение двух векторов в Excel, мы можем использовать следующие шаги:

1. Введите данные.Введите значения данных для каждого вектора в их собственные столбцы. Например, введите значения данных для вектора a = [2, 5, 6] в столбец A и значения данных для вектора b = [4, 3, 2] в столбец B:

2. Вычислите скалярный продукт. Чтобы вычислить скалярный продукт, мы можем использовать функцию Excel СУММПРОИЗВ() , которая использует следующий синтаксис:

СУММПРОИЗВ(массив1, [массив2], …)

• array — первый массив или диапазон, который необходимо умножить, а затем добавить.
• array2 — второй массив или диапазон для умножения, а затем добавления.

В этом примере мы можем ввести следующее в ячейку D1 , чтобы вычислить скалярное произведение между вектором a и вектором b :

=СУММПРОИЗВ(A1:A3, B1:B3)

Это дает значение 35 , которое соответствует ответу, который мы получили вручную.

Обратите внимание, что мы можем использовать СУММПРОИЗВ() для нахождения скалярного произведения векторов любой длины. Например, предположим, что вектор a и b имеют длину 20. Затем мы можем ввести следующую формулу в ячейку D1 , чтобы вычислить их скалярное произведение:

=СУММПРОИЗВ(A1:A20, B1:B20)

Возможные ошибки при вычислении скалярного произведения

Функция СУММПРОИЗВ() вернет #ЗНАЧ! ошибка, если векторы не имеют одинаковой длины.

Например, если вектор a имеет длину 20, а вектор b имеет длину 19, то формула =СУММПРОИЗВ(A1:A20, B1:B19) вернет ошибку.

Два вектора должны иметь одинаковую длину, чтобы можно было вычислить скалярное произведение.

Дополнительные ресурсы

В следующих руководствах объясняется, как рассчитать скалярный продукт в различных статистических программах:

Как рассчитать скалярный продукт в Google Sheets
Как рассчитать скалярный продукт в R
Как рассчитать скалярный продукт на калькуляторе TI-84

Скалярное произведение векторов

П усть даны векторы и , угол между которыми обозначим буквой (см.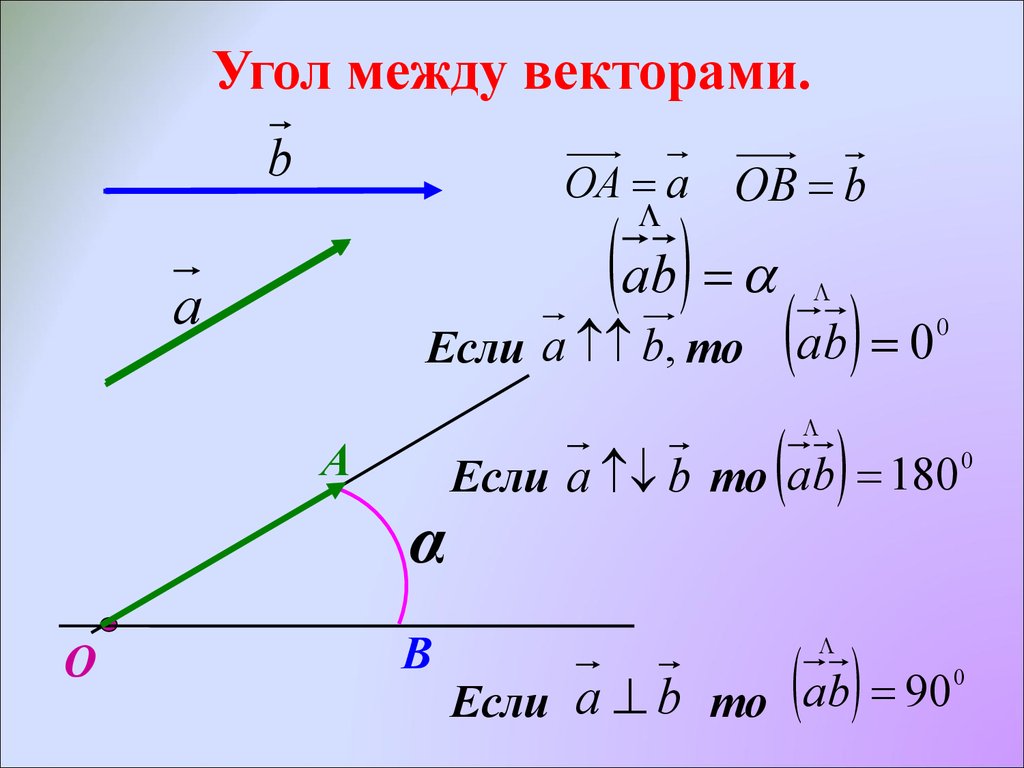 рисунок) . Их скалярным произведением (обозначается или ) называется число, равное произведению длин этих векторов и косинуса угла между ними :

(8) .

Рассмотрим свойства скалярного произведения .

1. Перестановочность (коммутативность) : . Это свойство следует сразу из определения скалярного произведения (8).

2. Раскрытие скобок: .

3. Пусть − число , тогда . Эти три свойства позволяют проводить преобразования векторных выражений точно также, как числовых (выносить за скобки множитель, раскрывать скобки, переставлять местами сомножители и т.п. ) . 4. Скалярный квадрат вектора : .

Доказательство сразу следует из определения (8), если учесть, что сам с собой вектор составляет угол в , а . Это свойство, читаемое как в приведенном порядке, так и в обратном порядке ( ) часто используется в задач нахождения длины вектора, являющегося комбинацией других векторов (пример будет ниже).

5. Векторы и перпендикулярны только если . Доказательство сразу следует из определения (8), если учесть, что угол между перпендикулярными векторами составляет , а . Это свойство используется в задачах, когда необходимо проверить перпендикулярность (или отсутствие таковой) векторов.

Пример 1. Найти скалярные произведения друг с другом единичных векторов осей координат и .

Решение. Поскольку эти векторы перпендикулярны друг другу (они находятся на взаимно перпендикулярных координатных осях) и имеют длину 1, то из свойств 4 и 5 получаем:

(9) , .

Свойство 4 помогает узнать, перпендикулярны ли данные векторы или нет. Для такой проверки это свойство предлагает найти скалярное произведение векторов и посмотреть, будет оно равно нулю или нет. Но для вычисления скалярного произведения у нас есть только определение (8), которое для вычисления скалярного произведения векторов требует знать, какой угол между ними.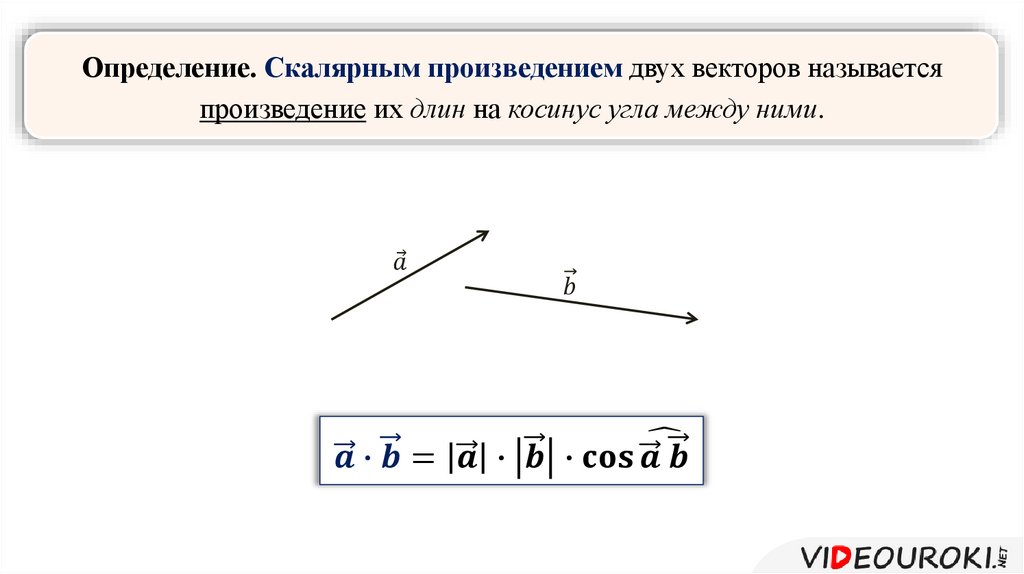

Получился замкнутый круг: мы хотим выяснить, равен ли угол между векторами (т.е. перпендикулярны ли они), а для этого нам нужно знать, чему равен угол между векторами. Но если бы мы его знали, то мы бы сразу могли сказать, равен ли он или нет. Выйти из такого круга помогает следующее свойство, которое предлагает другой (чаще гораздо более удобный) способ вычисления скалярного произведения векторов, отличный от формулы (8). Ранее при использовании различных векторных комбинаций мы уже убеждались, что значительное облегчение вносит использование координат вектора, которые не только полностью определяют все характеристики самих векторов , но и значительно облегчают строить различные комбинации векторов, сводя все операции, содержащиеся в этой комбинации, к более простым операциям над числами. Вычисление скалярного произведения векторов тоже может быть выполнено с использованием их координат, что чаще всего сделать проще, чем по формуле (8).

6. Выражение скалярного произведения через координаты векторов: если , , то

(10) .

Для доказательства (10) вспомним, что координаты вектора есть коэффициенты в разложении вектора по единичным векторам осей координат (была такая теорема в параграфе «Координаты вектора»), а потому если , , то , а . Тогда раскрывая обычным образом скобки (что делать можно) в выражении и используя полученные выше формулы (9), приходим к доказываемому равенству. Формула (10) очень часто используется при решении различных задач. С помощью формулы (10) можно вычислять скалярные произведения векторов по их координатам. Если оно получилось равным нулю, то векторы перпендикулярны. А если нет, то нет. Каков же тогда угол между векторами?

7 . Угол между векторами и может быть вычислен по формуле :

(11) .

Это свойство сразу следует из определения скалярного произведения (8) (если, конечно, не полениться на него взглянуть). До появления формулы (10) считать углы между векторами по формуле (11) не имело смысла, так как если при вычислении скалярного произведения в правой части этой формулы использовать определение (8), то требуется знать угол между векторами, а нам как раз и надо его найти.

Рассмотрим примеры на использование приведенных свойств скалярного произведения векторов.

Пример 2. Даны точки в пространстве : . Найти скалярное произведение .

Решение. Для вычисления скалярного произведения по формуле (10) нужно знать координаты векторов и . Их найдем по формуле (4), зная координаты начальных и конечных точек этих векторов: , . Тогда по формуле (10) получаем .

Пример 3. Даны векторы . Найти значение , при котором векторы перпендикулярны.

Решение. По критерию перпендикулярности векторов (свойство 5) требуется найти такое значение , при котором . С другой стороны, по формуле (10) получаем

. Тогда из уравнения , получаем .

Пример 4. Найти угол между векторами и .

Решение. Для того, чтобы воспользоваться формулой (11) для косинуса угла между векторами, нежно узнать длины векторов и , а также их скалярное произведение. И то и другое можно вычислить, если известны координаты этих векторов. Поэтому начнем с их поиска. Поскольку координаты вектора являются одновременно и коэффициентами в разложении этого вектора по единичным векторам осей координат , и (уже упоминалась такая теорема в параграфе «Координаты вектора»), то поскольку и , то , а . По формуле (1) предыдущего параграфа находим длины векторов по их координатам: , . По формуле (10) находим : . Наконец, по формуле (11) находим . Поскольку такое значение косинуса нам знакомо (должно быть) и соответствует углу , то угол между векторами .

Замечание. Если отложить векторы и (по найденным их координатам), то видно, что они пойдут по биссектрисам координатных углов хОу и yOz.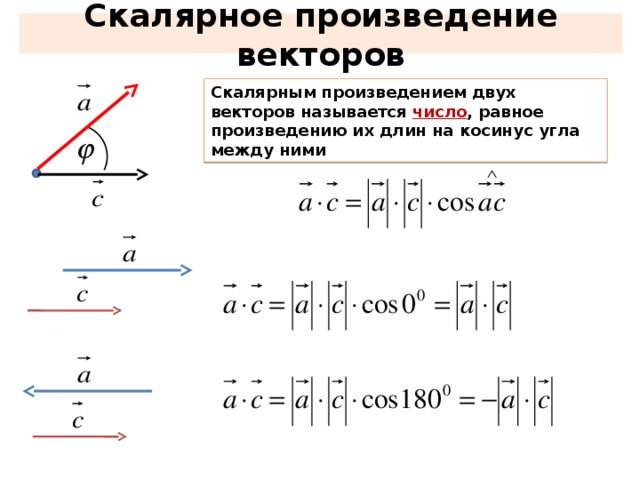 Таким образом мы получили, что угол между биссектрисами координатных углов равен .

Пример 5. Даны длины векторов и и угол между ними : , . Вектор . Найти − длину вектора .

Решение. Данные задачи относятся к векторам и , поэтому желательно выразить длину вектора через эти данные. Далее, по свойству 4: {раскрываем скобки} ={используем свойства 4 и 1} {используем данные задачи и формулу (8)} . Итак, , а потому .

Объяснение урока: скалярные и векторные величины

В этом объяснении мы научимся различать скалярные величины с величинами и векторные величины как с направлениями, так и с величинами.

Давайте начнем с рассмотрения некоторых примеров физических величин, чтобы определить, обладает ли каждая из них свойством направленности.

Пример 1. Определение скалярных и векторных величин

Какая из следующих величин является векторной?

1. Энергия
2. Разность потенциалов
3. Заряд
4. Сила
5. Давление

Ответ

Помните, что вектор имеет и величину, и направление, в отличие от скаляра 02, 9 который имеет только величину. Подумаем о возможных значениях этих величин. мог иметь, выраженный в единицах СИ. Например, мы могли бы иметь 200 Дж энергии, 12 В разности потенциалов, 1,6×10 С заряда силой 50 Н вверх или 900 Па давления.

Все эти величины имеют величины, но чтобы быть вектором, величина должна и включают направление. Определим, есть ли смысл задавать направление каждой из этих величин. Энергия измеряет способность объекта выполнять работу в силу его движение, положение или внутренние свойства. Например, если мы знаем мяч на холме в диаграмма ниже имеет 200 Дж потенциальной энергии, мы знаем величину энергии, но не можем осмысленно задать ей направление. Мяч имеет возможность скатиться с холма в любом направлении, но все пути вниз с холма неразличимы с точки зрения энергии, потому что количество не связано с каким-либо конкретным направление.

Разность потенциалов и заряд – это величины, связанные с электрической силой, которые могут указывать в любом направлении.

Например, положительный точечный заряд создает электрическое поле, которое указывает радиально наружу, как показано черными стрелками на рисунке ниже. Если бы рядом был помещен какой-либо положительный пробный заряд, положительный заряд оказал бы на него отталкивающую силу, т.к. представлен фиолетовыми стрелками, что приводит к ускорению отрицательного заряда через потенциал разница. Однако направление силы отталкивания зависит от положения положительных и отрицательные заряды, и на самом деле ни заряд, ни разность потенциалов не указывают в направлении. Таким образом, бессмысленно связывать какую-либо величину с направлением.

Давление — это сила, распределенная по площади. Представьте, что вы нажимаете на крышку контейнера, наполненного замазки, с отверстиями со всех сторон контейнера, как показано ниже. Обратите внимание, как нажимая на крышку оказывает давление на всю замазку в контейнере, как показано желтыми стрелками, и замазка вытекает через отверстия во всех сторонах контейнера.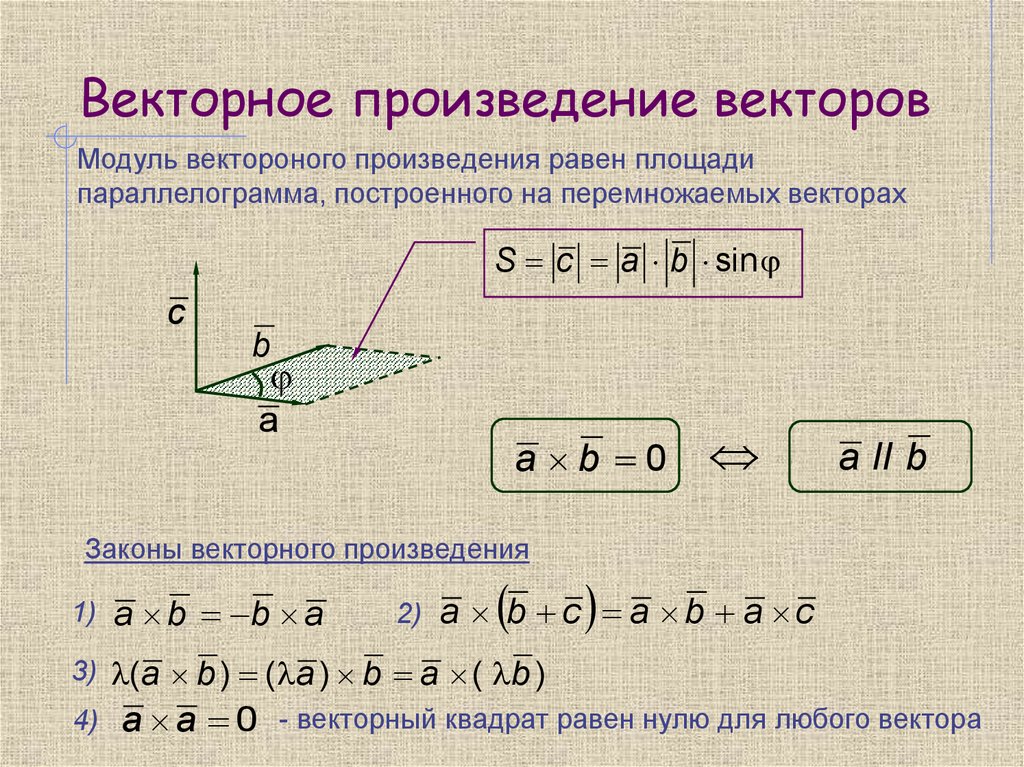 Давление применяется в все направления сразу , поэтому мы не можем связать его с каким-то одним конкретным направлением и вместо этого представьте давление как скалярную величину.

Единственная из перечисленных выше величин, с которой связано направление, это сила , поскольку она указано как направленное вверх. Представьте, что мяч брошен с силой 50 Н вверх, и другой мяч брошен с усилие 50 Н вправо, как показано на рисунке ниже. Несмотря на то, что они имеют одинаковые величины, силы можно отличить друг от друга. так, как скаляры не могут. Здесь разница в направлении является значимой частью измерения. Для полного описания силы необходимо указать как величину, так и направление.

Следовательно, сила является векторной величиной.

Теперь, когда мы рассмотрели примеры обоих типов величин, давайте посмотрим на их формальные определения.

Определение: Скаляр

Скаляр количество выражает только величину, или сколько существует количества. Скаляр может есть единицы, чтобы помочь описать его величину, но не направление.

Определение: Вектор

Величина вектора выражает как величину, так и направление. Вектор может иметь единицы для описания его величина, а количество должен быть связан с указанным направлением.

Хотя эти два термина кажутся похожими, их основное различие заключается в том, что вектору присваивается определенный направление, а скаляр — нет.

Помните, что единицы измерения могут быть присвоены обоим типам величин. Например, если мы знаем, что собака пробежал 20 м, расстояние, которое он пробежал, выражается скаляром. Но если наша подруга сказала, что видела, как собака пробежала 20 м по направлению к парку , то у нас есть векторная величина, которую мы можем использовать для описания бега собаки. смещение , которое сообщает, как далеко он пробежал в определенном направлении . Оба этих примера скаляра и вектора имеют одну и ту же единицу измерения, метры, но дают разные результаты, так как указание направление говорит нам больше о движении собаки.

Пример 2: Идентификация скалярных и векторных величин

Набор измеренных значений величины записывается как имеющий значения 7 единиц, 4 единицы, отрицательные 2 единицы и 6 единиц. Какой из перечисленных видов величин могут ли эти измерения представлять?

1. Только векторная величина
2. Только скалярная величина
3. Либо скалярная величина, либо векторная величина
4. Ни скалярная величина, ни векторная величина имеют только величину и векторы являются величинами, которые имеют величину и направление, и обратите внимание, что ни одно из перечисленных значений выше включают письменное направление. Однако это не означает, что эти величины могут никогда не ассоциироваться с направлением, поэтому давайте представим, будет ли это иметь смысл для вектора величины принимать значения 7,4,−2 и 6,

   Сила — это векторная величина, обычно используемая в физике, так что представьте, что у нас есть значения выражается в единице силы СИ, ньютонах, как 7 Н, 4 Н, −2 Н и 6 N. Отрицательное значение может вызвать некоторое подозрение, но следует отметить, что отрицательные векторные величины часто представляют значения, которые указывают на направление, противоположное положительным силам. Например, представьте, что вы толкаете коробку по полу с помощью силой 100 Н вправо, а трение по коробка вызывает силу сопротивления 25 Н к левый. Если мы найдем результирующую силу, действующую на коробку, решив представить правое направление как положительное, а левое отрицательное, мы можем рассчитать результирующую силу как 100−25=75NNN. Таким образом, мы знаем, что на коробку действует результирующая сила 75 Н. действуя на него вправо.

   Мы смогли осмысленно присвоить отрицательное значение вектору, поэтому разумно заключить что набор значений 7,4,−2 и 6 может представлять векторную величину.

   Теперь мы должны решить, может ли наш набор значений потенциально представлять скалярную величину, поэтому давайте подумайте, что будет означать для скаляра отрицательное значение. Хотя некоторые единицы измерения, например, время, не может осмысленно принимать отрицательное значение, существуют некоторые скалярные величины, которые могут обоснованно имеют отрицательные значения. Например, рассмотрим электрический заряд: протоны имеют значение заряда 1,6×10 С, и электроны имеют заряд −1,6 × 10 Кл. Обратите внимание, что значения имеют одинаковые величины, но поскольку один положительный и один отрицательный, важно их различать. Следовательно, заряд скалярная величина, которая может осмысленно иметь отрицательное значение.

   Таким образом, возможно, что набор измеренных значений 7,4,−2 и 6 может представляют либо скалярную, либо векторную величину, что соответствует варианту ответа C .

   Как показано выше, мы сталкиваемся со скалярными и векторными значениями в реальной жизни на протяжении всего нашего изучения физики, поэтому полезно рассмотреть, как эти типы величин взаимодействуют математически.

   Вектор может быть представлен графически с помощью стрелки, так что длина стрелки представляет величина вектора, а стрелка указывает направление вектора. Это представление может помочь нам лучше понять векторные свойства и то, как они взаимодействуют с другими величинами. В следующем примере демонстрируется метод сложения векторов «кончик к хвосту», в результате которого в новом векторе.

   Пример 3. Определение правильного графического представления сложения векторов

   Два показанных вектора можно сложить, чтобы получить результирующий вектор. Какой из нижеуказанных диаграммы правильно показывает сравнение обоих этих векторов с равнодействующей векторов?

   Обратите внимание, что длины векторов указаны не в масштабе.

   Ответ

   При графическом сложении векторов мы используем метод «кончик к хвосту».

   Векторы добавляются по коммутативное свойство , что означает, что они всегда будут приводить к одному и тому же результату. сумма, независимо от порядка их добавления. Итак, начиная с любого вектора, найдите его «кончик». (конец со стрелкой). Затем найдите «хвост» (конец без наконечника) другой вектор. Мы будем использовать кончик синего вектора и хвост зеленого вектора, как показано ниже.

   Затем переместите или сдвиньте без вращения второй вектор так, чтобы его хвост находился в той же точке как кончик первого вектора. Этот шаг проиллюстрирован ниже.

   Теперь, когда они расположены «кончик к хвосту», мы можем нарисовать новый вектор, представляющий их сумму, начиная с хвоста первого вектора и заканчивая кончиком второго вектора. Эта сумма представлена желтым вектором ниже.

   Кроме того, обратите внимание, что из-за свойства коммутативности мы могли бы сложить векторы в другом порядке. и достигли той же суммы, как показано ниже.

   Итак, знайте, что вариант ответа B правильно показывает, как сложить два вектора.

   При сложении и вычитании скаляров или векторов правило простое: мы должны обязательно только складывать или вычитать подобные количества . Невозможно осмысленно сложить или вычесть две величины с разными единицами измерения. Например, попробуйте добавить 25 Дж и 10 герц в один понятный термин, и это будет становится ясно, что добавление терминов с несовпадающими единицами совсем не полезно.

   Кроме того, невозможно сложить или вычесть скаляр с вектором. Даже если две величины используют одно и то же единицы, скаляры и векторы по-прежнему принципиально отличаются друг от друга; если у нас нет направления компонента или элемента для одного количества, то мы не можем оправдать прибавление или вычитание его с количеством, которое включает ли направление, поскольку у нас не было бы всей информации, необходимой для нахождения истинного и полный результат.

   Давайте представим себе ситуацию, в которой мы могли бы попытаться сложить скаляр и вектор. Представьте, что мы находим направления к спрятанному сокровищу, которое гласило: «Пройдите 60 шагов, затем пройдите 40 шагов на запад». Мы бы знали точную местонахождение клада, если бы мы могли рассчитать его полное перемещение по заданным инструкциям, что принять вид: 60 шагов + 40 шагов на запад. Но есть проблема, потому что мы не знать направление , в котором нужно пройти первые 60 шагов, поэтому нет четкой интерпретации добавления две величины вместе. Мы могли бы предположить и, возможно, попытаться пройти первые 60 шагов на север, юг, восток или запад, но также возможно, что шаги должны быть предприняты в каком-то промежуточном направлении. Это означает, что существует множество различные пути, которые можно было бы попробовать, хотя на самом деле работает только один путь. Если бы в инструкции был начальное направление вместе с величиной 60 шагов, мы могли бы сразу узнать местонахождение сокровища.

   Ключевой момент, который следует помнить при сложении или вычитании, заключается в том, что мы должны использовать одинаковые термины: скаляр со скаляром или вектор с вектором, всегда следя за тем, чтобы задействованные единицы совпадали.

   Следует отметить, что разделить на вектор невозможно, поэтому мы не будем пытаться это сделать. Но возможно удивительно, но можно разделить вектор на скаляр и перемножить скаляры и векторы вместе. Делать при этом мы умножаем или делим величины величин, как обычно, а также умножаем или делим их единицы, стараясь рассмотреть, что означает это изменение единиц для результирующей величины. Направление вектора количество по-прежнему относится к произведению или частному, поэтому умножение или деление скаляров и векторов вместе приводит к вектору . Представление векторов графически помогает понять эту концепцию, так как умножение или деление вектора на скаляр просто включает изменение длины стрелки, оставляя ее как вектор.

   Представьте, что мы знаем, что велосипед движется направо на 8мс, и мы хотим узнать его смещение через 2 с. Поскольку это векторная величина, мы можем представить скорость велосипеда со стрелкой, такой как синяя стрелка ниже, которая указывает вправо и имеет длину 8 единиц.

   Время является скалярной величиной, поэтому его нельзя представить стрелкой. Тем не менее, мы все еще можем выполнить математическое операция с нашим вектором и скаляром. Чтобы найти перемещение велосипеда, нужно умножить скорость по времени, поэтому мы умножаем величину вектора на два, что просто удваивает длину стрелки. Этот продукт представлен зеленой стрелкой ниже, и направление по-прежнему имеет значение, поскольку смещение является векторной величиной. Значит, через две секунды велосипед переместится на 16 м. право.

   Важно помнить, что умножение или деление вектора на скаляр дает новый вектор с тем же направлении, но другой величины. Применим это понятие к некоторым примерам.

   Пример 4. Определение того, является ли произведение двух величин скалярным или векторным

   Если скорость умножается на время, является ли результирующая величина векторной или скалярной величиной?

   Ответ

   Мы хотим умножить скорость на время; давайте сначала подумаем о свойствах этих величин. Мы должны будьте осторожны, чтобы не спутать скорость со скоростью, ее векторным эквивалентом. Скорость не имеет элемента направления, так что это скалярная величина.

   Время также является скалярной величиной, поэтому мы хотим перемножить два скаляра, с которыми мы уже знакомы: просто умножьте их величины и единицы. Поскольку нет направления, связанного со временем или скоростью, их результирующий продукт также будет скаляром .

   Пример 5. Определение того, является ли произведение двух величин скаляром или вектором

   Если время умножается на скорость, является ли результирующая величина векторной или скалярной величиной?

   Ответ

   Мы хотим умножить время на скорость, поэтому, чтобы проверить, верно ли это, давайте подумаем о двух величинах и их свойства. Время является скалярной величиной, поскольку его можно полностью описать, используя только величину, и помните эта скорость является -векторной величиной : ⃑𝑣=⃑𝑑𝑡.

   Не путать со скоростью, ее скалярным аналогом, скорость определяется как перемещение, деленное на время, и помните это смещение является вектором, потому что оно имеет как величину, так и направление.

   Мы хотим умножить скаляр на вектор, что можно сделать, перемножив их величины и единиц и присвоение исходного направления вектора произведению. Так как мы закончим с направлением, связанным с нашим продуктом результирующее количество равно вектору .

   Мы можем проверить это еще раз — умножив время и скорость, мы получим 𝑡×⃑𝑣=𝑡×⃑𝑑𝑡=⃑𝑑.

   Единицы времени уравновешиваются, и наша величина превращается в перемещение, имеющее как величину, так и направление, поэтому полученное количество равно вектор .

   Обратите внимание, что, как упоминалось в приведенном выше примере, само определение скорости включает в себя деление вектора (смещение) на скаляр (время), в результате чего получается векторная величина, точно так же, как мы видели раньше с велосипедом.

   Давайте закончим резюмированием нескольких важных понятий из этого объяснения.

   Ключевые моменты

   • Скалярные величины имеют только величину, а векторные величины имеют и величину, и направление.
   • При сложении и вычитании мы должны использовать либо вектор и вектор, либо скаляр и скаляр. В обоих случаях все участники единицы должны совпадать.
   • Мы можем добавлять векторы графически «кончик к хвосту», создавая новый вектор.
   • Мы можем определить, имеют ли значения, рассчитанные с использованием скалярных и векторных величин, скалярное или векторное значение.
   • При умножении или делении вектора и скаляра вместе умножайте или делите их величины и единиц, а произведение сохранит элемент направления вектора, в результате чего получится вектор.

   2.2 Векторы, скаляры и системы координат

   Цели обученияСистемы координат для одномерного движения

   Цели обучения

   К концу этого раздела вы сможете делать следующее:

   • Определение и различие между скалярными и векторными величинами
   • Назначение системы координат для сценария с одномерным движением

   Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:

   • 3. A.1.2 Учащийся может разработать экспериментальное исследование движения объекта.

   Рис. 2.6 Движение этой струи можно описать в терминах пройденного ею расстояния (скалярная величина) или ее смещения в определенном направлении (векторная величина). Чтобы указать направление движения, его перемещение должно быть описано на основе системы координат. В этом случае может быть удобно выбрать движение влево как положительное движение — это прямое направление для плоскости — хотя во многих случаях координата х-х-размера 12{х} {} проходит слева направо, движение вправо считается положительным, а движение влево отрицательным. (Фото: кресло «Авиатор», Flickr)

   В чем разница между расстоянием и перемещением? В то время как смещение определяется как направлением, так и величиной, расстояние определяется только величиной. Перемещение является примером векторной величины. Расстояние является примером скалярной величины. Вектор — это любая величина, имеющая как величину , так и направление . Другие примеры векторов включают скорость 90 км/ч на восток и силу 500 ньютонов прямо вниз.

   Направление вектора в одномерном движении задается просто плюсом (+)(+) размера 12{ \( + \) } {} или минус (-)(-) размером 12{ \( — \ ) } {} подписать. Векторы представлены графически стрелками. Стрелка, используемая для представления вектора, имеет длину, пропорциональную величине вектора, например, чем больше величина, тем больше длина вектора, и она указывает в том же направлении, что и вектор.

   Некоторые физические величины, такие как расстояние, либо не имеют направления, либо не указываются. Скаляром называется любая величина, имеющая величину, но не имеющую направления. Например, температура 20 ºC20 ºC, 250 килокалорий (250 калорий) энергии в шоколадном батончике, ограничение скорости 90 км/ч, рост человека 1,8 м и расстояние 2,0 м — все это скаляры — величины, не имеющие указанное направление. Обратите внимание, однако, что скаляр может быть отрицательным, например, температура от −20 ºC до 20 ºC. В этом случае знак минус указывает точку на шкале, а не направление. Скаляры никогда не изображаются стрелками.

   Системы координат для одномерного движения

   Чтобы описать направление векторной величины, вы должны указать систему координат в системе отсчета. Для одномерного движения это простая система координат, состоящая из одномерной координатной линии. В общем, при описании горизонтального движения движение вправо обычно считается положительным, а движение влево считается отрицательным. При вертикальном движении движение вверх обычно положительное, а движение вниз отрицательное. Однако в некоторых случаях, как в случае со струей на рис. 2.6, удобнее поменять местами положительное и отрицательное направления. Например, если вы анализируете движение падающих объектов, может быть полезно определить положительное направление вниз. Если люди в гонке бегут налево, полезно определить лево как положительное направление. Это не имеет значения, пока система ясна и последовательна. Как только вы задаете положительное направление и начинаете решать проблему, вы не можете изменить его.

   Рисунок 2.7 Обычно удобно рассматривать движение вверх или вправо как положительное (+)(+) значение 12{ \( + \) } {}, а движение вниз или влево как отрицательное (-).(-) .

   Проверьте свое понимание

   Скорость человека может оставаться неизменной, когда он поворачивает за угол и меняет направление. Учитывая эту информацию, является ли скорость скалярной или векторной величиной? Объяснять.

   Решение

   Скорость является скалярной величиной. Он совсем не меняется при изменении направления; следовательно, он имеет только величину. Если бы это была векторная величина, она менялась бы при изменении направления, даже если бы ее величина оставалась постоянной.

   Переключение систем отсчета

   Фундаментальный принцип физики заключается в том, что информацию о событии можно собрать из различных систем отсчета. Например, представьте, что вы — пассажир, идущий впереди автобуса. Когда вы идете, за вашим движением наблюдает другой пассажир автобуса и наблюдатель, стоящий на тротуаре.

   И пассажир автобуса, и наблюдатель на тротуаре смогут собирать информацию о вас. Они могут определить, как далеко вы продвинулись и сколько времени вам потребовалось для этого. Однако пока вы двигаетесь с постоянной скоростью, оба наблюдателя получат разные результаты. Для пассажира, сидящего в автобусе, вы двигались вперед в темпе, который можно было бы считать нормальным, что-то вроде того, как быстро вы идете по улице в солнечный день. Однако для наблюдателя с тротуара вы будете двигаться гораздо быстрее. Поскольку автобус также движется вперед, расстояние, которое вы продвигаетесь вперед по тротуару с каждой секундой, увеличивается, и наблюдатель тротуара должен сделать вывод, что вы двигаетесь с большей скоростью.

   Чтобы показать, что вы понимаете эту концепцию, вам нужно создать событие и придумать способ просмотра этого события с двух разных точек зрения. Для того, чтобы обеспечить наблюдение за событием одновременно с обоих кадров, вам понадобится помощь помощника.