Что такое скаляр и вектор

Физические величины различной природы могут иметь различную математическую структуру описания.

Из элементарного курса известны простейшие определения скаляра (скалярной величины) и вектора (векторной величины):

¾ скаляром называется величина, которая при определенном выборе единицы измерения однозначно характеризуется числом, ее измеряющим;

¾ вектор определяется своей величиной (модулем) и направлением в пространстве и складывается с другим вектором той же физической размерности по правилу треугольника или параллелограмма.

Для описания вектора в трехмерном пространстве (рис. П.1.1) необходимо одновременно задать три параметра (три проекции, или модуль вектора и углы между направлением вектора и какими-либо двумя из трех координатных направлений). Очевидное различие в математических структурах скалярной и векторной величин приводит к различию в свойствах указанных объектов.

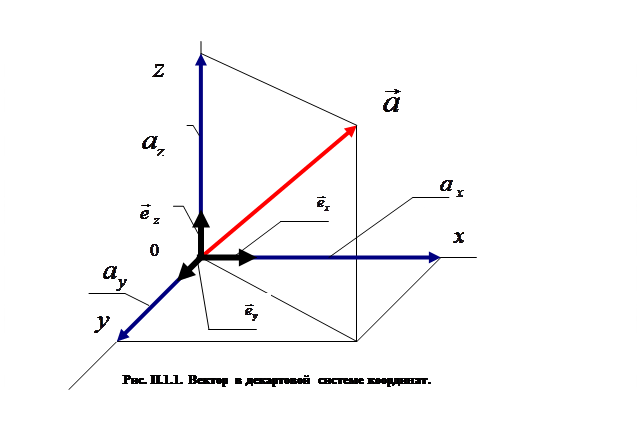
Строгая классификация физических объектов основана на изучении характера изменения их компонент при преобразованиях систем координат (т.е. при переходе от одной координатной системы к другой). В физике чаще всего имеют дело с преобразованиями систем координат в обычном трехмерном пространстве или в четырехмерном пространстве-времени Минковского.

Трансформационные свойства физических величин могут быть различны в этих случаях. К примеру, кинетическая энергия материальной точки — скаляр относительно преобразований системы координат в трехмерном пространстве и одна из компонент 4-вектора относительно преобразований в пространстве Минковского.

Важно отметить, что и вид преобразований системы координат может оказаться существенным. Так “вращения” и “сдвиги” координатных систем отличаются тем, что переводят “правые” координатные системы в “правые”, а «отражение» относительно одной из координатных поверхностей переводит «правую» координатную систему в «левую». Физическая величина может оказаться инвариантной (неизменной) при преобразовании «вращения» и неинвариантной при преобразовании «отражения».

При изучении преобразований систем координат в основной части курса мы ограничимся преобразованиями сдвига и вращения правых декартовых систем координат.

В общем, указание трансформационных свойств физической величины (т.е. ее тензорного характера) имеет смысл только по отношению к определенной группе преобразований координат в данном пространстве. С рассматриваемой точки зрения, скаляр — это величина, инвариантная относительно (разрешенных) преобразований координат, а вектор — совокупность компонент, которые при преобразовании координат трансформируются по определённому правилу, с этим правилом мы познакомимся ниже. Многокомпонентные физические объекты более сложной математической структуры, чем вектор, будут подробно описаны ниже по мере рассмотрения соответствующих физических ситуаций.

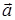Ниже для описания скалярной величины или функции используются общепринятые обозначения. Векторные величины принято описывать или в символической форме (т.е. без указания конкретной системы координат), например, вектор , или в координатной форме 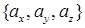, где упорядоченные величины в фигурных скобках представляют собой проекции вектора 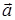на соответствующие координатные линии декартовой системы координат.

Сложение векторных величин по правилу треугольника или параллелограмма (рис. П.1.2)

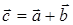
эквивалентно покоординатному сложению:

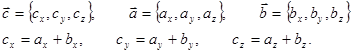
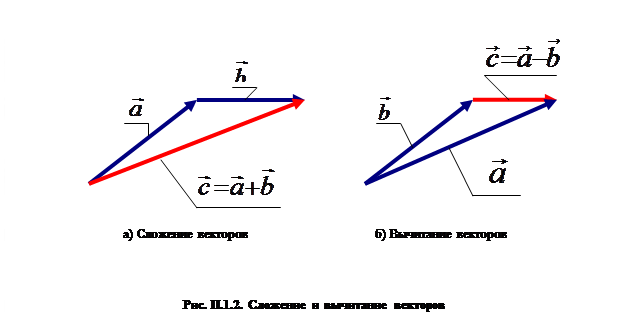
Для векторных величин определено умножение на скалярную величину:

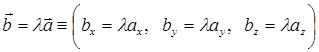
Геометрический образ описанной операции очень нагляден: вектор 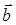направлен так же как и вектор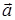

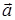, но его величина в «l раз больше» (если l>0 и размерности не имеет). Если l<0, то направление векторов и 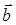противоположны. Если l физически размерная величина, сравнить непосредственно величины векторов 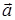и 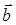не представляется возможным.

Поскольку вектор определен величиной и направлением в пространстве, его можно представить в форме:

,

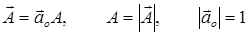где 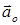– единичный безразмерный вектор (орт), совпадающий по направлению с исходным вектором 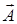; обозначение 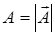используется для записи абсолютной величины (модуля) вектора .

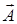Заметим, что в декартовой системе координат имеет место соотношение:

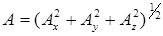
Для декартовой системы координат в трехмерном пространстве удобно ввести орты координатных линий: 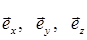(используемые иногда обозначения 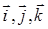не всегда удобны). В этом случае вектор 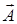можно представить в форме:

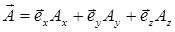
Определение операций «сложение» и «умножение на скалярную величину» позволяет ввести операцию «

вычитания» векторов (рис. П.1.2) по следующему правилу:

.

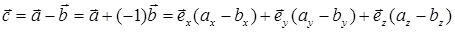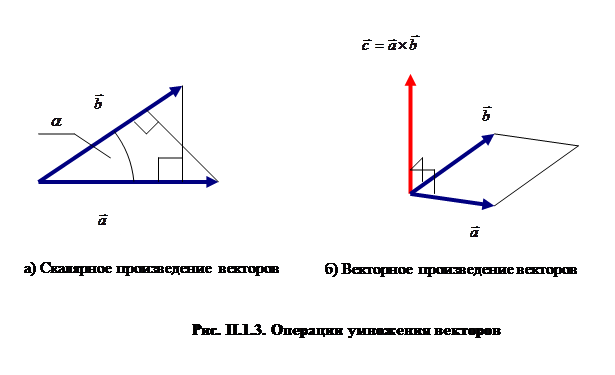
Для векторных величин известны три различные операции умножения. Первая из них, скалярное произведение двух векторов, определена правилом:

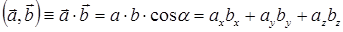
где a— угол между направлениями векторов 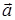и 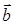, результат операции —скалярная величина (рис. П.1.3).

Если для произвольных векторов 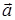и 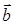, таких, что 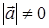и 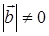, имеет место соотношение 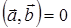, то такие векторы называются ортогональными друг другу. Геометрический смысл скалярного произведения двух векторов становится очевидным, если заметить, что выражение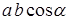

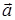представляет собой либо произведение проекции вектора на направление 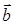на модуль вектора 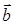, то есть 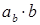, либо произведение проекции вектора 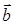на направление вектора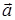

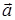на модуль вектора , то есть 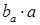. Легко проверить, что .

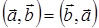Векторное произведение векторов 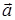и 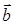определено правилом:

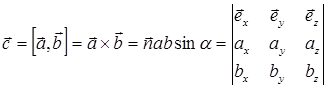
где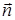

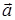– орт, направленный по нормали к плоскости, в которой расположены векторы и 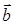, причем система направлений 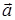, , 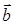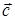является «правой» системой: кратчайшее угловое расстояние между направлениями векторов 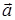и 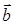(угол a) соответствует движению от 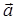к 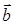против часовой стрелки, если смотреть с конца орта 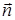(или с конца вектора 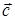). Очевидно, что направление орта нормали 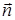совпадает с направлением вектора .

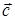Легко видеть, что результатом векторного произведения двух векторов является вектор, причем 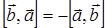. В координатной форме записи имеют место соотношения

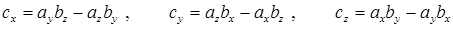
Если 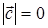, то векторы 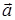и 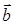либо параллельны друг другу, т.е. 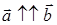, либо антипараллельны, т.е. .

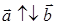Геометрический смысл векторного произведения становится наглядным, если векторы 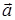и 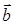представляют собой направленные отрезки двух прямых, исходящих из одной точки пространства, в этом случае величина представляет собой площадь параллелограмма, построенного на векторах 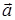и .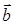

В качестве упражнения рекомендуется проверить соотношения:

 

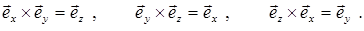
Прямое или тензорное произведение двух векторов определено следующим образом. Если имеем вектор 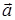, или в координатной форме 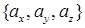, и вектор 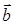, или в координатной форме {b_x,, b_y, b_z}, то можно построить двухиндексный объект – матрицу

=

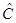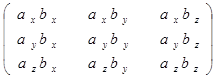
как результат тензорного произведения 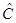= 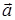Ä 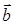, что в координатной форме имеет вид

С_ij = a_i b_j , i,j=1,2,3.

Объект, построенный таким образом, обладает свойствами тензора второго ранга. Тензоры второго и более высокого ранга используются при описании физических явлений в механике сплошных сред, электродинамике, теории относительности и т.д.

Описание алгебраических операций над векторными величинами заключим напоминанием, что операция деления векторных величин не определена.

 

 

---

Дата добавления: 2017-09-01; просмотров: 5355;

---

Похожие статьи:

СКАЛЯРЫ И ВЕКТОРЫ

Министерство общего и профессионального образования РФ ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Физический факультет Кафедра теоретической физики

ЗАПРЯГАЕВ С. А.

ЭЛЕКТРОДИНАМИКА. Векторный анализ

Методические укзания к практическим занятиям по курсу «ЭЛЕКТРОДИНАМИКА»

для студентов 3-го курса дневного отделения

Рекомендовано Учебно МетодическимОбъединением университетов РФ в качестве учебного пособия

1

1.1Исходные определения

Скаляром называется величина, определяемая одним численным значением. Вектором называется величина, задаваемая численным значением и направлением в пространстве. Математическое изображение

вектора есть:	~	A, или	~	(ниже используется обозначение — A).
	A, или		A

Геометрически, вектор изображается отрезком прямой линии, направление которой совпадает с направлением величины A в данной точке, а длина (или модуль вектора A = |A|) равна численному значению вектора (в определенных единицах измерения). Введено понятие нулевой вектор — это вектор, модуль которого равен нулю. Направление такого вектора не задано. Два вектора равны между собой, если модули их одинаковы и направления совпадают (обозначение A = B). Для векторов введен ряд математических операций (но не все в сравнении с числами). Суммой двух векторов A и B называется вектор C, являющийся диагональю параллелограмма, построенного на слагаемых векторах (рис. 1.a). Суммой N векторов является вектор C, замыкающий N + 1 — угольник,

1

q q

q q

*

HY

A2

6

A

YH

q q

q Hq

Hq q qCq q 3q q

q q q q

q q q q

—

HH

C —

AN

B

C —

−B

A

H

Bq

A1

H

?

a)

q q q

q

б)

в)

Рис. 1: Сложение векторов

построенный на слагаемых векторах (рис. 1.б). Из определения суммы векторов следует коммутативность A + B = B + A и ассоциативность

(A + B) + C = A + (B + C) векторного сложения. Вектор называется противоположным заданному A (обозначается −A), если модуль его равен |A|, а направление прямо противоположно вектору A. Разностью двух векторов A и B называется сумма уменьшаемого вектора с вектором, противоположным вычитаемому A − B = A + (−B) (рис. 1.в). Проекция вектора A на ось e есть число, равное:

где ϕ -угол между напрвлением вектора A и положительным направлением оси e. Умножение вектора A на скаляр a определяет вектор, модуль

P3 k=1

2

которого равен a · A, а направление совпадает с направлением вектора

A, если a > 0 и противоположно направлению вектора A, если a			<
0. Умножение вектора на число удовлетворяет соотношениям: a(b A)			=
(a · b)A,	a(A + B) =	aA + aB. Линейно зависимыми называются
векторы,	для которых	выполняется равенство PiN=1 αiAi = 0, где	αi

-числа, не все равные нулю. Два линейно зависимых вектора параллельны (коллиниарны) друг другу. Три линейно зависимых вектора лежат в одной плоскости (компланарны). Если три вектора линейно независимы, то любой вектор единственным образом разлагается по этим векторам. Базисом трехмерного пространства называется произвольная система трех линейно независимых векторов ei, i 1 ÷ 3. При заданном базисе для любого вектора имеем:

	3
	kX	(2)
A = A1 e1 + A2 e2 + A3 e3 =	Ak ek
	=1
Откладывая тройку базисных векторов из	одной точки	пространства

(начало координат) и называя прямые, являющиеся продолжением ek, осями координат, получим косоугольную декартову систему координат. Если базисные векторы взаимно ортогональны и |ek| = 1, то они называются ортами прямоугольной декартовой системы координат. Часто используются следующие общепринятые обозначения e1 = i -орт оси X, e2 = j -орт оси Y , e3 = k -орт оси Z. Радиусвектор точки (r) — есть вектор, проведенный из начала координат к заданной точке пространства r = x i+y j+z k. Здесь x, y, z — декартовы координаты точки. В дальнейшем будут использованы обозначения x1 ≡ x; x2 ≡ y; x3 ≡ z. В результате

r = xk ek. Модуль радиус вектора обозначается r и равен r =

√

x2 + y2 + z2. Единичный радиусвектор — есть вектор, равный n = r/r.

1.2 Произведения векторов

Для векторов определены два типа произведения — скалярное и векторное. Скалярное произведение двух векторов A и B есть число, равное произведению модулей векторов на косинус угла между ними. Скалярное произведение двух векторов обозначается (A · B) или A · B и по определению (1) равно произведению модуля одного вектора на проекцию

εi j k

	3
второго вектора на направление первого:
A · B = A B cos(Ad· B) = AB · B = A · BA	(3)

По определению скалярное произведение коммутативно A · B = B · A и дистрибутивно (A + B) · C = A · C + B · C. На основании (3) проекция вектора на ось равна скалярному произведению орта оси на вектор. Из равенства скалярного произведения нулю следует взаимная ортогональность векторов. Орты прямоугольной декартовой системы

координат ортогональны между собой ei · ej		= δij. Используя (2) для
скалярного произведения (3), имеем
	3	3
A · B =	X	kX	(4)
	Ak Bn (en · ek) =	Ak Bk
	k,n=1	=1

Векторным произведением двух векторов A и B называется вектор, обозначаемый [A × B], равный по величине произведению модулей векторов на синус угла между ними и направленный перпендикулярно плоскости векторов сомножителей в ту сторону, откуда поворот от первого сомножителя A ко второму B на меньший угол виден против хода часовой стрелки. Векторное произведение некоммутативно, так как [A × B] = −[B × A], но дистрибутивно [A × (B + C)] = [A × B] + [A × C]. Из равенства [A × B] = 0 следует параллельность векторов A и B. Векторное произведение имеет простой геометрический смысл: |[A × B]| равен площади параллелограмма, построенного на этих векторах. Векторное произведение ортов прямоугольной декартовой системы координат равно:

3
kX	i, j 1, 2, 3	(5)
[ei × ej] = εi j k ek
=1

— символ Леви-Чевита, равный нулю, если хотя бы два индекса совпадают; равный +1, если i, j, k образуют циклическую; и −1, если i, j, k образуют нециклическую перестановку от последовательности 1, 2, 3. В практических приложениях используются следующие соотношения для εi j k

3						3
εi k l · εi s t =		δks	δkt		;	εi k l · εi k t = 2δlt	(6)
X						X
i=1		ls	lt			i,k=1

Определитель квадратной матрицы 3 × 3 можно представить в следующем виде:

	3
det A = ||A|| =	X	(7)
	A1 i A2 j A3 k εi j k.

i,j,k=1

4

Используя (2), (5), получаем общее выражение для вычисления векторного произведения:

[A B] =

3

3

e1

e2

e3

(8)

AiBj [ei ej] =

εi j kAiBj ek

=

A1

A2

A3

X

X

×

×

B1

B2

B3

i,j=1

i,j,k=1

Смешанное произведение трех векторов

3

3

X

X

εi j kAnBiCj (en · ek) =

A · [B × C] =

AnBiCj en · [ei × ej] =

i,j,n=1

i,j,n,k=1

3

εi j k

AkBiCj =

3

A1

A2

A3

(9)

=

εk i j AkBiCj =

B1

B2

B3

X

X

C1

C2

C3

i,j,k=1

k,i,j=1

Из (9) вытекает, что значение смешанного произведения не меняется при циклической перестановке векторов, входящих в него. Численно смешанное произведение равно объему параллелепипеда, построенного на векторах, входящих в произведение. Если любые два вектора в смешанном произведении одинаковы или параллельны, то такое произведение равно нулю. Наконец, если все три вектора лежат в одной плоскости, смешанное произведение также равно нулю. Таким образом, если для трех векторов A · [B × C] 6= 0, то данные векторы образуют базис. При этом, если A · [B × C] > 0, базис называется правым. Если A · [B × C] < 0, базис называется левым. Используя (9), εi j k можно представить в следующем виде

εi j k = [ei × ej] · ek

(10)

Двойное векторное произведение обозначается [A×[B×C]] и для его вычисления справедлива формула

D ≡ [A × [B × C]] = B (A · C) − C (A · B)

(11)

Для доказательства равенства (11) перепишем двойное векторное произведение с учетом (2), используя равенство (5), получим:

	3		3
	X		X
D =	AiBjCk [ei × [ej × ek]] =		AiBjCkεl j k εl n i en
	i,j,k=1		i,j,k,l,n=1
Выполняя суммирование по l на основании (6) и (4), получим:
	3	en = B (A · C) − C (A · B)
D = i,n=1 AiBnCi − AiBiCn
	X

Геометрия данных 3. Скалярное произведение пар / Habr

Инвариант дистанции (квадрат расстояния) между элементами можно обобщить, если умножать разность элементов не на саму себя, а на другую разность элементов. Полученное значение будет отражать скалярное произведение упорядоченных пар.

Упорядоченная пара

Координаты вектора могут быть получены на как разность координат элементов, но обратное неверное — по координатам вектора невозможно восстановить координаты образовавших его элементов. Координаты двух элементов несут в себе больше информации, чем координаты вектора. Поэтому из элементов можно образовать пару — улучшенный аналог вектора. Такой набор из двух элементов называют упорядоченной парой.

Каждой упорядоченной паре можно сопоставить вектор — разность элементов, образующих пару. Для двух векторов можно определить скалярное произведение, которое можно также рассматривать как характеристику четырех элементов пространства.

Скалярное произведение

Для уменьшения громоздкости в данной части будем обозначать элементы строчными символами. Пара — это совокупность двух элементов: . Вектор, соответствующий паре, — это разность элементов пары:

Норма элемента — это его скалярное произведение с самим собой:

Это же определение можно использовать для вектора пары, которая, как известно, отражает квадрат расстояния между элементами пары:

Если заданы две разных пары и , то можно определить скалярное произведение между соответствующими векторами:

Индексы задают одну пару, а индексы — другую.

Выражение (3.4) определяет скаляр, зависящий от взаимного положения 4-х элементов. Важно, что данный скаляр может быть выражен через расстояния между элементами .

Как известно, расстояние между элементами связано со скалярным произведением между ними:

.

Раскрывая произведение (3.4) с учетом (3.5), получаем:

Это общая формула скалярного произведения пар. Порядок индексов важен — задает пары и направление соответствующих им векторов.

Выражения, подобные (3.6), часто возникают в разных местах математики. Связано это с общностью вывода данной формулы. Отметим, что мы использовали только самые общие свойства алгебраического выражения. Поэтому в качестве элементов могут использоваться любые объекты, для которых определена операция произведения. Тождество будет справедливо и для них, в общей форме оно выглядит так:

Пары с общей вершиной — смежные пары

Если пары имеют общую вершину , то формула (3.6) упрощается:

Формула (3.7) — это теорема косинусов для треугольника. Здесь пары, между которыми определена взаимная норма, имеют общий элемент k — смежные пары.

На 3-х вершинах можно определить три скалярных произведения. Их сумма выражается через сумму дистанций между вершинами:

Квадрат скалярного произведения на 3-х вершинах связан с площадью образуемого ими треугольника (формула Герона):

Независимые пары — четыре разных вершины

В общем случае вершины пар могут не лежать в одной плоскости, поэтому данному определению скалярного произведения не всегда можно сопоставить косинус угла между направлениями.

Перечислим свойства скалярного произведения (3.6).

1) Не зависит от перестановки пар:

2) Антисимметрично относительно перестановки элементов в паре или :

3) Для 4-х элементов существует только два независимых скалярных произведения пар ввиду тождества:

Математики увидят в формуле (3.9.3) первое тождество Бьянки. Из чего можно сделать вывод, что структуры тензора кривизны (Римана) и скалярного произведения пар — подобны.

4) Норма независимых пар может быть выражена через разность норм смежных пар:

Этим тождеством воспользуемся в следующей статье.

5) Дистанция между элементами и может быть выражена через значения скалярных произведений смежных и независимых пар:

Пары на элементах базиса

В качестве элементов, образующих пару, могут быть выбраны вершины базиса. Тогда скалярное произведение пар становится тензором — набором скалярных произведений между всеми возможными парами элементов данного базиса. Чтобы отличать тензоры от скаляров будем использовать для первых заглавные буквы. То есть вместо скаляра для элементов базиса получаем тензор .

Скалярное произведение и кофакторы лапласиана

Скалярное произведение пар, образованных элементами базиса, может быть выражено через свойства лапласиана базиса.

Если заданы две пары вершин и , то значение их скалярного произведения можно получить делением кофактора 2-го порядка на скалярный потенциал лапласиана :

Кофактором называется определитель минора квадратной матрицы (с учетом знака). Скалярный потенциал — это кофактор 1-го порядка от лапласиана (см. (1.12) из первой статьи).

Таким образом необходимо из матрицы лапласиана удалить столбцы, соответствующие одному вектору (в формуле это -й столбцы), и строки, соответствующие другому (), после чего разделить определитель получившегося минора на скалярный потенциал . Если удаляемые столбцы и строки лапласиана — одни и те же, то получим значение дистанции между узлами.

Скалярное произведение пар на графе

Между любыми парами вершин графа можно определить их взаимную норму — скалярное произведение. Поскольку граф обычно задан лапласианом, то для расчета можно использовать формулу (3.10.1).

Пусть, например, в качестве образующих вершин двух пар выбраны — и . Тогда скалярное произведение между данными парами дается формулой (3.6):

Для графа, представляющего собой электрическую цепь, значение скалярного произведения отражает понятие обобщенного сопротивления в электрической цепи. Для измерения такого («кажущегося») сопротивления источник тока (напряжение) прикладывается к одним узлам (A и B), а разность потенциалов измеряется между другими (M и N). Взаимная норма (скалярное произведение) пар равна нулю, если внешняя разность потенциалов не приводит к разности потенциалов на измеряемой паре.

Граф не обязательно должен быть дискретным,- грунт является примером сплошного (непрерывного) графа, на котором можно проводить измерения скалярного произведения между выбранными элементами.

Схема установки для исследования методом сопротивления: A и B – питающие заземления; M и N – измерительные заземления; 1 – измерительный прибор (из книги «Электроразведка», Якубовский Ю. B., M., 1980).

На рисунке показана схема измерения скалярного произведения пар и на грунте.

В следующей статье разберем подробнее, почему отношение заданной и измеряемой разностей потенциалов узлов оказалось связанным со скалярным произведением пар.

Обращение минора лапласиана

Подматрицу значений взаимных норм (скалярных произведений) пар можно получить обращением минора лапласиана. Обозначим лапласиан, из которого удалены -я строка и -й столбец, как . Тогда имеет место тождество:

Отметим, что в матрице отсутствуют -я строка и -й столбец.

Если известна матрица скалярных произведений пар , то можно восстановить дистанционную матрицу на основании преобразования дистанции. Вначале расширяем подматрицу отсутствующей строкой и столбцом с нулевыми значениями. К полученной матрице применяем преобразование дистанции:

которое в нашем случае принимает вид тождества (3.9.5):

Совокупность формул (3.10.2) и (3.10.3) — один из способов получить дистанционную матрицу по заданному лапласиану. Удаляем из лапласиана какой-либо из узлов (пусть будет ) и обращаем. Получаем матрицу скалярных произведений пар (ее другое название — фундаментальная матрица, см. следующую часть). Значение индекса фиксировано — базовая вершина. В матрице первая вершина пар находится в базовом узле , а вторая пробегает по остальным вершинам базиса.

Далее применяем к матрице преобразование дистанции (3.10.3).

Квадрат скалярного произведения, матрица Якоби

Если в графе изменить значение проводимости ребра (элемент лапласиана), то очевидно, что изменятся и все дистанции между вершинами (нормы векторов) . При увеличении проводимости дистанции должны сократиться (уменьшиться). Подарок богов в том, что можно оценить изменение дистанций не только качественно, но и количественно. Обозначим производную матрицы дистанций по лапласиану как

Тензор — это матрица Якоби, то есть выражение изменений значений дистанционной матрицы при изменении значений лапласиана . Оказывается, что данный тензор выражается через квадрат скалярного произведения пар:

То есть изменение величины связи узлов приводит к изменению дистанции между узлами пропорционально величине скалярного произведения пар и .

Тензор квадросвязности вершин

Тензор квадратов скалярного произведения обратим. Представим выражение (3.11) в следующем эквивалентном виде:

Данную формулу можно трактовать как отклик на воздействие . Тензор играет роль передаточной функции (реакции на воздействие).

Возможна и обратная ситуация, при которой воздействие и отклик меняются местами. Прямая и обратная передаточные функции связаны соотношением:

Снова удача — тензор можно выразить через лапласиан:

Значения тензора назовем квадросвязностью.

Свойства тензора квадросвязности

Значения тензора определены через значения лапласиана для 4-х вершин. Будем считать данные вершины вершинами графа. Допустим, что все 4 вершины различны:

Здесь векторами обозначены пары вершин, между которыми считается квадросвязность. Пары имеют отличную от нуля квадросвязность только тогда, когда их вершины попарно связаны (необходимые связи показаны на рисунке одинаковым цветом). Если все связи в графе положительны, то квадросвязность между разными вершинами также всегда больше или равна нулю.

Если пары имеют общую вершину, то смысл квадросвязности меняется. Это связано с тем, что диагональные элементы лапласиана не равны нулю (как в дистанционной матрице), а отражают общую связность (проводимость) узла.

Пары вершин могут совпадать — диагональные элементы тензора квадросвязности.

Здесь характеризует связь двух узлов i и j. Считается как сумма произведения их суммарной проводимости (степени вершины) и квадрата связи между узлами .

Несмотря на то, что формально для тензора могут вычисляться элементы вида (одна из пар вырождена), данные (вырожденные) элементы являются линейно-зависимыми от остальных. Могут быть вычислены через сумму тензора по одному из индексов пары:

___
Подведем итоги. Рассмотрено полезное во всех отношениях понятие скалярного произведения пар элементов. В следующей статье поработаем с подпространством графа — что это такое, и каковы его свойства.

Скаляры и векторы | LCME Wiki

Понятие вектор в геометрии отлично от определяемого в алгебре. Различают понятие свободного и связанного (закреплённого) вектора.

• Связанный вектор или направленный отрезок — упорядоченная пара точек эвклидова пространства.
• Свободный вектор — класс эквивалентности направленных отрезков.

При этом два направленных отрезка считаются эквивалентными, если они:

• коллинеарны
• равны по длине
• одинаково направлены (сонаправлены)

Линейные операции над векторами Править

Сложение векторов Править

Сложение трех свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника. Править

Правило треугольника Править

Для сложения двух векторов $ \overrightarrow u $ и $ \overrightarrow v $ по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Правило параллелограмма Править

Для сложения двух векторов $ \overrightarrow u $ и $ \overrightarrow v $ по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

Модуль суммы Править

Модуль (длину) вектора суммы определяют по теореме косинусов, где $ \alpha $ — угол между векторами, когда начало одного совпадает с концом другого.

Умножение вектора на скаляр Править

Произведением вектора $ \overrightarrow u $ и числа $ \lambda $ называется вектор, модуль которого равен $ \lambda u $, а направление совпадает с направлением вектора $ u $, если $ \lambda > 0 $, и противоположно ему, если $ \lambda < 0 $. Если же $ \lambda = 0 $, или вектор $ \overrightarrow u $ нулевой, тогда и только тогда произведение — нулевой вектор.

Скалярное произведение векторов ℹ️ определение, основные свойства, формулы и условия вычисления, примеры задач с решениями, онлайн-калькулятор



Трактовка понятий

Под скалярным произведением (СП) в пространстве над полем вещественных чисел подразумевается функция (x, y) для соответствующих элементов, принадлежащих указанному координатному пространству. Из определения вытекает линейность СП по первичному аргументу.

Для косинуса и синуса справедливо смешанное сопряжение. СП принимает положительную определённость, если соблюдается условие, что x=0. Для вычислений показателя в алгебре используется следующая форма: а = [a1, a2, …, an] и b = [b1, b2, …, bn].

Пример: нужно найти в трёхмерном пространстве произведение двух скаляров [1, 3, −5] и [4, −2, −1]. Решение: необходимо перемножить градиенты (вектора). [1, 3, −5] х [4, −2, −1] = 1 х 4 + 3 х (-2) + (-5) х (-1) = 3.



Геометрическое определение отличается от физического и алгебраического. Чтобы вычислить СП, используя длину и угол между градиентами, которые введены независимым способом, используется следующее выражение: (а, b) = lal x lbl x cos (a, b). Базисом аксиоматики считается скалярное произведение. После его нахождения определяется длина основного вектора и угла.

В современных теоремах понятие СП находится в основе некоторых производных, включая евклидову норму. Термин «длина» используется по отношению к конечномерным векторам. Если имеет смысл криволинейный путь, тогда применяются векторы ненулевой длины. Чаще они находятся в бесконечномерном пространстве.

Угол между такими величинами отличен от нуля. Его значением является число, косинус которого — отношение их СП к произведению их длин. Если пространство псевдоевклидовое (конечномерное, для которого характерна невырожденная индефинитная метрика), понятие «угол» применяется относительно скаляров без изотропных прямых.

Сам угол является числом. Чтобы дать ему значение, вычисляется гиперболический косинус: отношение модуля СП к произведению длин векторов. При перпендикулярности либо ортогональности на плоскости СП равняется нулю. Это свойство скалярного произведения векторов характерно для любого промежутка с положительно определённым СП.



При соблюдении такого условия пространство называется вещественным либо комплексным. Конечномерный вещественный промежуток с положительным СП называется евклидовым, а комплексный — унитарным (эрмитовым).

Если скалярное произведение отрицательное либо не считается знакоопределённым, промежуток называется индефинитной метрикой. Примером такого промежутка является пространство Минковского. СП на таких участках не порождает нормы. Из бесконечномерных выделяются пространства:

• Крейна.
• Понтрягина.

Описание свойств

С помощью специальных математических онлайн сервисов или калькулятора легко находится значение СП через теорему косинусов: a = arccos (a, b)/√(а, а)(b, b). Знак зависит от косинуса угла. В норме значения векторов только положительные. СП больше нуля, если угол острый, и меньше, когда он тупой.

Главные свойства умножения скаляров:


1. Если умножить СП само на себя, получится значение, равное либо большее нуля.
2. СП, умноженное само на себя, равно нулю, если скаляр равен нулевому вектору.
3. СП скаляра самого на себя равняется квадрату его модуля.
4. Для скалярного умножения характерна коммуникативность.
5. Если СП двух отличных от нуля векторов равно 0, тогда множители считаются ортогональными.
6. Для операции скалярного умножения характерна дистрибутивность (согласованные бинарные операции, определённые на одном множестве).

Задача 1: вычислить СП векторов а = {1;2} и b = {4;8}. Решение: а х b = 1 х 4 + 2 х 8 = 20.

Задача 2: найти СП скаляров а и b, если из длины равны 3 и 6, а угол — 60 градусов. Решение: а х b = lal x lbl cos α = 3 х 6 х cos60 = 9. Для лучшего усвоения материала два вектора перемножается с помощью матрицы. Чтобы различать множители, первый оформляется в строку, а второй — в столбец. Если в условиях задачи указываются три величины, тогда последняя оформляется в скобки в форме квадратов. Их скалярное произведение вычисляется путём умножения матриц. Результат — единственное число.

Задача 3: нужно найти СП пар векторов: а = (1; 5; 1), b = (1; -5; 2) и с = (2; 1; 3/2), d = (0; 0; 1). Решение: вычисления проводятся с помощью матричного представления. Первый вектор записывается в строку, а второй — в столбец. Чтобы найти скалярное произведение векторов, потребуется умножить матрицу-строку на матрицу-столбец. Если вектор а умножить на вектор b, получится -22. Аналогично находится значение второй пары. Результат равен 3/2. Простым обобщением конечномерного СП в тензорной (линейной) алгебре считается свёртка с повторяющимся индексом.

Применение в физике

Впервые скалярное произведение ввёл У. Гамильтон в 1846 году. Одновременно учёные начали использовать в своих работах векторное произведение, сумму скаляров. Понятие получило широкое применение и в физике. На его основе сформулированы главные законы электродинамики и механики.

Скаляр является физической величиной. Чтобы его задать, используется одно число. Примеры скаляров в физике:

• масса тела, равная 4 кг;
• температура воздуха на уровне +10 градусов.


В каждом предложенном варианте величина задаётся с помощью одного числа, поэтому масса тела и температура относятся к скалярам. Но это понятие в физике не считается простым числом. Для него характерна размерность.

Если в условиях задачи известно, что масса тела равна 3, необходимо указывать единицу измерения (килограммы, граммы). В математике можно сложить числа 3 и 10, а в физике суммируются только скаляры с одинаковой размерностью: массы с массой, градусы с градусами.

Если рассматривать векторную физическую величину, она характеризуется следующим образом:

1. Неотрицательность.
2. Направленность в пространстве.

Понятие скаляр — модуль вектора либо абсолютная величина. Если предположить, что транспортное средство двигается со скоростью 60 км/ч, такая информация считается неполной. В физике важно знать направление движения. Кроме модуля скорости как абсолютной величины, потребуется знать направление в пространстве, поэтому скорость считается векторной величиной.

Если на земле лежит кирпич массой в 1 кг и на него действует сила в 100 Н (модуль), потребуется найти направление движения объекта. Невозможно выяснить параметр, если нет информации о направлении действия силы. Если она идёт вверх, тогда и кирпич будет двигаться в аналогичном направлении.

Если сила идёт вдоль горизонта, тогда объект поедет горизонтально. При вертикальном воздействии силы вниз кирпич останется на прежнем месте. Он будет вжиматься в землю. Подобные явления указывают на то, что сила является вектором, поэтому для неё характерна размерность, модуль.

Для обозначения вектора в физике используются латинские буквы и стрелка:

• вектор скорости: →v;
• вектор силы: →F.


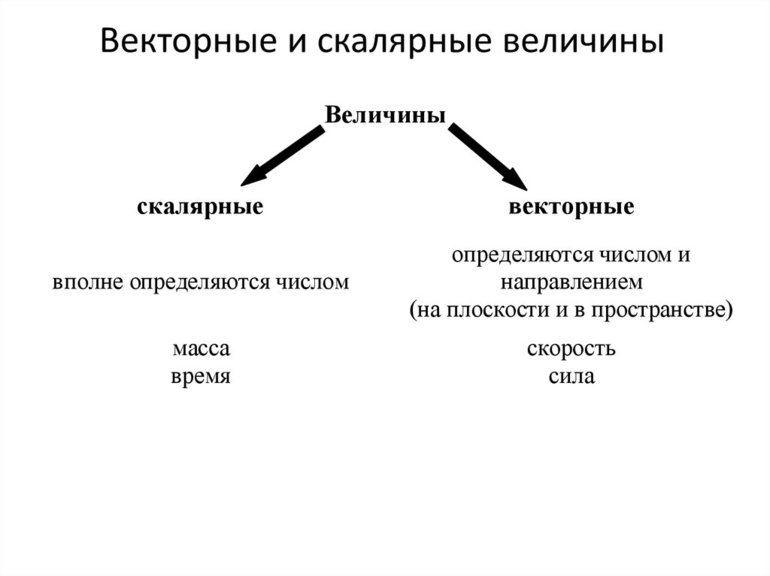
Стрелка является направленным отрезком. Её начальная точка — начало вектора, а конечная или остриё — конец вектора. В математике величина с начальной точкой А и концом В обозначается →АВ. Если начало и конец направленного отрезка совпадают, тогда получается нулевой вектор. Он обозначается →0.

Такой отрезок считается точкой. У него нет конкретного направления, а длина равняется нулю. К безразмерным скалярам относятся коэффициенты трения и полезного действия, показатель преломления света.