Калькулятор скалярного произведения векторов через длину и косинус угла между векторами
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Скалярное произведение двух ненулевых векторов — это число, которое равно произведению длин этих векторов на косинус угла между ними.
a ⋅ b = |a| ⋅ |b| ⋅ cos α
Модуль (длина) вектора |a| =
Модуль (длина) вектора |b| =
Косинус угла между векторами (cos α)Угол между векторами (в градусах)
Скалярное произведение двух векторов
Скалярное произведение вектора a на вектор b – есть произведение их модулей на косинус угла между ними.
|Модулем| вектора называется число, равное расстоянию между начальной и конечной точками вектора.
a ⋅ b = |a| ⋅ |b| ⋅ cos αСкалярное произведение обозначается как:
a ⋅ b или a ⋅ b либо ab.
Скалярное произведение двух векторов a и b можно также определить, как модуль одного из векторов умноженный на алгебраическую проекцию другого вектора:
a ⋅ b = |a| прa b
a ⋅ b = |b| прb a
Знак скалярного произведения может быть определен следующим образом:
a ⋅ b > 0
скалярное произведение больше нуля, если угол между векторами a и b острый
a ⋅ b
a ⋅ b = 0
скалярное произведение равно нулю, если угол между векторами a и b прямой
Скалярное произведение равно нулю, если хотя бы один из векторов нулевой.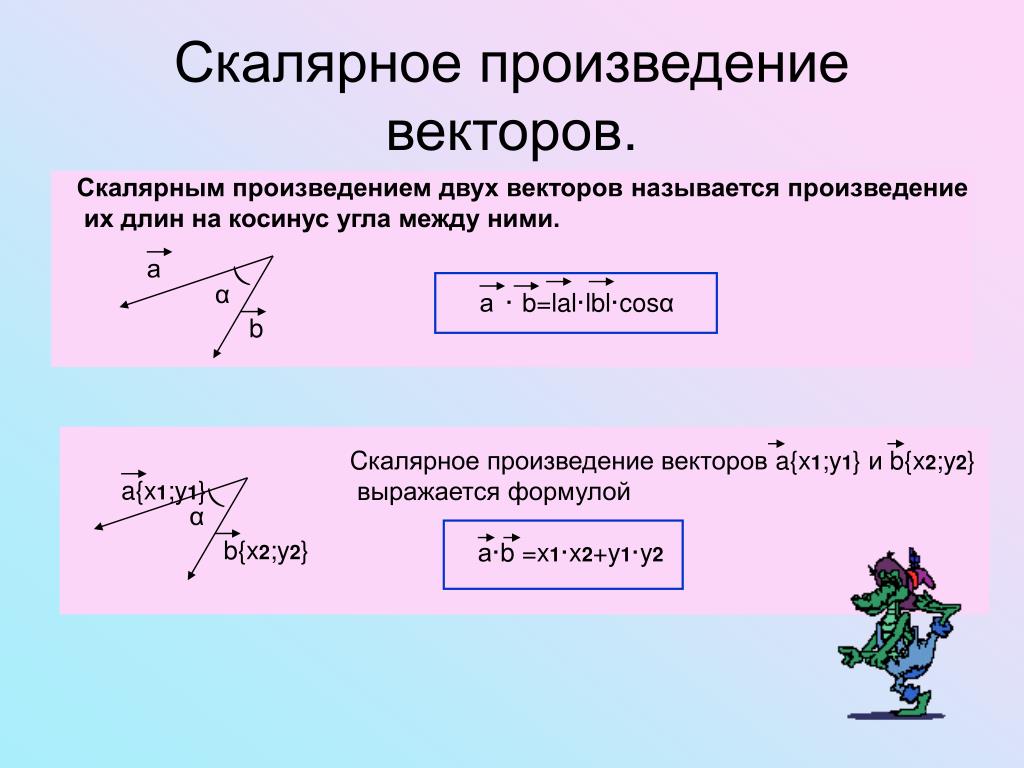
Приведем пример, найдем скалярное произведение двух векторов a и b:
Угол между векторами a и b = 120.96 градусов
Модуль (длина) вектора |a| = 3
Модуль (длина) вектора |
cos(120.96°) = -0.514439533781506
Тогда, скалярное произведение двух векторов a и b:
a ⋅ b = |a| ⋅ |b| ⋅ cos α = 3 ⋅ 2.33 ⋅ (-0.514439533781506) = -3.5959323411327264
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
Длина отрезка.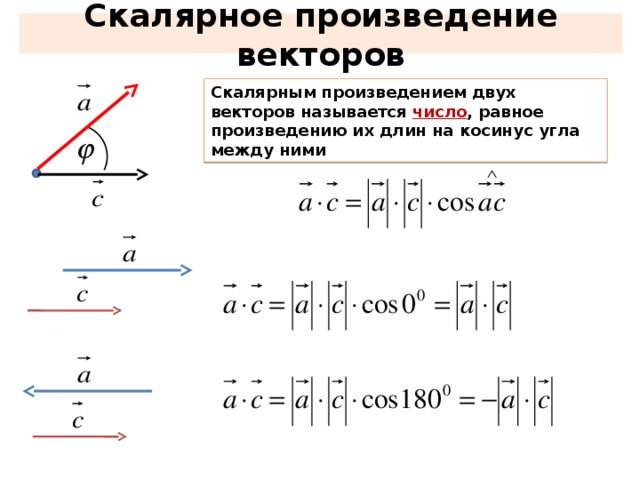 Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона.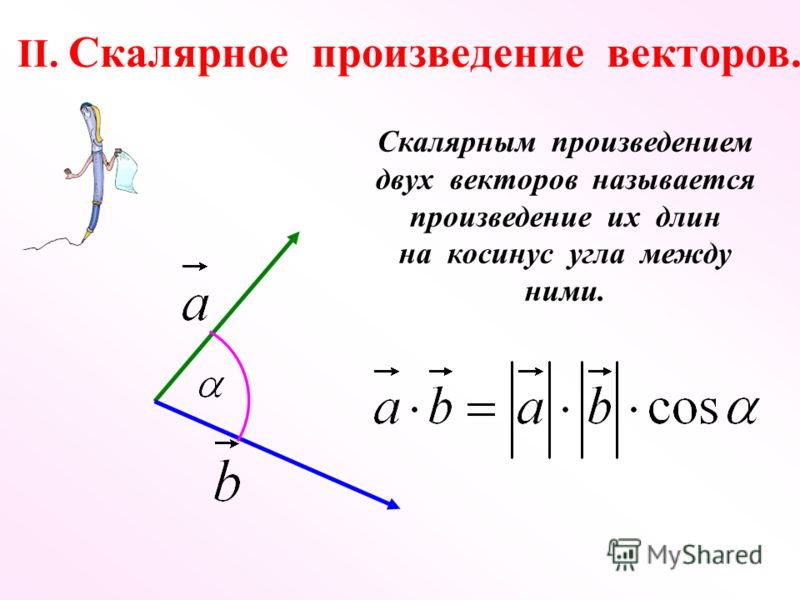 Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
12. Скалярное произведение векторов, свойства, приложения.
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Скалярное
произведение векторов
и:где-
угол между векторамии;
еслилибо,
тоИз определения скалярного произведения
следует, чтогде,
например,есть
величина проекции векторана
направление вектора.
Скалярный квадрат вектора:
Свойства скалярного произведения:
теорема косинусов легко выводится с использованием скалярного произведения:
Угол между векторами:
Оценка угла между векторами: в формулезнак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.
Проекция вектора на направление, определяемое единичным вектором:,
условие ортогональности[2] (перпендикулярности) векторови:
Площадь параллелограмма, натянутого на два вектораи, равна
Скалярное произведение в координатах
Если то
Угол между векторами
13.
Векторное произведение векторовВекторное произведение векторов.
Векторным произведением вектора на векторв пространственазывается вектор, удовлетворяющий следующим требованиям:
длина вектора равна произведению длин векторовина синус угламежду ними:;
вектор ортогонален каждому из векторови;
вектор направлен так, что тройка векторовявляется правой.
14.Смешанное произведение векторов
Сме́шанное произведе́ние векторов— скалярное произведение векторана векторное произведение векторови:
.
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрический
смысл: Модуль смешанного произведения
численно равен объёму параллелепипеда,
образованного векторами
.
Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
Смешанное произведение в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторови:
Смешанное произведение в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторови, взятому со знаком «минус»:
В частности,
Если любые два вектора параллельны, то с любым третьим вектором они образуют смешанное произведение равное нулю.
Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.
Геометрический
смысл — Смешанное произведение
по абсолютному значению равно объёму
параллелепипеда образованного векторамии;
знак зависит от того, является ли эта
тройка векторов правой или левой.
15.Прямая линия на плоскости, её общее уравнение и его исследование.
Пусть на плоскости введена прямоугольная декартова система координат Оxy.
Теорема.
Всякое уравнение первой степени вида , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и любая прямая в прямоугольной системе координат Oxy на плоскости задается уравнением видапри некотором наборе значений A, B и C.
Докажемсначала, что уравнение видазадает прямую на плоскости.
Пусть координаты точки удовлетворяют уравнению, то есть,. Вычтем из левой и правой частей уравнениясоответственно левую и правую части равенства, при этом получаем уравнение вида, которое эквивалентно.
Уравнение
представляет
собой необходимое и достаточное условие
перпендикулярности двух векторови.
То есть, множество всех точекопределяет
в прямоугольной системе координат Oxy
прямую линию, перпендикулярную направлению
вектора.
Если бы это было не так, то векторыине
были бы перпендикулярными и равенствоне
выполнялось бы.
Таким образом, уравнение задает прямую линию в прямоугольной декартовой системе координат Oxy на плоскости, следовательно, эквивалентное ему уравнение видазадает эту же прямую. На этом первая часть теоремы доказана.
Теперь докажем, что всякая прямая в прямоугольной системе координат Oxy на плоскости определяется уравнением первой степени вида .
Пусть в прямоугольной системе координат Oxy на плоскости задана прямая a, проходящая через точку,- нормальный вектор прямойa, и пусть- плавающая точка этой прямой. Тогда векторыиперпендикулярны, следовательно, их скалярное произведение равно нулю, то есть,. Полученное равенство можно переписать в виде. Если принять, то получим уравнение, которое соответствует прямойa.
На этом доказательство теоремы завершено.
Внутреннее (точечное) произведение двух векторов.
Приложения в машинном обученииВыделите : В этом посте мы рассмотрим один из основных операторов в линейной алгебре. Он известен как точечный продукт или внутренний продукт двух векторов. Большинство из вас уже знакомы с этим оператором, и на самом деле это довольно легко объяснить. И все же мы дадим некоторые дополнительные идеи, а также некоторую базовую информацию о том, как использовать его в Python.
Обзор учебника:
- Скалярный продукт :: Определение и свойства
- Линейные функции
- Примеры и реализация
Скалярный продукт :: Определение и свойства
Прежде всего, когда вы применяете скалярное произведение к двум векторам, они должны быть одного размера .
Например, у нас есть два вектора или два упорядоченных списка векторов. Мы применяем скалярное произведение таким образом, что сначала поэлементно умножаем эти два упорядоченных вектора. Давайте посмотрим на пример. Умножаем поэлементно: \(2\cdot 8\), \(7\cdot 2\), \(1\cdot 8\).
Затем мы суммируем эти члены умножения. Интересно, что результатом скалярного произведения является скаляр.
Сначала, как обычно, рассмотрим векторы в 2D-плоскости. Их легко визуализировать, и они дают нам интуитивное представление о том, что такое точечный продукт. Итак, мы будем наблюдать два вектора \(\vec{v} \) и \(\vec{w} \). Скалярное произведение этих двух векторов можно интерпретировать как проекцию вектора \(\vec{w} \) на вектор \(\vec{v} \) . Затем мы умножаем длину спроецированного вектора \(\vec{w} \) на \(\vec{v} \) и длину \(\vec{v} \). 9{\circ} \) (острый угол).
Если векторы перпендикулярны, то внутренний продукт равен нулю. Это важное свойство! О таких векторах говорят, что они ортогональны.
В случае, если векторы образуют тупой угол, внутренний продукт будет отрицательным.
Так сказать, еще один трюк со скалярным произведением. Итак, мы видим, что скалярный продукт — это коммутативная векторная операция.
По сути, это означает, что мы можем спроецировать \(\vec{v} \) на \(\vec{w} \), в этом случае у нас будет длина спроецированного \(\vec{v} \), умноженная на длину из \(\vec{w} \), поэтому мы получим тот же результат.
Давайте подробнее рассмотрим свойство коммутативности скалярного произведения.
Если \(\vec{v} \) и \(\vec{w} \) имеют одинаковую длину, мы могли бы использовать симметрию. Итак, мы видим, что длина проекции \(\vec{w} \) на \(\vec{v} \) такая же, как длина \(\vec{v} \), проецируемая на \ (\vec{ш} \). Таким образом, становится ясно, что внутренний продукт одинаков для обоих подходов к расчету.
Кроме того, можно предположить, что один из векторов, скажем, \(\vec{v} \), в три раза длиннее, чем \(\vec{w} \). Теперь мы видим, что у нас не может быть проекций одинаковой длины. Однако мы можем интерпретировать это \(3\vec{v} \) как простое масштабирование вектора \(\vec{v} \).
Напомним, что масштабирование вектора с помощью скаляра на самом деле является масштабированием его длины.
Следовательно, мы можем наблюдать вектор, имеющий тот же размер, что и \(\vec{w} \), масштабированный с помощью скаляра. Теперь у нас есть скаляр, умноженный на вектор \(\vec{v} \), и скалярное произведение с \(\vec{w} \) будет таким же, как умножение \(3 \) на \(\vec{ v} \) и \(\vec{w} \). Это показывает, что внутренний продукт действительно является коммутативной операцией.
Линейные функции
Теперь снова поговорим о линейных функциях. Но теперь мы рассмотрим функции, в которых входные и выходные размерности не совпадают. Например, у нас есть двумерный входной вектор, и с помощью функции \(L \) он даст нам одномерный выходной вектор.
Для линейных преобразований выполняются следующие свойства:
Например, линия с равномерно расположенными на ней точками будет преобразована в 1D-линию. Здесь обратите внимание, что на самом деле мы отображаем точек с координатами ( x , y ) в одну координату (например, на какую-то линию z )! Важно, чтобы расстояние между точками на отображаемой линии было равноудаленным. Это свойство линейного преобразования.
Теперь давайте посмотрим, что произойдет, если мы применим линейное преобразование [1-2] к вектору \(\vec{w} \). Он отображается так, что его значение равно \(-2 \). Это преобразование отображает 2D-пространство в 1D-пространство, которое представляет собой линию. И это преобразование \(\begin{bmatrix}1 & -2\end{bmatrix} \) показывает, как мы отображаем один базисный вектор. Таким образом, это \(1 \) не изменит наш вектор \(\hat{i} \) (остается прежним), но изменит наш вектор \(\hat{j} \). \(\hat{j} \)vector будет сопоставлен с -2. Итак, используя эту идею о том, что любой вектор можно разложить на комбинацию базисных векторов, мы можем получить следующую формулу.
Все это можно пояснить на этом примере. Вы можете подумать об этом: как 2-D точки будут проецироваться на одну линию.
У нас есть вектор, который идет от \(0 \) до \(\hat{u} \). Кроме того, у нас много двумерных точек. Нас интересует, где эти двумерные точки (векторы!) будут проецироваться на одну линию?
Давайте посмотрим, где вектор \(\hat{i} \) приземлится на единичный вектор \(\hat{u} \), определяющий эту линию. Если мы воспользуемся так называемой линией симметрии, то придем к выводу, что \(u_{x} \) будет проекцией \(\hat{i} \). это тоже x – координата вектора \(\hat{u} \).
То же верно и для вектора \(\hat{i} \). Он будет спроецирован в вектор длины \(u_{y} \). Итак, какой будет проекция произвольного вектора, имеющего две ненулевые ( x , y ) координаты.
Мы видим, что \(u_{x} \) и \(u_{y} \) определяют нашу проекционную матрицу. Они сообщат нам, где приземлится наш базисный вектор: \(u_{x} \) и \(u_{y} \)
Другими словами, если мы представим наш вектор с помощью базисных векторов, мы получим координаты ( х , и ). Если мы умножим эти координаты на \(u_{x} \) и \(u_{y} \) соответственно и суммируем эти два произведения, мы получим положение, в котором наш исходный вектор (x, y) попадет на линия, заданная вектором \(\hat{u} \). Эта позиция будет нашей новой координатой для одномерной системы координат \(\hat{u} \).
Как только мы определим это преобразование, мы сможем рассматривать каждый вектор как разложение этих двух векторов, и, следовательно, мы можем получить результат. Теперь мы видим, что векторные произведения матриц двойственны интерпретации скалярного произведения.
Примеры и реализация
Умножение строки на столбец является основой для всех матричных умножений. Из двух векторов получается одно число. Это число называется внутренним произведением двух векторов. Другими словами, произведение матрицы \(1\) на \(n\) (вектор-строка) и матрицы \(n\times 1\) (вектор-столбец) является скаляром.
Для начала несколько простых примеров:
\(\vec{v}= \begin{bmatrix}1\\2\end{bmatrix} \), \(\vec{w}= \begin{ bmatrix}4\\5\end{bmatrix} \)
Скалярное произведение равно
$$ \vec{v}\cdot\vec{w} = 1\cdot 4+2\cdot 5= 4+10= 14 $$
Другой пример показывает два вектора, внутреннее произведение которых равно \(0\).
\(\vec{v}= \begin{bmatrix}1\\3\\2\end{bmatrix} \), \(\vec{w}= \begin{bmatrix}4\\-4\\ 4\end{bmatrix} \)
$$ \vec{v}\cdot\vec{w} = 0 $$
$$ 1\cdot 4+3\cdot \left (-4 \right )+2 \cdot 4= 0 $$
Теперь наши векторы \(\vec{v} \) и \(\vec{w} \) имеют размер \(3 \).
С другой стороны, мы можем вычислить длину отдельного вектора, используя скалярное произведение, и применить квадратный корень. Это иногда называют «нормой» вектора.
$$ \vec{v}= \begin{bmatrix}1\\3\\2\end{bmatrix} $$
$$ \vec{v}\cdot\vec{v}= 1+9+ 4= 14 $$
Длина равна \(\left \| \vec{v} \right \|= \sqrt{14} \)
Это может быть очень полезно, когда нам нужно нормализовать наши векторы. В этом случае мы хотим, чтобы вектор имел длину \(1 \). В принципе, если у нас есть длина нашего вектора, равная \(4\), то понятно, что нам нужно разделить его на \(4\). В этом случае, когда у нас есть \(\sqrt{14} \), и мы просто разделим каждый элемент нашего вектора на \(\sqrt{14} \), и это будет наш результирующий вектор:
$$ \vec{u}= \frac{\vec{v}}{\left \| \vec{v} \right \|}= \frac{1}{\sqrt{14}}\begin{bmatrix}1\\3\\2\end{bmatrix} $$
$$ \left \| \vec{u} \right \|= 1 $$
$$ \frac{1}{14}+\frac{9}{14}+\frac{4}{14} = 1 $$
Мы с помощью этого подхода также можно получить угол между двумя векторами. Возьмем скалярное произведение между векторами \(\vec{v} \) и \(\vec{w} \), и если мы нормализуем это произведение, то получим угол между векторами \(\vec{v} \) и \ (\vec{ш} \).
Это уравнение доказывает, что на самом деле все абсолютные значения косинуса меньше единицы. Итак, у нас есть следующая форма, где абсолютное значение скалярного произведения всегда меньше размера вектора \(\vec{v} \), умноженного на вектор \(\vec{w} \).
$$ \слева | \cos \theta \right |\leq 1 $$
$$ \left | \vec{v}\cdot \vec{w} \right |\leq \left \| \vec{v} \право \|\лево \| \vec{w} \право \| $$
Один из способов определить скалярное произведение — записать его следующим образом:
$$ \vec{v}\cdot \vec{w}= v_{1}w_{1}+ v_{2}w_{2} $$
Кроме того, определение единичного вектора очень интересно . Например, вектор \(\vec{v} \) с координатами \(\left (1,1 \right ) \) можно нормализовать следующим образом. Мы можем разделить \(\vec{v} \) на длину \(\vec{v} \), и это будет наш единичный вектор, который имеет длину \(\frac{1}{\sqrt{2}} \).
С другой стороны, мы можем видеть, что векторы длины \(1 \), которые начинаются в центре системы координат, определяют единичную окружность. Итак, каждый единичный вектор должен лежать на этой окружности. Кроме того, интересно, что длина — это одно, но другое свойство возникает, если мы возьмем скалярное произведение с нашим базисным вектором \(\hat{i} \) и нашим единичным вектором \(\hat{u} \). Эта проекция является хорошо известным результатом тригонометрии. Получаем \(\cos\theta\) по оси \(x\) и \(\sin\theta\) по оси \(y\). Более того, мы можем получить наши координаты единичного вектора, поставив \(\cos\theta\) для компонента \(x\) и \(\sin\theta\) для компонента \(y\). Таким образом, мы можем определить угол между двумя векторами.
Сводка
Вау! Действительно, мы представили множество идей и концепций, связанных с внутренним или скалярным произведением двух векторов. Мы понимаем, насколько важна линейная алгебра. Также очень часто у нас будут похожие приложения. Например, мы будем использовать нормализацию наших данных, используя идеи скалярного произведения. Это лишь одно из множества приложений с точечными продуктами. Посидим, а в следующем посте продолжим наше путешествие и поговорим подробнее о линейных преобразованиях .
Каков физический смысл этого? – Глубокая физика
Скалярное произведение – это математическая операция между двумя векторами, в результате которой получается скаляр (число). Он также широко используется в физике, но каков на самом деле физический смысл скалярного произведения?
Физический смысл скалярного произведения заключается в том, что оно показывает, насколько перекрываются любые две векторные величины. Например, скалярное произведение между силой и смещением описывает количество силы в направлении, в котором изменяется положение, и это составляет работу, выполняемую этой силой.
В этой статье мы обсудим это более подробно, а также рассмотрим некоторые примеры использования скалярных произведений в физике.
Мы также обсудим некоторые более общие понятия скалярных произведений, которые полезны, среди прочего, для теории относительности и квантовой механики .
Подсказка: Моя любимая книга по векторам и векторному исчислению (включая скалярное произведение) для начинающих — . Руководство для студентов по векторам и тензорам Дэна Флейша (ссылка на Амазон). Это очень удобное для начинающих введение, в котором основное внимание уделяется тому, как векторы (и тензоры) применяются в физике. У него также есть много отличных практических задач для вас.
Содержание
Значение скалярного произведения в физике: интуитивное объяснение + примеры
В интуитивном смысле скалярное произведение является мерой того, насколько два вектора выровнены . Итак, если у нас есть два вектора, u и v, скалярное произведение этих двух даст длина вектора v вдоль вектора u , или, если хотите, проекция v вдоль u .
Если мы знаем угол между двумя векторами (θ на рисунке выше), то скалярное произведение можно рассчитать по следующей формуле: процент совпадения» между двумя векторами; если cos(θ)=1, то векторы полностью выровнены (поскольку θ=0°), а если cos(θ)=0 (что означает θ=90°), векторы вообще не выровнены. Более того, что-то вроде cos(θ)=0,97 (θ≈15°) будет соответствовать векторам, «почти выровненным».
Скалярный продукт также можно рассчитать через компоненты этих векторов, используя следующую формулу: В общем, эта формула действительна для любого количества измерений, но здесь я записал только в трех измерениях.
Какое значение все это имеет для физики? Что ж, многие физические величины описываются векторами (например, скорость и силы), поэтому имеет смысл только то, что скалярное произведение также имеет некоторое физическое значение.
В частности, та же самая геометрическая картина применима и в физике; скалярное произведение дает длину одного вектора вдоль другого вектора, но теперь векторы представляют что-то физическое.
Лучший способ объяснить физику этого — пример. А именно, скалярное произведение между вектором смещения и вектором силы , которое можно описать как «изменение положения (смещение) в направлении действия силы».
Это количество дает работа, совершаемая силой , которая по сути является изменением энергии , вызванным этой силой. Точнее, работа, проделанная на некотором пути, на самом деле определяется линейным интегралом этого скалярного произведения, которое я объясню в этой статье.
Здесь dr — вектор смещения, описывающий изменение положения в некотором направлении, а F — вектор силы. Их скалярное произведение дает мгновенных работы (т. е. работу, выполненную на каком-то очень маленьком отрезке этого пути). Надеюсь, этого достаточно, чтобы установить, почему скалярные произведения действительно полезны в физике. Существуют тысячи различных применений скалярного произведения, начиная от базовой механики и заканчивая электромагнетизмом и даже графическим дизайном и анимацией .
Теперь, в физике более высокого уровня скалярные произведения также полезны, но по несколько иным причинам, чем элементарная геометрическая интерпретация, данная выше.
А именно, скалярное произведение полезно, потому что оно имеет хорошие математические свойства , которые можно очень хорошо обобщить на более абстрактные и более сложные области физики.
Например, обычным способом решения задач механики является использование законов Ньютона, которые по сути являются векторными уравнениями.
Однако альтернативным способом является использование только энергий (которые являются скалярами), и это делается в формулировке механики, называемой лагранжевой механикой . На самом деле у меня есть целая вводная статья, посвященная лагранжевой механике, которую вы можете найти здесь.
Лагранжева механика — очень элегантная формулировка механики, и отчасти эта элегантность проистекает из того факта, что энергия является скалярной величиной , что отчасти обусловлено математическими свойствами скалярного произведения.
Это потому, что кинетическая энергия является скаляром, поскольку она включает только точечное произведение скоростей (я объясняю это и многое другое о формуле кинетической энергии в этой статье).
Это напрямую подводит нас к одному из определяющих свойств скалярного произведения; это математическая операция, дающая в результате скаляр .
Это особенно важно, поскольку скаляры — это инвариантные величины (я объясню это позже), которые широко используются, например, в специальной и общей теории относительности.
Для наших целей основными свойствами скалярного произведения являются:
- Скалярное произведение является скаляром .
- Скалярное произведение коммутативно (хотя это неверно для операторов больше; этот факт на самом деле является частью того, откуда исходит богатство квантовой механики).
- Скалярный продукт определяет понятие ортогональности (если скалярный продукт между двумя величинами равен нулю).
Мы поговорим об этих свойствах позже, но стоит отметить, что, хотя они могут показаться очевидными, если смотреть на них только через призму этого «базового» определения скалярного произведения, они действительно являются тем, что определяет точка. сам продукт.
Вот почему эти свойства важны, если мы хотим обобщить понятие скалярного произведения на более сложные ситуации, такие как искривленное пространство-время в общей теории относительности . Об этом мы поговорим далее.
Скалярный продукт в специальной и общей теории относительности
В общей теории относительности сила тяжести и движение объектов под действием силы тяжести объясняется искривлением самого пространства-времени (то есть и пространства, и времени), что приводит к эффектам гравитация и гравитационное ускорение.
Все, что нас интересует в общей теории относительности, по существу происходит в искривленном пространстве-времени . Таким образом, вы можете думать о математике общей теории относительности как об обычной математике, но выполненной в «криволинейной геометрии». В простом смысле вы можете думать об искривленном пространстве-времени как о системе координат с некоторыми произвольными искривленными осями времени и пространства. Обратите внимание, однако, что эту картину не следует воспринимать слишком буквально; во-первых, пространство-время является 4-мерным (не 2D) с временным измерением и тремя пространственными измерениями, а во-вторых, эта картина на самом деле представляет собой просто «плоское» пространство с искривленными осями координат, а не буквально искривленное геометрическое пространство.
Стоит отметить, что специальная теория относительности — это всего лишь «частный случай» общей теории относительности, поэтому здесь мы будем обсуждать в основном общую теорию относительности.
Трудность здесь заключается в том, что если мы имеем дело с некоторыми произвольно искривленными пространствами, то как может существовать универсальное понятие скалярного произведения ? Ответ в том, что не может, по крайней мере, не так, как мы привыкли.
На самом деле проблема возникает из-за того, что в искривленном пространстве-времени базисные векторы (которые используются для выражения компонентов векторов) не являются постоянными и могут меняться от места к месту . Базисные векторы обычно обозначаются эти e с маркировкой индекса, с которой связан базисный вектор.
Если базисные векторы непостоянны, мы не можем определить скалярное произведение просто как сумму произведений компонентов:
Вместо этого мы используем объект, называемый метрическим тензором , который можно представить как добавление «поправочного коэффициента» к каждому члену в этом скалярном произведении, чтобы учесть тот факт, что базисные векторы могут отличаться от места к месту : Обратите внимание, что эти метрические компоненты (г здесь) на самом деле являются компонентами двухиндексного тензорные, а не векторные компоненты. Поэтому у них два индекса. Более того, метрика, как правило, является функцией, которая также может меняться от места к месту, как базисные векторы.
В более общем случае скалярное произведение можно записать так: Вместо обычной формулы скалярного произведения теперь у нас есть двойная сумма, которая на самом деле МОЖЕТ иметь перекрестные члены, включающие произведения компонентов вектора, такие как v 1 u 2 . Это действительно возможно, если базисные векторы непостоянны, но не в типичной декартовой (x, y, z) системе координат.
Это формула скалярного произведения между двумя векторами в любой произвольной системе координат или пространстве (хотя есть некоторые математические ограничения, в которые мы сейчас вдаваться не будем).
Теперь метрика для любого заданного пространства-времени обычно рассчитывается из уравнений поля Эйнштейна общей теории относительности, которые определяют геометрию этого пространства-времени по содержанию энергии и импульса. Это обычный способ расчета различных метрик пространства-времени в общей теории относительности.
Используя метрику, можно получить все виды физических результатов общей теории относительности, например замедление времени вблизи черной дыры . Я подробно обсуждаю это и его геометрические, а также физические интерпретации в этой статье.
Суть всего этого в том, что можно определить понятие скалярного произведения в искривленных пространствах и системах координат с помощью метрического тензора .
Физический смысл этого более или менее тот же; скалярное произведение — это мера того, насколько совпадают два вектора, хотя это немного сложнее изобразить, если мы имеем дело с криволинейной геометрией.
В любом случае, математика искривленных пространств (и дифференциальная геометрия в целом) увлекательна и содержит так много интересных понятий, которые находят применение во многих областях физики.
Если вы хотите узнать об этом больше, я рекомендую мою статью о символах Кристоффеля , одном из центральных математических инструментов, используемых в общей теории относительности, а также мою статью о тензоре Риччи , имеющую интересную физическую имея в виду гравитационные приливы.
Скалярный продукт в квантовой механике (внутренний продукт)
Скалярный продукт в квантовой механике несколько более абстрактен, чем любое из понятий, о которых мы говорили ранее.
Кроме того, скалярное произведение обычно даже не называется по имени, а скорее является внутренним произведением (точнее, скалярное произведение на самом деле относится к более общему «классу» математических операций, чем скалярное произведение). ).
Внутренний продукт между двумя векторами обозначается «сэндвичем» вместе вектора бюстгальтера (вещь слева) и кет-вектора (вещь справа):
Теперь это эквивалентно типичному скалярному произведению, за исключением того, что в квантовой механике мы обычно имеем дело с комплексные числа . Таким образом, это внутреннее произведение на самом деле:Здесь звездочка обозначает комплексное сопряжение компонентов v. Обратите внимание, что это почти то же самое, что и скалярное произведение для «обычных» векторов, за исключением обобщения на комплексные числа.
Теперь эти лифчики и кеты (v и u с этими странными скобками вокруг них) действительно являются векторами . Однако они не являются типичными векторами в трехмерном пространстве, а представляют собой абстрактные векторов состояния в комплексном векторном пространстве 9.0026 .
Физический смысл их в том, что они представляют квантовых состояний системы.
