Скалярное умножение
Скалярное умножениеВ. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников
Суперобложка / Обложка / Содержание
..Скалярное умножение векторов
Впервые слово «скаляр» ввел в математику Виет, но современное значение ему придал Гамильтон (1843 г.), назвав скалярной величину отличную от векторной. Скалярная величина – это величина, которая может, в отличие от векторной, быть задана одним числовым значением. Проще говоря, скаляр – это число. По смыслу названия, при скалярном умножении векторов должно получаться число.
Определение скалярного произведения векторов (22)
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Скалярное умножение обычно обозначается точкой: .
Введение такой странной, на первый взгляд, операции находит как физическое, так и геометрическое оправдание.
Если – постоянная сила, которая действует на точку, а – вектор перемещения этой точки, то работа A, которая совершается силой на этом перемещении, может быть вычислена как скалярное произведение силы на перемещение: .
С геометрическими приложениями скалярного умножения мы познакомимся в дальнейшем.
Вспомнив, что и , мы можем записать: .
Свойства скалярного умножения
1. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда векторы взаимно ортогональны.
Пусть векторы и не равны нулю. Тогда из равенства нулю скалярного произведения следует, что , а это и означает, что .
Если же хотя бы один из векторов нулевой, то . С другой стороны, для нулевого вектора понятие направления не имеет смысла. Но раз смысла нет, то любое соглашение не погрешит против правды. Мы можем принять, что нулевой вектор параллелен любому другому, если захотим, или, что он ортогонален к любому направлению, что мы и сделаем. Но если нулевой вектор ортогонален к любому другому, в том числе и нулевому же, то и этот случай не является исключением.
2. Скалярное умножение векторов коммутативно (перестановочно).
– это сразу следует из определения.
3. Скалярное умножение ассоциативно по отношению к числовому множителю.
так же непосредственно следует из определения.
4. Скалярное умножение дистрибутивно (распределительно) относительно сложения векторов.
.
Данное свойство, несмотря на привычный вид, не является очевидным.
Рис. 17В самом деле (рис. 17), ,
а . Глядя на рис. 17, трудно предположить, что эти два выражения равны, однако это так.
Доказательство
Для доказательства мы используем свойства проекций.
.
Можно это свойство доказать и непосредственно вычисляя соответствующие длины и углы, но этот путь значительно дольше.
Скалярное умножение в декартовых координатах
Общее выражение для скалярного произведения в произвольных координатах значительно сложнее, и мы займемся им позже.
Для начала найдем результат скалярного умножения базисных векторов декартовой системы координат.
и аналогично .
и аналогично .
|
Полученные результаты можно свести в таблицу скалярного умножения базисных векторов. |
Теперь мы можем доказать следующее утверждение:
Скалярное произведение двух векторов равно сумме произведений их соответствующих координат: .
Доказательство
В самом деле,
. Воспользовавшись свойствами скалярного умножения и таблицей умножения для векторов базиса, мы получаем: .
..Некоторые примеры использования скалярного умножения
Длина или модуль вектора в координатной форме
Пусть произвольный вектор. Скалярное произведение этого вектора самого на себя равно:
С другой стороны, , следовательно,
и .
Расстояние между двумя точками
Рис. 18
.
Если расстояние между двумя точками мы обозначим , полученное выражение перепишется в виде:
.
В качестве следующих примеров рассмотрим доказательство двух теорем элементарной геометрии. Этим мы убьем двух зайцев: во-первых, вспомним элементарную геометрию, во-вторых, получим удовольствие от эффективности метода.
Теорема
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Рис. 19Совместим векторы и со сторонами параллелограмма (рис. 19), тогда сумма и разность этих векторов совпадут с его диагоналями.
и соответственно
.
Сложив эти выражения, мы получим:
.
Мы видим, что левая часть равенства – это сумма квадратов диагоналей. Правая же часть, как и следовало ожидать – сумма квадратов сторон.
Теорема
Квадрат стороны треугольника равен сумме квадратов двух других его сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.
Рис. 20Совместим векторы и со сторонами треугольника (рис. 20), тогда вектор совпадет с третьей его стороной.
И окончательно: .
Напомним, что a и b означают модули соответствующих векторов.
Умножение векторов, формулы и примеры
Скалярное умножение векторов
Замечание. Если один из векторов нулевой, то скалярное произведение равно нулю.
Замечание. Из определения скалярного произведения получаем, что угол (а точнее его косинус) между векторами-сомножителями вычисляется по формуле:
Скалярное произведение вектора на самого себя называется скалярным квадратом и обозначается .
Скалярный квадрат вектора равен квадрату его модуля:
Тогда длина вектора может быть найдена по формуле:
Скалярное произведение двух векторов положительно, если угол между векторами острый; и отрицательно, если угол тупой.
Критерий ортогональности векторов. Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда угол между ними прямой, то есть когда эти векторы ортогональны (перпендикулярны):
Если векторы и заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат:
Векторное умножение векторов
Замечание. Таким образом, длина (модуль) вектора численно равна площади параллелограмма, построенного на векторах и :
Критерий коллинеарности векторов. Два вектора и коллинеарны тогда и только тогда, когда их векторное произведение равно нулю:
Если векторы и заданы своими координатами в пространстве, то их векторное произведение определяется формулой:
Смешанное умножение векторов
Геометрический смысл смешанного произведения. Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами :
Критерий компланарности векторов. Если три вектора компланарны, то их смешанное произведение равно нулю.
Если векторы заданы в пространстве своими координатами: , то их смешанное произведение можно вычислить по формуле:
Псевдоскалярное произведение — Википедия
Материал из Википедии — свободной энциклопедии
Псевдоскалярным[1] или косым произведением векторов a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} } на плоскости называется число
- a∧b=|a|⋅|b|sinθ,{\displaystyle \mathbf {a} \wedge \mathbf {b} =|\mathbf {a} |\cdot |\mathbf {b} |\sin \theta ,}
где θ=∠(a,b){\displaystyle \theta =\angle (\mathbf {a} ,\mathbf {b} )} — угол вращения (против часовой стрелки) от a{\displaystyle \mathbf {a} } к b{\displaystyle \mathbf {b} }. Если хотя бы один из векторов a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} } нулевой, то полагают a∧b=0{\displaystyle \mathbf {a} \wedge \mathbf {b} =0}. Геометрически псевдоскалярное произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора. С её помощью удобно работать с площадями многоугольников, выражать условия коллинеарности векторов и находить углы между ними.
Псевдоскалярное произведение существует только для 2-мерных векторов, его аналогом в трехмерном пространстве является тройное скалярное произведение.
- Линейность: a∧(λb+μc)=λa∧b+μa∧c.{\displaystyle \mathbf {a} \wedge (\lambda \mathbf {b} +\mu \mathbf {c} )=\lambda \mathbf {a} \wedge \mathbf {b} +\mu \mathbf {a} \wedge \mathbf {c} .} Здесь λ{\displaystyle \lambda }, μ{\displaystyle \mu } — произвольные вещественные числа.
- Антикоммутативность: a∧b=−b∧a{\displaystyle \mathbf {a} \wedge \mathbf {b} =-\mathbf {b} \wedge \mathbf {a} }.
- a∧b{\displaystyle \mathbf {a} \wedge \mathbf {b} } является псевдоскаляром, то есть инвариантом при всех невырожденных изометриях, не включающих отражений.
- Псевдоскалярное произведение a∧b{\displaystyle \mathbf {a} \wedge \mathbf {b} } — это ориентированная площадь параллелограмма, натянутого на векторы a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} }.
- Абсолютная величина псевдоскалярного произведения |a∧b|{\displaystyle |\mathbf {a} \wedge \mathbf {b} |} — это площадь такого параллелограмма.
- Ориентированная площадь треугольника △ABC{\displaystyle \triangle ABC} выражается формулой
- S(A,B,C)=12(AB→∧AC→),{\displaystyle S(A,B,C)={\frac {1}{2}}({\overrightarrow {AB}}\wedge {\overrightarrow {AC}}),}
- а его площадь, следовательно, равна модулю этой величины.
- Если рассматривать плоскость в трёхмерном пространстве, то
- a∧b=±(a×b)⋅n,{\displaystyle \mathbf {a} \wedge \mathbf {b} =\pm (\mathbf {a} \times \mathbf {b} )\cdot \mathbf {n} ,}
- где «×{\displaystyle \times }» и « ⋅{\displaystyle \ \cdot }» соответственно — векторное и скалярное произведение, а n{\displaystyle \mathbf {n} } — единичный вектор нормали к плоскости. Знак плюс берется в случае, если правый базис на плоскости, дополненный вектором n{\displaystyle \mathbf {n} }, образует также правый базис; в противном случае минус.
- a∧b=0{\displaystyle \mathbf {a} \wedge \mathbf {b} =\mathbf {0} } — необходимое и достаточное условие коллинеарности ненулевых векторов на плоскости. Нулевой вектор для удобства работы с более употребительным скалярным произведением обычно считают ортогональным любому другому вектору, хотя это является произвольным соглашением.
- Из линейности и антикоммутативности следует, что если на плоскости задан ортонормированный базис ⟨e1,e2⟩, ∠(e1,e2)=π2,{\displaystyle \langle \mathbf {e} _{1},\mathbf {e} _{2}\rangle ,~~\angle (\mathbf {e} _{1},\mathbf {e} _{2})={\tfrac {\pi }{2}},} и два вектора, имеющих в нём координаты a=(a1,a2), b=(b1,b2),{\displaystyle \mathbf {a} =(a_{1},a_{2}),~~\mathbf {b} =(b_{1},b_{2}),} то их псевдоскалярное произведение равно определителю
- a∧b=|a1a2b1b2|{\displaystyle \mathbf {a} \wedge \mathbf {b} ={\begin{vmatrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{vmatrix}}}
- a∧b=∑i,j=12εijaibj{\displaystyle \mathbf {a} \wedge \mathbf {b} =\sum _{i,\;j=1}^{2}\varepsilon _{ij}a^{i}b^{j}}
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Понятие вектора. Действия с векторами, их свойства — сложение и вычитание векторов, умножение на число, коллинеарность. Скалярное умножение (произведение) векторов. Проекции, разложение векторов, координаты, действия в координатах, взаимное расположение Поделиться:
| |||
Скалярное произведение векторов: теория и решения задач
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Почему скалярное произведение векторов называется именно скалярным и что представляет собой? Чем оно отличается от результатов других операций над векторами? Что такое скаляр? Скаляр — это число. И скалярное произведение векторов — это тоже число. Этим оно и отличается от уже рассмотренной суммы векторов, и от векторного произведения векторов, которое ещё предстоит рассмотреть. В отличие от скалярного произведения, сумма векторов — это вектор, и векторное произведение — тоже вектор.
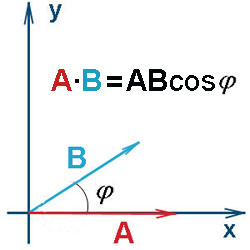
Определение 1. Скалярным произведением векторов называется число (скаляр), равное произведению длин (модулей) этих векторов на косинус угла между ними. Формула скалярного произведения векторов согласно определению 1:
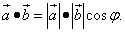(1)
Можно встретить и другое название этой операции: внутреннее произведение.
Скалярное произведение вектора на себя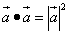 
называется скалярным квадратом.
На этом уроке будем решать распространённые задачи не только на непосредственное вычисление скалярного произведения, но и на выяснение ортогональности (перпендикулярности) векторов, вида угла (тупой, острый, прямой) между векторами, вычисление скалярного произведения векторов, которые даны в координатах, вычисление длин диагоналей параллелограма, построенного на вектора. Но все по порядку. Перед каждым видом задач будем обращать внимание на то, что на этот счёт гласит теория. По ходу урока вам пригодится онлайн-калькулятор для проверки решения задач на скалярное произведение векторов.
Если в задаче и длины векторов, и угол между ними преподнесены «на блюдечке с голубой каёмочкой», то условие задачи и её решение выглядят так:
Пример 1. Даны векторы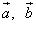 
.
Найти скалярное произведение векторов
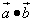, если их длины и угол между ними представлены
следующими значениями:
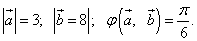
Решение:
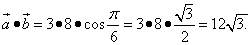
Справедливо и другое определение, полностью равносильное определению 1.
Определение 2. Скалярным произведением векторов называется число (скаляр), равное произведению длины одного их этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов. Формула согласно определению 2:
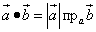(2)
или
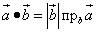(3)
Задачу с применением этой формулы решим после следующего важного теоретического пункта.
То же самое число можно получить, если перемножаемые векторы заданы своими координатами.
Определение 3. Скалярное произведение векторов — это число, равное сумме попарных произведений их соответствующих координат.
На плоскости
Если два вектора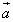 
и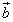 
на плоскости определены своими двумя декартовыми прямоугольными координатами
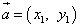
и
,
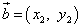то скалярное произведение этих векторов равно сумме попарных произведений их соответствующих координат:
.
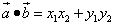Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
В пространстве
Если два вектора 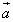и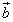
в пространстве определены своими тремя декартовыми прямоугольными координатами
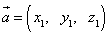
и
,
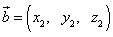то скалярное произведение этих векторов также равно сумме попарных произведений их соответствующих координат, только координат уже три:
.
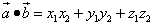Задача на нахождение скалярного произведения рассмотренным способом — после разбора свойств скалярного произведения. Потому что в задаче потребуется определить, какой угол образуют перемножаемые векторы.
Геометрические свойства
В определениях изучаемой операции мы уже касались понятия угла между двумя векторами. Пора уточнить это понятие.
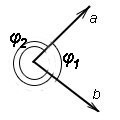
На рисунке выше видны два вектора, которые приведены к общему началу. И первое, на что нужно обратить внимание: между этими векторами существуют два угла — φ1 и φ2. Какой из этих углов фигурирует в определениях и свойствах скалярного произведения векторов? Сумма рассмотренных углов равна 2π и поэтому косинусы этих углов равны. В определение скалярного произведения входит только косинус угла, а не значение его выражения. Но в свойствах рассматривается только один угол. И это тот из двух углов, который не превосходит π, то есть 180 градусов. На рисунке этот угол обозначен как φ1.
1. Два вектора называют ортогональными и угол между этими векторами — прямой (90 градусов или π/2), если скалярное произведение этих векторов равно нулю:
.
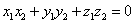Ортогональностью в векторной алгебре называется перпендикулярность двух векторов.
2. Два ненулевых вектора составляют острый угол (от 0 до 90 градусов, или, что тоже самое — меньше π/2) тогда и только тогда, когда их скалярное произведение положительно.
3. Два ненулевых вектора составляют тупой угол (от 90 до 180 градусов, или, что то же самое — больше π/2) тогда и только тогда, когда их скалярное произведение отрицательно.
Пример 3. В координатах даны векторы:
.
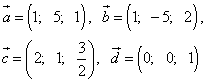Вычислить скалярные произведения всех пар данных векторов. Какой угол (острый, прямой, тупой) образуют эти пары векторов?
Решение. Вычислять будем путём сложения произведений соответствующих координат.
.
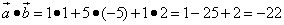Получили отрицательное число, поэтому векторы образуют тупой угол.
.
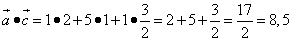Получили положительное число, поэтому векторы образуют острый угол.
.
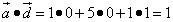Получили положительное число, поэтому векторы образуют острый угол.
.
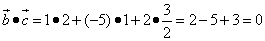Получили нуль, поэтому векторы образуют прямой угол.
.
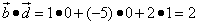Получили положительное число, поэтому векторы образуют острый угол.
.
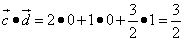Получили положительное число, поэтому векторы образуют острый угол.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
Пример 4. Даны длины двух векторов и угол между ними:
.
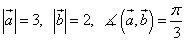Определить, при каком значении числа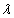 
векторы 
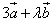и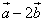 
ортогональны (перпендикулярны).
Решение. Перемножим векторы по правилу умножения многочленов:
.
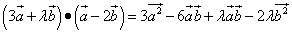Теперь вычислим каждое слагаемое:
.
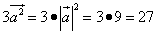
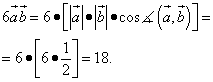
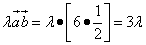
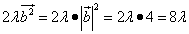Составим уравнение (равенство произведения нулю), приведём подобные члены и решим уравнение:
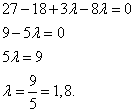
Ответ: мы получили значение λ = 1,8, при котором векторы ортогональны.
Решить задачу самостоятельно, а затем посмотреть решение
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
Иногда выигрышным для наглядности является представление двух перемножаемых векторов в виде матриц. Тогда первый вектор представлен в виде матрицы-строки, а второй — в виде матрицы-столбца:
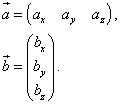
Тогда скалярное произведение векторов будет произведением этих матриц:
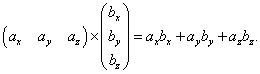
Результат тот же, что и полученный способом, который мы уже рассмотрели. Получили одно единственное число, и произведение матрицы-строки на матрицу-столбец также является одним единственным числом.
В матричной форме удобно представлять произведение абстрактных n-мерных векторов. Так, произведение двух четырёхмерных векторов будет произведением матрицы-строки с четырьмя элементами на матрицу-столбец также с четырьмя элементами, произведение двух пятимерных векторов — произведением матрицы-строки с пятью элементами на матрицу-столбец также с пятью элементами и так далее.
Пример 7. Найти скалярные произведения пар векторов
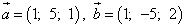
и
,
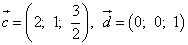используя матричное представление.
Решение. Первая пара векторов. Представляем первый вектор в виде матрицы-строки, а второй — в виде матрицы-столбца. Находим скалярное произведение этих векторов как произведение матрицы-строки на матрицу-столбец:
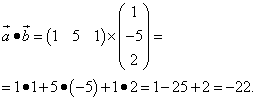
Аналогично представляем вторую пару и находим:
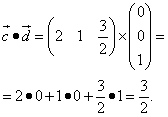
Как видим, результаты получились те же, что и у тех же пар из примера 2.
Вывод формулы косинуса угла между двумя векторами очень красив и краток.
Чтобы выразить скалярное произведение векторов
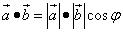(1)
в координатной форме, предварительно найдём скалярные произведение ортов. Скалярное произведение вектора на само себя по определению:
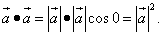
То, что записано в формуле выше, означает: скалярное произведение вектора на самого себя равно квадрату его длины. Косинус нуля равен единице, поэтому квадрат каждого орта будет равен единице:
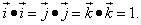
Так как векторы
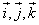
попарно перпендикулярны, то попарные произведения ортов будут равны нулю:
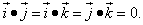
Теперь выполним умножение векторных многочленов:
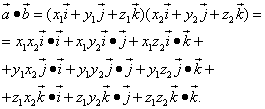
Подставляем в правую часть равенства значения соответствующих скалярных произведений ортов:
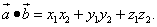
Получаем формулу косинуса угла между двумя векторами:
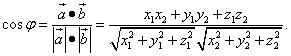
Пример 8. Даны три точки A(1;1;1), B(2;2;1), C(2;1;2).
Найти угол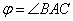 
.
Решение. Находим координаты векторов:
,
.
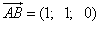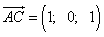По формуле косинуса угла получаем:
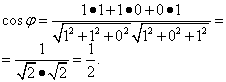
Следовательно,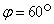 
.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
Пример 9. Даны два вектора
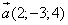
и
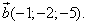
Найти сумму, разность, длину, скалярное произведение и угол между ними.
Решение.
1.Сумма
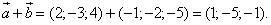
2.Разность
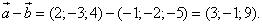
3.Длина
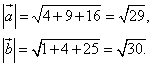
4.Скалярное произведение
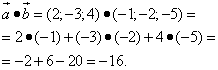
5.Угол между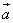 
и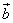 
:
Решить задачи самостоятельно, а затем посмотреть решения
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
Пример 13. Среди векторов
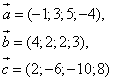
Найти а) коллинеарные; б) ортогональные.
Решение.
а) проверим пропорциональность соответствующих координат векторов — условие коллинеарности (повторение материала предыдущей части темы «Векторы»).
Для векторов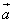 
и 
:
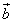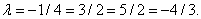
Равенство не выполняется.
Для векторов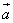 
и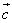 
:
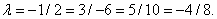
Равенство выполняется.
Для векторов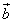 
и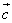 
:
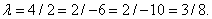
Равенство не выполняется.
Наше исследование показало, что коллинеарны векторы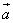 
и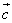 
.
б) найдём скалярные произведения векторов.
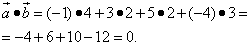
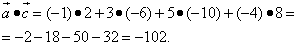
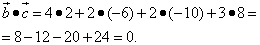
Наше исследование показало, что ортогональны векторы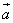 
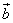и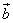 
и 
и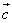 
.
Расчёт работы постоянной силы
Посмотрите ещё раз на рисунок в начале статьи. Пусть материальная
точка перемещается прямолинейно из начала координат в конец вектора B под
действием постоянной силы F = A, образующей угол
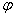с перемещением S = A.
Из физики известно, что работа силы F при перемещении S равна
.
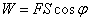Таким образом, работа постоянной силы при прямолинейном перемещении её точки
приложения равна скалярному произведению вектора силы F = B на
вектор перемещения S = A.
Скалярное произведение векторов позволяет находить угол между двумя векторами. Поэтому оно часто встречается в последующих разделах математики, особенно, аналитической геометрии. Стоит ли говорить о том, что нахождение скалярного произведения векторов — фундаментальный навык для любого будущего инженера, проектирующего всё что угодно, от гладильных досок и лестниц-стремянок до зданий, или для программиста, собирающегося разрабатывать игры?
Экономический смысл скалярного произведения векторов
В экономических задачах можно рассматривать скалярное произведение вектора цен p
на вектор объёма проданных товаров x . Скалярное произведение px в этом случае даёт суммарную стоимость проданных товаров x при ценах p . Например, если объём всех товаров, проданных предприятием, выражается вектором x = (400; 750; 200; 300), элементы которого означают соответственно количество товаров различных групп, а цены в одних и тех же денежных единицах заданы в соответствующем порядке вектором p = (3; 2,1; 1,2; 0,5), то скалярное произведение
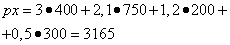
выражает суммарную стоимость всех товаров x.
Поделиться с друзьями
Начало темы «Векторы»
Продолжение темы «Векторы»
Свойства скалярного произведения векторов
ОПРЕДЕЛЕНИЕ Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:
Замечание. Если хотя бы один из двух векторов нулевой, то их скалярное произведение равно нулю.
Свойства скалярного произведения векторов
1. Скалярное произведение вектора самого на себя называется скалярным квадратом:
Скалярный квадрат вектора равен квадрату его модуля:
2. .
3. .
4. .
5. Длина вектора равна
6. Величина угла (а точнее косинус этого угла) между ненулевыми векторами и равна частному скалярного произведения этих векторов и произведения их длин:
7. Два ненулевых вектора и ортогональны (перпендикулярны) тогда и только тогда, когда их скалярное произведение равно нулю:
8. Угол между двумя ненулевыми векторами и является острым тогда и только тогда, когда их скалярное произведение положительно; и является тупым – когда скалярное произведение отрицательно.
9. Длина проекции вектора на ось, образованную вектором , равна скалярному произведению этих векторов, деленному на модуль вектора :
10. Если векторы и заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат:
Примеры решения задач
ПРИМЕР| Задание | Найти модуль вектора , если |
| Решение | Модуль вектора равен корню квадратному из скалярного квадрата этого вектора:
|
| Ответ |
| Задание | Найти скалярное произведение векторов и |
| Решение | Искомое скалярное произведение равно сумме произведений соответствующих координат рассматриваемых векторов, то есть
|
| Ответ |
Скалярное произведение векторов, формула и примеры
Определение и формула скалярного произведения векторов
Если векторы заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат:
Свойства скалярного произведения векторов
1. Скалярное произведение вектора самого на себя всегда больше или равно нуля:
Выражение называется скалярным квадратом вектора .
2. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:
3. Скалярное произведение вектора самого на себя равно квадрату его модуля:
4. Операция скалярного умножения коммуникативна:
5. Если скалярное произведение двух ненулевых векторов равно нулю, то эти вектора ортогональны (перпендикулярны):
6. .
7. Операция скалярного умножения дистрибутивна:
8. Если угол между векторами острый, то скалярное произведение этих векторов будет положительным числом (так как косинус острого угла – положительное число). Если угол между векторами тупой, то скалярное произведение будет отрицательным (так как косинус тупого угла есть величина отрицательная). Имеют место и обратные утверждения.
9. Если векторы сонаправлены, то угол между ними будет равен , а скалярное произведение будет положительным. Угол между противоположно направленными векторами равен и их скалярное произведение отрицательно.
| Понравился сайт? Расскажи друзьям! | |||
