Ошибка

Перейти к основному содержанию

Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)

Извините, не удалось найти запрашиваемый Вами файл

Подробнее об этой ошибке

Перейти на… Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ).

Применение СЛАУ в экономике»Лекционный материал по теме «Линейные операторы»Примеры решения по теме «Системы линейных алгебраических уравнений»ЛИНЕЙНАЯ АЛГЕБРАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийЛинейная алгебра для экономистовМатрицы. ОпределителиВекторная алгебра.Аналитическая геометрияЛекционный материал по теме «Векторная алгебра. Линейные операции над векторами»Примеры решения задач по теме «Векторная алгебра. Линейные операции над векторами»Примеры решения задач по теме «Скалярное, векторное и смешанное произведения векторов»ВЕКТОРНАЯ АЛГЕБРАВекторная алгебра и аналитическая геометрияПрезентация по теме «Векторная алгебра»Векторная алгебра.Аналитическая геометрияТеоретический материал по теме «Метод координат на плоскости и в пространстве»Лекционный материал по теме «Прямая на плоскости»Лекционный материал по теме «Кривые второго порядка»Лекционный материал по теме «Прямая в пространстве»Лекционный материал по теме «Плоскость в пространстве»Лекционный материал по теме «Поверхности второго порядка»Примеры решения задач по теме «Прямая на плоскости»Примеры решения задач по теме «Кривые второго порядка»Примеры решения задач по темам «Прямая и плоскость в пространстве»АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯВекторная алгебра и аналитическая геометрияСправочный материал «Прямая на плоскости»Справочный материал «Кривые второго порядка»Справочный материал «Прямая и плоскость в пространстве»Линейная алгебра для экономистовПрезентация по теме «Прямая на плоскости»Презентация по теме «Уравнения плоскости и прямой в пространстве»▶ Виртуальный тренажер «Прямая на плоскости» 👨‍🎓Введение в анализНачала анализаЛекционный материал по теме «Множества, функции, основные характеристики функций.

Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨‍🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления. Правила Лопиталя»Лекционный материал по теме «Формулы Тейлора и Маклорена»Лекционный материал по теме «Приложения дифференциального исчисления»Примеры решения задач по теме «Дифференциальное исчисление функций одной переменной»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙТест «Основные правила и формулы дифференцирования»Тест «Дифференциальное исчисление функций одной переменной»Основы дифференцирования. Часть 1Основы дифференцирования. Часть 2Основы дифференцирования. Часть 3Приложения производной Исследование функций, Примеры решения задачПрименение производных при решении экономических задачИнтегральное исчисление функции одной переменнойЛекционный материал по теме «Неопределенный интеграл»Лекционный материал по теме «Определенный интеграл»Практическое занятие 1. Непосредственное интегрирование (неопределённый интеграл)Практическое занятие 2. Интегрирование заменой переменной (неопределённый интеграл)Практическое занятие 3. Интегрирование по частям. Интегрирование выражений, содержащих квадратный многочлен (неопределённый интеграл)Практическое занятие 4. Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1. Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»Примеры решения задач по теме «Дифференциальные уравнения»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1.

Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий. Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 6. Дискретные случайные величины. Числовые характеристикиПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Комбинаторика»Примеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности.

Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме «Непрерывные случайные величины»Примеры решения задач по теме «Основные числовые характеристики непрерывных случайных величин»Примеры решения задач по теме «Классические законы распределения дискретных случайных величин»Примеры решения задач по теме «Классические законы распределения непрерывных случайных величин»Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу «Случайные события»Тест по теме «Числовые характеристики случайных величин»Тест по теме «Дискретные случайные величины»Тест по теме «Непрерывные случайные величины»Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу «Математическая статистика». Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа. Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)

Скалярное, векторное и смешанное произведения векторов — Студопедия

Поделись  

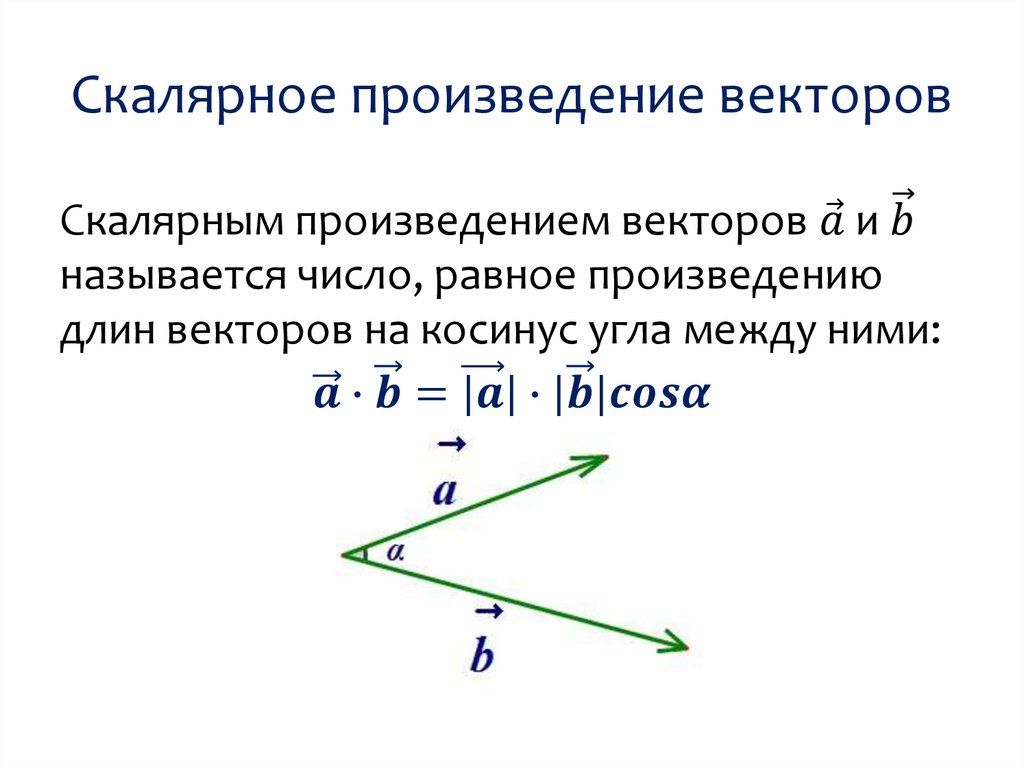
Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: , где — угол между векторами и (рис. 4).

Рис.4

Пусть заданы два вектора в координатной форме и

Скалярное произведение двух ненулевых векторов в координатной форме равно сумме произведений соответствующих координат этих векторов: .

Косинус угла между векторами вычисляется по формуле: .

Условием перпендикулярности ненулевых векторов и является равенство нулю их скалярного произведения:

.

Векторным произведением двух векторов и называется вектор , который:

1) имеет модуль, численно равный площади параллелограмма, построенного на векторах и : ;

2) перпендикулярен к плоскости этого параллелограмма;

3) направлен в такую сторону, с которой кратчайший поворот от к рассматривается совершающимся против часовой стрелки (такое расположение векторов , и называется правой тройкой векторов) (рис.5).

Рис.5

Векторное произведение ненулевых векторов вычисляется через координаты данных векторов и

следующим образом:

Равенство нулю векторного произведения двух ненулевых векторов является условием их коллинеарности, т. е. ½½ .

Смешанное произведение трех векторов , и , которое обозначается или , есть скаляр, абсолютная величина которого равна объему параллелепипеда, построенного на векторах , и , как на ребрах.

Смешанное произведение трех векторов вычисляется в координатной форме по формуле:

.

Равенство нулю смешанного произведения трех ненулевых векторов является условием их компланарности: .

Задача. Определить внутренние углы и треугольника c вершинами в точках

Решение. Внутренний угол — это угол между векторами и , который вычисляется через скалярное произведение векторов по формуле:

Координаты векторов: .

Отсюда,

Аналогично, находя предварительно , получим

Отсюда

Задача.Вычислить площадь треугольника с вершинами в точках и высоту (рис.6).

Решение.

Рис.6

Найдем координаты векторов Площадь треугольника вычисляется через векторное произведение векторов по формуле: .

Векторное произведение

Тогда .

С другой стороны , отсюда высота .

Так как ,

то высота .

Задача. Вычислить объем пирамиды с вершинами в точках и высоту, опущенную из точки на основание (рис.7).

Решение.

Рис.7

Найдем координаты векторов : .

Объем пирамиды вычисляется через смешанное произведение векторов по формуле: .

Смешанное произведение векторов

.

Следовательно,

С другой стороны . Откуда высота пирамиды , где площадь треугольника

Векторное произведение

Тогда,

Следовательно, высота пирамиды =



3$ скалярное произведение используется для получения информации о проекции одного вектора на другой, а перекрестное произведение используется для получения информации об отклонении одного вектора от другого.

Скалярный продукт

Если у нас есть два вектора $\mathbf a$ и $\mathbf b$, что нам нужно, чтобы указать проекцию $\operatorname{proj}_{\mathbf b}\mathbf a$? Нам нужны те же вещи, что и для указания любого вектора: величина (длина) и направление. Геометрически мы видим, что величина $\operatorname{proj}_{\mathbf b}\mathbf a$ равна $\|\mathbf a\||\cos(\theta)|$, где $\|\mathbf a\ |$ — величина $\mathbf a$, а $\theta$ — угол между $\mathbf a$ и $\mathbf b$. Абсолютное значение косинуса есть, так что формула продолжает работать для тупых углов (убедитесь, что вы понимаете, что эта формула работает для всех углов между $0$ и $\pi$ радиан).

А как же направление? По определению направление проекции будет либо в направлении $\mathbf b$ (острый угол), либо в направлении $-\mathbf b$ (тупой угол). Затем обратите внимание, что на самом деле нам не нужно использовать вектор для кодирования этой информации — это было бы излишним. Мы могли бы просто использовать знак ($+$ или $-$) для его кодирования. Допустим, мы хотим, чтобы наше произведение было положительным, когда угол $\theta$ острый, и отрицательным, когда угол $\theta$ тупой. т.е. $$\operatorname{предлагаемая операция} = \begin{case} \|\mathbf a\||\cos(\theta)|, & \theta \in \left[0, \frac{\pi}2\right] \\ -\|\mathbf a\||\cos(\theta)|, & \theta \in \left[\frac{\pi}2, \pi\right]\end{cases}$$ Но вот что интересно: $\cos(\theta) = |\cos(\theta)|$, когда $\theta\in\left[0, \dfrac{\pi}2\right]$ и $\cos( \theta) = -|\cos(\theta)|$, когда $\theta\in\left[\dfrac{\pi}2, \pi\right]$. Таким образом, мы можем просто заменить эту кусочно определенную формулу более простой $$\operatorname{предлагаемая операция} = \|\mathbf a\|\cos(\theta)$$

Итак, мы должны определить скалярный продукт как просто $$\mathbf a \cdot \mathbf b = \|\mathbf a\|\cos(\theta)$$ верно? На самом деле, мы получаем два очень хороших свойства, если масштабируем правую часть (RHS) на величину $\mathbf b$: $$\mathbf a \cdot \mathbf b = \|\mathbf a\|\|\mathbf b\|\cos(\theta)$$ мы получаем, что $\mathbf a\cdot \mathbf b = \mathbf b \cdot \mathbf a$ (это легко увидеть из симметрии RHS), и мы получаем, что это произведение билинейно . Это может не иметь смысла для вас прямо сейчас, но это очень желательное свойство. И заметьте, что этот дополнительный фактор совсем не мешает нам реконструировать проекцию. На самом деле, вы должны подтвердить для себя, что $$\operatorname{proj}_{\mathbf b}\mathbf a = (\mathbf a \cdot \hat {\mathbf b})\hat {\mathbf b}$$ где $\hat {\mathbf b} = \dfrac{\mathbf b}{\|\mathbf b\|}$. 93$ существует бесконечно много направлений, ортогональных $\mathbf b$. Таким образом, мы не можем просто закодировать эту информацию в одном скаляре — нам понадобится векторное произведение, чтобы получить векторную величину.

Если нам нужно хоть какое-то подобие симметрии скалярного произведения, мы также не можем иметь векторное произведение, указывающее только в направлении отказа, потому что тогда направление $\mathbf a\times \mathbf b$ не имело бы реальное отношение к направлению $\mathbf b \times \mathbf a$. Вместо этого нам нужен способ кодировать направления обоих отказов вместе. К счастью, у трехмерного пространства есть полезное свойство: каждая плоскость (содержащая начало координат) ортогональна уникальной линии (содержащей начало координат). Тогда умная идея состоит в том, чтобы построить плоскость из $\operatorname{rej}_{\mathbf a}\mathbf b$ и $\operatorname{rej}_{\mathbf b}\mathbf a$, а затем указать векторное произведение в одном из двух направлений вдоль линии, ортогональной этой плоскости. Тогда мы свели наш выбор из бесконечного множества направлений всего к двум вариантам (одно из двух направлений вдоль линии).

Тогда нам просто нужен способ всегда делать последовательный выбор. Правило правой руки — это (несколько произвольный) способ сделать такой выбор.

Еще одно замечание (которое вы могли бы попытаться доказать): плоскость, натянутая на $\operatorname{rej}_{\mathbf a}\mathbf b$ и $\operatorname{rej}_{\mathbf b} \mathbf a$ точно такая же, как плоскость, состоящая только из $\mathbf a$ и $\mathbf b$. Таким образом, при определении направления вектора векторного произведения проще сделать это непосредственно в терминах $\mathbf a$ и $\mathbf b$.

Затем мы можем восстановить отклонение $\operatorname{rej}_{\mathbf b}\mathbf a$ по несколько более сложной формуле (из-за того, что перекрестное произведение на самом деле ортогонально отклонению, а не указывает в его направлении): $$\operatorname{rej}_{\mathbf b}\mathbf a = \hat{\mathbf b}\times(\mathbf a\times \hat{\mathbf b})$$ который вы можете найти, сначала показав, что $$\mathbf a \times \mathbf b = \operatorname{rej} _{\mathbf b}\mathbf a \times \mathbf b$$

Прошлые мотивы

Приведенные выше «конструкции» на самом деле являются лишь одним из способов мотивировать определения, но вы все равно можете спросить, почему, например, мы используем скаляр вместо вектора при определении скалярного произведения. Надеюсь, я убедил вас, что вектор нам не нужен, но ничто не говорит о том, что мы не можем определить его таким образом. Причина на самом деле исходит из частей, которые я упустил из виду о свойствах, которые мы хотим, чтобы точечные и перекрестные произведения имели. В частности, мы хотим, чтобы точечные и перекрестные произведения были равны 9.0013 инвариант при некоторых преобразованиях. Вы можете подождать, пока вы действительно не доберетесь до линейной алгебры, чтобы узнать об этом, но заголовок состоит в том, что скалярное произведение будет иметь требуемое свойство инвариантности только в том случае, если это скалярная величина, а не векторная величина.

Wedge Product

Мотивируя векторное произведение, я использовал свойство трехмерного пространства. Это имеет довольно печальное последствие: векторное произведение (как билинейное произведение векторов на векторы) можно определить только в трех измерениях (и, как ни странно, в семи измерениях, но мы не будем вдаваться в эту конструкцию здесь). Но на самом деле есть способ обобщить векторное произведение до чего-то, что работает в любое измерение , если мы готовы отказаться от свойства, которое должно привести к вектору. Фактически, это также не может привести к скаляру. Если мы введем новые объекты, называемые бивекторами , то мы можем получить гораздо более элегантный и общий продукт, называемый произведением клина. Это почти наверняка не будет рассмотрено в вашем курсе многомерного исчисления или даже в вашем будущем курсе линейной алгебры, но если вы хотите изучить самые основы этого, я предлагаю прочитать мой ответ здесь. Внизу я даю пару ссылок, из которых вы можете узнать больше. 93$ векторное пространство, нам нужно базовое поле (и мы решили использовать $k=\Bbb R$) и действие $k$, т. е. кольцевой гомоморфизм $\phi\colon k\to \operatorname{End} (V)$ и для удобства запишем $x\cdot v$ вместо $\phi(x)(v)$, что дает нам новую операцию $\cdot\colon k\times V\to V$, которая автоматически обладает некоторыми хорошими свойствами : Например, $1\cdot v=v$ следует, потому что в гомоморфизме между унитарными кольцами мы постулируем, что 1-элемент отображается в 1-элемент.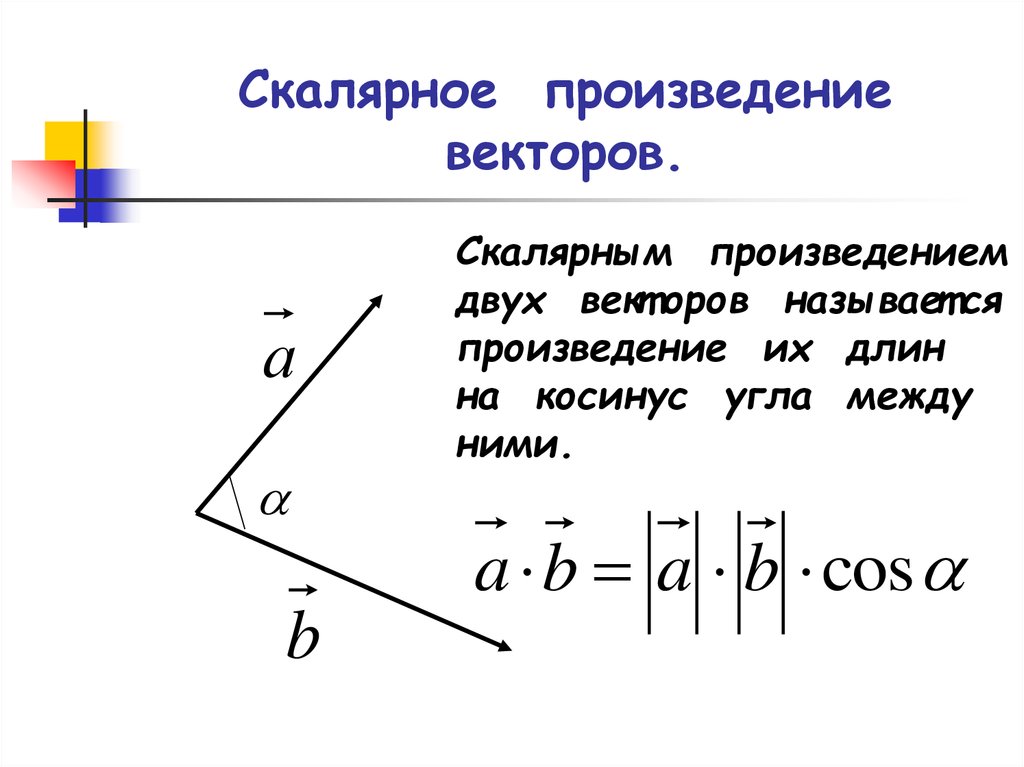 И такие вещи, как $(x+y)\cdot v=x\cdot v+y\cdot v$ или $x\cot(v+w)=x\cdot v+x\cdot w$ или $(x\cdot w$ y)\cdot v = x\cdot(y\cdot v))$ также непосредственно следуют из определения гомоморфизма колец. Все работает вместе настолько хорошо, что использование одних и тех же символов операций $+$ и $\cdot$ для различных операций не сбивает нас с толку (и на самом деле настолько наводит на размышления, что сильно упрощает нашу жизнь). 9n$), у нас есть естественный способ определить скалярный продукт. Но повторю: векторное пространство, вообще говоря, не наделено (или даже не наделено) таким скалярным произведением.

Наконец, векторное произведение. Чтобы дать более широкую картину этого, мне пришлось бы довольно глубоко погрузиться в абстрактные структуры (даже по сравнению с тем, что я делал до сих пор). Давайте остановимся на этом: точно так же, как не всякое векторное пространство является топологическим пространством, или алгеброй, или пространством со скалярным произведением, также не каждое векторное пространство допускает векторное произведение.