7.2.2. Скалярное произведение MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

• Главная
/
• База знаний
/
• CAD / CAM
/
• org/Breadcrumb»>MathCAD 12

• Линейная алгебра
• 7.1. Простейшие матричные операции
  • 7.1.1. Транспонирование
  • 7.1.2. Сложение и вычитание
  • 7.1.3. Умножение
• 7.2. Векторная алгебра
  • 7.2.1. Модуль вектора
  • 7.2.2. Скалярное произведение
  • 7.2.3. Векторное произведение
  • 7.2.4. Векторизация массива
• 7.3. Вычисление определителей и обращение квадратных матриц
  • 7.3.1. Определитель квадратной матрицы
  • 7.3.2. Ранг матрицы
  • 7.3.3. Обращение квадратной матрицы
  • 7.3.4. Возведение квадратной матрицы в степень
  • 7.3.5. Матричные нормы
  • 7.3.6. Число обусловленности квадратной матрицы
• 7.4. Вспомогательные матричные функции
  • 7.4.1. Автоматическая генерация матриц
  • 7.4.2. Разбиение и слияние матриц
  • 7. 4.3. Сортировка элементов матриц
  • 7.4.4. Вывод размера матрицы

Скалярное произведение векторов (vector inner product) определяется как скаляр, равный сумме попарных произведений соответствующих элементов. Векторы должны иметь одинаковую размерность, скалярное произведение имеет ту же размерность. Скалярное произведение двух векторов u и v равно uv=|u||v|cos0, где 0— угол между векторами. Если векторы ортогональны, то их скалярное произведение равно нулю. Обозначается скалярное произведение тем же символом, что и умножение (листинг 7.9).

ВНИМАНИЕ!

Для обозначения скалярного произведения пользователю позволяется выбирать представление оператора умножения при помощи контекстного меню (подобно умножению скалярных величин). Однако никогда не применяйте для обозначения скалярного произведения символ х, который является общеупотребительным символом векторного произведения (см. разд. 7.2.3).

Листинг 7.9. Скалярное произведение векторов

С осторожностью перемножайте несколько (более двух) векторов. По-разному расставленные скобки полностью изменяют результат умножения. Примеры такого умножения приведены в листинге 7.10.
Листинг 7.10. Скалярное произведение векторов, умноженное на третий вектор

Нравится

Твитнуть

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

9909 0

Глава 10 Работа с информационными ресурсами Mathcad 11

6933 0

Глава 2 Работа с файлами Mathcad 11

12368 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2219 s

Почему векторное произведение дает нам вектор? И почему скалярное произведение полученного вектора с другим дает нам объем параллелепипеда?

Математика и математики

Популярное

Сообщества

Представьте векторное произведение axb=i(p)+j(p)+k(p). P — это полученный вектор. Я понимаю, что если бы в матрице 3 на 3 вместо (i, j, k) были координаты, то мы бы получили параллелепипед. Но каким образом скалярное произведение (i,j,k) и (p1,p2,p3) дает нам тот же самый результат? Нас учили, что скалярное произведение дает длину (magnitude), но не объем или площадь. Что я не так понимаю?

МатематикаЛинейная алгебра

Лок Эрстед

Математика и математики

16 октября 2021  ·

14,7 K

ОтветитьУточнить

Лучший

Борис Державец

Data science

2,7 K

Openstack DevOps and IBM/Informix Certified DBA . Phd in Math (Duality of spaces of…  · 16 окт 2021

Далее смотрим детально последную строку

Здесь z = [a (x) b] есть вектор перпендикулярный плоскости натянутой на вектора «а» и «b» , длина которого есть площадь параллелограмма натянутого на вектора «а» и «b». Скалярное произведение (z,d) = |z|*|d|* cos(psi), где «psi» есть угол между z и d . Но |d|* cos(psi) есть длина проекции d на направление z ( where z is actually normal to plane containing vectors «a» and b» ). То есть |d|* cos(psi) есть высота наклонного параллепипеда натянутого на {a,b,d}.

Таким образом, мы доказываем, что ([a (x) b],d) есть его объем.

==================================================

Would you need all explanations above to be provided to you in English, make a direct request to give you feedback in English. Otherwise, YANDEXQ will just drop my answer due to YANDEXQ POLICY to reply only in Russian.

Борис Державец

17 октября 2021

@Лок Эрстед, После корректировке моего ответа Убрал из «стороку» лишнюю букву «о» => «строку». Пропало… Читать дальше

Комментировать ответ…Комментировать…

Виктор Патринов

Физика

796

Научный журналист  · 16 окт 2021

«Почему векторное произведение дает нам вектор?» Потому что по определению положено так. «И почему скалярное произведение полученного вектора с другим дает нам объем параллелепипеда.» Т. к. длина вектора, полученного в результате векторного произведения, равна площади параллелограмма, построенного на векторах векторного произведения. То по определению скалярного… Читать далее

вадим жуков

16 октября 2021

Скалярное произведение двух векторов есть ab = |a||b| * Cos ab и представляет собой, по сути, проекцию вектора а… Читать дальше

Комментировать ответ…Комментировать…

aburov

171

когда-то изучал математику.  · 17 окт 2021

Векторное произведение — «не очень вектор», раз размерность его компонент измеряется в квадратных метрах. но история эта довольно длинная. Заметим лишь, что с векторным произведением «не очень хорошо» в зеркале: векторное произведение зеркальных отражений векторов — совсем не зеркальное отражение векторного произведения.

1 эксперт согласен

Комментировать ответ…Комментировать…

Вы знаете ответ на этот вопрос?

Поделитесь своим опытом и знаниями

Войти и ответить на вопрос

О сообществе

Математика и математики

Сообщество практикующих математиков разного уровня. Оригинальные решения, нетворкинг и общение. Не отвечаем на школьные задачки!

1.5: Точечное и векторное произведение

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

603

• Ларри Грин
• Общественный колледж Лейк-Тахо

93 \)

Если

\[\textbf{v} = a \hat{\textbf{i}} + b \hat{\textbf{j}} + c \hat{\textbf{k}} \; \;\; \текст{и}\;\;\; \textbf{w}= d \hat{\textbf{i}} + e \hat{\textbf{j}} + f \hat{\textbf{k}} \nonumber \]

, затем

\[ \ textbf{v} \cdot \textbf{w} = объявление + быть + ср. \номер\]

Пример \(\PageIndex{1}\)

Если

\[\textbf{v} = 2\; \ шляпа {\ textbf {я}} + 4 \; \шляпа{\textbf{j}} \;\;\; \текст{и} \;\;\; \textbf{w} = \hat{\textbf{i}} + 5\; \ шляпа {\ textbf {j}} \ не номер \]

, затем

\[ \textbf{v} \cdot \textbf{w} = (2)(1) + (4)(5) = 22. \nonumber \]

Упражнение \(\PageIndex{1}\)

Найдите скалярное произведение \(2 \hat{\textbf{i}}+ \hat{\textbf{j}} — \hat{\textbf{k}} \) и \( \hat{\textbf{i}} + 2 \hat{\textbf{j}} \).

Угол между двумя векторами

Определим угол \(\theta \) между двумя векторами v и w по формуле

\[ \cos q = \dfrac{\textbf{v} \cdot \ textbf{w} }{|| \textbf{v} || || \textbf{ш}|| }\номер\]

, так что

\[ \textbf{v} \cdot \textbf{w} = ||\textbf{v}|| || \textbf{ш} || \cos кв. \nonumber \]

Два вектора называются ортогональными , если их угол прямой. Мы видим, что углы ортогональны тогда и только тогда, когда

\[ \textbf{v} \cdot \textbf{w} = 0. \nonumber \]

угол между

\[ \textbf{v} = 2 \hat{\textbf{i}} + 3 \hat{\textbf{j}} + \hat{\textbf{k}} \nonumber \] 9{-1}\left( \dfrac{13}{\sqrt{14} \sqrt{21}} \right). \nonumber \]

Определение: Направленные косинусы

Пусть

\[\textbf{v} = a \hat{\textbf{i}} + b \hat{\textbf{j}} + c \hat{\ textbf{k}} \nonumber \]

вектор, то мы определяем направляющих косинусов следующим образом:

1.

\[ \cos a = \dfrac{a}{||\textbf {v} ||},\nonumber \]

2.

\[\cos b = \dfrac{b}{ ||\textbf{v} || }, \номер\]

3.

\[ \cos c = \dfrac{c}{||\textbf{v}||}. \nonumber \]

Выступы и компоненты Предположим, что автомобиль остановился на крутом холме, и пусть g будет силой тяжести, действующей на него. Мы можем разделить вектор g на составляющую, толкающую машину по дороге, и составляющую, толкающую машину на дорогу. Определим

Определение: Проекция

Пусть u и v будут векторами. Затем u можно разбить на две составляющие: r и s , так что r параллельно v , а s перпендикулярно v . r называется проекцией u на v и называется компонентой u , перпендикулярной v .

Мы видим, что

\[\begin{align*} \textbf{u} \cdot \textbf{v} = || \textbf{и} || \; || \textbf{v}|| \cos q &= \dfrac{|| \textbf{и} || \; || \textbf{v} || \text{proj}_{\textbf{v}} \textbf{u} }{||\textbf{u}||} \\ &= ||\textbf{v} || \; || \text{proj}_{\textbf{v}} \textbf{u} ||. \end{align*} \nonumber \] 92 } || \textbf{v}|| \nonumber \]

, а правая часть упрощается до приведенной выше формулы. Направление правильное, так как правая часть формулы постоянно кратна v , поэтому вектор проекции имеет направление v , как и требуется.

Чтобы найти вектор s , обратите внимание на диаграмму, что

\[ \text{proj}_{\textbf{v}} \textbf{u} + \textbf{s} = \textbf{u} \ nonumber \]

, так что

\[ \textbf{s} = \textbf{u} — \text{proj}_{ \textbf{v} } \textbf{u}. \номер\]

Работа

Работа, совершенная постоянной силой F вдоль PQ, равна

\[W=\textbf{F}\cdot PQ. \nonumber \]

Пример \(\PageIndex{3}\)

Найдите работу, совершенную против силы тяжести, чтобы переместить 10-килограммового ребенка из точки \((2,3)\) в точку \((5, 7)\)?

Решение

Мы имеем, что вектор силы равен

\[ \textbf{F} = m \textbf{a} = (10 )(-9,8 \hat{\textbf{j}}) = -98 \ шляпа {\ textbf {j}} \ не номер \]

, а вектор смещения равен

\[\textbf{v} = (5-2) \hat{\textbf{i}} + (7-3) \hat{\textbf{j}} = 3 \hat{ \textbf{i}} + 4 \hat{\textbf{j}}.\nonumber \]

Работа представляет собой скалярное произведение

\[\begin{align*} W = \textbf{F} \cdot \ textbf{v} &= (-98 \hat{\textbf{j}} ) \cdot (3 \hat{\textbf{i}} + 4 \hat{\textbf{j}} ) \\ &= (0 )(3) + (-98) (4) \\ &= -392. \end{align*} \nonumber \]

Обратите внимание, что отрицательный знак подтверждает, что работа выполняется против силы тяжести. Следовательно, требуется 392 Дж работы по перемещению ребенка.

Крутящий момент

Предположим, вы катаетесь на лыжах и ужасно падаете. Ваше тело вращается, а лыжи остаются на месте (не пытайтесь делать это дома). При правильном креплении ваши крепления отстегнутся, и лыжа оторвется. Крепления распознают, что была применена сила. Эта сила называется крутящим моментом. Чтобы вычислить его, мы используем перекрестное произведение двух векторов, которое не только дает крутящий момент, но и дает направление, перпендикулярное как силе, так и направлению ноги.

Определение: перекрестное произведение

Пусть \(\textbf{u} = a \hat{\textbf{i}} + b \hat{\textbf{j}} + c \hat{\textbf{k}}\ ) и \(\textbf{v} = d \hat{\textbf{i}} + e \hat{\textbf{j}} + f \hat{\textbf{k}} \) — векторы. Затем мы определяем перекрестное произведение \(\textbf{v} \times \textbf{w} \) определителем матрицы:

\[\begin{pmatrix} \hat{\textbf{i}} & \hat{\textbf{j}} &\hat{\textbf{k}} \\ a & b &c \\ d & e & f \end{pmatrix}.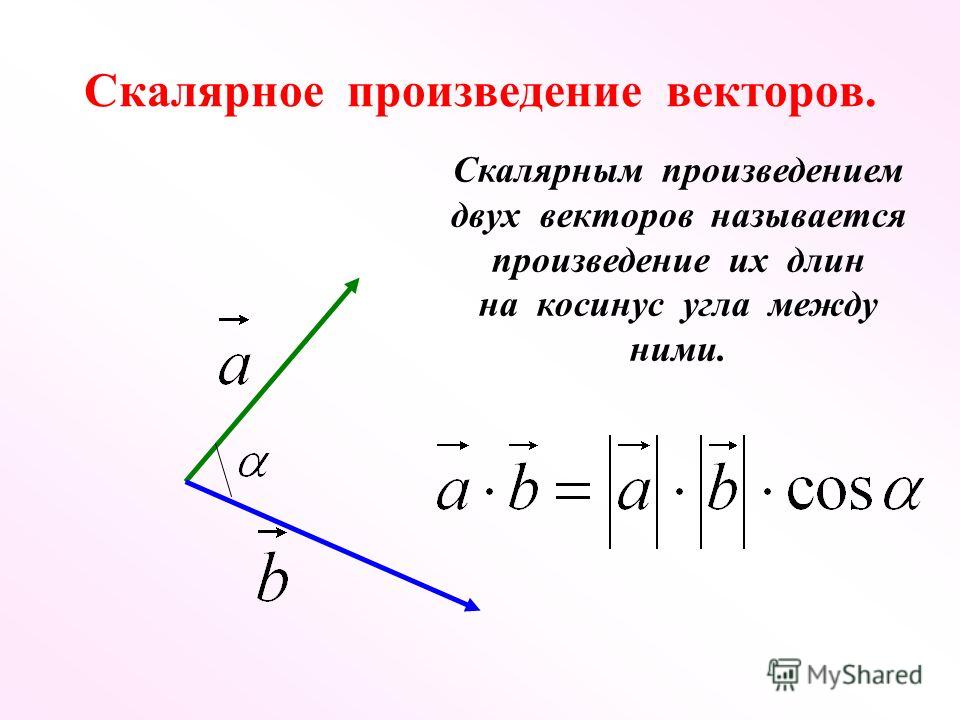 \номер\]

Мы можем вычислить этот определитель как

\[\begin{vmatrix} b & c \\ e & f \end{vmatrix} \hat{\textbf{i}} — \begin{vmatrix} a & c \\ d & f \end{vmatrix} \hat{\textbf{j}} + \begin{vmatrix} a & b \\ d & e \end{vmatrix} \hat{\textbf{k}} \nonumber \]

\[ =(bf — ce) \hat{\textbf{i}} + (cd — af) \hat{\textbf{j}} + (ae — bd)\hat{\textbf{k}}. \nonumber \]

Пример \(\PageIndex{4}\)

Найдите векторное произведение \(\textbf{u} \times \textbf{v} \), если

\[\textbf{u} = 2 \hat{\textbf{i}} + \hat{\textbf{j}} -3 \hat{\textbf{k}}, \;\;\; \textbf{v} = 4 \hat{\textbf{j}} + 5 \hat{\textbf{k}}.\nonumber \]

Решение

Мы вычисляем

\[\begin{align* }\begin{vmatrix} \hat{\textbf{i}} & \hat{\textbf{j}} & \hat{\textbf{k}} \\ 2 & 1 & -3 \\ 0 & 4 & 5 \end{vmatrix} & = \begin{vmatrix} 1 & -3 \\ 4 & 5 \end{vmatrix} \hat{\textbf{i}} — \begin{vmatrix} 2 & -3 \\ 0 & 5 \end{vmatrix} \hat{\textbf{j}} + \begin{vmatrix} 2 & 1 \\ 0 & 4 \end{vmatrix} \hat{\textbf{k}} \\ &= 17 \hat{ \textbf{i}} — 10 \шляпа{\textbf{j}} + 8 \шляпа{\textbf{к}}. \end{align*} \nonumber \]

Если вам нужна дополнительная помощь, см. конспект лекций по математике 103 B по матрицам.

Упражнения

Найдите \(\textbf{u} \times \textbf{v}\), когда

1. \(\textbf{u} = 3 \hat{\textbf{i}} + \hat{\textbf {j}} — 2 \hat{\textbf{k}}\), \( \textbf{v} = \hat{\textbf{i}} — \hat{\textbf{k}} \),
2. \(\textbf{u} = 2 \hat{\textbf{i}} — 4 \hat{\textbf{j}} — \hat{\textbf{k}} \), \(\textbf{v} = 3 \hat{\textbf{i}} — \hat{\textbf{j}} + 2k \hat{\textbf{k}} \),

Обратите внимание, что поскольку переключение порядка двух строк определителя меняет знак определителя, мы имеем

\[ \textbf{u} \times \textbf{v} = — \textbf{v} \times \textbf{ у}. \nonumber \]

Геометрия и векторное произведение

Пусть u и v — векторы, и рассмотрим параллелограмм, который составляют два вектора.

Затем

\[||\textbf{u} \times \textbf{v} || = \text{Площадь параллелограмма}\nonumber \]

и направление \(\textbf{u} \times \textbf{v}\) является прямым углом к ​​параллелограмму, который следует правилу правой руки.

Примечание. Для \( \hat{\textbf{i}} \times \hat{\textbf{j}}\) величина равна 1, а направление равно \(\hat{\textbf{k}}\) , следовательно, \(\hat{\textbf{i}} \times \hat{\textbf{j}} = \hat{\textbf{k}}\).

Упражнение \(\PageIndex{3}\)

Найдите \(\hat{\textbf{j}} \times \hat{\textbf{k}}\) и \(\hat{\textbf{i} } \times \hat{\textbf{k}}\).

Новый взгляд на крутящий момент

Мы определяем крутящий момент (или момент \(M\) силы \(F\) относительно точки \(Q\)) как

\[M = PQ \times F. \nonumber \]

Пример \(\PageIndex{5}\)

Гаечный ключ на 20 дюймов находится под углом 30 градусов к земле. Сила в 40 фунтов, которая поворачивает ключ под углом 45 градусов к ключу. Найдите крутящий момент.

Решение

Ключ можно записать в виде вектора

\[ 20 \cos 30\; \hat{\textbf{i}} + 20 \sin 30 \; \hat{\textbf{j}} = 17,3 \hat{\textbf{i}} + 10 \hat{\textbf{j}} \nonumber \]

и сила как

\[ -40 \cos 75\; \hat{\textbf{i}} — 40 \sin 75 \; \hat{\textbf{j}} = -10,3 \hat{\textbf{i}} — 38,6 \hat{\textbf{j}}\nonumber \]

, следовательно, крутящий момент представляет собой величину их векторного произведения:

\[\begin{vmatrix} \hat{\textbf{i}} & \hat{\textbf{j}} & \hat{\textbf{k}} \\ 17,3 & 10 & 0 \\ -10,3 & -38,6 & 0 \end{vmatrix}\nonumber \]

\[= -564 \text{дюйм-фунт}. \номер \]

Параллелепипеды

Чтобы найти объем параллелепипеда, натянутого на три вектора u , v и w , находим тройное произведение:

\[\text{Объем}= \textbf{u} \cdot ( \textbf{v} \times \textbf{w}). \nonumber \]

Это можно найти, вычислив определитель трех векторов:

\[\begin{vmatrix} u_1 & v_1 & w_1 \\ u_2 & v_2 & w_2 \\ u_3& v_3 & w_3 \end{vmatrix }.\номер \]

Пример \(\PageIndex{6}\)

Найдите объем параллелепипеда, натянутого на векторы

\[\textbf{u} = <1,0,2>, \;\;\; \textbf{v} = <0,2,3>, \;\;\; \textbf{v} = <0,1,3>.\nonumber \]

Решение

Находим

\[\begin{vmatrix} 1 &0 &2 \\ 0 &2 &3 \\ 0 &1 &3 \end{vmatrix} = 3. \nonumber \]

Авторы и авторство

---

Эта страница под названием 1.5: The Dot and Cross Product распространяется по незаявленной лицензии и была создана, изменена и/или курирована Ларри Грином.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Ларри Грин

   Показать страницу TOC

   нет

2. Теги

   1. компоненты
   2. перекрестное произведение
   3. НАПРАВЛЕННЫЕ КОСИНУСЫ
   4. скалярное произведение
   5. выступ

Различие между скалярным произведением и перекрестным произведением.

Ответить

Проверено

174,4 тыс.+ просмотров

Подсказка : Произведение двух векторов может быть двух типов: скалярное произведение и векторное произведение. Выполняя любое из двух действий над двумя векторами, то есть скалярное произведение или векторное произведение, в результате получается скалярная или векторная величина.

Полный пошаговый ответ:
Величины, полностью заданные как по величине, так и по направлению, известны как векторные величины. В то время как величины, которые полностью определяются только величинами, известны как скалярные величины.

Вектор можно умножить, используя два основных типа произведений. Эти продукты являются точечным продуктом и перекрестным продуктом, и они имеют много различий.

Скалярное произведение двух векторов также называется скалярным произведением. Это произведение величины двух векторов и косинуса угла, который они образуют друг с другом.
Перекрестное произведение двух векторов также называется векторным произведением. Это произведение величины двух векторов и синуса угла, который они образуют друг с другом.
Разница между скалярным произведением и векторным произведением двух векторов заключается в том, что результатом скалярного произведения является скалярная величина, тогда как результатом векторного произведения является векторная величина.

Дополнительная информация:
(i) Скалярное произведение: скалярное произведение двух векторов представляет собой произведение их модулей и косинуса угла, образуемого одним вектором над другим. Его также называют внутренним продуктом или проекционным продуктом. Он представлен как:

\[\overrightarrow{A}.\overrightarrow{B}=\left| А \право|\лево| B \right|\cos \theta \]

Результатом является скалярная величина, поэтому она имеет только величину, но не направление.

(ii) Взаимное произведение: Взаимное произведение или векторное произведение двух векторов представляет собой произведение их величин и синуса угла, стягиваемого одним вектором с другим.