Подготовительный курс по математике для начинающих студентов-физиков
Подготовительный курс по математике для начинающих студентов-физиков
9.8 Преобразование произведений векторов
9.8.4 Преобразование произведений векторов
В конце данного курса, мы хотели бы еще проверить, как ведут себя наши векторные произведения при вращениях и отражениях:
Мы уже знаем, что составляющие вектора , которые представляют собой проекции вектора на оси координат , преобразуются при помощи трансляции так же как и сами базисные векторы:
То есть
.
В частности, знаки компонент меняются при отражении относительно начала координат, т.е. преобразовании чётности. Поэтому такие векторы называют полярными векторами.
В качестве первого произведения давайте исследуем скалярное произведение двух полярных векторов и :
,
где
Мы сначала подставили покомпонентное представление для скалярного произведения в новой системе отсчёта с суммированием по
, затем применили закон преобразования для составляющих полярных векторов, использовали соотношение ортогональности матриц преобразования и, в конце, после суммирования по
, получили покомпонентное представление скалярного произведения в первоначальной системе координат.
Таким образом мы показали, что наше скалярное произведение является инвариантным относительно вращений и отражений, а значит, не зря называется скаляром.
Теперь давайте изучим свойства преобразования составляющих
векторного произведения
двух полярных векторов
и
,
где
Здесь мы подставили разложение на составляющие k-ой компоненты векторного произведения в преобразованной системе координат с суммированием по
и
, затем провели преобразование векторных составляющих обоих сомножителей и ввели для последнего символа Леви-Чивиты дополнительный символ Кронекера с суммированием по
. Этот
мы заменили на две прямоугольные матрицы преобразования, а три матрицы
при помощи нашей
формулы вычисления детерминанта
объединили в один детерминант, и в конце векторное произведение снова записали в старой системе координат.
Таким образом, векторное произведение преобразуется как вектор при вращениях. Однако, присутствие детерминанта
дает дополнительный знак минус при отражениях, так что векторное произведение векторов является инвариантом относительно отражений. Такие векторы называются аксиальными векторами; все векторы, выступающие в физике как векторные произведения полярных векторов, являются инвариантными относительно отражений. Все они, как мы видели, связанны с вращательными процессами и обозначают, в отличии от стрелки направления векторов смещения,
Рисунок 9.29: Отражение круга направления вращения и стрелка трансляции у начала координат
|
Задание 9.48: Полярные и аксиальные векторы Распределите следующие примеры физических векторов по их поведению при отражении на две группы — на полярные и аксиальные векторы: |
В качестве последнего примера рассмотрим смешанное произведение трех полярных векторов , и в преобразованной системе координат :
,
где
Мы снова преобразовали составляющие полярных векторов и применили формулу для вычисления детерминанта .
Смешанное произведение векторов предстает при этом в виде скаляра по отношению к поворотам, но не является инвариантным по отношению к отражениям, в результате которых оно меняет знак. Такая величина называется псевдоскаляром.
|
Задание 9.49: Нарушение четности
|
Мы рассмотрели здесь лишь простейшие правила векторной алгебры. На протяжении всей Вашей учебы Вы еще не раз будете иметь дело с векторами. Вы будете изучать векторы как функции скаляра, прежде всего, времени, но также и скаляры и векторы как функции векторов, прежде всего, координаты или импульса — так называемые поля. Вы изучите, как дифференцировать векторы, раскладывать их в ряд Тейлора и интегрировать их различными способами. Все эти векторы будут показывать характерное поведение по отношению к поворотам системы координат и будут различаться относительно отражений на полярные и аксиальные векторы. Рассматривая теорию относительности, Вы будете делать вычисления с векторами, которые имеют четыре составляющие. А рассматривая теорию поля, Вы будете учиться обходиться с бесконечно-мерными векторами. Но базовые структуры, с которыми мы здесь вместе познакомились, всегда останутся неизменными.
На протяжении всей Вашей учебы Вы еще не раз будете иметь дело с векторами. Вы будете изучать векторы как функции скаляра, прежде всего, времени, но также и скаляры и векторы как функции векторов, прежде всего, координаты или импульса — так называемые поля. Вы изучите, как дифференцировать векторы, раскладывать их в ряд Тейлора и интегрировать их различными способами. Все эти векторы будут показывать характерное поведение по отношению к поворотам системы координат и будут различаться относительно отражений на полярные и аксиальные векторы. Рассматривая теорию относительности, Вы будете делать вычисления с векторами, которые имеют четыре составляющие. А рассматривая теорию поля, Вы будете учиться обходиться с бесконечно-мерными векторами. Но базовые структуры, с которыми мы здесь вместе познакомились, всегда останутся неизменными.
В некоторых разделах физики Вы, кроме скаляров и векторов, столкнетесь с тензорами второго ранга, например, рассматривая момент инерции, тензор напряжения или электрический квадрупольный момент.
Дополнительная литература
Скалярное произведение — Wikiwand
- ВведениеСкалярное произведение
- Определение и свойства
- Определение и свойства в евклидовом пространствеВещественные векторыКомплексные векторыСвойстваТеорема косинусов в вещественном пространстве
- Связанные определения
- Вариации и обобщения
- См. также
- Примечания
- Литература
- Ссылки
Скаля́рное произведе́ние (иногда называемое внутренним произведением) — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат. Используется в определении длины векторов и угла между ними.
Используется в определении длины векторов и угла между ними.
- (a,b){\displaystyle (\mathbf {a} ,\mathbf {b} )}
- a⋅b, a→⋅b→{\displaystyle \mathbf {a} \cdot \mathbf {b} ,\ {\vec {a}}\cdot {\vec {b}}} или просто ab{\displaystyle \mathbf {a} \mathbf {b} }
- ⟨a,b⟩{\displaystyle \langle \mathbf {a} ,\mathbf {b} \rangle } и ⟨a|b⟩;{\displaystyle \langle a|b\rangle ;} второе обозначение применяется в квантовой механике для векторов состояния[1].
В простейшем случае, а именно в случае конечномерного вещественного евклидового пространства, иногда используют «геометрическое» определение скалярного произведения ненулевых векторов a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} } как произведения длин этих векторов на косинус угла между ними[2]:
- (a,b)=|a||b|cos(θ).
 {\displaystyle (\mathbf {a} ,\mathbf {b} )=|\mathbf {a} ||\mathbf {b} |\cos(\theta ).}
{\displaystyle (\mathbf {a} ,\mathbf {b} )=|\mathbf {a} ||\mathbf {b} |\cos(\theta ).}
Равносильное определение: скалярное произведение есть произведение длины проекции первого вектора на второй и длины второго вектора (см. рисунок). Если хотя бы один из векторов нулевой, то произведение считается равным нулю[3].
У понятия скалярного произведения существует также большое количество обобщений для различных векторных пространств, то есть для множеств векторов с операциями сложения и умножения на скаляры
Скалярное произведение и его обобщения играют чрезвычайно большую роль в векторной алгебре, теории многообразий, механике и физике. Например, работа силы при механическом перемещении равна скалярному произведению вектора силы на вектор перемещения[5].
Например, работа силы при механическом перемещении равна скалярному произведению вектора силы на вектор перемещения[5].
линейная алгебра — Понимание умножения / скалярного произведения двух чисел / двух векторов
Я думаю, что изучение абстрактной алгебры (вот введение) ответит на некоторые из этих вопросов. Оператор (сложение/умножение/и т. д.) и тип объектов (целые числа/действительные числа/векторы/и т. д.), на которые он действует, объединяются. Вам нужно определить что такое умножение для этого типа объектов. Например:
- Умножение 2 целых чисел может быть представлено повторным добавлением, как вы упомянули
- (Скаляр) Умножение геометрического вектора (стрелка) — это растяжение и сжатие этого вектора. Представьте себе физическое растяжение стрелки без умножения ее компонентов. У вас просто есть инструкция растянуться в 2 раза, и это то, что вы делаете с ручкой и бумагой.
Вы можете придумать любую математическую операцию, которая делает самые сумасшедшие вещи.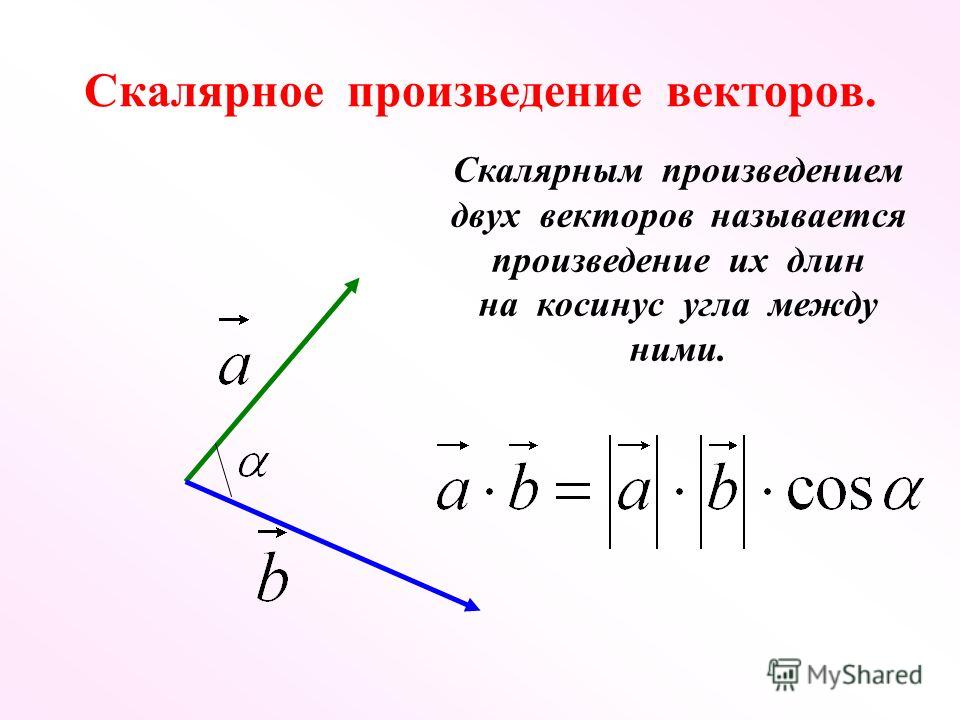 Но большая часть таких операций будет бесполезной. Например. они не помогут найти неизвестное $x$ в уравнении: $a*x=b$ где $*$ равно — ваша новая математическая операция, а $a, x, b$ — ваш новый тип объектов (я не знаю… допустим, это круги — вы умножаете круги). Хотя настоящая математика уже существует, она создает эти структуры и операции таким образом, чтобы они были полезны для какой-то цели.
Но большая часть таких операций будет бесполезной. Например. они не помогут найти неизвестное $x$ в уравнении: $a*x=b$ где $*$ равно — ваша новая математическая операция, а $a, x, b$ — ваш новый тип объектов (я не знаю… допустим, это круги — вы умножаете круги). Хотя настоящая математика уже существует, она создает эти структуры и операции таким образом, чтобы они были полезны для какой-то цели.
Скалярный продукт не является умножением в типичном для смысле . Например. вы не можете решить $a\cdot x=b$. У этой операции совершенно другая цель — она полезна по разным причинам. Например. можно использовать:
- Чтобы определить длину вектора: $|a|=\sqrt{a\cdot a}$
- Чтобы найти единичный вектор (длины 1), указывающий в том же направлении: $\frac{a}{|a|}$
- Чтобы узнать, перпендикулярны ли векторы (когда $a\cdot b=0$)
- Чтобы найти проекции одного вектора на другой ($b\cdot \frac{a}{|a|}$)
Именно поэтому точечные продукты полезны, а не потому, что они могут, например. решать уравнения. Кстати, всю эту математику можно обобщить. Обратите внимание, что, например. такие функции, как полиномы, также имеют свойства, схожие с геометрическими векторами: их можно умножать на скаляр, можно их складывать. Но тогда — какой длины будет такой «вектор»? Что такое точечный продукт? Чтобы ответить на эти вопросы, вводится список требований к таким произведениям, взятым из того, что мы только что видели, например, длина единичного вектора $\frac{a}{|a|}$ равна 1 и другие. Итак, если бы мы могли придумать новую операцию, которая подчиняется этим свойствам, мы могли бы использовать ее так же, как мы использовали скалярные произведения.
решать уравнения. Кстати, всю эту математику можно обобщить. Обратите внимание, что, например. такие функции, как полиномы, также имеют свойства, схожие с геометрическими векторами: их можно умножать на скаляр, можно их складывать. Но тогда — какой длины будет такой «вектор»? Что такое точечный продукт? Чтобы ответить на эти вопросы, вводится список требований к таким произведениям, взятым из того, что мы только что видели, например, длина единичного вектора $\frac{a}{|a|}$ равна 1 и другие. Итак, если бы мы могли придумать новую операцию, которая подчиняется этим свойствам, мы могли бы использовать ее так же, как мы использовали скалярные произведения.
Такие продукты теперь называются Внутренние продукты , а Dot Product — лишь одна из реализаций. Например, для функций вы можете определить другую реализацию, например $\int{f(x)f(x)dx}$, которая будет похожа на $a \cdot a$. Для внутреннего продукта можно определить все виды реализации, но они все равно должны подчиняться этим ролям. И теперь мы можем определить, что такое длина и что значит быть перпендикулярным для функций и других объектов, которые подчиняются аналогичным правилам. И мы можем повторно использовать всю математику из векторов с этими объектами — при таком использовании эти объекты и их соответствующие операции называются абстрактными векторами. 92$ (площадь апельсинового поля) имеет смысл — тогда идите и делайте операцию.
И теперь мы можем определить, что такое длина и что значит быть перпендикулярным для функций и других объектов, которые подчиняются аналогичным правилам. И мы можем повторно использовать всю математику из векторов с этими объектами — при таком использовании эти объекты и их соответствующие операции называются абстрактными векторами. 92$ (площадь апельсинового поля) имеет смысл — тогда идите и делайте операцию.
Если вы используете апельсины в качестве одного из компонентов вашего вектора, т.е. тогда $|o|=\sqrt{o \cdot o}$ по-прежнему является длиной вектора, поэтому он дает вам количество апельсинов в нем (которое вы уже знали из компонента вектора).
Векторные продукты
Векторные продуктыВекторные скалярные произведения и перекрестные произведения
Предыдущий материал познакомил вас с векторами и некоторыми манипуляциями с ними в виде сложения и вычитания векторов. В этом материале речь пойдет о произведении двух векторов. В частности, мы рассмотрим векторное скалярное произведение и векторное перекрестное произведение. Мы будем использовать маленькую полужирную букву с линией сверху для обозначения вектора. Скаляры не будут выделены жирным шрифтом и не будут иметь линии сверху.
Мы будем использовать маленькую полужирную букву с линией сверху для обозначения вектора. Скаляры не будут выделены жирным шрифтом и не будут иметь линии сверху.
Скалярные произведения
Скалярное произведение двух векторов u = (u1, u2) и v = (v1, v2) определяется как u • v = u1*v1 + u2*v2. Я использовал векторы с двумя компонентами (x, y), но сказанное здесь также применимо к векторам с тремя компонентами (x, y и z). Если мы вычислим скалярное произведение двух векторов, перпендикулярных друг другу, то скалярное произведение будет равно нулю. Когда мы берем скалярное произведение двух векторов, результатом является скаляр. Для точечных произведений порядок не имеет значения. u • v = v • u . Вот пример скалярного произведения. Инструмент, расположенный ниже, можно использовать для расчета результатов с использованием других векторов.- Пример — скалярный продукт
- г = (2, -3)
- с = (4 ,8)
- r • с = 2*4 + (-3)*8 = 8 — 24 = -16
Перекрестные произведения
Перекрестное произведение двух векторов u = (u1, u2, u3) и v = (v1, v2, v3) определяется как u x v = (u2v3 — u3v2, u3v1 — u1v3, u1v2 — u2v1).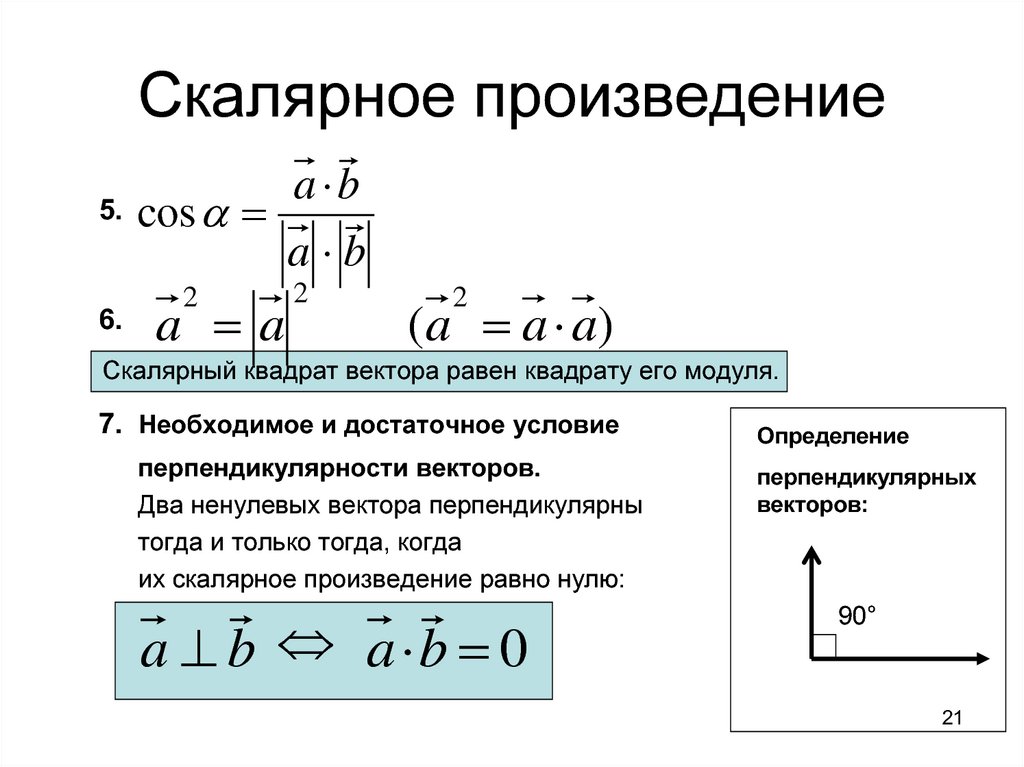



 {\displaystyle (\mathbf {a} ,\mathbf {b} )=|\mathbf {a} ||\mathbf {b} |\cos(\theta ).}
{\displaystyle (\mathbf {a} ,\mathbf {b} )=|\mathbf {a} ||\mathbf {b} |\cos(\theta ).}