Напомним основные свойства скалярного произведения.
1. Симметричность, $(\textbf {u},\textbf {v})=(\textbf {v},\textbf {u})$ для любых векторов $\textbf {u},\textbf {v}$.
2. Линейность по обоим сомножителям: $(\lambda \textbf {u},\textbf {v})=\lambda (\textbf {u},\textbf {v})$,
$(\textbf {u}_1+\textbf {u}_2,\textbf {v})=(\textbf {u}_1,\textbf {v})+(\textbf {u}_2,\textbf {v})$ для любых чисел $\lambda$ и любых векторов
$\textbf {u}, \,\textbf {v},\,\textbf {u}_1, \, \textbf {u}_1$, то же для второго сомножителя.
3. $ (\textbf {u},\textbf {u}) \geq 0$, причем $ (\textbf {u},\textbf {u}) = 0$ $ \leftrightarrow$ $ \textbf {u}=\textbf {0} $.
4. Неравенство Коши-Буняковского: $ |( \textbf {u},\textbf {v})|\leq |\textbf {u}|\cdot |\textbf {v}|$ для любых $\textbf {u},\,\textbf {v}$.
 
Пример.
Вычислим скалярное произведение двух векторов $\textbf {a}=(2,\,3,\,4)^T,\, \textbf {b}=(-1,\,1,\,-1)^T$.
Решение.
Найдем скалярное произведение этих векторов: $(\textbf {a},\textbf {b}) = 4m + 3m — 28 = 7m — 28$. Поскольку эти вектора перпендикулярны, их скалярное произведение равно нулю, так что $7m — 28 = 0$. Отсюда имеем $m=4$.
Задача 2.
Какой угол образуют единичные вектора $\textbf {p}$ и $\textbf {q}$, если известно, что $\textbf {a}= \textbf {p} + 2\textbf {q} $ и $ \textbf {b} =5\textbf {p} — 4\textbf {q}$ взаимно перпендикулярны?
Решение.
Найдем скалярное произведение $\textbf {a}$ и $\textbf {b}$, воспользовавшись свойствами
скалярного произведения:
\[
(\textbf {a},\textbf {b}) = (\textbf {p} + 2\textbf {q}, 5\textbf {p} — 4\textbf {q}) = (\textbf {p},5\textbf {p}) + (2\textbf {q},5\textbf {p}) +
(\textbf {p},- 4\textbf {q}) + (2\textbf {q},- 4\textbf {q}) =
\]
\[
= 5(\textbf {p},\textbf {p}) + 6(\textbf {p},\textbf {q}) — 8 (\textbf {q}, \textbf {q}) = 5 |\textbf{p}|^2 + 6 |\textbf{p}| |\textbf{q}| cos(\textbf{p},\textbf{q}) — 8 |\textbf{q}|^2 .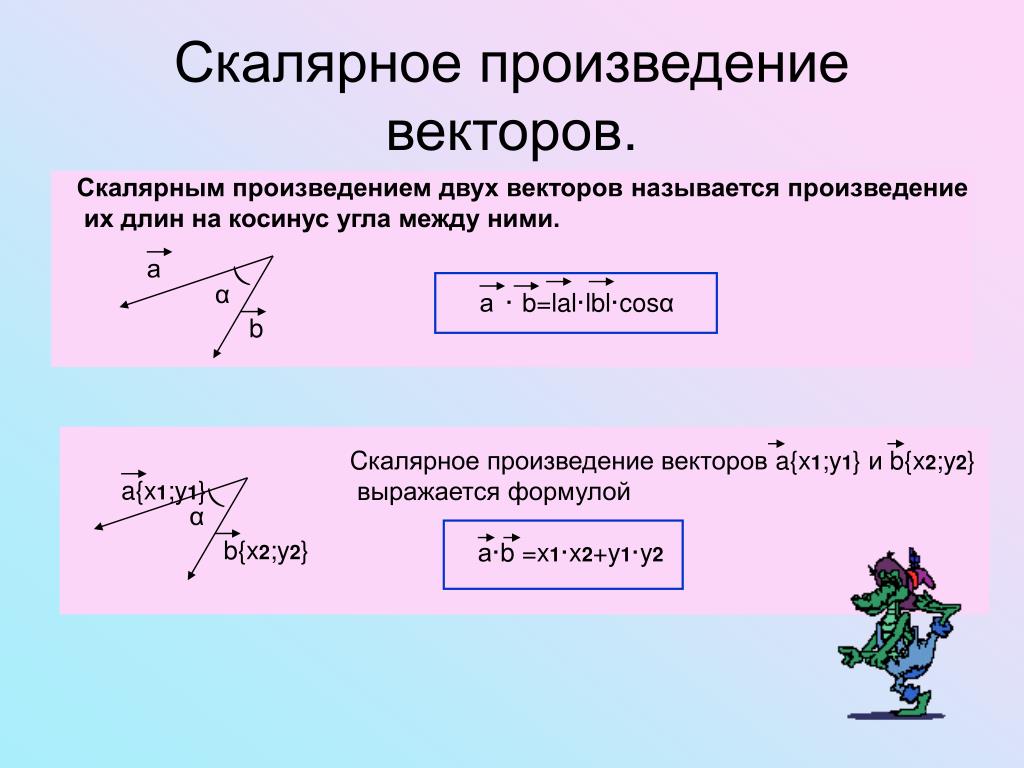 \]
Учитывая, что $\textbf {a}$ и $\textbf {b}$ перпендикулярны, а вектора $\textbf {p}$ и
$\textbf {q}$ имеют единичную длину, из последнего равенства имеем:
\[
5 + 6 cos(\textbf{p},\textbf{q}) — 8 = 6 cos(\textbf{p},\textbf{q})-3 = 0
\]
Отсюда получим $cos(\textbf{p},\textbf{q}) =1/2$, так что угол между векторами
$\textbf {p}$ и $\textbf {q}$ составляет 60 градусов.
\]
Учитывая, что $\textbf {a}$ и $\textbf {b}$ перпендикулярны, а вектора $\textbf {p}$ и
$\textbf {q}$ имеют единичную длину, из последнего равенства имеем:
\[
5 + 6 cos(\textbf{p},\textbf{q}) — 8 = 6 cos(\textbf{p},\textbf{q})-3 = 0
\]
Отсюда получим $cos(\textbf{p},\textbf{q}) =1/2$, так что угол между векторами
$\textbf {p}$ и $\textbf {q}$ составляет 60 градусов.
 
Задачи.
1. Зная, что $|\textbf {a}| =2$, $|\textbf {b}| = 5$ и угол между $\textbf {a}$ и $\textbf {b}$ равен 120 градусов, определить, при каком значении коэффициента m векторы $\textbf {p} = m\textbf {a} + 17\textbf {b}$ и $\textbf {q} = 3\textbf {a} — \textbf {b}$ окажутся взаимно перпендикулярными.
2. Вычислить длину диагоналей параллелограмма, построенного на векторах $\textbf {A}= 5\textbf {p} + 2\textbf {q} $ и $ \textbf {B} =\textbf {p} — 3\textbf {q}$, если известно, что $|\textbf {p}| = 21,5$, $|\textbf {q}| = 3$ и угол между $\textbf {p}$ и $\textbf {q}$ равен 45 градусов. T$. Вычислить вектор $\textbf{x}$ из условий $(\textbf{x},\textbf{a})=10, \,(\textbf{x},\textbf{b})=22,\, (\textbf{x},\textbf{c})=-40$.
T$. Вычислить вектор $\textbf{x}$ из условий $(\textbf{x},\textbf{a})=10, \,(\textbf{x},\textbf{b})=22,\, (\textbf{x},\textbf{c})=-40$.
5. Найти единичный вектор, перпендикулярный векторам $\textbf{a}=3\textbf{i}-\textbf{j}+2\textbf{k}, \, \textbf{b}=-\textbf{i}+3\textbf{j}-\textbf{k}$.  
16.3: Дополнительный продукт — Инженерные тексты LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 55333
- Jacob Moore & Contributors
- Pennsylvania State University Mont Alto via Mechanics Map
Скалярное произведение (также иногда называемое скалярным произведением) — это математическая операция, которая может выполняться над любыми двумя векторами с одинаковым количеством элементов. Результатом является скалярное число, равное величине первого вектора, умноженной на величину второго вектора и умноженной на косинус угла между двумя векторами.
Результатом является скалярное число, равное величине первого вектора, умноженной на величину второго вектора и умноженной на косинус угла между двумя векторами.
В инженерной механике скалярное произведение используется почти исключительно со вторым вектором, равным 9.0032 единичный вектор . Если второй вектор в операции скалярного произведения является единичным вектором (таким образом, имеет величину 1), тогда скалярное произведение будет представлять величину первого вектора в направлении единичного вектора. В этом отношении скалярное произведение полезно для определения компонента данного вектора в любом заданном направлении, где направление задается в терминах единичного вектора.
Рисунок \(\PageIndex{1}\): Скалярное произведение вектора на единичный вектор даст вам величину первого вектора в направлении единичного вектора.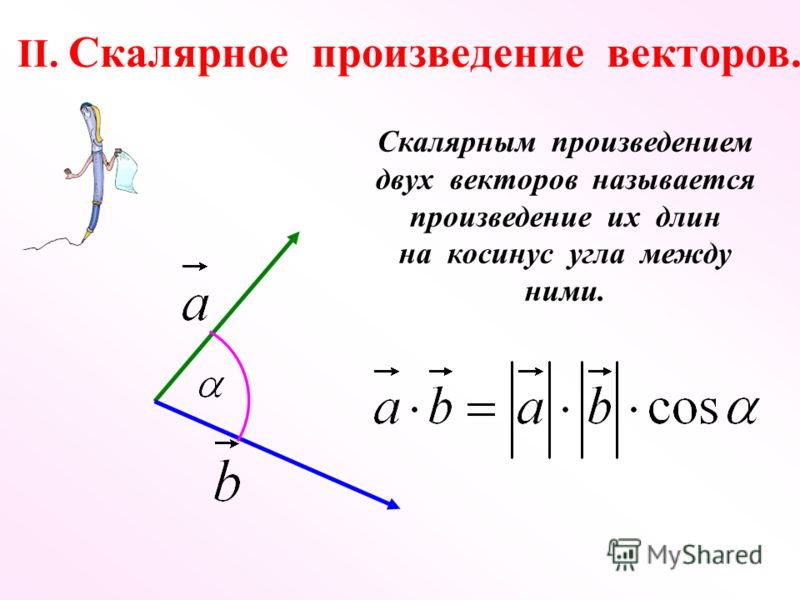 Для этого метода мы разбиваем каждый вектор на компоненты и берем сумму каждого набора компонентов, умноженных вместе, как показано в уравнении ниже.
Для этого метода мы разбиваем каждый вектор на компоненты и берем сумму каждого набора компонентов, умноженных вместе, как показано в уравнении ниже.\[ \vec{A} \cdot \vec{B} = (A_x * B_x) + (A_y * B_y) + (A_z * B_z) \]
Наконец, как и во многих векторных операциях, истинная сила скалярного произведения заключается в том, что компьютеры могут вычислять их очень быстро. И MATLAB, и калькулятор Wolfram Alpha Vector Operation Calculator могут вычислять скалярные произведения за вас.
Пример \(\PageIndex{1}\)
Найдите скалярное произведение вектора силы \(\vec{A}\) на заданный единичный вектор \(\hat{B}\).
Рисунок \(\PageIndex{2}\): схема проблемы для примера \(\PageIndex{1}\). Вектор силы и единичный вектор исходят из начала двумерной декартовой системы координат.
- Решение:
- Видео \(\PageIndex{2}\): рабочее решение примера проблемы \(\PageIndex{1}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/JJ3aXtIZwZ0.
Пример \(\PageIndex{2}\)
Рассчитайте скалярное произведение \(\vec{A}\) на \(\vec{B}\) вручную.
Рисунок \(\PageIndex{3}\): схема проблемы для примера \(\PageIndex{2}\).- Решение:
- Видео \(\PageIndex{3}\): рабочее решение примера проблемы \(\PageIndex{2}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/NuuYcDNeja4.
Пример \(\PageIndex{3}\)
Вычислить скалярное произведение \(\vec{A}\) на \(\vec{B}\) с помощью MATLAB.
- Решение:
- Видео \(\PageIndex{4}\): рабочее решение примера проблемы \(\PageIndex{3}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/B8PKJtL63C0.
Пример \(\PageIndex{4}\)
Рассчитайте скалярное произведение \(\vec{A}\) на \(\vec{B}\) с помощью калькулятора векторных операций Wolfram.
Рисунок \(\PageIndex{5}\): схема проблемы для примера \(\PageIndex{4}\).- Решение:
- Видео \(\PageIndex{5}\): рабочее решение примера проблемы \(\PageIndex{4}\), предоставленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/2FZSXFASFiQ.

Эта страница под названием 16.3: Dot Product распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Джейкобом Муром и участниками (Mechanics Map) с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Джейкоб Мур и авторы
- Лицензия
- CC BY-SA
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- скалярное произведение
- источник@http://mechanicsmap.
 psu.edu
psu.edu - единичных вектора
Скалярные произведения и двойственность — Примечания Лекса
Это ноты из Точечных произведений и двойственности | Глава 9, Сущность линейной алгебры) от 3Blue1Brown.
Обычно мы преподаем скалярное произведение во введении в курс линейной алгебры.
Однако мы можем полностью понять роль скалярного произведения, если сначала поймем матричные преобразования.
Типичный способ, которым мы вводим скалярное произведение, состоит в том, чтобы выстроить компоненты в 2 вектора с точными размерами и кратными значениями, а затем сложить результаты.
Это вычисление имеет геометрическую интерпретацию.
Для скалярного произведения v⃗⋅w⃗\vec{v} \cdot \vec{w}v⋅w мы начинаем с рисования линии через w⃗\vec{w}w, проходящей через начало координат. Затем проведите линию от кончика v⃗\vec{v}v до первой линии, которую вы нарисовали.
Скалярное произведение будет равно длине вектора от начала координат до конца второй линии, умноженной на длину w⃗\vec{w}w (см. обложку).
Примечание для моего понимания: полезно понимать взаимосвязь между формулой скалярного произведения: v⃗⋅w⃗=∣v∣∣w∣cosθ\vec{v} \cdot \vec{w} = |v| |ш| \cos\thetav⋅w=∣v∣∣w∣cosθ и к чему стремится 3Blue1Brown. Скалярное произведение будет равно 0, когда углы перпендикулярны, потому что θ\thetaθ равно 0. В визуализации v⃗\vec{v}v не имеет проекции на w⃗\vec{w}w, поэтому мы умножаем на 0,
Несмотря на то, что это кажется асимметричным, порядок не имеет значения: вы можете начать с прямой через w⃗\vec{w}w и получить те же результаты.
Интуитивное объяснение того, почему порядок не имеет значения:
- Если v⃗\vec{v}v и w⃗\vec{w}w имеют одинаковую длину, мы проводим между ними линию симметрии.
- Затем мы проецируем w⃗\vec{w}w на v⃗\vec{v}v, это будет идентично защите v⃗\vec{v}v на w⃗\vec{w}w.
- Теперь, если мы увеличим вектор v⃗\vec{v}v в 2 раза, симметрия нарушится.
 Однако мы можем видеть, что если мы спроецируем w⃗\vec{w}w на v⃗\vec{v}v, длина проекции www не изменится, но изменится вектор, на который мы проецируем.
Однако мы можем видеть, что если мы спроецируем w⃗\vec{w}w на v⃗\vec{v}v, длина проекции www не изменится, но изменится вектор, на который мы проецируем.
С другой стороны, если мы проецируем v⃗\vec{v}v на w⃗\vec{w}w, мы удваиваем длину проекции, что дает тот же эффект.
Можно задать один вопрос: почему процесс сопоставления координат, перемножения пар и сложения имеет какое-то отношение к проекции? Чтобы понять это, мы должны раскрыть то, что называется двойственностью .
Но сначала нам нужно понять линейные преобразования из нескольких измерений в одно измерение: числовую прямую.
Линейные преобразования обладают формальными свойствами, которые делают их линейными:
L(v⃗+w⃗)=L(v⃗)+L(w⃗)L(\vec{v} + \vec{w}) = L(\vec{ v}) + L(\vec{w})L(v+w)=L(v)+L(w)
L(cv⃗)=cL(v⃗)L(c\vec{v}) = cL (\vec{v})L(cv)=cL(v)
Но видео будет посвящено визуальным свойствам, что эквивалентно формальным вещам. Интуиция такова, что если у вас есть диагональная линия точек в двумерном пространстве, точки останутся равномерно расположенными на числовой линии после линейного преобразования.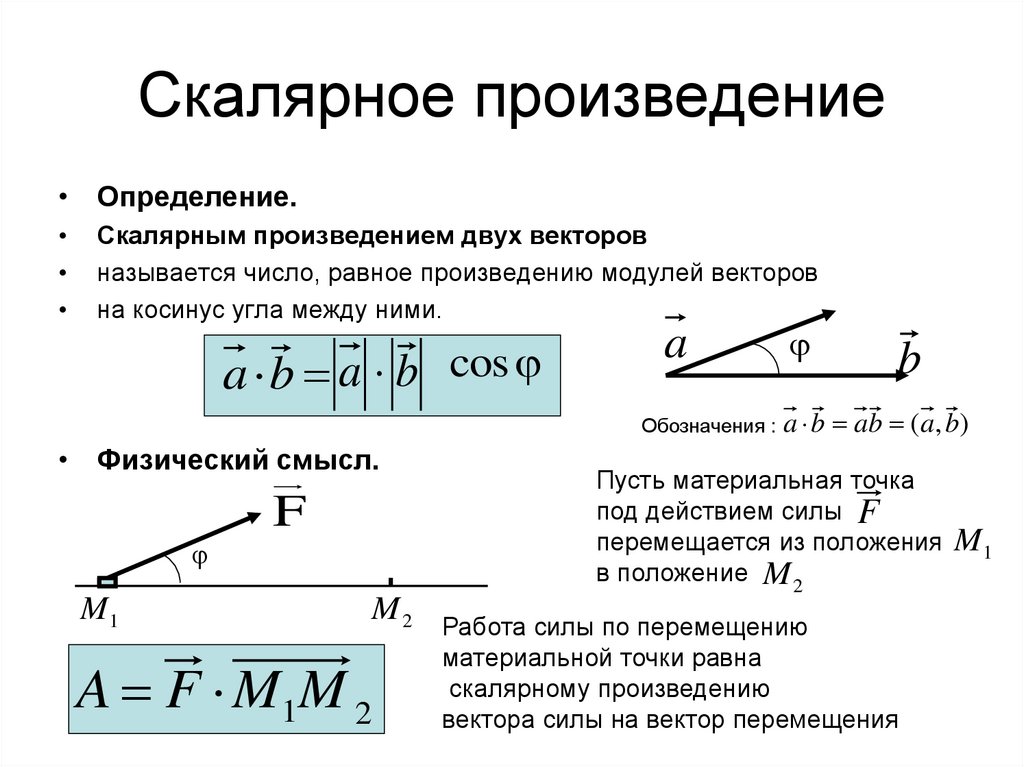



 psu.edu
psu.edu Однако мы можем видеть, что если мы спроецируем w⃗\vec{w}w на v⃗\vec{v}v, длина проекции www не изменится, но изменится вектор, на который мы проецируем.
Однако мы можем видеть, что если мы спроецируем w⃗\vec{w}w на v⃗\vec{v}v, длина проекции www не изменится, но изменится вектор, на который мы проецируем.