(adsbygoogle = window.adsbygoogle || []).push({});

Выбор двоичной системы для применения в вычислительной технике объясняется тем, что электронные элементы — триггеры, из которых состоят микросхемы ЭВМ, могут находиться только в двух рабочих состояниях.

С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе. Телеграфист, используя только два символа этой азбуки — точки и тире, может передать практически любой текст.

Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост.

Ниже приведена таблица соответствия чисел, записанных в разных системах.

 

Таблица 3. Соответствие чисел, записанных в различных системах счисления

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
1	001	1	1
2	010	2	2
3	011	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10

 

Правила перевода чисел из одной системы счисления в другую

 

Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.

1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней двойки:

 

Таблица 4. Степени числа 2

 

n (степень)	0	1	2	3	4	5	6	7	8	9	10
	1	2	4	8	16	32	64	128	256	512	1024

 

 

Пример .  Число  перевести в десятичную систему счисления.

2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:

 

При переводе удобно пользоваться таблицей степеней восьмерки:

Таблица 5. Степени числа 8

 

n (степень)	0	1	2	3	4	5	6
	1	8	64	512	4096	32768	262144

 

 

Пример .  Число  перевести в десятичную систему счисления.

3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней числа 16:

Таблица 6. Степени числа 16

 

n (степень)	0	1	2	3	4	5	6
	1	16	256	4096	65536	1048576	16777216

 

 

Пример .  Число  перевести в десятичную систему счисления.

4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.

Пример. Число  перевести в двоичную систему счисления.

5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

Пример. Число перевести в восьмеричную систему счисления.

 

6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

Пример. Число перевести в шестнадцатеричную систему счисления.

 

7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).

Пример. Число перевести в восьмеричную систему счисления.

8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).

Пример. Число  перевести в шестнадцатеричную систему счисления.

9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.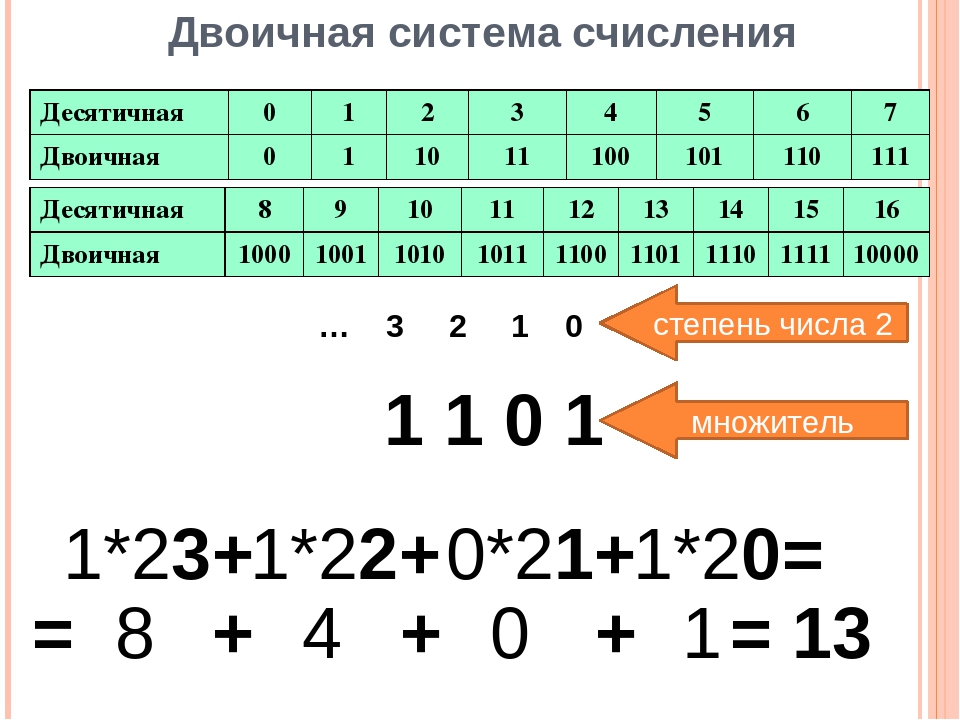

Пример. Число  перевести в двоичную систему счисления.

10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.

Пример. Число  перевести в двоичную систему счисления.

11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.

Пример 1. Число  перевести в восьмеричную систему счисления.

Пример 2. Число  перевести в шестнадцатеричную систему счисления.

Перевод чисел из одной системы счисления в другую

Цели урока:

• повторить изученный материал по теме система счисления ;
• научится переводить число из десятичной системы в любую другую позиционную систему счисления и наоборот;
• освоить принципы перевода чисел из одной системы в другую;
• развивать логическое мышление.

Ход урока

Вначале урока краткое повторение и проверка домашнего задания..

Вопросы:

— В каком виде представлена числовая информация в памяти компьютера?

— Для чего используются системы счисления?

— Какие виды систем счисления вы знаете? Привести свои примеры.

— Чем отличаются позиционные системы от непозиционных?.

Цель нашего урока научится переводить число из десятичной системы в любую другую позиционную систему счисления и наоборот. Но в начале мы рассмотрим, как можно

представить любое целое неотрицательное чисело:

В позиционных системах значение записи целого числа определяется по следующему правилу: пусть a _na _n-1a _n-2…a ₁a ₀ — запись числа A, а _i – цифры, тогда

A = a n·pn+a n-1·pn-1 +a n-2·pn-2+. ..+a 1·p1+ a0·p0        (1),

где p — целое число большее 1, которое называется основанием системы счисления

 Для того, чтобы при заданном p любое неотрицательное целое число можно было бы   записать по формуле (1) и притом единственным образом, числовые значения различных цифр должны быть различными целыми числами, принадлежащими отрезку от 0 до p-1.

Пример:

1) Десятичная система

p = 10

цифры: 0,1,2,3,4,5,6,7,8,9

число 5735 = 5·10³+7·10²+3·10¹+8·10⁰

2) Троичная система

p = 3

цифры: 0,1,2

число 201₃ = 2·3²+0·3¹+1·3⁰

Замечание: нижним индексом в записи числа обозначается основание системы счисления, в которой записано число. Для десятичной системы счисления индекс можно не писать.

Представление отрицательных и дробных чисел:

Во всех позиционных системах для записи отрицательных чисел так же как и в десятичной системе используется знак ‘–‘.  Для отделения целой части числа от дробной используется запятая. Значение записи a _na _n-1a _n-2…a ₁a ₀, a _-1 a _-2…a _m-2 a _m-1a _m числа A определяется по формуле, являющейся обобщением формулы (1):

A = an·pn+a n-1·p n-1+a n-2·p n-2+…+a1·p1+a0·p0+a-1·p-1+a -2·p-2+…+am-2·p–(m–2)+am–1·p–(m–1)+amp–m     (2),

Пример:

75,6 = 7·10¹+5·10⁰+6·10^–1

 –2,314₅ = –(2·5⁰+3·5^–1+1·5^–2+4·5^–3)

Перевод чисел из произвольной системы счисления в десятичную:

Следует понимать, что при переводе числа из одной системы счисления в другую количественное значение числа не изменяется, а меняется только форма записи числа, так же как при переводе названия числа, например, с русского языка на английский.

Перевод чисел из произвольной системы счисления в десятичную выполняется непосредственным вычислением по формуле (1) для целых и формуле (2) для дробных чисел.

Перевод чисел из десятичной системы счисления в произвольную.

Перевести число из десятичной системы в систему с основанием p – значит найти коэффициенты в формуле (2). Иногда это легко сделать простым подбором. Например, пусть нужно перевести число 23,5 в восьмеричную систему. Нетрудно заметить, что 23,5 = 16+7+0,5 = 2·8+7+4/8 = 2·8¹+7·8⁰+4·8^–1 =27,48. Понятно, что не всегда ответ столь очевиден. В общем случае применяется способ перевода отдельно  целой и дробной частей числа.  

Для перевода целых чисел применяется следующий алгоритм (полученный на основании формулы (1)):

1. Найдем частное и остаток от деления числа на p. Остаток  будет очередной цифрой ai (j=0,1,2 …) записи числа в новой системе счисления.

2. Если частное равно нулю, то перевод числа закончен, иначе применяем к частному пункт 1.

Замечание 1. Цифры ai в записи числа нумеруются справа налево.

Замечание 2. Если p>10, то необходимо ввести обозначения для цифр с числовыми значениями, большими или равными 10.

Пример:

Перевести число 165 в семеричную систему счисления.

165:7 = 23 (остаток 4) => a₀ = 4

23:7 = 3 (остаток 2) => a₁ = 2

3:7 = 0 (остаток 3) => a₂ = 3

Выпишем результат: a₂a₁a₀, т.е. 3247.

Выполнив проверку по формуле (1), убедимся в правильности перевода:

3247=3·7²+2·7¹+4·7⁰=3·49+2·7+4 = 147+14+4 = 165.

Для перевода дробных частей чисел применяется алгоритм, полученный на основании формулы (2):

1. Умножим дробную часть числа на p.

2. Целая часть результата будет очередной цифрой am (m = –1,–2, –3 …) записи  числа в новой системе счисления. Если дробная часть результата равна нулю, то перевод числа закончен, иначе применяем к ней пункт 1.

Замечание 1.  Цифры a_m в записи числа располагаются слева направо в порядке возрастания абсолютного значения m.

Замечание 2.  Обычно количество дробных разрядов в новой записи числа ограничивается заранее. Это позволяет выполнить приближенный перевод с заданной точностью. В случае бесконечных дробей такое ограничение обеспечивает конечность алгоритма.

Пример 1:

Перевести число 0,625 в двоичную систему счисления.

 0,625·2 = 1,25 (целая часть 1) => a_-1 =1

0,25·2  = 0,5 (целая часть 0) => a-₂ = 0

0,5·2 = 1,00 (целая часть 1) => a-₃ = 1

Итак, 0,62510 = 0,1012

Выполнив проверку по формуле (2), убедимся в правильности перевода:

0,1012=1·2^-1+0·2-²+1·2^-3=1/2+1/8 = 0,5+0,125 = 0,625.

 Пример 2:

Перевести число 0,165 в четверичную систему счисления, ограничившись четырьмя четверичными разрядами.

0,165·4 = 0,66 (целая часть 0) => a_-1=0

0,66·4  = 2,64 (целая часть 2) => a_-2= 2

0,64·4 = 2,56 (целая часть 2) => a_-3= 2

0,56·4 = 2,24 (целая часть 2) => a_-4= 2

Итак, 0,16510 ” 0,02224

Выполним обратный перевод, чтобы убедиться, что абсолютная погрешность не превышает 4–4:

0,02224 = 0·4^-1+2·4^-2+2·4^-3+2·4^-4= 2/16+2/64+2/256 = 1/8+1/32+1/128 = 21/128 = 0,1640625

|0,1640625–0,165| = 0,00094 < 4–4 = 0,00390625

Перевод чисел из одной произвольной системы в другую

В этом случае сначала следует выполнить перевод числа в десятичную систему, а затем из десятичной в требуемую.

Особым способом выполняется перевод чисел для систем с кратными основаниями.

Пусть p и q – основания двух систем счисления. Будем называть эти системы системами счисления с кратными основаниями, если p = qn или q = pn, где n – натуральное число. Так, например, системы счисления с основаниями 2 и 8 являются системами счисления с кратными основаниями.

Пусть p = qn и требуется перевести число из системы счисления с основанием q в систему счисления с основанием p.  Разобьем целую и дробную части записи числа на группы по n последовательно записанных цифр влево и вправо от запятой. Если количество цифр в записи целой части  числа не кратно n, то надо дописать слева соответствующее количество нулей. Если количество цифр в записи дробной части  числа не кратно n, то нули дописываются справа. Каждая такая группа цифр числа в старой системе счисления будет соответствовать одной цифре числа в новой системе счисления.

Пример:

Переведем 1100001,111₂  в четверичную систему счисления.

Дописав нули и выделив пары цифр, получим 01100001,11102.

Теперь выполним перевод отдельно каждой пары цифр, пользуясь пунктом Перевод чисел из одной   произвольной системы в другую.

01₂=1₁₀=1₄

10₂=2₁₀=2₄

00₂=0₁₀=0₄

01₂=1₁₀=1₄

11₂=3₁₀=3₄

10₂=2₁₀=2₄

Итак,  1100001,1112 = 01100001,11102 = 1201,324.

Пусть теперь требуется выполнить перевод из системы с большим основанием q, в систему с меньшим основанием p, т.е. q = p_n. В этом случае одной цифре числа в старой системе счисления соответствует n цифр числа в новой системе счисления.

Пример: Выполним проверку предыдущего перевода числа.

1201,324 = 1100001,11102=1100001,1112

В шестнадцатеричной системе есть цифры с числовыми значениями 10,11,12, 13,14,15. Для их обозначения используют первые шесть  букв латинского алфавита A, B, C, D, E, F.

Приведем таблицу чисел от 0 до 16, записанных в системах счисления с основаниями 10, 2, 8 и 16.

Число в десятичной системе счисления	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
В восьмеричной	0	1	2	3	4	5	6	7	10	11	12	13	14	15	16	17	20
В двоичной	0	1	10	11	100	101	110	111	1000	1001	1010	1011	1100	1101	1110	1111	10000
В шестнадцатеричной	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10

 Для записи шестнадцатеричных цифр можно использовать также строчные латинские буквы a-f.

Пример: Переведем число 110101001010101010100,11₂ в шестнадцатеричную систему счисления.

Воспользуемся кратностью оснований систем счисления (16=2⁴). Сгруппируем цифры по четыре, дописав, слева и справа  нужное количество нулей

000110101001010101010100,1100₂

и, сверяясь с  таблицей, получим: 1A9554,C₁₆

Вывод:

В какой системе счисления лучше записывать числа – это вопрос удобства и традиций. С технической точки зрения, в ЭВМ удобно использовать двоичную систему, так как в ней для записи числа используются только  две цифры 0 и 1, которые можно представить двумя легко различимыми состояниями “нет сигнала ” и “есть сигнал”.

А человеку, напротив, неудобно иметь дело с двоичными записями чисел из-за того, что они более длинные, чем десятичные и в них много повторяющихся цифр. Поэтому, при необходимости работать с машинными представлениями чисел используют восьмеричную или шестнадцатеричную системы счисления. Основания этих систем – целые степени двойки, и поэтому числа легко переводятся из этих систем в двоичную и обратно.

Записываем задание на дом:

а) Запишите дату рождения всех членов вашей семьи в различных системах счисления.

б) Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:

а) 1001111110111,011₂ ;

б) 1110101011,1011101₂

Страница не найдена | Кафедра физики твердого тела ПетрГУ

หน้าหลัก

http://rtlabs.nitk.ac.in/ http://www.ei.ksue.edu.ua/ http://www.unajma.edu.pe/ http://www.drbrambedkarcollege.ac.in/ https://esperanza.eastern.edu/ https://www.hsri.or.th/ https://www.agrft.uni-lj.si/ http://www4.fe.usp.br/ https://www.cnba.uba.ar/

Home

bak hocam 2yildir kullandigim siteye gelip kod ekliyorsun not yazip kodlarini siliyorum (insan olan utanir kusura bakma hocam diyip giderdi) kendine dusmanmi ariyorsun? belliki sen disli birine denk gelmemissin hayatin boyunca ama ben cok ugrastim cokta denk geldim bu sekilde tanimadigin birini tehtit etmen ya deli oldugunu gosterir yada tecrubesizligini sen bana isimi ogretecegine once baskalarina ait olan sitelere girmemeyi ogren ondan sonra bana isimi ogretirsin ben cok takintili bir adamim beni kotu bir insan olmaya zorlama rica ediyorum bak lutfen birbirimizi uzmeyelim emin ol bu site felan umrumdami saniyorsun? olay tamamen prensip meselesi sen benim yatakodama gelip beraber yatacagiz diyorsun oyle bir olay yok isine bak oldu 10 kisi daha cagir 500 kod eklesin herkes yorumbacklink isimi yapiyorsun? sacmalamissin daha fazla beni muatap etme kendinle yaptigin terbiyesizligin farkina var illa darbe yiyincemi aklin basina gelecek anlamiyorum ki o kadar yaziyorum ki birbirimize kotuluk yapmayalim kalp kirmayalim birbirimizi uzmeyelim sana daha once boyle notlar yazan bir linkci gordun mu Allah askina ben bazen goruyorum ana baci duymadigim kufurler yaziyor adamlar birbirine sen benim gibi bir insani uzuyorsun ama lutfen. . 8yildir ben kimseyle ortak site kullanmadim babam gelse onunlada kullanmam en hassas oldugum konudur bu bir daha kod eklememeni siddetle tavsiye ediyorum yoksa farkli seyler olur ve kendine nur topu gibi manyak bir dusman edinirsin bos yere bu polemigi uzatiyorsun haksiz olan sensin kod disinde birsey yazmak istersen yazabilirsin ama rica ediyorum isi inada bindirme senden ERDEMLİ DÜRÜST VE OLGUN bir davranis bekliyorum beni anladigini umuyorum ve tekrar inşAllah kod eklemeyecegini umuyorum olumlu olumsuz notunu buraya yazablirsin bende bir daha bu siteyi kullanmiyacagim sanada kullandirmam tabiki is site isi degil prensip isi.. ihtiyacin olabilir site sayin azdir bunlar dogal seyler ben gerekirse kendim eklerim senin kodlarini oyle bir durumda kendi kodlarimida silerim sadece senin olur ama o son not garip bir insan oldugunu dusunduruyor bana ve inan ugrasacak vaktim de kafamda yok kendine sardirma hepimiz ekmek davasindayiz senle isim yok benden sana kotulukte gelmez ama beni zorlama lutfen. . zaten kafamda bir dunya sorun var hayat acimasiz hayat zor benim derdim bana yetiyor butun ictenligim ve iyi niyetim ile sana bu notu yaziyorum bu kadar sozden sonra kod ekleyecegini sanmiyorum birde seninle ugrasmayayim guzel kardesim arkadasim lutfen rica ediyorum LUTFEN barış her zaman erdemli insanlarin isidir lutfen ayni olgunluk ile senden olumlu donusunu bekliyorum eger yazdiklarimda kalp kirici yada incitici birsey varsa lutfen kusura bakma 1-2defa kontrol ettim ama belki gozumden kacmis olabilir hakkini helal et ve en iyisi ikimiz icinde helallesip bu isi noktalamaktir inan kotu biri degilim selam ve sevgiyle..

Формулы и Задачи (Информатика 10) — Школа N61 г.Ульяновска

Формулы

N = 2ⁱ

N — мощность алфавита (количество знаков в алфавите)
i — информационный вес символа алфавита (количество информации в одном символе)

I = K * i

I — количество информации, содержащееся в выбранном сообщении (информационный объем сообщения)
K — число символов в сообщении
i — информационный вес символа (количество информации в одном символе)

Q = N^L

Q — количество разных сообщений
N — количество символов
L — длина сообщения

Формула Хартли:

I = log₂N

I — количество информации, содержащееся в выбранном сообщении
N — количество сообщений

---

Римская система счисления

I – 1 (палец),
V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони),
L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)

Перевод чисел из других систем счисления в десятичную систему счисления

Развернутая запись целого числа:

a₃a₂a₁a₀ = a₃ * p³ + a₂ * p² + a₁ * p¹ + a₀ * p⁰

Правило перевода числа из любой системы счисления в десятичную систему счисления — умножаем каждую цифру исходного числа на основание системы счисления в степени разряда, в котором находится эта цифра, а затем всё складываем.

Запись через схему Горнера:

a₃a₂a₁a₀ = ((a₃ * p + a₂) * p + a₁) * p + a₀

p — основание системы счисления в котором представлено число.

Пример:

6375₁₀ = 6 * 10³ + 3 * 10² + 7 * 10¹ + 5 * 10⁰
6375₁₀ = ((6 * 10 + 3) * 10 + 7) * 10 + 5
1234₅ = 1 * 5³ + 2 * 5² + 3 * 5¹ + 4 * 5⁰ = 194₁₀
1234₅ = ((1 * 5 + 2) * 5 + 3) * 5 + 4 = 194₁₀

Развернутая запись дробного числа:

0,a₁a₂a₃a₄ = a₁*p^-1 + a₂*p^-2 + a₃*p^-3 + a₄*p^-4

Запись через схему Горнера:

0,a₁a₂a₃a₄ = p^-1 * (a₁ + p^-1 * (a₂ + p^-1 * (a₃ + p^-1 * a₄)))
p * (0,a₁a₂a₃a₄) = a₁ + p^-1 * (a₂ + p^-1 * (a₃ + p^-1 * a₄))

p — основание системы счисления в котором представлено число.

Пример:

0,6375 = 6 * 10^-1 + 3 * 10^-2 + 7 * 10^-3 + 5 * 10^-4
0,6375 = 10^-1 * (6 + 10^-1 * (3 + 10^-1 * (7 + 10^-1 * 5)))
0,1234₅ = 1 * 5^-1 + 2 * 5^-2 + 3 * 5^-3 + 4 * 5^-4
0,1234₅ = 5^-1 * (1 + 5^-1 * (2 + 5^-1 * (3 + 5^-1 * 4)))

Задачи

Алфавитный подход к измерению количества информации

Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа) при использовании алфавита из 256 символов.

1. информационная ёмкость символа: 256 = 2⁸      =>>      i = 8 бит = 1 байт
2. количество символов на странице:
   32 * 64 = 2⁵ * 26 = 2¹¹
3. общее количество символов:
   L = 10 * 2¹¹
4. информационный объём сообщения:
   I = L * i = 10 * 2¹¹ * 1 байт = 20 Кбайт

---

Системы счисления

  X10     X16     X8       X2
 0      0      0        0  1      1      1        1  2      2      2       10  3      3      3       11  4      4      4      100  5      5      5      101  6      6      6      110  7      7      7      111  8      8     10     1000  9      9     11     1001 10      A     12     1010 11      B     13     1011 12      C     14     1100 13      D     15     1101 14      E     16     1110 15      F     17     1111 16     10     20    10000 17     11     21    10001 18     12     22    10010 19     13     23    10011 20     14     24    10100 21     15     25    10101 22     16     26    10110 23     17     27    10111 24     18     30    11000 25     19     31    11001 26     1A     32    11010 27     1B     33    11011 28     1C     34    11100 29     1D     35    11101 30     1E     36    11110 31     1F     37    11111 32     20     40   100000

Логические операции

Логической операцией называется выбор решения (действия), исходя из  заданной ситуации, определяемой набором факторов (условий).
Зависимости между логическими функциями (операциями) и логическими переменными устанавливаются с помощью таблиц истинности. Используются следующие логические операции: НЕ, И, ИЛИ, исключающее ИЛИ, тождество.

---

Логическая операция НЕ (инверсия, операция логического отрицания). Действие, которое определяется операцией НЕ произойдет, если отсутствует фактор его определяющий.

Таблица истинности для операции НЕ имеет вид:

A
0	1
1	0

Действие, связанное с операцией НЕ можно записать следующим образом:

---

Логическая операция И (конъюнкция, операция логического умножения). Действие, которое определяется операцией И произойдет, если выполняются все влияющие на него факторы (условия). B

---

Логическая операция ИЛИ (дизъюнкция, операция логического сложения). Действие, которое определяется операцией ИЛИ произойдет, если выполняются хотя бы одно (любое), определяющее его условие.

Таблица истинности для операции ИЛИ имеет вид:

A	B	X=A v B
0	0	0
0	1	1
1	0	1
1	1	1

Действие, связанное с операцией ИЛИ можно записать следующим образом:

X = A + B = A v B

---

Логическая операция Исключающее ИЛИ. Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.

Таблица истинности имеет вид:

A	B	X=AB
0	0	0
0	1	1
1	0	1
1	1	0

Действие, связанное с операцией Исключающее ИЛИ можно записать следующим образом:

X = A B

---

Действие, связанное с операцией Импликации можно записать следующим образом:

X = A → B

Таблица истинности Импликации имеет вид:

A	B	A → B
0	0	1
0	1	1
1	0	0
1	1	1

---

Операция тождество. Операция тождество определяет тождественность аргументов.

Таблица истинности для операции тождество имеет вид:

A	B	A Ξ B
0	0	1
0	1	0
1	0	0
1	1	1

Действие, связанное с операцией тождество можно записать следующим образом:

X = A Ξ B

---

   

Диаграммы Венна (круги Эйлера)

 

Поиск номера сети

Необходимо найти номер сети по IP-адресу 12.16.196.10 и маске 255.255.224.0.

маска сети	255.	255.	224.	0
IP-адрес	12.	16.	196.	10	— ip-адрес (узла, компьютера и т.п.)
IP-адрес	0000 1100.	0001 0000.	1100 0100.	0000 1010
маска сети	1111 1111.	1111 1111.	1110 0000.	0000 0000
адрес сети	0000 1100.	0001 0000.	110x xxxx.	xxxx xxxx	— эта часть относится к адресу сети — она взята из ip-адреса, но взяты те цифры, напротив которых стоят единицы остальные цифры справа надо дополнить нулями, чтобы общее число цифр стало равным 32. Получится следующее:
адрес сети	0000 1100.	0001 0000.	1100 0000.	0000 0000	— полный адрес сети теперь каждую октаду (последовательность из 8 цифр, разделены точками) переводим в десятичный вид. Получаем:
адрес сети	12.	16.	192.	0	— полный адрес сети (в десятичном виде)

 

Перевод чисел в различные системы счисления

 

Задача перевода заключается в следующем: Пусть известна запись числа x в системе счисления с каким-либо основанием P:

x = p_n·Pⁿ+p_n-1·P^n-1+…+p₁·P¹+p₀·P⁰+p_-1·P^-1+…+p_-m·P^-m

где p_i – цифры P-ичной системы. Требуется найти запись этого числа x в системе счисления с основанием Q:

x = q_u·Q^u+q_u-1·Q^u-1+…+q₁·Q¹+q₀·Q⁰+q_-1·Q^-1+…+q_-v·Q^-v

где q_i – искомые цифры Q-ичной системы.

Для перевода любого числа достаточно отдельно перевести его целую и дробную части.

Перевод целых чисел

Представим число x в Q-ичной системе в виде полинома

x = q_u·Q^u+q_u-1·Q^u-1+…+q₁·Q¹+q₀·Q⁰

Разделим обе части этого равенства на основание искомой системы счисления Q, причем в левой части произведем фактическое деление, поскольку запись числа x в P-ичной системе нам известна, а в правой части деление выполним аналитически:

x/Q = q_u·Q^u-1+q_u-1·Q^u-2+…+q₁·Q⁰;   q₀ — остаток от деления

Таким образом, младший коэффициент числа x в Q-ичной системе счисления является остатком от деления x на Q. Число x/Q  является целым, и к нему тоже можно применить описанную процедуру:

x/Q² = q_u·Q^u-2+q_u-1·Q^u-3+…+q₂·Q⁰;   q₁ — остаток от деления

Этот процесс продолжается до тех пор, пока не получено x/Q^u=0. Для записи числа x в Q-ичной системе счисления запишем каждый из полученных коэффициентов q_i одной Q-ичной цифрой:

x_Q=q_uq_u-1…q₁q₀

Пример 1: Перевести число 47₁₀ в двоичную систему счисления (Q=2).

Искомое число 47₁₀ = 101111₂.
Пример 2: Перевести число 3060₁₀ в шестнадцатеричную систему счисления (Q = 16).

Таким образом,  4₁₀ = 4₁₆,  15₁₀ = F₁₆,  11₁₀ = B₁₆. Искомое число
3060₁₀ = BF4₁₆.

Перевод дробных чисел

Пусть необходимо перевести в Q-ичную систему правильную дробь x (0<x<1), заданную в P-ичной системе счисления.
Поскольку x<1, то в Q-ичной системе запись числа x будет иметь вид

x = q_-1·Q^-1+q_-2·Q^-2+…+q_-v·Q^-v

Умножив обе части этого выражения на Q, получим

x·Q = q_-1·Q⁰+q_-2·Q^-1+…+q_-v·Q^-v+1

где q_-1 является целой частью, а (x·Q — q_-1)  – правильная дробь. Таким образом, искомые коэффициенты q_i  могут быть определены по формуле

q_-(i+1)=[x_i·Q]

где [ ] – целая часть. Процесс продолжается до тех пор, пока не будет получено x_i+1=0, либо не будет достигнута требуемая точность числа.

Пример 3: Перевести число 0,273₁₀ в двоичную систему счисления

Искомое число x = 0,273₁₀ = 0,0100010111…₂.

Назад: Представление данных и архитектура ЭВМ

Расчет числа палиндромов в двоичной системе счисления Текст научной статьи по специальности «Математика»

29

Вестник Самарского университета. Естественнонаучная серия. Том 24 № 4 2018

УДК 511(075.8)

Б01: 10.18287/2541-7525-2018-24-4-29-32

В.В. Любимов, Р.В. Меликджанян1

РАСЧЕТ ЧИСЛА ПАЛИНДРОМОВ В ДВОИЧНОЙ СИСТЕМЕ

СЧИСЛЕНИЯ

В работе рассматриваются симметричные числа в двоичной системе счисления, называемые палиндромами. Целью работы является вывод зависимости количества палиндромов от их разряда. Отдельно получены зависимости числа палиндромов для четных и нечетных разрядов.

Ключевые слова: палиндромы, двоичная система счисления, теория чисел, формула.

Цитирование. Любимов В.В., Меликджанян Р.В. Расчет числа палиндромов в двоичной системе счисления // Вестник Самарского университета. Естественнонаучная серия. 2018. Т. 24. № 4. С. 29-32. БО!: http://doi.org/10.18287/2541-7525-2018-24-4-29-32.

Введение

Числовой палиндром — это натуральное число, которое читается слева направо и справа налево одинаково.оя — «бег, движение») [1]. Примерами палиндромов являются числа 101; 12321; 55688655 и т.д. В частности, в статье «Применение числовых палиндромов» Гундиной М.А. и Гусачека Д.А. на основе алгоритма итеративного процесса «перевернуть и сложить» исследовалось количество шагов получения палиндромов для чисел от 1 до 500 [2]. Существует мнение, пишет М. Гарднер, что описанная процедура в применении к любому целому числу даст палиндром после конечного числа сложений [3]. Но калифорнийский математик Чарльз Тригг сомневается в справедливости этого предположения. Среди чисел меньше 10000 он нашел 251 число, каждое из которых не дает палиндрома при первых ста сложениях. При этом наименьшее из этих чисел равно 196. Дьюи Дункан, показал, что в двоичной системе описанный процесс не всегда дает палиндром. Действительно, из двоичного числа 10110 никогда не получится палиндром.

Существуют так же палиндромные матрицы, которые подробно исследуются в следующих работах

[4-6].

Наша же задача состоит в том, чтобы определить количество числовых палиндромов двоичной системы счисления для конкретного разряда. Далее кратко «Палиндром двоичной системы счисления» будет обозначаться ПДСС. Для ответа на этот вопрос разберемся в структуре ПДСС.

1. Структура ПДСС для нечетных разрядов

Исследование проведем на примере ПДСС 7 разряда. Запишем всевозможные их варианты. В результате получим:

1000001 1001001 1010101 1011101 1100011 1101011

х© Любимов В.В., Меликджанян Р.В., 2018

Любимов Владислав Васильевич ([email protected]), кафедра высшей математики, Самарский национальный исследовательский университет имени академика С.П. Королева, 443086, Российская Федерация, г. Самара, Московское шоссе, 34.

Меликджанян Регина Валерьевна ([email protected]), Институт информатики, математики и электроники, Самарский национальный исследовательский университет имени академика С.П. Королева, 443086, Российская Федерация, г. Самара, Московское шоссе, 34.

1110111 1111111

Число 7 разряда состоит из 7 цифр (в нашем случае, из нулей и единиц). Так как палиндром симметричен, следовательно, для 7 разряда первые и последние 3 цифры должны быть «зеркальными»; цифра же, стоящая посередине (четвертая), может быть любой для двоичный системы: либо 0, либо 1. На рисунке 1 представлено условное изображение палиндрома 7 разряда.

**

* * * * * *

Рис. 1. Условное изображение палиндрома 7 разряда

На месте первых и последних трех цифр может стоять любая комбинация цифр 1 и 0, кроме той, где 0 стоит на первом месте, например, 000; 001; 010; 011, так как число не может начинаться с нуля. Из этого следует вывод, что задача нахождения количества ПДСС 7 разряда сводится к задаче нахождения количества всех существующих чисел двоичной системы счисления 3 разряда. Запишем всевозможные их варианты. В результате получаем:

100 101 110 111

Следовательно, их количество равно четырем.

Для того, чтобы понять, как связано количество чисел некого разряда с номером разряда, запишем числа в двоичной системе для первых четырех разрядов:

Разряд 1: 1

Разряд 2: 10; 11

Разряд 3: 100; 101; 110; 111

Разряд 4: 1000; 1001; 1010; 1011; 1100; 1101; 1110; 1111

Заметим, что с каждым разрядом количество чисел увеличивается в два раза.

Далее запишем формулу для вычисления количества существующих чисел двоичной системы счисления для п разряда:

■1п = 2п-1, п — номер разряда

Вернемся к нашему палиндрому 7 разряда. Так как цифра, стоящая посередине (четвертая), может быть любой (для двоичной системы либо 0, либо 1), то количество палиндромов будет в два раза больше, чем значение ,1п. Действительно, сначала перебираются варианты, когда посередине стоит нуль, затем — те же числа, когда посередине стоит единица.

Из данных рассуждений выведем формулу для определения количества палиндромов нечетных разрядов. Она примет следующий вид:

Б к = 2 *

где к — нечетный номер разряда для палиндрома.

Пусть числа п и к зависят между собой следующим образом:

к —17 «

п = , к — нечетный номер разряда для палиндрома

Тогда получаем следующую формулу для определения количества палиндромов нечетных разрядов:

Би = 2—, (1.1)

где к — нечетный номер разряда для палиндрома.

2. Структура ПДСС для четных разрядов

Рассмотрим всевозможные палиндромы четных разрядов, в частности, для шестого разряда имеем:

100001 101101 111111

Расчет числа палиндромов в двоичной системе счисления

31

110011

Они также состоят из всех существующих чисел двоичной системы счисления третьего разряда, но их отличие заключается в отсутствии единицы или нуля посередине (т.к. количество цифр четное, оно нацело делятся на две симметричные части). На рисунке 2 представлено условное изображение палиндрома для шестого разряда., к* =2т, т = 0,1, 2 …п

Литература

[1] Nishiyama Y. Numerical palindromes and the 196 problem // IJPAM. Vol. 80. № 3. 2012. P. 375-384. URL: https://ijpam.eu/contents/2012-80-3/9/9.pdf.

[2] Гундина М.А., Гусачек Д.А. Применение числовых палиндромов // IX Машеровские чтения: материалы Международной научно-практической конференции студентов, аспирантов и молодых ученых, Витебск, 25 сентября 2015 г. Витебск: Изд-во ВГУ им. П.М. Машерова, 2015. С. 13-15.

[3] Гарднер М. Этот левый, правый мир. М.: Мир, 1967. 267 с.

[4] Iannazzo B., Meini B. Palindromic matrix polynomials, matrix functions and integral representations // Linear Algebra Appl. Vol. 434. Issue 1. 2011. P. 174-184. DOI: https://doi.org/10.1016/j4aa.2010.09.013.

[5] Structured polynomial eigenvalue problems: Good vibrations from good linearizations / D.S. Mackey [et al.] // SIAM J. Matrix Anal. Appl. Vol. 28. 2006. P. 1029-1051. URL: http://eprints.maths.manchester.ac.uk/id/eprint/190.

[6] Gemignani L., Noferini V. The Ehrlich-Aberth method for palindromic matrix polynomials represented in the Dickson basis // Linear Algebra Appl. Vol. 438. 2013. P. 1645-1666. DOI: 10.1016/j.laa.2011.10.035.

References

[1] Nishiyama Y. Numerical palindromes and the 196 problem. IJPAM, Vol. 80, no. 3, 2012, pp. 375-384. Available at: https://ijpam.eu/contents/2012-80-3/9/9.pdf [in English].

[2] Gundina M.A., Gusachek D.A. Primenenie chislovykh palindromov [Application of numerical palindromes]. In: IX Masherovskie chteniya: materialy Mezhdunarodnoi nauchno-prakticheskoi konferentsii studentov, aspirantov i molodykh uchenykh, Vitebsk, 25 sentyabrya 2015 g. [IX Masherovskie readings: materials of the International research and practical conference of students, postgraduate students and young scientists, Vitebsk, 25 September, 2015]. Vitebsk: Izd-vo VGU im. P.M. Masherova, 2015, pp. 13-15 [in Russian].

[3] Gardner M. Etot levyi, pravyi mir [This left, right world]. M.: Mir, 1967, 267 p. [in Russian].

[4] Iannazzo B., Meini B. Palindromic matrix polynomials, matrix functions and integral representations. Linear Algebra Appl., Vol. 434, Issue 1, 2011, pp. 174-184. DOI: https://doi.org/10.1016/j4aa.2010.09.013 [in English].

[5] D.S. Mackey [et al.] Structured polynomial eigenvalue problems: Good vibrations from good linearizations. SIAM J. Matrix Anal. Appl., Vol. 28, 2006, pp. 1029-1051. Available at: http://eprints.maths.manchester.ac.uk/id/eprint/190 [in English].

[6] Gemignani L., Noferini V. The Ehrlich-Aberth method for palindromic matrix polynomials represented in the Dickson basis. Linear Algebra Appl., Vol. 438, 2013, pp. 1645-1666. DOI: 10.1016/j.laa.2011.10.035 [in English].

V.V. Lyubimov, R.V. Melikdzhanyan2

CALCULATION OF THE NUMBER OF PALINDROMS IN A BINARY

SYSTEM

The work deals with symmetric numbers in the binary number system, called palindromes. The aim of the work is to derive the dependence of the number of palindromes on their digit. The dependences of the number of palindromes for even and odd digits are obtained separately.

Key words: palindromes, binary number system, number theory, formula.

Citation. Lyubimov V.V., Melikdzhanyan R.V. Raschet chisla palindromov v dvoichnoi sisteme schisleniya [Calculation of the number of palindroms in a binary system] [Calculation of the number of palindroms in a binary system]. Vestnik Samarskogo universiteta. Estestvennonauchnaia seriia [Vestnik of Samara University. Natural Science Series], 2018, no. 24, no. 4, pp. 29-32. DOI: http://doi.org/10.18287/2541-7525-2018-24-4-29-32 [in Russian].

Статья поступила в редакцию 15/Х/2018. The article received 15/X/2018.

This work is licensed under a Creative Commons Attribution 4.0 International License.

2Lyubimov Vladislav Vasilievich ([email protected]), Department of Higher Mathematics, Samara National Research University, 34, Moskovskoye shosse, Samara, 443086, Russian Federation.

Melikdzhanyan Regina Valerievna ([email protected]), Institute of Informatics, Mathematics and Electronics, Samara National Research University, 34, Moskovskoye shosse, Samara, 443086, Russian Federation.

1.3. СИСТЕМЫ СЧИСЛЕНИЯ. — Основы информатики

1.3.1.ПОНЯТИЕ СИСТЕМЫ СЧИСЛЕНИЯ.

Все фантастические возможности вычислительной техники (ВТ) реализуются путем создания разнообразных комбинаций сигналов высокого и низкого уровней, которые условились называть «единицами» и «нулями».

Система счисления(СС) — это система записи чисел с помощью определенного набора цифр.CС называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе. Десятичная СС является позиционной: 999.Римская СС является непозиционной. Значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.Количество различных цифр, употребляемых в позиционной СС, называется основанием СС.

Развернутая форма числа — это запись, которая представляют собой сумму произведений цифр числа на значение позиций.

Например: 8527=8*10³+5*10²+2*10¹+7*10⁰

Развернутая форма записи чисел произвольной системы счисления имеет вид

, где

X — число;
a — основа системыисчисления;
i — индекс;
m — количество разрядов числа дробной части;
n — количество разрядов числа целой части.

Например: 327.46 n=3, m=2, q=10

Если основание используемой СС больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение.

Например: если 10=А, а 11=В, то число 7А.5В₁₂ можно расписать так:

7А.5В₁₂ = В·12^-2 + 5 ·2^-1 +А ·12⁰ + 7 ·12¹.

В шестнадцатеричной СС основа — это цифры 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 с соответствующими обозначениями 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Примеры чисел: 17D.ECH, F12AH.

ДвоичнаяСС— это система, в которой для записи чисел используются две цифры 0 и 1. Основанием двоичной системы счисления является число 2.

Двоичный код числа — запись этого числа в двоичной системе счисления. Например,

0=0₂
1=1₂
2=10₂
3=11₂ …
7=111₂
120=1111000₂.

В ВТ применяют позиционные СС с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную. Для обозначения используемой СС число снабжают верхним или нижним индексом, в котором записывают основание СС. Другой способ – использование латинских букв после записи числа:

D – десятичная СС
В – двоичная СС
О – восьмеричная СС
Н – 16-ричная СС.

Несмотря на то, что 10-тичная СС имеет широкое распространение, цифровые ЭВМ строятся на двоичных элементах, т.к. реализовать элементы с 10 четко различимыми состояниями сложно. Историческое развитие ВТ сложилось таким образом, что ЭВМ строятся на базе двоичных цифровых устройств: триггеров, регистров, счетчиков, логических элементов и т.д.

16-ричная и 8-ричная СС используются при составлении программ на языке машинных кодов для более короткой и удобной записи двоичных кодов – команд, данных, адресов и операндов.

Задача перевода из одной СС в другую часто встречается при программировании, особенно, на языке Ассемблера. Например, при определении адреса ячейки памяти. Отдельные стандартные процедуры языков программирования Паскаль, Бейсик, Си, HTML требуют задания параметров в 16-ричной СС. Для непосредственного редактирования данных, записанных на жесткий диск, также необходимо умение работать с 16-ричными числами. Отыскать неисправность в ЭВМ невозможно без представлений о двоичной СС.

В таблице приведены некоторые числа, представленные в различных СС.

Двоичные числа	Восьмеричные числа	Десятичные числа	Шестнадцатеричные числа
0	0	0	0
1	1	1	1
10	2	2	2
11	3	3	3
100	4	4	4
101	5	5	5
110	6	6	6
111	7	7	7
1000	10	8	8
1001	11	9	9
1010	12	10	A
1011	13	11	B
1100	14	12	C
1101	15	13	D
1110	16	14	E
1111	17	15	F

1.3.2. ПЕРЕВОД ЧИСЕЛ ИЗ ПРОИЗВОЛЬНОЙ СС В ДЕСЯТИЧНУЮ И ОБРАТНО.

Перевод чисел из произвольной системы в десятичную. Для перевода числа из любой позиционной СС в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:

1101₂=1*2³+1*2²+0*2¹+1*2⁰=13₁₀

17D.ECH=12·16^-2 + 14·16^-1 +13·16⁰ + 7·16¹ + 1·16²=381.921875

Перевод чисел из десятичной СС в заданную.

1) Для преобразования целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание СС, пока не получат нуль. Числа, которые возникают как остаток от деления на основание СС, представляют собой последовательную запись разрядов числа в выбранной СС от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

Например:

Читая остатки от деления снизу вверх, получим 111011011.

Проверка:

1*2⁸+1*2⁷+1*2⁶+0*2⁵+1*2⁴+1*2³+0*2 ²+1*2¹+1*2⁰=1+2+8+16+64+128+256=475₁₀.

2) Для преобразования десятичных дробей десятичной СС в число любой СС последовательно выполняют умножение на основание системы счисления , пока дробная часть произведения не станет равной нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.

Например: перевести число 0.375 ₁₀ в двоичную СС.

Полученный результат — 0.011₂.

Необходимо отметить, что не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части, округляя последний разряд.

1.3.3. ПЕРЕВОД МЕЖДУ ОСНОВАНИЯМИ, СОСТАВЛЯЮЩИМИ СТЕПЕНЬ 2.

Для того, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.

Например:

1234.777₈ = 001 010 011 100.111 111 111₂ = 1 010 011 100.111 111 111₂

1234567₈ = 001 010 011 100 101 110 111₂ = 1 010 011 100 101 110 111₂

Обратный перевод: каждая триада двоичных цифр заменяется восьмеричной цифрой, при этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.

Например:

1100111₂ = 001 100 111₂ = 147₈

11.1001₂ = 011.100 100₂ = 3.44₈

110.0111₂ = 110.011 100₂ = 6.34₈

При переводах между двоичной и шестнадцатеричной СС используются четверки цифр. При необходимости выравнивание выполняется до длины двоичного числа, кратной четырем.

Например:

1234.AB77₁₆ = 0001 0010 0011 0100.1010 1011 0111 0111₂ =1 0010 0011 0100.1010 1011 0111 0111₂

CE4567₁₆ = 1100 1110 0100 0101 0110 0111₂

0.1234AA₁₆ = 0.0001 0010 0011 0100 1010 1010₂

1100111₂ = 0110 0111₂ = 67₁₆

11.1001₂ = 0011.1001₂ = 3.9₁₆

110.0111001₂ = 0110.0111 0010₂ = 65.72₁₆

При переходе из восьмеричного счисления в шестнадцатеричное счисление и обратно используется вспомогательный двоичный код числа.

Например:

1234567₈ = 001 010 011 100 101 110 111₂ = 0101 0011 1001 0111 0111₂ = 53977₁₆

0.12034₈ = 0.001 010 000 011 100₂ = 0.0010 1000 0011 1000₂ = 0.2838₁₆

120.34₈ = 001 010 000. 011 100₂ = 0101 0000.0111 0000₂ = 50.7₁₆

1234.AB77₁₆ = 0001 0010 0011 0100.1010 1011 0111 0111₂ =

= 001 001 000 110 100.101 010 110 111 011 100₂ = 11064.526734₈

CE4567₁₆ = 1100 1110 0100 0101 0110 0111₂ = 110 011 100 100 010 101 100 111₂ = 63442547₈

0.1234AA₁₆ =0.0001 0010 0011 0100 1010 1010₂ =0.000 100 100 011 010 010 101 010₂ =0.04432252₈

CBSE Класс 9 Математические системы счисления Формулы

Вам сложно справляться с математическими формулами и уравнениями? Кажется, сложно запомнить математические формулы? Не о чем беспокоиться. Что, если мы скажем вам, что вам больше не нужно изо всех сил разбираться со всеми математическими формулами 9 класса? Да! Вы получите формулы системы счисления класса 9 в Таблицах формул математики для класса 9, разработанных экспертами в данной области в Веданту. Этот лист включает в себя все формулы 9-го класса системы счисления.

Математические формулы 9-го класса

Математические формулы 9-го класса CBSE Все главы доступны для свободного доступа и редактирования на сайте Vedantu.com. Вы можете просто загрузить важные математические формулы и уравнения в формате PDF для девятого класса, чтобы легко и быстро решать задачи и получать более высокие оценки на экзаменах класса 9 CBSE Board в Веданту.

Формула числовой системы Класс 9

Натуральные числа: Они представлены в числовой форме -1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ………. обозначаются Н.

Целые числа: они представлены в числовой форме — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ………. обозначаются W.

Целые числа : -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 обозначаются Z

Рациональные числа: Все числа, которые можно математически записать в форме p / q, q ≠ 0, известны как рациональные числа, где p и q относятся к целым числам.

Иррациональные числа: число называется иррациональным, если оно не может быть математически записано в форме p / q, где p и q — целые числа, а q 0.

Десятичное расширение: Такое алгебраическое расширение в десятичной форме рационального числа является либо завершающим, либо непрерывным повторяющимся. Следовательно, мы можем сказать, что число, десятичное расширение которого является завершающим или непрекращающимся повторяющимся, является тем, что мы называем рациональным числом. Существуют следующие свойства десятичного раскрытия, которые приведены ниже:

• Для иррационального числа десятичное раскрытие не завершается и не повторяется.

• Все рациональные и иррациональные числа можно взять вместе.

• Можем составить сборник реальных чисел.

• Действительное число может быть как рациональным, так и иррациональным.

• Если «r» рационально, а «s» иррационально, тогда r + s, r — s, r. s неизменно будет иррациональными числами, однако r / s может быть рациональным или иррациональным

• Мы можем представить любое иррациональное число на числовых линиях, используя теорему Пифагора.

• Рационализация — это метод извлечения квадратных корней из знаменателя.Например, для математического выражения 2 + √6 / √4, чтобы удалить, мы умножим числитель и знаменатель на √4.

Важное число Системная формула Класс 9

1. Формулы полиномиальных выражений

Биномиальные	(2x + 3y), (3x — 2y) и т. Д.
Одночлен	3, 2x, 23y и т. Д.
Трехчлен	x 2 + 4x + 5 и т. Д.
Линейный многочлен	x + 2, 3x + 5 и т. Д.
Квадратичный многочлен	ax 2 + bx + c и т.д.	x 4 + 5x 3 + 2x 2 + 3
Кубический многочлен	x 3 + 4x 2 + 5 и т. Д.

2 .Формулы координатной геометрии

Уравнение прямой	ax + by + c = 0
Уравнение окружности	x² + y² = r² Здесь ‘r’ обозначает радиус окружности
Уравнение эллипса	x² / a² + y² / b² = 1
Уравнение параболы	y² = 4ax
Уравнение гиперпараболы	x² / a² — y² / b² = 1
Угол между двумя линиями	θ = tan² − 1 (м / 1 + m1m2)
Формула расстояния	√ [(x2 − x1) ² + (y2 − y1) ²]

3.Формулы окружностей

Площадь круга	πr²
Диаметр окружности	2r
Окружность окружности 0
Угол окружности сектора	θ = (360 / (πr)
Площадь сектора	(θ / 2) × r²
Площадь круговое кольцо	π × (R² − r²)
r = радиус внутреннего круга. R = Радиус внешнего круга. θ = угол между двумя радиусами.

Числа — вопросы, приемы и ярлыки для проверки способностей

Каждый установочный тест на количественные способности будет содержать не менее 30% вопросов по системам счисления и рядам. Вопросы о способностях по системе счисления составляют основу подготовки к поступлению. Вы можете легко набрать балл в разделе количественных способностей, если понимаете основы системы счисления.Поскольку вопросы по системам счисления просты, важно приобрести правильные навыки для быстрого решения этих проблем.

Практика задач по числовым системам не только помогает улучшить вашу скорость, но также обеспечивает прочную основу для решения других количественных разделов, таких как HCF и LCM , среднее , процентов , время и скорость , трубы а также цистерны и т. д. В этом уроке давайте посмотрим, как легко и быстро решать проблемы с системой счисления.

Цифры интересно учить. Если вы изучите концепции досконально, вы обнаружите, что решение вопросов о способностях по системе счисления — это легкая прогулка для вас. Здесь задействовано множество концепций, и поэтому даже простой вопрос может показаться слишком сложным или сложным для решения.

Мы по адресу a4academics предоставим вам необходимые инструменты для проведения количественных тестов по системе счисления. Ниже приведен список важных формул для систем счисления и советы, которые помогут вам понять и подготовиться к вопросам количественных способностей по системам счисления.

Перед изучением советов и приемов просмотрите руководство, приведенное ниже, чтобы подробно понять математические концепции системы счисления. Это руководство улучшит ваши навыки решения проблем.

Важные формулы системы счисления

Формулы числового ряда

1. 1 + 2 + 3 + 4 + 5 +… + n = n (n + 1) / 2
2. (1 ² + 2 ² + 3 ² + ….. + n ² ) = n (n + 1) (2n + 1) / 6
3. (1 ³ + 2 ³ + 3 ³ +….. + n ³ ) = (n (n + 1) / 2) ²
4. Сумма первых n нечетных чисел = n ²
5. Сумма первых n четных чисел = n (n + 1)

---

Математические формулы

1. (a + b) (a — b) = (a ² — b ² )
2. (a + b) ² = (a ² + b ² + 2ab)
3. (a — b) ² = (a ² + b ² — 2ab)
4. (a + b + c) ² = a ² + b ² + c ² + 2 (ab + bc + ca)
5. (a ³ + b ³ ) = (a + b) (a ² — ab + b ² )
6. (a ³ — b ³ ) = (a — b) (a ² + ab + b ² )
7. (a ³ + b ³ + c ³ — 3abc) = (a + b + c) (a ² + b ² + c ² — ab — bc — ac)
8. Когда a + b + c = 0, тогда a ³ + b ³ + c ³ = 3abc
9. (a + b) ⁿ = a ⁿ + ( ⁿ C ₁ ) a ^n-1 b + ( ⁿ C ₂ ) a ^n-2 b ² +… + ( ⁿ C _n-1 ) ab ^n-1 + b ⁿ

---

Ярлыки для проверки делимости чисел

1. Число делится на 2, если цифра его единицы — 0, 2, 4, 6, 8.
2. Число делится на 3, если сумма его цифр делится на 3.
3. Число делится на 4, если число, образованное двумя последними цифрами, делится на 4.
4. Число делится на 5, если его единица измерения равна 0 или 5.
5. Число делится на 6, если оно делится как на 2, так и на 3.
6. Число делится на 8, если число, образованное последними тремя цифрами данного числа, делится на 8.
7. Число делится на 9, если сумма его цифр делится на 9.
8. Число делится на 10, если заканчивается на 0.
9. Число делится на 11, если разница суммы его цифр в нечетных местах и ​​суммы цифр в четных местах равна 0 или числу, делящемуся на 11.
10. Число делится на 12, если оно делится как на 4, так и на 3.
11. Число делится на 14, если оно делится как на 2, так и на 7.
12. Два числа называются взаимно простыми, если их H.C.F. равно 1. Чтобы определить, делится ли число, скажем, y на x, найдите такие m и n, что m * n = x, а m и n — простые числа. Если y делится как на m, так и на n, то оно делится на x.

---

Ярлыки для преобразования повторяющегося десятичного числа в дробное

1. Для повторяющихся десятичных знаков формата ‘0.abababab …’ (ab повторяется) эквивалентной дробью будет «повторяющаяся группа (здесь ab)» / «столько девяток, сколько цифр в повторяющейся группе»
2. Для повторяющихся десятичных знаков формата ‘0.abbbbb … ‘(b повторяется), эквивалентная дробь будет (вся десятичная группа — неповторяющаяся десятичная группа) / (столько девяток, сколько количество повторяющихся цифр в десятичной части с таким количеством нулей, сколько не- повторяющиеся цифры в десятичной части)

Часто задаваемые вопросы о системе счисления

• Для числа x вам будет предложено найти наибольшее n -значное число, делящееся на x .
• Вам будет предоставлен набор чисел ( n1, n2, n3… ) и попросили найти, сколько из этих чисел делится на указанное число x .
• Для числового ряда найдите сумму n членов, найдите n ^{-й член} и т. Д.
• Найдите произведение двух чисел, если дана их сумма / разность и сумма их квадратов.
• Найдите число, когда задана делимость его цифр на определенные числа.
• Найдите наименьшее n -значное число, делящееся на x .
• Какие из заданных чисел являются простыми числами.
• Число x при делении на y дает остаток r , каким будет остаток при делении x ² на y .
• Зная соотношение между цифрами числа, найдите число.
• Найти результат операций (сложение, вычитание, умножение, деление и т. Д.) Над заданными целыми числами. Эти целые числа могут быть большими, и вопрос может показаться сложным и трудоемким.Но в основном вопрос будет отображаться на одно из известных алгебраических уравнений, приведенных в этой первой вкладке.

Примеры вопросов и ответов по системе счисления

натуральных, целых, рациональных, иррациональных, действительных чисел и выше

Натуральные числа

натуральное число (или , считая ) чисел — это 1,2,3,4,5 и т. Д. много натуральных чисел. Набор натуральных чисел, {1,2,3,4,5, …}, иногда для краткости пишут N .

Целые числа — натуральные числа вместе с 0.

(Примечание: некоторые учебники не согласны с этим и говорят, что натуральные числа включают 0.)

Сумма любые два натуральных числа также являются натуральными числами (например, 4 + 2000 = 2004), а произведение любых двух натуральных чисел натуральное число (4 × 2000 = 8000). Этот однако это неверно для вычитания и деления.

Целые числа

Целые числа — это набор действительных чисел, состоящий из натуральных чисел, их аддитивных обратных чисел и нуля.

{…, — 5, −4, −3, −2, −1,0,1,2,3,4,5, …}

Набор целых чисел иногда написано J или Z для краткости.

The сумма, произведение и разность любых двух целых чисел также являются целыми числами. Но это не относится к делению … просто попробуйте 1 ÷ 2.

Рациональные числа

Рациональные числа те числа, которые можно выразить как отношение между два целых числа. Например, дроби 13 и −11118 являются рациональное число.Все числа входят в рациональные числа, поскольку любое целое число z можно записать как отношение z1.

Все десятичные дроби, которые заканчиваются, являются рациональными числами (с версии 8.27 можно записать как 827100.) Десятичные дроби которые после некоторой точки имеют повторяющийся узор, также являются рациональными: например,

0,0833333 …. = 112.

Множество рациональных чисел замкнуто относительно всех четырех основных операций, то есть для любых двух рациональных чисел их сумма, разница, произведение и частное также являются рациональным числом (пока мы не делим на 0).

Иррациональные числа

Иррациональное число — это число, которое нельзя записать в виде отношения (или дроби). В десятичной форме он никогда не заканчивается и не повторяется. В древние греки обнаружили, что не все числа рациональны; там — это уравнения, которые нельзя решить с помощью отношений целых чисел.

Первое такое уравнение для изучения было 2 = x2. Какие само число раз равно 2?

2 является около 1,414, поскольку 1,4142 = 1,999396, что близко к 2. Но вы никогда не попадете точно, возведя дробь в квадрат (или завершив десятичный).Квадратный корень из 2 — иррациональное число, то есть его десятичный эквивалент продолжается вечно, без повторяющегося образца:

2 = 1,41421356237309 …

Другой известный иррациональный числа золотое сечение , число с большим значение для биологии:

1 + 52 = 1,61803398874989 …

π (пи), отношение длины окружности к ее диаметру:

π = 3,14159265358979 …

и е, самое важное число в исчислении:

е = 2.71828182845904 …

Иррациональные числа могут быть далее подразделены на алгебраических чисел, которые являются решениями некоторого полиномиального уравнения (например, 2 и золотое сечение), и трансцендентных чисел, которые не являются решениями какого-либо полиномиального уравнения. π и e оба трансцендентны.

The Реальные числа

Действительные числа — это набор чисел, содержащий все рациональные числа и все иррациональные числа. Настоящие числа — это «все числа» в числовой строке.Существует бесконечно много действительных чисел, как и бесконечно много чисел в каждом из других наборов чисел. Но можно доказать, что бесконечность действительных чисел на больше бесконечности.

«Меньше», или счетных бесконечности целых чисел и rationals иногда называют ℵ0 (alef-naught), и бесчисленных бесконечности реалов называется ℵ1 (алеф-он).

Есть еще «большие» бесконечности, но для этого вам следует пройти курс теории множеств!

The Комплексные числа

Комплексные числа — множество {a + bi | a и b — действительные числа}, где i — мнимая единица, −1.(нажмите здесь, чтобы подробнее о мнимых числах и операциях с комплексными числами).

Комплексные числа включают набор действительных чисел. Действительные числа в сложной системе записываются в виде a + 0i = a. реальное число.

Этот набор иногда бывает записывается как C для краткости. Набор комплексных чисел важно, потому что для любого полинома p (x) с коэффициентами действительного числа все решения p (x) = 0 будут в C .

За пределами …

Есть и «большие» наборы чисел, используемых математиками.Кватернионы , открытые Уильямом Х. Гамильтоном в 1845 году, образуют систему счисления с тремя разные мнимые единицы!

CDSE Математическая формула системы счисления

Уважаемые кандидаты, ниже вы можете найти большинство важных и основных формул из системы счисления CDSE . Эта формула поможет вам решить большинство вопросов, которые появляются в математической статье CDSE. Математическая работа CDSE обычно состоит из вопросов по алгебре, арифметике, измерениям, геометрии, тригонометрии, тригонометрии, логарифму и статистике.

CDSE Математические формулы системы счисления

• Десять — это основа нашей системы счисления.
• Набор целых чисел Z = {…… -4, -3, -2, -1, 0, 1, 2, 3, 4 …….}
• Целые положительные числа 1, 2, 3, 4,… называются натуральными числами. Наименьшее натуральное число равно 1, а наибольшего натурального числа не существует. Множество натуральных чисел N бесконечно.
• Все натуральные числа вместе с нулем являются целыми числами. 0 — наименьшее целое число. Множество целых чисел W бесконечно.
• Набор натуральных чисел — это подмножество набора целых чисел, за исключением 0
• Четные числа делятся на 2, а набор четных чисел E включает 0. E = {0, 2, 4, 6,…}.
• Нечетные числа не делятся на 2. O = {1, 3, 5, 7….}
• Простые числа — это натуральные числа, имеющие два точных различных множителя, то есть 1 и само число (2, 3, 5, 7, 11…). 2 — наименьшее простое число.
• Натуральные числа, имеющие более двух множителей, называются составными числами.Например. 4, 6, 8, 9, 10,…
• 1 не является ни простым, ни составным. Все четные числа, кроме 2, являются составными.
• Сочетание простых или относительно простых чисел — это два натуральных числа, которые могут не быть простыми числами и у которых есть только 1 в качестве общего делителя. Например. 8 и 9, 15 и 16, 26 и 33.
• Пары простых чисел, между которыми есть только одно составное число, называются двойными простыми числами. Например. 3,5; 5,7; 11,13
• Числа, которые могут быть выражены в форме p / q, где p и q — целые числа, а q не равно 0, называются рациональными числами.Набор рациональных чисел обозначается Q.
.
• Число, которое не может быть выражено как завершающее или повторяющееся десятичное число, называется иррациональным числом.
• Чистая повторяющаяся десятичная дробь — это десятичная дробь, в которой повторяются все цифры после десятичной точки. Смешанное повторяющееся десятичное число — это десятичное число, в котором по крайней мере одна цифра после десятичной точки не повторяется.
• Сокращенный метод преобразования чистого повторяющегося десятичного числа в рациональное число.
• Запишите повторяющуюся цифру или цифры только один раз в числитель и возьмите в знаменателе столько девяток, сколько повторяющихся цифр в данном числе.
• Например, 0,33333 = 3/9 = 1/3 или 0,387387387 = 387/999
• Сокращенный метод преобразования смешанного повторяющегося десятичного числа в рациональное число
• Сформируйте дробь, в которой числитель представляет собой разницу между числом, состоящим из всех цифр после десятичной точки с повторяющимися цифрами только один раз, и числом, образованным неповторяющимися цифрами, а знаменателем является число, состоящее из такого же количества девяток поскольку за повторяющимися цифрами следует столько нулей, сколько неповторяющихся цифр.например 0,74353535 = 7435-74 / 9900 = 7361/9900 или 0,1272727 = 127? 1/990 = 7/55
• Наборы рациональных и иррациональных чисел, взятые вместе, известны как наборы действительных чисел. Абсолютное значение действительного числа | x | определяется как | x | = x, если x> 0 и | x | = -x, если x <0

CDSE Вопросы из системы счисления

Также проверьте

О редакционной группе SSBCrack Редакционная группа SSBCrack состоит из группы профессиональных писателей и соискателей.Их главная цель — предоставить актуальную информацию об интервью SSB и обмен качественной информацией об обороне Индии, чтобы помочь соискателям. Напишите нам, чтобы присоединиться к нашей редакционной команде прямо сейчас. Система счисления

: формулы, советы и рекомендации для решения вопросов

Привет друзья!

В разделе «Система счисления : формулы, советы и приемы решения вопросов » мы обсудим некоторые важные формулы, советы и приемы, позволяющие легко решать задачи, основанные на системе счисления.

Некоторые важные основные формулы:

1. ( a + b ) ( a — b ) = ( a ² — b ² )

2. ( a + b ) ² = ( a ² + b ² + 2 ab )

3. ( a — b ) ² = ( a ² + b ² -2 ab )

4. ( a + b + c ) ² = a ² + b ² + c ² + 2 ( ab + bc + ca )

5. ( a ³ + b ³ ) = ( a + b ) ( a ² — ab + b ² )

6. ( a ³ — b ³ ) = ( a — b ) ( a ² + ab + b ² )

7. ( a ³ + b ³ + c ³ — 3 abc ) = ( a + b + c ) ( a ² + b ² + c ² — ab — bc — ac )

8. Если a + b + c = 0, тогда a ³ + b ³ + c ³ = 3 abc

Основные сведения, которые необходимо знать перед решением проблем с системой счисления:

• Дивиденд = (делитель x коэффициент) + остаток

• Если число n делится на два непростых числа a, b, то n делится на ab.Другими словами, чтобы найти число, скажем, b делится на a, найдите два числа m и n, такие что m * n = a, где m и n — взаимно простые числа, и если b делится как на m, так и на n тогда он делится на a.

• (a-b) всегда делит (a ⁿ — b ⁿ ), если n — натуральное число.

• (a + b) всегда делит (a ⁿ — b ⁿ ), если n — четное число.

• (a + b) всегда делит (a ⁿ + b ⁿ ), если n — нечетное число.

Некоторые основные серии чисел, которые необходимо знать:

1. (1 + 2 + 3 + … + n) = (1/2) n (n + 1)

2. (1 ² +2 ² +3 ² + … + n ² ) = (1/6) n (n + 1) (2n + 1)

3. (1 ³ +2 ³ +3 ³ + … + n ³ ) = (1/4) n ² (n + 1) ²

4. Сумма первых n нечетных чисел = n ²


5. Сумма первых n четных чисел = n (n + 1)

Наконец, спасибо за выбор Loud Study.

Пожалуйста, поделитесь этой статьей, Подписывайтесь на нас в социальных сетях, Подпишитесь на наш сайт

Важные формулы числовой системы для CAT

Системы счисления — самая важная тема в количественном разделе. Это очень обширная тема, и каждый год в CAT появляется значительное количество вопросов из этого раздела.

Важные формулы числовой системы для CAT:

1) Наибольшая степень n в метрах! равно [m / n] + [m / n ² ] + [m / n ³ ] +…..

Пример: максимальная степень 7 из 100! = [100/7] + [100/49] = 16

2) Найти количество нулей в n! найти наивысшую степень 5 в n!

3) Если сложить все возможные перестановки n различных цифр, получится сумма = (n-1)! * (сумма n цифр) * (11111… n раз)

4) Если число может быть представлено как N = a ^p ∗ b ^q ∗ c ^r . . . количество факторов равно (p + 1) * (q + 1) * (r + 1)

5) Сумма факторов:

(((a ^ (p + 1)) — 1) / (a-1)) * ((b ^ (q + 1)) — 1) / (b-1)) * ((c ^ (r +1)) — 1) / (с-1))

6) Если количество множителей нечетное, то N — полный квадрат.

7) Если имеется n факторов, то количество пар факторов будет n / 2. Если N — полный квадрат, то количество пар (включая квадратный корень) равно (n + 1) / 2

.

8) Если число можно выразить как N = 2 ^p ∗ a ^q ∗ b ^r . . . где степень двойки равна p, а a, b — простые числа

• Тогда количество четных делителей N = p (1 + q) (1 + r). . .

• Количество нечетных множителей N = (1 + q) (1 + r)…

9) Число положительных интегральных решений уравнения x ² — y ² = k определяется как

• Общее количество множителей k (если k нечетно, но не является полным квадратом)

• (общее количество множителей k) — 1 (если k нечетное и является полным квадратом)

• Общее количество множителей k (если k четно, но не является полным квадратом)

• (общее количество множителей k) — 1 (если k четное и полный квадрат)

10) Количество цифр в a ^b = [b log _m (a)] + 1; где m — основание числа, а [.] обозначает наибольшую целую функцию

11) Четное число, не кратное 4, никогда не может быть выражено как разность двух полных квадратов.

12) Сумма первых n нечетных чисел равна n ²

13) Сумма первых n четных чисел равна n (n + 1)

14) Произведение множителей N равно N ^{a / 2} , где a — количество множителей

15) Последние две цифры номера ² , (50 — a) ² , (50 + a) ² , (100 — a) ² .. … . . . такие же.

16) Если число записано как 2 ¹⁰ⁿ

Если n нечетное, последние 2 цифры равны 24.

Когда n четно, последние 2 цифры равны 76.

Также посмотрите 7 советов по системе счисления для CAT.

Просмотры сообщений: 10 683

CBSE Класс 10 Математика Формулы вещественных чисел

CBSE Класс 10 Математика Действительные числа Формулы для простого решения задач и получения большего количества баллов на экзамене CBSE Class 10 Board.Математические формулы для 10 класса составляют основу для решения всех задач на самых сложных конкурсных экзаменах.

Книга: Национальный совет по образовательным исследованиям и обучению (NCERT)
Класс: 10-й класс
Предмет: математика
Название главы: Действительные числа

CBSE Класс 10 Математика Формулы вещественных чисел

С. №	Типы номеров	Описание
1	Натуральные числа	N = {1,2,3,4,5> Это счетные числа
2	Целое число	W = {0,1,2,3,4,5> Это счетные числа + ноль
3	Целые числа	Все целые числа, включая Отрицательное число + Положительное число …… -4, -3, -2, -1,0,1,2,3,4,5… и так далее. Как и целые числа, целые числа не включают дроби и десятичные дроби.
4	Целые положительные числа	Z + = 1,2,3,4,5, ……
5	Целые отрицательные числа	Z — = -1, -2, -3, -4, -5, ……
6	Рациональное число	Число называется рациональным, если его можно выразить в форме p / q, где p и q — целые числа (q> 0). Пример: P / q, 4/5
7	Иррациональное число	Число называется рациональным, если оно не может быть выражено в форме p / q, где p и q — целые числа (q> 0). Пример: √2, Pi и т. Д.
8	Реальные числа	Действительное число — это число, которое можно найти в числовой строке. Действительные числа — это числа, которые мы обычно используем и применяем в реальных приложениях. Действительные числа включают натуральные числа, целые числа, целые числа, дроби, рациональные числа и иррациональные числа

Лемма Евклида о делении | CBSE Класс 10 Математика Формулы вещественных чисел

Лемма Евклида о делении определяется как «для заданных положительных целых чисел a и b существуют уникальные целые числа q и r, удовлетворяющие [a = bq + r, 0≤r

HCF (Наивысший общий множитель) |

CBSE Класс 10 Математика Формулы вещественных чисел

HCF двух натуральных чисел можно найти с помощью алгоритма леммы Евклида о делении
Мы знаем, что для любых двух целых чисел a. б. мы можем написать следующее выражение

a = bq + r, 0≤r Если r = 0, тогда
HCF (a. B) = b
Если r ≠ 0, то
HCF (a. B) = HCF (br)
Снова выражая целое число b.r в лемме Евклида о делении, получаем
b = pr + r1
HCF (b, r) = HCF (r, r1)

Аналогично последовательное деление Евклида может быть записано до тех пор, пока мы не получим нулевой остаток, делитель в этой точке называется HCF a и b

• HCF (a, b) = 1 — Тогда a и b взаимно простые числа.

• Произведение простых чисел Теорема арифметики — составное число = произведение простых чисел

• HCF и LCM методом разложения на простые множители:
  HCF = произведение наименьшей степени каждого общего множителя в числах
  LCM = произведение наибольшей степени каждого простого множителя, входящего в число

• Важная формула HCF (a, b) X LCM (a, b) = a X b

• Важная концепция рационального числа — Завершающее десятичное выражение может быть записано в форме p / 2 ⁿ 5 ^m

Основная теорема арифметики | CBSE Класс 10 Математика Формулы вещественных чисел

Эта теорема утверждает, что «каждое составное число может быть выражено (разложено на множители) как произведение простых чисел, и эта факторизация уникальна, за исключением порядка, в котором встречаются простые множители.