Система счисления двоичная примеры: Двоичная система счисления — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Page not found — Сайт skobelevserg!

Главная
Информатика
Практикумы
Подготовка к ОГЭ
Рабочие программы
Используемая литература
Об авторах

Unfortunately the page you’re looking doesn’t exist (anymore) or there was an error in the link you followed or typed. This way to the home page.

Главная
Информатика
- 5 класс (ФГОС)
- - Информация вокруг нас
  - Компьютер — универсальная машина для работы с информацией
  - Ввод информации в память компьютера
  - Управление компьютером
  - Хранение информации
  - Передача информации
  - Кодирование информации
  - Текстовая информация
  - Представление информации в виде таблиц
  - Наглядные формы представления информации
  - Компьютерная графика
  - Обработка информации
- 6 класс (ФГОС)
- - Объекты окружающего мира
  - Компьютерные объекты
  - Отношения объектов и их множеств
  - Разновидности объектов и их классификация
  - Системы объектов
  - Персональный компьютер как система
  - Как мы познаем окружающий мир
  - Понятие как форма мышления
  - Информационное моделирование
  - Знаковые информационные модели
  - Табличные информационные объекты
  - Графики и диаграммы
  - Схемы
  - Что такое алгоритм
  - Исполнители вокруг нас
  - Формы записи алгоритмов
  - Типы алгоритмов
  - Управление исполнителем Чертежник
  - Компьютерный практикум
- 7 класс (ФГОС)
- - Информация и информационные процессы
  - Компьютер универсальное устройство для работы с информацией
  - Обработка графической информации
  - Обработка текстовой информации
  - Технология мультимедиа
- 8 класс (ФГОС)
- - Математические основы информатики
  - Основы алгоритмизации
  - Начала программирования
- 9 класс (ФГОС)
- - Моделирование и формализация
  - Алгоритмизация и программирование
  - Обработка числовой информации в электронных таблицах
  - Коммуникационные технологии
- 10 класс (ФГОС)
- - Информация и информационные процессы
  - Компьютер и его программное обеспечение
  - Представление информации в компьютере
  - Элементы теории множеств и алгебры логики
  - Современные технологии создания и обработки информационных объектов
- 11 класс (ФГОС)
- - Обработка информации в электронных таблицах
  - Алгоритмы и элементы программирования
  - Информационное моделирование
  - Сетевые информационные технологии
  - Основы социальной информатики
Практикумы
- Google формы
- Основы работы в Microsoft PowerPoint
- Создание анимации в презентациях
- Основы работы в Microsoft Word
- Основы работы в Microsoft Excel
- Создание простейшей базы данных
- Практикум по MS Excel
Подготовка к ОГЭ
Рабочие программы

Используемая литература
Об авторах
- Блоги
- Сайты

Двоичная арифметика : сложение, вычитание, умножение, деление

Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.

Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения.

Таблица сложения, вычитания и умножения для двоичной системы счисления

Сложение	Вычитание	Умножение
0 + 0 = 0	0 — 0 = 0	0 ∙ 0 = 0
0 + 1= 1	1 — 0 = 1	0 ∙ 1 = 0
1 + 0 = 1	1 — 1 = 0	1 ∙ 0 = 0
1 + 1 = 10	10 — 1 = 1	1 ∙ 1 = 1

Сложение двоичных чисел

Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.

Пример: 1011,1₂ + 1010,11₂

Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример: 111,1₂ + 111₂ + 101,1₂

При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают 100₂. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1.
Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = 101₂. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.

Вычитание двоичных чисел

В случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает по одной единице во всех промежуточных нулевых разрядах и две единицы в том разряде, для которого занималась.
Пример: 10110,01₂ — 1001,1₂

Умножение и деление двоичных чисел

Зная операции двоичной арифметики, можно переводить числа из двоичной системы счисления в любую другую.
Пример: Перевести число 101111011₂ в десятичную систему счисления.
Поскольку 10₁₀ = 1010₂, запишем

Полученные остатки, 1001₂ = 9₁₀, =111₂ = 7₁₀, 11₂ = 3₁₀. Искомое число 101111011₂ = 379₁₀.

Назад: Представление данных и архитектура ЭВМ

Двоичная система счисления Определение и значение

Лучшие определения
Викторина
Примеры

Сохраните это слово!

Метод представления чисел, основанный на 2 и использующий только цифры 0 и 1. Каждая последующая цифра представляет степень числа 2. Например, 10011 представляет (1 X 24) + (0 X 23) + ( 0 х 22) + (1 х 21) + (1 х 20), или 16 + 0 + 0 + 2 + 1, или 19.

Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!

Вопрос 1 из 7

Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.

Слова рядом с двоичной системой счисления

двоичная цифра, двоичное деление, двоичная форма, двоичная запись, двоичное число, двоичная система счисления, двоичная операция, двоичная оппозиция, двоичный пульсар, двоичная звезда, двоичная система

Как использовать двоичную систему счисления в предложении

Было много положительных отзывов от людей, интересующихся небинарными людьми.
Проблема трансгендерных знакомств Grindr|Дэвид Левсли|9 января 2015 г. |DAILY BEAST
«Наши участники продолжают сталкиваться с рядом проблем», — сказала она.
Война республиканцев с Кале|Патриция Мерфи|7 января 2015 г.|DAILY BEAST
В 2014 году на регулярных рейсах коммерческой авиации не было ни одного случая смерти в системе, которая выполняет 68 000 рейсов в день.
Раздражающие задержки в аэропорту могут помешать вам стать следующей AirAsia 8501|Клайв Ирвинг|6 января 2015 г.|DAILY BEAST
Количество несогласных беспрецедентно для современной эпохи.
Демократы случайно спасли Бонера от республиканского переворота|Бен Джейкобс, Джеки Кусинич|6 января 2015 г.|DAILY BEAST

Она наполняет своих персонажей — сильных женщин, сопротивляющихся сексистской системе — с таким сердцем.
Оскар 2015: Выбор The Daily Beast, от Скарлетт Йоханссон до «Отрочества»|Марлоу Стерн|6 января 2015 г.|DAILY BEAST
Страна хорошо населена, так как в ней пятьдесят один город, около сотни городов-крепостей и множество деревень.
Путешествия Гулливера|Джонатан Свифт
Швеция исключила британские товары в соответствии с континентальной системой, установленной Бонапартом.
Книга истории и хронологии на каждый день|Джоэл Манселл
У нас было шесть полевых орудий, но мы взяли только четыре, запряженных вдвое большим количеством лошадей.
Эдинбургский журнал Blackwood, № CCCXXXIX. Январь 1844 г. Том. LV.|Various
Однако, поскольку Испания пала с высокого положения, которое она когда-то занимала, ее колониальная система также рухнула.
Табак; Его история, разновидности, культура, производство и торговля|E. Р. Биллингс.
Реформаторы более раннего периода не были равнодушны к необходимости централизованной организации банковской системы.
Чтения по деньгам и банковскому делу | Честер Артур Филлипс

Что такое двоичная система счисления? Определение, подсчет, пример, использование и преимущества двоичной системы счисления

Определение : Система счисления, которая соответствует только двум числовым цифрам, то есть 0 и 1, известна как двоичная система счисления.

Поскольку это двузначная система, известная как система с основанием 2 . Работа компьютерной системы зависит исключительно от двоичной системы счисления. Поскольку он понимает только двоичные значения, то есть 0 и 1.

Теперь возникает вопрос, почему компьютерная система понимает только двоичные значения?

Ответ на поставленный выше вопрос заключается в том, что компьютер является электронным устройством, а все электрические и электронные устройства воспринимают только электрические сигналы. Таким образом, двоичные цифры 0 и 1 просто соответствуют состоянию устройства

на и на соответственно.

Цифры 0 и 1 имеют то же значение, что и в десятичной системе счисления. Однако изменение положения двоичных чисел зависит от представляемого значения.

Так как с увеличением позиции справа налево вес показывает последовательное увеличение степени 2.

Давайте посмотрим, как мы можем записать число в двоичном разряде в степени 2:

Две двоичные цифры 0 и 1 известны как биты . Бит считается первичной единицей информации. Слово BIT образовано от комбинации

BI nary и digit T . Однако сочетание 8 бит дает начало другой единице, известной как « байт» . Кроме того, когда 4 бита объединяются, формируется блок «полубайт» .

Здесь следует отметить, что основные булевы функции основаны на двоичной системе счисления. Можно изменить двоичное представление значения в десятичной, восьмеричной или шестнадцатеричной системе счисления. Кроме того, мы можем преобразовать любую систему счисления в двоичную систему счисления, выполнив соответствующую операцию.

Подсчет двоичных чисел

Как мы знаем, в десятичной системе счисления существует 10 цифр, т. е. от 0 до 9. Однако, используя комбинацию этих слов при изменении их положения, можно представить несколько величин.

Давайте сначала разберемся, как ведется счет в двоичной системе счисления, а затем мы перейдем к пониманию ее десятичного представления.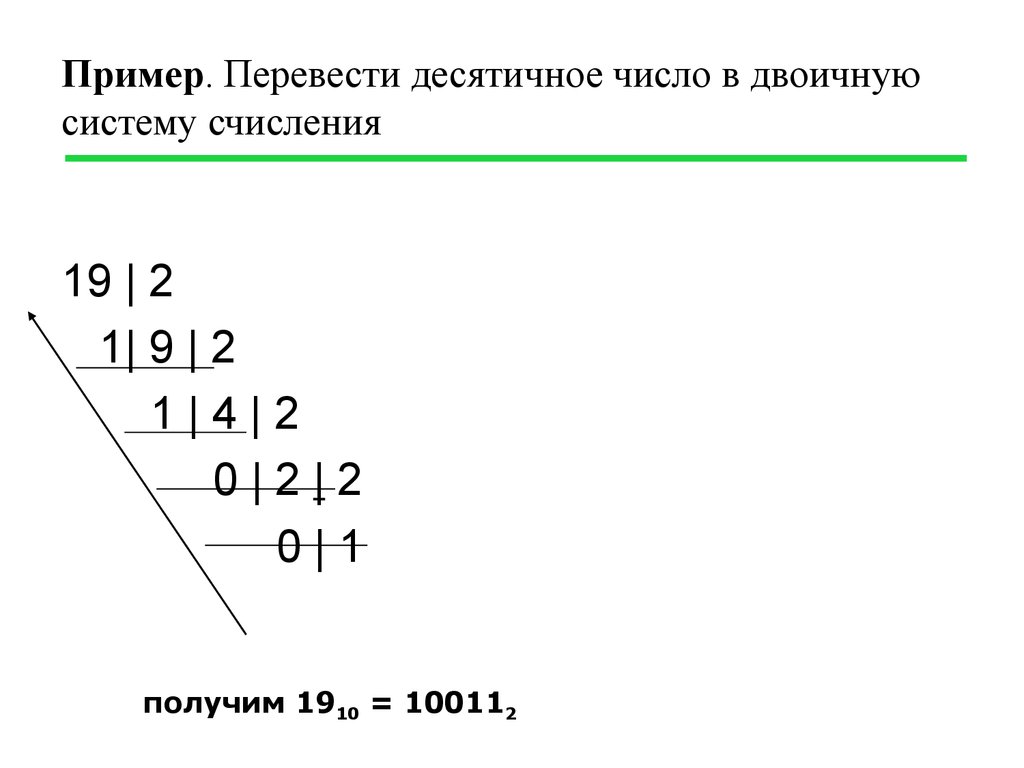

Здесь у нас есть только 2 цифры, так как счет начинается с 0 и заканчивается на 1. Однако из-за наличия только 2 цифр при последовательном счете цифра 1 сдвигается влево, а цифра справа становится 0 таким образом предоставляя 10 в двоичном формате, который представляет собой не что иное, как 2 в десятичной системе счисления.

Приведенная ниже таблица даст вам лучшее представление о представлении десятичного числа в двоичном формате и формате его подсчета:

Из приведенного выше табличного представления ясно, что двоичное число превосходит в степени 2, начиная с 0, о котором мы уже говорили ранее.

Чтобы получить двоичный эквивалент десятичного числа, мы последовательно выполняем деление частного члена, пока оно не станет 0. Также последовательно отмечаем остаток, полученный после каждого деления. Затем эти напоминания записываются в порядке, обратном их приходу. Таким образом, мы просто получаем двоичный эквивалент любого десятичного значения.

Теперь перейдем к математической реализации рассмотренного выше метода:

Например, пусть число будет 15 :

Метод известен как метод двойного мазка .

Иногда в реальной жизни мы сталкиваемся с десятичными числами в дробном формате. Итак, давайте возьмем пример дробного десятичного числа, которое необходимо преобразовать в дробное двоичное число.

Например, пусть число будет 0,65 :

Чтобы преобразовать 0,65 в дробное двоичное число, число сначала умножается на 2. Результат, полученный после умножения, последовательно умножается на 2. Кроме того, после умножения полученный результат является десятичным значением, таким образом, цифра перед десятичное число служит переносным битом.

Преобразование дробно-десятичной системы в двоичную в виде математической реализации показано ниже:

Здесь в данном случае отмечен перенос в нисходящем направлении. Здесь следует отметить, что двоичное умножение обычно продолжается до восьми двоичных разрядов. Следовательно, можно сказать, что полученный результат не является точно эквивалентным, а рассматривается как приблизительное значение.

Характеристики двоичной системы счисления

Это двузначная система счисления.
Это обычно называют системой счисления с основанием 2.
Различные позиции двоичных систем счисления показывают эквивалентное значение в степени 2.
Крайняя левая позиция двоичного представления показывает 2 в степени x. Здесь x представляет крайнее положение слева.

Преимущества двоичной системы счисления

С развитием двоичной системы счисления выполнение различных задач упростилось. Используя двоичные значения, можно легко решить различные логические задачи, основанные на булевой алгебре.

Использование двоичной системы счисления

В электронных устройствах : Электронные устройства, такие как компьютер, диод, BJT, MOSFET и т. д., работают только с низким и высоким значением, т. е. 0 и 1 двоичной системы счисления.
В перфокартах : Они широко используются в перфокартах, которые показывают 0 для неперфокарты и 1 для перфокарты.