Оптимальная система счисления: sevabashirov — LiveJournal
Давно хотел определить с точки зрения банальной эрудиции и формальной математики, какая из позиционных систем счисления является наиболее удобной, в некотором смысле — эргономичной. Потому что — как многим известно — привычная современной цивилизации десятичная система выбрана не из соображений оптимальности, а прямо вытекает из анатомии человека. Было бы не 10 пальцев на руках — укоренилось бы другое основание. Когда люди считали окружающие предметы буквально по пальцам, десятичная система была разумным выбором, да и то: почему именно пальцы-«штуки»? Кому-то было удобнее по фалангам 4 пальцев одной руки, указывая на них большим — так получила некоторую популярность 12-ричная система. Но дальше — просто сила привычки, QWERTY-эффект в чистом виде: используем не потому, что удобнее всего, а потому, что так сложилось исторически, в силу традиции.___
Как математически определить удобство использования той или иной системы счисления? Во-первых можно рассмотреть, как в них записываются числа.
Так вот, эти выкладки — давно уже не секрет, кто их только не делал. В непрерывном случае максимум приходится на число e=2,718…, так что основание 3 выглядит лучше всех, 2 и 4 — одинаково чуть похуже: http://phg.su/basis2/X51.HTM — наглядно.
___
Но этого явно мало. При таком подходе учтено удобство записи чисел, но есть же еще и вычисления, операции над ними. Частично это уже учтено (см. выше фразу про таблицы сложения-умножения). И здесь приходится к месту аргумент, который — если кто в курсе — был основным доводом у сторонников двенадцатеричной системы: 12 делится нацело на 1, 2, 3, 4, 6 и собственно 12 против 1, 2, 5 и 10 у десятки. Это еще Перельман описывал в «Занимательной арифметике». И действительно, чем больше круглых чисел в произведениях и чем меньше периодических дробей в частных — очевидно, тем удобнее и быстрее подсчеты.
Итоговая формула: коэффициент эргомичности системы счисления q(n) = lg(n) / n * d(n) * 2,5 — домножил для приведения коэффициента десятичной системы к единице. Мы вправе это делать, поскольку основание логарифма все равно взято произвольно, у абсолютных значений q(n) нет смыслового наполнения. Ниже — таблица 25 лидеров:
| n | lg(n) | d(n) | q(n) |
| 12 | 1,079 | 6 | 1,349 |
| 6 | 0,778 | 4 | 1,297 |
| 24 | 1,380 | 8 | 1,150 |
| 4 | 0,602 | 3 | 1,129 |
| 8 | 0,903 | 4 | 1,129 |
| 18 | 1,255 | 6 | 1,046 |
| 10 | 1,000 | 4 | 1,000 |
| 30 | 1,477 | 8 | 0,985 |
| 20 | 1,301 | 6 | 0,976 |
| 36 | 1,556 | 9 | 0,973 |
| 16 | 1,204 | 5 | 0,941 |
| 60 | 1,778 | 12 | 0,889 |
| 48 | 1,681 | 10 | 0,876 |
| 14 | 1,146 | 4 | 0,819 |
| 40 | 1,602 | 8 | 0,801 |
| 3 | 0,477 | 2 | 0,795 |
| 9 | 0,954 | 3 | 0,795 |
| 15 | 1,176 | 4 | 0,784 |
| 28 | 1,447 | 6 | 0,775 |
| 72 | 1,857 | 12 | 0,774 |
| 42 | 1,623 | 8 | 0,773 |
| 2 | 0,301 | 2 | 0,753 |
| 32 | 1,505 | 6 | 0,706 |
| 5 | 0,699 | 2 | 0,699 |
| 120 | 2,079 | 16 | 0,693 |
Итак, «дозеналисты» были правы, у основания 12 действительно отличная репутация! А привычная нам десятка занимает седьмую позицию — достойную, но существенно уступающую.
 Если отойти в бытовую сферу, то главный недочет десятки — то, что она не делится на 3, а между тем на 3 делить приходится крайне часто. Ну и чтобы четвертые доли содержали лишь один знак после запятой вместо двух — тоже хороший бонус. Вкупе с сокращением длины больших чисел на 8% это оправдывает заучивание чуть большей таблицы умножения.
Если отойти в бытовую сферу, то главный недочет десятки — то, что она не делится на 3, а между тем на 3 делить приходится крайне часто. Ну и чтобы четвертые доли содержали лишь один знак после запятой вместо двух — тоже хороший бонус. Вкупе с сокращением длины больших чисел на 8% это оправдывает заучивание чуть большей таблицы умножения.Само собой, прикидка крайне грубая и многих вещей не учитывает. Но тут, как говорится, выделяйте гранты на дальнейшие исследования.
Тема поста интересна в первую очередь френдам aaamibor, doncunita, lrlay777, sly2m, spamsink, vmenshov и другим.
ПРОДОЛЖЕНИЕ ПОСТА С УТОЧНЕНИЕМ ФОРМУЛЫ
 livejournal.com/270269.html
livejournal.com/270269.htmlЗадача №1. Перевод из одной системы в другую, сравнение чисел в различных системах.
Автор материалов — Лада Борисовна Есакова.
Системы счисления и их разновидности.
Система счисления – это способ представления, записи чисел с помощью письменных знаков. Количество этих самых знаков (цифр), используемых для записи чисел, называется основанием системы счисления.
Различных систем счисления у разных народов существовало великое множество. Но все их можно поделить на непозиционные и позиционные. Позиционные системы в свою очередь подразделяются на однородные и смешанные.
1. Непозиционные системы счисления.
В непозиционных системах счисления число, обозначаемое цифрой, не зависит от положения цифры в записи числа.
Самым простым примером непозиционной системы счисления является единичная (унарная) система счисления. Это запись числа с помощью повторения зарубок на дощечке или узелков на веревке. Все зарубки, узелки или другие «цифры» абсолютно одинаковы, а потому их порядок не имеет значения, число получается простым суммированием количества символов.
Это запись числа с помощью повторения зарубок на дощечке или узелков на веревке. Все зарубки, узелки или другие «цифры» абсолютно одинаковы, а потому их порядок не имеет значения, число получается простым суммированием количества символов.
Унарной системой счисления до сих пор пользуются маленькие дети, показывая количество на пальцах.
Еще одной используемой до сих пор почти непозиционной системой счисления является Римская:
Она названа почти непозиционной, потому что в Римской системе, кроме обычного сложения цифр в числе, действует правило: если младшая цифра стоит слева от старшей, она вычитается из суммы.
Т.е. число , а число
Непозиционных систем счисления известно очень много, но мы завершим на этом их рассмотрение. Использование непозиционных систем неудобно, а для очень больших чисел практически невозможно, и к тому же нет возможности записать дроби.
2. Позиционные системы счисления.
В позиционных системах счисления число, обозначаемое цифрой, зависит от положения цифры в записи числа.
Самой популярной позиционной системой является, конечно же, десятичная.
Мы видим, что числа 15 и 51 имеют совсем разные значения, хотя состоят из одних и тех же цифр. Разница обусловлена положением цифры в числе.
Но десятичная система ничем не лучше и не хуже другой позиционной системы, она просто привычная. Число 10 выбрано основанием по количеству пальцев на двух руках (для удобства счета). Однако, в Китае популярной была пятиречная система счисления (по количеству пальцев на одной руке), а двадцатиричная система использовалась у Ацтеков, Майя и некоторых народов Африки (по количеству пальцев на ногах и руках).
Еще одной известной позиционной системой счисления является двенадцатиричная (считали фаланги пальцев (кроме большого) на руке. Элементы двенадцатиричной системы сохранились в Англии: 1 фут = 12 дюймов, 1 шиллинг = 12 пенсов.
Ну и, наконец, незаменимая в наш компьютерный век двоичная система. Почему именно двоичная? Да потому что у компьютера только 2 «пальца», точнее два состояния: «есть ток», «нет тока».
2.1. Однородные системы счисления.
В однородной системе в каждой позиции числа может находиться любая цифра. Примером может быть запись числа в любой позиционной системе счисления (десятичной, двоичной и пр.). Т.е. когда мы пишем число в десятичной системе, в любой позиции мы можем написать цифру от 0 до 9.
2.2. Смешанные системы счисления.
В смешанной системе счисления набор используемых цифр может отличаться в зависимости от позиции. В качестве примера удобно рассмотреть запись времени в формате ЧЧ.ММ.СС (часы.минуты.секунды). В качестве часов может быть использовано число от 00 до 23, в качестве минут и секунд – число от 00 до 59.
Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа.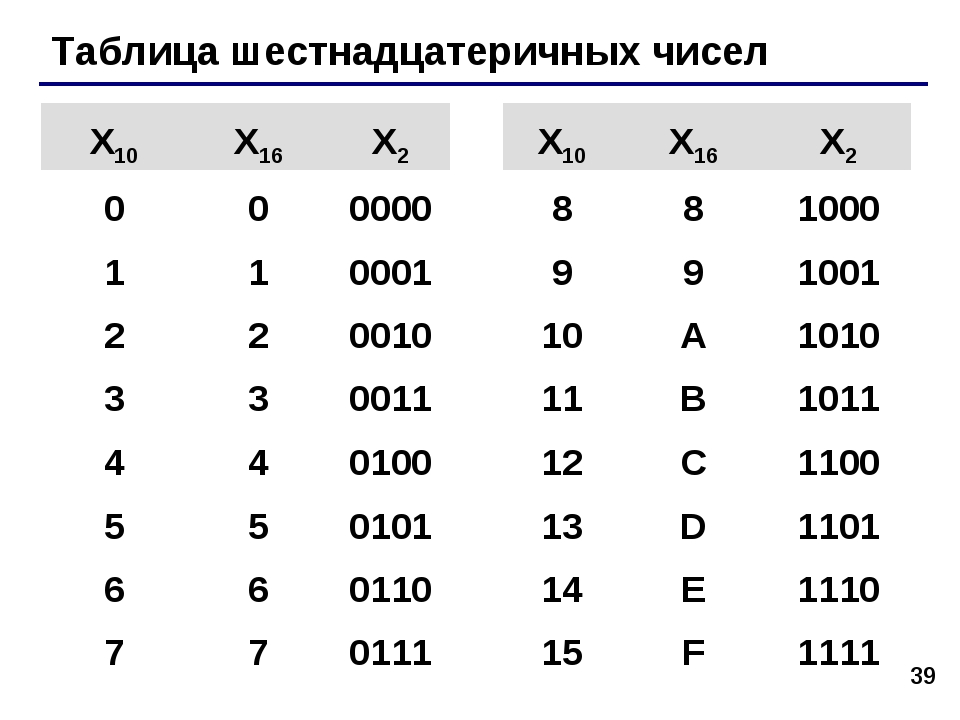 Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
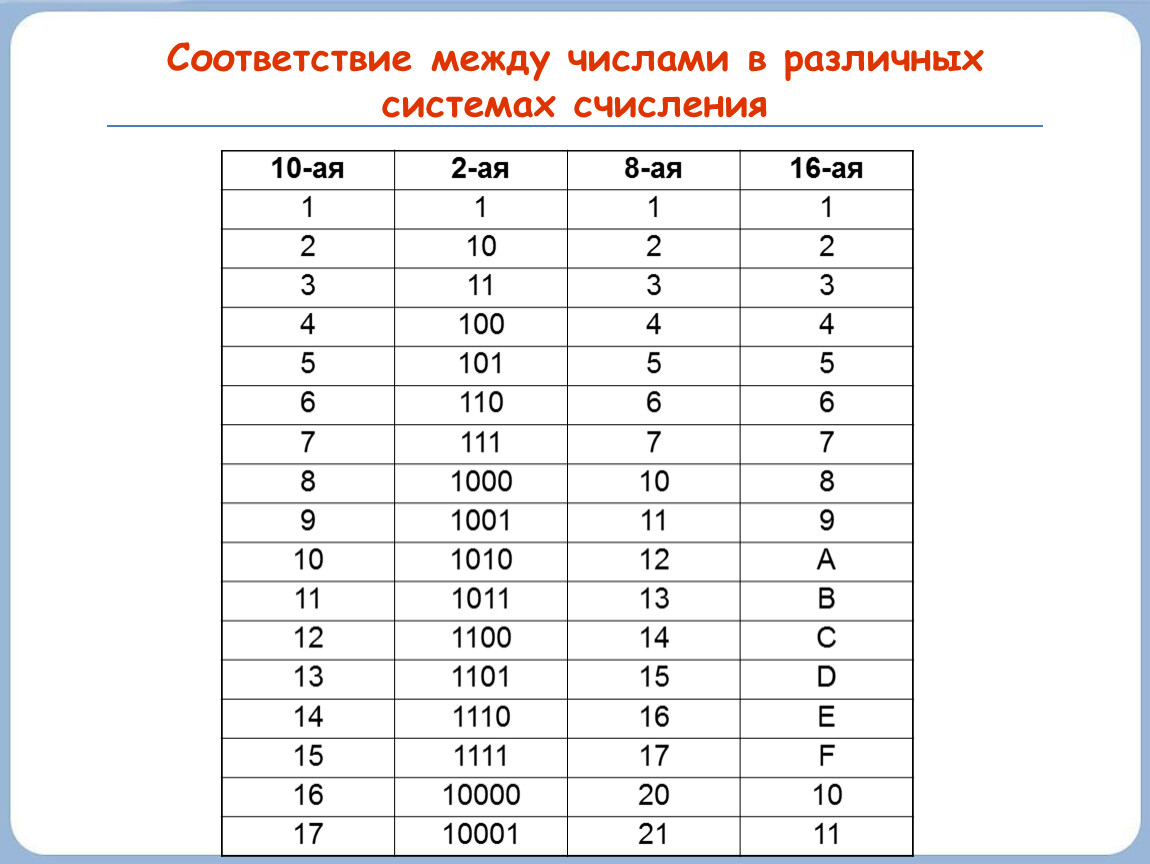
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита.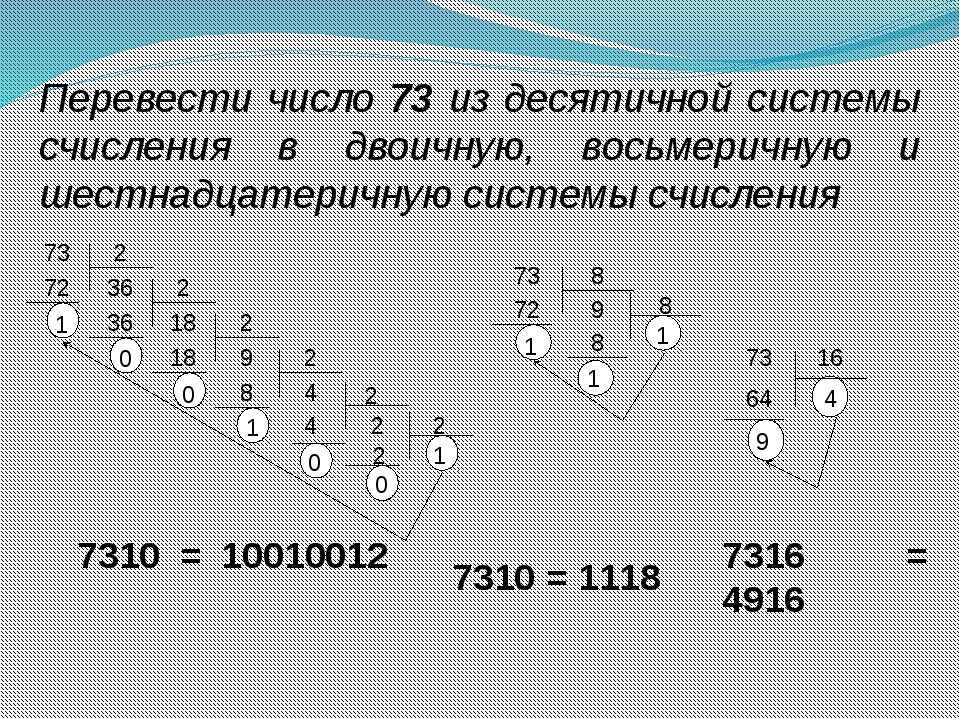 Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.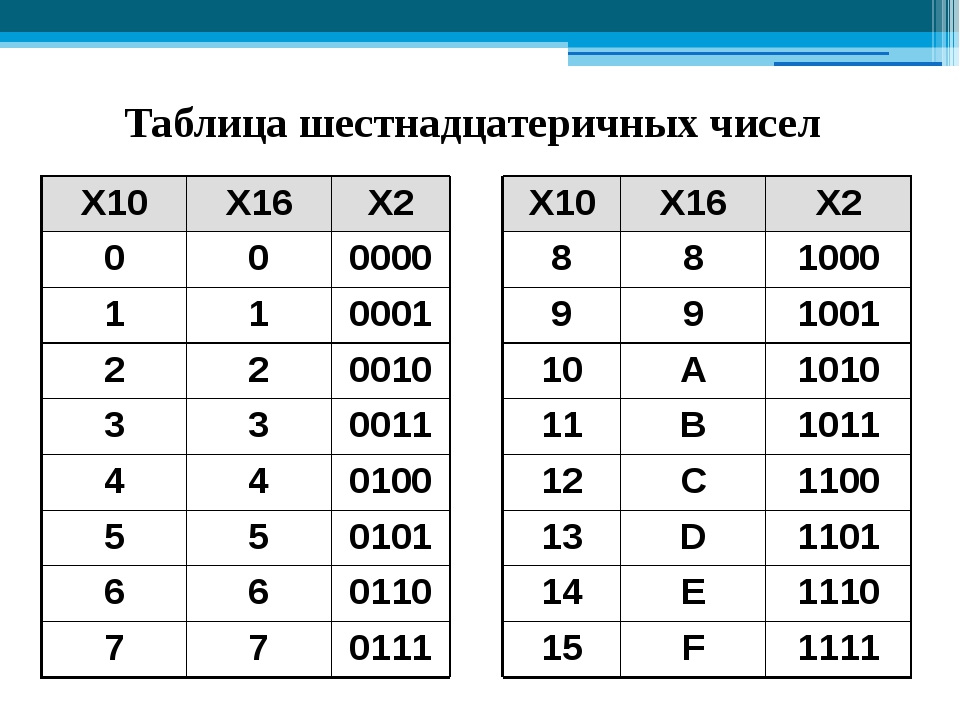 е.
е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т. е.
е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.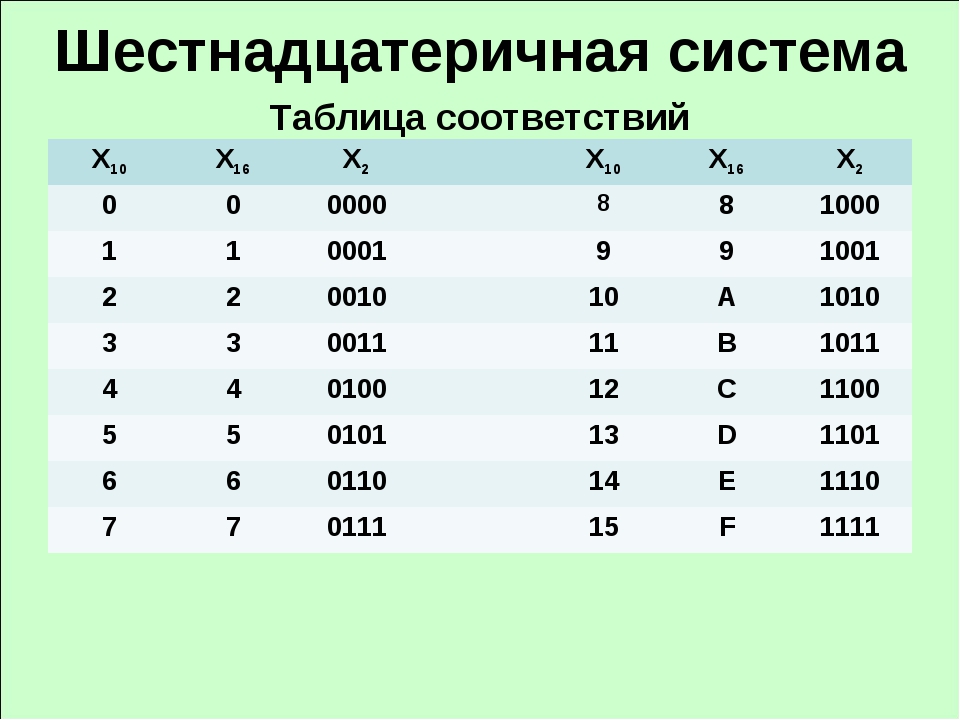
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Десятичные дроби и смешанные числа в разных системах счисления.
Автор — Лада Борисовна Есакова.
Перевод целых чисел из одной системы счисления в другую обычно не вызывает проблем. А вот необходимость перевести десятичную дробь или смешанное число (число с целой и дробной частью) из системы в систему часто ставит в тупик даже сильных учеников.
1. Перевод смешанного числа в десятичную систему счисления из любой другой.
Для перевода смешанного числа в десятичную систему из любой другой следует пронумеровать разряды числа, начиная с нуля, справа налево от младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.
Пример 1.
Переведите число 105,4 из восьмеричной системы в десятичную.
Решение:
Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :
Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа:
Ответ:
2. Перевод десятичных дробей из десятичной системы счисления в любую другую.
Для перевода десятичной дроби из десятичной системы в любую другую следует умножать дробь, а затем дробные части произведений, на основание новой системы пока дробная часть не станет равной 0 или до достижения указанной точности. Затем целые части выписать, начиная с первой.
Пример 2
Переведите десятичное число 0,816 в двоичную систему с точностью до сотых.
Решение:
Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на 2 и выписываем целые части, начиная с первой:
Ответ:
Пример 3.
Переведите десятичное число 0,8125 в восьмеричную систему.
Решение:
Умножаем дробь 0,8125, а затем дробную часть произведения (0,5) на 8 и выписываем целые части, начиная с первой:
Ответ:
3. Перевод смешанных чисел из десятичной системы счисления в любую другую
Если необходимо перевести смешанное число из десятичной системы в любую другую, следует перевести целую и дробную части, а затем записать, разделив десятичной запятой.
Пример 4.
Сколько единиц в двоичной записи десятичного числа 14,125?
Решение:
Переведем целую часть числа в двоичную систему:
Переведем дробную часть числа в двоичную систему:
Соединим целую и дробную части:
14,12510 = 1110,0012
Количество единиц равно 4.
Ответ: 4
Ты нашел то, что искал? Поделись с друзьями!
ДЕС (функция ДЕС) — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование DECIMAL
в Microsoft Excel.
Описание
Преобразует текстовое представление числа с указанным основанием в десятичное число.
Синтаксис
ДЕС(текст;основание)
Синтаксис функции ДЕС имеет аргументы, указанные ниже.
-
Текст Обязательный аргумент.
-
Основание. Обязательный аргумент. Основание системы счисления должно быть целым числом.
 53, может привести к потере точности.
53, может привести к потере точности. -
Основание системы счисления должно быть больше или равно 2 (двоичная система) или меньше или равно 36 (36-ричная система).
Для основания более 10 используются числовые значения 0–9 и буквы A–Z. Например, для основания 16 (шестнадцатеричного) используются цифры 0–9 и буквы A–F, а для основания 36 — цифры 0–9 и буквы A–Z. -
Если хотя бы один из аргументов находится за пределами своих ограничений, то decIMAL может вернуть #NUM! или значение ошибки #ЗНАЧ!.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание | Результат | Принцип действия |
|---|---|---|---|
|
‘=ДЕС(«FF»,16) |
Преобразует шестнадцатеричное значение FF (с основанием 16) в эквивалентное ему десятичное значение (с основанием 10). Результат — 255. |
=ДЕС(«FF»;16) |
«F» в позиции 15 в шестнадцатеричной системе счисления. Так как все системы счисления начинаются с 0, 16-й символ в шестнадцатеричной системе будет стоять на 15-й позиции. |
|
‘=ДЕС(111;2) |
Преобразует двоичное значение 111 (с основанием 2) в эквивалентное ему десятичное значение (с основанием 10). Результат — 7. |
=ДЕС(111;2) |
«1» в позиции 1 в двоичной системе счисления. В приведенной ниже формуле показано, как число преобразуется в десятичное. |
|
Функция ДВ.В.ДЕС в ячейке C6 подтверждает этот результат. |
=ДВ.В.ДЕС(111) |
Формула |
|
|
=(1*(2^2))+(1*(2^1))+(1*(2^0)) |
|||
|
‘=ДЕС(«zap»;36) |
Преобразует значение «zap» с основанием 36 в эквивалентное десятичное значение (45745). |
К началу страницы
Преимущества двенадцатеричной системы над десятичной | Техночтиво
Привет любителям математики!
Не забудьте поставить лайк. Приятного прочтения!
Считаем до 12 на пальцах одной рукиСчитаем до 12 на пальцах одной руки
Очень занятную для себя находку я не так давно сделал. Двенадцатеричная система счисления.
Честно сказать, никогда я о ней не слышал. Двоичную знаю, десятичную, шестнадцатеричную, но двенадцать…
Но, несмотря на то, что о ней я почти ничего не знал, сталкивался ежедневно. Те же часы как пример.
Как оказалось, многие бытовые вещи с ней считать куда проще! Но, обо всем поподробнее.
Сначала, познакомимся с самими числами.
Так выглядит стандартная десятичная система. Все последующие цифры создаются именно из этих 10
Все последующие цифры создаются именно из этих 10
Цифры десятичной системы
А теперь, взглянем на дюжину.
Цифры двенадцатиричной системы счисленияЦифры двенадцатиричной системы счисления
Дальше, как ни странно, идет 10, только произносится она не «десять», а «До». Далее пойдет 11 — «Два до один», 12 — «Два до два» и так далее.
Последние две цифры имеют такие названия:
Кое где их пишут просто как «А» и «В»Кое где их пишут просто как «А» и «В»
Двузначные и трехзначные числа получаются возведением десяти в соответствующие степени, с двенадцатью — то же самое.
Красным — числа в десятичной системеКрасным — числа в десятичной системе
По сути, если смотреть с точки зрения математики, не изменится ничего. Нужно только привыкнуть к «новым» цифрам. Математические законы останутся прежними. Вот только у такой системы есть ряд преимуществ.
Если в десятичной системе, десятка кратна четырем числам:
То в двенадцатеричной уже шести!
Представьте себе дробь 1/3. В десятичной системе это число будет выглядеть как то так — 0,333(3).
В десятичной системе это число будет выглядеть как то так — 0,333(3).
В двенадцатеричной — никаких троек в периоде!
«Четыре двенадцатеричных» 🙂«Четыре двенадцатеричных» 🙂
С 1/6 также не получится никаких бесконечных цифр после запятой, это будет просто 0,2.
Согласитесь, в бытовом плане довольно удобно. Правда, уже те же 1/5 будет выглядеть не совсем презентабельно:
Бесконечная двенадцатеричная дробь…Бесконечная двенадцатеричная дробь…
Да, бесконечные дроби здесь тоже есть, но их меньше.
Стоит отметить, что некоторые малые народы Тибета и Нигерии пользуются такой системой. Да и в давние времена она была распространена из-за своего удобства. Но, в какой-то момент ее просто вытеснили.
Если честно, несмотря на некоторые свои преимущества, переход на эту систему, как по мне, не возможен и не нужен. А потому, забивать ею голову не стоит. Воспринимайте это просто как интересную информацию к размышлению.
Спасибо, что дочитали до конца.Подписывайтесь, ставьте лайки и не болейте!
parseInt() — JavaScript | MDN
Функция parseInt() принимает строку в качестве аргумента и возвращает целое число в соответствии с указанным основанием системы счисления.
The source for this interactive example is stored in a GitHub repository. If you’d like to contribute to the interactive examples project, please clone https://github.com/mdn/interactive-examples and send us a pull request.
Параметры
string- Значение, которое необходимо проинтерпретировать. Если значение параметра
stringне принадлежит строковому типу, оно преобразуется в него (с помощью абстрактной операцииToString). Пробелы в начале строки не учитываются.
radix- Целое число в диапазоне между 2 и 36, представляющее собой основание системы счисления числовой строки
string, описанной выше. В основном пользователи используют десятичную систему счисления и указывают 10. Всегда указывайте этот параметр, чтобы исключить ошибки считывания и гарантировать корректность исполнения и предсказуемость результата. Когда основание системы счисления не указано, разные реализации могут возвращать разные результаты.
В основном пользователи используют десятичную систему счисления и указывают 10. Всегда указывайте этот параметр, чтобы исключить ошибки считывания и гарантировать корректность исполнения и предсказуемость результата. Когда основание системы счисления не указано, разные реализации могут возвращать разные результаты.
Возвращаемое значение
Целое число, полученное парсингом (разбором и интерпретацией) переданной строки. Если первый символ не получилось сконвертировать в число, то возвращается NaN.
Функция parseInt преобразует первый переданный ей аргумент в строковый тип, интерпретирует его и возвращает целое число или значение NaN. Результат (если не NaN) является целым числом и представляет собой первый аргумент (string), рассматривающийся как число в указанной системе счисления (radix). Например, основание 10 указывает на преобразование из десятичного числа, 8 — восьмеричного, 16 — шестнадцатеричного и так далее. Если основание больше
Если основание больше 10, то для обозначения цифр больше 9 используются буквы. Например, для шестнадцатеричных чисел (основание 16) используются буквы от A до F.
Если функция parseInt встречает символ, не являющийся числом в указанной системе счисления, она пропускает этот и все последующие символы (даже, если они подходящие) и возвращает целое число, преобразованное из части строки, предшествовавшей этому символу. parseInt отсекает дробную часть числа. Пробелы в начале и конце строки разрешены.
Так как некоторые числа включают символ e в своём строковом представлении (например, 6.022e23), то использование parseInt для усечения числовых значений может дать неожиданные результаты, когда используются очень малые или очень большие величины. parseInt не должна использоваться как замена для Math.floor().
Если основание системы счисления имеет значение undefined (не определено) или равно 0 (или не указано), то JavaScript по умолчанию предполагает следующее:
- Если значение входного параметра
stringначинается с «0x» или «0X«, за основание системы счисления принимается 16, и интерпретации подвергается оставшаяся часть строки. - Если значение входного параметра
stringначинается с «0», за основание системы счисления принимается либо 8, либо 10, в зависимости от конкретной реализации. В спецификации ECMAScript 5 прописано использование 10 (десятичная система), но это поддерживается ещё не всеми браузерами, поэтому необходимо всегда указывать основание системы счисления при использовании функцииparseInt. - Если значение входного параметра
stringначинается с любого другого символа, система счисления считается десятичной (основание 10).
Если первый символ строки не может быть преобразован в число, parseInt возвращает значение NaN.
С точки зрения математики, значение NaN не является числом в какой-либо системе счисления. Чтобы определить, вернёт ли parseInt значение NaN в качестве результата, можно вызвать функцию isNaN. Если NaN участвует в арифметических операциях, результатом также будет NaN.
Для преобразования числа в строку в указанной системе счисления, используйте intValue.toString(radix).
Пример: Использование
parseIntВсе следующие примеры возвращают 15:
parseInt(" 0xF", 16);
parseInt(" F", 16);
parseInt("17", 8);
parseInt(021, 8);
parseInt("015", 10);
parseInt(15.99, 10);
parseInt("FXX123", 16);
parseInt("1111", 2);
parseInt("15*3", 10);
parseInt("15e2", 10);
parseInt("15px", 10);
parseInt("12", 13);
Все следующие примеры возвращают NaN:
parseInt("Hello", 8);
parseInt("546", 2);
Все следующие примеры возвращают -15:
parseInt("-F", 16);
parseInt("-0F", 16);
parseInt("-0XF", 16);
parseInt(-15.1, 10)
parseInt(" -17", 8);
parseInt(" -15", 10);
parseInt("-1111", 2);
parseInt("-15e1", 10);
parseInt("-12", 13);
Все следующие примеры возвращают 4:
parseInt(4.7, 10);
parseInt(4.7 * 1e22, 10);
parseInt(0.00000000000434, 10); Следующий пример возвращает 224:
parseInt("0e0", 16);
Хотя это не поощряется в спецификацией ECMAScript 3 и запрещено в ECMAScript 5, многие реализации интерпретируют числовую строку, начинающуюся с 0, как восьмеричную. Следующий пример может иметь как восьмеричный, так и десятичный результат. Чтобы избежать непредвиденного результата, всегда указывайте основание системы счисления.
parseInt("0e0");
parseInt("08");
ECMAScript 5 устраняет восьмеричную интерпретацию
Спецификация ECMAScript 5 функции parseInt больше не разрешает трактовать в восьмеричной системе счисления строки, начинающиеся с 0. ECMAScript 5 провозглашает:
Функция parseInt производит целочисленное значение в результате интерпретации содержимого строкового аргумента в соответствии с указанным основанием системы счисления.(\-|\+)?([0-9]+|Infinity)$/.test(value))
return Number(value);
return NaN;
} console.log(filterInt(‘421’));
console.log(filterInt(‘-421’));
console.log(filterInt(‘+421’));
console.log(filterInt(‘Infinity’));
console.log(filterInt(‘421e+0’));
console.log(filterInt(‘421hop’));
console.log(filterInt(‘hop1.61803398875’));
console.log(filterInt(‘1.61803398875’));
BCD tables only load in the browser
Перевод чисел из десятичной системы счисления в восьмеричную и наоборот.
Скачать урок в pdf формате.
В этом уроке информатики мы рассмотрим как перевести любое число из десятичной системы счисления в восьмеричную, а затем переведем произвольное число из восьмиричной системы счисления в десятичную, то есть сделаем обратное действие.
Итак в десятичной системе счисления мы пользуемся 10 цифрами с помощью которых можем составить любое число. Это цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В восьмеричной системе счисления у нас только восемь цифр 0, 1, 2, 3, 4, 5, 6, 7, с помощью которых мы можем составлять любые числа.
В восьмеричной системе счисления после семерки идет цифра 10 т.к. цифры 8 в ней нет. Почему? А потому что когда мы работаем в десятичной системе счисления то когда доходим до 9 то при прибавлении к ней единицы 9+1 получаем, что 9 заменяется на ноль, слева от которого добавляется 1 (к старшему разряду).
Таким образом мы можем попробовать составить небольшую таблицу соответствия чисел десятичной и восьмиричной системы счисления.
|
Десятичная |
Восьмеричная |
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
4 |
4 |
|
5 |
5 |
|
6 |
6 |
|
7 |
7 |
|
8 |
10 |
|
9 |
11 |
|
10 |
12 |
|
11 |
13 |
|
12 |
14 |
|
13 |
15 |
|
14 |
16 |
|
15 |
17 |
|
16 |
20 |
|
17 |
21 |
|
18 |
22 |
|
19 |
23 |
|
20 |
24 |
|
21 |
25 |
|
22 |
26 |
|
23 |
27 |
|
24 |
30 |
|
25 |
31 |
|
26 |
32 |
|
27 |
33 |
|
28 |
34 |
|
29 |
35 |
|
30 |
36 |
|
31 |
37 |
То есть, смотрите, когда мы выписывали правый столбец (числа в восьмеричной системе счисления) мы руководствовались тем правилом, которое описали выше таблицы. Как только у нас заканчиваются цифры системы счисления мы пишем ноль и добавляем единицу к старшему разряду.
А теперь рассмотрим как перевети число из десятичной системы счисления в восьмеричную. Давайте возьмем число 259 в десятичной системе счисления.
Число в десятичной системе счисления делим на основание степени (восьмерку). Получаем какую то целую часть и остаток. Если целая часть больше либо равна 8, то опять делим на основание степени и получаем целую часть и остаток. Как только целая часть становится меньше восьми, начинаем выписывать, сначала последнюю целую часть, а затем все остатки в обратном порядке. Это и будет число в новой системе счисления, в нашем случае в восьмиричной.
И сделаем обратное преобразование переведем число 403 в восьмеричной системе счисления в десмятичную.
То есть вначале мы нумеруем числа справа налево для того, чтобы затем каждое из чисел в восьмиричной системе счисления умножить на восьмерку в соответствующей степени. Сложив все, мы получим результат в десятичной системе счисления.
Скачать урок в pdf формате.
Числа: целые, вещественные, комплексные | Python 3 для начинающих и чайников
Числа в Python 3: целые, вещественные, комплексные. Работа с числами и операции над ними.
Целые числа (int)
Числа в Python 3 ничем не отличаются от обычных чисел. Они поддерживают набор самых обычных математических операций:
| x + y | Сложение |
| x — y | Вычитание |
| x * y | Умножение |
| x / y | Деление |
| x // y | Получение целой части от деления |
| x % y | Остаток от деления |
| -x | Смена знака числа |
| abs(x) | Модуль числа |
| divmod(x, y) | Пара (x // y, x % y) |
| x ** y | Возведение в степень |
| pow(x, y[, z]) | xy по модулю (если модуль задан) |
Также нужно отметить, что целые числа в python 3, в отличие от многих других языков, поддерживают длинную арифметику (однако, это требует больше памяти). y
Дополнительные методы
int.bit_length() — количество бит, необходимых для представления числа в двоичном виде, без учёта знака и лидирующих нулей.
>>> n = -37 >>> bin(n) '-0b100101' >>> n.bit_length() 6
int.to_bytes(length, byteorder, *, signed=False) — возвращает строку байтов, представляющих это число.
>>> (1024).to_bytes(2, byteorder='big') b'\x04\x00' >>> (1024).to_bytes(10, byteorder='big') b'\x00\x00\x00\x00\x00\x00\x00\x00\x04\x00' >>> (-1024).to_bytes(10, byteorder='big', signed=True) b'\xff\xff\xff\xff\xff\xff\xff\xff\xfc\x00' >>> x = 1000 >>> x.to_bytes((x.bit_length() // 8) + 1, byteorder='little') b'\xe8\x03'
classmethod int.from_bytes(bytes, byteorder, *, signed=False) — возвращает число из данной строки байтов.
>>> int.from_bytes(b'\x00\x10', byteorder='big') 16 >>> int.from_bytes(b'\x00\x10', byteorder='little') 4096 >>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=True) -1024 >>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=False) 64512 >>> int.from_bytes([255, 0, 0], byteorder='big') 16711680
Системы счисления
Те, у кого в школе была информатика, знают, что числа могут быть представлены не только в десятичной системе счисления. К примеру, в компьютере используется двоичный код, и, к примеру, число 19 в двоичной системе счисления будет выглядеть как 10011. Также иногда нужно переводить числа из одной системы счисления в другую. Python для этого предоставляет несколько функций:
- int([object], [основание системы счисления]) — преобразование к целому числу в десятичной системе счисления. По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.
- bin(x) — преобразование целого числа в двоичную строку.
- hex(х) — преобразование целого числа в шестнадцатеричную строку.
- oct(х) — преобразование целого числа в восьмеричную строку.
Примеры:
>>> a = int('19') # Переводим строку в число
>>> b = int('19.5') # Строка не является целым числом
Traceback (most recent call last):
File "", line 1, in
ValueError: invalid literal for int() with base 10: '19.5'
>>> c = int(19.5) # Применённая к числу с плавающей точкой, отсекает дробную часть
>>> print(a, c)
19 19
>>> bin(19)
'0b10011'
>>> oct(19)
'0o23'
>>> hex(19)
'0x13'
>>> 0b10011 # Так тоже можно записывать числовые константы
19
>>> int('10011', 2)
19
>>> int('0b10011', 2)
19Вещественные числа (float)
Вещественные числа поддерживают те же операции, что и целые. Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:
>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 0.9999999999999999
Для высокой точности используют другие объекты (например Decimal и Fraction)).
Также вещественные числа не поддерживают длинную арифметику:
>>> a = 3 ** 1000 >>> a + 0.1 Traceback (most recent call last): File "", line 1, in OverflowError: int too large to convert to float
Простенькие примеры работы с числами:
>>> c = 150 >>> d = 12.9 >>> c + d 162.9 >>> p = abs(d - c) # Модуль числа >>> print(p) 137.1 >>> round(p) # Округление 137
Дополнительные методы
float.as_integer_ratio() — пара целых чисел, чьё отношение равно этому числу.
float.is_integer() — является ли значение целым числом.
float.hex() — переводит float в hex (шестнадцатеричную систему счисления).
classmethod float.fromhex(s) — float из шестнадцатеричной строки.
>>> (10.5).hex()
'0x1.5000000000000p+3'
>>> float.fromhex('0x1.5000000000000p+3')
10.5Помимо стандартных выражений для работы с числами (а в Python их не так уж и много), в составе Python есть несколько полезных модулей.
Модуль math предоставляет более сложные математические функции.
>>> import math >>> math.pi 3.141592653589793 >>> math.sqrt(85) 9.219544457292887
Модуль random реализует генератор случайных чисел и функции случайного выбора.
>>> import random >>> random.random() 0.15651968855132303
Комплексные числа (complex)
В Python встроены также и комплексные числа:
>>> x = complex(1, 2) >>> print(x) (1+2j) >>> y = complex(3, 4) >>> print(y) (3+4j) >>> z = x + y >>> print(x) (1+2j) >>> print(z) (4+6j) >>> z = x * y >>> print(z) (-5+10j) >>> z = x / y >>> print(z) (0.44+0.08j) >>> print(x.conjugate()) # Сопряжённое число (1-2j) >>> print(x.imag) # Мнимая часть 2.0 >>> print(x.real) # Действительная часть 1.0 >>> print(x > y) # Комплексные числа нельзя сравнить Traceback (most recent call last): File "", line 1, in TypeError: unorderable types: complex() > complex() >>> print(x == y) # Но можно проверить на равенство False >>> abs(3 + 4j) # Модуль комплексного числа 5.0 >>> pow(3 + 4j, 2) # Возведение в степень (-7+24j)
Для работы с комплексными числами используется также модуль cmath.
Что такое система счисления по основанию 10?
Если вы когда-либо считали от 0 до 9, значит, вы использовали base-10, даже не зная, что это такое. Проще говоря, основание 10 — это способ присвоения числовым значениям разрядных значений. Иногда ее называют десятичной системой, потому что значение цифры в числе определяется ее положением относительно десятичной точки.
Силы 10
В системе base-10 каждая цифра числа может иметь целочисленное значение от 0 до 9 (10 возможных вариантов) в зависимости от ее положения.Позиции или позиции чисел основаны на степени 10. Каждая позиция числа в 10 раз больше значения справа от нее, отсюда и термин основание-10. Превышение числа 9 в позиции инициирует отсчет в следующей наивысшей позиции.
Цифры больше 1 появляются слева от десятичной точки и имеют следующие разрядные значения:
- Единицы
- Десятки
- Сот
- тыс.
- Десятки тысяч
- Сотни тысяч и т. Д.
Справа от десятичной точки отображаются значения, составляющие долю или меньше 1:
- Десятые
- сотых
- тысячных
- Десятитысячные
- Стотысячные и так далее
Каждое действительное число может быть выражено в десятичной системе счисления.Каждое рациональное число, знаменатель которого состоит только из 2 и / или 5 в качестве простых множителей, может быть записано как десятичная дробь. Такая дробь имеет конечное десятичное разложение. Иррациональные числа могут быть выражены как уникальные десятичные числа, в которых последовательность не повторяется и не заканчивается, например π. Начальные нули не влияют на число, хотя конечные нули могут иметь значение при измерениях.
Использование Base-10
Давайте посмотрим на пример большого числа и воспользуемся основанием 10 для определения разрядного значения каждой цифры.Например, если использовать целое число 987 654 125, положение каждой цифры будет следующим:
- 9 имеет номинальную стоимость 900 000
- 8 имеет значение 80 000
- 7 имеет значение 7000
- 6 имеет значение 600
- 5 имеет значение 50
- 4 имеет значение 4
- 1 имеет значение 1/10
- 2 имеет значение 2/100
- 5 имеет значение 5/1000-е
Происхождение Base-10
База-10 используется в большинстве современных цивилизаций и была наиболее распространенной системой для древних цивилизаций, скорее всего, потому, что у людей 10 пальцев.Египетские иероглифы, датируемые 3000 годом до нашей эры. показать свидетельство десятичной системы. Эта система была передана Греции, хотя греки и римляне также обычно использовали base-5. Десятичные дроби впервые стали использоваться в Китае в I веке до нашей эры.
Некоторые другие цивилизации использовали другие системы счисления. Например, майя использовали основание 20, возможно, из-за счета пальцев рук и ног. В калифорнийском языке юки используется основание 8 (восьмеричное), при котором считается, что расстояние между пальцами, а не цифры.
Другие системы счисления
Базовые вычисления основаны на двоичной системе счисления или системе счисления с основанием 2, в которой всего две цифры: 0 и 1. Программисты и математики также используют систему счисления с основанием 16 или шестнадцатеричную систему, которая, как вы, вероятно, догадались, имеет 16 различных цифровых символов. . Компьютеры также используют основание 10 для выполнения арифметических операций. Это важно, поскольку позволяет производить точные вычисления, что невозможно при использовании дробных двоичных представлений.
Числовые основы: введение и двоичные числа
Purplemath
Преобразование между различными системами счисления на самом деле довольно просто, но идея, лежащая в основе этого, поначалу может показаться немного запутанной.И хотя тема различных основ может показаться вам несколько бессмысленной, рост компьютеров и компьютерной графики увеличил потребность в знаниях о том, как работать с различными (недесятичными) базовыми системами, особенно с двоичными системами (с единицами и нулями) и шестнадцатеричная система (числа от нуля до девяти, за которыми следуют буквы от A до F).
MathHelp.com
В нашей обычной десятичной системе у нас есть цифры для чисел от нуля до девяти. У нас нет однозначного числа для «десяти». (Римляне использовали иероглиф «X».) Да, мы пишем «10», но это означает «1 десять и 0 единиц». Это две цифры; у нас нет единственной цифры, обозначающей «десять».
Вместо этого, когда нам нужно считать на единицу больше девяти, мы обнуляем столбец единиц и добавляем единицу к столбцу десятков. Когда мы становимся слишком большими в столбце десятков — когда нам нужно на один больше, чем девять десятков и девяти единиц («99»), мы обнуляем столбцы десятков и единиц и добавляем единицу к десятикратным или сотням. , столбец. Следующий столбец — это столбец десять, десять, десять, или тысячи. И так далее, причем каждый столбец большего размера в десять раз больше предыдущего. Мы помещаем цифры в каждый столбец, сообщая нам, сколько копий этой степени десяти нам нужно.
Единственная причина, по которой математика по основанию десять кажется «естественной», а другие — нет, заключается в том, что вы использовали десятичную систему с детства. И (почти) каждая цивилизация использовала математику по основанию десять, вероятно, по той простой причине, что у нас десять пальцев. Если бы вместо этого мы жили в мире мультфильмов, где у нас было бы только четыре пальца на каждой руке (сосчитайте их в следующий раз, когда вы смотрите телевизор или читаете комиксы), тогда «естественной» базовой системой, вероятно, была бы система с основанием восемь, или «восьмеричный».
двоичный
Давайте посмотрим на числа с основанием два или двоичные. Как бы вы записали, например, 12 10 («двенадцать по основанию десять») в виде двоичного числа? Вам нужно будет преобразовать в столбцы с основанием два, аналог столбцов с основанием десять. В десятичной системе счисления у вас есть столбцы или «места» для 10 0 = 1, 10 1 = 10, 10 2 = 100, 10 3 = 1000 и так далее. Точно так же в основании два у вас есть столбцы или «места» для 2 0 = 1, 2 1 = 2, 2 2 = 4, 2 3 = 8, 2 4 = 16 и т. Д. вперед.
Первый столбец в математике с основанием два — это столбец единиц. Но в столбце единиц может быть только «0» или «1». Когда вы дойдете до «два», вы обнаружите, что нет ни одной единственной цифры, которая обозначает «два» в математике с основанием два. Вместо этого вы помещаете «1» в столбец двоек и «0» в столбец единиц, указывая «1 два и 0 единиц». Двойка по основанию десять (2 10 ) записывается в двоичной системе как 10 2 .
«Тройка» в основании два на самом деле означает «1, два и 1, один», поэтому записывается как 11 2 .«Четыре» на самом деле означает дважды два, поэтому мы обнуляем столбец двоек и столбец единиц и помещаем «1» в столбец четверок; 4 10 записывается в двоичной форме как 100 2 . Вот список первых чисел:
Преобразование между двоичными и десятичными числами довольно просто, если вы помните, что каждая цифра в двоичном числе представляет собой степень двойки.
Преобразует 101100101
2 в соответствующее десятичное число.
Я перечислю цифры по порядку, так как они появляются в номере, который они мне дали. Затем в другом ряду я отсчитываю эти цифры от ПРАВА, начиная с нуля:
Первая строка выше (помеченная как «цифры») содержит цифры из двоичного числа; вторая строка (обозначенная как «нумерация») содержит степень двойки (основание), соответствующую каждой цифре. Я буду использовать этот список для преобразования каждой цифры в степень двойки, которую он представляет:
1 × 2 8 + 0 × 2 7 + 1 × 2 6 + 1 × 2 5 + 0 × 2 4 + 0 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0
= 1 × 256 + 0 × 128 + 1 × 64 + 1 × 32 + 0 × 16 + 0 × 8 + 1 × 4 + 0 × 2 + 1 × 1
= 256 + 64 + 32 + 4 + 1
= 357
Затем 101100101 2 преобразуется в 357 10 .
Преобразование десятичных чисел в двоичные почти так же просто: просто разделите на 2.
Преобразует 357
10 в соответствующее двоичное число.
Чтобы выполнить это преобразование, мне нужно несколько раз делить на 2, отслеживая остатки по ходу дела. Смотрите ниже:
Приведенный выше рисунок анимирован на «живой» веб-странице.
Как видите, после многократного деления на 2 я получил следующие остатки:
Эти остатки говорят мне, что такое двоичное число. Я читаю числа с внешней стороны деления, начиная сверху с конечного значения и его остатка, и заканчиваю свой путь вокруг и вниз по правой части последовательного деления. Тогда:
357 10 преобразуется в 101100101 2 .
Партнер
Этот метод преобразования работает для преобразования в любое недесятичное основание. Только не забудьте включить эту первую цифру вверху, перед списком остатков. Если вам интересно, объяснение того, почему этот метод работает, доступно здесь.
Вы можете преобразовать десятичную систему счисления в любую другую. Когда вы изучаете эту тему в классе, вы, вероятно, должны будете преобразовывать числа в различные другие основы, поэтому давайте рассмотрим еще несколько примеров …
URL: https://www.purplemath.com/modules/numbbase.htm
Системы счисления и основы — Лучшее объяснение
Базовые системы, такие как двоичная и шестнадцатеричная, сначала кажутся немного странными.Ключ в понимании того, как разные системы «работают», как одометр, когда они заполнены. База 10, наша десятичная система, «переключает», когда она получает 10 элементов, создавая новую цифру. Мы ждем 60 секунд, прежде чем «перейти» к новой минуте. Шестнадцатеричный и двоичный значения похожи, но отметьте галочкой каждые 16 и 2 элемента соответственно.
Попробуйте преобразовать числа в шестнадцатеричное и двоичное здесь:
Путь назад, когда: унарные числа
Раньше у нас не было базовых систем! Он шел в обе стороны, сквозь снег и палящую жару.Если вы хотите сосчитать один, вы пишете:
л
Если вам нужно 5, вы должны написать
lllll
И ясно, 1 + 5 = 6
l + lllll = llllll
Это самый простой способ подсчета.
Введите римлян
В римских цифрах два означает один, дважды. Три было один, трижды:
один = я два = II три = III
Однако они решили, что могут добиться большего успеха, чем старая традиция линий на песке. Для пяти мы могли бы использовать V для представления lllll и получить что-то вроде
л + V = Vl
Неплохо, а? И, конечно же, есть еще много символов (L, C, M и т. Д.) ты можешь использовать.
Ключевым моментом является то, что V и lllll — это два способа кодирования числа 5.
Дайте каждому номеру имя
Еще одним прорывом стало осознание того, что каждое число может быть отдельной концепцией. Вместо того, чтобы представлять три как ряд единиц, дайте ему собственный символ: «3 ″. Проделайте это от одного до девяти, и вы получите символы:
1 2 3 4 5 6 7 8 9
Римляне были близки, так близки, но давали уникальные символы только 5, 10, 50, 100, 1000 и т. Д.
Используйте свою позицию
Теперь ясно, что вы не можете давать каждому номеру свой собственный символ. Их просто слишком много.
Но обратите внимание на одну особенность римских цифр: они используют позицию символов для обозначения значения.
IV означает «вычесть 1 из 5»
и VI означает «прибавить 1 к 5».
В нашей системе счисления мы используем позицию аналогичным образом. Мы всегда прибавляем и никогда не вычитаем. И каждая позиция на 10 больше, чем предыдущая.
Итак, 35 означает «прибавить 3 * 10 к 5 * 1 », а 456 означает 4 * 100 + 5 * 10 + 6 * 1 . Эта «позиционная десятичная» система исчисления является индуистско-арабской системой счисления, которую мы используем сегодня.
Наш выбор базы 10
Почему мы решили каждый раз умножать на 10? Скорее всего потому, что у нас 10 пальцев.
Следует понимать, что вам нужно достаточно цифр, чтобы «заполнить», пока вы не наберете следующее число. Позвольте мне продемонстрировать.
Если мы хотим, так сказать, проверять одометр каждые 10, нам нужны символы для чисел от одного до девяти; мы еще не достигли десяти.Представьте, что числа медленно тикают вверх — в какой момент вы переворачиваете следующую единицу и начинаете с нуля?
Введите ноль
А что будет, когда мы дойдем до десяти? Как показать, что мы хотим ровно одну «десять» и ничего в столбце «единицы»?
Мы используем ноль, число, которого не существует. Ноль — это довольно концептуальная концепция, это заполнитель, пробел, пробел и многое другое. Достаточно сказать, что Зеро — одно из величайших изобретений всех времен.
Zero позволяет нам иметь пустой заполнитель, чего не было у римлян.Посмотрите, как без него их численность огромна.
Знаменитый роман Джорджа Оруэлла «1984» будет «MCMLXXXIV»! Слетает с языка, не так ли?
С учетом других баз
Помните, что мы, , выбрали , чтобы проверять одометр каждые десять. Наш подсчет выглядит так:
1 2 3 4 5 6 7 8 9 (ох, я наелась!) 10 (отмечено галочкой - начало новой цифры)
Что, если бы мы отметили 60, когда считаем, как мы делаем секунды и минуты?
1 секунда 2 3 4 5 … 58 59 1:00 (60 секунд или 1 минута.Мы начали новую цифру.)
Пока все в порядке, верно? Обратите внимание, что мы используем двоеточие (:), указывающее, что мы находимся на новой «цифре». В базе 10 каждая цифра может стоять сама по себе.
Пробная база 16
Если нам нужна основа 16, мы могли бы сделать что-то подобное:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 (мы набираемся) 1:00 (16 - мы начали новую цифру)
Однако мы не хотим записывать шестнадцатеричные числа с двоеточием (хотя мы могли бы).Мы лучше приготовим отдельные символы для 10–15, чтобы можно было просто писать числа, как мы привыкли. У нас закончились числа (1–9 уже использованы, 0 в качестве заполнителя), поэтому нам нужны другие символы. Мы могли бы использовать какие-то волнистые линии или другие формы, но обычно используются буквы в римском стиле. Так же, как 5 превратилось в V, программисты используют буквы A-F, чтобы получить достаточно цифр до 16. То есть
1 2 3 4 5 6 7 8 9 A (10 - мы используем символ «A») В (11) С (12) D (13) E (14) F (15 - ох, мы набираемся) 10 (16 - начинаем новую цифру)
Ага! Теперь мы можем использовать одну цифру для каждого «места», и мы знаем, что 10 на самом деле означает, что мы «перешли на 16 ″ один раз.
20 означает, что мы дважды отметили 16 (32).
25 означает, что мы дважды повысили до 16 (что дает нам 32) и получили еще 5. Итого 32 + 5 = 37.
Быстрый просмотр
Со мной так далеко? Это круто, правда? Мы можем считать в любой системе, какой захотим. Также обратите внимание, что основание 16 более экономно по пространству в том смысле, что мы можем записать число вроде 11 одной цифрой: B.
База 16 не сильно отличается от базы 10, просто нам нужно больше времени для заполнения.
Удивительный мир двоичной системы
Мы видели множество базовых систем, от очень простых унарных до несвязных римских цифр, устойчивой базы 10 и компактной базы 16.
Что хорошего в двоичном формате? В духе простоты это самая простая система счисления, в которой есть понятие «тиканье». Унарный, где мы просто пишем 1, 11, 111 … просто продолжается вечно. Бинарный, с двумя вариантами (1 и 0) выглядит так:
1: 1 2:10 (мы полны - отметьте галочкой) 3: 11 4: 100 (мы снова наелись - отметьте галочкой) 5: 101 6: 110 7: 111 8: 1000 (отметьте еще раз) …
и так далее.
Поскольку двоичный файл настолько прост, его очень легко встроить в оборудование. Вам просто нужны вещи, которые могут включаться или выключаться (представляющие 1 и 0), а не вещи, которые имеют 10 возможных состояний (для представления десятичных чисел).
Благодаря своей простоте двоичный файл устойчив к ошибкам. Если ваш сигнал «частично включен» (допустим, 0,4), вы можете считать, что это ноль. А если в основном он (скажем, 0,8), то вы можете предположить, что это 1. Если вы используете систему с 10 возможными состояниями, трудно определить, когда произошла ошибка.Это одна из причин, по которой цифровые сигналы настолько устойчивы к шумам.
Другие примеры баз
Мы постоянно используем другие базы, даже динамически меняющиеся. Обычно мы так не думаем:
Часы, минуты, секунды: 1:32:04
- Мы знаем, что это 1 час 32 минуты 4 секунды. В секундах это 1 60 60 + 32 * 60 + 4.
Футы и дюймы: 3 фута 5 дюймов
- Это 3 фута, 5 дюймов или 3 * 12 + 5 дюймов.
Фунты и унции: 8 фунтов, 5 унций
- Поскольку фунт равен 16 унциям, это 8 * 16 + 5 унций.Мы все время использовали систему счисления с основанием 16!
Расставания
«10» в любой системе счисления означает основание и означает, что мы один раз отметили галочкой. 10 в двоичной системе счисления означает два, 10 в десятичной системе счисления означает десять, а 10 в шестнадцатеричной системе счисления означает шестнадцать.
Как вы разделяете эти числа? Программисты часто пишут «0b» перед двоичными числами. Итак, 2 в двоичном формате — это
0b10
Точно так же они пишут 0x перед шестнадцатеричными числами. Итак, 16 в шестнадцатеричном формате:
0 × 10
Если впереди нет никаких символов (0b или 0x), мы предполагаем, что это обычное число с основанием 10.
А теперь вперед и наслаждайтесь новыми знаниями!
Другие сообщения этой серии
- Системы счисления и базы
- Краткое руководство по GUID
- Понимание быстрого обратного квадратного корня Quake
- Простое введение в компьютерные сети
- Поменять местами две переменные с помощью XOR
- Общие сведения о порядке байтов с прямым и обратным порядком байтов
- Юникод и вы
- Немного о форматах двоичных файлов
- Алгоритмы сортировки
Системы счисления (двоичная, восьмеричная, десятичная, шестнадцатеричная)
Прежде чем мы сможем объяснить некоторые конкретные системы счисления, нам нужно знать, что такое система счисления.Проще говоря, система счисления — это способ представления чисел.
Мы можем классифицировать системы счисления по типу нотации в зависимости от того, используют ли они позиционную нотацию (также известную как нотация с числовыми значениями), и произвести дальнейшую категоризацию по основанию или основанию.
1. Непозиционная система счисления
Для объяснения непозиционной системы счисления возьмем в качестве примера римские цифры. В таблице ниже вы можете найти десятичные значения для основных символов римской системы счисления.
Вы можете спросить, есть ли какой-то узор для формирования всех остальных символов? Ответ положительный.
- Когда символ с меньшим значением помещается на после символа, имеющего такое же или большее значение, значения складываются. Примеры приведены в таблице ниже.
- Когда символ с меньшим значением помещается перед символом, имеющим большее значение, меньшее значение вычитается из большего. Примеры приведены в таблице ниже.
2. Система позиционных чисел
Позиционная система счисления позволяет расширить исходный набор символов, чтобы их можно было использовать для представления любого произвольно большого (или маленького) значения.В разных системах число может быть представлено по-разному.
Например, два числа $ (2A) _ {16} $ и $ (52) _ {8} $ оба относятся к одному и тому же количеству, $ (42) _ {10} $.
Система счисления, которую мы используем каждый день, называется десятичной системой счисления или системой счисления с основанием десять. Как видно из названия системы счисления, основание определяет всю систему.
Десятичная система счисления имеет основание 10, потому что мы работаем с 10 цифрами (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), и любое другое большее число может быть составлено из этих 10 цифр.{0}
долл. США$ = 3 \ cdot 100 + 4 \ cdot 10 + 2 \ cdot 1 $
$ = 300 + 40 + 2 $
В этом уроке мы не будем подробно объяснять десятичную систему, так как на странице, посвященной ей, есть много уроков.
Помимо десятичной системы счисления, существует множество других систем счисления. Мы упомянем только три из них, так как это наиболее часто используемые системы счисления после десятичной. Это: двоичная система счисления, восьмеричная система счисления и шестнадцатеричная система счисления. Мы дадим краткое объяснение каждой из них и узнаем, как преобразовывать числа из одной системы в другую.
2.1. Двоичная система счисления
Двоичная система счисления содержит две уникальные цифры (0 и 1). Таким образом, эта система является системой счисления с основанием 2. Относительные величины символов равны 0 <1. Символы в этой системе часто называются двоичными цифрами или просто битами. Двоичная система счисления - это позиционная система счисления. Позже мы увидим, что, например, $ 1010_ {2} \ neq 1100_ {2} $.
2.2. Восьмеричная система счисления
Восьмеричная система счисления содержит 8 уникальных цифр (0, 1, 2, 3, 4, 5, 6, 7).Таким образом, эта система является системой счисления с основанием 8. Относительные величины символов: 0 <1 <2 <3 <4 <5 <6 <7. Восьмеричная система счисления - еще один пример позиционной системы счисления.
2.3. Шестнадцатеричная система счисления
Шестнадцатеричная система счисления содержит 16 уникальных цифр. Поскольку в десятичной системе всего 10 арабских цифр, нам нужно использовать другие символы для представления оставшихся 6 цифр. Мы используем буквенные
символы A – F, чтобы расширить систему до 16 цифр.16 цифр в шестнадцатеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Относительные величины символов равны
0. <1 <2 <3 <4 <5 <6 <7 <8 <9 Шестнадцатеричная система счисления также является позиционной системой счисления.
3. Базовое преобразование
Каждая позиция цифры в числе с основанием b представляет степень $ b $. Итак, когда мы пишем число с основанием b, каждая цифра с основанием b умножается на соответствующую степень $ b $ в зависимости от позиции в числе.
3.1. Преобразование в десятичное число
Преобразовать число из любой системы счисления в десятичную довольно просто. Мы знаем, что значение каждой цифры в числе основано на индивидуальном значении цифры и позиции цифры. Мы узнали это, когда узнали о десятичных числах. Используя это правило, мы можем преобразовать число из любой системы счисления в десятичное число.
Давайте посмотрим на общий пример:
Представьте, что у нас есть число $ d_ {2} d_ {1} d_ {0}.{-2} = 3 \ cdot 8 + 4 \ cdot 1 + 1 \ cdot \ displaystyle {\ frac {1} {8}} + 5 \ cdot \ displaystyle {\ frac {1} {64}} = 28.203125 $
3.2. Преобразование из десятичного числа в любое другое основание
Мы можем преобразовать десятичное число в любое другое, используя всего несколько простых шагов:
- Разделите десятичное число, которое нужно преобразовать, на значение нового основания.
- Запишите остаток в сторону
- Разделите частное от предыдущего деления на новое основание.
- Запишите остаток в сторону
- Повторяйте шаги 3 и 4, пока частное на шаге 3 не станет равным нулю.
Требуемое число состоит из остатков, записываемых снизу вверх, слева направо.
Пример 2. Преобразуйте 25 в двоичное число.
Согласно правилу преобразования десятичных чисел в любое другое основание, необходимое число — $ 11001_ {2} $.
Пример 3. Преобразует 2489 в шестнадцатеричное число.
Помните, что эквивалент числа 11 в шестнадцатеричной системе счисления — буква B.
Согласно правилу преобразования десятичных чисел в любое другое основание, необходимое число — $ 9B9_ {16} $.
3.3. Эквивалентность различных систем счисления
4. Быстрые клавиши для переключения между основанием 2 и основанием 8 и между основанием 2 и основанием 16
Мы узнали, что можно преобразовать число из любого основания в число из любого основания, предварительно преобразовав его в десятичное. Например, если мы хотим преобразовать число с основанием 3 в число с основанием 7, сначала нужно преобразовать число с основанием 3 в десятичное, а затем преобразовать это десятичное число в число с основанием 7.
Мы можем использовать ту же процедуру для преобразования двоичного числа в восьмеричное или шестнадцатеричное, но есть несколько полезных сокращений, которые упростят этот процесс. Давайте посмотрим на следующий пример:
Пример 4. Преобразует $ 100100010101111_ {2} $ в шестнадцатеричное число.
Чтобы преобразовать двоичное число в шестнадцатеричное, мы могли бы просто разбить двоичное число на группы из 4 цифр (начиная справа и добавляя ведущие нули, если цифры заканчиваются), а затем заново интерпретировать эти группы из 4 как перечисленные шестнадцатеричные значения в таблице выше.При этом у нас есть:
$ 100100010101111_ {2} = 0100 1000 1010 1111 $
$ 0100 = 4 $, 1000 $ = 8 $, 1010 $ = A $, 1111 $ =
F $$ 100100010101111_ {2} = 48AF_ {16}
$Аналогично этому, чтобы преобразовать двоичное число в восьмеричное, мы могли бы просто разбить двоичное число на группы по 3 цифры, а остальная часть процедуры такая же, как преобразование двоичного числа в шестнадцатеричное число. Давайте превратим то же двоичное число в восьмеричное:
$ 100100010101111_ {2} = 100 100 010 101 111 $
100 долларов = 4
долларов010 долларов = 2
доллара101 доллар = 5
доллара111 долларов = 7
долларов$ 100100010101111_ {2} = 44257_ {8}
$Обратить процесс еще проще.Предположим, мы хотим преобразовать $ FC7_ {16} $ в двоичную форму. Из таблицы мы можем прочитать двоичные значения для каждой цифры шестнадцатеричного числа:
$ F_ {16} = 1111_ {2} $ C_ {16} = 1100_ {2} $ 7_ {16} = 0111_ {2}
$$ FC7_ {16} = 111111000111_ {2}
$Процесс преобразования восьмеричного числа в двоичную форму такой же.
двоичная система счисления | Encyclopedia.com
Двоичная система счисления, также называемая системой счисления с основанием 2 и , представляет собой метод представления чисел, который считает, используя комбинации только двух цифр: нуля (0) и единицы (1).Компьютеры используют двоичную систему счисления для управления и хранения всех своих данных, включая числа, слова, видео, графику и музыку.
Термин бит, наименьшая единица цифровой техники, означает «двоичную цифру». Байт — это группа из восьми бит. Килобайт равен 1024 байтам или 8192 битам.
Используя двоичные числа, 1 + 1 = 10, потому что «2» не существует в этой системе. Другая система счисления, обычно используемая десятичная система счисления или система счисления с основанием 10, , считается с использованием 10 цифр (0,1,2,3,4,5,6,7,8,9), поэтому 1 + 1 = 2 и 7 + 7 = 14.Другая система счисления, используемая компьютерными программистами, — это шестнадцатеричная система счисления с основанием 16 , в которой используется 16 символов (0,1,2,3,4,5,6,7,8,9, A, B, C, D , E, F), поэтому 1 + 1 = 2 и 7 + 7 = E. Системы счисления с основанием 10 и 16 более компактны, чем двоичная. Программисты используют шестнадцатеричную систему счисления как удобный и более компактный способ представления двоичных чисел, поскольку ее очень легко преобразовать из двоичной системы в шестнадцатеричную и наоборот. Сложнее преобразовать из двоичного в десятичное и из десятичного в двоичное.
Преимуществом двоичной системы является ее простота. Вычислительное устройство может быть создано из всего, что имеет ряд переключателей, каждый из которых может переключаться между положением «включено» и положением «выключено». Эти переключатели могут быть электронными, биологическими или механическими, если их можно перемещать по команде из одного положения в другое. Большинство компьютеров имеют электронные переключатели.
Когда переключатель находится в положении «включено», он представляет значение единицы, а когда переключатель находится в положении «выключено», он представляет значение нуля.Цифровые устройства выполняют математические операции, включая и выключая двоичные переключатели. Чем быстрее компьютер может включать и выключать переключатели, тем быстрее он выполняет свои вычисления.
| Двоичное | Десятичное | Шестнадцатеричное | |||||||
| Число | Число | 9026 Система||||||||
| 0 | 0 | 0 | |||||||
| 1 | 1 | 1 | |||||||
| 10 | 2 | 2 | |||||||
| 100 | 4 | 4 | |||||||
| 101 | 5 | 5 | |||||||
| 110 | 6 | 6 | |||||||
| 111 | 111 | 7 | 8 | ||||||
| 1001 | 9 | 9 | |||||||
| 1010 | 10 | A | |||||||
| 1011 | 11 | B | |||||||
| 1100 | 12 | C | |||||||
| 1101 | 69026 9026 9026 9026 | E | |||||||
| 1111 | 15 | F | |||||||
| 10000 | 16 | 10 |
Позиционная нотация
Каждая цифра в двоичном числе принимает значение, которое число .Это называется позиционным обозначением. Это понятие также применимо к десятичным числам.
Например, десятичное число 123 представляет десятичное значение 100 + 20 + 3. Число один представляет сотни, число два представляет десятки, а число три представляет единицы. Математическая формула для создания числа 123 может быть создана путем умножения числа в столбце сотен (1) на 100, или 10 2 ; умножение числа в столбец десятков (2) на 10, или 10 1 ; умножение числа в столбце единиц (3) на 1, или 10 0 ; а затем сложить продукты вместе.Формула: 1 × 10 2 + 2 × 10 1 + 3 × 10 0 = 123.
Это показывает, что каждое значение умножается на основание (10), возведенное в возрастающую степень. Значение мощности начинается с нуля и увеличивается на единицу в каждой новой позиции в формуле.
Эта концепция позиционного обозначения также применяется к двоичным числам с той разницей, что основание равно 2. Например, чтобы найти десятичное значение двоичного числа 1101, формула имеет вид 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 13.
Двоичные операции
Двоичными числами можно управлять с помощью тех же знакомых операций, которые используются для вычисления десятичных чисел, но с использованием только нулей и единиц. Чтобы сложить два числа, нужно запомнить только четыре правила:
Следовательно, чтобы решить следующую задачу сложения, начните с самого правого столбца и сложите 1 + 1 = 10; запишите 0 и перенесите 1. Работая с каждым столбцом слева, продолжайте добавлять, пока проблема не будет решена.
Чтобы преобразовать двоичное число в десятичное, каждая цифра умножается на степень двойки.Затем продукты складываются. Например, чтобы преобразовать двоичное число 11010 в десятичное, формула будет иметь следующий вид:
Чтобы преобразовать двоичное число в шестнадцатеричное, разделите двоичное число на группы по четыре, начиная справа, а затем преобразуйте каждую группу в свое шестнадцатеричный эквивалент. Слева от двоичного числа можно добавить нули, чтобы завершить группу из четырех человек. Например, чтобы перевести число 11010 в шестнадцатеричное, формула будет иметь следующий вид:
Цифровые данные
Биты являются фундаментальным элементом цифровых вычислений.Термин «оцифровка» означает преобразование аналогового сигнала — диапазона напряжений — в цифровой сигнал, или ряд чисел, представляющих напряжения. Музыкальное произведение можно оцифровать, взяв из него очень частые сэмплы, называемые сэмплами, и переведя их в дискретных чисел, которые затем преобразуются в нули и единицы. Если сэмплы берутся очень часто, музыка при воспроизведении звучит как непрерывный тон.
Черно-белую фотографию можно оцифровать, наложив на изображение мелкую сетку и вычислив количество серого на каждом пересечении сетки, называемое пикселем .Например, используя 8-битный код, чисто белая часть изображения может быть оцифрована как 11111111. Аналогичным образом, чисто черная часть может быть оцифрована как 00000000. Каждое из 254 чисел, находящихся между этими двумя крайностями. (числа от 00000001 до 11111110) представляет собой оттенок серого. Когда приходит время восстановить фотографию, используя набор двоичных цифр, компьютер декодирует изображение, присваивает каждому пикселю правильный оттенок серого и появляется изображение. Чтобы улучшить разрешение, можно использовать более мелкую сетку, чтобы изображение можно было увеличить до большего размера без потери деталей.
Цветная фотография оцифровывается аналогичным образом, но для сохранения цвета пикселя требуется гораздо больше битов. Например, 8-битная система использует восемь битов, чтобы определить, какой из 256 цветов представлен каждым пикселем (2 8 равно 256). Точно так же 16-битная система использует шестнадцать бит для определения каждого из 65 536 цветов (2 16 равно 65 536). Поэтому для цветных изображений требуется гораздо больше места для хранения, чем для черно-белых.
см. Также Ранние компьютеры; Объем памяти.
Энн МакИвер МакХоуз
Библиография
Блиссмер, Роберт Х. Знакомство с компьютерными концепциями, системами и приложениями. Нью-Йорк: John Wiley & Sons, Inc., 1989.
Диллиган, Роберт Дж. Вычислительная техника в эпоху Интернета: интерактивное веб-введение. Нью-Йорк: Plenum Press, 1998.
White, Ron. Как работают компьютеры: издание тысячелетия. Индианаполис: Que Corporation, 1999.
Числа до 10 цифр
10-значное число по-разному читается и записывается в индийской и международной системах разметки.Он имеет любое число от 1 до 9 вместо 10 -й цифры от крайнего правого положения. 10-значное число читается или записывается, начиная с крайней левой цифры. Топоним из 10 -й цифры называется «миллиард» в международной системе и «арабским» в индийской системе счисления.
Как записывать числа до 10 цифр?
10-значный номер можно записать двумя способами: один — это международная система счисления, а другой — индийская.
В международной системе счисления , 10-значное число выражается запятыми сразу после каждых трех цифр справа. Наименьшее 10-значное число записывается как 1 000 000 000 и называется миллиардом или одним миллиардом и записывается как 1 с 9 нулями. Поскольку третья запятая после 9 -й цифры справа обозначает начало миллиарда, это число будет называться 1 миллиардом в Международной системе счисления.
В индийской системе счисления первая запятая идет после трех цифр справа после разряда сотни, а следующая запятая идет после каждых двух цифр и так далее.Таким образом, наименьшее 10-значное число в индийской системе записывается как 1,00,00,00,000. Поскольку третья запятая после седьмой цифры справа обозначает начало крора, это число будет называться 100 крор или один араб в индийской системе счисления.
Сравнение индийской системы и международной системы
Посмотрите на приведенные ниже таблицы, которые показывают числа до 10 цифр в соответствии с системами.
Как разложить 10-значные числа?
Любое 10-значное число может иметь разряд до одного миллиарда или арабского.
Это названия значений разряда (начиная справа) в 10-значном числе:
- Цифра 1 — единицы
- Цифра 2 — десятки
- Цифра 3 — сотни
- Цифра 4 — тысячи
- Цифра 5 — десять тысяч
- Цифра 6 — лакхи
- Цифра 7 — десять лакхов / миллион
- Цифра 8 — кроры / десять миллионов
- Цифра 9 — десять крор / сто миллионов
- Цифра 10 — один араб (сто крор) / миллиард
Итак, возьмем случайное 10-значное число — 5448626840 и посмотрим, как оно разложится.
Здесь PV означает стоимость места:
- Цифра 1 PV = 0 × 1 = 0
- Цифра 2 PV = 4 × 10 = 40
- Цифра 3 PV = 8 × 100 = 800
- Цифра 4 PV = 6 × 1000 = 6000
- Цифра 5 PV = 2 × 10000 = 20000
- Цифра 6 PV = 6 × 100000 = 600000
- Цифра 7 PV = 8 × 1000000 = 8000000
- Цифра 8 PV = 4 × 10000000 = 40000000
- Цифра 9 PV = 4 × 100000000 = 400000000
- Цифра 10 PV = 5 × 1000000000 = 5000000000
Важные примечания:
- Обратите внимание на различные способы размещения запятых в числе 5000000000: Международная система определения стоимости: 5,000,000,000; Индийская система значений места: 5,00,00,00,000
- Обратите внимание на разные имена в соответствии с индийской системой счисления и международной системой счисления:
- Один лакх равен ста тысячам
- Десять лакхов равняется одному миллиону
- Один крор равен десяти миллионам
- Десять крор равняется сотне миллионов
- Один араб (сто кроров) равен одному миллиарду
Статьи по теме
Ознакомьтесь с важными темами, упомянутыми ниже, чтобы узнать больше о числах до 10 цифр.
Часто задаваемые вопросы о номерах до 10 цифр
10-значное число называется миллиардом?
Да, 10-значное число в международной системе счисления разряда называется миллиардом, потому что название места из 10 -й цифры справа называется миллиардом. Например, 3 000 000 000 читается как три миллиарда.
Какой самый большой 10-значный номер?
Наибольшее 10-значное число содержит 9 из всех 10-значных цифр. Это число записывается как девять миллиардов девятьсот девяносто девять миллионов девятьсот девяносто девять тысяч девятьсот девяносто девять слов в Международной системе счисления, а в цифрах оно записывается как 9 999 999 999.
Какое наименьшее 10-значное число?
Наименьшее 10-значное число имеет 9 нулей, а начальная цифра — 1. Это число называется миллиардом, а в цифрах оно записывается как 1 000 000 000.
Сколько запятых в 10-значном числе согласно международной системе?
В международной системе исчисления миллиард состоит из трех запятых. Миллиард представляет собой 10-значное число в международной системе ценностей. Написано как 1 000 000 000.
Что такое 10-значный номер?
10-значное число — это число, состоящее из 10 цифр, где первая цифра должна быть 1 или больше единицы. Например, 3,456,788,805.
Системы счисления — Викиверситет
Ознакомьте учащегося с методом выражения чисел и преобразуйте один метод в другой.
Метод записи чисел называется «системой счисления». В наиболее распространенной системе счисления мы пишем числа с комбинациями из 10 символов {0,1,2,3,4,5,6,7,8,9}.Эти символы называются цифрами, а числа, выраженные с помощью 10 цифр, называются десятичными числами или числами с основанием 10. Другие наиболее распространенные системы счисления — двоичная, шестнадцатеричная и восьмеричная. Двоичная система счисления, или система счисления с основанием 2, представляет числовые значения с использованием двух символов: 0 и 1. Более конкретно, обычная система счисления с основанием 2 представляет собой позиционную систему счисления с основанием 2. 0,1,2,3 ,.3 = 1000
и т. Д.
Например:
20 = (2 * 10) + (0 * 1) = 20 + 0 = 20
456 = (4 * 100) + (5 * 10) + (6 * 1) = 400 + 50 + 6
84568 = (8 * 10000) + (4 * 1000) + (5 * 100) + (6 * 10) + (8 * 1) = 80000 + 4000 + 500 + 60 + 8
Числа, выраженные двумя символами (0, 1), называются двоичными числами или числами с основанием 2.
Например:
1 (однозначное чтение: 1)
10 (двузначное чтение: 1, 0)
100 (трехзначное чтение: 1,0,0)
1101 (четырехзначное чтение: 1, 1, 0, 1)
и т. Д.0) = 1 * 32 + 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 = 32 + 16 + 8 + 0 + 2 + 1 = 59 → 111011 (двоичный) = 59 (десятичный )
Преобразование десятичного числа в двоичное [править | править источник]
Для преобразования десятичного числа в двоичное
Разделите десятичное число на 2
- Если есть остаток, крайний правый столбец будет 1
- Если нет остатка, крайний правый столбец будет 0.
Затем повторите процесс, перемещая один столбец влево каждый раз, пока вы не разделите его до 1.
Пример 1
15/2 = 7 остаток 1 (двоичное число = ??? 1)
7/2 = 3 остатка 1 (двоичное число = ?? 11)
3/2 = 1 остаток 1 (двоичное число =? 111)
Окончательный результат всегда будет 1 в крайнем левом столбце (двоичное число = 1111)
Пример 2
74/2 = 37 остаток 0 (двоичное число = ?????? 0)
37 / 2 = 18 остаток 1 (двоичное число = ????? 10)
18/2 = 9 остаток 0 (двоичное число = ???? 010)
9/2 = 4 остаток 1 (двоичное число = ??? 1010)
4/2 = 2 остатка 0 (двоичное число = ?? 01010)
2/2 = 1 остаток 0 (двоичное число =? 001010)
Окончательный результат всегда будет 1 в крайнем левом столбце (двоичное число = 1001010 )
NB — Хотя я ставил? на каждом этапе вы не узнаете, сколько столбцов необходимо, пока не завершите процесс.
Чтобы быстро узнать, сколько столбцов необходимо, найдите наибольший множитель 2, который меньше десятичного числа, с которого вы начали, например
Пример 1: Наибольший множитель меньше 74 равен 64, что равно 2 в степени 6. Поскольку крайний правый столбец равен 2 в степени 0, это означает, что нам нужно 7 столбцов.
Шестнадцатеричная система счисления [править | править источник]
Числа, написанные с помощью 16 символов {0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F}, называются числами с основанием 16. Например:
A (одна цифра)
B5 (две цифры)
6C3 (трехзначный)
AF85 (четыре цифры)
и т. Д.0) = 10 * 4096 + 15 * 256 + 8 * 16 + 5 * 1 = 40960 + 3840 + 128 + 5 = 44933 → AF85 (шестнадцатеричный) = 44933 (десятичный)
Преобразование десятичного числа в шестнадцатеричное [править | править источник]
Для преобразования десятичного числа в шестнадцатеричное
• Разделите десятичное число на 16 — полученный остаток является последним шестнадцатеричным значением.
• Затем частное делится на 16, чтобы получить другой остаток. Как и при двоичном вычислении, значения читаются справа налево (первое значение остатка — последнее в шестнадцатеричном числе, затем предпоследнее, третье до последнего и т. Д.)
• Процесс завершается, когда достигается значение дивиденда (числитель) меньше 16. Если продолжить деление на 16, получится неделимое частное 0.
• Имейте в виду, что 10-15 представлены как односимвольные «числа» в шестнадцатеричной системе. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15 — остатки должны отражать соответствующее шестнадцатеричное значение.
Примеры
• Десятичный 15
- o остаток 15/16 равен 15 (> 16, поэтому процесс завершается), поэтому «числовое» значение равно F
• Десятичное число 16
- o остаток 16/16 равен 0 [шестнадцатеричный? 0]
- o Затем частное от 1 делится — 1/16, в результате чего остается 1 (частное равно 0, поэтому процесс завершается) [шестнадцатеричное 10]
• Десятичное число 45
- o 45/16 — остаток 13 [шестнадцатеричный? D]
- o Коэффициент 2 | 2/16 — остаток 2 [шестнадцатеричное 2D]
• Десятичное число 47825
- o 47825/16 — остаток 1 [шестнадцатеричный ??? 1]
- или Частное 2989 | 2989/16 — остаток 13 [шестнадцатеричный ?? D1]
- o Частное 186 | 186/16 — остаток 10 [шестнадцатеричный? AD1]
- o Коэффициент 11 | 11/16 — остаток 11 [шестнадцатеричный BAD1]


 53, может привести к потере точности.
53, может привести к потере точности. 0))
0))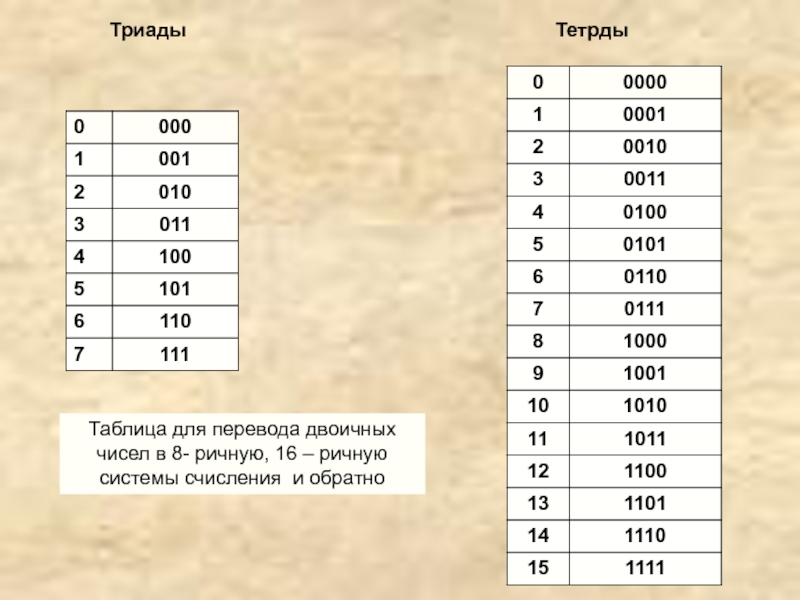 0))
0)) Подписывайтесь, ставьте лайки и не болейте!
Подписывайтесь, ставьте лайки и не болейте! В основном пользователи используют десятичную систему счисления и указывают 10. Всегда указывайте этот параметр, чтобы исключить ошибки считывания и гарантировать корректность исполнения и предсказуемость результата. Когда основание системы счисления не указано, разные реализации могут возвращать разные результаты.
В основном пользователи используют десятичную систему счисления и указывают 10. Всегда указывайте этот параметр, чтобы исключить ошибки считывания и гарантировать корректность исполнения и предсказуемость результата. Когда основание системы счисления не указано, разные реализации могут возвращать разные результаты.