СИГНАЛЫ. Синусоидальные сигналы

ОСНОВЫ ЭЛЕКТРОНИКИ

Сигналы

Следующий раздел главы посвяшен конденсаторам — элементам, свойства которых зависят от того, как изменяются в схеме напряжения и токи. Закономерности, с которыми мы познакомили вас при изучении цепей постоянного тока (закон Ома, эквивалентные преобразования схем и др.), сохраняют свою силу и в тех случаях, когда напряжения и токи изменяются по времени. Для лучшего понимания работы цепей переменного тока полезно изучить некоторые распространенные типы сигналов (напряжений, которые определенным образом изменяются во времени).

1.07. Синусоидальные сигналы

Синусоидальные сигналы распространены наиболее широко; именно их мы извлекаем из стенной розетки. Если вы услышите выражение «10 мкВ на частоте 1 МГц», то знайте, что речь идет о синусоидальном сигнале. Математическое выражение, описывающее синусоидальное напряжение, имеет вид

U = A sin2πƒt,

где А — амплитуда сигнала, ƒ — частота в циклах в секунду или в герцах. Синусоидальный сигнал показан на рис. 1.17. Иногда бывает полезно переместить начало координат (t = 0) в точку, соответствующую произвольному моменту времени; в этом случае в выражение для синусоидального напряжения следует включить фазу

U = A sin(2πƒt + Ø).

Можно также воспользоваться понятием угловая частота и переписать выражение для синусоидального сигнала в другом виде:

U = A sin ωt,

где ω — угловая частота в радианах в 1 с. Если вы вспомните, что ω = 2πf, то все станет на свои места.

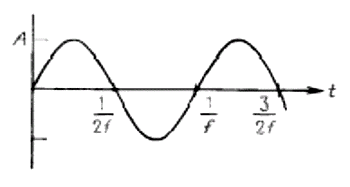
Рис.1.17. Синусоидальная зависимость изменения амплитуды А от частоты ƒ.

Основное достоинство синусоидальной функции (а также основная причина столь широкого распространения синусоидальных сигналов) состоит в том, что эта функция является решением целого ряда линейных дифференциальных уравнений, выходных сигналов, каждый из которых порожден входными сигналами, действующими не в совокупности, а отдельно: иначе говоря, если Вых. (А) — выходной сигнал, порожденный сигналом А, то для линейной цепи справедливо следующее равенство: Вых. (А + В) = Вых. (А) + Вых. (В). Если на входе линейной цепи действует синусоидальный сигнал, то на выходе также получим синусоидальный сигнал, но в общем случае его амплитуда и фаза будут другими. Это утверждение справедливо только для синусоидального сигнала. На практике принято оценивать поведение схемы по ее

амплитудно-частотной характеристике, показывающей, как изменяется амплитуда синусоидального сигнала в зависимости от частоты. Усилитель звуковой частоты, например, имеет «плоскую» амплитудно-частотную характеристику в диапазоне от 20 Гц до 20 кГц.

Частота синусоидальных сигналов, с которыми чаще всего приходится работать, лежит в диапазоне от нескольких герц до нескольких мегагерц. Для получения очень низких частот, от 0,0001 Гц и ниже, достаточно аккуратно построить нужную схему. Получение более высоких частот, например до 2000 МГц, также не вызывает принципиальных трудностей, но для сигналов такой частоты нужны специальные линии передач и специальные приемы передачи. Кроме того здесь приходится иметь дело с микроволновыми сигналами, для которых не подходят привычные схемы, состоящие из отдельных элементов, соединенных между собой проводами, а нужны специальные волноводы.

Конденсаторы и цепи переменного тока

Синусоидальный сигнал.

 

Такой сигнал имеет вид, представленный на рис. 1.3.

 

 

Рис. 1.3. Синусоидальный сигнал.

 

Величина пикового значения Up называется амплитудой волны. Синусоидальная форма волны является периодической, т.е. она повторяется. Время полного цикла обозначено буквой Т и называется периодом синусоидальной волны. С периодом связано понятие частота, обозначаемое f. Соотношение между частотой и периодом имеет вид: f= 1/T. Единицей частоты является герц (Гц). 1 Гц = 1 цикл/сек. Выражение, объединяющее информацию об амплитуде и частоте для напряжения, показанного на рисунке, имеет вид:

 

 

Каждый раз, когда угол 2ft увеличивается на 2рад. или 360 град., форма волны повторяется. Отсюда можно определить круговую частоту, обозначаемую через:

 

 

Единица измерения круговой частоты – радиан/секунда (т.е. частота, равная 1 Гц ) соответствует круговой частоте 2рад/с. С пиковой амплитудой связана величина, которая называется СРЕДНЕ КВАДРАТИЧНОЙ (ЭФФЕКТИВНОЙ) амплитудой и часто применяется для обозначения синусоиды. Среднеквадратичная амплитуда равна корню квадратному из усредненного по времени значения квадрата величины сигнала данной формы. Для синусоиды эффективная амплитуда Uэфф и пиковая Uр связаны следующим образом:

 

 

Следовательно, синусоида в уравнении (1.1) может быть записана в виде:

 

 

Имея дело с синусоидальными сигналами, удобно вместо амплитудных значений использовать эффективные. Например, напряжение в энергосети, питающей дома, предприятия, изменяется с частотой 50 Гц по синусоидальному закону. Считают, что это напряжение равно 220 В. Значит, амплитудное пиковое напряжение в линии составляет:

 

 

Кроме синусоидального сигнала, часто используются другие типы сигналов.

 

Прямоугольный (меандровый) сигнал.

 

Такой сигнал имеет вид, представленный на рис.1.4.

 

 

Рис. 1.4. Меандровый сигнал.

 

 

Как и синусоидальный прямоугольный сигнал характеризуется амплитудой и частотой. Для такого сигнала эффективное значение равно просто амплитуде. Форма реального прямоугольного сигнала отличается от идеального прямоугольника. Обычно в электромагнитной схеме время нарастания сигнала tн составляет от нескольких наносекунд до нескольких микросекунд.

 

Линейно-меняющиеся сигналы.

 

Линейно-меняющийся сигнал – это напряжение, возрастающее (или убывающее) с постоянной скоростью. Примером такого сигнала является пилообразное напряжение (рис. 1.5) и сигнал треугольной формы (рис. 1.6).

 

рис. 1.5. Пилообразный сигнал.

 

 

рис. 1.6. Сигнал треугольной формы.

Импульсные сигналы.

 

 

рис. 1.7. Периодический импульсный сигнал.

 

Импульсные сигналы характеризуются амплитудой и длительностью. Если импульсы периодически повторяются, то в этом случае говорят о частоте повторения и о скважности импульсов. Скважность импульсов равна отношению длительности импульса к периоду повторения (рис. 1.7.)

 

Импульсы могут иметь положительную и отрицательную полярность (пьедестал) (рис. 1.8).

 

рис. 1.8. Импульсные сигналы различной полярности.

 

Сигнал шумов.

 

Сигналы шумов являются теми сигналами, которые мешают нормальной работе приборов и устройств, ограничивая их возможности. Например, минимальные напряжения и токи, которые могут быть измерены электронными приборами (вольтметрами и амперметрами) ограничены уровнем шума, действующим на вход прибора совместно с измеряемым сигналом. Одним из наиболее распространенных типов шумовых сигналов является белый шум с гауссовским распределением в ограниченном спектре частот. Шумовой сигнал такого типа генерирует, например, резистор, он создает неприятности при всевозможных измерениях, в которых требуется высокая чувствительность.

 

Синусоидальный ток и его характеристики

Синусоидальный ток и основные характеризующие его величины.

Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (рис. 3.1):

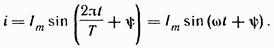
Максимальное значение функции называют амплитудой. Амплитуду тока обозначают 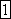. Период Т — это время, за которое совершается одно полное колебание.

Частота равна числу колебаний в 1 с (единица частоты 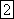 — герц (Гц) или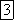 

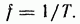
Угловая частота (единица угловой частоты — рад/с или )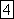

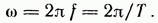
Аргумент синуса, т. е.  называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени 

Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.

В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.

Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ).

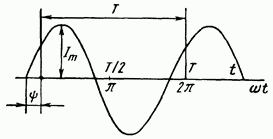
Рис. 3.1

Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их  и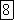 

Синусоидальный ток

Синусоидальный ток представляет собой функцию времени. То есть в отличие от постоянного тока его значение меняется с течением времени. Основными характеристиками синусоидального тока являются. Амплитуда частота и начальная фаза.

 Частота f это количество колебаний в единицу времени. За единицу времени в системе СИ принимается одна секунда. Таким образом, количество колебаний за секунду это и есть частота синусоидального тока. И измеряется она в Герцах. Названа в честь ученого Герца. Величина обратная частоте называется периодом колебания T=1/f. Период измеряется в секундах. Определение периода звучит так период это время полного колебания. Если представить себе маятник часов то период это время за которое он совершит движение из одного крайнего положения в другое и обратно.

 Амплитуда синусоидального тока это максимальное значение тока, которое он достигает за период колебания. Опять же если рассматривать на примере маятника, то амплитуда это расстояние от положения равновесия до одного из крайних положений.

 Начальная фаза синусоидального тока это то время, на которое отстает либо опережает синусоида начальный момент времени. Представим две синусоиды одна, из которых начинается условно в нуле а другая в 1. То можно сказать, что вторая синусоида отстаёт по фазе от первой. Если обе синусоиды начинаются в одной точке то можно сказать что они синфазные, то есть имеют одну фазу. При этом они обе могут отставать от начального момента времени на одну и ту же величину, то есть иметь одинаковую начальную фазу.

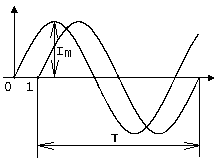
Рисунок 1  — Графическое представление синусоидального тока

 Математически синусоидальный ток описывается уравнением:

i=Im*sin(wt+j)

где

   i     мгновенное значение тока это величина тока в определенный момент времени с учетом частоты и начальной фазы тока.

   Im    амплитуда тока.

   j начальная фаза  

   w     угловая частота выражается как 

Синусоидальный ток и его характеристики

Синусоидальный ток и основные характеризующие его величины.

Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (рис. 3.1):

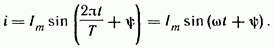
Максимальное значение функции называют амплитудой. Амплитуду тока обозначают 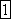. Период Т — это время, за которое совершается одно полное колебание.

Частота равна числу колебаний в 1 с (единица частоты 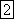 — герц (Гц) или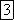 

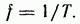
Угловая частота (единица угловой частоты — рад/с или )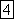

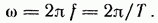
Аргумент синуса, т. е.  называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени 

Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.

В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.

Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ).

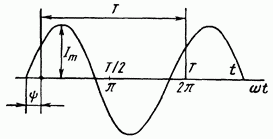
Рис. 3.1

Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их  и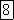 

Синусоидальный ток

Синусоидальный ток представляет собой функцию времени. То есть в отличие от постоянного тока его значение меняется с течением времени. Основными характеристиками синусоидального тока являются. Амплитуда частота и начальная фаза.

 Частота f это количество колебаний в единицу времени. За единицу времени в системе СИ принимается одна секунда. Таким образом, количество колебаний за секунду это и есть частота синусоидального тока. И измеряется она в Герцах. Названа в честь ученого Герца. Величина обратная частоте называется периодом колебания T=1/f. Период измеряется в секундах. Определение периода звучит так период это время полного колебания. Если представить себе маятник часов то период это время за которое он совершит движение из одного крайнего положения в другое и обратно.

 Амплитуда синусоидального тока это максимальное значение тока, которое он достигает за период колебания. Опять же если рассматривать на примере маятника, то амплитуда это расстояние от положения равновесия до одного из крайних положений.

 Начальная фаза синусоидального тока это то время, на которое отстает либо опережает синусоида начальный момент времени. Представим две синусоиды одна, из которых начинается условно в нуле а другая в 1. То можно сказать, что вторая синусоида отстаёт по фазе от первой. Если обе синусоиды начинаются в одной точке то можно сказать что они синфазные, то есть имеют одну фазу. При этом они обе могут отставать от начального момента времени на одну и ту же величину, то есть иметь одинаковую начальную фазу.

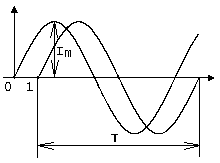
Рисунок 1  — Графическое представление синусоидального тока

 Математически синусоидальный ток описывается уравнением:

i=Im*sin(wt+j)

где

   i     мгновенное значение тока это величина тока в определенный момент времени с учетом частоты и начальной фазы тока.

   Im    амплитуда тока.

   j начальная фаза  

   w     угловая частота выражается как 

1.2.3. Измерение параметров синусоидального сигнала

1. На функциональном генераторе измерительного стенда (см. лаб. работу № 3, рис. 3.7) кнопкой 2 выбрать синусоидальную форму генерируемого напряжения.

2. Выполнить синхронизацию осциллографа. При необходимости подобрать цену деления по YиX. Получить осциллограмму измеряемого напряжения на экране осциллографа.

3. Ручкой 4 функционального генератора установить размах напряжения, чтобы оно касалось горизонтальных линий шкалы и занимало максимум шкалы экрана. Число периодов сигнала, наблюдаемых на экране, не должно превышать двух.

4. Зарисовать осциллограмму, используя шаблон рис. 1.12, а. Записать значения цены делений поYиX.

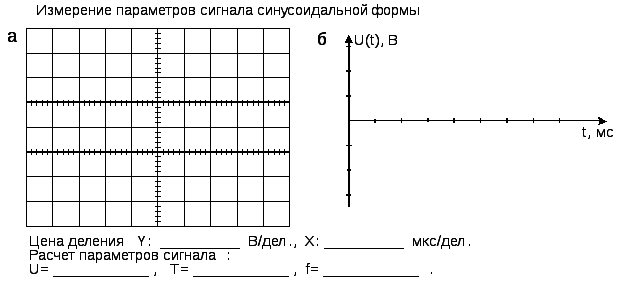
Рис. 1.12. Отчет «Измерение напряжения синусоидальной формы»

1.2.4. Измерение параметров импульсного сигнала

1. На функциональном генераторе кнопкой 3 выбрать импульсную форму генерируемого напряжения. Сигнал двухполярный, при этом 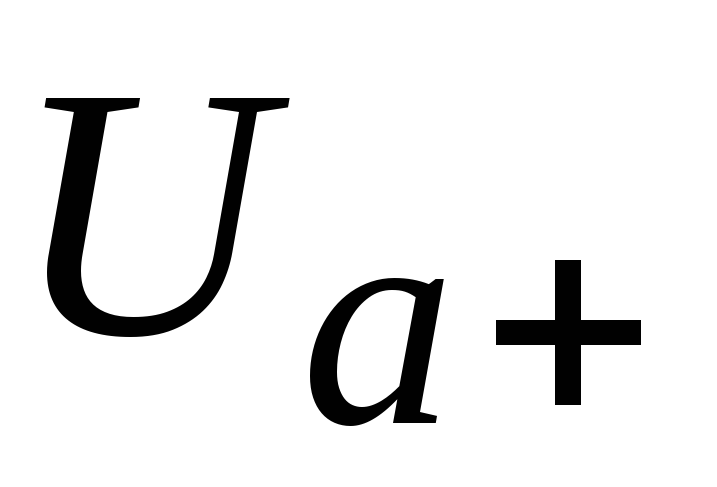и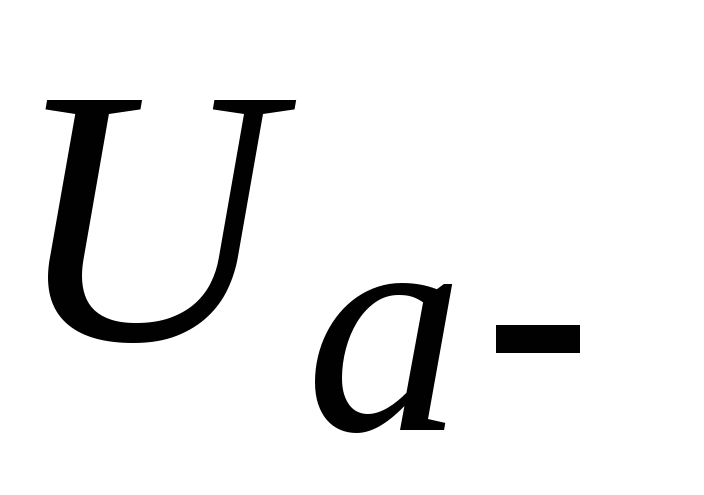равны по модулю, размах напряжения равен удвоенному значению амплитуды.

2. На блоке СИНХРОНИЗАЦИЯ осциллографа переключатель «+/–» установить в положение «+», на блоке УСИЛИТЕЛЬ YI переключатель «/~» – в положение «».

3. Выполнить синхронизацию осциллографа. При необходимости подобрать цену деления по YиX. Получить осциллограмму измеряемого напряжения на экране осциллографа.

4. Параметры развертки осциллографа выбрать таким образом, чтобы число периодов сигнала, наблюдаемых на экране, не превышало двух.

5. По заданию преподавателя ручкой 5 функционального генератора установить отношение длительности положительного и отрицательного импульсов, а ручкой 4 – амплитудное значение сигнала.

6. Зарисовать осциллограмму, используя шаблон рис. 1.13, а. Записать значения цены делений поYиX.

7. Перевести переключатель «/~» в положение «~».

8. Зарисовать осциллограмму на шаблоне рис. 1.13, а пунктирной линией.

9. Вернуть переключатель «/~» в положение «~», переключатель «+/–» установить в положение «–». При необходимости выполнить синхронизацию осциллографа.

10. Зарисовать осциллограмму, используя шаблон рис. 1.14, в.

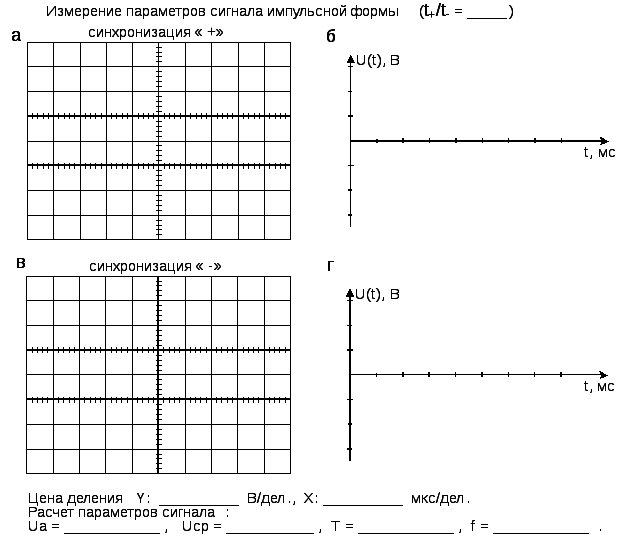
Рис. 1.13. Отчет «Измерение напряжения импульсной формы»

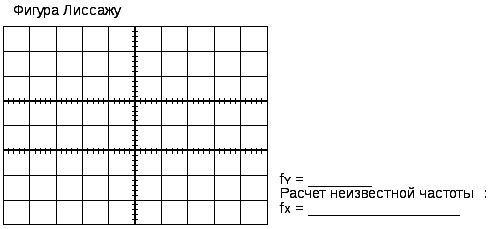
Рис. 1.14. Отчет «Построение фигур Лиссажу»

1.2.5. Получение фигур Лиссажу

1. На функциональном генераторе кнопкой 2 выбрать синусоидальную форму генерируемого напряжения.

2. Соединить выход II (600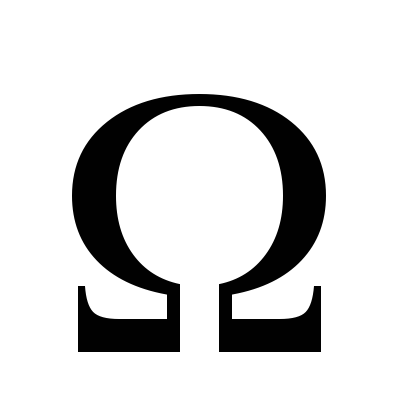) генератора Г3-118 (лицевая панель приведена на рис. 1.15) и ВХОД блока СИНХРОНИЗАЦИЯ осциллографа. На блоке СИНХРОНИЗАЦИЯ установить переключатель в положение ВХОД Х. На генераторе установить ручкамиHz, МНОЖИТЕЛЬ частоту сигнала, равную или кратную рассчитанной по результатам измерений, выполненных в п. 1.2.3.

3. Регулируя амплитуды напряжений сигналов, подаваемых на входы YиXосциллографа, меняя цену деления поY, добиться, чтобы размеры изображения по осямY иXбыли примерно равны.

4. Меняя частоту сигнала на генераторе Г3-118 дискретно и плавно регулятором РАССТРОЙКА, добиться устойчивого изображения в виде фигуры Лиссажу.

5. Зарисовать осциллограмму. Записать значение частоты сигнала на выходе генератора Г3-118.

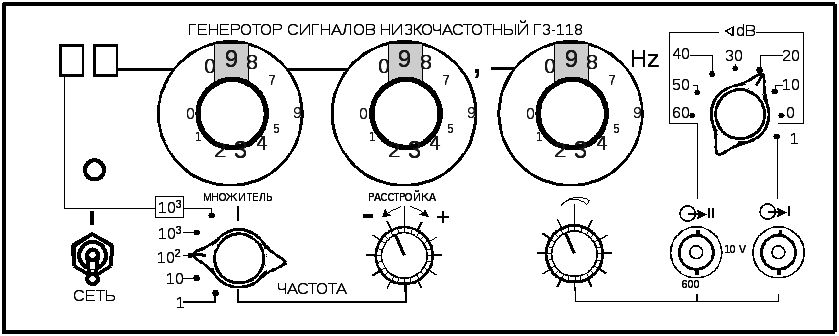
Рис. 1.15. Лицевая панель генератора Г3-118

1.2.6. Обработка результатов измерений

1. По данным п. 1.2.2 и полученной осциллограмме рассчитать относительные погрешности измерения амплитуды и периода сигнала до калибровки осциллографа. Погрешности рассчитываются по формулам:

,.

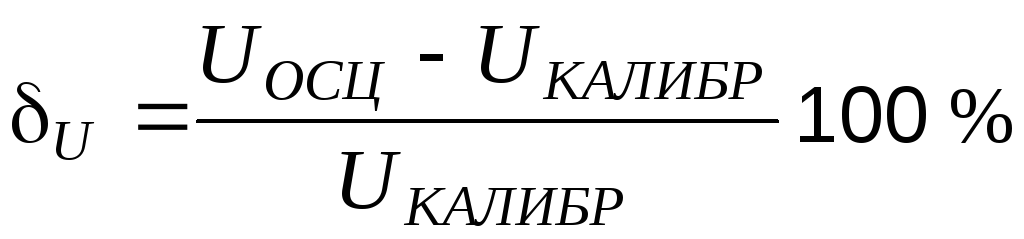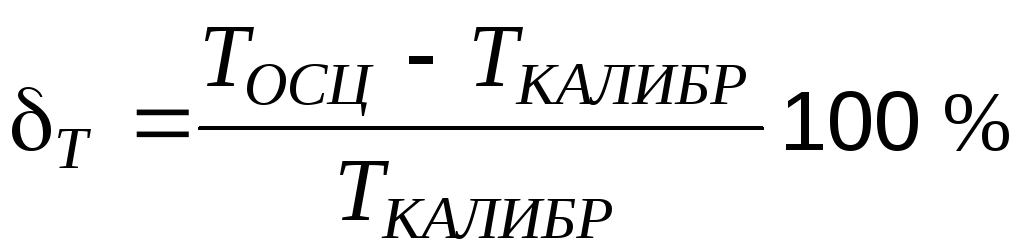2. Построить график сигнала в декартовой системе координат (см. рис. 1.11, б).

3. По данным п. 1.2.3 и полученной осциллограмме рассчитать параметры сигнала: амплитудное значение, период, частоту. Построить график сигнала в декартовой системе координат (см. рис. 1.12, б).

4. По данным п. 1.2.4 и полученным осциллограммам рассчитать параметры сигнала: амплитудное значение напряжения, среднее значение напряжения, период, частоту. Построить графики сигнала в декартовой системе координат (см. рис. 1.13, б,г).

5. По данным п. 1.2.5 и полученной осциллограмме (фигуре Лиссажу) рассчитать частоту сигнала, поданного на вход Х осциллографа (см. рис. 1.14).

Отчет должен содержать:

1) описание цели работы;

2) структурную схему осциллографа;

3) схемы и графики, поясняющие принцип работы осциллографа;

4) осциллограммы исследуемых сигналов;

5) расчеты.

Синусоидальный (гармонический) сигнал — Мегаобучалка

Дельта-функция (функция Дирака)

Эту физически нереализуемую функцию можно представить как импульс бесконечно малой длительности и бесконечно большой амплитуды, т.е. как предел, к которому стремится прямоугольный импульс с основанием Δt и площадью, равной единице, если Δt → 0 так, чтобы площадь импульса сохранялась равной единице.

Синусоидальный (гармонический) сигнал

Управляющее воздействие в замкнутой системе формируется в большинстве случаев в зависимости от величины и знака отклонения истинного значения управляемой величины от ее заданного значения:

y(t) = Ay[ε(t)],

где ε(t) = xз(t) — x (t) – сигнал ошибки (сигнал рассогласования).

Замкнутую систему называют часто системой управления по отклонению.

В замкнутой системе контролируется непосредственно управляемая величина и тем самым при выработке управляющего воздействия учитывается действие всех возмущений, влияющих на управляемую величину. В этом заключается преимущество замкнутых систем.

Но из-за наличия замкнутой цепи воздействий в этих системах могут возникать колебания, которые в некоторых случаях делают систему неработоспособной. Кроме того, сам принцип действия замкнутых систем (принцип управления по отклонению) допускает нежелательные изменения управляемой величины: вначале возмущение должно проявиться на выходе, система “почувствует” отклонение и лишь потом выработает управляющее воздействие, направленное на устранение этого отклонения. Такая “медлительность” снижает эффективность управления. Несмотря на наличие определенных недостатков, этот принцип управления широко применяется при создании АСУ.

Гармонический сигнал характеризуется параметрами: амплитуда – А; период – Т; фаза – ϕ.

Пример 1. Если на исследуемом объекте резко открыть вентиль, в результате чего расход подаваемого вещества изменится скачком с F1 до F2, то говорят, что на входе объекта реализован скачкообразный сигнал величиной F2 – F1 , и если эта разность равна единице, то на входе реализуется единичный скачок.

Изменение в установке вентиля расход пара не мгновенно будет изменять выходную величину температуры. Теплоёмкость воды будет заставлять температуру медленно перемещаться в новое положение.

Пример 2. При управлении расходом динамический ответ быстрый. Изменение в положении вентиля вызовет немедленное изменение расхода, так что изменение в объёмном расходе почти немедленно повторяет изменение во входном положении вентиля.

Рис. 12 Характеристики управляемой системы «вентиль»

Ответ системы на внезапное изменение входной переменной называется (step response— ответ на входное ступенчатое изменение). Каждую систему можно характеризовать её step response. Вид step response позволяет описывать поведение системы математическими уравнениями, это поведение ещё известно как динамический ответ системы (Dynamic response).

Статическая характеристика – зависимость выходной величины объекта у, т.е. величины, характеризующей объект управления, от величины подаваемого на его вход воздействия х, при условии, что подаваемое воздействие постоянно, т.е. х = const.

Почти все объекты (системы) управления обладают инерцией – механической, тепловой, гидродинамической.

При мгновенном изменении входных сигналов выходной сигнал системы меняется не мгновенно, а постепенно. Изменение выходного сигнала часто продолжается и после того, как входной сигнал уже не меняется. Это явление последействия – называется инерцией. Если инерция системы меньше, чем у остальных элементов, то такие системы называются безынерционными. Инерция (механическая, тепловая) – это способность объекта накапливать вещество или энергию. Инерция характеризуется емкостью системы управления. Объекты управления с монотонным изменением выходного сигнала называются апериодическими. При переходных процессах в инерционных объектах запас вещества или энергии может меняться не только монотонно, но и колебательно. Системы управления, обладающий этим свойством, называется колебательными системами.

Статический режим– состояние элемента АСУ, при котором выходная величина не изменяется во времени, т. е. y(t) = const.

Очевидно, что статический режим (или состояние равновесия) может иметь место лишь тогда, когда входные воздействия постоянны во времени. Связь между входными и выходными величинами в статическом режиме описывают алгебраическими уравнениями.

Динамический режим– состояние элемента АСУ, при котором входная величина непрерывно изменяется во времени, т. е. y(t) = var.

Динамический режим имеет место, когда в элементе после приложения входного воздействия происходят процессы установления заданного состояния или заданного изменения выходной величины. Эти процессы описываются в общем случае дифференциальными уравнениями.

Неустановившийся (переходный) режим– режим, существующий от момента начала изменения входного воздействия до момента, когда выходная величина начинает изменяться по закону этого воздействия.

Установившийся режим– режим, наступающий после того, когда выходная величина начинает изменяться по такому же закону, что и входное воздействие, т. е. наступающий после окончания переходного процесса.

В установившемся режиме элемент совершает вынужденное движение. Очевидно, что статический режим является частным случаем установившегося (вынужденного) режима приx(t) = const.

При последовательном соединении звеньев их передаточные функции перемножаются.

W_об = W₁^.W₂^.W₃…

Сигнал — синусоидальная форма — Большая Энциклопедия Нефти и Газа, статья, страница 4

Сигнал — синусоидальная форма

Cтраница 4

НЭ, регулирующий коэффициент Передачи инвертора так, что установленный выходной уровень сигнала остается неизменным. Предусматривается преобразователь сигнала синусоидальной формы в прямоугольный короткий синхроимпульс, для чего используется соответствующее формирующее устройство ФУ.  [47]

Таким образом, во вторичной обмотке 4 — 5 трансформатора Tpl появляются разнополярные прямоугольные импульсы, которые поступают на вход полосового фильтра типа К, предназначенного для подавления гармонических составляющих сигнала, поступающего с выхода передатчика. С выхода фильтра сигнал синусоидальной формы через устройство уплотнения поступает в линию связи.  [48]

Нелинейные искажения определяются нелинейностью ВАХ транзисторов, на которых собран усилитель. Так, при подаче на вход сигнала синусоидальной формы выходной сигнал не будет чисто синусоидальным, а будет содержать составляющие высших гармоник.  [49]

В генераторах с самовозбуждением для получения на выходе напряжения синусоидальной формы не требуется подавать на вход сигнал этого же вида. Они без внешнего воздействия преобразовывают энергию источника питания в энергию сигнала синусоидальной формы.  [50]

ЛС-генераторы нашли наибольшее применение, поскольку имеют достаточно 1Хорошую стабильность, небольшой коэффициент гармоник и просты по устройству. Основой i C-генератрра является усилитель, охваченный ПОО через фазо-сдвигающую цепь, обеспечивающую генерацию сигнала синусоидальной формы. Установку необходимой частоты выходного сигнала осуществляют изменением сопротивлений резисторов или емкостей конденсаторов, входящих в фазосдви-гаювдую цепь.  [51]

При возникновении нелинейных искажений внутри измеряемого четырехполюсника его амплитудная характеристика ивыхР ( иЯ1) перестает быть линейной и возникают искажения формы передаваемых сигналов. В частности, при подведении ко входу четырехполюсника измерительных синусоидальных сигналов на выходе последнего нередко возникают сигналы усеченной синусоидальной формы. На рис. 1.14 а показана синусоида, симметрично усеченная в зонах максимальных мгновенных значений, на рис. 1.146 — синусоида, несимметрично усеченная в зонах минимальных значений.  [52]

Умножитель применяется в устройствах радиосвязи и автоматического контроля, спектроскопии и частотноизмерительнои технике. Он позволяет измерять константы кварцевых резонаторов; настраивать узкополосные фильтры и снимать их резонансные кривые; калибровать по частоте шкалы приемников, передатчиков и различных частотомеров; оценивать фазовые и частотные характеристики узкополосных радиотрактов; определять нестабильность частоты и спектральные характеристики сигналов синусоидальной формы и других радиосигналов. Прибор работает при температуре от 5 до 40 С и относительной влажности 90 — 95 % при температуре 30 С.  [53]

Подключить осциллограф к гнездам КС, предварительно загрузив их на сопротивление 600 Ом. На осциллографе должен быть виден сигнал синусоидальной формы с частотой 2100 Гц в режиме ПЕРЕДАЧА и 450 Гц в режиме ПРИЕМ.  [54]

Контрольное устройство рассчитано на работу с двухлучевыми и однолучевыми трубками. Его действие состоит в следующем. Задающий генератор блока опорного устройства создает сигнал синусоидальной формы с частотой 22 5 Мгц. Одновременно он подводится с некоторым сдвигом по фазе к смесителю устройства выделения импульсов.  [55]

При идентичной конструкции плеч — отношение сопротивлений резисторов R1 и R2 не зависит от паразитных емкостей. Емкости между экранами Э1, Э4и землей представляют собой емкость Сб-включенную параллельно источнику питания; емкость между эк, раном ЭЗ и землей — емкость Са; емкость экрана Э4 — емкость С; емкость трансформаторной обмотки — Ст. Для питания моста может быть использован генератор сигналов синусоидальной формы, индикатором равновесия может служить усилитель с высокоомным входом и стрелочным прибором.  [56]

При этом на частоте квазирезонанса цепь имеет максимальный коэффициент передачи, равный / з, и нулевой фазовый сдвиг. Перестройка генерируемой частоты обычно производится либо изменением величины обоих сопротивлений, либо изменением величины обоих конденсаторов. Мост Вина включается в цепь положительной ОС УНТ, обеспечивая на частоте квазирезонанса выполнение условия баланса фаз. Так как коэффициент усиления УПТ велик и глубина положительной ОС слишком большая, сигнал на выходе генератора близок к гармоническому сигналу прямоугольной формы. Для получения сигнала синусоидальной формы в усилитель вводится с помощью сопротивлений R3, R4 дополнительная отрицательная ОС. Она снижает коэффициент усиления и обеспечивает выполнение условия баланса амплитуд лишь для узкого частотного спектра сигнала, определяемого настройкой: моста Вина.  [57]

Назначение четвертьволновой пластинки как раз в том и состоит, чтобы обеспечить работу модулятора на линейном участке модуляционной характеристики. Это выполняется следующим образом. Тогда при электрическом поле на модуляторе, равном нулю, через анализатор проходит 50 % света. В этом случае подача на модулятор сигнала синусоидальной формы вызывает периодические увеличение и уменьшение коэффициента светопропускания системы. Аналогичный эффект достигается и при подаче на электрооптический кристалл напряжения смещения, соответствующего пропусканию 50 % света. Модуляционная характеристика системы, содержащей четвертьволновую пластинку, показана на фиг.  [58]

Страницы:      1    2    3    4